Noktaların Doğrusallığı
Birbirinden farklı üç noktanın doğrusal olması bu noktalardan geçen tek bir doğru çizilebilmesi anlamına gelir. Analitik düzlemdeki üç nokta doğrusal değilse bir üçgen oluşturur.
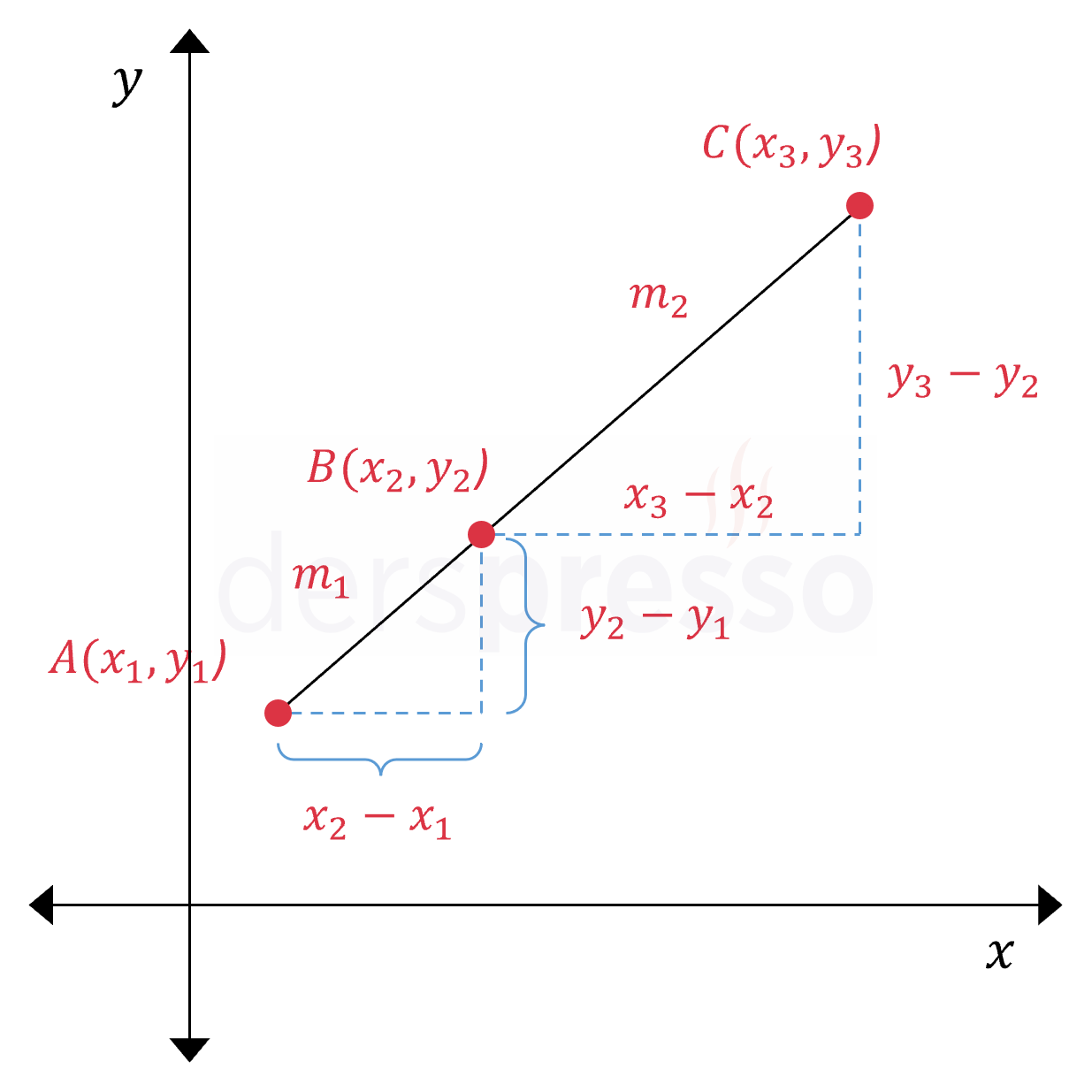
Verilen üç noktanın doğrusal olup olmadığını anlamak için bu noktalar içinden seçilen herhangi iki nokta ikilisini birleştiren doğru parçalarının eğimleri hesaplanır. Eğimler birbirine eşitse noktalar doğrusaldır, farklı ise doğrusal değildir.
\( m_1 = \dfrac{y_2 - y_1}{x_2 - x_1} \)
\( m_2 = \dfrac{y_3 - y_2}{x_3 - x_2} \)
\( m_1 = m_2 \) ise noktalar doğrusaldır.
\( m_1 \ne m_2 \) ise noktalar doğrusal değildir.
\( A(-3, 8) \), \( B(-1, 2) \) ve \( C(5, -16) \) noktalarının doğrusallığını inceleyelim.
\( A \) ve \( B \) noktalarını birleştiren doğru parçasının eğimini hesaplayalım.
\( m_{AB} = \dfrac{2 - 8}{-1 - (-3)} = -3 \)
\( B \) ve \( C \) noktalarını birleştiren doğru parçasının eğimini hesaplayalım.
\( m_{BC} = \dfrac{-16 - 2}{5 - (-1)} = -3 \)
İki eğim birbirine eşit olduğu için bu üç nokta doğrusaldır.
Bu örnekte ikinci eğimin \( A \) ve \( C \) noktaları arasında hesaplanması bu noktaların doğrusallığını gösterme anlamında sonucu değiştirmez.
\( A \) ve \( C \) noktalarını birleştiren doğru parçasının eğimini hesaplayalım.
\( m_{AC} = \dfrac{-16 - 8}{5 - (-3)} = -3 \)
Analitik düzlemde \( A(-2, 0), B(4, 2) \) ve \( C(6, k) \) noktaları doğrusal olduğuna göre, \( k \) kaçtır?
Çözümü GösterVerilen noktaları analitik düzlemde işaretleyelim.
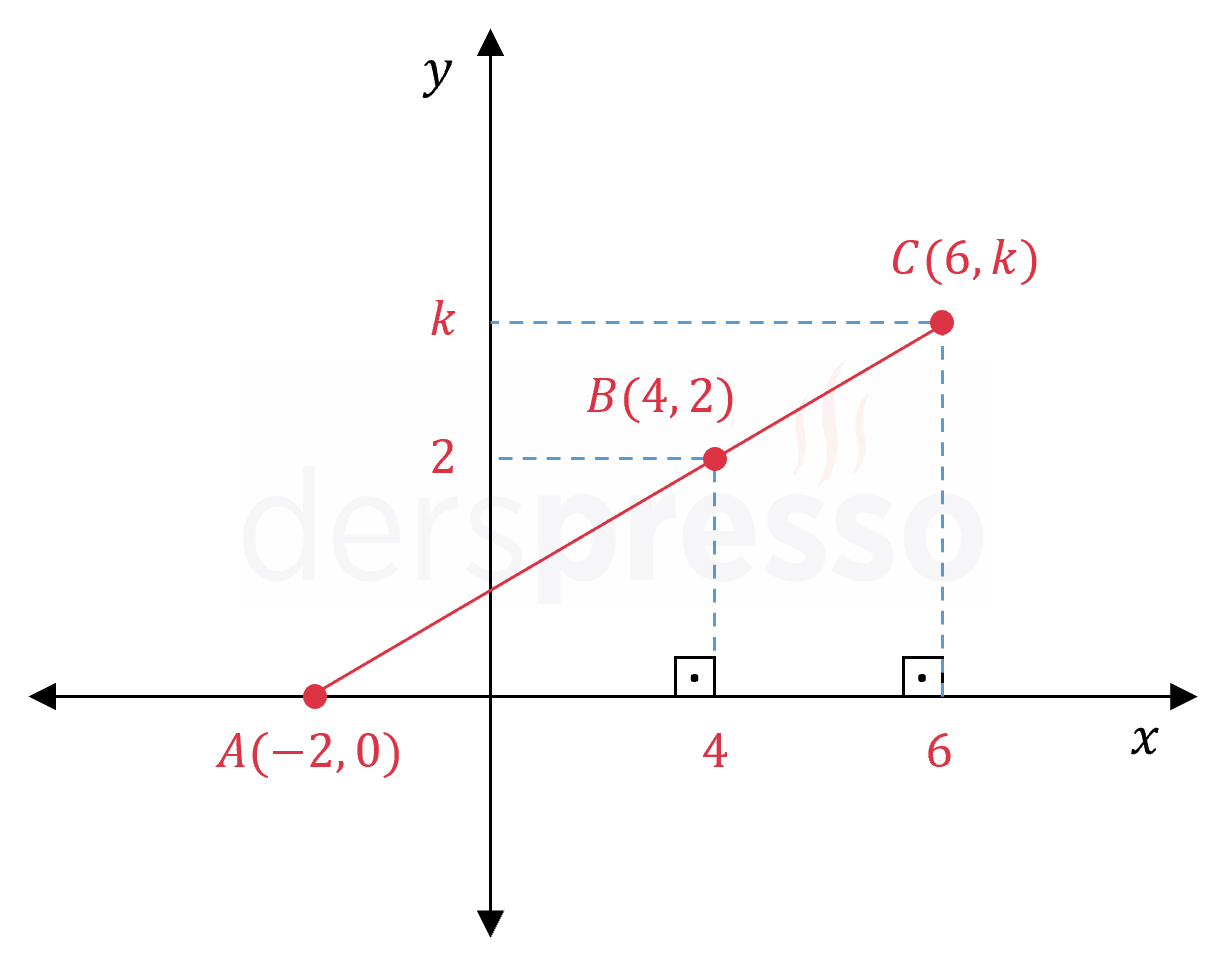
Bu noktaların oluşturduğu doğrunun eğimi hangi iki nokta ikilisini seçersek seçelim eşit olmalıdır.
\( m_{AB} = m_{BC} \)
\( \dfrac{2 - 0}{4 - (-2)} = \dfrac{k - 2}{6 - 4} \)
\( \dfrac{2}{6} = \dfrac{k - 2}{2} \)
\( k - 2 = \dfrac{2}{3} \)
\( k = \dfrac{8}{3} \) bulunur.
\( A(1, 4), B(a, 0), C(6, -2) \) olmak üzere,
\( \abs{AB} + \abs{BC} \) toplamının en küçük olması için \( a \) kaç olmalıdır?
Çözümü GösterUzaklıklar toplamının en küçük olması için bu üç nokta doğrusal olmalıdır, aksi takdirde noktalar bir üçgen oluşturur.
\( m_{AB} = m_{BC} \)
\( \dfrac{0 - 4}{a - 1} = \dfrac{-2 - 0}{6 - a} \)
\( \dfrac{-4}{a - 1} = \dfrac{-2}{6 - a} \)
İçler - dışlar çarpımı yapalım.
\( -24 + 4a = -2a + 2 \)
\( 6a = 26 \)
\( a = \dfrac{13}{3} \) bulunur.
\( k \)'nın hangi değerleri için \( (k + 1, 2k - 3) \), \( (2k - 1, 3k - 2) \) ve \( (2k + 3, 5k - 4) \) noktaları doğrusaldır?
Çözümü GösterVerilen noktaların doğrusal olabilmesi için noktaların sınırlandırdığı üçgenin alanı sıfır olmalıdır.
Üç noktasının koordinatları bilinen üçgenin alanı aşağıdaki formülle bulunur.
\( A = \dfrac{1}{2} \abs{(x_1y_2 + x_2y_3 + x_3y_1) - (x_2y_1 + x_3y_2 + x_1y_3)} \)
\( A(x_1, y_1) = A(k + 1, 2k - 3) \)
\( B(x_2, y_2) = B(2k- 1, 3k - 2) \)
\( C(x_3, y_3) = C(2k + 3, 5k - 4) \)
Noktaların koordinatlarını denklemde yerine koyalım.
\( A(ABC) = \dfrac{1}{2} \abs{[(k + 1)(3k - 2) + (2k- 1)(5k - 4) + (2k + 3)(2k - 3)] - [(2k- 1)(2k - 3) + (2k + 3)(3k - 2) + (k + 1)(5k - 4)]} \)
\( = \dfrac{1}{2} \abs{(3k^2 + k - 2 + 10k^2 - 13k + 4 + 4k^2 - 9) - (4k^2 - 8k + 3 + 6k^2 + 5k - 6 + 5k^2 + k - 4)} \)
\( A(ABC) = \dfrac{1}{2} \abs{(2k^2 - 10k)} \)
Verilen noktaların doğrusal olması için bu noktaların sınırlandırdığı alan 0 olmalıdır.
\( \dfrac{1}{2} \abs{(2k^2 - 10k)} = 0 \)
\( k(k - 5) = 0 \)
Buna göre \( k \in \{ 0, 5 \} \) değerleri için verilen üç nokta doğrusal olur.
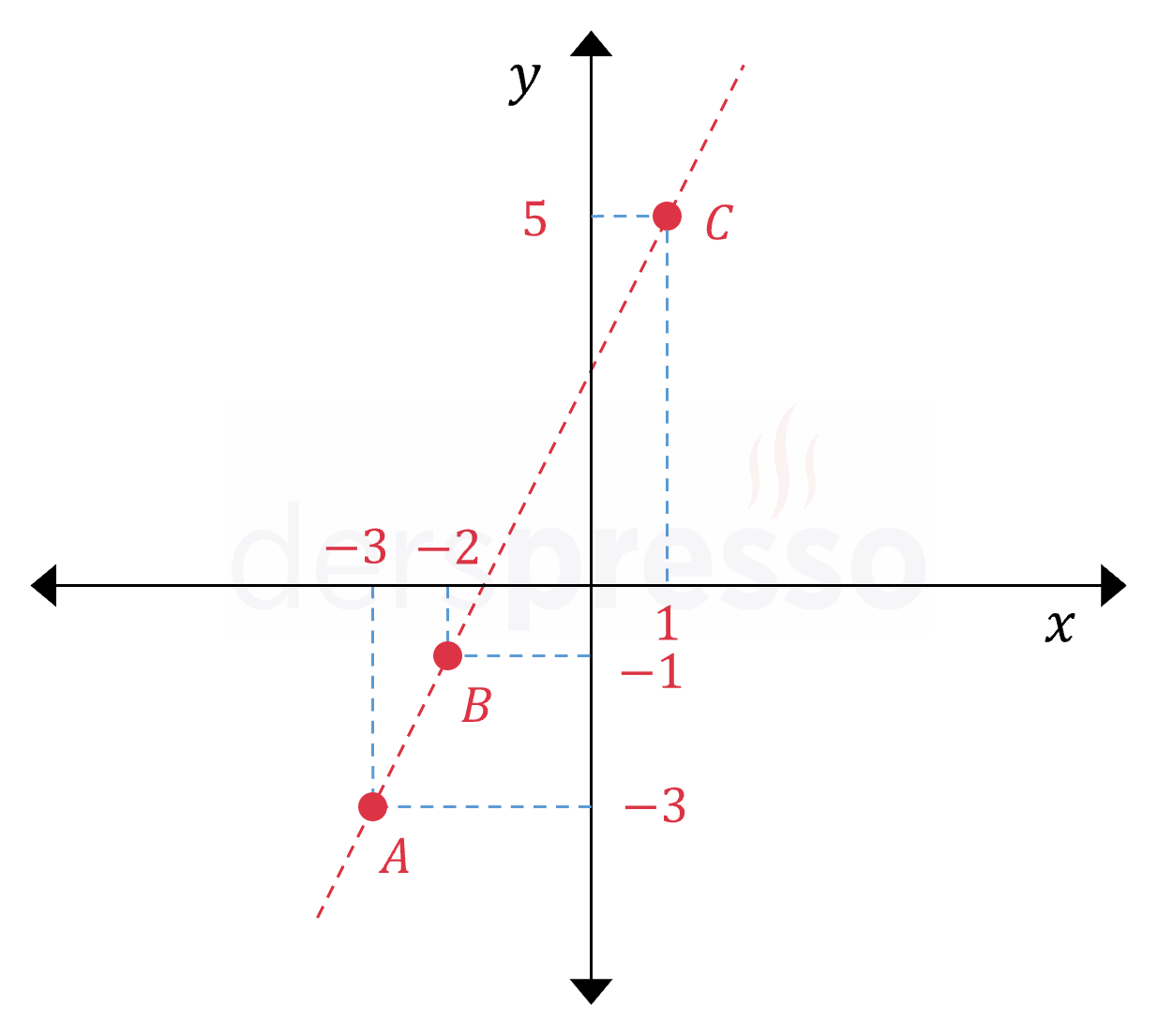
\( A(-3, -3), B(-2, -1), C(1, 5) \) noktalarının doğrusal olup olmadığını uzaklık formülünü kullanarak bulunuz.
Çözümü GösterBu üç nokta arasındaki uzaklıkları bulalım.
\( \abs{AB} = \sqrt{(-2 - (-3))^2 + (-1 - (-3))^2} \)
\( = \sqrt{1^2 + 2^2} = \sqrt{5} \)
\( \abs{BC} = \sqrt{(1 - (-2))^2 + (5 - (-1))^2} \)
\( = \sqrt{3^2 + 6^2} = 3\sqrt{5} \)
\( \abs{AC} = \sqrt{(1 - (-3))^2 + (5 - (-3))^2} \)
\( = \sqrt{4^2 + 8^2} = 4\sqrt{5} \)
\( [AC] \) uzunluğunun \( [AB] \) ve \( [BC] \) uzunlukları toplamına eşit olduğunu görüyoruz.
\( \abs{AC} = \abs{AB} + \abs{BC} \)
\( 4\sqrt{5} = \sqrt{5} + 3\sqrt{5} \)
Üçgen eşitsizliğine göre, bir üçgende bir kenar uzunluğu her zaman diğer iki kenar uzunlukları toplamından küçüktür. Bu eşitlik bize bu üç noktanın bir üçgen oluşturmadıklarını, dolayısıyla doğrusal olduklarını gösterir.
Noktaların doğrusal olduğunu aşağıdaki şekilde de görebiliriz.