Nesnelerin Dağıtımı

Bazıları ilk bakışta benzer problemler olarak gözükmese de, bir grup sayma problemini bu bölümde tanımlayacağımız nesnelerin dağıtımı başlığı altında inceleyebiliriz.

Nesnelerin dağıtımı problemleri, özdeş ya da birbirinden farklı nesnelerin yine özdeş ya da birbirinden farklı kutulara farklı dağıtım sayılarını inceler. Bu tip problemlerde dağıtılacak nesneler ve nesnelerin dağıtılacağı kutular aşağıda örnekleri verildiği gibi farklı şekillerde karşımıza çıkabilir.

Nesneler: Top, oyuncak, meyve, kişi, bir kümenin elemanları vb.
Kutular: Kutu, koltuk, kişi, hayvan, bir kümenin alt kümeleri vb.

Dağıtılacak nesneler fiziksel özellikleri (renk, büyüklük vb.) itibariyle birbirinden ayırt edilemiyorsa bu nesneler özdeş nesneler olarak adlandırılır ve belirli bir dağıtımda iki özdeş nesnenin aralarında yer değiştirmesi yeni bir dağıtım oluşturmaz. Aksi durumda nesneler farklı nesneler olarak adlandırılır ve belirli bir dağıtımda iki farklı nesnenin aralarında yer değiştirmesi yeni bir dağıtıma karşılık gelir.

Nesnelerin dağıtılacağı kutular da fiziksel özellikleri ya da birbirlerine göre konumları itibariyle birbirinden ayırt edilemiyorsa bu kutular özdeş kutular olarak adlandırılır ve iki kutunun içindeki nesnelerin kutular arasında yer değiştirmesi yeni bir dağıtım oluşturmaz. Aksi durumda kutular farklı kutular olarak adlandırılır ve belirli bir dağıtımda iki kutunun içindeki farklı nesnelerin kutular arasında yer değiştirmesi yeni bir dağıtıma karşılık gelir.

Nesnelerin dağıtımı başlığı altında nesne sayısı için \( n \), kutu sayısı için \( k \) değişkenini kullanacağız.

Aşağıdaki şekilde nesnelerin ve kutuların özdeş ya da farklı olmalarına göre oluşan dört durum gösterilmiştir.

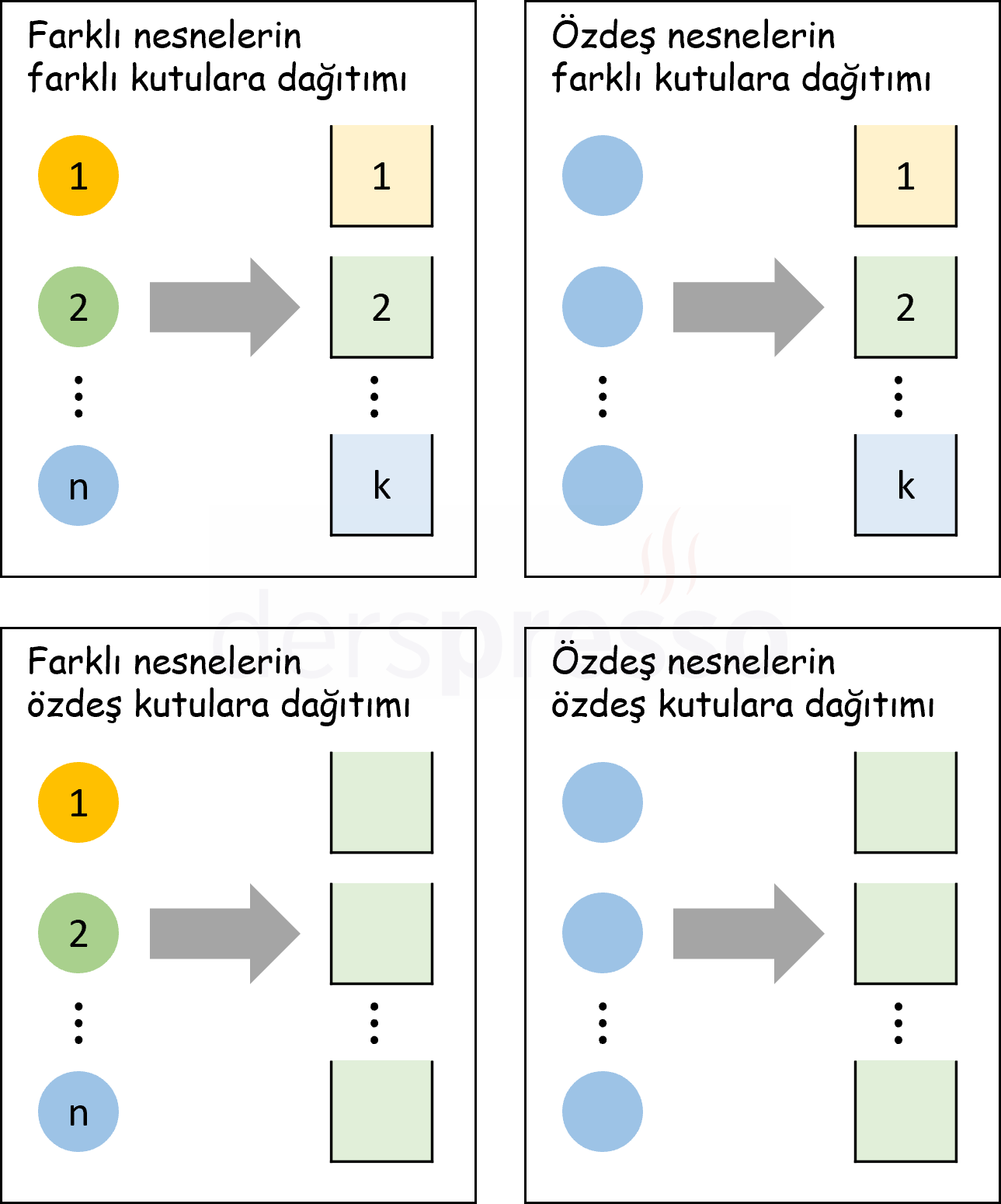
Bu dört durum için oluşan problem tiplerine aşağıdaki gibi örnekler verebiliriz.

Problem Tipi	Örnek Problemler
Farklı nesnelerin farklı kutulara dağıtımı	\( n \) kişinin bir sinema salonundaki \( k \) boş koltuğa farklı oturma sayısı \( n \) elemanlı bir kümeden \( k \) elemanlı bir kümeye yazılabilecek fonksiyon sayısı
Özdeş nesnelerin farklı kutulara dağıtımı	\( n \) özdeş oyuncağın \( k \) çocuğa farklı dağıtım sayısı \( n \) özdeş broşürün \( k \) posta kutusuna farklı dağıtım sayısı
Farklı nesnelerin özdeş kutulara dağıtımı	\( n \) elemanlı bir kümenin elemanlarının \( k \) alt kümeye farklı parçalanış sayısı \( n \) farklı çiçeğin \( k \) özdeş vazoya farklı konma sayısı
Özdeş nesnelerin özdeş kutulara dağıtımı	\( n \) pozitif tam sayısının \( k \) pozitif tam sayının toplamı şeklinde farklı yazılış sayısı \( n \) özdeş kayısının \( k \) saklama poşetine farklı dağıtım sayısı

Bu problem tiplerinin her biri kendi içlerinde aşağıdaki dört alt probleme ayrılır.

Her kutuya herhangi bir sayıda nesne konabilir.
Her kutuya en fazla bir nesne konur.
Her kutuya en az bir nesne konur (kutular boş olamaz).
Her kutuya sadece bir nesne konur.

Aşağıdaki tabloda bu \( 4 \times 4 = 16 \) problem tipinin her birinde kullanılabilecek sayma yöntemi, ilgili yöntemin konu anlatım sayfasına bir link ve örnek bir problem ile birlikte verilmiştir.

Farklı Nesnelerin Farklı Kutulara Dağıtımı

Bu problemler permütasyon ve dahil etme - hariç tutma prensibi ile çözülür.

Koşul	Sayma Yöntemi
Herhangi bir sayıda nesne	Çarpma yoluyla sayma \( k^n \) 5 farklı oyuncak 6 çocuğa kaç farklı şekilde dağıtılabilir?
En fazla bir nesne (\( n \le k \))	\( k \)'lı permütasyon \( P(k, n) \) 6 yolcu bir dolmuştaki 10 boş koltuğa kaç farklı şekilde oturabilir?
En az bir nesne (\( n \ge k \))	Dahil etme - hariç tutma prensibi \( k!\ S(n, k) \) 10 elemanlı bir kümeden 6 elemanlı bir kümeye kaç örten fonksiyon yazılabilir?
Tek bir nesne (\( n = k \))	Permütasyon \( n! \) Bir mağazadaki 5 müşteri 5 deneme kabinini kaç farklı şekilde kullanabilir?

Özdeş Nesnelerin Farklı Kutulara Dağıtımı

Bu problemler kombinasyon yöntemi ile çözülür.

Koşul	Sayma Yöntemi
Herhangi bir sayıda nesne	Ayraç yöntemi \( C(n + k - 1, k - 1) \) 8 özdeş muz 5 maymuna kaç farklı şekilde dağıtılabilir?
En fazla bir nesne (\( n \le k \))	Kombinasyon \( C(k, n) \) 5 özdeş muz 8 maymuna, hiçbir maymun birden fazla muz almamak koşuluyla kaç farklı şekilde dağıtılabilir?
En az bir nesne (\( n \ge k \))	Ayraç yöntemi \( C(n - 1, k - 1) \) 8 özdeş muz 5 maymuna, her maymun en az bir muz almak koşuluyla kaç farklı şekilde dağıtılabilir?
Tek bir nesne (\( n = k \))	\( 1 \) 5 özdeş muz 5 maymuna, her maymun tek bir muz almak koşuluyla kaç farklı şekilde dağıtılabilir?

Farklı Nesnelerin Özdeş Kutulara Dağıtımı

Bu problemler kümelerin parçalanışı yöntemi ve ikinci türden Stirling sayıları ile çözülür.

Koşul	Sayma Yöntemi
Herhangi bir sayıda nesne	İkinci türden Stirling sayıları \( \displaystyle\sum_{i = 1}^{k} S(n, i) \) 6 kişi 3 özdeş balona kaç farklı şekilde binebilir?
En fazla bir nesne (\( n \le k \))	\( 1 \) 4 çocuk bir havuzdaki 6 özdeş deniz yatağına her deniz yatağında en fazla bir çocuk olacak şekilde kaç farklı şekilde binebilir?
En az bir nesne (\( n \ge k \))	İkinci türden Stirling sayıları \( S(n, k) \) 6 öğrenci okul bahçesinde kaç farklı şekilde 3 gruba ayrılabilirler?
Tek bir nesne (\( n = k \))	\( 1 \) 5 bebek 5 özdeş bebek arabasına kaç farklı şekilde konabilir?

Özdeş Nesnelerin Özdeş Kutulara Dağıtımı

Koşul	Sayma Yöntemi
Herhangi bir sayıda nesne	Tam sayıların parçalanışı \( \displaystyle\sum_{i = 1}^{k} p_i(n) \) 8 özdeş bilye 3 özdeş kavanoza kaç farklı şekilde atılabilir?
En fazla bir nesne (\( n \le k \))	\( 1 \) 3 özdeş yumurta 5 özdeş yumurtalığa kaç farklı şekilde konabilir?
En az bir nesne (\( n \ge k \))	Tam sayıların parçalanışı \( p_k(n) \) 9 özdeş kayısı 3 saklama poşetine her poşette en az bir kayısı olmak koşuluyla kaç farklı şekilde konabilir?
Tek bir nesne (\( n = k \))	\( 1 \) 3 özdeş biberon üçüz bebeklere kaç farklı şekilde verilebilir?