Uzaklık Formülleri
İki Nokta Arasındaki Uzaklık
Analitik düzlemde iki nokta arasındaki uzaklık, noktaların apsis ve ordinat değerleri arasındaki farkların kareleri toplamının kareköküne eşittir. Bu iki noktayı birleştiren doğru parçası hipotenüs olacak şekilde bir dik üçgen çizildiğinde bu formülün Pisagor teoreminden türetildiği görülebilir.
\( A \) ve \( B \) noktaları arasındaki uzaklık \( \abs{AB} \) şeklinde gösterilir.
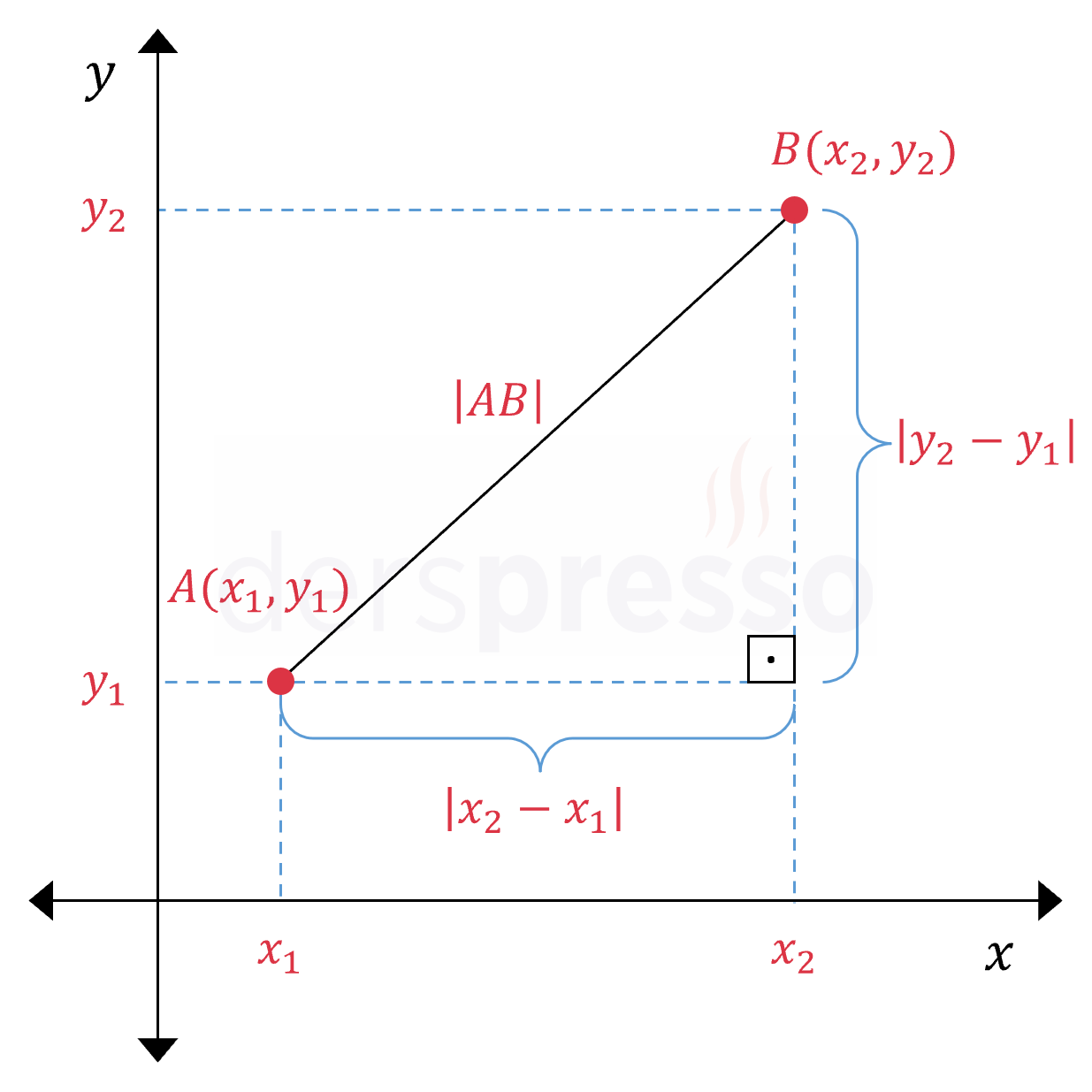
\( {\abs{AB}}^2 = (x_2 - x_1)^2 + (y_2 - y_1)^2 \)
\( \abs{AB} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \)
\( A(8, -3) \) ve \( B(2, 5) \) noktaları arasındaki uzaklık:
\( \abs{AB} = \sqrt{(2 - 8)^2 + (5 - (-3))^2} \)
\( = \sqrt{(-6)^2 + 8^2} = 10 \)
\( A(x_1, y_1) \) noktasının orijine (\( O(0, 0) \)) olan uzaklığı aşağıdaki formülle bulunur.
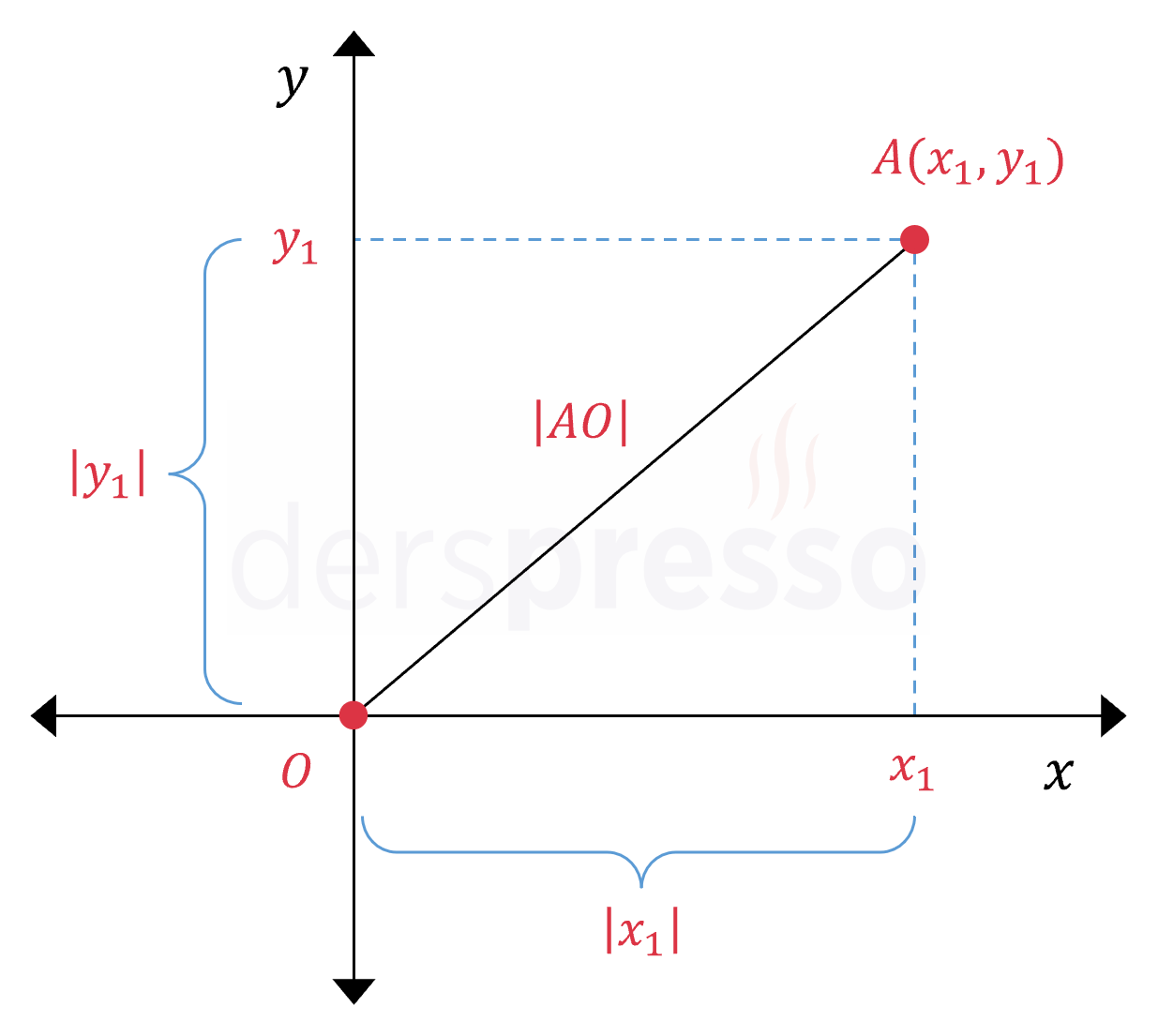
\( \abs{AO} = \sqrt{(x_1 - 0)^2 + (y_1 - 0)^2} \)
\( \abs{AO} = \sqrt{x_1^2 + y_1^2} \)
\( A(-12, 5) \) noktasının orijine uzaklığı:
\( \abs{AO} = \sqrt{(-12)^2 + 5^2} = 13 \)
Uzaklık formülünde iki noktanın apsis ve koordinat değerlerinin hangi sırada birbirinden çıkarıldığının bir önemi yoktur, noktalar arasındaki yatay ve dikey uzaklıkların karesi alındığı için her iki durumda da aynı sonuç elde edilir.
Bunun bir sonucu olarak \( A \) noktasının \( B \) noktasına olan uzaklığı \( B \) noktasının \( A \) noktasına olan uzaklığına eşittir.
\( \abs{AB} = \abs{BA} \)
İki nokta arasındaki uzaklık sıfır ise bu iki noktanın apsis ve ordinat değerleri ayrı ayrı birbirine eşittir. Koordinatları farklı iki nokta arasındaki uzaklık her zaman pozitiftir.
\( A(x_1, y_2) \) ve \( B(x_2, y_2) \) olmak üzere,
\( \abs{AB} = 0 \) ise,
\( x_1 = x_2 \) ve \( y_1 = y_2 \)
\( x_1 \ne x_2 \) veya \( y_1 \ne y_2 \) ise,
\( \abs{AB} \ne 0 \)
\( A(1, -3) \) ve \( B(m, 3) \) olmak üzere,
\( \abs{AB} = 10 \) birim olduğuna göre, \( m \)'nin alabileceği değerler nedir?
Çözümü Göster\( \abs{AB} \) uzaklığını hesaplayalım.
\( \sqrt{(m - 1)^2 + (3 - (-3))^2} = 10 \)
\( (m - 1)^2 + 36 = 100 \)
\( (m - 1)^2 = 64 \)
\( \sqrt{(m - 1)^2} = \sqrt{64} \)
\( \abs{m - 1} = 8 \)
Bu eşitlik iki durumda sağlanır.
Durum 1:
\( m - 1 = 8 \)
\( m = 9 \)
Durum 2:
\( m - 1 = -8 \)
\( m = -7 \)
\( m \)'nin alabileceği değerler -7 ve 9 olur.
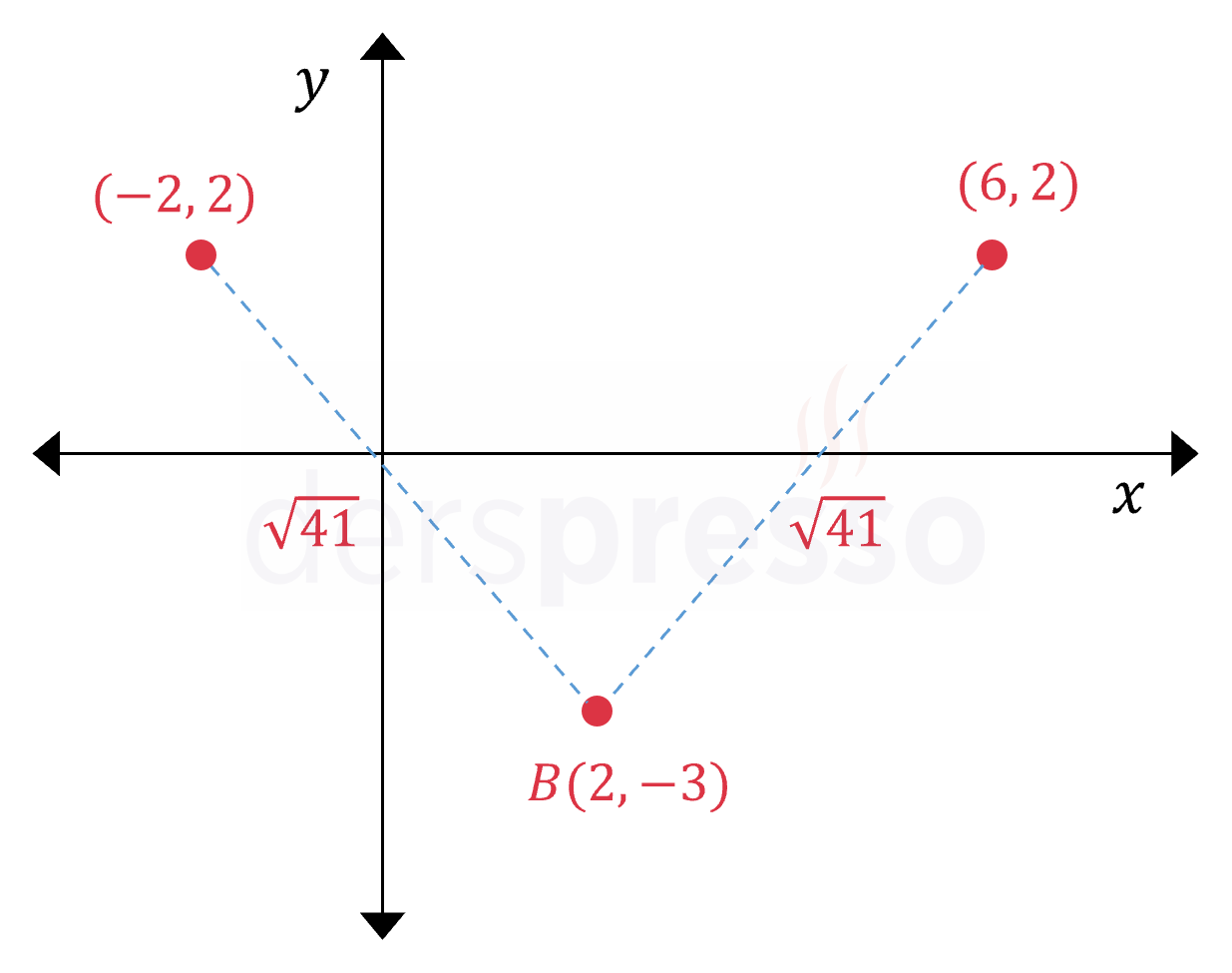
\( A(a, 2) \) ve \( B(2, -3) \) noktaları arasındaki uzaklık \( \sqrt{41} \) olduğuna göre, \( a \)'nın alabileceği değerlerin çarpımı kaçtır?
Çözümü Gösterİki nokta arasındaki uzaklık formülünü yazalım.
\( \abs{AB} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \)
\( \sqrt{41} = \sqrt{(2 - a)^2 + (-3 - 2)^2} \)
\( 41 = (2 - a)^2 + (-5)^2 \)
\( (2 - a)^2 = 16 \)
\( \sqrt{(2 - a)^2} = \sqrt{16} \)
\( \abs{2 - a} = 4 \)
Bu eşitlik iki durumda sağlanır.
Durum 1:
\( 2 - a = 4 \)
\( a = -2 \)
Durum 2:
\( 2 - a = -4 \)
\( a = 6 \)
Buna göre \( a \)'nın alabileceği değerlerin çarpımı \( -2 \cdot 6 = -12 \) olarak bulunur.
Bu iki nokta aşağıdaki şekilde gösterilmiştir.
\( x \) ekseni üzerinde ve \( A(1, 2) \) ve \( B(-3, 1) \) noktalarına eşit uzaklıkta bulunan \( C \) noktasının apsisi nedir?
Çözümü Göster\( C \) noktası \( x \) ekseni üzerinde olduğuna göre koordinatları \( C(a, 0) \) şeklinde olur.
\( \abs{CA} = \abs{CB} \) olduğu biliniyor.
\( \sqrt{(a - 1)^2 + (0 - 2)^2} = \sqrt{(a - (-3))^2 + (0 - 1)^2} \)
\( (a - 1)^2 + 4 = (a + 3)^2 + 1 \)
\( a^2 - 2a + 1 + 4 = a^2 + 6a + 9 + 1 \)
\( -8a = 5 \)
\( a = -\dfrac{5}{8} \) bulunur.
\( A(-2, 2) \) ve \( B(2, 6) \) noktalarının \( y = x \) doğrusu üzerindeki \( C \) noktasına uzaklıkları eşit olduğuna göre, \( C \) noktasının koordinatları nedir?
Çözümü Göster\( C \) noktasının koordinatlarına \( C(a, a) \) diyelim.
\( \abs{AC} \) uzaklığını bulalım.
\( \abs{AC} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \)
\( = \sqrt{(a - (-2))^2 + (a - 2)^2} \)
\( = \sqrt{(a + 2)^2 + (a - 2)^2} \)
\( \abs{BC} \) uzaklığını bulalım.
\( \abs{BC} = \sqrt{(a - 2)^2 + (a - 6)^2} \)
\( \abs{AC} = \abs{BC} \) olarak veriliyor.
\( \sqrt{(a + 2)^2 + (a - 2)^2} = \sqrt{(a - 2)^2 + (a - 6)^2} \)
Eşitliğin iki tarafının karesini alalım
\( (a + 2)^2 + (a - 2)^2 = (a - 2)^2 + (a - 6)^2 \)
\( (a + 2)^2 = (a - 6)^2 \)
\( a^2 + 4a + 4 = a^2 - 12a + 36 \)
\( a = 2 \)
\( C(a, a) = C(2, 2) \) olarak bulunur.
\( A(5, 8) \) noktasının \( x \) eksenine uzaklığı \( B(5, p) \) noktasına uzaklığının 4 katı olduğuna göre, \( p \)'nin alabileceği değerler çarpımı kaçtır?
Çözümü Göster\( A \) noktasının \( x \) eksenine olan uzaklığı 8 birimdir. Buna göre \( A \) noktasının \( B \) noktasına olan uzaklığı 2 birimdir.
İki nokta arasındaki uzaklık formülünü yazalım.
\( {\abs{AB}}^2 = (x_2 - x_1)^2 + (y_2 - y_1)^2 \)
\( 2^2 = (5 - 5)^2 + (p - 8)^2 \)
\( 4 = (p - 8)^2 \)
\( p - 8 = 2 \) ya da \( p - 8 = -2 \)
\( p - 8 = 2 \Longrightarrow p = 10 \)
\( p - 8 = -2 \Longrightarrow p = 6 \)
\( p \)'nin alabileceği değerler çarpımı \( 10 \cdot 6 = 60 \) olarak bulunur.
\( A(-3, -3), B(-2, -1), C(1, 5) \) noktalarının doğrusal olup olmadığını uzaklık formülünü kullanarak bulunuz.
Çözümü GösterBu üç nokta arasındaki uzaklıkları bulalım.
\( \abs{AB} = \sqrt{(-2 - (-3))^2 + (-1 - (-3))^2} \)
\( = \sqrt{1^2 + 2^2} = \sqrt{5} \)
\( \abs{BC} = \sqrt{(1 - (-2))^2 + (5 - (-1))^2} \)
\( = \sqrt{3^2 + 6^2} = 3\sqrt{5} \)
\( \abs{AC} = \sqrt{(1 - (-3))^2 + (5 - (-3))^2} \)
\( = \sqrt{4^2 + 8^2} = 4\sqrt{5} \)
\( [AC] \) uzunluğunun \( [AB] \) ve \( [BC] \) uzunlukları toplamına eşit olduğunu görüyoruz.
\( \abs{AC} = \abs{AB} + \abs{BC} \)
\( 4\sqrt{5} = \sqrt{5} + 3\sqrt{5} \)
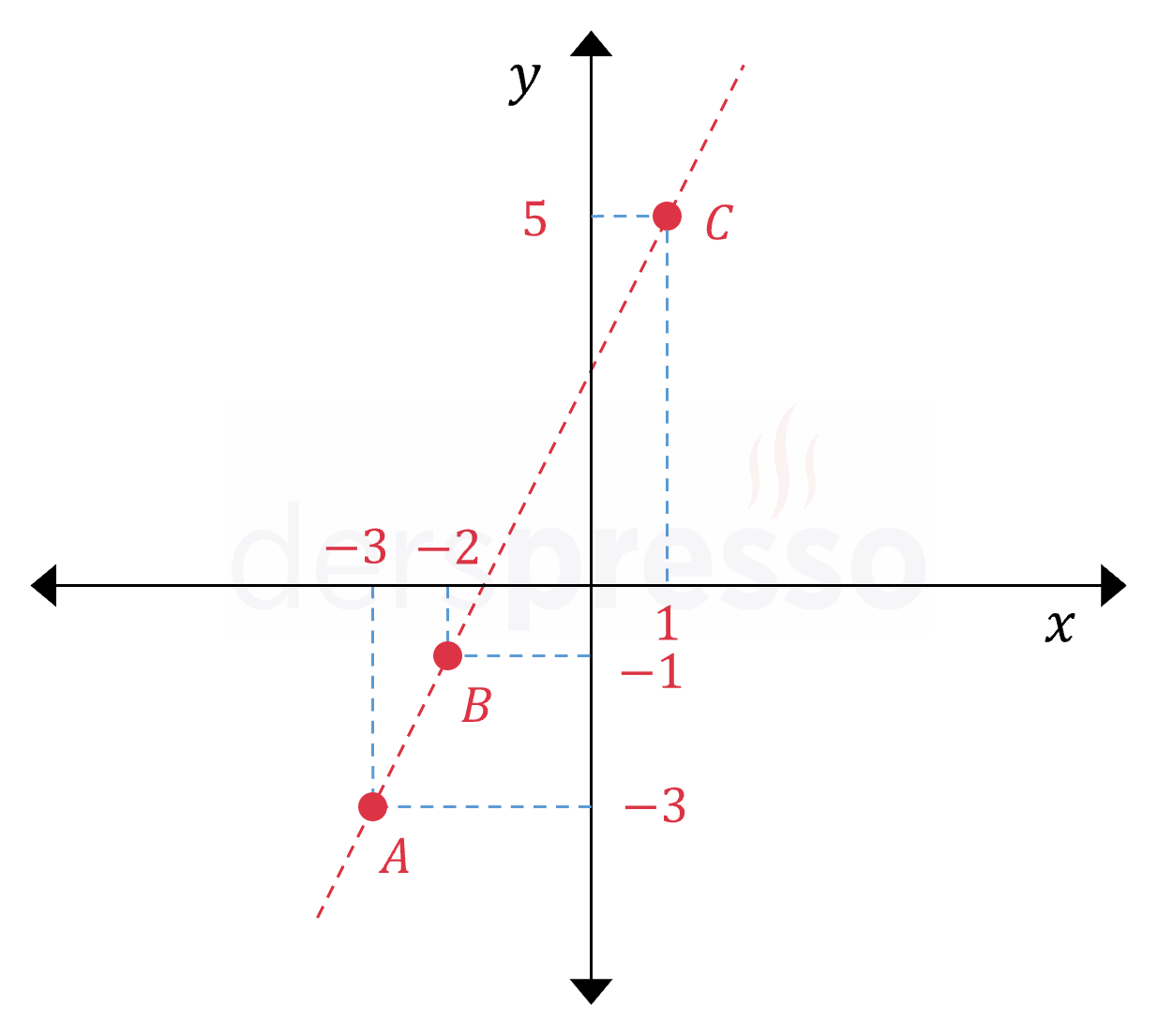
Üçgen eşitsizliğine göre, bir üçgende bir kenar uzunluğu her zaman diğer iki kenar uzunlukları toplamından küçüktür. Bu eşitlik bize bu üç noktanın bir üçgen oluşturmadıklarını, dolayısıyla doğrusal olduklarını gösterir.
Noktaların doğrusal olduğunu aşağıdaki şekilde de görebiliriz.
İki Noktanın Orta Noktası
İki noktanın orta noktası, bu iki noktayı birleştiren doğru parçası üzerinde bulunan ve her iki noktaya eşit uzaklıktaki noktadır. Benzer üçgenlerden görülebileceği üzere, bu orta noktanın apsis ve ordinat değerleri verilen iki noktanın apsis ve ordinat değerlerinin toplamının yarısına (aritmetik ortalamasına) eşittir.
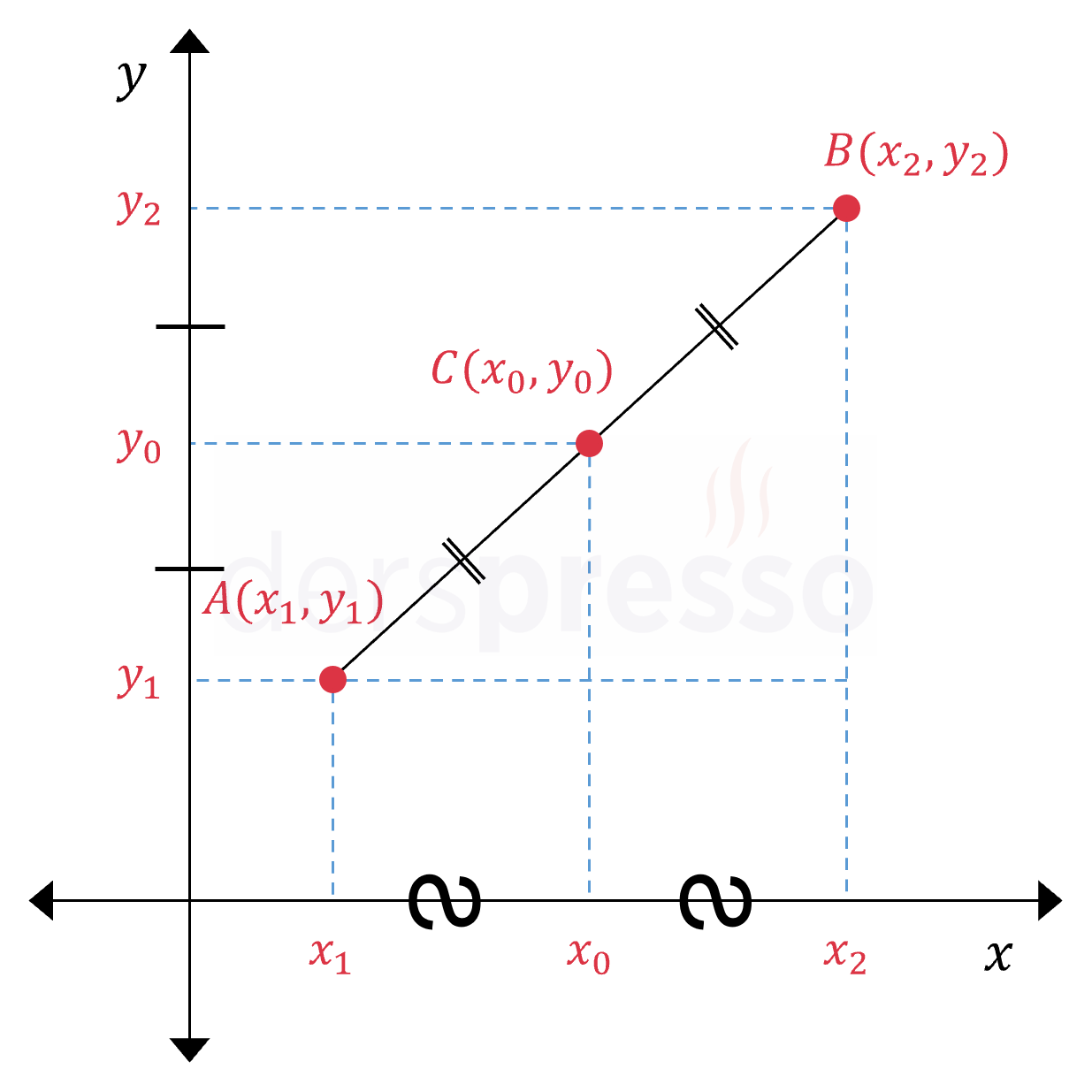
\( A(x_1, y_1) \) ve \( B(x_2, y_2) \) noktalarının orta noktası \( C(x_0, y_0) \) olmak üzere,
\( \abs{AC} = \abs{CB} \)
\( x_0 = \dfrac{x_1 + x_2}{2} \)
\( y_0 = \dfrac{y_1 + y_2}{2} \)
\( A(-1, 4) \) ve \( B(5, -4) \) noktalarının orta noktası \( C(x_0, y_0) \) ise,
\( x_0 = \dfrac{-1 + 5}{2} = 2 \)
\( y_0 = \dfrac{4 + (-4)}{2} = 0 \)
Orta nokta: \( C(2, 0) \)
\( \abs{AC} = \sqrt{(2 - (-1))^2 + (0 - 4)^2} = 5 \)
\( \abs{CB} = \sqrt{(5 - 2))^2 + (-4 - 0)^2} = 5 \)
Şekilde görülebileceği gibi, \( C \) noktasının eksenler üzerindeki izdüşümleri de \( A \) ve \( B \) noktalarının eksenler üzerindeki izdüşümlerinin orta noktalarıdır.
\( A(-2, -6) \) ve \( B(4, b) \) noktalarının orta noktası \( C(a, -2) \) olduğuna göre, \( ab \) çarpımı kaçtır?
Çözümü Gösterİki noktanın orta noktasının apsis ve ordinat değerleri, bu iki noktanın apsis ve ordinat değerlerinin aritmetik ortalamasına eşittir.
\( a = \dfrac{-2 + 4}{2} \)
\( a = 1 \)
\( -2 = \dfrac{-6 + b}{2} \)
\( b = 2 \)
\( ab = 1 \cdot 2 = 2 \) bulunur.
Koordinat düzleminde \( A(t - 1, 2t + 3) \) ve \( B(t + 3, 4t - 1) \) noktaları veriliyor.
\( [AB] \) doğru parçasının orta noktalarının geometrik yerinin denklemi nedir?
Çözümü Gösterİki noktanın orta noktasının apsis ve ordinat değerleri, bu iki noktanın apsis ve ordinat değerlerinin aritmetik ortalamasına eşittir.
İki noktanın orta noktasına \( C \) diyelim.
\( C\left( \dfrac{t - 1 + t + 3}{2}, \dfrac{2t + 3 + 4t - 1}{2} \right) \) \( = C(t + 1, 3t + 1) \)
\( t \) cinsinden parametrik denklemini bulduğumuz doğrunun denklemini bulalım.
\( x = t + 1 \Longrightarrow t = x - 1 \)
Birinci denklemde bulduğumuz \( t \) değerini ikinci denklemde yerine koyalım.
\( y = 3t + 1 \Longrightarrow y = 3(x - 1) + 1 \)
\( y = 3x - 2 \) bulunur.
Buna göre, farklı \( t \) değerleri için oluşan \( [AB] \) doğru parçalarının orta noktaları bir doğru oluşturur.
Bir Doğru Parçasını Belirli bir Oranda İçten Bölen Nokta
İki noktayı birleştiren doğru parçasını belirli bir oranda içten bölen noktanın koordinatları aşağıdaki formülle bulunur.
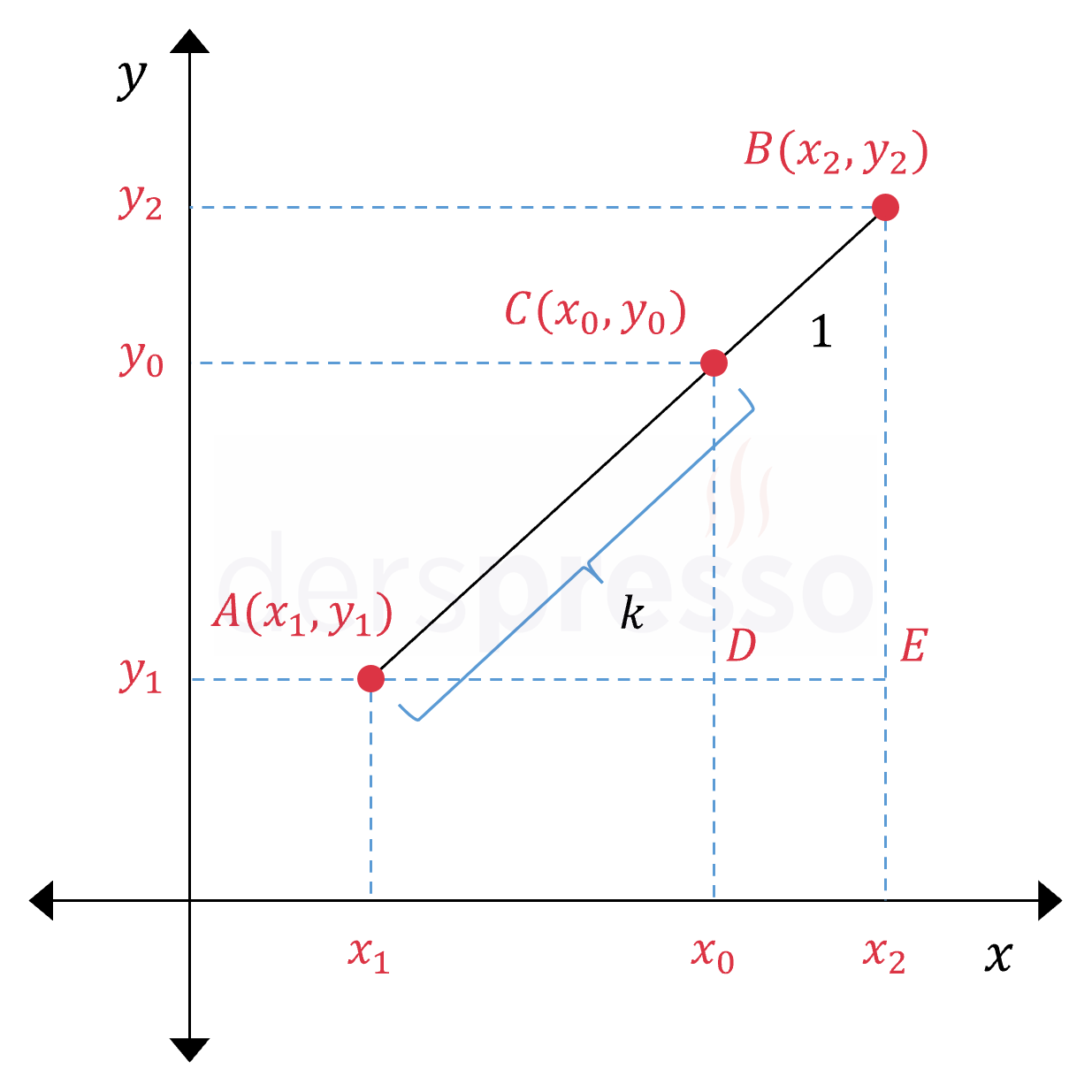
\( A(x_1, y_1) \) ve \( B(x_2, y_2) \) noktaları birleştiren doğru parçasını \( \frac{\abs{CA}}{\abs{CB}} = k \) oranında içten bölen \( C(x_0, y_0) \) noktasının koordinatları:
\( x_0 = \dfrac{x_1 + kx_2}{1 + k} \)
\( y_0 = \dfrac{y_1 + ky_2}{1 + k} \)
\( A(-1, 1) \) ve \( B(11, 9) \) noktalarını birleştiren doğru parçasını \( \frac{\abs{CA}}{\abs{CB}} = 3 \) oranında bölen \( C(x_0, y_0) \) noktasının koordinatları:
\( x_0 = \dfrac{-1 + 3 \cdot 11}{1 + 3} = 8 \)
\( y_0 = \dfrac{1 + 3 \cdot 9}{1 + 3} = 7 \)
İSPATI GÖSTER
\( ADC \) ve \( AEB \) üçgenlerinin tüm açıları eşit olduğu için benzer üçgenlerdir.
\( \overset{\triangle}{ADC} \sim \overset{\triangle}{AEB} \)
Buna göre temel orantı teoremini kullanarak bu iki üçgenin kenar uzunluk oranları arasında aşağıdaki orantıyı kurabiliriz.
\( \dfrac{x_0 - x_1}{x_2 - x_1} = \dfrac{y_0 - y_1}{y_2 - y_1} = \dfrac{k}{k + 1} \)
Bu orantıda birinci ve üçüncü oranlar arasında içler - dışlar çarpımı yaparak \( x_0 \)'ı yalnız bırakalım.
\( \dfrac{x_0 - x_1}{x_2 - x_1} = \dfrac{k}{k + 1} \)
\( (k + 1)(x_0 - x_1) = k(x_2 - x_1) \)
\( kx_0 - kx_1 + x_0 - x_1 = kx_2 - kx_1 \)
\( x_0 = \dfrac{x_1 + kx_2}{1 + k} \)
Şimdi de ikinci ve üçüncü oranlar arasında içler - dışlar çarpımı yaparak \( y_0 \)'ı yalnız bırakalım.
\( \dfrac{y_0 - y_1}{y_2 - y_1} = \dfrac{k}{k + 1} \)
\( (k + 1)(y_0 - y_1) = k(y_2 - y_1) \)
\( ky_0 - ky_1 + y_0 - y_1 = ky_2 - ky_1 \)
\( y_0 = \dfrac{y_1 + ky_2}{1 + k} \)
\( C \) noktasının eksenler üzerindeki izdüşümleri de \( A \) ve \( B \) noktalarının eksenler üzerindeki izdüşümlerini içten aynı oranda böler.
Bir Doğru Parçasını Belirli bir Oranda Dıştan Bölen Nokta
İki noktayı birleştiren doğru parçasını belirli bir oranda dıştan bölen noktanın koordinatları aşağıdaki formülle bulunur.
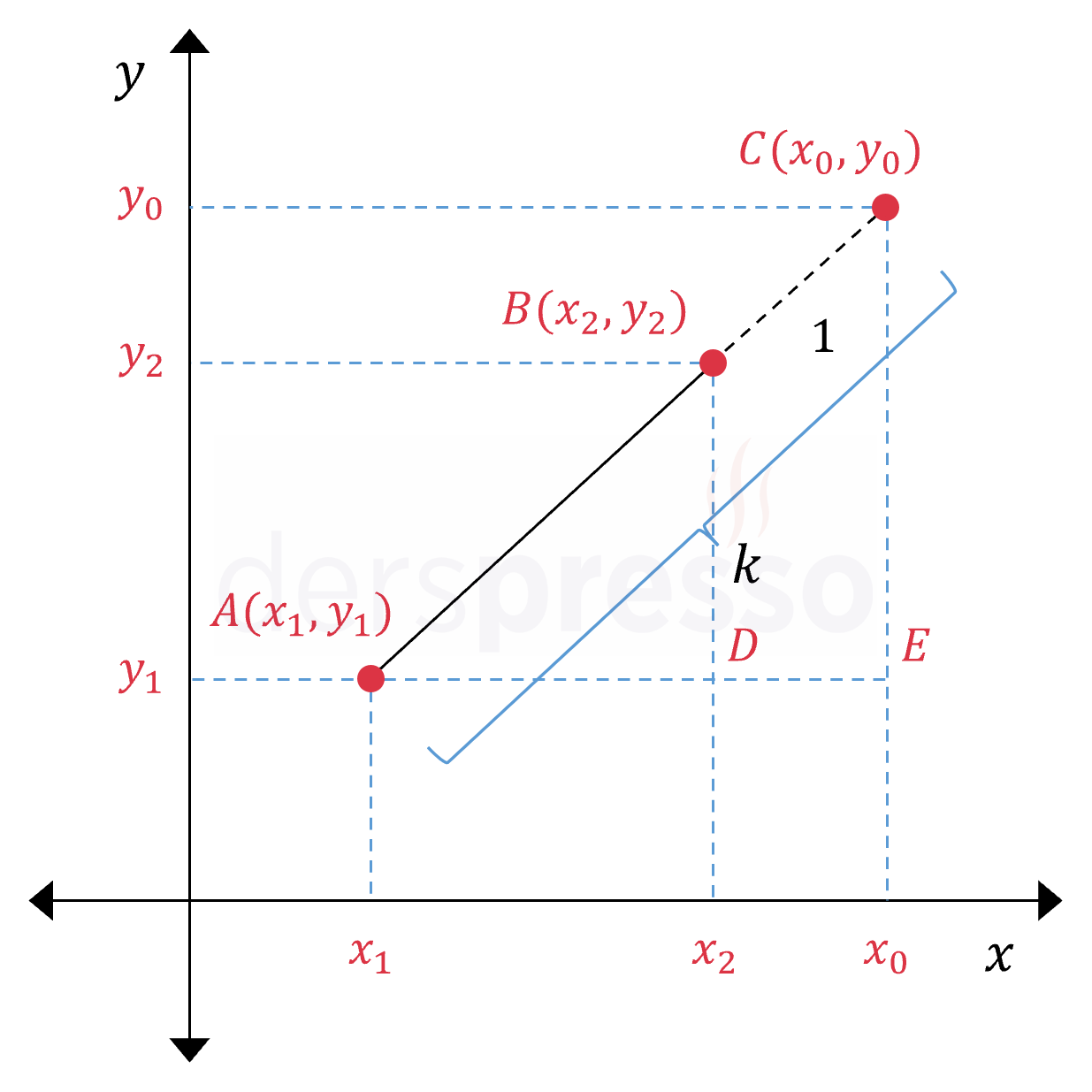
\( A(x_1, y_1) \) ve \( B(x_2, y_2) \) noktaları birleştiren doğru parçasını \( \frac{\abs{CA}}{\abs{CB}} = k \) oranında dıştan bölen \( C(x_0, y_0) \) noktasının koordinatları:
\( x_0 = \dfrac{x_1 - kx_2}{1 - k} \)
\( y_0 = \dfrac{y_1 - ky_2}{1 - k} \)
\( A(-1, 1) \) ve \( B(8, 7) \) noktalarını birleştiren doğru parçasını \( \frac{\abs{CA}}{\abs{CB}} = 4 \) oranında bölen \( C(x_0, y_0) \) noktasının koordinatları:
\( x_0 = \dfrac{-1 - 4 \cdot 8}{1 - 4} = 11 \)
\( y_0 = \dfrac{1 - 4 \cdot 7}{1 - 4} = 9 \)
İSPATI GÖSTER
\( ADB \) ve \( AEC \) üçgenlerinin tüm açıları eşit olduğu için benzer üçgenlerdir.
\( \overset{\triangle}{ADB} \sim \overset{\triangle}{AEC} \)
Buna göre temel orantı teoremini kullanarak bu iki üçgenin kenar uzunluk oranları arasında aşağıdaki orantıyı kurabiliriz.
\( \dfrac{x_2 - x_1}{x_0 - x_1} = \dfrac{y_2 - y_1}{y_0 - y_1} = \dfrac{k - 1}{k} \)
Bu orantıda birinci ve üçüncü oranlar arasında içler - dışlar çarpımı yaparak \( x_0 \)'ı yalnız bırakalım.
\( \dfrac{x_2 - x_1}{x_0 - x_1} = \dfrac{k - 1}{k} \)
\( (k - 1)(x_0 - x_1) = k(x_2 - x_1) \)
\( kx_0 - kx_1 - x_0 + x_1 = kx_2 - kx_1 \)
\( x_0 = \dfrac{x_1 - kx_2}{1 - k} \)
Şimdi de ikinci ve üçüncü oranlar arasında içler - dışlar çarpımı yaparak \( y_0 \)'ı yalnız bırakalım.
\( \dfrac{y_2 - y_1}{y_0 - y_1} = \dfrac{k - 1}{k} \)
\( (k - 1)(y_0 - y_1) = k(y_2 - y_1) \)
\( ky_0 - ky_1 - y_0 + y_1 = ky_2 - ky_1 \)
\( y_0 = \dfrac{y_1 - ky_2}{1 - k} \)
\( C \) noktasının eksenler üzerindeki izdüşümleri de \( A \) ve \( B \) noktalarının eksenler üzerindeki izdüşümlerini dıştan aynı oranda böler.
Bir Noktaya Eşit Uzaklıktaki Noktalar
Analitik düzlemde bir noktaya eşit uzaklıktaki noktaların kümesi bir çember oluşturur.
Aşağıdaki şekilde \( A \) noktasına \( d \) birim uzaklıktaki noktalar kümesi olan çember gösterilmiştir.
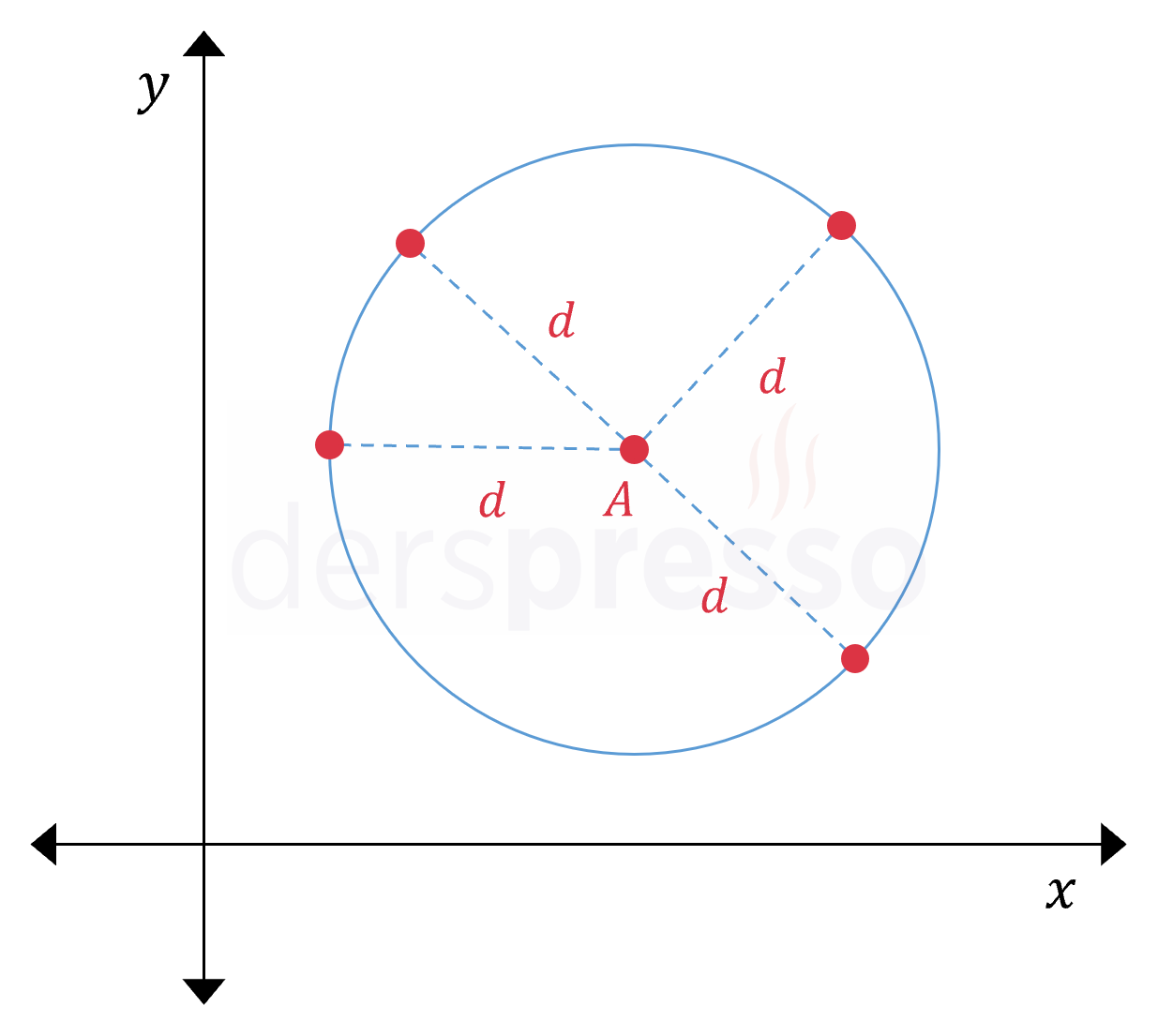
Bu konuyu daha detaylı şekilde çemberin analitiği bölümünde inceleyeceğiz.
İki Noktaya Eşit Uzaklıktaki Noktalar
Analitik düzlemde iki farklı noktaya eşit uzaklıktaki noktaların kümesi, bu iki noktayı birleştiren doğru parçasının orta noktasından geçen ve bu doğru parçasına dik olan doğrudur.
Aşağıdaki şekilde \( A \) ve \( B \) noktalarına eşit uzaklıktaki noktalar kümesi olan \( d \) doğrusu gösterilmiştir.

\( A \) ve \( B \) noktalarına eşit uzaklıktaki tüm noktalara \( D(x, y) \) diyelim.
\( D \) noktasının geometrik yer denklemini aşağıdaki şekilde yazabiliriz.
\( \abs{AD} = \abs{BD} \)
\( \sqrt{(x - x_1)^2 + (y - y_1)^2} \) \( = \sqrt{(x - x_2)^2 + (y - y_2)^2} \)
Eşitliğin iki tarafının karesini alalım.
\( (x - x_1)^2 + (y - y_1)^2 \) \( = (x - x_2)^2 + (y - y_2)^2 \)
\( x^2 - 2xx_1 + x_1^2 + y^2 \) \( - 2yy_1 + y_1^2 \) \( = x^2 - 2xx_2 + x_2^2 + y^2 \) \( - 2yy_2 + y_2^2 \)
İki taraftaki \( x^2 \) ve \( y^2 \)'ler birbirlerini götürür.
\( - 2xx_1 + x_1^2 \) \( - 2yy_1 + y_1^2 \) \( = - 2xx_2 + x_2^2 \) \( - 2yy_2 + y_2^2 \)
Tüm terimleri tek tarafta toplayalım.
\( 2(x_1 - x_2)x + 2(y_1 - y_2)y \) \( - (x_1^2 - x_2^2 + y_1^2 - y_2^2) \) \( = 0 \)
Bu denklemdeki \( x_1, y_1, x_2, y_2 \) değerleri \( A \) ve \( B \) noktalarının sabit koordinat değerleri olduğu için, o değerleri yerine koyduğumuzda \( ax + by + c = 0 \) formunda bir doğru denklemi elde ederiz.
Bu yüzden, iki noktaya eşit uzaklıktaki noktalar bir doğru oluşturur.
Üç Noktaya Eşit Uzaklıktaki Noktalar
Analitik düzlemde doğrusal olmayan üç farklı noktaya eşit uzaklıktaki noktaların kümesi tek bir noktadır.
İki noktaya eşit uzaklıktaki noktalar kümesini bulmak için kullandığımız yöntemi bu üç nokta arasından seçeceğimiz herhangi iki nokta ikilisine uyguladığımızda, elde edeceğimiz iki doğrunun kesişim noktası üç noktaya eşit uzaklıktaki noktayı verir.
Aşağıdaki şekilde \( A \), \( B \) ve \( C \) noktalarına eşit uzaklıktaki \( D \) noktası gösterilmiştir.
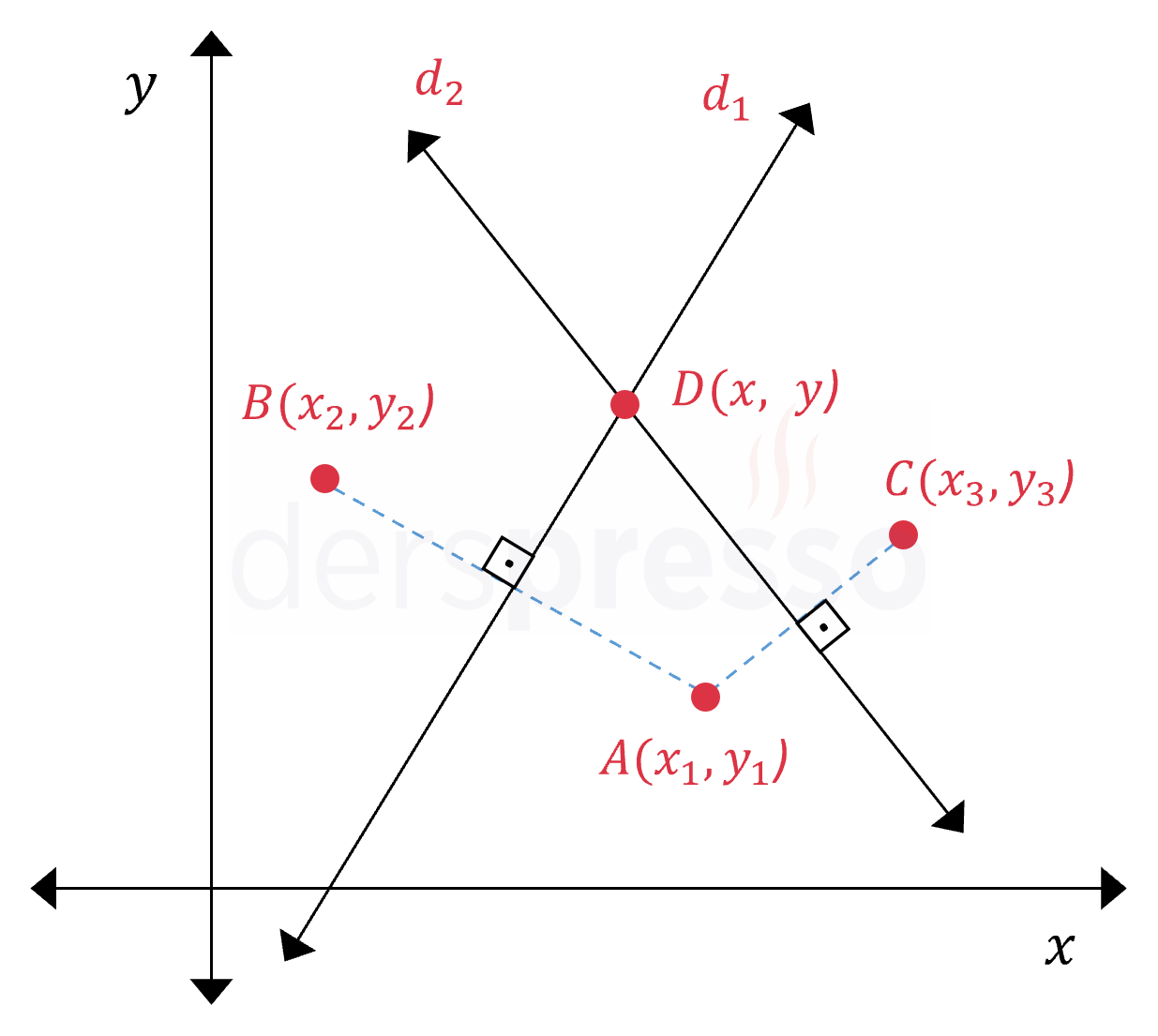

Şekildeki \( A(1, 2) \) ve \( B(5, -2) \) noktalarını birleştiren doğru parçasını \( \frac{\abs{AC}}{\abs{BC}} = \frac{1}{3} \) oranında içten bölen \( C \) noktasının koordinatlarını bulunuz.
Çözümü Göster\( A(x_1, y_1) \) ve \( B(x_2, y_2) \) noktalarını birleştiren doğru parçasını \( k \) oranında içten bölen \( C(x_0, y_0) \) noktasının koordinatları aşağıdaki formülle bulunur.
\( x_0 = \dfrac{x_1 + kx_2}{1 + k} \)
\( y_0 = \dfrac{y_1 + ky_2}{1 + k} \)
Verilen noktaların koordinatlarını bu formüllerde yerine koyalım.
\( x_0 = \dfrac{1 + \frac{1}{3} \cdot 5}{1 + \frac{1}{3}} \)
\( = \dfrac{\frac{8}{3}}{\frac{4}{3}} = 2 \)
\( y_0 = \dfrac{2 + (\frac{1}{3} \cdot -2)}{1 + \frac{1}{3}} \)
\( = \dfrac{\frac{4}{3}}{\frac{4}{3}} = 1 \)
\( C \) noktasının koordinatları \( C(2, 1) \) olarak bulunur.

Şekildeki \( A(2, 3) \) ve \( B(6, -1) \) noktalarını birleştiren doğru parçasını \( \abs{AC} : \abs{BC} = 1:2 \) oranında dıştan bölen \( C \) noktasının koordinatlarını bulunuz.
Çözümü Göster\( A(x_1, y_1) \) ve \( B(x_2, y_2) \) noktalarını birleştiren doğru parçasını \( k \) oranında dıştan bölen \( C(x_0, y_0) \) noktasının koordinatları aşağıdaki formülle bulunur.
\( x_0 = \dfrac{x_1 - kx_2}{1 - k} \)
\( y_0 = \dfrac{y_1 - ky_2}{1 - k} \)
Verilen noktaların koordinatlarını bu formüllerde yerine koyalım.
\( x_0 = \dfrac{2 - \frac{1}{2} \cdot 6}{1 - \frac{1}{2}} \)
\( = \dfrac{-1}{\frac{1}{2}} = -2 \)
\( y_0 = \dfrac{3 - (\frac{1}{2} \cdot -1)}{1 - \frac{1}{2}} \)
\( = \dfrac{\frac{7}{2}}{\frac{1}{2}} = 7 \)
\( C \) noktasının koordinatları \( C(-2, 7) \) olarak bulunur.
\( 2x - 3y + 7 = 0 \) doğrusu \( A(n - 4, 2n - 3) \) noktasından geçtiğine göre, \( A \) noktasının orijine olan uzaklığı kaçtır?
Çözümü Göster\( 2x - 3y + 7 = 0 \) doğrusu \( A \) noktasından geçtiğine göre, \( A \) noktasının koordinatları doğru denklemini sağlar.
\( 2(n - 4) - 3(2n - 3) + 7 = 0 \)
\( 2n - 8 - 6n + 9 + 7 = 0 \)
\( n = 2 \)
\( A(n - 4, 2n - 3) = A(-2, 1) \)
\( A \) noktasının orijine olan uzaklığını bulalım.
\( \abs{AO} = \sqrt{x_1^2 + y_1^2} \)
\( = \sqrt{(-2)^2 + 1^2} \)
\( = \sqrt{5} \) bulunur.
Analitik düzlemde \( A(-3, 4) \) noktası 1 birim sola, 7 birim yukarı ötelendiğinde \( B \) noktası elde ediliyor.
Buna göre \( \abs{AB} \) uzaklığı kaçtır?
Çözümü GösterBir nokta 1 birim sola ötelendiğinde apsisi 1 birim azalır.
\( A(-3, 4) \longmapsto A'(-4, 4) \)
Bir nokta 7 birim yukarı ötelendiğinde ordinatı 7 birim artar.
\( A'(-4, 4) \longmapsto B(-4, 11) \)
İki nokta arası uzaklık formülünü kullanarak \( \abs{AB} \) uzaklığını hesaplayalım.
\( \abs{AB} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \)
\( = \sqrt{(-4 - (-3))^2 + (11 - 4)^2} \)
\( = \sqrt{(-1)^2 + 7^2} \)
\( = \sqrt{50} = 5\sqrt{2} \) bulunur.
Analitik düzlemde \( A \) noktası \( y = -2 \) doğrusu üzerinde ve \( B(2, 4) \), \( C(-3, -5) \) noktalarına eşit uzaklıktadır.
Buna göre \( A \) noktasının apsisi kaçtır?
Çözümü GösterVerilen bilgileri analitik düzlemde gösterelim.
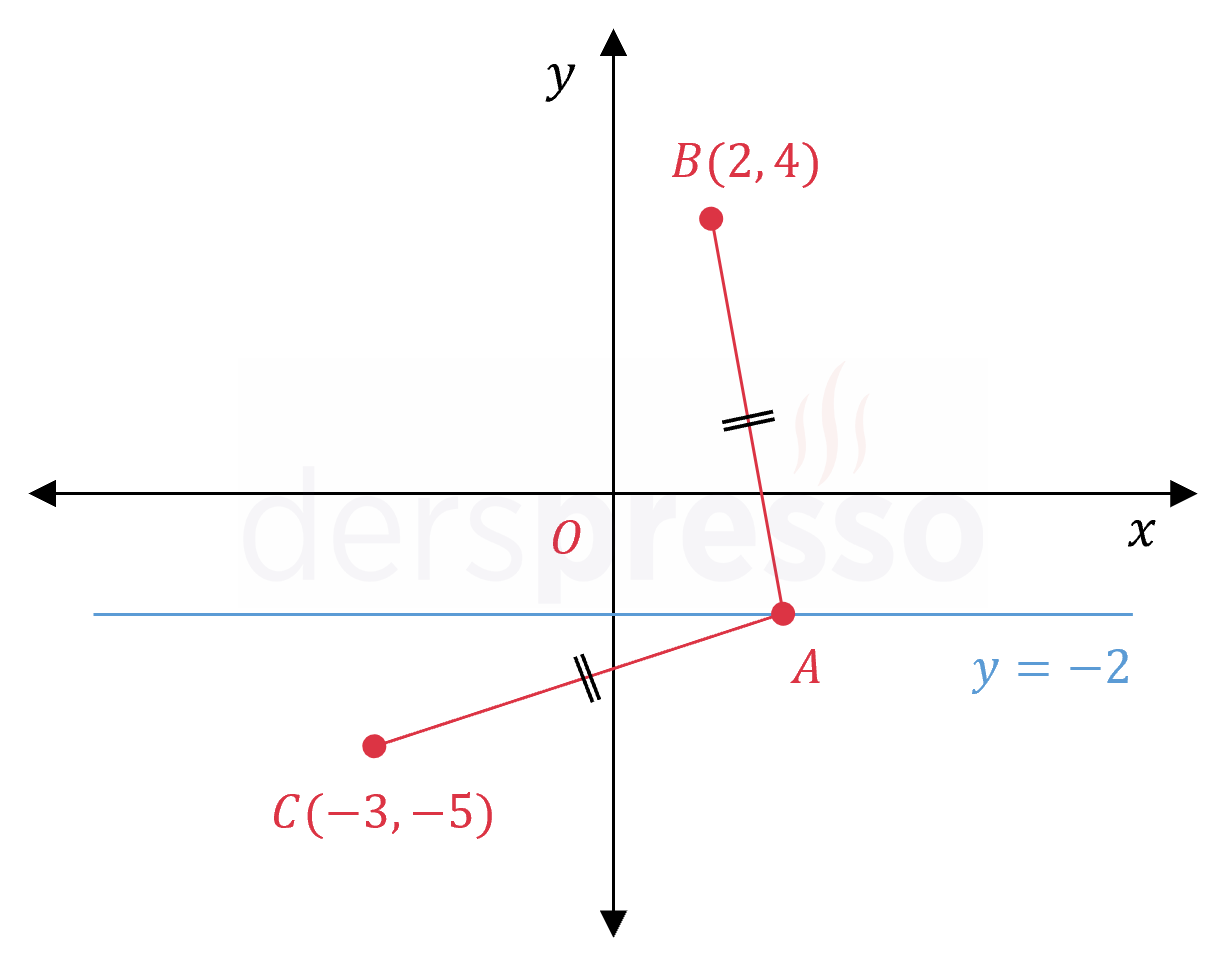
\( A \) noktasının apsisine \( k \) diyelim.
\( A \) noktası \( y = -2 \) doğrusu üzerindedir.
\( A(k, -2) \)
\( A \) noktasının verilen iki noktaya olan uzaklıklarını birbirine eşitleyelim.
\( \abs{AB}^2 = (x_2 - x_1)^2 + (y_2 - y_1)^2 \)
\( = (k - 2)^2 + (-2 - 4)^2 \)
\( = (k - 2)^2 + 36 \)
\( \abs{AC}^2 = (k - (-3))^2 + (-2 - (-5))^2 \)
\( = (k + 3)^2 + 9 \)
\( \abs{AB}^2 = \abs{AC}^2 \)
\( (k - 2)^2 + 36 = (k + 3)^2 + 9 \)
\( k^2 - 4k + 4 + 36 = k^2 + 6k + 9 + 9 \)
\( 10k = 22 \)
\( k = \dfrac{11}{5} \) bulunur.
Analitik düzlemde köşeleri \( A(-2, 2) \), \( B(10, 2) \) ve \( C(-2, -3) \) olan üçgenin çevresi kaç birimdir?
Çözümü GösterNoktaları analitik düzlemde işaretlediğimizde oluşan üçgenin dik kenarları eksenlere paralel olan bir dik üçgen olduğunu görürüz.
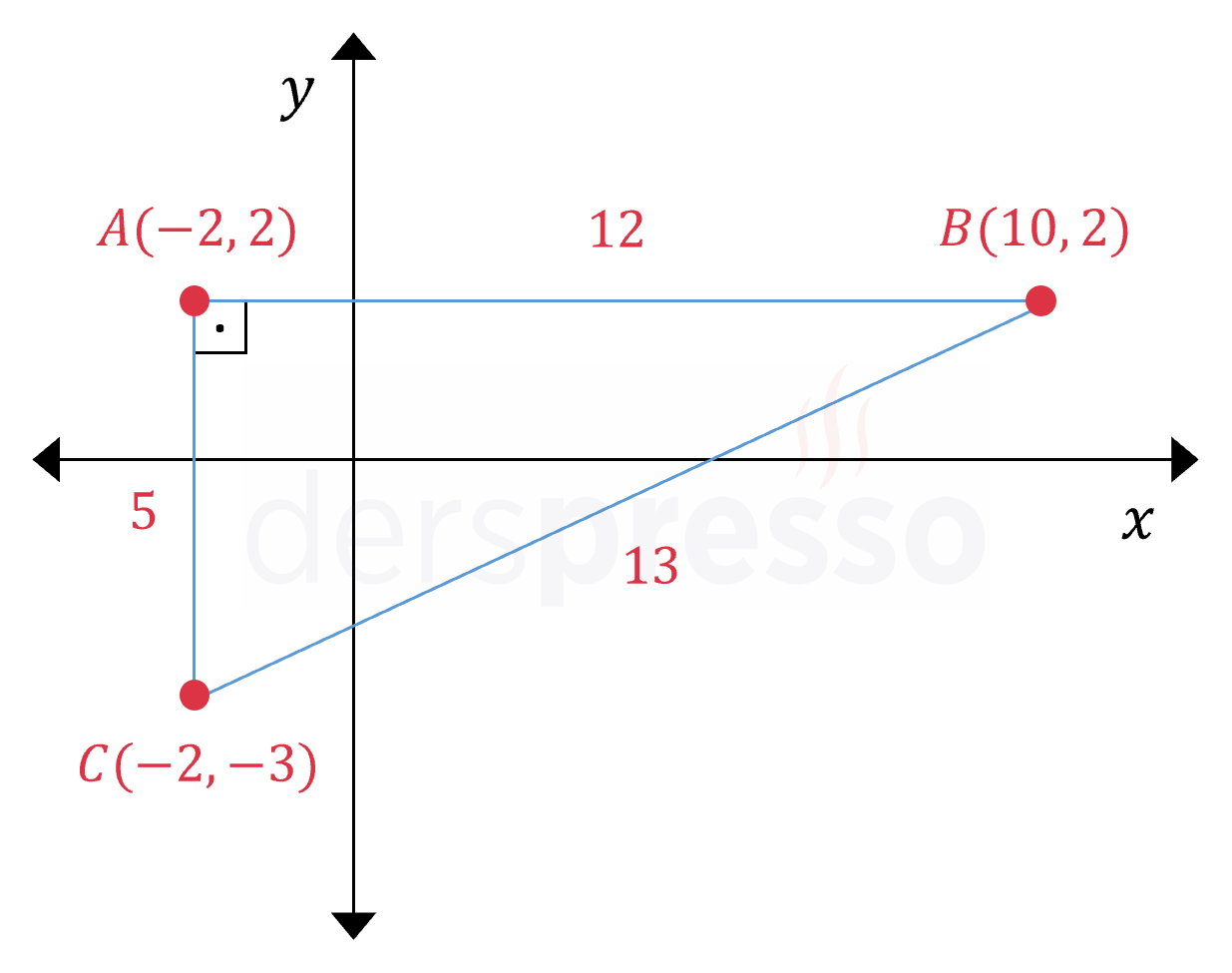
Üçgenin kenar uzunluklarını bulalım.
\( \abs{AB} = \abs{10 - (-2)} = 12 \) br
\( \abs{AC} = \abs{-3 - 2} = 5 \) br
\( \abs{BC} = \sqrt{12^2 + 5^2 } = 13 \) br
Buna göre üçgenin çevresi aşağıdaki gibi bulunur.
\( Ç(ABC) = 12 + 5 + 13 = 30 \) br
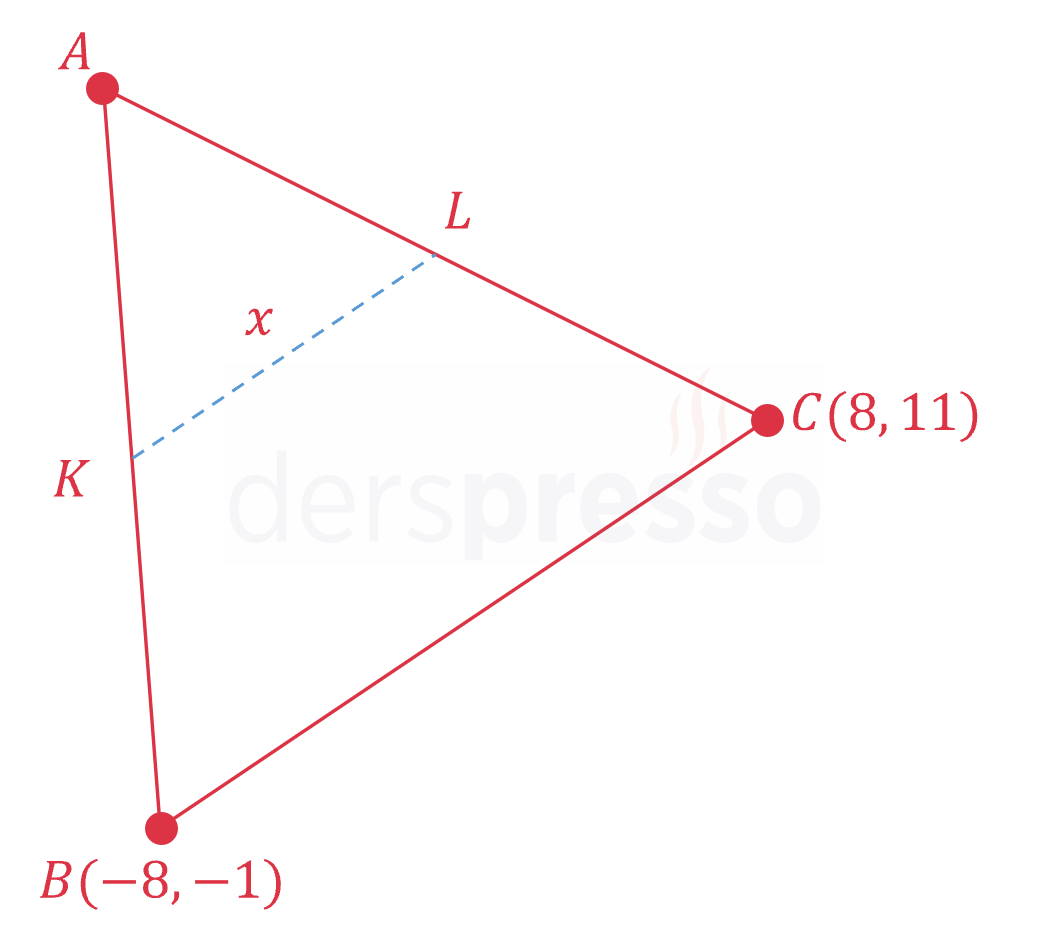
Analitik düzlemde \( ABC \) üçgeni verilmiştir.
\( \abs{AK} = \abs{KB} \) ve \( \abs{AL} = \abs{LC} \) olduğuna göre \( \abs{KL} = x \) değerini bulunuz.
Çözümü Göster\( K \) ve \( L \) noktaları bulundukları kenarların orta noktaları olduğu için \( [KL] \) doğru parçası \( ABC \) üçgeninin orta tabanı olur.
Bir üçgende orta taban uzunluğu taban uzunluğunun yarısıdır.
\( [BC] \) taban uzunluğunu iki nokta arasındaki uzaklık formülü ile bulalım.
\( \abs{BC} = \sqrt{(8 - (-8))^2 + (11 - (-1))^2} \)
\( = \sqrt{12^2 + 16^2} = 20 \)
Buna göre \( x = 10 \) bulunur.

Yukarıdaki şekilde \( A \) noktasının apsis değeri 4 olduğuna göre, \( \abs{AB} \) kaç birimdir?
Çözümü GösterAşağıdaki şekildeki gibi \( A \) noktasından \( x \) eksenine bir dikme çizelim.

\( \abs{OD} = 4 \)
\( \abs{DB} = 5 - 4 = 1 \)
Trigonometrik oranları kullanarak \( \abs{AD} \) uzunluğunu bulalım.
\( \tan{60°} = \dfrac{\abs{AD}}{\abs{OD}} \)
\( \sqrt{3} = \dfrac{\abs{AD}}{4} \)
\( \abs{AD} = 4\sqrt{3} \)
\( ADB \) üçgeninde Pisagor teoremini kullanarak \( \abs{AB} \) uzunluğunu bulalım.
\( \abs{AB} = \sqrt{(4\sqrt{3})^2 + 1^2} \)
\( = \sqrt{48 + 1} = 7 \) bulunur.

Analitik düzlemde \( A \) ve \( B \) noktaları şekildeki gibi veriliyor.
Buna göre aşağıdaki koordinatlardan hangisi \( A \) ve \( B \) noktalarına eşit uzaklıktadır.
(a) \( (3, 6) \)
(b) \( (1, 0) \)
(c) \( (3, 3) \)
(d) \( (2, -9) \)
(e) \( (0, 2) \)
Çözümü GösterAnalitik düzlemde iki noktaya eşit uzaklıktaki noktaların kümesi, bu iki noktayı birleştiren doğru parçasının orta noktasından geçen ve bu doğru parçasına dik olan doğrudur.
Verilen iki noktanın ordinat değerleri aynı olduğundan bu noktalara eşit uzaklıktaki noktalar kümesini oluşturan doğru dikey bir doğrudur.
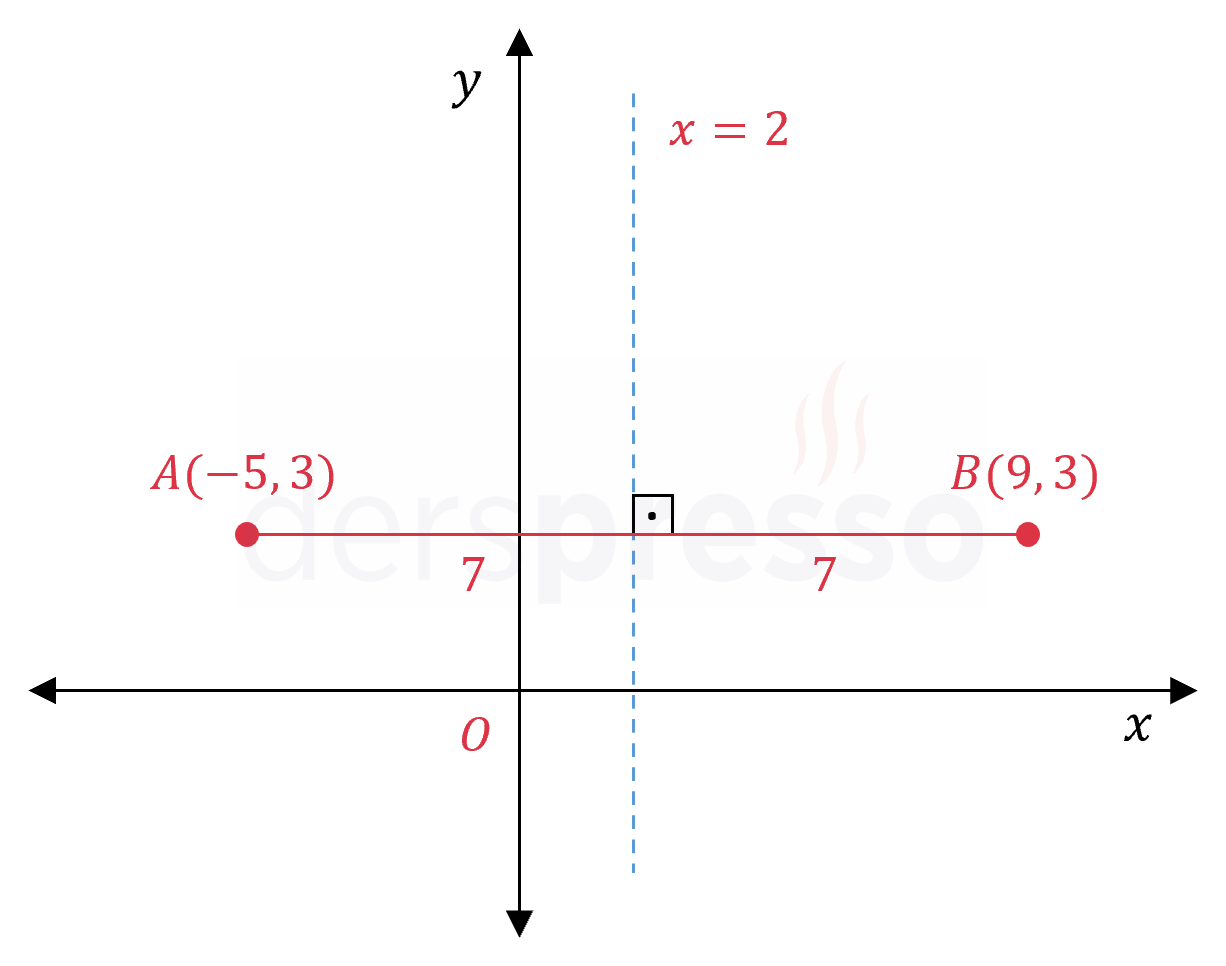
\( A \) ve \( B \) noktalarının orta noktasının apsisini bulalım.
\( x = \dfrac{x_0 + x_1}{2} \)
\( = \dfrac{-5 + 9}{2} = 2 \)
Buna göre \( A \) ve \( B \) noktalarına eşit uzaklıktaki noktalar kümesi \( x = 2 \) doğrusu üzerindeki noktalardır.
\( x = 2 \) doğrusu üzerindeki tek nokta (d) seçeneğindeki \( (2, -9) \) noktasıdır.
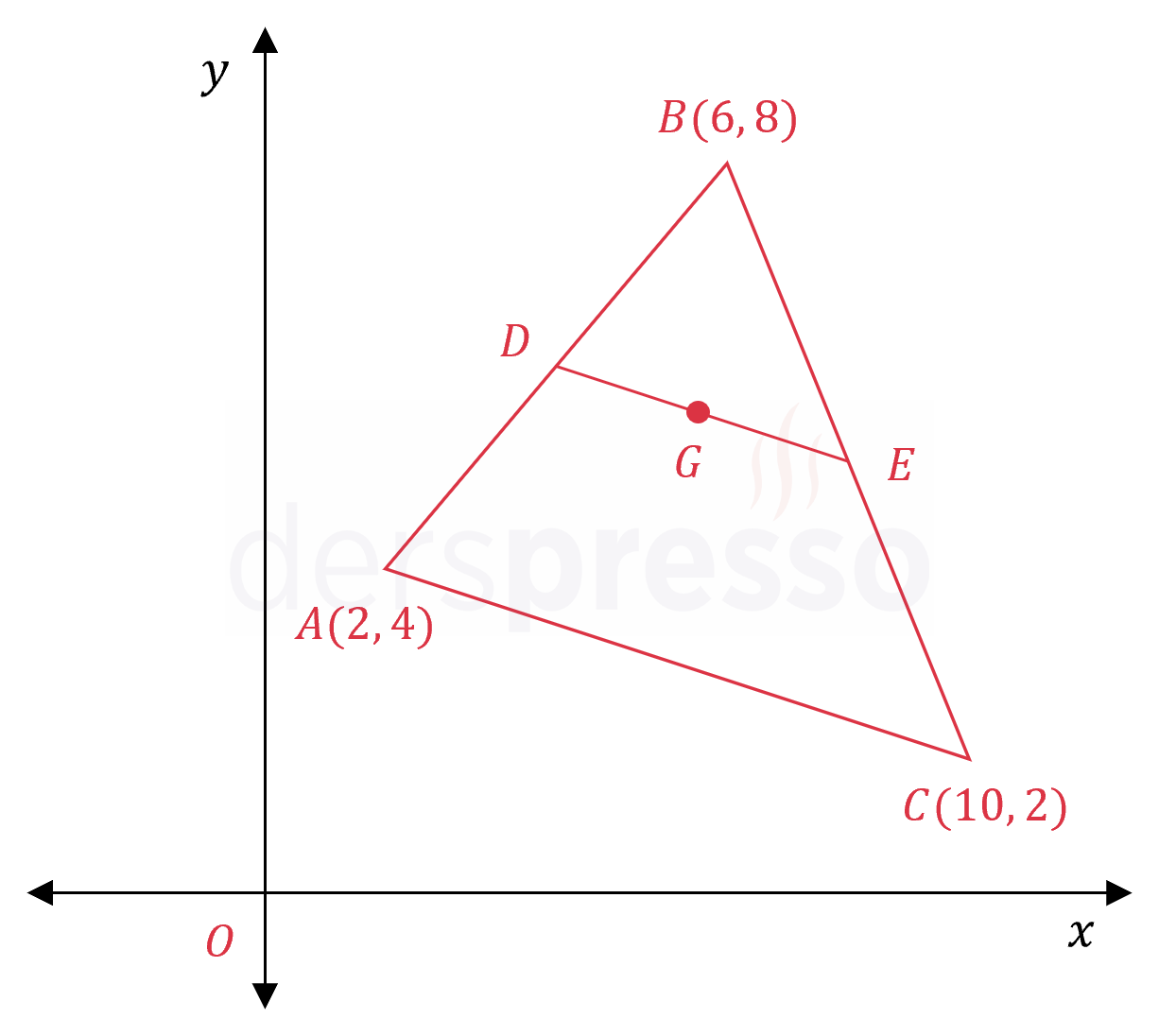
Verilen şekilde \( D, E, G \) noktaları bulundukları kenarların orta noktalarıdır.
Buna göre \( G \) noktasının koordinatları nedir?
Çözümü Göster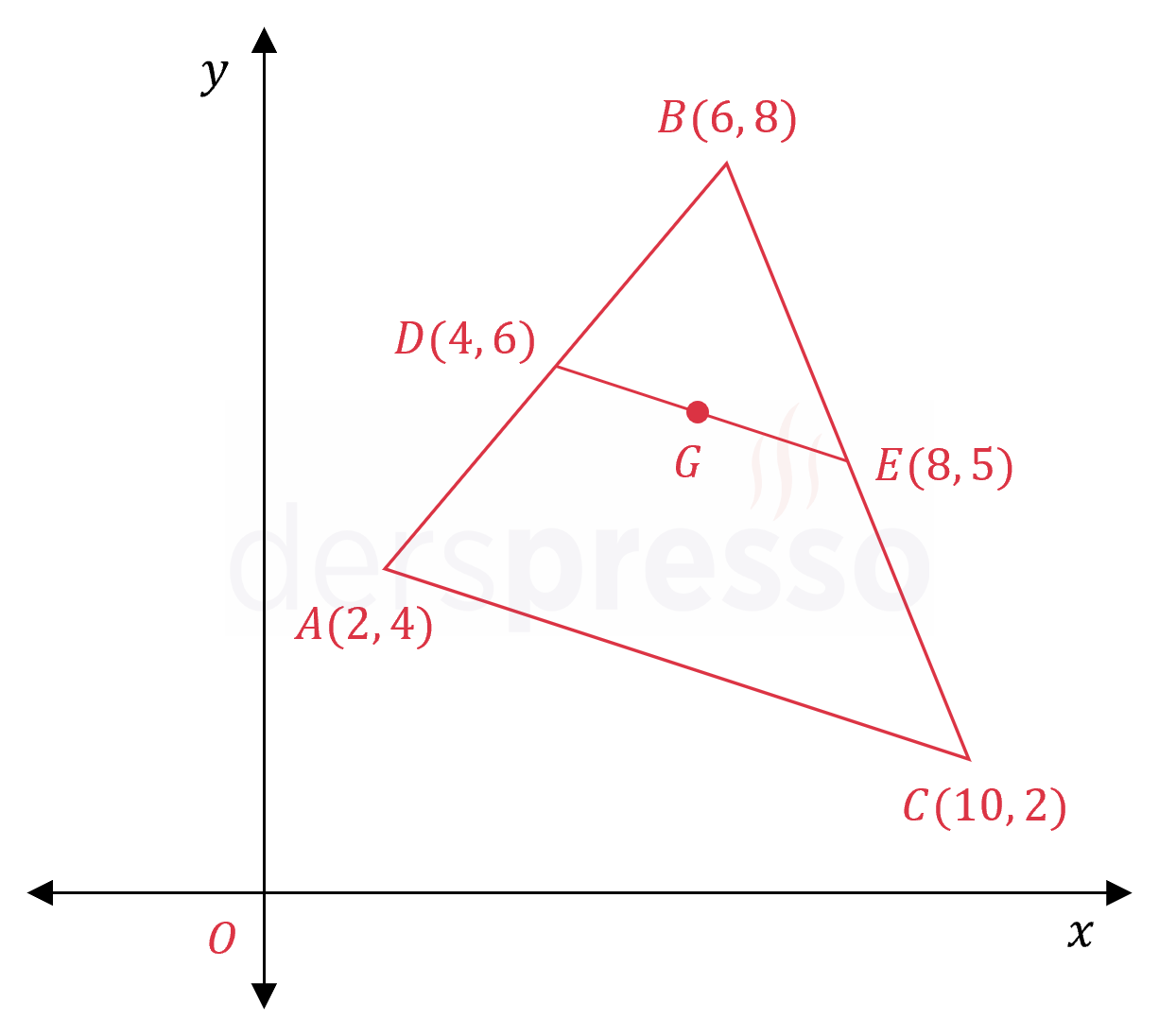
\( D, E, G \) noktaları bulundukları kenarların orta noktaları olduğuna göre, iki noktanın orta noktası formülü ile bu noktaların koordinatlarını bulalım.
\( x_0 = \dfrac{x_1 + x_2}{2} \)
\( y_0 = \dfrac{y_1 + y_2}{2} \)
\( D \) noktası \( [AB] \) kenarının orta noktasıdır.
\( x_0 = \dfrac{2 + 6}{2} = 4 \)
\( y_0 = \dfrac{4 + 8}{2} = 6 \)
\( D(4, 6) \)
\( E \) noktası \( [BC] \) kenarının orta noktasıdır.
\( x_0 = \dfrac{6 + 10}{2} = 8 \)
\( y_0 = \dfrac{8 + 2}{2} = 5 \)
\( E(8, 5) \)
\( G \) noktası \( [DE] \) kenarının orta noktasıdır.
\( x_0 = \dfrac{4 + 8}{2} = 6 \)
\( y_0 = \dfrac{6 + 5}{2} = \dfrac{11}{2} \)
\( G \) noktasının koordinatları \( G(6, \frac{11}{2}) \) olarak bulunur.
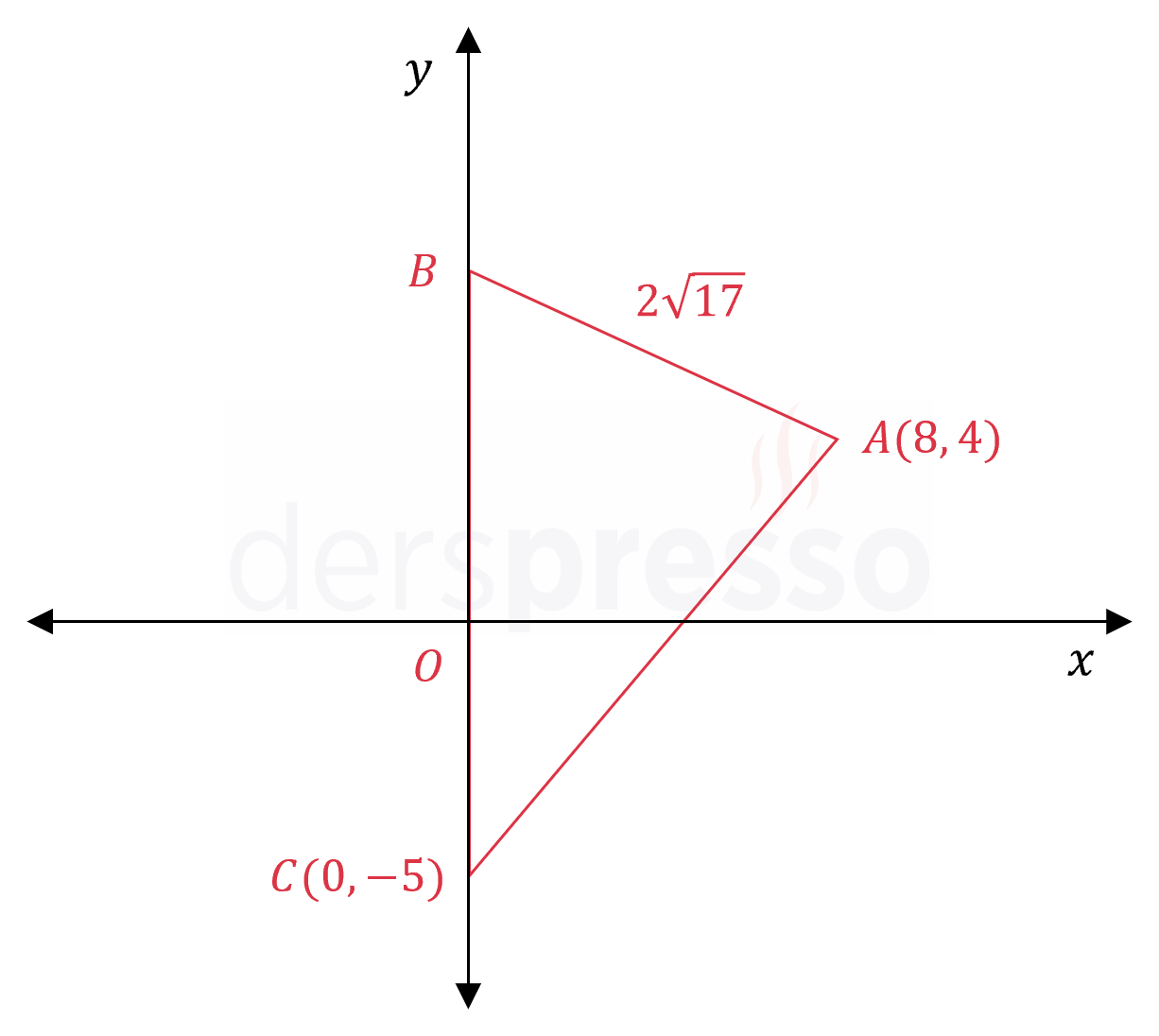
\( A(8, 4) \), \( C(0, -5) \)
\( \abs{AB} = 2\sqrt{17} \)
\( m(\widehat{ABC}) \lt 90° \) olduğuna göre, \( A(ABC) \) kaçtır?
Çözümü Göster\( B \) noktasının koordinatlarına \( B(0, n) \) diyelim.

\( B \) noktasının koordinatlarını \( A-B \) noktaları arasındaki uzaklık formülünü kullanarak bulalım.
\( {\abs{AB}}^2 = (x_2 - x_1)^2 + (y_2 - y_1)^2 \)
\( (2\sqrt{17})^2 = (8 - 0)^2 + (4 - n)^2 \)
\( 68 = 64 + (4 - n)^2 \)
\( (4 - n)^2 = 4 \)
\( 4 - n = 2 \) ya da \( 4 - n = -2 \)
\( 4 - n = 2 \Longrightarrow n = 2 \)
\( 4 - n = -2 \Longrightarrow n = 6 \)
\( m(\widehat{ABC}) \lt 90° \) olduğuna göre, \( A \) noktasının ordinatı \( B \) noktasının ordinatından daha küçük olmalıdır.
\( n \gt 4 \)
Buna göre \( B(0, 6) \) olur.
\( ABC \) üçgeninin alanını bulalım.
\( A \) noktasının \( y \) eksenine olan uzaklığı 8 birimdir.
\( A(ABC) = \dfrac{\abs{BC} \cdot 8}{2} \)
\( = \dfrac{11 \cdot 8}{2} \)
\( = 44 \) bulunur.

Yukarıdaki şekilde \( K, L, M, N, P \) noktaları verilmiştir.
\( L, M, N \) noktaları \( [KP] \) doğru parçasını 4 eşit parçaya böldüğüne göre, \( a + b + c + d + e + f \) kaçtır?
Çözümü Göster\( L, M, N \) noktaları \( [KP] \) doğru parçasını 4 eşit parçaya böldüğüne göre, \( M \) noktası \( [KP] \) doğru parçasının, \( N \) noktası \( [MP] \) doğru parçasının, \( L \) noktası da \( [KM] \) doğru parçasının orta noktasıdır.
\( [MP] \) doğru parçası için orta nokta bulma formülünü kullanarak \( N \) noktasının ordinatını bulalım.
\( y_0 = \dfrac{y_1 + y_2}{2} \)
\( f = \dfrac{2 + 6}{2} = 4 \)
\( N(10, f) = N(10, 4) \)
Aynı doğru parçasını kullanarak \( M \) noktasının apsisini bulalım.
\( x_0 = \dfrac{x_1 + x_2}{2} \)
\( 10 = \dfrac{e + 12}{2} \)
\( e = 8 \)
\( M(e, 2) = M(8, 2) \)
\( M(8, 2) \) noktası \( [LN] \) doğru parçasının da orta noktasıdır.
\( [LN] \) doğru parçası için orta nokta bulma formülü kullanarak \( L \) noktasının koordinatlarını bulalım.
\( 8 = \dfrac{c + 10}{2} \)
\( c = 6 \)
\( 2 = \dfrac{d + 4}{2} \)
\( d = 0 \)
\( L(c, d) = L(6, 0) \)
\( [KP] \) doğru parçası için orta nokta bulma formülü kullanarak \( K \) noktasının koordinatlarını bulalım.
\( e = 8 = \dfrac{a + 12}{2} \)
\( a = 4 \)
\( 2 = \dfrac{b + 6}{2} \)
\( b = -2 \)
\( K(a, b) = K(4, -2) \)
\( a + b + c + d + e + f = 4 + (-2) + 6 + 0 + 8 + 4 \)
\( = 20 \) bulunur.
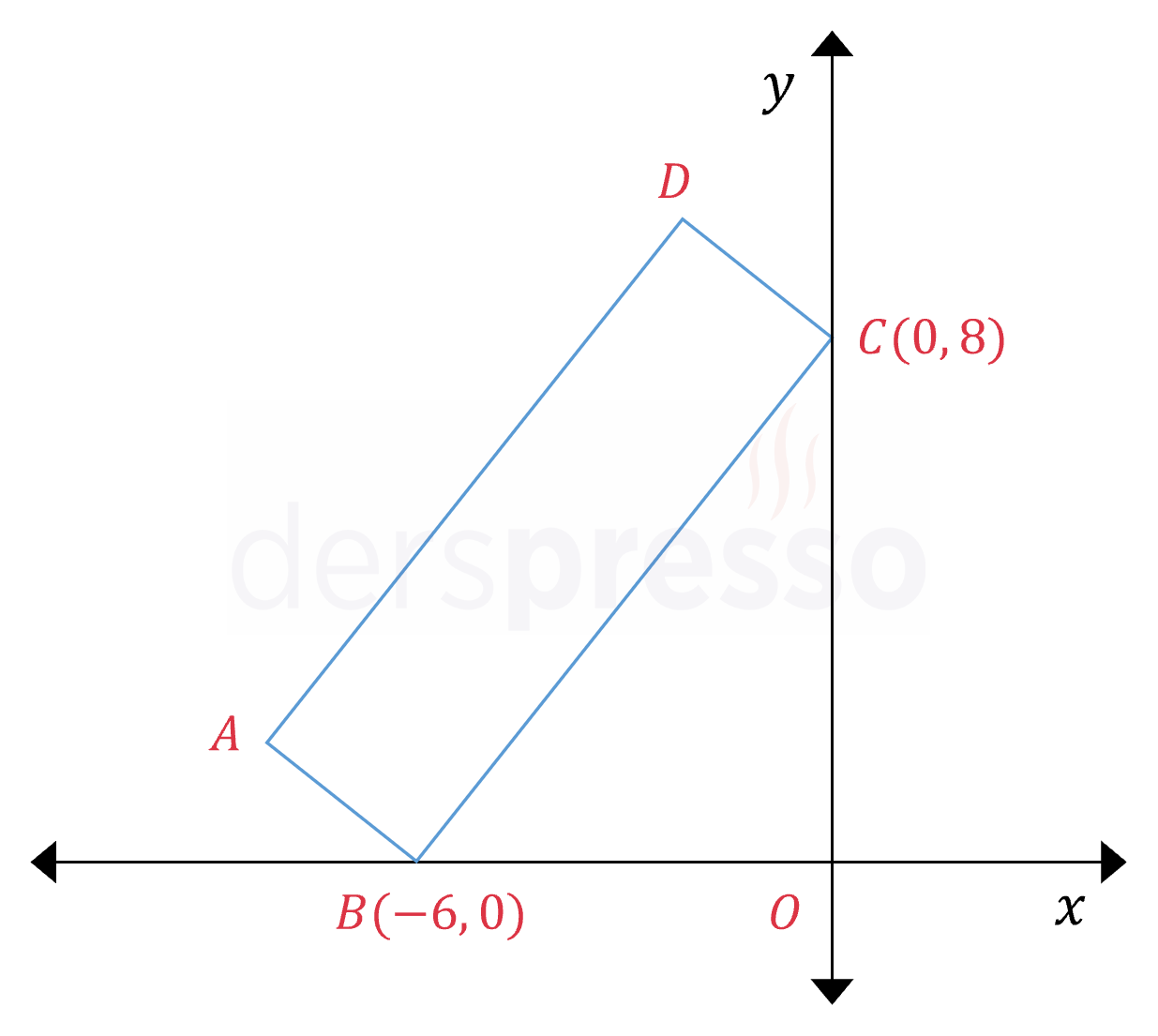
\( ABCD \) dikdörtgeninin çevresi 30 birim olduğuna göre, \( D \) noktasının koordinatları çarpımı kaçtır?
Çözümü GösterAşağıdaki şekildeki gibi \( D \) noktasından \( y \) eksenine bir dikme indirerek \( DEC \) üçgenini oluşturalım.
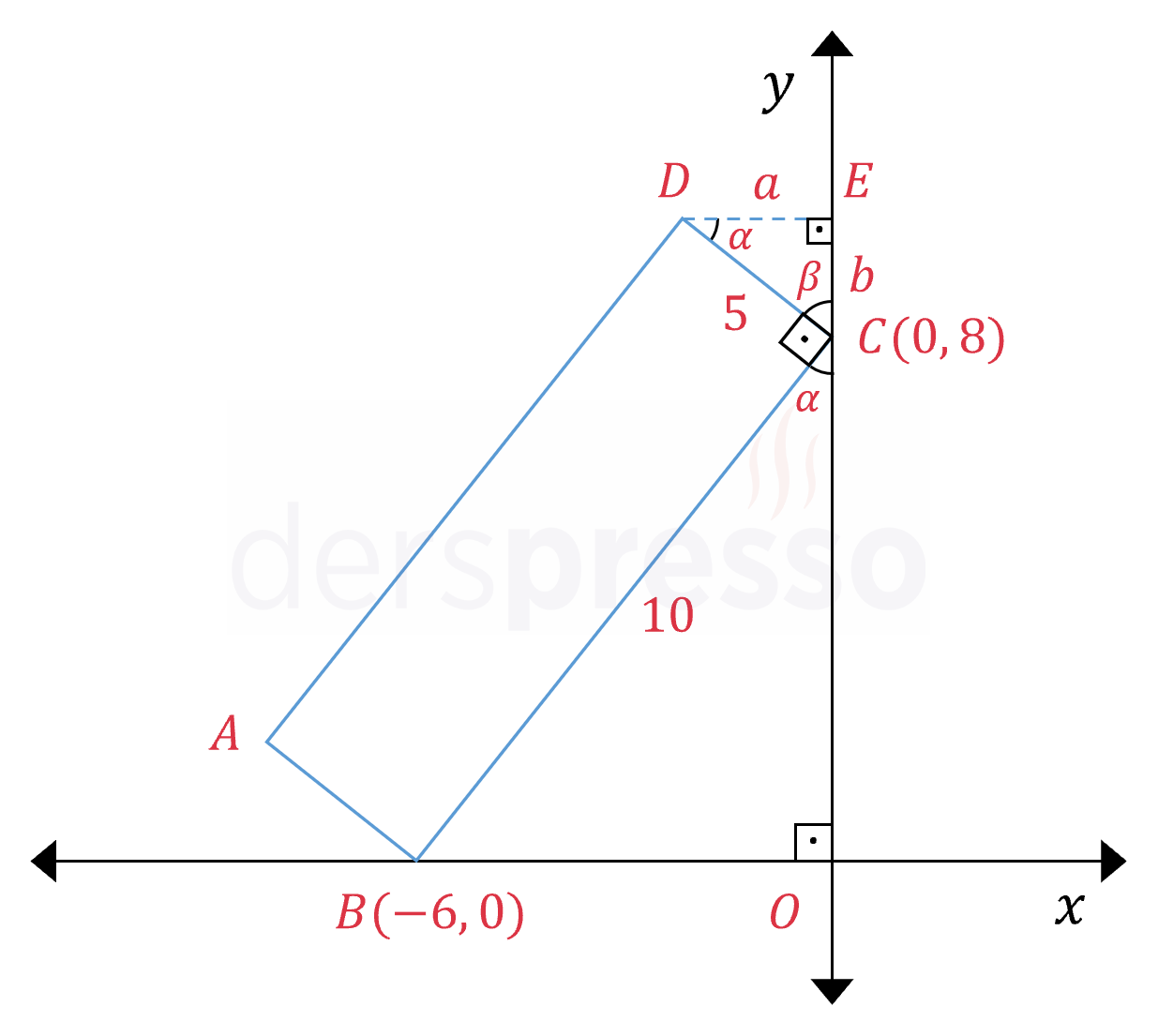
\( m(\widehat{DEC}) = m(\widehat{COB}) = 90° \)
\( m(\widehat{EDC}) = m(\widehat{OCB}) = \alpha \)
Buna göre tüm iç açıları eşit aşağıdaki iki üçgen benzer üçgenlerdir.
\( \overset{\triangle}{DEC} \sim \overset{\triangle}{COB} \)
Pisagor teoremini kullanarak \( \abs{BC} \) uzunluğunu bulalım.
\( \abs{BC} = \sqrt{8^2 + 6^2} = 10 \)
Dikdörtgenin çevresi 30 birimdir.
\( 2(\abs{BC} + \abs{DC}) = 30 \)
\( \abs{DC} = 5 \) br
Benzer üçgenlerde benzer kenarların uzunlukları oranı birbirine eşittir.
\( \dfrac{5}{10} = \dfrac{a}{8} = \dfrac{b}{6} \)
\( a = 4 \) br
\( b = 3 \) br
\( D \) noktasının koordinatları aşağıdaki gibi olur.
\( D(-a, 8 + b) = D(-4, 11) \)
\( D \) noktasının koordinatları çarpımı \( -4 \cdot 11 = -44 \) bulunur.
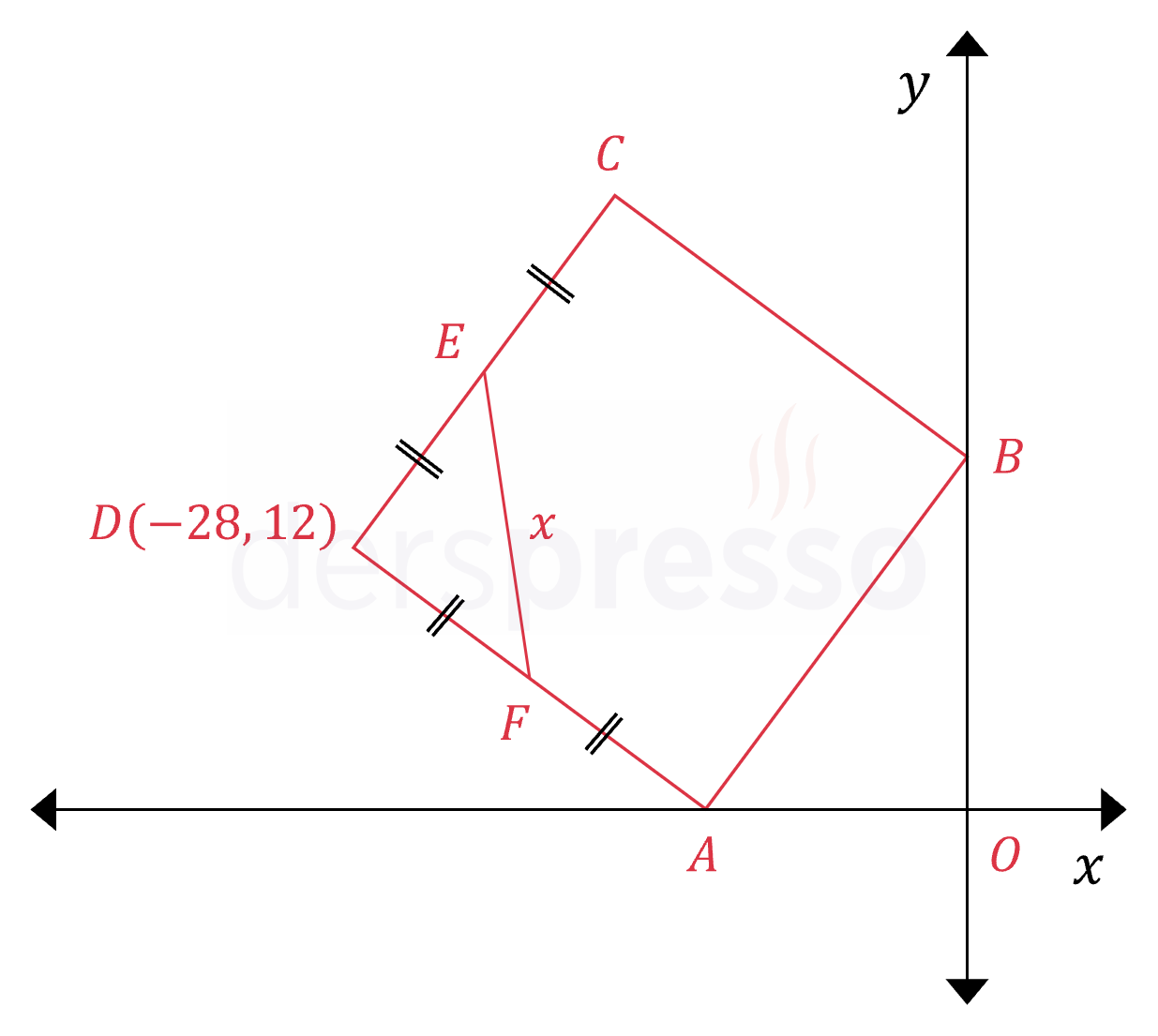
\( ABCD \) bir kare olmak üzere,
\( \abs{DE} = \abs{EC}, \quad \abs{DF} = \abs{FA} \)
\( D(-28, 12) \)
olduğuna göre, \( \abs{EF} = x \) kaç birimdir?
Çözümü GösterAşağıdaki şekildeki gibi \( D \) noktasından \( x \) eksenine bir dikme indirerek \( DGA \) üçgenini oluşturalım.
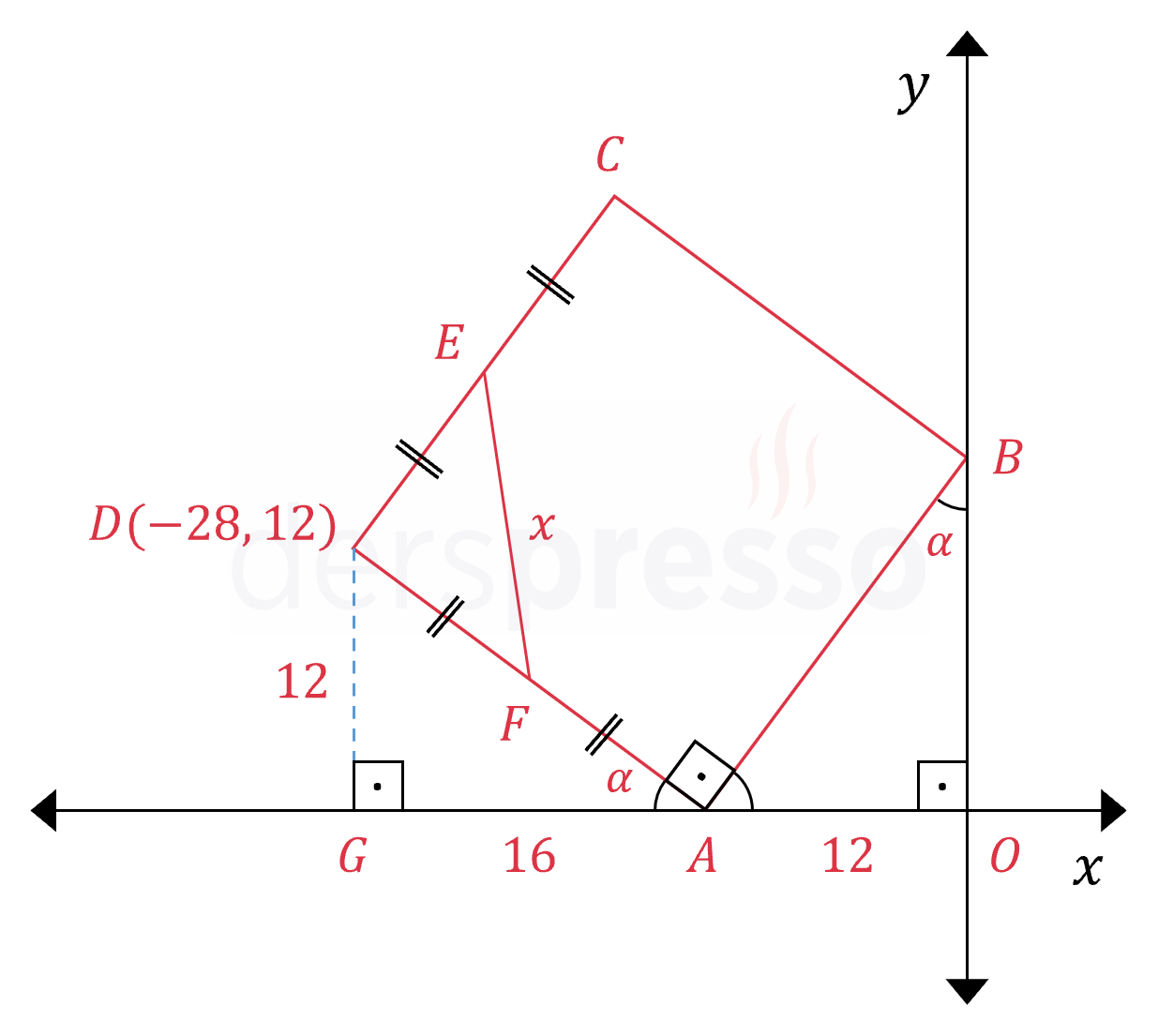
\( m(\widehat{DGA}) = m(\widehat{AOB}) = 90° \)
\( m(\widehat{GAD}) = m(\widehat{OBA}) = \alpha \)
\( ABCD \) bir karedir.
\( \abs{DA} = \abs{AB} \)
Buna göre tüm iç açıları ve birer benzer kenar uzunluğu eşit aşağıdaki iki üçgen eş üçgenlerdir.
\( \overset{\triangle}{DGA} \cong \overset{\triangle}{AOB} \)
Eş üçgenlerin birbirine karşılık gelen kenarlarının uzunlukları birbirine eşittir.
\( \abs{AO} = \abs{DG} = 12 \)
\( \abs{GA} = \abs{GO} - \abs{AO} \)
\( = 28 - 12 = 16 \)
Pisagor teoremini kullanarak \( \abs{DA} \) uzunluğunu bulalım.
\( \abs{DA} = \sqrt{12^2 + 16^2} = 20 \)
\( \abs{DF} = \dfrac{\abs{DA}}{2} = 10 \)
Pisagor teoremini kullanarak \( \abs{EF} \) uzunluğunu bulalım.
\( \abs{EF} = \sqrt{10^2 + 10^2} = 10\sqrt{2} \) bulunur.
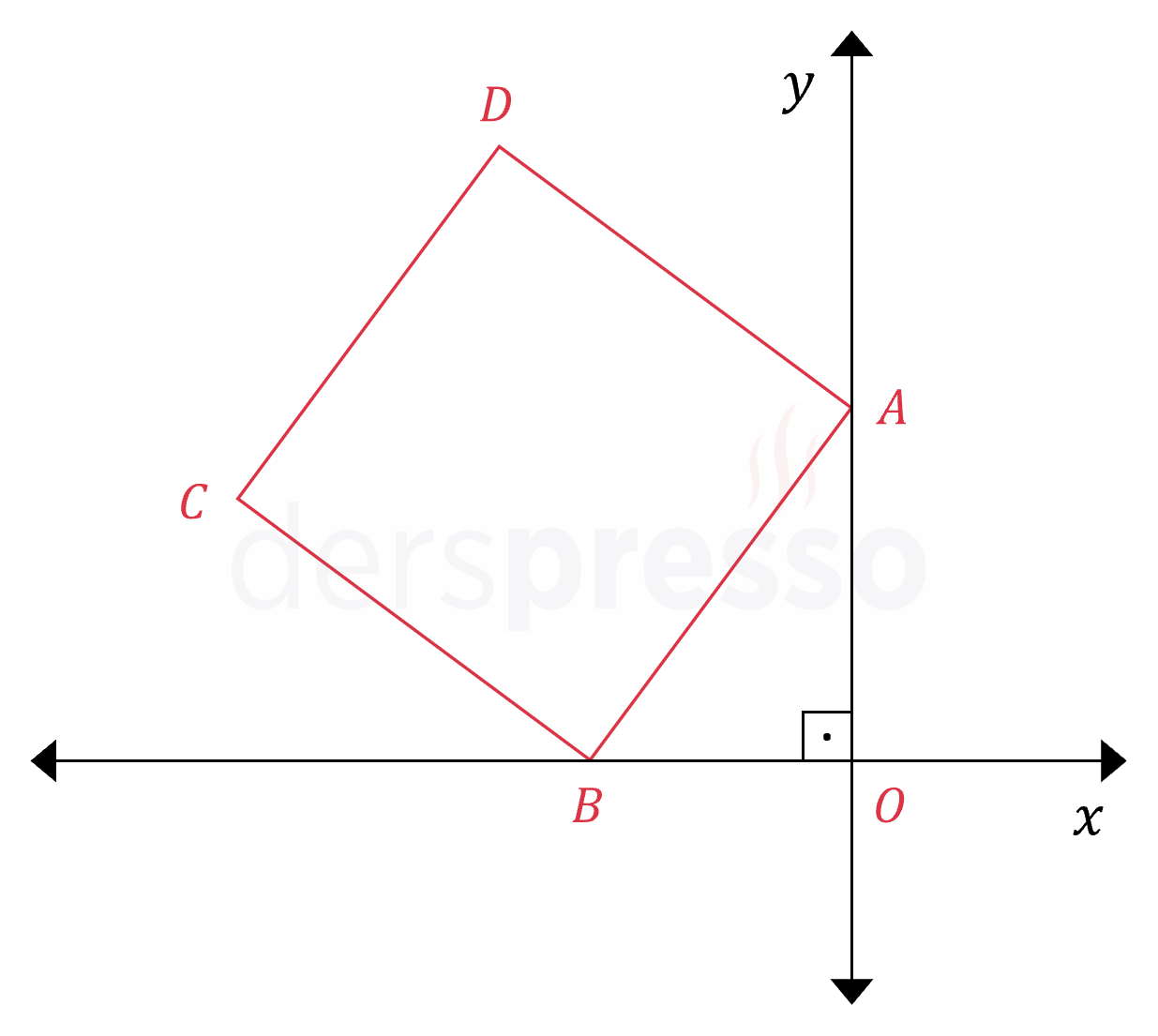
\( ABCD \) bir kare olduğuna göre, \( C \) noktasının koordinatları toplamı kaçtır?
Çözümü GösterAşağıdaki şekildeki gibi \( C \) noktasından \( x \) eksenine bir dikme çizerek \( CEB \) üçgenini oluşturalım.
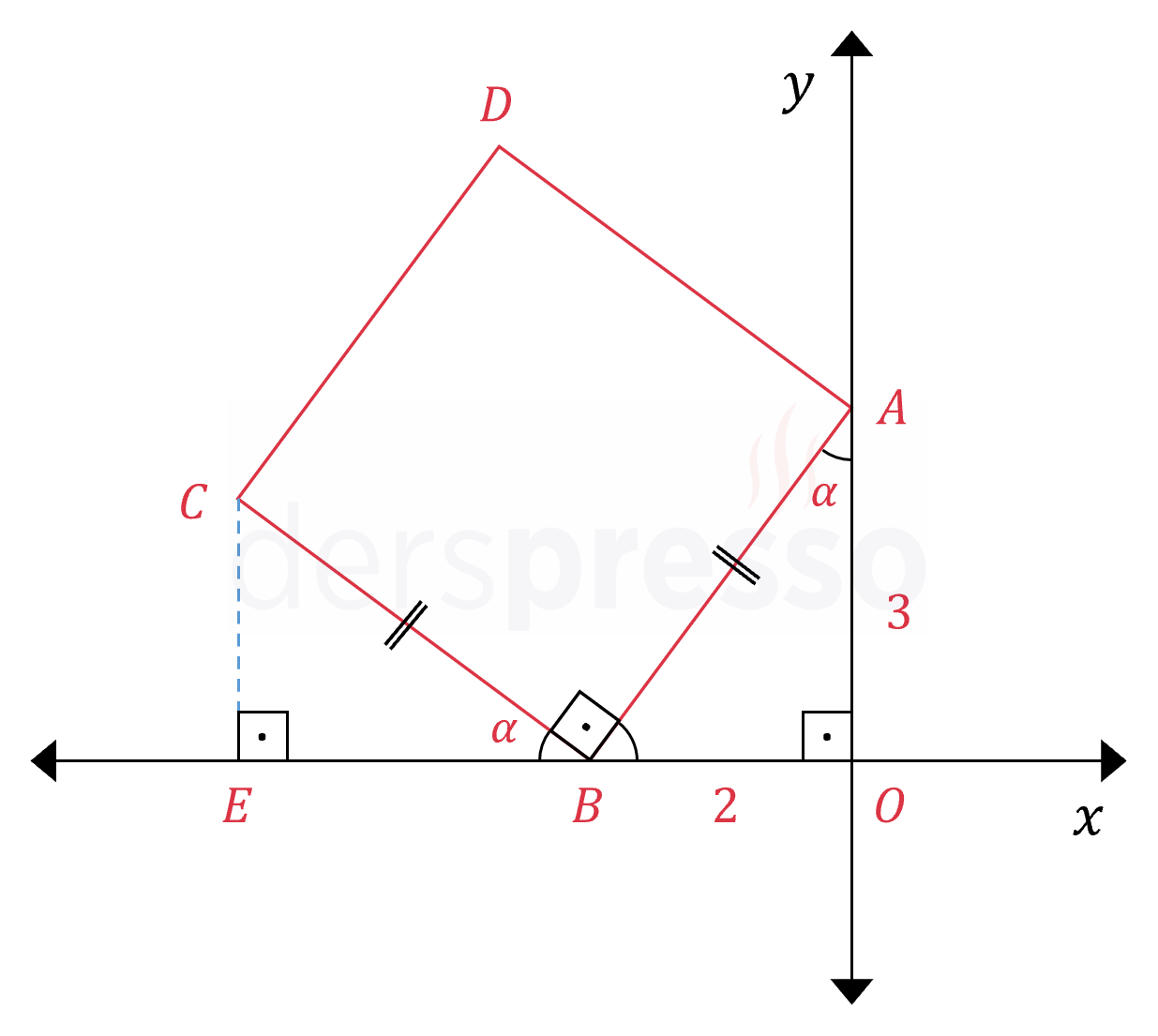
\( m(\widehat{CEB}) = m(\widehat{BOA}) = 90° \)
\( m(\widehat{EBC}) = m(\widehat{OAB}) = \alpha \)
\( ABCD \) bir karedir.
\( \abs{CB} = \abs{BA} \)
Buna göre tüm iç açıları ve birer benzer kenar uzunluğu eşit aşağıdaki iki üçgen eş üçgenlerdir.
\( \overset{\triangle}{CEB} \cong \overset{\triangle}{BOA} \)
Eş üçgenlerin birbirine karşılık gelen kenarlarının uzunlukları birbirine eşittir.
\( \abs{CE} = \abs{BO} = 2 \)
\( \abs{EB} = \abs{OA} = 3 \)
\( C \) noktasının koordinatları aşağıdaki gibi olur.
\( C(-(3 + 2), 2) = C(-5, 2) \)
Buna göre \( C \) noktasının koordinatları toplamı \( -5 + 2 = -3 \) olarak bulunur.
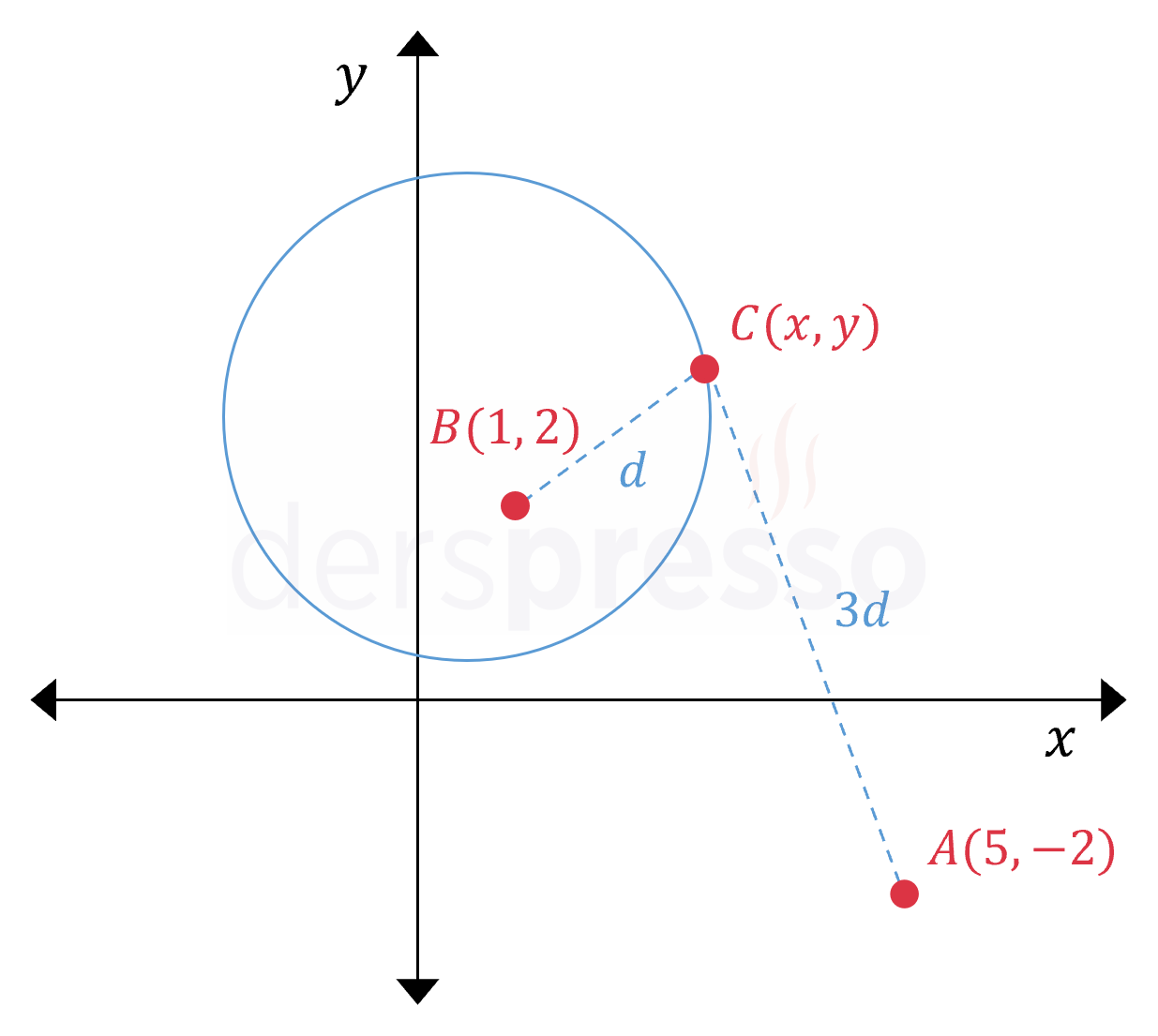
\( A(5, -2) \) noktasına olan uzaklığı \( B(1, 2) \) noktasına olan uzaklığının 3 katı olan noktaların geometrik yer denklemi nedir?
Çözümü GösterBelirtilen koşulu sağlayan noktalar kümesine \( C(x, y) \) diyelim.
\( C \) noktasının \( A \) noktasına olan uzaklığı \( B \) noktasına olan uzaklığının 3 katıdır.
\( \abs{CA} = 3\abs{CB} \)
\( \sqrt{(x - 5)^2 + (y - (-2))^2} = 3\sqrt{(x - 1)^2 + (y - 2)^2} \)
\( \sqrt{(x - 5)^2 + (y + 2)^2} = 3\sqrt{(x - 1)^2 + (y - 2)^2} \)
İki tarafın karesini alalım.
\( x^2 - 10x + 25 + y^2 + 4y + 4 = 9(x^2 - 2x + 1 + y^2 - 4y + 4) \)
\( x^2 - 10x + 25 + y^2 + 4y + 4 = 9x^2 - 18x + 9 + 9y^2 - 36y + 36 \)
\( 8x^2 - 8x + 8y^2 - 40y + 16 = 0 \)
Verilen koşulu sağlayan noktalar kümesi aşağıdaki denklemle ifade edilir.
\( x^2 - x + y^2 - 5y + 2 = 0 \)
Çemberin analitiği bölümünde göreceğimiz üzere, bu denklem aşağıdaki şekildeki gibi bir çember ifade eder.
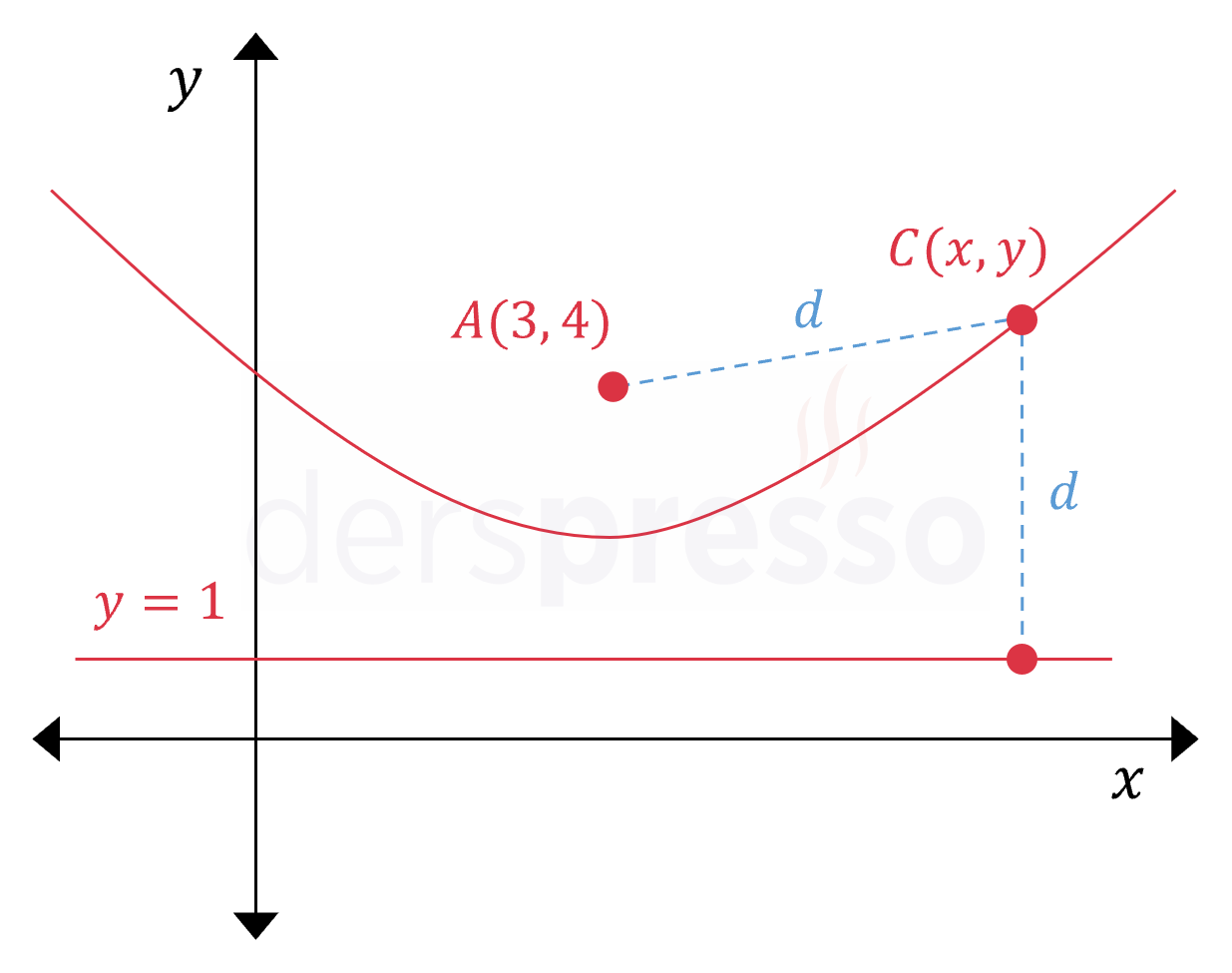
\( A(3, 4) \) noktasına ve \( y = 1 \) doğrusuna olan uzaklıkları eşit olan noktaların geometrik yeri denklemi nedir?
Çözümü GösterBelirtilen koşulu sağlayan noktalar kümesine \( C(x, y) \) diyelim.
\( C \) noktasının \( A \) noktasına ve doğruya uzaklığına \( d \) diyelim. \( d \) değerini hem \( A \) noktası hem de doğru için ayrı ayrı hesaplayalım.
\( C \) noktasının \( A \) noktasına uzaklığını bulalım.
\( d = \sqrt{(x - 3)^2 + (y - 4)^2} \)
\( y = 1 \) yatay bir doğru olduğu için \( C \) noktasının doğruya uzaklığı ordinat değerleri arasındaki farka eşittir.
\( d = \abs{y - 1} \)
İki uzaklık değeri birbirine eşittir.
\( \sqrt{(x - 3)^2 + (y - 4)^2} = \abs{y - 1} \)
İki tarafın karesini alalım.
\( (x - 3)^2 + (y - 4)^2 = (y - 1)^2 \)
\( x^2 - 6x + 9 + y^2 - 8y + 16 = y^2 - 2y + 1 \)
\( x^2 - 6x + 24 = 6y \)
Verilen koşulu sağlayan noktalar kümesi aşağıdaki denklemle ifade edilir.
\( y = \dfrac{1}{6}x^2 - x + 4 \)
Elde ettiğimiz denklem bir parabol denklemidir. Parabol bölümünde göreceğimiz üzere, parabol aynı zamanda bir nokta ve doğruya eşit uzaklıktaki noktalar kümesidir.

Şekildeki \( ABC \) üçgeninde \( D, E, F \) noktaları bulundukları kenarların orta noktalarıdır.
Buna göre \( B \) noktasının koordinatları nedir?
Çözümü Göster\( B \) noktasının koordinatlarına \( B(a, b) \) diyelim.
Orta noktaları kullanarak \( [AB] \) ve \( [BC] \) kenarlarına paralel olacak şekilde orta tabanları çizelim.

\( [EF] \parallel [AB] \)
\( [DE] \parallel [BC] \)
Çizilen doğrular \( DEFB \) parelelkenarını oluşturur.
Bir paralelkenarda karşılıklı köşelerin koordinatları toplamları birbirine eşittir.
Köşe noktalarını kullanarak \( B \) noktasının koordinatlarını bulalım.
\( B \) noktasının apsisini bulalım.
\( a + (-2) = -4 + (-3) \)
\( a = -5 \)
\( B \) noktasının ordinatını bulalım.
\( b + 6 = 5 + 2 \)
\( b = 1 \)
\( B(a, b) = B(-5, 1) \) bulunur.
\( A(3, 5), B(6, -1), C(2, -3), D(-1, 3) \) noktaları veriliyor.
Bu noktaların oluşturduğu \( ABCD \) dörtgeninin tipini bulunuz (kare, dikdörtgen, paralelkenar, eşkenar dörtgen vb).
Çözümü GösterDörtgenin köşe noktaları arasındaki uzaklıkları bulalım.
\( \abs{AB} = \sqrt{(6 - 3)^2 + (-1 - 5)^2} \)
\( = \sqrt{3^2 + (-6)^2} = \sqrt{45} \)
\( \abs{BC} = \sqrt{(2 - 6)^2 + (-3 - (-1))^2} \)
\( = \sqrt{(-4)^2 + (-2)^2} = \sqrt{20} \)
\( \abs{CD} = \sqrt{(-1 - 2)^2 + (3 - (-3))^2} \)
\( = \sqrt{(-3)^2 + 6^2} = \sqrt{45} \)
\( \abs{DA} = \sqrt{(3 - (-1))^2 + (5 - 3)^2} \)
\( = \sqrt{4^2 + 2^2} = \sqrt{20} \)
Dörtgenin karşılıklı kenar uzunlukları birbirine eşittir, ancak tüm kenar uzunlukları eşit olmadığı için şekil kare ya da eşkenar dörtgen olamaz.
Dörtgenin paralelkenar mı dikdörtgen mi olduğunu anlamak için köşegen uzunluklarını karşılaştıralım.
\( \abs{AC} = \sqrt{(2 - 3)^2 + (-3 - 5)^2} \)
\( = \sqrt{(-1)^2 + (-8)^2} = \sqrt{65} \)
\( \abs{BD} = \sqrt{(-1 - 6)^2 + (3 - (-1))^2} \)
\( = \sqrt{(-7)^2 + 4^2} = \sqrt{65} \)
Dörtgenin köşegen uzunlukları eşit olduğu için şekil bir dikdörtgendir (paralelkenarın köşegen uzunlukları birbirinden farklıdır).
\( A(-1, 4), B(-3, -1), C(3, -3) \) noktaları veriliyor.
Bu noktaların oluşturduğu \( ABC \) üçgeninin iç açıları cinsinden tipini bulunuz (dar, dik, geniş açılı vb).
Çözümü GösterÜçgenin köşe noktaları arasındaki uzaklıkları bulalım.
\( \abs{AB} = \sqrt{(-3 - (-1))^2 + (-1 - 4)^2} \)
\( = \sqrt{(-2)^2 + (-5)^2} = \sqrt{29} \)
\( \abs{BC} = \sqrt{(3 - (-3))^2 + (-3 - (-1))^2} \)
\( = \sqrt{6^2 + (-2)^2} = \sqrt{40} \)
\( \abs{CA} = \sqrt{(-1 - 3)^2 + (4 - (-3))^2} \)
\( = \sqrt{(-4)^2 + 7^2} = \sqrt{65} \)
Üçgenin uzun kenarının karesi ile diğer iki kenar uzunluklarının kareleri toplamını karşılaştıralım.
\( (\abs{CA})^2 \overset{?}{=} (\abs{AB})^2 + (\abs{BC})^2 \)
\( (\sqrt{65})^2 \overset{?}{=} (\sqrt{29})^2 + (\sqrt{40})^2 \)
\( 65 \overset{?}{=} 29 + 40 \)
\( 65 \lt 69 \)
Eşitlik sağlansaydı Pisagor teoreminden üçgenin bir dik üçgen olduğu sonucuna varabilirdik. Uzun kenarın karesi diğer iki kenar uzunluklarının kareleri toplamından küçük olduğu için uzun kenarı gören açı 90°'den küçük olmalıdır, dolayısıyla üçgen dar açılı bir üçgendir.
\( x \) ekseni \( (4, -3) \) ve \( (7, 6) \) noktalarını birleştiren doğru parçasını hangi oranda böler?
Çözümü Göster\( (4, -3) \) noktasına \( A \), \( (7, 6) \) noktasına \( B \) diyelim.
\( x \) ekseninin \( [AB] \) doğru parçasını böldüğü orana \( k \) diyelim.
\( A \) noktası IV. bölgede, \( B \) noktası I. bölgede olduğu için \( x \) ekseni \( [AB] \) doğru parçasını içten böler.
\( A(x_1, y_1) \) ve \( B(x_2, y_2) \) noktalarını birleştiren doğru parçasını \( k \) oranda içten bölen \( C(x_0, y_0) \) noktasının koordinatları aşağıdaki formülle bulunur.
\( x_0 = \dfrac{x_1 + kx_2}{1 + k} \)
\( y_0 = \dfrac{y_1 + ky_2}{1 + k} \)
\( [AB] \) doğru parçasının \( x \) eksenini kestiği noktaya \( C \) diyelim. \( C \) noktası \( x \) ekseni üzerinde olduğu için ordinatı sıfırdır.
\( C(x_0, 0) \)
\( y_0 = \dfrac{-3 + 6k}{1 + k} = 0 \)
\( 0 = -3 + 6m \)
\( m = \dfrac{1}{2} \)
Buna göre \( x \) ekseni verilen iki noktayı birleştiren doğru parçasını \( \frac{1}{2} \) oranında içten böler.
\( d: 2x + 3y - 12 = 0 \) doğrusu \( (2, -1) \) ve \( (4, 3) \) noktalarını birleştiren doğru parçasını hangi oranda böler?
Çözümü Göster\( (2, -1) \) noktasına \( A \), \( (4, 3) \) noktasına \( B \) diyelim.
\( d \) doğrusunun \( [AB] \) doğru parçasını böldüğü noktaya \( C \), böldüğü orana \( m \) diyelim.
\( A(x_1, y_1) \) ve \( B(x_2, y_2) \) noktalarını birleştiren doğru parçasını \( k \) oranda içten bölen \( C(x_0, y_0) \) noktasının koordinatları aşağıdaki formülle bulunur.
\( x_0 = \dfrac{x_1 + kx_2}{1 + k} \)
\( y_0 = \dfrac{y_1 + ky_2}{1 + k} \)
\( d \) doğrusu üzerindeki \( C \) noktasının koordinatlarını bulalım.
\( x_0 = \dfrac{2 + 4m}{1 + m} \)
\( y_0 = \dfrac{-1 + 3m}{1 + m} \)
\( C(\dfrac{2 + 4m}{1 + m}, \dfrac{-1 + 3m}{1 + m}) \)
\( C \) noktası \( d \) doğrusu üzerinde olduğuna göre koordinatları doğru denklemini sağlar.
\( 2(\dfrac{2 + 4m}{1 + m}) + 3(\dfrac{-1 + 3m}{1 + m}) - 12 = 0 \)
\( \dfrac{4 + 8m - 3 + 9m}{1 + m} = 12 \)
\( 17m + 1 = 12 + 12m \)
\( m = \dfrac{11}{5} \)
Buna göre \( d \) doğrusu \( [AB] \) doğru parçasını \( \frac{11}{5} \) oranında içten böler.

\( ABCD \) bir paralelkenardır.
\( \dfrac{\abs{DE}}{\abs{CE}} = \dfrac{5}{2} \) olduğuna göre, \( F \) noktasının koordinatları nedir?
Çözümü Göster
Köşelerinin koordinatları \( A(x_1, y_1) \), \( B(x_2, y_2) \), \( C(x_3, y_3) \) ve \( D(x_4,y_4) \) olan bir paralelkenarının köşe koordinatları arasında aşağıdaki ilişki vardır.
\( x_1 + x_3 = x_2 + x_4 \)
\( y_1 + y_3 = y_2 + y_4 \)
\( D \) noktasının apsisini bulalım.
\( 6 + 8 = 13 + x_4 \)
\( x_4 = 1 \)
\( D \) noktasının ordinatını bulalım.
\( 18 + 10 = 20 + y_4 \)
\( y_4 = 8 \)
\( D(x_4, y_4) = (1, 8) \)
\( \dfrac{\abs{DE}}{\abs{CE}} = \dfrac{5}{2} \) oranı için doğru uzunluklarını yazalım.
\( \abs{DE} = 5k \) ve \( \abs{CE} = 2k \) diyelim.
Paralelkenarda karşılıklı kenar uzunlukları eşittir.
\( \abs{AB} = \abs{CD} = 7k \)
\( ABF \) ve \( EDF \) üçgenleri paralellikten dolayı benzer üçgenlerdir.
\( \overset{\triangle}{ABF} \sim \overset{\triangle}{EDF} \)
Benzer üçgenlerin kenar uzunlukları arasında orantı kuralım.
\( \dfrac{\abs{AB}}{\abs{BF}} = \dfrac{\abs{ED}}{\abs{DF}} \)
\( \dfrac{7k}{\abs{BF}} = \dfrac{5k}{\abs{DF}} \)
\( \abs{BF} = 7m \) ve \( \abs{DF} = 5m \) diyelim.
\( A(x_1, y_1) \) ve \( B(x_2, y_2) \) noktalarını birleştiren doğru parçasını \( k \) oranında içten bölen \( C(x_0, y_0) \) noktasının koordinatları aşağıdaki formülle bulunur.
\( x_0 = \dfrac{x_1 + kx_2}{1 + k} \)
\( y_0 = \dfrac{y_1 + ky_2}{1 + k} \)
Bu formülleri \( D \) ve \( B \) noktalarını \( \frac{5}{7} \) oranında bölen \( F \) noktasına uygulayalım.
\( x_0 = \dfrac{1 + \frac{5}{7} \cdot 13}{1 + \frac{5}{7}} \)
\( = \dfrac{\frac{72}{7}}{\frac{12}{7}} = 6 \)
\( y_0 = \dfrac{8 + \frac{5}{7} \cdot 20}{1 + \frac{5}{7}} \)
\( = \dfrac{\frac{156}{7}}{\frac{12}{7}} = 13 \)
\( F(6, 13) \) olarak bulunur.