İkinci Dereceden Eşitsizlikler
Tüm terimleri aynı tarafta toplandığında \( ax^2 + bx + c \) formunda yazılabilen eşitsizliklere ikinci dereceden eşitsizlik denir. Diğer eşitsizliklerde olduğu gibi ikinci dereceden eşitsizliklerde de \( \lt \), \( \le \), \( \gt \), \( \ge \) sembollerinden herhangi biri kullanılabilir.
\( a \ne 0 \) olmak üzere,
\( ax^2 + bx + c \lt 0 \)
\( x^2 - 5x + 6 \le 0 \)
\( 2x^2 \ge 5x + 12 \)
\( 3x^2 \lt x \)
İkinci dereceden eşitsizliklerin çözüm kümesi grafik yorumu ile ve işaret tablosu yardımıyla olmak üzere iki yöntemle bulunabilir. Her iki yöntemde de önce tüm terimleri eşitsizliğin sol tarafında toplamamız ve sağ tarafında 0 bırakmamız gerekir.
Grafik Yorumu ile Çözüm
İkinci dereceden bir ifadenin işareti başkatsayısının pozitif/negatif ve deltasının pozitif/negatif/sıfır olmasına göre 6 farklı şekilde olabilir.
| Grafik | İfadenin İşareti |
|---|---|
|
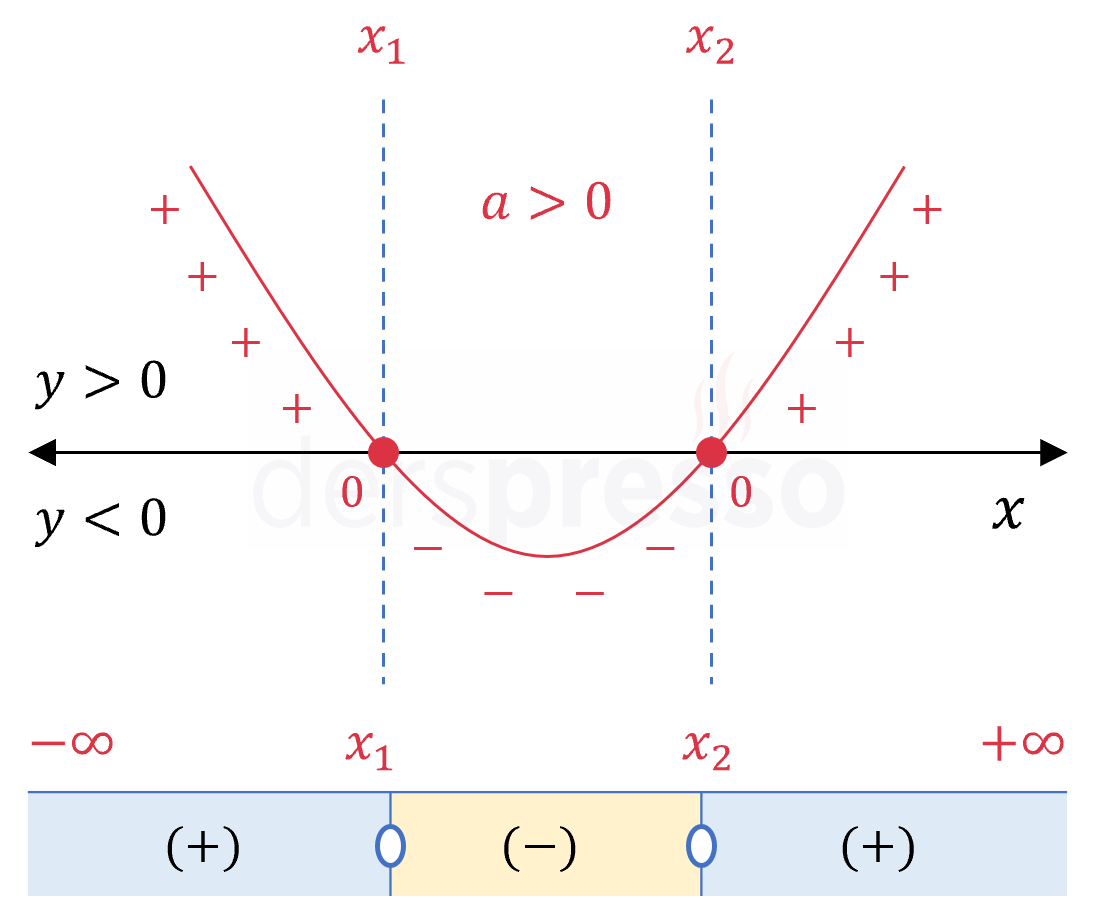
Başkatsayı ve delta pozitif: \( a \gt 0, \quad \Delta \gt 0 \) İfade kökler arasındaki aralıkta negatif, kökler dışındaki aralıkta pozitif, kök değerlerinde sıfır olur. Örnek: \( (x - 2)(x - 5) \lesseqgtr 0 \) \( x = 4 \Longrightarrow (4 - 2)(4 - 5) = -2 \lt 0 \) \( x = 5 \Longrightarrow (5 - 2)(5 - 5) = 0 \) \( x = 6 \Longrightarrow (6 - 2)(6 - 5) = 4 \gt 0 \) |
|
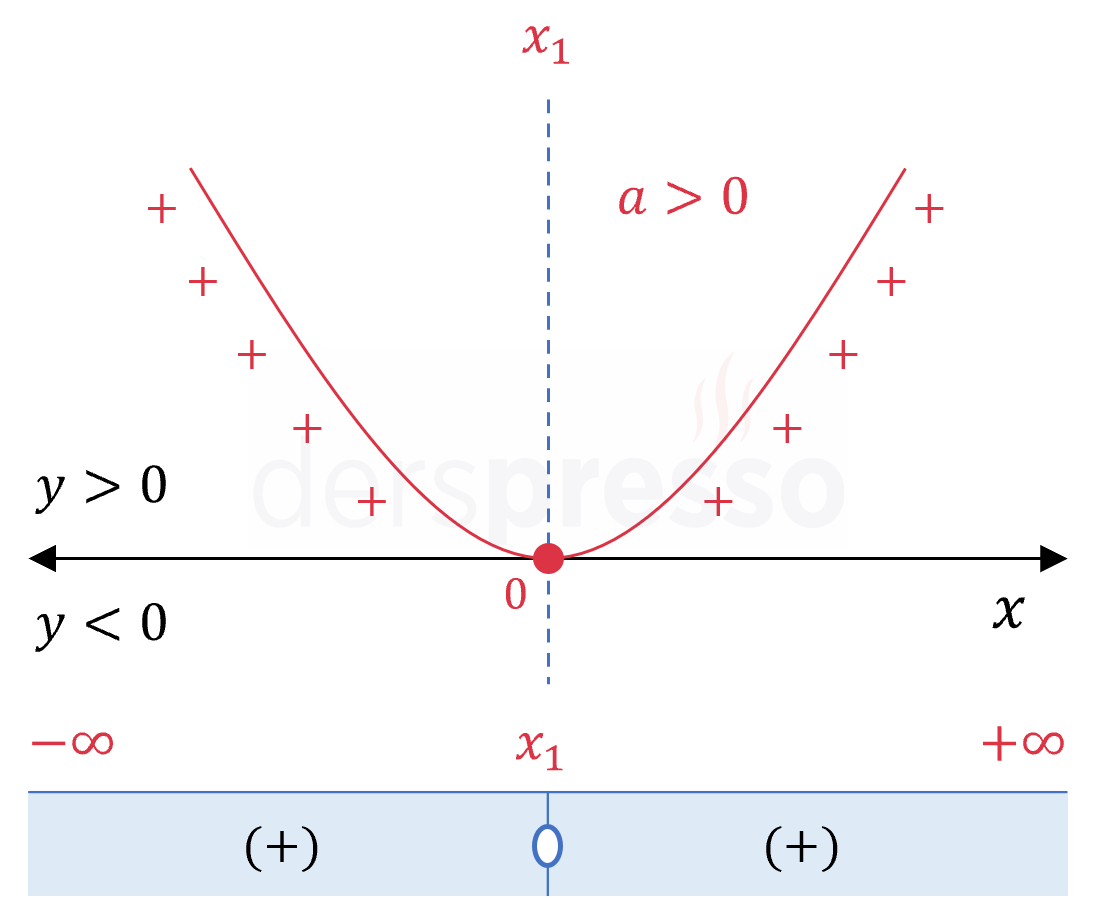
Başkatsayı pozitif, delta sıfır: \( a \gt 0, \quad \Delta = 0 \) İfade kök değerinde sıfır, diğer tüm değerlerde pozitif olur. Örnek: \( (x - 5)^2 \lesseqgtr 0\) \( x = 4 \Longrightarrow (4 - 5)^2 = 1 \gt 0 \) \( x = 5 \Longrightarrow (5 - 5)^2 = 0 \) \( x = 6 \Longrightarrow (6 - 5)^2 = 1 \gt 0 \) |
|
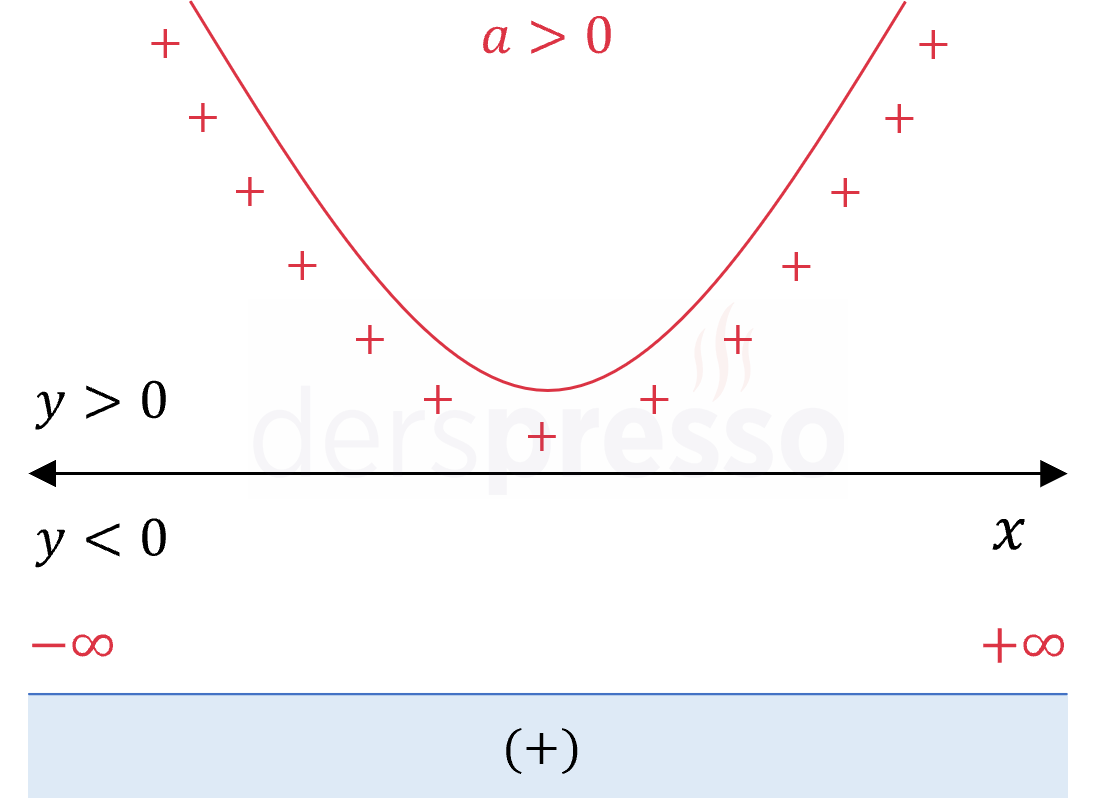
Başkatsayı pozitif, delta negatif: \( a \gt 0, \quad \Delta \lt 0 \) İfade tüm reel sayılarda pozitif olur. Örnek: \( x^2 - 2x + 2 \lesseqgtr 0\) \( x = 0 \Longrightarrow 0^2 - 2(0) + 2 = 2 \gt 0 \) \( x = 1 \Longrightarrow 1^2 - 2(1) + 2 = 1 \gt 0 \) \( x = 2 \Longrightarrow 2^2 - 2(2) + 2 = 2 \gt 0 \) |
|
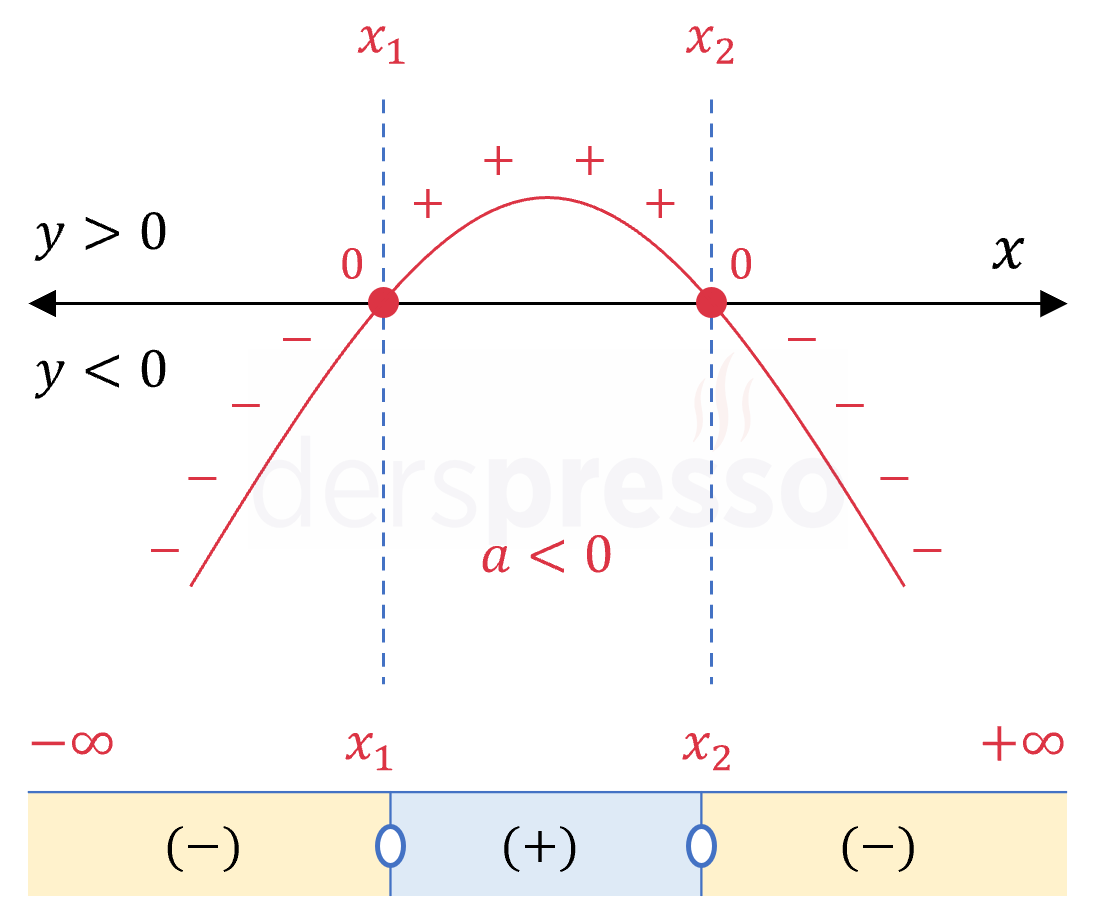
Başkatsayı negatif, delta pozitif: \( a \lt 0, \quad \Delta \gt 0 \) İfade kökler arasındaki aralıkta pozitif, kökler dışındaki aralıkta negatif, kök değerlerinde sıfır olur. Örnek: \( -(x - 2)(x - 5) \lesseqgtr 0\) \( x = 4 \Longrightarrow -(4 - 2)(4 - 5) = 2 \gt 0 \) \( x = 5 \Longrightarrow -(5 - 2)(5 - 5) = 0 \) \( x = 6 \Longrightarrow -(6 - 2)(6 - 5) = -4 \lt 0 \) |
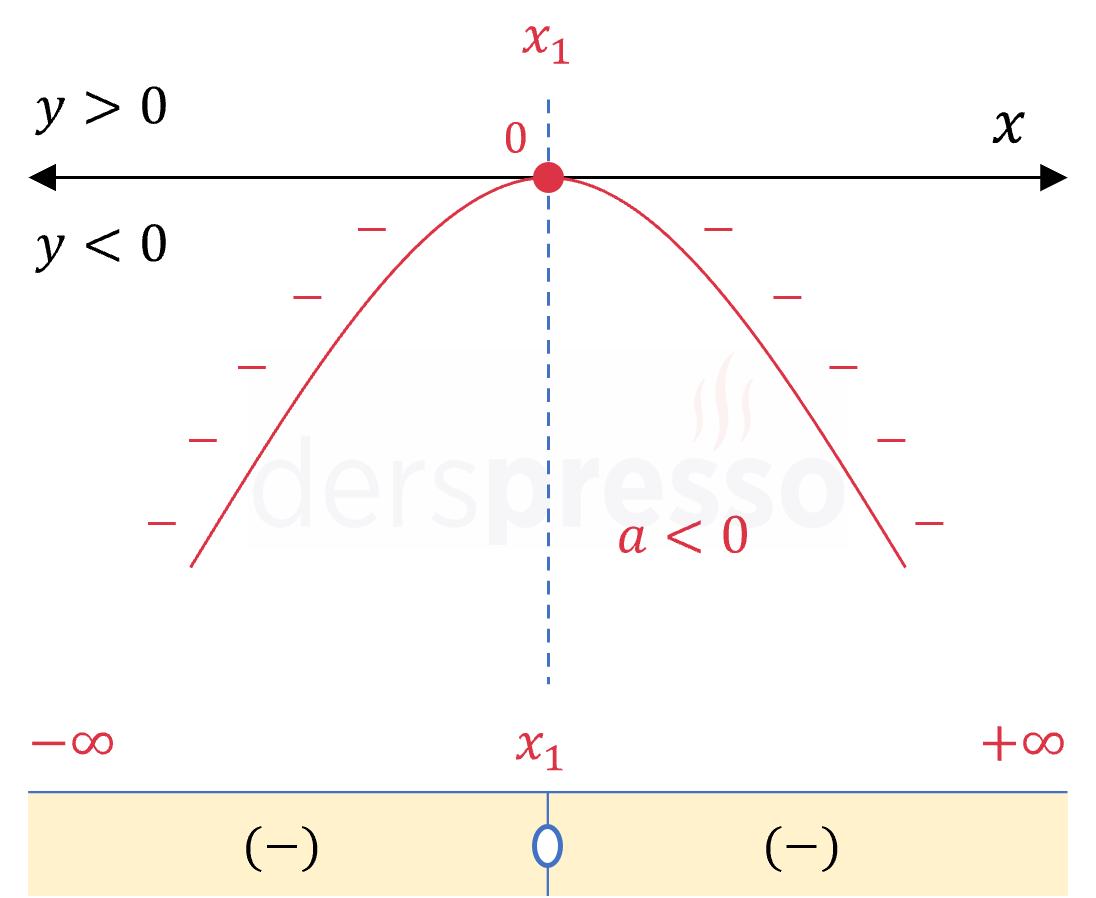
|
Başkatsayı negatif, delta sıfır: \( a \lt 0, \quad \Delta = 0 \) İfade kök değerinde sıfır, diğer tüm değerlerde negatif olur. Örnek: \( -(x - 5)^2 \lesseqgtr 0\) \( x = 4 \Longrightarrow -(4 - 5)^2 = -1 \lt 0 \) \( x = 5 \Longrightarrow -(5 - 5)^2 = 0 \) \( x = 6 \Longrightarrow -(6 - 5)^2 = -1 \lt 0 \) |

|
Başkatsayı ve delta negatif: \( a \lt 0, \quad \Delta \lt 0 \) İfade tüm reel sayılarda negatif olur. Örnek: \( -x^2 + 2x - 2 \lesseqgtr 0\) \( x = 0 \Longrightarrow -0^2 + 2(0) - 2 = -2 \lt 0 \) \( x = 1 \Longrightarrow -1^2 + 2(1) - 2 = -1 \lt 0 \) \( x = 2 \Longrightarrow -2^2 + 2(2) - 2 = -2 \lt 0 \) |
İkinci dereceden ifadelerin yukarıda paylaştığımız farklı durumları ve her durumdaki grafikleri iyi anlaşıldığı takdirde tüm ikinci dereceden eşitsizliklerin çözüm kümesi ek bir yönteme ihtiyaç duyulmadan bulunabilir.
İkinci dereceden ifadeleri aynı aşağıdaki dört eşitsizliğin çözüm kümelerini bulalım.
\( 2x^2 - 5x - 12 \lt 0 \)
\( 2x^2 - 5x - 12 \le 0 \)
\( 2x^2 - 5x - 12 \gt 0 \)
\( 2x^2 - 5x - 12 \ge 0 \)
İkinci dereceden ifadenin katsayılarını yazalım.
\( a = 2, \quad b = -5, \quad c = -12 \)
Başkatsayı pozitif olduğu için grafiğin kolları yukarı yönlüdür.
\( a = 2 \gt 0 \)
İfadenin deltasını bulalım.
\( \Delta = b^2 - 4ac \)
\( = (-5)^2 - 4 \cdot 2 \cdot (-12) = 121 \gt 0 \)
Delta pozitif olduğu için ikinci dereceden ifadenin iki reel kökü vardır.
İfadeyi çarpanlarına ayıralım.
\( (2x + 3)(x - 4) \le 0 \)
Başkatsayısı ve deltası pozitif olan ikinci dereceden ifadelerin grafiklerini düşündüğümüzde, ifade her bir çarpanı sıfır yapan \( x = -\frac{3}{2} \) ve \( x = 4 \) kök değerlerinde sıfır, \( (-\frac{3}{2}, 4) \) aralığında negatif, köklerin dışındaki aralıkta pozitif olur.
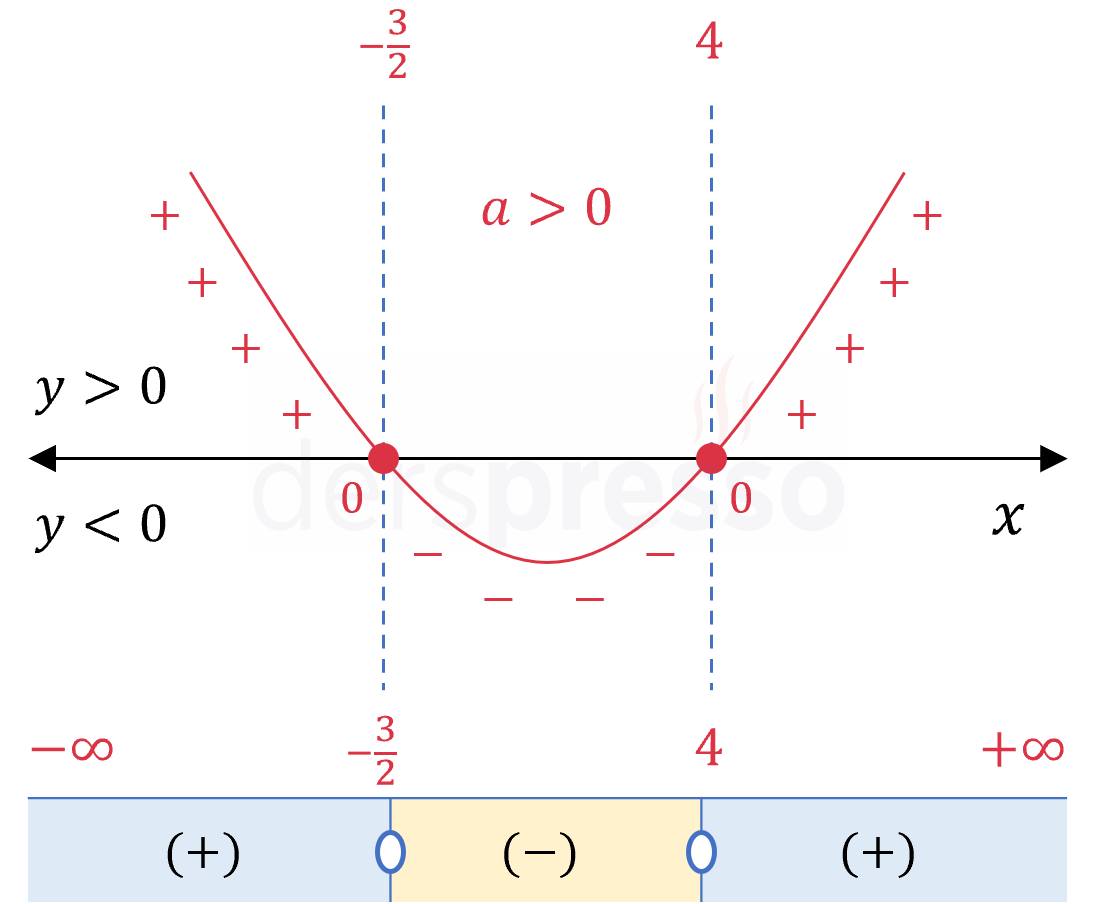
Bu doğrultuda verilen dört eşitsizliğin çözüm kümelerini bulalım.
\( 2x^2 - 5x - 12 \lt 0 \) için:
\( \quad x \in (-\frac{3}{2}, 4) \)
\( 2x^2 - 5x - 12 \le 0 \) için:
\( \quad x \in [-\frac{3}{2}, 4] \)
\( 2x^2 - 5x - 12 \gt 0 \) için:
\( \quad x \in (-\infty, -\frac{3}{2}) \cup (4, \infty) \)
\( 2x^2 - 5x - 12 \ge 0 \) için:
\( \quad x \in (-\infty, -\frac{3}{2}] \cup [4, \infty) \)
Aşağıdaki eşitsizliklerin çözüm kümelerini bulunuz.
(a) \( x^2 + 2x - 24 \ge 0 \)
(b) \( x^2 - 5x - 14 \le 0 \)
(c) \( x^2 - 24x + 23 \gt 0 \)
(d) \( x^2 + x - 42 \lt 0 \)
Çözümü Göster(a) eşitsizliği:
\( x^2 + 2x - 24 \ge 0 \)
İkinci dereceden ifadeyi çarpanlarına ayıralım.
\( (x + 6)(x - 4) \ge 0 \)
Pozitif başkatsayılı ve birbirinden farklı iki reel kökü olan ikinci dereceden bir ifade kök değerlerinde sıfır, köklerin arasındaki aralıkta negatif, dışındaki aralıkta pozitif olur.

Verilen eşitsizlikte \( \ge \) sembolü kullanıldığı için ikinci dereceden ifadenin pozitif ya da sıfır olduğu aralıklar eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in (-\infty, -6] \cup [4, \infty) \)
(b) eşitsizliği:
\( x^2 - 5x - 14 \le 0 \)
İkinci dereceden ifadeyi çarpanlarına ayıralım.
\( (x + 2)(x - 7) \le 0 \)
Pozitif başkatsayılı ve birbirinden farklı iki reel kökü olan ikinci dereceden bir ifade kök değerlerinde sıfır, köklerin arasındaki aralıkta negatif, dışındaki aralıkta pozitif olur.

Verilen eşitsizlikte \( \le \) sembolü kullanıldığı için ikinci dereceden ifadenin negatif ya da sıfır olduğu aralıklar eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in [-2, 7] \)
(c) eşitsizliği:
\( x^2 - 24x + 23 \gt 0 \)
İkinci dereceden ifadeyi çarpanlarına ayıralım.
\( (x - 1)(x - 23) \gt 0 \)
Pozitif başkatsayılı ve birbirinden farklı iki reel kökü olan ikinci dereceden bir ifade kök değerlerinde sıfır, köklerin arasındaki aralıkta negatif, dışındaki aralıkta pozitif olur.

Verilen eşitsizlikte \( \gt \) sembolü kullanıldığı için ikinci dereceden ifadenin pozitif olduğu aralıklar eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in (-\infty, 1) \cup (23, \infty) \)
(d) eşitsizliği:
\( x^2 + x - 42 \lt 0 \)
İkinci dereceden ifadeyi çarpanlarına ayıralım.
\( (x + 7)(x - 6) \lt 0 \)
Pozitif başkatsayılı ve birbirinden farklı iki reel kökü olan ikinci dereceden bir ifade kök değerlerinde sıfır, köklerin arasındaki aralıkta negatif, dışındaki aralıkta pozitif olur.

Verilen eşitsizlikte \( \lt \) sembolü kullanıldığı için ikinci dereceden ifadenin negatif olduğu aralıklar eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in (-7, 6) \)
Aşağıdaki eşitsizliklerin çözüm kümelerini bulunuz.
(a) \( (1 - x)(x + 8) \ge 0 \)
(b) \( (2x + 5)(3x - 7) \lt 0 \)
(c) \( (4 - 3x)^2 \le 0 \)
(d) \( (6 - 2x)(9 - x) \lt 0 \)
Çözümü Göster(a) eşitsizliği:
\( (1 - x)(x + 8) \ge 0 \)
Negatif başkatsayılı ve birbirinden farklı iki reel kökü olan ikinci dereceden bir ifade kök değerlerinde sıfır, köklerin arasındaki aralıkta pozitif, dışındaki aralıkta negatif olur.

Verilen eşitsizlikte \( \ge \) sembolü kullanıldığı için ikinci dereceden ifadenin pozitif ya da sıfır olduğu aralıklar eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in [-8, 1] \)
(b) eşitsizliği:
\( (2x + 5)(3x - 7) \lt 0 \)
Pozitif başkatsayılı ve birbirinden farklı iki reel kökü olan ikinci dereceden bir ifade kök değerlerinde sıfır, köklerin arasındaki aralıkta negatif, dışındaki aralıkta pozitif olur.

Verilen eşitsizlikte \( \lt \) sembolü kullanıldığı için ikinci dereceden ifadenin negatif olduğu aralıklar eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in (-\frac{5}{2}, \frac{7}{3}) \)
(c) eşitsizliği:
\( (4 - 3x)^2 \le 0 \)
\( (3x - 4)^2 \le 0 \)
Pozitif başkatsayılı ve tek bir (çift katlı) reel kökü olan ikinci dereceden bir ifade kök değerinde sıfır, kökün dışındaki aralıkta pozitif olur.

Verilen eşitsizlikte \( \le \) sembolü kullanıldığı için ikinci dereceden ifadenin negatif ya da sıfır olduğu aralıklar eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in \{\frac{4}{3}\} \)
(d) eşitsizliği:
\( (6 - 2x)(9 - x) \lt 0 \)
\( 2(x - 3)(x - 9) \lt 0 \)
Pozitif başkatsayılı ve birbirinden farklı iki reel kökü olan ikinci dereceden bir ifade kök değerlerinde sıfır, köklerin arasındaki aralıkta negatif, dışındaki aralıkta pozitif olur.

Verilen eşitsizlikte \( \lt \) sembolü kullanıldığı için ikinci dereceden ifadenin negatif olduğu aralıklar eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in (3, 9) \)
Aşağıdaki eşitsizliklerin çözüm kümelerini bulunuz.
(a) \( x^2 + 5x + 7 \lt 0 \)
(b) \( x^2 + 6x + 9 \gt 0 \)
(c) \( -x^2 + 3x - 3 \le 0 \)
(d) \( -x^2 + 4x - 4 \ge 0 \)
Çözümü Göster(a) eşitsizliği:
(a) \( x^2 + 5x + 7 \lt 0 \)
\( \Delta = 5^2 - 4 \cdot 1 \cdot 7 = -3 \lt 0 \)
İkinci dereceden ifadenin deltası negatif olduğu için reel kökü yoktur ve ifade çarpanlarına ayrılmaz.
Pozitif başkatsayılı ve deltası sıfırdan küçük olan ikinci dereceden bir ifade tüm reel sayılarda pozitif olur.

Verilen eşitsizlikte \( \lt \) sembolü kullanıldığı için ikinci dereceden ifadenin negatif olduğu aralıklar eşitsizliğin çözüm kümesi olur, ancak ifadenin negatif olduğu bir aralık yoktur.
Çözüm kümesi: \( x \in \emptyset \)
(b) eşitsizliği:
\( x^2 + 6x + 9 \gt 0 \)
İkinci dereceden ifadeyi çarpanlarına ayıralım.
\( (x + 3)^2 \gt 0 \)
Pozitif başkatsayılı ve tek bir (çift katlı) reel kökü olan ikinci dereceden bir ifade kök değerinde sıfır, kökün dışındaki aralıkta pozitif olur.

Verilen eşitsizlikte \( \gt \) sembolü kullanıldığı için ikinci dereceden ifadenin pozitif olduğu aralıklar eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in \mathbb{R} - \{-3\} \)
(c) eşitsizliği:
\( -x^2 + 3x - 3 \le 0 \)
\( \Delta = 3^2 - 4 \cdot (-1) \cdot (-3) = -3 \lt 0 \)
İkinci dereceden ifadenin deltası negatif olduğu için reel kökü yoktur ve ifade çarpanlarına ayrılmaz.
Negatif başkatsayılı ve deltası sıfırdan küçük olan ikinci dereceden bir ifade tüm reel sayılarda negatif olur.

Verilen eşitsizlikte \( \le \) sembolü kullanıldığı için ikinci dereceden ifadenin negatif ya da sıfır olduğu aralıklar eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in \mathbb{R} \)
(d) eşitsizliği:
\( -x^2 + 4x - 4 \ge 0 \)
İkinci dereceden ifadeyi çarpanlarına ayıralım.
\( -(x^2 - 4x + 4) \ge 0 \)
\( -(x - 2)^2 \ge 0 \)
Negatif başkatsayılı ve tek bir (çift katlı) reel kökü olan ikinci dereceden bir ifade kök değerinde sıfır, kökün dışındaki aralıkta negatif olur.

Verilen eşitsizlikte \( \ge \) sembolü kullanıldığı için ikinci dereceden ifadenin pozitif ya da sıfır olduğu aralıklar eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in \{2\} \)
Aşağıdaki eşitsizliklerin çözüm kümelerini bulunuz.
(a) \( x^2 + 24 \lt -11x \)
(b) \( x^2 \gt -3x - 7 \)
(c) \( -x^2 + 12x \gt 32 \)
(d) \( -2x^2 - 98 \ge 28x \)
Çözümü Göster(a) eşitsizliği:
\( x^2 + 24 \lt -11x \)
\( x^2 + 11x + 24 \lt 0 \)
İkinci dereceden ifadeyi çarpanlarına ayıralım.
\( (x + 8)(x + 3) \lt 0 \)
Pozitif başkatsayılı ve birbirinden farklı iki reel kökü olan ikinci dereceden bir ifade kök değerlerinde sıfır, köklerin arasındaki aralıkta negatif, dışındaki aralıkta pozitif olur.

Verilen eşitsizlikte \( \lt \) sembolü kullanıldığı için ikinci dereceden ifadenin negatif olduğu aralıklar eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in (-8, -3) \)
(b) eşitsizliği:
(b) \( x^2 \gt -3x - 7 \)
(b) \( x^2 + 3x + 7 \gt 0 \)
\( \Delta = 3^2 - 4 \cdot 1 \cdot 7 = -19 \lt 0 \)
İkinci dereceden ifadenin deltası negatif olduğu için reel kökü yoktur ve ifade çarpanlarına ayrılmaz.
Pozitif başkatsayılı ve deltası sıfırdan küçük olan ikinci dereceden bir ifade tüm reel sayılarda pozitif olur.

Verilen eşitsizlikte \( \gt \) sembolü kullanıldığı için ikinci dereceden ifadenin pozitif olduğu aralıklar eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in \mathbb{R} \)
(c) eşitsizliği:
\( -x^2 + 12x \gt 32 \)
\( -x^2 + 12x - 32 \gt 0 \)
İkinci dereceden ifadeyi çarpanlarına ayıralım.
\( -(x - 4)(x - 8) \gt 0 \)
Negatif başkatsayılı ve birbirinden farklı iki reel kökü olan ikinci dereceden bir ifade kök değerlerinde sıfır, köklerin arasındaki aralıkta pozitif, dışındaki aralıkta negatif olur.

Verilen eşitsizlikte \( \gt \) sembolü kullanıldığı için ikinci dereceden ifadenin pozitif olduğu aralıklar eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in (4, 8) \)
(d) eşitsizliği:
\( -2x^2 - 98 \ge 28x \)
\( -2x^2 - 28x - 98 \ge 0 \)
Eşitsizliğin taraflarını 2'ye bölelim.
\( -x^2 - 14x - 49 \ge 0 \)
Eşitsizliğin taraflarını -1 ile çarpalım. Bir eşitsizliğin tarafları negatif bir sayı ile çarpıldığında eşitsizlik yön değiştirir.
\( x^2 + 14x + 49 \le 0 \)
İkinci dereceden ifadeyi çarpanlarına ayıralım.
\( (x + 7)^2 \le 0 \)
Pozitif başkatsayılı ve tek bir (çift katlı) reel kökü olan ikinci dereceden bir ifade kök değerinde sıfır, kökün dışındaki aralıkta pozitif olur.

Verilen eşitsizlikte \( \le \) sembolü kullanıldığı için ikinci dereceden ifadenin negatif ya da sıfır olduğu aralıklar eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in \{-7\} \)
Aşağıdaki eşitsizliklerin çözüm kümelerini bulunuz.
(a) \( \dfrac{3x^2 + 13x}{2} \lt 5 \)
(b) \( 6x^2 \gt 7x + 3 \)
(c) \( -4x^2 + 3x \gt -1 \)
(d) \( \dfrac{-3x^2 + 10x}{-8} \gt 1 \)
Çözümü Göster(a) eşitsizliği:
\( \dfrac{3x^2 + 13x}{2} \lt 5 \)
Eşitsizliğin taraflarını 2 ile çarpalım.
\( 3x^2 + 13x \lt 10 \)
\( 3x^2 + 13x - 10 \lt 0 \)
İkinci dereceden ifadeyi çarpanlarına ayıralım.
\( (3x - 2)(x + 5) \lt 0 \)
Pozitif başkatsayılı ve birbirinden farklı iki reel kökü olan ikinci dereceden bir ifade kök değerlerinde sıfır, köklerin arasındaki aralıkta negatif, dışındaki aralıkta pozitif olur.

Verilen eşitsizlikte \( \lt \) sembolü kullanıldığı için ikinci dereceden ifadenin negatif olduğu aralıklar eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in (-5, \frac{2}{3}) \)
(b) eşitsizliği:
\( 6x^2 \gt 7x + 3 \)
\( 6x^2 - 7x - 3 \gt 0 \)
İkinci dereceden ifadeyi çarpanlarına ayıralım.
\( (3x + 1)(2x - 3) \gt 0 \)
Pozitif başkatsayılı ve birbirinden farklı iki reel kökü olan ikinci dereceden bir ifade kök değerlerinde sıfır, köklerin arasındaki aralıkta negatif, dışındaki aralıkta pozitif olur.

Verilen eşitsizlikte \( \gt \) sembolü kullanıldığı için ikinci dereceden ifadenin pozitif olduğu aralıklar eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in (-\infty, -\frac{1}{3}) \cup (\frac{3}{2}, \infty) \)
(c) eşitsizliği:
\( -4x^2 + 3x \gt -1 \)
\( -4x^2 + 3x + 1 \gt 0 \)
İkinci dereceden ifadeyi çarpanlarına ayıralım.
\( -(4x + 1)(x - 1) \gt 0 \)
Negatif başkatsayılı ve birbirinden farklı iki reel kökü olan ikinci dereceden bir ifade kök değerlerinde sıfır, köklerin arasındaki aralıkta pozitif, dışındaki aralıkta negatif olur.

Verilen eşitsizlikte \( \gt \) sembolü kullanıldığı için ikinci dereceden ifadenin pozitif olduğu aralıklar eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in (-\frac{1}{4}, 1) \)
(d) eşitsizliği:
\( \dfrac{-3x^2 + 10x}{-8} \gt 1 \)
Eşitsizliğin taraflarını \( -8 \) ile çarpalım. Bir eşitsizliğin tarafları negatif bir sayı ile çarpıldığında eşitsizliklik yön değiştirir.
\( -3x^2 + 10x \lt -8 \)
\( -3x^2 + 10x + 8 \lt 0 \)
İkinci dereceden ifadeyi çarpanlarına ayıralım.
\( -(3x + 2)(x - 4) \lt 0 \)
Negatif başkatsayılı ve birbirinden farklı iki reel kökü olan ikinci dereceden bir ifade kök değerlerinde sıfır, köklerin arasındaki aralıkta pozitif, dışındaki aralıkta negatif olur.

Verilen eşitsizlikte \( \lt \) sembolü kullanıldığı için ikinci dereceden ifadenin negatif olduğu aralıklar eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in (-\infty, -\frac{2}{3}) \cup (4, \infty) \)
Aşağıdaki eşitsizliklerin çözüm kümelerini bulunuz.
(a) \( \dfrac{7x^2}{2} \gt \dfrac{-6x - 2}{3} \)
(b) \( -8x^2 \ge -5x + 2 \)
(c) \( \dfrac{4x^2 - 20x}{5} \le -5 \)
(d) \( -2x^2 \gt -3x + 7 \)
Çözümü Göster(a) eşitsizliği:
\( \dfrac{7x^2}{2} \gt \dfrac{-6x - 2}{3} \)
Eşitsizliğin taraflarını 6 ile çarpalım.
\( 21x^2 \gt -12x - 4 \)
\( 21x^2 + 12x + 4 \gt 0 \)
\( \Delta = 12^2 - 4 \cdot 21 \cdot 4 = -192 \lt 0 \)
İkinci dereceden ifadenin deltası negatif olduğu için reel kökü yoktur ve ifade çarpanlarına ayrılmaz.
Pozitif başkatsayılı ve deltası sıfırdan küçük olan ikinci dereceden bir ifade tüm reel sayılarda pozitif olur.

Verilen eşitsizlikte \( \gt \) sembolü kullanıldığı için ikinci dereceden ifadenin pozitif olduğu aralıklar eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in \mathbb{R} \)
(b) eşitsizliği:
\( -8x^2 \ge -5x + 2 \)
\( -8x^2 + 5x - 2 \ge 0 \)
\( \Delta = 5^2 - 4 \cdot (-8) \cdot (-2) = -39 \lt 0 \)
İkinci dereceden ifadenin deltası negatif olduğu için reel kökü yoktur ve ifade çarpanlarına ayrılmaz.
Negatif başkatsayılı ve deltası sıfırdan küçük olan ikinci dereceden bir ifade tüm reel sayılarda negatif olur.

Verilen eşitsizlikte \( \ge \) sembolü kullanıldığı için ikinci dereceden ifadenin pozitif ya da sıfır olduğu aralıklar eşitsizliğin çözüm kümesi olur, ancak ifadenin pozitif ya da sıfır olduğu bir aralık yoktur.
Çözüm kümesi: \( x \in \emptyset \)
(c) eşitsizliği:
\( \dfrac{4x^2 - 20x}{5} \le -5 \)
Eşitsizliğin taraflarını 5 ile çarpalım.
\( 4x^2 - 20x \le -25 \)
\( 4x^2 - 20x + 25 \le 0 \)
İkinci dereceden ifadeyi çarpanlarına ayıralım.
\( (2x - 5)^2 \le 0 \)
Pozitif başkatsayılı ve tek bir (çift katlı) reel kökü olan ikinci dereceden bir ifade kök değerinde sıfır, kökün dışındaki aralıkta pozitif olur.

Verilen eşitsizlikte \( \le \) sembolü kullanıldığı için ikinci dereceden ifadenin negatif ya da sıfır olduğu aralıklar eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in \{\frac{5}{2}\} \)
(d) eşitsizliği:
\( -2x^2 \gt -3x + 7 \)
\( -2x^2 + 3x - 7 \gt 0 \)
\( \Delta = 3^2 - 4 \cdot (-2) \cdot (-7) = -47 \lt 0 \)
İkinci dereceden ifadenin deltası negatif olduğu için reel kökü yoktur ve ifade çarpanlarına ayrılmaz.
Negatif başkatsayılı ve deltası sıfırdan küçük olan ikinci dereceden bir ifade tüm reel sayılarda negatif olur.

Verilen eşitsizlikte \( \gt \) sembolü kullanıldığı için ikinci dereceden ifadenin pozitif olduğu aralıklar eşitsizliğin çözüm kümesi olur, ancak ifadenin pozitif olduğu bir aralık yoktur.
Çözüm kümesi: \( x \in \emptyset \)
Aşağıdaki eşitsizliklerin çözüm kümelerini bulunuz.
(a) \( 2x^2 - 7x \ge 30 \)
(b) \( 8x - 21 \le -5x^2 \)
(c) \( 4x^2 + 28x + 45 \gt 0 \)
(d) \( 3x(-3x + 4) \lt 4 \)
Çözümü Göster(a) eşitsizliği:
\( 2x^2 - 7x \ge 30 \)
\( 2x^2 - 7x - 30 \ge 0 \)
İkinci dereceden ifadeyi çarpanlarına ayıralım.
\( (2x + 5)(x - 6) \ge 0 \)
Pozitif başkatsayılı ve birbirinden farklı iki reel kökü olan ikinci dereceden bir ifade kök değerlerinde sıfır, köklerin arasındaki aralıkta negatif, dışındaki aralıkta pozitif olur.

Verilen eşitsizlikte \( \ge \) sembolü kullanıldığı için ikinci dereceden ifadenin pozitif ya da sıfır olduğu aralıklar eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in (-\infty, -\frac{5}{2}] \cup [6, \infty) \)
(b) eşitsizliği:
\( 8x - 21 \le -5x^2 \)
\( 5x^2 + 8x - 21 \le 0 \)
İkinci dereceden ifadeyi çarpanlarına ayıralım.
\( (5x - 7)(x + 3) \le 0 \)
Pozitif başkatsayılı ve birbirinden farklı iki reel kökü olan ikinci dereceden bir ifade kök değerlerinde sıfır, köklerin arasındaki aralıkta negatif, dışındaki aralıkta pozitif olur.

Verilen eşitsizlikte \( \le \) sembolü kullanıldığı için ikinci dereceden ifadenin negatif ya da sıfır olduğu aralıklar eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in [-3, \frac{7}{5}] \)
(c) eşitsizliği:
\( 4x^2 + 28x + 45 \gt 0 \)
İkinci dereceden ifadeyi çarpanlarına ayıralım.
\( (2x + 9)(2x + 5) \gt 0 \)
Pozitif başkatsayılı ve birbirinden farklı iki reel kökü olan ikinci dereceden bir ifade kök değerlerinde sıfır, köklerin arasındaki aralıkta negatif, dışındaki aralıkta pozitif olur.

Verilen eşitsizlikte \( \gt \) sembolü kullanıldığı için ikinci dereceden ifadenin pozitif olduğu aralıklar eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in (-\infty, -\frac{9}{2}) \cup (-\frac{5}{2}, \infty) \)
(d) eşitsizliği:
\( 3x(-3x + 4) \lt 4 \)
\( -9x^2 + 12x - 4 \lt 0 \)
İkinci dereceden ifadeyi çarpanlarına ayıralım.
\( -(3x - 2)^2 \lt 0 \)
Negatif başkatsayılı ve tek bir (çift katlı) reel kökü olan ikinci dereceden bir ifade kök değerinde sıfır, kökün dışındaki aralıkta negatif olur.

Verilen eşitsizlikte \( \lt \) sembolü kullanıldığı için ikinci dereceden ifadenin negatif olduğu aralıklar eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in \mathbb{R} - \{\frac{2}{3}\} \)
Aşağıdaki eşitsizliklerin çözüm kümelerini bulunuz.
(a) \( (2x + 5)(3x - 2) \ge x + 6 \)
(b) \( (3x + 4)^2 - 5x \gt 2x + 5 \)
(c) \( (2x - 9)^2 - 45 \le x(7x - 3) \)
(d) \( (2x - 3)(x - 4) \gt (x + 5)(x - 6) \)
Çözümü Göster(a) eşitsizliği:
\( (2x + 5)(3x - 2) \ge x + 6 \)
\( 6x^2 + 11x - 10 \ge x + 6 \)
\( 6x^2 + 10x - 16 \ge 0 \)
Eşitsizliğin taraflarını 2'ye bölelim.
\( 3x^2 + 5x - 8 \ge 0 \)
İkinci dereceden ifadeyi çarpanlarına ayıralım.
\( (3x + 8)(x - 1) \ge 0 \)
Pozitif başkatsayılı ve birbirinden farklı iki reel kökü olan ikinci dereceden bir ifade kök değerlerinde sıfır, köklerin arasındaki aralıkta negatif, dışındaki aralıkta pozitif olur.

Verilen eşitsizlikte \( \ge \) sembolü kullanıldığı için ikinci dereceden ifadenin pozitif ya da sıfır olduğu aralıklar eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in (-\infty, -\frac{8}{3}] \cup [1, \infty) \)
(b) eşitsizliği:
\( (3x + 4)^2 - 5x \gt 2x + 5 \)
\( 9x^2 + 24x + 16 - 5x \gt 2x + 5 \)
\( 9x^2 + 17x + 11 \gt 0 \)
\( \Delta = 17^2 - 4 \cdot 9 \cdot 11 = -107 \lt 0 \)
İkinci dereceden ifadenin deltası negatif olduğu için reel kökü yoktur ve ifade çarpanlarına ayrılmaz.
Pozitif başkatsayılı ve deltası sıfırdan küçük olan ikinci dereceden bir ifade tüm reel sayılarda pozitif olur.

Verilen eşitsizlikte \( \gt \) sembolü kullanıldığı için ikinci dereceden ifadenin pozitif olduğu aralıklar eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in \mathbb{R} \)
(c) eşitsizliği:
\( (2x - 9)^2 - 45 \le x(7x - 3) \)
\( 4x^2 - 36x + 81 - 45 \le 7x^2 - 3x \)
\( -3x^2 - 33x + 36 \le 0 \)
Eşitsizliğin taraflarını 3'e bölelim.
\( -x^2 - 11x + 12 \le 0 \)
İkinci dereceden ifadeyi çarpanlarına ayıralım.
\( -(x + 12)(x - 1) \le 0 \)
Negatif başkatsayılı ve birbirinden farklı iki reel kökü olan ikinci dereceden bir ifade kök değerlerinde sıfır, köklerin arasındaki aralıkta pozitif, dışındaki aralıkta negatif olur.

Verilen eşitsizlikte \( \le \) sembolü kullanıldığı için ikinci dereceden ifadenin negatif ya da sıfır olduğu aralıklar eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in (-\infty, -12] \cup [1, \infty) \)
(d) eşitsizliği:
\( (2x - 3)(x - 4) \gt (x + 5)(x - 6) \)
\( 2x^2 - 11x + 12 \gt x^2 - x - 30 \)
\( x^2 - 10x + 42 \gt 0 \)
\( \Delta = (-10)^2 - 4 \cdot 1 \cdot 42 = -68 \lt 0 \)
İkinci dereceden ifadenin deltası negatif olduğu için reel kökü yoktur ve ifade çarpanlarına ayrılmaz.
Pozitif başkatsayılı ve deltası sıfırdan küçük olan ikinci dereceden bir ifade tüm reel sayılarda pozitif olur.

Verilen eşitsizlikte \( \gt \) sembolü kullanıldığı için ikinci dereceden ifadenin pozitif olduğu aralıklar eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in \mathbb{R} \)
İşaret Tablosu ile Çözüm
İkinci dereceden eşitsizliklerin çözüm kümesi bir işaret tablosu yardımıyla da bulunabilir.
Eşitsizliklerin çözümünde işaret tablosu kullanımını birkaç örnek üzerinden gösterelim.
\( x^2 \lt 7x -10 \) eşitsizliğinin çözüm kümesini bulalım.
Adım 1: Tüm terimler eşitsizliğin sol tarafına alınır.
Bu işlem sonucunda eşitsizliğin sağ tarafı sıfır olur.
\( x^2 - 7x + 10 \lt 0 \)
Adım 2: İkinci dereceden ifade çarpanlarına ayrılır.
İfadeyi çarpanlarına ayırmak için çarpanlara ayırma yöntemleri ya da kök bulma formülü kullanılır.
İkinci dereceden ifadenin deltası;
- Sıfırdan büyükse ifadenin iki reel kökü vardır ve ifade \( a(x - x_1)(x - x_2) \) şeklinde çarpanlarına ayrılır.
- Sıfıra eşitse ifadenin (çift katlı) tek reel kökü vardır ve ifade \( a(x - x_1)^2 \) şeklinde çarpanlarına ayrılır.
- Sıfırdan küçükse ifadenin reel kökü yoktur ve ifade çarpanlarına ayrılmaz.
Verilen ifadeyi çarpanlarına ayıralım.
\( (x - 2)(x - 5) \lt 0 \)
Adım 3: Her bir çarpanı sıfır yapan kritik noktalar belirlenir ve işaret tablosunda işaretlenir.
Eşitsizliğin kritik noktaları her bir çarpanı sıfır yapan \( x = 2 \) ve \( x = 5 \) değerleridir. Bu değerleri işaret tablosunda reel sayı doğrusunu üç aralığa ayıracak şekilde işaretleyelim.

Adım 4: Çarpanlar ve her aralıktaki işaretleri tabloya birer satır olarak eklenir.
\( x - 2 \) çarpanı \( x = 2 \) için sıfır, bu noktanın solunda negatif, sağında pozitif olur.
\( x - 5 \) çarpanı \( x = 5 \) için sıfır, bu noktanın solunda negatif, sağında pozitif olur.

Adım 5: İkinci dereceden ifadenin kendisi ve her aralıktaki işareti tabloya eklenir.
İkinci dereceden ifadenin her aralıktaki işareti, çarpanların ilgili aralıktaki işaretlerinin çarpımına eşittir.
\( (-\infty, 2) \) aralığında \( (-) \cdot (-) = (+) \) olduğu için ifadenin işareti pozitif olur.
\( (2, 5) \) aralığında \( (+) \cdot (-) = (-) \) olduğu için ifadenin işareti negatif olur.
\( (5, \infty) \) aralığında \( (+) \cdot (+) = (+) \) olduğu için ifadenin işareti pozitif olur.
Ayrıca her bir çarpanı sıfır yapan kritik noktalarda ikinci dereceden ifade de sıfır olur.

Adım 6: Eşitsizliğin çözüm kümesi bulunur.
İkinci dereceden ifadenin farklı aralıklardaki işaretine ve eşitsizlik sembolüne göre çözüm kümesi bulunur.
Verilen eşitsizlikte \( \lt \) sembolü kullanıldığı için \( x^2 - 7x + 10 \) ifadesinin negatif olduğu aralık eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in (2, 5) \)
İkinci bir örnekte başkatsayısı negatif olan bir ikinci dereceden eşitsizliğin çözüm kümesini bulalım.
\( -x^2 - 10 \le - 7x \) eşitsizliğinin çözüm kümesini bulalım.
Adım 1: Tüm terimler eşitsizliğin sol tarafına alınır.
\( -x^2 + 7x - 10 \le 0 \)
Adım 2: İkinci dereceden ifade çarpanlarına ayrılır.
Verilen ifadeyi çarpanlarına ayıralım.
\( -(x - 2)(x - 5) \lt 0 \)
Negatif işaretini birinci çarpanın içine alalım (işareti ikinci çarpanın içine almamız sonucu değiştirmeyecektir).
\( (2 - x)(x - 5) \lt 0 \)
Adım 3: Her bir çarpanı sıfır yapan kritik noktalar belirlenir ve işaret tablosunda işaretlenir.
Eşitsizliğin kritik noktaları her bir çarpanı sıfır yapan \( x = 2 \) ve \( x = 5 \) değerleridir.
Adım 4: Çarpanlar ve her aralıktaki işaretleri tabloya birer satır olarak eklenir.
\( 2 - x \) çarpanı \( x = 2 \) için sıfır, bu noktanın solunda pozitif, sağında negatif olur.
\( x - 5 \) çarpanı \( x = 5 \) için sıfır, bu noktanın solunda negatif, sağında pozitif olur.

Adım 5: İkinci dereceden ifadenin tümü ve her aralıktaki işareti tabloya eklenir.
İkinci dereceden ifadenin her aralıktaki işareti, çarpanların ilgili aralıktaki işaretlerinin çarpımına eşittir.
\( (-\infty, 2) \) aralığında \( (+) \cdot (-) = (-) \) olduğu için ifadenin işareti negatif olur.
\( (2, 5) \) aralığında \( (-) \cdot (-) = (+) \) olduğu için ifadenin işareti pozitif olur.
\( (5, \infty) \) aralığında \( (-) \cdot (+) = (-) \) olduğu için ifadenin işareti negatif olur.
Ayrıca her bir çarpanı sıfır yapan kritik noktalarda ikinci dereceden ifade de sıfır olur.

Adım 6: Eşitsizliğin çözüm kümesi bulunur.
Verilen eşitsizlikte \( \le \) sembolü kullanıldığı için \( -x^2 + 7x - 10 \) ifadesinin negatif ya da sıfır olduğu aralıklar eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in (-\infty, 2] \cup [5, \infty) \)
Üçüncü bir örnekte çift katlı kökü olan bir ikinci dereceden eşitsizliğin çözüm kümesini bulalım.
\( -x^2 + 6x \lt 9 \) eşitsizliğinin çözüm kümesini bulalım.
Adım 1: Tüm terimler eşitsizliğin sol tarafına alınır.
\( -x^2 + 6x - 9 \lt 0 \)
Adım 2: İkinci dereceden ifade çarpanlarına ayrılır.
Verilen ifadeyi çarpanlarına ayıralım.
\( -(x - 3)^2 \lt 0 \)
Adım 3: Her bir çarpanı sıfır yapan kritik noktalar belirlenir ve işaret tablosunda işaretlenir.
Eşitsizliğin kritik noktası çift katlı çarpanı sıfır yapan \( x = 3 \) değeridir.
Adım 4: Çarpanlar ve her aralıktaki işaretleri tabloya birer satır olarak eklenir.
\( (x - 3)^2 \) çarpanı \( x = 3 \) için sıfır, diğer tüm reel sayılarda pozitif olur.

Adım 5: İkinci dereceden ifadenin tümü ve her aralıktaki işareti tabloya eklenir.
İfade \( x = 3 \) için sıfır, diğer tüm reel sayılarda negatif olur.

Adım 6: Eşitsizliğin çözüm kümesi bulunur.
Verilen eşitsizlikte \( \lt \) sembolü kullanıldığı için \( -x^2 + 6x - 9 \) ifadesinin negatif olduğu aralık eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in \mathbb{R} - \{3\} \)
Yukarıdaki örnekte çift katlı kök işaret tablosuna \( (x - 3)^2 \) şeklinde tek çarpan ve satır olarak değil de \( (x - 3) \) şeklinde iki çarpan ve satır olarak eklense de, tek katlı çarpanın negatif olduğu aralıkta iki negatif değerin çarpımı pozitif olacağı için sonuç değişmeyecektir.
\( k \in \mathbb{R} \) olmak üzere,
\( (k + 3)x^2 + (2k + 1)x + k \gt 0 \)
eşitsizliği daima sağlandığına göre, \( k \)'nın değer aralığını bulunuz.
Çözümü Gösterİkinci dereceden bir ifade daima pozitif ise aşağıdaki iki koşul sağlanmalıdır.
(1) İkinci dereceden ifadenin başkatsayısı sıfırdan büyük olmalıdır (grafiğin kolları yukarı yönlü olmalıdır).
\( k + 3 \gt 0 \)
\( k \gt -3 \)
(2) İkinci dereceden ifadenin deltası sıfırdan küçük olmalıdır (grafik \( x \) eksenini kesmemelidir).
\( \Delta = b^2 - 4ac \lt 0 \)
\( (2k + 1)^2 - 4 \cdot (k + 3) \cdot k \lt 0 \)
\( 4k^2 + 4k + 1 - 4k^2 - 12k \lt 0 \)
\( -8k + 1 \lt 0 \)
\( k \gt \dfrac{1}{8} \)
Bulduğumuz iki değer aralığının kesişim kümesi \( k \)'nın değer aralığını verir.
\( k \gt \dfrac{1}{8} \)
\( (x - 4)^2 \lt \abs{x - 4} + 12 \) eşitsizliğinin çözüm kümesi nedir?
Çözümü GösterMutlak değer içini sıfır yapan noktalar mutlak değer ifadesinin kritik noktalarıdır.
\( x - 4 = 0 \Longrightarrow x = 4 \)
Kritik noktanın oluşturduğu iki aralık için eşitsizliği ayrı ayrı çözelim.
Durum 1: \( x \lt 4 \)
Bu durumda mutlak değer içindeki ifade negatif olur ve mutlak değer dışına negatif işaretli çıkar.
\( (x - 4)^2 \lt -(x - 4) + 12 \)
\( x^2 - 8x + 16 \lt -x + 16 \)
\( x^2 - 7x \lt 0 \)
\( x(x - 7) \lt 0 \)
Pozitif başkatsayılı ve birbirinden farklı iki reel kökü olan ikinci dereceden bir ifade kök değerlerinde sıfır, köklerin arasındaki aralıkta negatif, dışındaki aralıkta pozitif olur.
Verilen eşitsizlikte \( \lt \) sembolü kullanıldığı için eşitsizliğin negatif olduğu aralıklar eşitsizliğin çözüm kümesi olur.
\( x \in (0, 7) \)
Bu aralık ile \( x \lt 4 \) aralığının kesişimi 1. durumun çözüm kümesi olur.
\( x \in (0, 4) \)
Durum 2: \( x \ge 4 \)
Bu durumda mutlak değer içindeki ifade sıfır ya da pozitif olur ve mutlak değer dışına olduğu gibi çıkar.
\( (x - 4)^2 \lt x - 4 + 12 \)
\( x^2 - 8x + 16 \lt x + 8 \)
\( x^2 - 9x + 8 \lt 0 \)
\( (x - 1)(x - 8) \lt 0 \)
Pozitif başkatsayılı ve birbirinden farklı iki reel kökü olan ikinci dereceden bir ifade kök değerlerinde sıfır, köklerin arasındaki aralıkta negatif, dışındaki aralıkta pozitif olur.
Verilen eşitsizlikte \( \lt \) sembolü kullanıldığı için eşitsizliğin negatif olduğu aralıklar eşitsizliğin çözüm kümesi olur.
\( x \in (1, 8) \)
Bu aralık ile \( x \ge 4 \) aralığının kesişimi 2. durumun çözüm kümesi olur.
\( x \in [4, 8) \)
Eşitsizliğin çözüm kümesi yukarıdaki iki aralık için bulduğumuz çözüm aralıklarının birleşim kümesidir.
Çözüm kümesi: \( x \in (0, 8) \)
\( x^2 + 11x \gt -28 \)
\( x^2 + 2x \lt 15 \)
eşitsizlik sisteminin çözüm kümesini bulunuz.
Çözümü GösterBirinci eşitsizliği çarpanlarına ayıralım.
\( x^2 + 11x + 28 \gt 0 \)
\( (x + 7)(x + 4) \gt 0 \)
İkinci dereceden ifadeyi sıfır yapan değerler \( x = -7 \) ve \( x = -4 \)'tür.
Eşitsizlik bu iki nokta arasında negatif, bu aralık dışında pozitif, bu iki noktada sıfır olur.
Eşitsizlikte \( \gt \) sembolü kullanıldığı için bu iki nokta dışındaki aralıkta eşitsizlik sağlanır.
İkinci eşitsizliği çarpanlarına ayıralım.
\( x^2 + 2x - 15 \lt 0 \)
\( (x + 5)(x - 3) \lt 0 \)
İkinci dereceden ifadeyi sıfır yapan değerler \( x = -5 \) ve \( x = 3 \)'tür.
Eşitsizlik bu iki nokta arasında negatif, bu aralık dışında pozitif, bu iki noktada sıfır olur.
Eşitsizlikte \( \lt \) sembolü kullanıldığı için bu iki nokta arasında eşitsizlik sağlanır.
Eşitsizlikler için bir işaret tablosu oluşturalım ve her bir eşitsizliğin sağlandığı aralıkları mavi ile işaretleyelim.

Eşitsizlik sisteminin çözüm kümesi her iki eşitsizliğin de sağlandığı (her iki eşitsizlik için de mavi olan) aralıklardır.
Çözüm kümesi: \( x \in (-4, 3) \)
\( x^2 - 5x - 24 \lt 0 \)
\( 3x - 4 \gt 11 \)
Yukarıdaki iki eşitsizliği tek bir eşitsizlik olarak ifade ediniz.
Çözümü GösterBirinci eşitsizliği çarpanlarına ayıralım.
\( (x + 3)(x - 8) \lt 0 \)
İkinci eşitsizliği düzenleyelim.
\( 3x - 15 \gt 0 \)
\( 3(x - 5) \gt 0 \)
Bir işaret tablosu hazırlayalım.

Birinci eşitsizliği bir satır olarak ekleyelim.
Pozitif başkatsayılı ve birbirinden farklı iki reel kökü olan ikinci dereceden bir ifade kök değerlerinde sıfır, köklerin arasındaki aralıkta negatif, dışındaki aralıkta pozitif olur.
Verilen eşitsizlikte \( \lt \) sembolü kullanıldığı için ikinci dereceden ifadenin negatif olduğu aralıklar eşitsizliğin çözüm kümesi olur (yeşil işaretli kutular).
İkinci eşitsizliği bir satır olarak ekleyelim.
Pozitif başkatsayılı birinci dereceden ifade kök değerinde sıfır, kökün sağında pozitif, solunda negatif olur.
Verilen eşitsizlikte \( \gt \) sembolü kullanıldığı için birinci dereceden ifadenin pozitif olduğu aralık eşitsizliğin çözüm kümesi olur (yeşil işaretli kutular).
Buna göre iki eşitsizliğin de sağlandığı aralık \( (5, 8) \) aralığıdır.
Bu aralığı belirten tek bir eşitsizlik kökleri 5 ve 8 olan ikinci dereceden bir ifade ile aşağıdaki şekilde oluşturulabilir.
\( (x - 5)(x - 8) \lt 0 \)
\( x^2 - 13x + 40 \lt 0 \)