Polinom Eşitsizlikleri
Eşitsizliğin her iki tarafı da birer polinom olan eşitsizliklere polinom eşitsizliği denir. Diğer eşitsizliklerde olduğu gibi polinom eşitsizliklerinde de \( \lt \), \( \le \), \( \gt \), \( \ge \) sembollerinden herhangi biri kullanılabilir.
Bu bölümde terimleri eşitsizliğin aynı tarafında toplanmış ve tüm çarpanlarına ayrılmış polinomlarla eşitsizlikleri inceleyeceğiz. Bu formda olmayan eşitsizlikler çarpanlara ayırma bölümünde incelediğimiz yöntemler kullanılarak bu forma getirilebilir.
\( (x + 1)(x - 2)(x - 5) \lt 0 \)
\( (2x + 3)^3(x - 1)(x - 4)^2 \ge 0 \)
\( 3x(x + 2)(3x - 5)(x - 7)^2 \lt 0 \)
Polinom eşitsizliklerinin çözüm kümesi test değeri vererek, grafik yöntemi ile ve işaret tablosu yardımıyla olmak üzere üç yöntemle bulunabilir.
Test Değeri ile Çözüm
Bu yöntemde polinom ifadesinin her bir çarpanını sıfır yapan kritik noktalar bulunur ve bu noktaların oluşturduğu aralıkların her birinden seçilen birer test değeri polinom ifadesinde yerine konarak ifadenin ilgili aralıktaki işareti bulunur.
Polinom fonksiyonları tüm reel sayılarda sürekli olduğu için, iki kök değeri arasındaki her noktada aynı işarete sahiptir, dolayısıyla belirli bir aralıkta seçeceğimiz test değeri için polinomun işareti aralıktaki tüm noktalar için aynı olur.
\( (x + 4)(x + 2)^2(x - 1)(x - 3) \le 0 \) eşitsizliğinin çözüm kümesini bulalım.
\( f(x) = (x + 4)(x + 2)^2(x - 1)(x - 3) \) olsun.
Adım 1: Her bir çarpanı sıfır yapan kritik noktalar ve bu noktaların reel sayı doğrusunda oluşturduğu aralıklar belirlenir.
Her bir çarpanı sıfır yapan \( x \in \{-4, -2, 1, 3\} \) değerleri eşitsizliğin kritik noktalarıdır.
Bu kritik noktalar reel sayı doğrusunda \( (-\infty, -4) \), \( (-4, -2) \), \( (-2, 1) \), \( (1, 3) \) ve \( (3, \infty) \) aralıklarını oluşturur.
Adım 2: Kritik noktaların oluşturduğu aralıklardan birer test değeri seçilir ve bu değerler için fonksiyonun işareti bulunur.
Bu aralıkların her birinden test değeri olarak \( x \in \{-5, -3, 0, 2, 4\} \) değerlerini seçelim.
Seçtiğimiz test değerleri için fonksiyonun işaretini bulalım.
\( f(-5) = (-5 + 4)(-5 + 2)^2(-5 - 1)(-5 - 3) = -432 \lt 0 \)
\( f(-3) = (-3 + 4)(-3 + 2)^2(-3 - 1)(-3 - 3) = 24 \gt 0 \)
\( f(0) = (0 + 4)(0 + 2)^2(0 - 1)(0 - 3) = 48 \gt 0 \)
\( f(2) = (2 + 4)(2 + 2)^2(2 - 1)(2 - 3) = -96 \lt 0 \)
\( f(4) = (4 + 4)(4 + 2)^2(4 - 1)(4 - 3) = 864 \gt 0 \)
Adım 3: Fonksiyonun test değerlerindeki işaretine göre bir tablo hazırlanır.
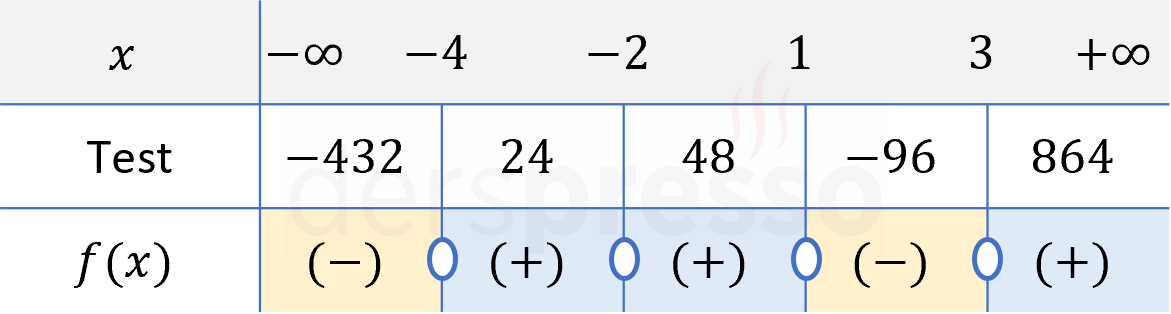
Adım 4: Eşitsizliğin çözüm kümesi bulunur.
Fonksiyonun farklı aralıklardaki işaretine ve eşitsizlik sembolüne göre çözüm kümesi bulunur.
Verilen eşitsizlikte \( \le \) sembolü kullanıldığı için fonksiyonun sıfır ya da negatif olduğu aralık ve değerler eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in (-\infty, -4] \cup \{-2\} \cup [1, 3] \)
Polinom eşitsizliklerinin test değeri kullanarak çözümü aşağıda bahsedeceğimiz diğer iki yönteme göre daha çok (ve kimi zaman kesirlerle) işlem gerektirebileceği için öncelikli olarak tercih edilmesi gereken yöntem değildir.
Grafik ile Çözüm
Çarpanlarına ayrılmış bir polinomun grafiği birkaç temel davranış dikkate alındığında genel hatlarıyla çizilebilir.
- Eğrinin \( x \) eksenini kestiği noktaların apsis değerleri her bir çarpanı sıfır yapan reel sayı değerlerdir.
- Eğrinin \( y \) eksenini kestiği noktanın ordinat değeri polinomun sabit terimine eşittir.
- Eğrinin \( x \) pozitif ve negatif sonsuza giderkenki davranışı polinomun derecesine ve başkatsayısına göre dört şekilde olabilir.
- Derece tek sayı ve başkatsayı pozitif: \( x \) artarken \( y \) negatif sonsuzdan gelir ve pozitif sonsuza gider. Eğri \( x \) eksenini en az bir noktada keser.
- Derece çift sayı ve başkatsayı pozitif: \( x \) artarken \( y \) pozitif sonsuzdan gelir ve pozitif sonsuza gider. Eğri \( x \) eksenini kesebilir ya da kesmeyebilir.
- Derece tek sayı ve başkatsayı negatif: \( x \) artarken \( y \) pozitif sonsuzdan gelir ve negatif sonsuza gider. Eğri \( x \) eksenini en az bir noktada keser.
- Derece çift sayı ve başkatsayı negatif: \( x \) artarken \( y \) negatif sonsuzdan gelir ve negatif sonsuza gider. Eğri \( x \) eksenini kesebilir ya da kesmeyebilir.
- Eğrinin \( x \) eksenini kestiği bir noktadaki davranışı iki şekilde olabilir.
- Tek katlı kök: Bir çarpanın üssü tek sayı ise eğri \( x \) eksenini bu noktada keser ve eksenin öteki tarafına geçer.
- Çift katlı kök: Bir çarpanın üssü çift sayı ise eğri \( x \) eksenini teğet keser ve eksenin öteki tarafına geçmeden geri döner.
Bu yöntemi yukarıda kullandığımız örneğe uygulayalım.
\( (x + 4)(x + 2)^2(x - 1)(x - 3) \le 0 \) eşitsizliğinin çözüm kümesini bulalım.
Adım 1: Eşitsizliğin kritik noktalarını belirleyelim.
Her bir çarpanı sıfır yapan \( x \in \{-4, -2, 1, 3\} \) değerleri eşitsizliğin kritik noktalarıdır.
Adım 2: \( x \) ekseninin pozitif tarafından başlayarak polinom grafiğinin \( x \) eksenine göre davranışını belirleyelim.
Derece tek sayı ve başkatsayı pozitif olduğu için \( x \) pozitif sonsuzdan gelirken \( y \) de pozitif sonsuzdan gelir.
Tek katlı \( (x - 3) \) çarpanı için, eğri \( x \) eksenini \( x = 3 \) noktasında keser ve eksenin öteki tarafına (negatif tarafa) geçer.
Tek katlı \( (x - 1) \) çarpanı için, eğri \( x \) eksenini \( x = 1 \) noktasında keser ve eksenin öteki tarafına (pozitif tarafa) geçer.
Çift katlı \( (x + 2)^2 \) çarpanı için, eğri \( x \) eksenini \( x = -2 \) noktasında keser ve eksenin aynı tarafına (pozitif tarafa) döner.
Tek katlı \( (x + 4) \) çarpanı için, eğri \( x \) eksenini \( x = -4 \) noktasında keser ve eksenin öteki tarafına (negatif tarafa) geçer.
Derece tek sayı ve başkatsayı pozitif olduğu için, beklediğimiz gibi \( x \) negatif sonsuza giderken \( y \) de negatif sonsuza gider.
Buna göre polinomun grafiği aşağıdaki gibi olur.
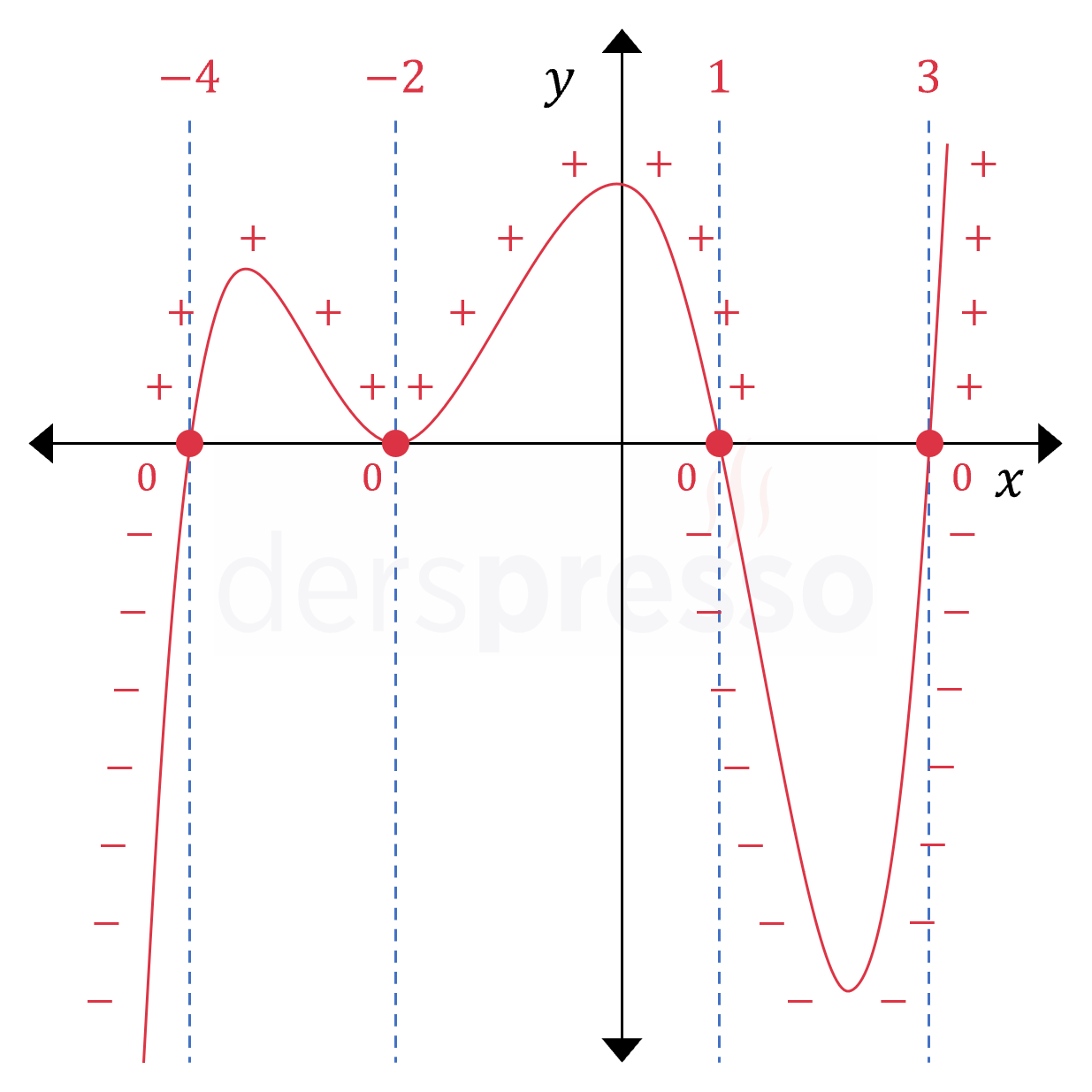
Adım 4: Eşitsizliğin çözüm kümesi bulunur.
İfadenin farklı aralıklardaki işaretine ve eşitsizlik sembolüne göre çözüm kümesi bulunur.
Verilen eşitsizlikte \( \le \) sembolü kullanıldığı için grafiğin sıfır ya da negatif olduğu aralık ve değerler eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in (-\infty, -4] \cup \{-2\} \cup [1, 3] \)
İşaret Tablosu ile Çözüm
Polinom eşitsizliklerinin çözüm kümesi, ikinci dereceden eşitsizliklerin çözümüne benzer şekilde bir işaret tablosu yardımıyla da bulunabilir.
Bu yöntemi yukarıda kullandığımız örneğe uygulayalım.
\( (x + 4)(x + 2)^2(x - 1)(x - 3) \le 0 \) eşitsizliğinin çözüm kümesini bulalım.
Adım 1: Her bir çarpanı sıfır yapan kritik noktalar belirlenir ve işaret tablosunda işaretlenir.
Eşitsizliğin kritik noktaları her bir çarpanı sıfır yapan \( x \in \{-4, -2, 1, 3\} \) değerleridir.
Bu kritik noktalar reel sayı doğrusunda \( (-\infty, -4) \), \( (-4, -2) \), \( (-2, 1) \), \( (1, 3) \) ve \( (3, \infty) \) aralıklarını oluşturur.
Adım 2: Çarpanlar ve her aralıktaki işaretleri tabloya birer satır olarak eklenir.
\( x + 4 \) çarpanı \( x = -4 \) için sıfır, bu noktanın solunda negatif, sağında pozitif olur.
\( (x + 2)^2 \) çarpanı \( x = -2 \) için sıfır, diğer tüm reel sayılarda pozitif olur.
\( x - 1 \) çarpanı \( x = 1 \) için sıfır, bu noktanın solunda negatif, sağında pozitif olur.
\( x - 3 \) çarpanı \( x = 3 \) için sıfır, bu noktanın solunda negatif, sağında pozitif olur.
Adım 3: Polinom ifadesinin kendisi ve her aralıktaki işareti tabloya eklenir.
Polinom ifadesinin her aralıktaki işareti, çarpanların ilgili aralıktaki işaretlerinin çarpımına eşittir.
Örneğin \( (-2, 1) \) aralığında \( (+) \cdot (+) \cdot (-) \cdot (-) = (+) \) olduğu için ifadenin işareti pozitif olur.
Ayrıca her bir çarpanı sıfır yapan kritik noktalarda polinom ifadesi de sıfır olur.
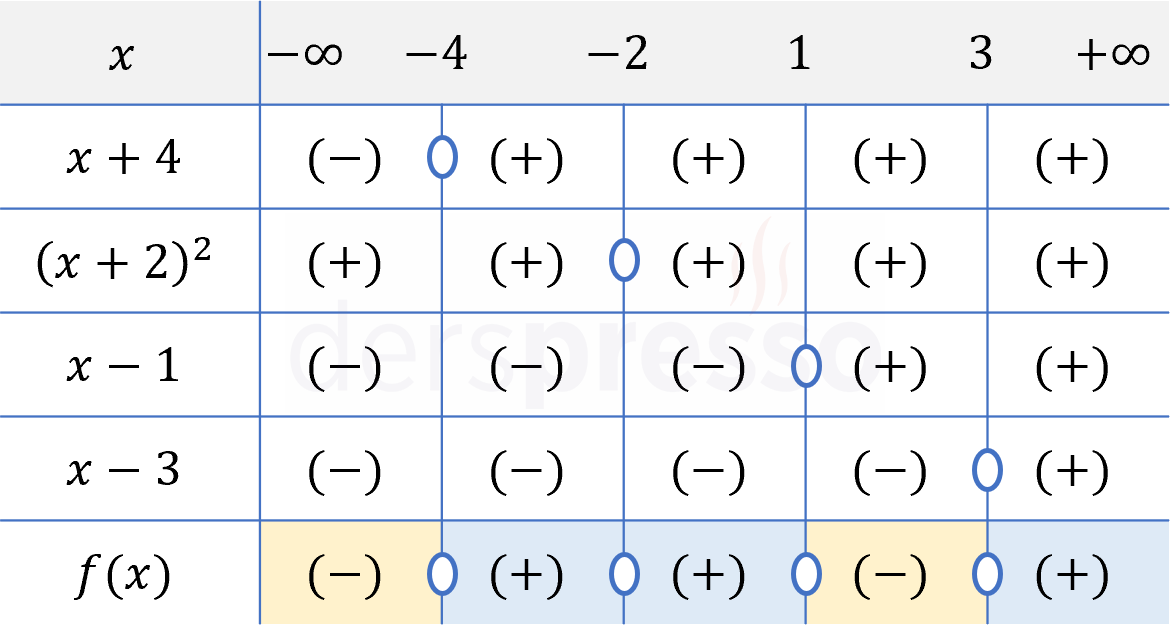
Adım 4: Eşitsizliğin çözüm kümesi bulunur.
Polinom ifadesinin farklı aralıklardaki işaretine ve eşitsizlik sembolüne göre çözüm kümesi bulunur.
Verilen eşitsizlikte \( \le \) sembolü kullanıldığı için polinom ifadesinin sıfır ya da negatif olduğu aralık ve değerler eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in (-\infty, -4] \cup \{-2\} \cup [1, 3] \)
\( x^4 \lt 4x^2 + 12 \) eşitsizliğinin çözüm kümesi nedir?
Çözümü GösterTüm terimleri aynı tarafta toplayalım.
\( x^4 - 4x^2 - 12 \lt 0 \)
Eşitsizliğin sol tarafını çarpanlarına ayıralım.
\( (x^2 - 6)(x^2 + 2) \lt 0 \)
\( (x - \sqrt{6})(x + \sqrt{6})(x^2 + 2) \lt 0 \)
Eşitsizliğin kritik noktaları her bir çarpanı sıfır yapan değerlerdir.
\( x - \sqrt{6} = 0 \Longrightarrow x = +\sqrt{6} \)
\( x + \sqrt{6} = 0 \Longrightarrow x = -\sqrt{6} \)
\( x^2 + 2 \) ifadesi her zaman pozitif olduğu için ifadeyi sıfır yapan reel sayı \( x \) değeri yoktur.
İşaret tablosunu çizelim.
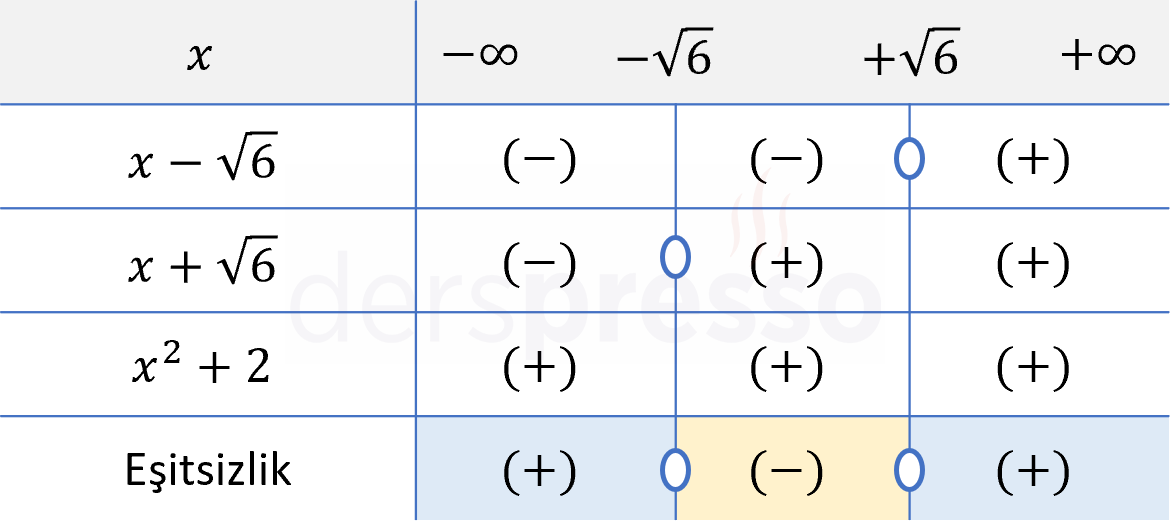
\( x^4 - 4x^2 - 12 \) ifadesinin negatif olduğu aralık eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in (-\sqrt{6}, \sqrt{6}) \)
\( x^5 - 179x^3 + 1690x \) ifadesini negatif yapan kaç farklı pozitif \( x \) tam sayı değeri vardır?
Çözümü GösterVerilen ifadeyi bir eşitsizlik şeklinde yazarak çözüm kümesini bulalım.
\( x^5 - 179x^3 + 1690x \lt 0 \)
5. dereceden ifadeyi çarpanlarına ayıralım.
\( x(x^4 - 179x^2 + 1690) \lt 0 \)
\( x(x^2 - 10)(x^2 - 169) \lt 0 \)
\( x(x - \sqrt{10})(x + \sqrt{10})(x - 13)(x + 13) \lt 0 \)
Her bir çarpanı sıfır yapan \( \{0, \pm \sqrt{10}, \pm 13\} \) değerleri eşitsizliğin kritik noktalarıdır.
Bu kritik noktalar reel sayı doğrusunda \( (-\infty, -13) \), \( (-13, -\sqrt{10}) \), \( (-\sqrt{10}, 0) \), \( (0, \sqrt{10}) \), \( (\sqrt{10}, 13) \) ve \( (13, \infty) \) aralıklarını oluşturur.
Bir işaret tablosu hazırlayalım.
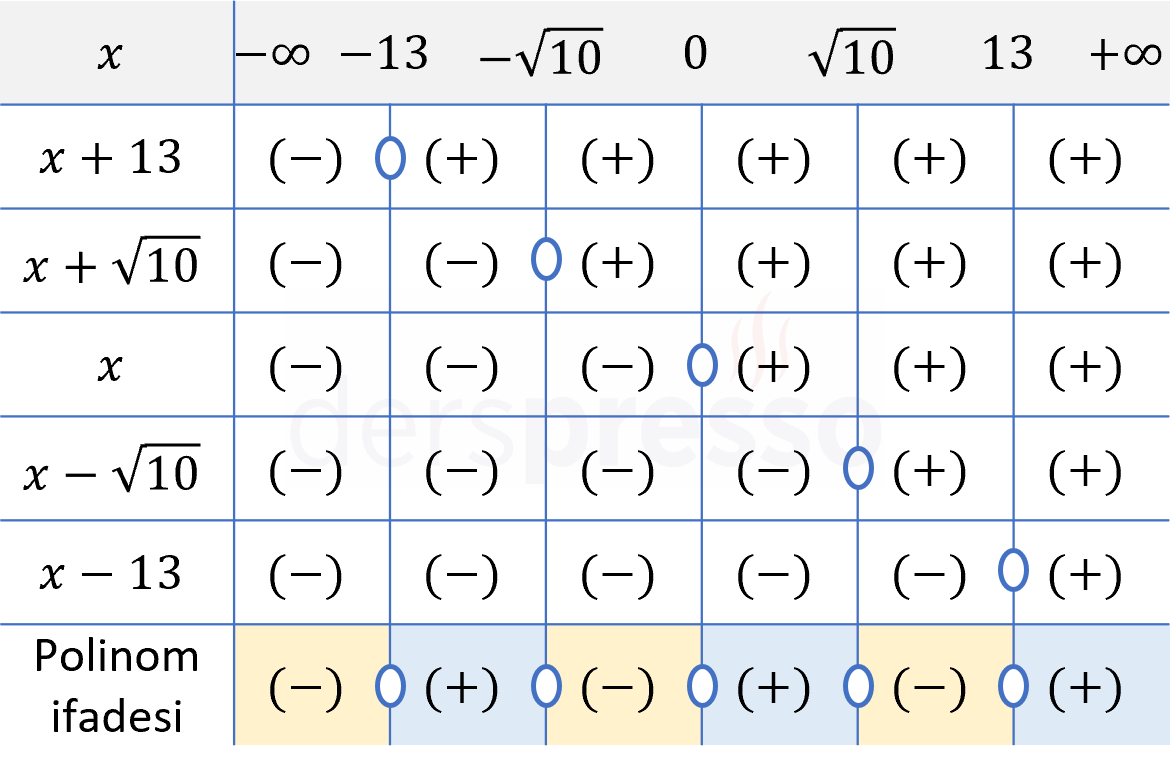
Çarpanları ve her aralıktaki işaretlerini tabloya birer satır olarak ekleyelim.
Polinom ifadesinin her aralıktaki işareti, çarpanların ilgili aralıktaki işaretlerinin çarpımına eşittir.
Polinom ifadesi her bir çarpanı sıfır yapan \( \{0, \pm \sqrt{10}, \pm 13\} \) değerlerinde sıfır olur.
Verilen eşitsizlikte \( \lt \) sembolü kullanıldığı için polinom ifadesinin negatif olduğu aralık ve değerler eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in (-\infty, -13) \cup (-\sqrt{10}, 0) \cup (\sqrt{10}, 13) \)
Bu aralıktaki pozitif \( x \) tam sayı değerleri aşağıdaki gibidir.
\( x \in \{4, 5, 6, 7, 8, 9, 10, 11, 12\} \)
Verilen ifadeyi negatif yapan 9 farklı pozitif tam sayı \( x \) değeri vardır.
\( \sqrt{x - 1} \cdot (x^2 - 3x - 10) = 0 \) ifadesinin kaç tane reel sayı kökü vardır?
Çözümü Gösterİfadeyi çarpanlarına ayıralım.
\( \sqrt{x - 1} \cdot (x - 5)(x + 2) = 0 \)
Her bir çarpanı sıfır yapan değerler denklemin kökleridir.
\( x_1 = 1 \), \( x_2 = 5 \) ya da \( x_3 = -2 \)
Bu değerlerden \( x = -2 \) köklü ifadeyi tanımsız yaptığı için denklemin geçerli bir çözümü olamaz.
Buna göre denklemin iki reel sayı kökü vardır.
Çözüm kümesi: \( x \in \{1, 5\} \)
\( (x + 4)(2^x - 8)(5^{-x} - 1) \lt 0 \) eşitsizliğinin çözüm kümesini bulunuz.
Çözümü GösterEşitsizlikteki her bir çarpanı sıfır yapan \( x \) değerleri eşitsizliğin kritik noktalarıdır.
Üstel ifadeleri sıfır yapan \( x \) değerlerini bulalım.
\( 2^x - 8 = 0 \Longrightarrow x = 3 \)
\( 5^{-x} - 1 = 0 \Longrightarrow x = 0 \)
Buna göre eşitsizlikteki her bir çarpanı sıfır yapan \( \{-4, 0, 3\} \) değerleri eşitsizliğin kritik noktalarıdır.
Bu kritik noktalar reel sayı doğrusunda \( (-\infty, -4) \), \( (-4, 0) \), \( (0, 3) \) ve \( (3, \infty) \) aralıklarını oluşturur.
Bir işaret tablosu hazırlayalım.
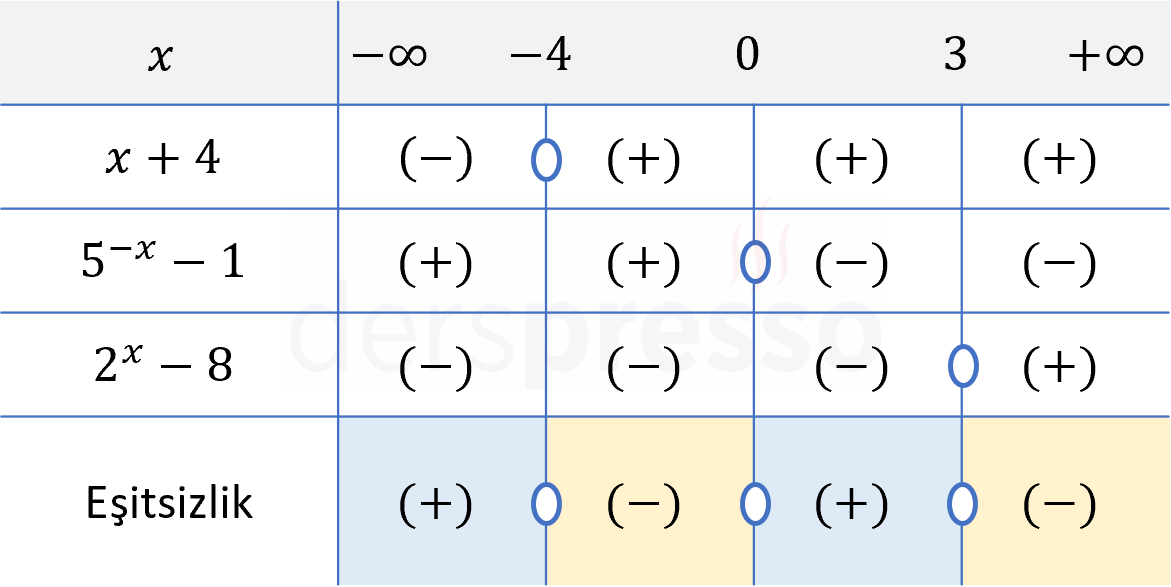
İfadedeki çarpanları ve her aralıktaki işaretlerini tabloya birer satır olarak ekleyelim.
\( a \gt 1 \) olmak üzere,
\( a^x - b \) formundaki bir çarpan (grafiği artan olduğu için) kritik noktada sıfır, kritik noktanın solunda negatif, sağında pozitif olur.
\( a^{-x} - b \) formundaki bir çarpan (grafiği azalan olduğu için) kritik noktada sıfır, kritik noktanın solunda pozitif, sağında negatif olur.
İfadenin her aralıktaki işareti, çarpanların ilgili aralıktaki işaretlerinin çarpımına eşittir.
Verilen eşitsizlikte \( \lt \) sembolü kullanıldığı için eşitsizliğin negatif olduğu aralık ve değerler eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in (-4, 0) \cup (3, \infty) \)