Koni
Bir düzlemde bulunan bir dairenin her noktasını, bu düzlem dışındaki bir noktayla birleştiren doğru parçalarının oluşturduğu üç boyutlu şekle koni denir.
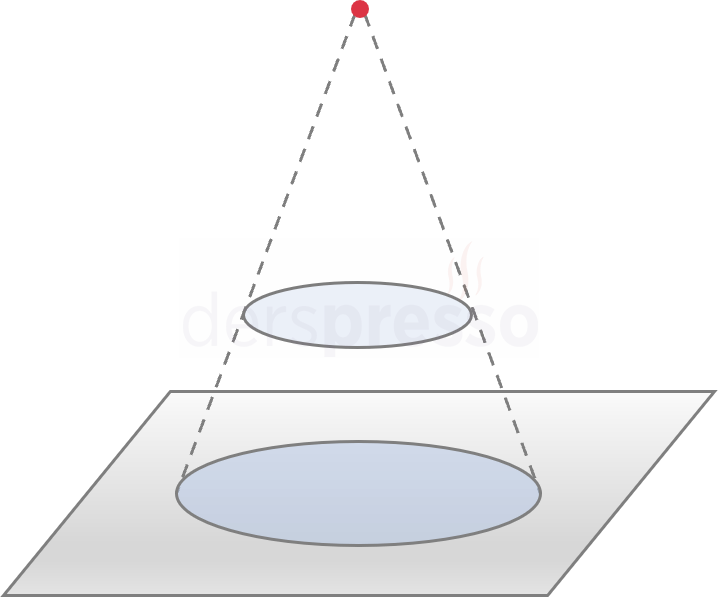
Dik ve Eğik Koni
Bir koninin tepe noktasının taban üzerindeki izdüşümü tabanın dairenin merkez noktası ise bu koniye dik koni denir. Bu izdüşüm farklı bir noktaya karşılık geliyorsa, bu koniye eğik koni denir.
Hem dik hem de eğik koninin yüksekliği, alt ve üst paralel tabanlar arasındaki dik ve en kısa mesafedir.
Bir koni ve açık hali aşağıdaki gibidir.
Dik koninin yan yüzü bir daire dilimidir. Taban yarıçapı ile yan yüz yüksekliği arasında aşağıdaki ilişkiyi kurabiliriz.
\( x \) koninin yan yüzünün oluşturduğu daire diliminin merkez açısı olmak üzere,
\( \dfrac{r}{l} = \dfrac{x}{360°} \)
Koninin Yüzey Alanı
Koninin toplam yüzey alanı, taban ve yan yüz (yanal) alanlarının toplamına eşittir.
\( \text{Yüzey Alanı} = \text{Taban Alanı} + \text{Yanal Alan} \)
\( \text{Yüzey Alanı} = \pi r^2 + \pi r \cdot l \)
İSPATI GÖSTER
Koninin Yanal Alan Formülü
Yan yüzünün açılımı bir daire dilimi olan koninin yanal alanını, yarıçapı \( l \) olan tam dairenin alanı ile açılımın merkez açısının 360'a oranını çarparak bulabiliriz.
\( A = \pi \cdot l^2 \cdot \dfrac{x}{360} \)
Bu daire diliminin yay uzunluğu aynı zamanda koninin tabanının çevre uzunluğuna eşittir.
\( 2\pi \cdot l \cdot \dfrac{x}{360} = 2\pi \cdot r \)
\( x = \dfrac{360r}{l} \)
Bu \( x \) değerini yukarıdaki alan formülünde yerine koyalım.
\( A = \pi \cdot l^2 \cdot \dfrac{\frac{360r}{l}}{360} \)
\( = \pi r \cdot l \)
Koninin Hacmi
Dik ve eğik konilerin hacmi, taban alanı ve yüksekliğin çarpımının üçte birine eşittir. Eğik konide bahsettiğimiz gibi, hem dik hem de eğik koninin yüksekliği alt ve üst tabanlar arasındaki dik ve en kısa mesafedir.
\( \text{Hacim} = \dfrac{1}{3} \cdot \text{Taban Alanı} \cdot \text{Yükseklik} \)
\( \text{Hacim} = \dfrac{1}{3} \pi r^2 \cdot h \)
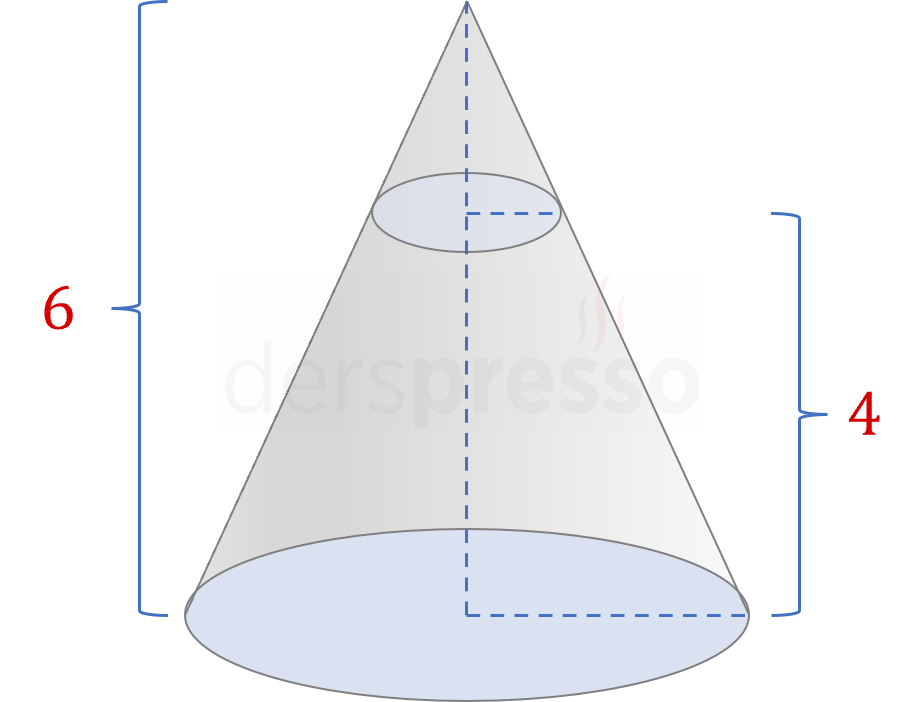
Yüksekliği 6 birim olan dik koni şeklindeki bir su deposu, tabandan 4 birim yükseklikte ve tabana paralel bir kesit kullanılarak iki bölmeye ayrılıyor.
Bölmelerin hacimleri farkı 200 birimküp olduğuna göre, su deposunun yarıçapı kaç birimdir? (\( \pi = 3 \))
Çözümü GösterÜstte kalan bölme yine koni şeklindedir.
Küçük koninin yüksekliği \( 6 - 4 = 2 \) birim olduğuna göre, konilerin benzerlik oranı \( \frac{1}{3} \) olur.
Buna göre konilerin hacimleri oranı \( \frac{1}{27} \) olur.
Küçük koninin hacmine \( V \) dersek büyük koninin hacmi \( 27V \) olur.
Buna göre oluşan iki bölmenin hacimleri \( V \) ve \( 27V - V = 26V \) olur.
Bölmelerin hacimleri farkı 200 birimküptür.
\( 26V - V = 25V = 200 \)
\( V = 8 \)
Buna göre küçük koninin hacmi 8 birimküptür.
\( V = \dfrac{1}{3}\pi r^2 \cdot h = 8 \)
\( \dfrac{1}{3}3 r^2 \cdot 2 = 8 \)
\( r^2 = 4 \)
\( r = 2 \)
Küçük koninin yarıçapı 2 birimdir.
Benzerlik oranı \( \frac{1}{3} \) olduğundan büyük koninin yani su deposunun yarıçapı 6 birim olarak bulunur.