Bir Örnekle Permütasyon
Bu bölümde örnek olarak 4 harfli "KEDİ" kelimesinin farklı uzunluklardaki permütasyonlarını inceleyeceğiz.
\( A = \{ \text{K, E, D, İ} \} \)
A Kümesinin 4'lü Permütasyonları
Permütasyon formülüne göre \( A \) kümesinin 4'lü permütasyonlarının sayısı 24'tür.
\( P(4, 4) = \dfrac{4!}{(4 - 4)!} = \dfrac{4!}{0!} = 24 \)
Permütasyon sayısı kutu yöntemiyle aşağıdaki şekilde hesaplanabilir.

Bu 24 permütasyon aşağıdaki gibidir.
KEDİ, KEİD, KDEİ, KDİE, KİED, KİDE
EKDİ, EKİD, EDKİ, EDİK, EİKD, EİDK
DKEİ, DKİE, DEKİ, DEİK, DİKE, DİEK
İKED, İKDE, İEKD, İEDK, İDKE, İDEK
A Kümesinin 3'lü Permütasyonları
Permütasyon formülüne göre \( A \) kümesinin 3'lü permütasyonlarının sayısı 24'tür.
\( P(4, 3) = \dfrac{4!}{(4 - 3)!} = \dfrac{4!}{1!} = 24 \)
Permütasyon sayısı kutu yöntemiyle aşağıdaki şekilde hesaplanabilir.
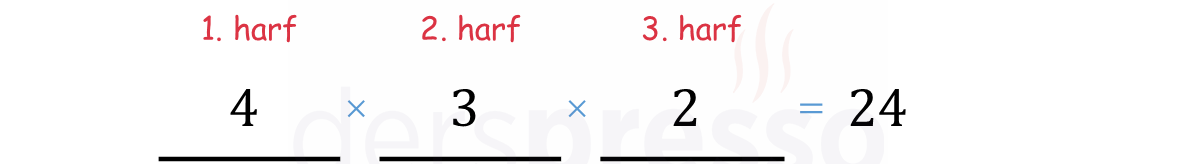
Bu 24 permütasyon aşağıdaki gibidir.
KED, KEİ, KDE, KDİ, KİE, KİD
EKD, EKİ, EDK, EDİ, EİK, EİD
DKE, DKİ, DEK, DEİ, DİK, DİE
İKE, İKD, İEK, İED, İDK, İDE
A Kümesinin 2'li Permütasyonları
Permütasyon formülüne göre \( A \) kümesinin 2'li permütasyonlarının sayısı 12'dir.
\( P(4, 2) = \dfrac{4!}{(4 - 2)!} = \dfrac{4!}{2!} = 12 \)
Permütasyon sayısı kutu yöntemiyle aşağıdaki şekilde hesaplanabilir.

Bu 12 permütasyon aşağıdaki gibidir.
KE, KD, Kİ
EK, ED, Eİ
DK, DE, Dİ
İK, İE, İD
A Kümesinin 1'li Permütasyonları
Permütasyon formülüne göre \( A \) kümesinin 1'li permütasyonlarının sayısı 4'tür.
\( P(4, 1) = \dfrac{4!}{(4 - 1)!} = \dfrac{4!}{3!} = 4 \)
Permütasyon sayısı kutu yöntemiyle aşağıdaki şekilde hesaplanabilir.

Bu 4 permütasyonun her biri KEDİ kelimesinin bir harfinden oluşur.
K, E, D, İ
A Kümesinin 0'lı Permütasyonları
Permütasyon formülüne göre \( A \) kümesinin (ve tüm sayıların) 0'lı permütasyonlarının sayısı 1'dir. Buna göre bir kümenin 0 elemanlı sadece bir dizilişi olabilir, o da boş kümedir.
\( P(4, 0) = \dfrac{4!}{(4 - 0)!} = \dfrac{4!}{4!} = 1 \)
Bu 1 permütasyon boş kümedir.
\( \emptyset \)