Açı Tipleri
Açılar ölçülerine ve birbirlerine göre durumlarına göre aşağıdaki şekilde tanımlanırlar.
Ölçülerine Göre Açı Tipleri
Açılar ölçülerine göre aşağıdaki şekilde adlandırılırlar.
Dar Açı
Ölçüsü \( (0°, 90°) \) aralığında olan açılara dar açı denir.

Dik Açı
Ölçüsü \( 90° \) olan açılara dik açı denir. Dik açılar içinde nokta bulunan küçük bir kare ile gösterilir.

Birbirini dik kesen iki doğru ya da doğru parçası \( \perp \) sembolü ile gösterilir.
\( d_1 \) ve \( d_2 \) doğruları birbirine dik ise,
\( d_1 \perp d_2 \)
Geniş Açı
Ölçüsü \( (90°, 180°) \) aralığında olan açılara geniş açı denir.
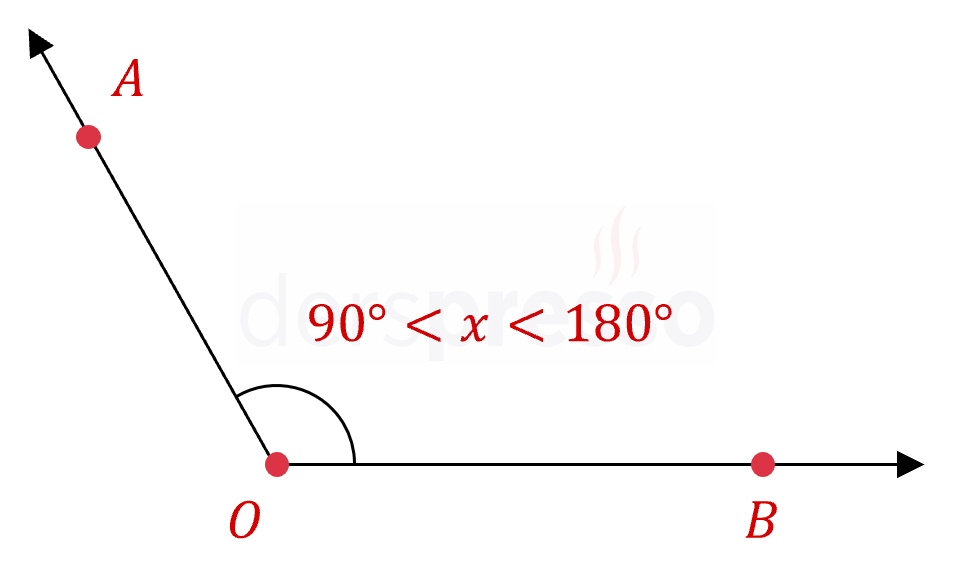
Doğru Açı
Ölçüsü \( 180° \) olan açılara doğru açı denir.

Tam Açı
Ölçüsü \( 360° \) olan açılara tam açı denir.

Birbirini Tamamlayan Açılar
Tümler Açılar
Birbirini \( 90° \)'ye tamamlayan açılara tümler açılar denir.
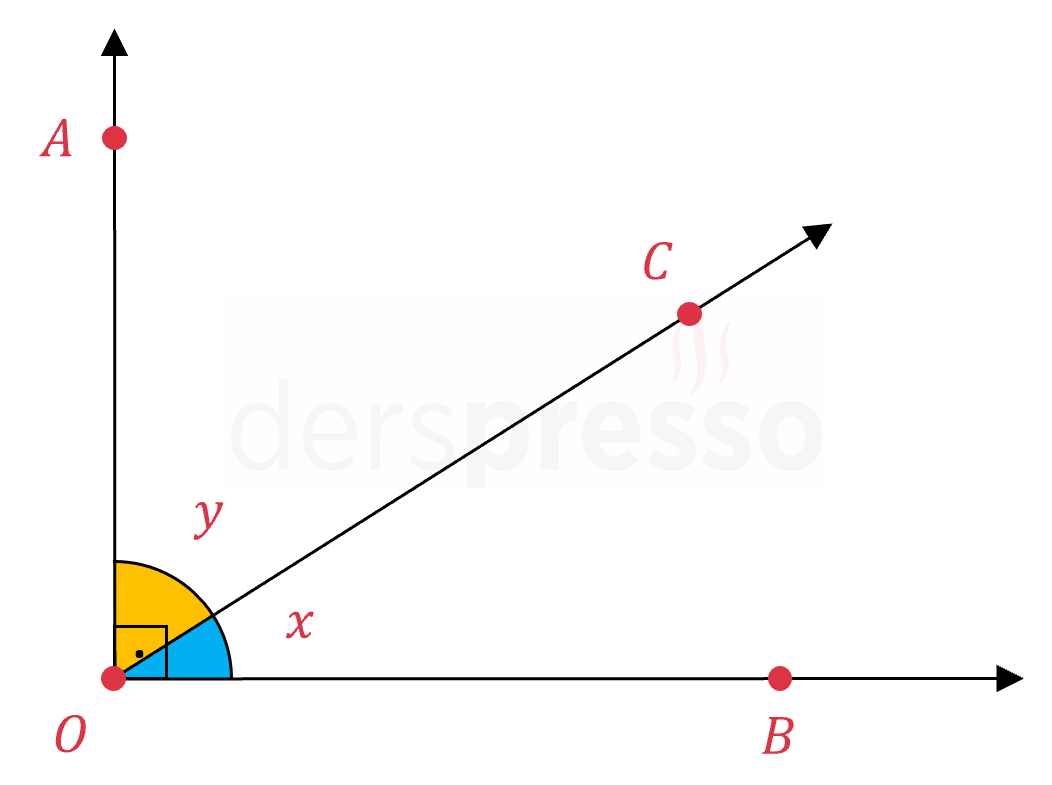
\( x + y = 90° \)
Aynı açıya tümler olan açılar eş açılardır.
Bütünler Açılar
Birbirini \( 180° \)'ye tamamlayan açılara bütünler açılar denir.

\( x + y = 180° \)
Aynı açıya bütünler olan açılar eş açılardır.
Diğer Açılar
Komşu Açılar
Köşeleri ve bir kenarları ortak, diğer kenarları ortak kenarın farklı taraflarında bulunan açılara komşu açı denir. Komşu açıların iç bölgeleri birbirinden ayrıktır.

Yukarıdaki şekle göre aşağıdaki açılar komşu açılardır.
\( \widehat{AOC} \) ve \( \widehat{COD} \): \( [OC \) kenarı ortak.
\( \widehat{AOD} \) ve \( \widehat{DOB} \): \( [OD \) kenarı ortak.
Yukarıdaki şekle göre aşağıdaki açılar komşu olmayan açılardır.
\( \widehat{AOC} \) ve \( \widehat{DOB} \): Ortak kenar yok.
\( \widehat{AOD} \) ve \( \widehat{COD} \): \( [OD \) kenarı ortak, ama diğer kenarlar ortak kenarın farklı taraflarında değil.
Birbirini \( 90° \)'ye tamamlayan komşu açılara komşu tümler açılar, birbirini \( 180° \)'ye tamamlayan komşu açılara komşu bütünler açılar denir.
İç/Dış Açılar
Kapalı bir geometrik şeklin iç bölgesinde bulunan açılara iç açı, bir iç açının komşu bütünleri olan açılara dış açı denir.

Tanımda belirttiğimiz gibi, bir iç açı ve bu iç açıya komşu olan dış açı bütünler açılardır ve toplamları \( 180° \)'dir.
Bir açı tümler açısının dörtte birine eşitse bu açının bütünler açısı kaç derecedir?
Çözümü GösterBu açının ölçüsüne \( x \) derece diyelim.
Ölçüsü \( x \) derece olan bir açının tümler açısı \( 90 - x \), bütünler açısı \( 180 - x \) derecedir.
Açı tümler açısının dörtte birine eşittir.
\( x = \dfrac{90 - x}{4} \)
\( x = 18° \)
\( x \) açısının bütünler açısını bulalım.
\( 180 - x = 180 - 18 \)
\( = 162° \) bulunur.

\( m(\widehat{ABC}) = 3x + 30 \)
\( \widehat{ABC} \) dar açı olduğuna göre, \( x \) değerinin alabileceği kaç farklı tam sayı değeri vardır?
Çözümü Göster\( m(\widehat{ABC}) \) dar açıdır.
\( 0° \lt m(\widehat{ABC}) \lt 90° \)
\( 0 \lt 3x + 30 \lt 90 \)
\( -30 \lt 3x \lt 60 \)
\( -10 \lt x \lt 20 \)
Buna göre \( x \)'in -9 ve 19 aralığında alabileceği \( 19 - (-9) + 1 = 29 \) farklı tam sayı değer vardır.

\( [FB] \perp [AC] \)
\( m(\widehat{ABD}) = 25° \)
\( m(\widehat{ABD}) = m(\widehat{DBE}\))
\( m(\widehat{EBF}) = m(\widehat{FBG}\))
\( m(\widehat{GBH}) = m(\widehat{HBC}\))
olduğuna göre, \( m(\widehat{HBE}\)) kaç derecedir?
Çözümü Göster\( m(\widehat{ABD}) = a = 25° \)
\( m(\widehat{EBF}) = b \)
\( m(\widehat{GBH}) = c \) diyelim.
\( \widehat{ABC} \) doğru açıdır.
\( 2a + 2b + 2c = 180° \)
\( 2 \cdot 25 + 2b + 2c = 180° \)
\( b + c = 65° \)
\( \widehat{FBC} \) dik açıdır.
\( b + 2c = 90° \)
İki denklemi ortak çözelim.
\( c = 25°, \quad b = 40° \)
\( m(\widehat{HBE}) = 2b + c = 105° \) bulunur.

\( [EF] \parallel [AD], [EF] \perp [BF] \)
\( m(\widehat{DBC}) = x \)
\( m(\widehat{ADB}) = 2x + 40 \)
olduğuna göre, \( \widehat{ADB} \) açısının ölçüsü nedir?
Çözümü Göster\( D \) noktasıdan \( [BF] \) doğru parçasına bir dik indirelim.
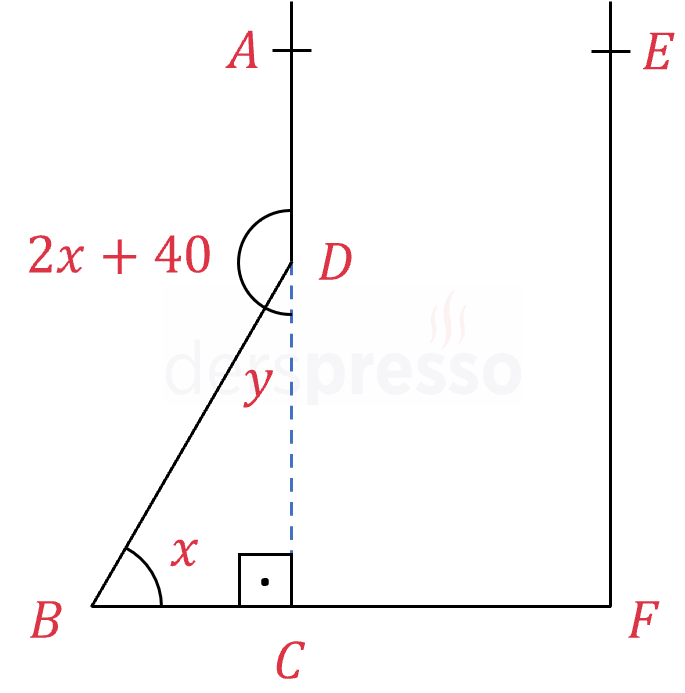
Oluşan üçgende \( \widehat{ADB} \) açısının bütünler açısına \( y \) diyelim.
\( y = 180 - (2x + 40) \)
\( y = 140 - 2x \)
\( \overset{\triangle}{BCD} \) dik üçgen olduğu için \( x \) ve \( y \) tümler açılardır.
\( x + y = 90 \)
İki denklemi ortak çözelim.
\( x = 50°, \quad y = 40° \)
\( m(\widehat{ADB}) = 2x + 40 = 140° \) bulunur.