Binom Açılımında Terim Bulma
\( (x + y)^n \) ifadesinin açılımındaki \( (k + 1) \). terim aşağıda formülle bulunur.
Binom açılımının \( (k + 1) \). terimi:
\( T_{k + 1} = \binom{n}{k} x^{n - k} y^k \)
Bu formülde dikkat edilmesi gereken husus, belirli bir \( k \) değeri için formülün açılımın \( k \). değil, \( (k + 1). \) terimini veriyor olmasıdır.
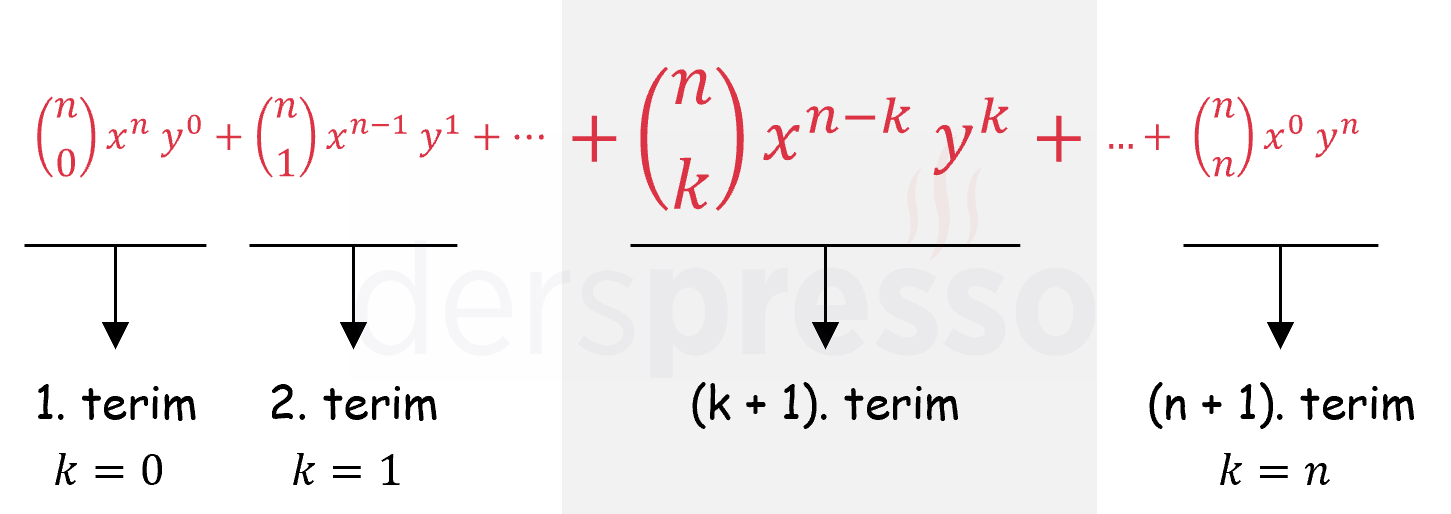
\( (2x - 3y^2)^5 \) ifadesinin açılımındaki 1., 2. ve sonuncu terimleri bulalım.
Birinci terim (\( k = 0 \)):
\( T_1 = \binom{5}{0} (2x)^5(-3y^2)^0 \)
\( = 32x^5 \)
İkinci terim (\( k = 1 \)):
\( T_2 = \binom{5}{1} (2x)^4(-3y^2)^1 \)
\( = 5(16x^4)(-3y^2) \)
Sonuncu terim (\( k = 5 \)):
\( T_6 = \binom{5}{5} (2x)^0(-3y^2)^5 \)
\( = -243y^{10} \)
Ortadaki Terim
\( n \) çift sayı ise \( n \). dereceden bir binom ifadenin \( (\frac{n}{2} + 1) \). terimi ortadaki terimdir. Bu terimi bulmak için formülde \( k = \frac{n}{2} \) koymamız gerekir.
\( n \) tek sayı ise terim sayısı çift sayı olacağı için açılımda ortadaki terim olmaz.
\( n \) çift sayı olmak üzere,
Ortadaki terim (\( k = \frac{n}{2} \)):
\( T_{\frac{n}{2} + 1} = \binom{n}{\frac{n}{2}} x^{\frac{n}{2}}y^{\frac{n}{2}} \)
\( (3x - y^2)^8 \) açılımındaki ortadaki terimi bulalım.
Ortadaki terim \( k = \frac{8}{2} = 4 \) verdiğimizde bulacağımız \( 4 + 1 = 5 \). terimdir.
\( T_5 = \binom{8}{4} (3x)^4(-y^2)^4 \)
\( = 70 (81x^4)(y^8) = 5670x^4y^8 \)
\( a = \tan{40°} \) ve \( b = \tan{50°} \) olmak üzere,
\( (a + b)^{10} \) ifadesinin açılımında ortadaki terim nedir?
Çözümü Göster\( n \) çift sayı olduğu için \( \frac{n}{2} + 1 = \frac{10}{2} + 1 = 6 \). terim ortadaki terimdir.
6. terimi bulmak için \( k = 5 \) verelim.
\( T_6 = \binom{10}{5} (\tan{40°})^5 (\tan{50°})^5 \)
\( \tan{50°} = \cot{40°} \) ve \( \tan{40°} \cdot \cot{40°} = 1 \) özdeşliklerini kullanalım.
\( = \binom{10}{5} (\tan{40°})^5 (\cot{40°})^5 \)
\( = \binom{10}{5} (\tan{40°} \cdot \cot{40°})^5 \)
\( = \binom{10}{5} 1^5 = 252 \) bulunur.
Baştan ve Sondan Terim Sayıları
Binom açılımındaki bir terimin baştan ve sondan kaçıncı terim olduğunu gösteren sayıların toplamı toplam terim sayısının bir fazlasına, yani binom ifadenin derecesinin iki fazlasına eşittir.
Bir örnek vermek gerekirse \( (x + y)^6 \) ifadesinin açılımında 7 terim vardır. Baştan 3. terim sondan 5. terimdir (3 + 5 = 7 + 1) ve sondan 2. terim baştan 6. terimdir (6 + 2 = 7 + 1).

Bir binom açılımında sondan belirli bir terimi bulmak için önce bu terimin baştan kaçıncı terim olduğu bulunur, daha sonra \( (k + 1). \) terim formülü ile istenen terim bulunur.
\( (x - 2y)^8 \) ifadesinin açılımında sondan 4. terimi bulalım.
8. dereceden bir binom ifadenin açılımında 9 terim vardır, dolayısıyla sondan 4. terim baştan 6. terimdir (\( 6 + 4 = 9 + 1 \)).
Baştan 6. terim (\( k = 5 \)):
\( T_6 = \binom{8}{5} x^3 (-2y)^5 \)
\( = 56 x^3(-32y^5) = -1792 x^3y^5 \)
Aşağıdaki ifadelerin açılımındaki istenen terimleri bulunuz.
(a) \( (x^2 - 2)^7 \) açılımındaki 5. terim
(b) \( (2x + \dfrac{y}{2})^{14} \) açılımındaki 12. terim
(c) \( (\sqrt{x} - 1)^{20} \) açılımındaki 17. terim
Çözümü Göster\( (x + y)^n \) formundaki bir ifadenin açılımındaki \( (k + 1) \). terim aşağıdaki formülle bulunur.
\( T_{k+1} = \binom{n}{k} x^{n - k}y^k \)
(a) seçeneği:
\( (x^2 - 2)^7 \) ifadesindeki 5. terimi bulmak için \( k = 4 \) verelim.
\( T_5 = \binom{7}{4}\ (x^2)^{7 - 4}\ (-2)^4 \)
\( = 35 \cdot x^6 \cdot 16 \)
\( = 560x^6 \)
(b) seçeneği:
\( (2x + \dfrac{y}{2})^{14} \) ifadesindeki 12. terimi bulmak için \( k = 11 \) verelim.
\( T_{12} = \binom{14}{11}\ (2x)^{14 - 11}\ (\dfrac{y}{2})^{11} \)
\( = 364 \cdot 2^3x^3 \cdot \dfrac{y^{11}}{2^{11}} \)
\( = \dfrac{91x^3y^{11}}{64} \)
(c) seçeneği:
\( (\sqrt{x} - 1)^{20} \) ifadesindeki 17. terimi bulmak için \( k = 16 \) verelim.
\( T_{17} = \binom{20}{16}\ (\sqrt{x})^{20 - 16}\ 1^{16} \)
\( = 4845 \cdot x^2 \cdot 1 \)
\( = 4845x^2 \)
\( (5 + 4x)^5 \) ifadesinin açılımındaki \( x^2 \)'li terimin katsayısı kaçtır?
Çözümü Göster\( (x + y)^n \) formundaki bir ifadenin açılımındaki \( (k + 1) \). terim aşağıdaki formülle bulunur.
\( T_{k + 1} = \binom{n}{k} x^{n - k}y^k \)
Binom ifadenin birinci terimi sabit olduğu için \( x^2 \)'li terim \( k = 2 \) olduğunda elde edilir.
\( k = 2 \) vererek açılımın 3. terimini bulalım.
\( T_3 = \binom{5}{2} \cdot 5^3 \cdot (4x)^2 \)
\( = 10 \cdot 125 \cdot 16x^2 \)
\( = 20000x^2 \)
\( x^2 \)'li terimin katsayısı \( 20000 \) olarak bulunur.
\( (a^4 + \dfrac{2}{a})^5 \) ifadesinin açılımındaki \( a^{10} \)'lu terimin katsayısı kaçtır?
Çözümü Göster\( (x + y)^n \) ifadesinin açılımındaki \( (k + 1). \) terim aşağıdaki formülle bulunur.
\( T_{k + 1} = \binom{n}{k} x^{n - k}y^k \)
Buna göre, \( (a^4 + \frac{2}{a})^5 \) ifadesinin açılımındaki \( (k + 1). \) terim aşağıdaki gibi olur.
\( T_{k + 1} = \binom{5}{k}(a^4)^{5 - k}(\frac{2}{a})^k \)
\( = \binom{5}{k}a^{20 - 4k}\frac{2^k}{a^k} \)
\( = \binom{5}{k}2^k a^{20 - 5k} \)
\( a \)'nın üssünün 10 olması için \( k \)'nın alması gereken değeri bulalım.
\( 20 - 5k = 10 \Longrightarrow k = 2 \)
Bu değeri yukarıdaki genel terim bulma formülünde yerine koyalım.
\( T_3 = \binom{5}{2}2^2 a^{20 - 5(2)} \)
\( = 40a^{10} \)
Buna göre \( a^{10} \)'lu terimin katsayısı 40'tır.
\( (x^3 - \dfrac{1}{x^2})^{10} \) açılımında \( x^5 \) 'li terimin katsayısı kaçtır?
Çözümü Göster\( (x + y)^n \) formundaki bir ifadenin açılımındaki \( (k + 1) \). terim aşağıdaki formülle bulunur.
\( T_{k + 1} = \binom{n}{k} x^{n - k}y^k \)
Bu formülü verilen ifadeye uygulayalım.
\( T_{k + 1} = \binom{10}{k}(x^3)^{10 - k}((-x)^{-2})^{k} \)
\( = \binom{10}{k}x^{30 - 3k}(-x)^{-2k} \)
\( = \binom{10}{k}x^{30 - 5k} \)
\( x \)'in üssünün 5 olması için \( k \)'nın alması gereken değeri bulalım.
\( 30 - 5k = 5 \Longrightarrow k = 5 \)
Bu değeri yukarıdaki genel terim bulma formülünde yerine koyalım.
\( T_6 = \binom{10}{5}x^{30 - 5(5)} \)
\( = 252x^5 \)
Buna göre \( a^5 \)'li terimin katsayısı 252'dir.
\( (\sqrt[3]{x} - \sqrt{x})^{13} \) ifadesinin açılımında \( x^5 \)'li terimin katsayısı kaçtır?
Çözümü Göster\( (x + y)^n \) formundaki bir ifadenin açılımındaki \( (k + 1) \). terim aşağıdaki formülle bulunur.
\( T_{k + 1} = \binom{n}{k} x^{n - k}y^k \)
Bu formülü verilen ifadeye uygulayalım.
\( T_{k + 1} = \binom{13}{k}(\sqrt[3]{x})^{13 - k}(-\sqrt{x})^k \)
\( = \binom{13}{k}(\sqrt[3]{x})^{13 - k}(\sqrt{x})^k(-1)^k \)
\( = \binom{13}{k}x^{\frac{13 - k}{3}}x^{\frac{k}{2}}(-1)^k \)
\( = \binom{13}{k}x^{\frac{13 - k}{3} + \frac{k}{2}}(-1)^k \)
\( = \binom{13}{k}x^{\frac{26 + k}{6}}(-1)^k \)
\( x \)'in üssünün 5 olması için \( k \)'nın alması gereken değeri bulalım.
\( \dfrac{26 + k}{6} = 5 \)
\( k = 4 \)
\( k = 4 \) vererek açılımın 5. terimini bulalım.
\( T_5 = \binom{13}{4}x^{\frac{26 + 4}{6}}(-1)^4 \)
\( = 715x^5 \)
Buna göre \( x^5 \)'li terimin katsayısı 715'tir.
\( (\dfrac{16}{3x} - \dfrac{27x^3}{4})^8 \) ifadesinin açılımındaki \( x^{20} \)'li terimin katsayısı kaçtır?
Çözümü Göster\( (x + y)^n \) formundaki bir ifadenin açılımındaki \( (k + 1) \). terim aşağıdaki formülle bulunur.
\( T_{k + 1} = \binom{n}{k} x^{n - k}y^k \)
Bu formülü verilen ifadeye uygulayalım.
\( T_{k + 1} = \binom{8}{k} \cdot (\dfrac{2^4}{3x})^{8 - k} \cdot (-\dfrac{3^3x^3}{2^2})^k \)
\( = \binom{8}{k} \cdot \dfrac{2^{32 - 4k}}{3^{8 - k} \cdot x^{8 - k}} \cdot \dfrac{(-1)^k \cdot 3^{3k} \cdot x^{3k}}{2^{2k}} \)
\( = \binom{8}{k} \cdot 2^{32 - 6k} \cdot (-1)^k \cdot 3^{4k - 8} \cdot x^{4k - 8} \)
\( x \)'in üssünün 20 olması için \( k \)'nın alması gereken değeri bulalım.
\( 4k - 8 = 20 \Longrightarrow k = 7 \)
\( k = 7 \) vererek açılımın 8. terimini bulalım.
\( T_8 = \binom{8}{7} \cdot 2^{32 - 6(7)} \cdot (-1)^7 \cdot 3^{4(7) - 8} \cdot x^{4(7) - 8} \)
\( = 8 \cdot 2^{-10} \cdot (-1) \cdot 3^{20} \cdot x^{20} \)
\( = -\dfrac{3^{20}}{2^7}x^{20} \)
\( x^{20} \)'li terimin katsayısı \( -\dfrac{3^{20}}{2^7} \) olarak bulunur.
\( (2x^2 + 8y)^n \) ifadesinin açılımındaki bir terim \( Ax^8y^5 \) olduğuna göre, \( n \) doğal sayısı kaçtır?
Çözümü Göster\( (x + y)^n \) formundaki bir ifadenin açılımındaki \( (k + 1) \). terim aşağıdaki formülle bulunur.
\( T_{k + 1} = \binom{n}{k} x^{n - k}y^k \)
Bu formülü verilen ifadeye uygulayalım.
\( T_{k + 1} = \binom{n}{k}(2x^2)^{n - k}(8y)^k \)
\( = \binom{n}{k}2^{n - k}x^{2n - 2k}2^{3k}y^k \)
\( = \binom{n}{k}2^{n + 2k}x^{2n - 2k}y^k \)
İfadenin açılımındaki bir terim \( Ax^8y^5 \) olduğuna göre iki ifadeyi eşitleyelim.
\( \binom{n}{k}2^{n + 2k}x^{2n - 2k}y^k = Ax^8y^5 \)
İfadenin her iki tarafındaki \( x \) ve \( y \) değişkenlerinin kuvvetleri birbirine eşit olmalıdır.
\( y \) için:
\( k = 5 \)
\( x \) için:
\( 2n - 2k = 8 \)
\( 2n - 2(5) = 8 \)
\( n = 9 \) olarak bulunur.
\( (x - 2y)^n \) ifadesinin açılımındaki terimlerden biri \( Ax^2y^4 \) olduğuna göre, \( \frac{A}{n} \) kaçtır?
Çözümü GösterTerimleri birinci dereceden değişkenler olan bir binom ifadenin açılımındaki her terimde dereceler toplamı \( n \) olur.
\( Ax^2y^4 \) açılımın terimlerinden biri olduğuna göre \( n = 2 + 4 = 6 \) olur.
\( (x + y)^n \) formundaki bir ifadenin açılımındaki \( (k + 1) \). terim aşağıdaki formülle bulunur.
\( T_{k + 1} = \binom{n}{k} x^{n - k}y^k \)
Bu formülü verilen ifadeye uygulayalım.
\( T_5 = \binom{6}{4} \cdot x^2 \cdot (-2y)^4 = Ax^2y^4 \)
\( = 15 \cdot x^2 \cdot 16y^4 = Ax^2y^4 \)
\( A = 15 \cdot 16 = 240 \)
\( \frac{A}{n} = \frac{240}{6} = 40 \) olarak bulunur.
\( x \gt y \) olmak üzere,
\( (a + b)^{17} \) ifadesinin açılımındaki terimlerden biri \( \binom{17}{x + y - 11}a^xb^y \) olduğuna göre, \( x - y \) kaçtır?
Çözümü GösterBinom açılımında çarpanların üslerinin toplamı tüm terimlerde \( n \)'ye eşit olur.
\( x + y = 17 \)
Buna göre verilen terim \( \binom{17}{6}a^xb^y \) olur.
\( \binom{17}{6} = \binom{17}{11} \) olduğu için \( (x, y) \) ikilisi \( (11, 6) \) ya da \( (6, 11) \) olabilir.
\( x \gt y \) olarak veriliyor.
Buna göre \( x = 11 \) ve \( y = 6 \) olur.
\( x - y = 5 \) bulunur.
\( (x^2y - \dfrac{x}{y})^9 = \ldots + m\dfrac{x^{13}}{y} + \ldots \)
eşitliğindeki \( m \) değeri kaçtır?
Çözümü Göster\( (x + y)^n \) formundaki bir ifadenin açılımındaki \( (k + 1) \). terim aşağıdaki formülle bulunur.
\( T_{k + 1} = \binom{n}{k} x^{n - k}y^k \)
Açılımda verilen terimi \( (k + 1) \). terim olarak kabul edelim.
\( T_{k + 1} = \binom{9}{k} (x^2y)^{9 - k} (-\dfrac{x}{y})^k \)
\( = \binom{9}{k} x^{18 - 2k} y^{9 - k} \dfrac{x^k}{y^k} (-1)^k \)
\( = \binom{9}{k} x^{18 - k} y^{9 - 2k} (-1)^k \)
Bu terimi soruda verilen açılımdaki terime eşitleyelim.
\( \binom{9}{k} x^{18 - k} y^{9 - 2k} (-1)^k = m\dfrac{x^{13}}{y} \)
\( 18 - k = 13 \)
\( 9 - 2k = -1 \)
Her iki eşitliği de sağlayan \( k \) değeri 5'tir.
\( k = 5 \) vererek açılımın 6. terimini bulalım.
\( T_6 = \binom{9}{5} x^{18 - 5} y^{9 - 2(5)} (-1)^k \)
\( = -126 x^{13} y^{-1} \)
Buna göre \( m = -126 \) bulunur.
\( (1 + \sqrt[3]{5})^6 \) ifadesinin açılımındaki tam sayı terimlerin toplamı kaçtır?
Çözümü GösterTam sayı terim elde etmek için \( \sqrt[3]{5} \) ifadesinin üssü 0, 3 ya da 6 olmalıdır.
\( k = 0 \) vererek açılımın 1. terimini bulalım.
\( T_1 = \binom{6}{0} \cdot 1^{6 - 0} \cdot (\sqrt[3]{5})^0 = 1 \cdot 1^6 \cdot 1 = 1 \)
\( k = 3 \) vererek açılımın 4. terimini bulalım.
\( T_4 = \binom{6}{3} \cdot 1^{6 - 3} \cdot (\sqrt[3]{5})^3 = 20 \cdot 1^3 \cdot 5^{\frac{3}{3}} = 100 \)
\( k = 6 \) vererek açılımın 7. terimini bulalım.
\( T_7 = \binom{6}{6} \cdot 1^{6 - 6} \cdot (\sqrt[3]{5})^6 = 1 \cdot 1^0 \cdot 5^{\frac{6}{3}} = 25 \)
Bulduğumuz tam sayı değerlerin toplamını alalım.
\( 1 + 100 + 25 = 126 \) bulunur.
\( (\sqrt[4]{3} + \sqrt{3})^6 \) ifadesinin açılımındaki rasyonel terimlerin toplamı kaçtır?
Çözümü Göster\( (x + y)^n \) formundaki bir ifadenin açılımındaki \( (k + 1) \). terim aşağıdaki formülle bulunur.
\( T_{k + 1} = \binom{n}{k} x^{n - k}y^k \)
Bu formülü verilen ifadeye uygulayalım.
\( T_{k + 1} = \binom{6}{k}(\sqrt[4]{3})^{6 - k}(\sqrt{3})^k \)
\( = \binom{6}{k}3^{\frac{6 - k}{4}} 3^{\frac{k}{2}} \)
\( = \binom{6}{k}3^{\frac{6 + k}{4}} \)
Bu terimin rasyonel olması için, \( \frac{6 + k}{4} \) ifadesi bir tam sayı olmalıdır. \( 0 \le k \le 6 \) olduğunu da dikkate alırsak \( k = 2 \) ve \( k = 6 \) bulunur.
\( k = 2 \) vererek açılımın 3. terimini bulalım.
\( T_3 = \binom{6}{2} (\sqrt[4]{3})^{6 - 2}(\sqrt{3})^2 \)
\( = 15 \sqrt[4]{3}^4\sqrt{3}^2 \)
\( = 15 \cdot 3 \cdot 3 = 135 \)
\( k = 6 \) vererek açılımın 7. terimini bulalım.
\( T_7 = \binom{6}{6} (\sqrt[4]{3})^{6 - 6}(\sqrt{3})^6 \)
\( = 1 \sqrt[4]{3}^0\sqrt{3}^6 \)
\( = 3^3 = 27 \)
Bulduğumuz rasyonel değerlerin toplamını alalım.
\( 135 + 27 = 162 \) bulunur.
\( (1 - \sqrt{5})^6 = m + k\sqrt{5} \) olduğuna göre \( m \) ve \( k \)'yı bulunuz.
Çözümü Göster\( (1 - \sqrt{5})^6 \) ifadesinin binom açılımını yazalım.
\( (1 - \sqrt{5})^6 = \binom{6}{0}1^6 (-\sqrt{5})^0 + \binom{6}{1}1^5 (-\sqrt{5})^1 + \binom{6}{2}1^4 (-\sqrt{5})^2 \) \( + \binom{6}{3}1^3 (-\sqrt{5})^3 \) \( + \binom{6}{4}1^2 (-\sqrt{5})^4 \) \( + \binom{6}{5}1^1 (-\sqrt{5})^5 \) \( + \binom{6}{6}1^0 (-\sqrt{5})^6 \)
\( = 1 + 6 \cdot (-\sqrt{5}) + 15 \cdot 5 \) \( + 20 \cdot (-5\sqrt{5}) \) \( + 15 \cdot 25 \) \( + 6 \cdot (-25\sqrt{5}) + 125 \)
\( = 1 - 6\sqrt{5} + 75 - 100\sqrt{5} + 375 - 150\sqrt{5} + 125 \)
\( = 576 - 256\sqrt{5} \)
\( m = 576 \) ve \( k = -256 \) olarak bulunur.
\( (\dfrac{3}{x} - \dfrac{x}{3})^8 \) ifadesinin açılımındaki \( x^6 \)'lı terimin katsayısı kaçtır?
Çözümü Göster\( (x + y)^n \) formundaki bir ifadenin açılımındaki \( (k + 1) \). terim aşağıdaki formülle bulunur.
\( T_{k + 1} = \binom{n}{k} x^{n - k}y^k \)
Bu formülü verilen ifadeye uygulayalım ve \( x^6 \)'lı terime \( (k + 1). \) terim diyelim.
\( T_{k + 1} = \binom{8}{k} \cdot (\dfrac{3}{x})^{8 - k} \cdot (\dfrac{-x}{3})^k \)
\( = \binom{8}{k} \cdot \dfrac{3^{8 - k}}{x^{8 - k}} \cdot \dfrac{(-x)^k}{3^k} \)
\( -x \)'in işareti \( k \)'ya bağlı olduğu için \( -1 \) çarpanını \( x \)'ten ayıralım.
\( = \binom{8}{k} \cdot 3^{8 - 2k} \cdot x^{2k - 8} \cdot (-1)^k \)
\( x \)'in üssünü 6 yapan \( k \) değerini bulalım.
\( 2k - 8 = 6 \Longrightarrow k = 7 \)
\( k = 7 \) vererek açılımın 8. terimini bulalım.
\( T_8 = \binom{8}{7} \cdot 3^{8 - 2(7)} \cdot x^{2(7) - 8} \cdot (-1)^7 \)
\( = 8 \cdot 3^{-6} \cdot x^6 \cdot (-1) \)
\( = -\dfrac{8}{729}x^6 \)
Buna göre \( x^6 \)'lı terimin katsayısı \( -\frac{8}{729} \) olarak bulunur.
\( m \lt 0 \) olmak üzere,
\( (x + \dfrac{1}{mx^2})^7 \) ifadesinin açılımında \( x \)'li terimin katsayısı \( \frac{525}{4} \) olduğuna göre, \( m \) kaçtır?
Çözümü Göster\( (x + y)^n \) formundaki bir ifadenin açılımındaki \( (k + 1) \). terim aşağıdaki formülle bulunur.
\( T_{k + 1} = \binom{n}{k} x^{n - k}y^k \)
Bu formülü verilen ifadeye uygulayalım ve \( x \)'li terimi \( (k + 1). \) terim olarak kabul edelim.
\( T_{k+1} = \binom{7}{k} x^{7 - k}{(\dfrac{1}{mx^2})^k} \)
\( = \binom{7}{k} x^{7 - k}{\dfrac{1}{m^kx^{2k}}} \)
\( = \binom{7}{k} \dfrac{x^{7 - 3k}}{m^k} \)
\( x \)'in üssünün 1 olması için \( k \)'nın alması gereken değeri bulalım.
\( 7 - 3k = 1 \Longrightarrow k = 2 \)
\( k = 2 \) vererek açılımın 3. terimini bulalım.
\( T_3 = \binom{7}{2} \dfrac{x^{7 - 3(2)}}{m^2} \)
\( = 21 \dfrac{x}{m^2} \)
Bu terimin katsayısı \( \frac{525}{4} \) olarak veriliyor.
\( \dfrac{21}{m^2} = \dfrac{525}{4} \)
\( m^2 = \dfrac{4}{25} \)
\( m \lt 0 \) olarak veriliyor.
\( m = -\dfrac{2}{5} \) olarak bulunur.
\( (1 + x^2)^{24} \) ifadesinin açılımındaki 12. ve 13. terimler birbirine eşit olduğuna göre, \( x \)'in alabileceği değerler nelerdir?
Çözümü Göster\( (x + y)^n \) formundaki bir ifadenin açılımındaki \( (k + 1) \). terim aşağıdaki formülle bulunur.
\( T_{k + 1} = \binom{n}{k} x^{n - k}y^k \)
\( k = 11 \) vererek açılımın 12. terimini bulalım.
\( T_{12} = \binom{24}{11} \cdot 1^{24 - 11} \cdot (x^2)^{11} \)
\( = \dfrac{24!}{11! \cdot 13!} \cdot x^{22} \)
\( k = 12 \) vererek açılımın 13. terimini bulalım.
\( T_{13} = \binom{24}{12} \cdot 1^{24 - 12} \cdot (x^2)^{12} \)
\( = \dfrac{24!}{12! \cdot 12!} \cdot x^{24} \)
Bu iki terim birbirine eşittir.
\( \dfrac{24!}{11! \cdot 13!} \cdot x^{22} = \dfrac{24!}{12! \cdot 12!} \cdot x^{24} \)
\( \dfrac{x^{22}}{13} = \dfrac{x^{24}}{12} \)
\( x^2 = \dfrac{12}{13} \)
\( x \in \{\sqrt{\frac{12}{13}}, -\sqrt{\frac{12}{13}}\} \) olarak bulunur.
\( (x^3 - \dfrac{1}{x^2})^m \) ifadesinin açılımında ilk 3 terimin katsayıları toplamı 15 olduğuna göre, \( x \)'li terimi katsayısı kaçtır?
Çözümü GösterAçılımın ilk üç terimini yazalım.
\( (x^3 - \dfrac{1}{x^2})^m = \binom{m}{0}(x^3)^m(\dfrac{-1}{x^2})^0 + \binom{m}{1}(x^3)^{m - 1}(\dfrac{-1}{x^2})^1 + \binom{m}{2}(x^3)^{m - 2}(\dfrac{-1}{x^2})^2 + \ldots \)
Bu üç terimin katsayılarının toplamını 15'tir.
\( \dfrac{m!}{0! \cdot m!} + \dfrac{m!}{(m - 1)! \cdot 1!} \cdot (-1) + \dfrac{m!}{(m - 2)! \cdot 2!} = 15 \)
\( 1 - m + \dfrac{m \cdot (m - 1)}{2} = 15 \)
\( \dfrac{-2m + m^2 - m}{2} = 14 \)
\( m^2 - 3m - 28 = 0 \)
\( (m - 7)(m + 4) = 0 \)
\( m = 7 \) veya \( m = -4 \)
\( m \) doğal sayı olabileceği için \( m = -4 \) geçerli bir çözüm değildir.
\( m = 7 \)
\( x \)'li terimin katsayısını bulalım.
\( (x + y)^n \) formundaki bir ifadenin açılımındaki \( (k + 1) \). terim aşağıdaki formülle bulunur.
\( T_{k + 1} = \binom{n}{k} x^{n - k}y^k \)
\( x \)'li terime \( (k + 1). \) terim diyelim.
\( T_{k + 1} = \binom{7}{k} \cdot (x^3)^{7 - k} \cdot (-x^{-2})^k \)
\( = \binom{7}{k} \cdot x^{21 - 3k} \cdot x^{-2k} \cdot (-1)^k \)
\( = \binom{7}{k} \cdot x^{21 - 5k} \cdot (-1)^k \)
\( x \)'in derecesini 1 yapan \( k \) değerini bulalım.
\( 21 - 5k = 1 \Rightarrow k = 4 \)
\( k = 4 \) vererek açılımın 5. terimini bulalım.
\( T_5 = \binom{7}{4} \cdot x^{21 - 5(4)} \cdot (-1)^4 \)
\( = 35x \)
Buna göre \( x \)'li terimin katsayısı 35 olarak bulunur.
\( (x^3 - \dfrac{1}{x^4})^7 \) ifadesinin açılımındaki sabit terim kaçtır?
Çözümü GösterBir ifadenin sabit terimini bilinmeyenlere 0 vererek bulabiliriz, ancak verilen ifadede 0 değeri tanımsızlık yaratacağı için farklı bir yol izlemeliyiz.
Bu ifadenin açılımındaki sabit terim her iki terimden gelen \( x \)'li çarpanlar birbirini götürdüğünde ve \( A \cdot x^0 \) şeklinde bir terim oluştuğunda oluşur.
\( (x + y)^n \) formundaki bir ifadenin açılımındaki \( (k + 1) \). terim aşağıdaki formülle bulunur.
\( T_{k + 1} = \binom{n}{k} x^{n - k}y^k \)
Sabit terimin oluştuğu terime \( ( k + 1) \). terim diyelim.
\( T_{k + 1} = \binom{7}{k}(x^3)^{7 - k}(-\frac{1}{x^4})^k \)
\( = \binom{7}{k}x^{21 - 3k}\frac{(-1)^k }{x^{4k}} \)
\( = \binom{7}{k} x^{21 - 7k}(-1)^k \)
\( x \)'in üssünün 0 olması için \( k \)'nın alması gereken değeri bulalım.
\( 21 - 7k = 0 \)
\( k = 3 \)
\( k = 3 \) vererek açılımın 4. terimini bulalım.
\( T_4 = \binom{7}{3} x^{21 - 7(3)}(-1)^3 \)
\( = 35 x^0(-1) \)
\( = -35 \)
Buna göre verilen ifadenin açılımının sabit terimi -35'tir.
\( (\dfrac{x^3}{3} - \dfrac{9}{x^2})^5 \) ifadesinin açılımındaki sabit terim kaçtır?
Çözümü GösterBir ifadenin sabit terimini bilinmeyenlere 0 vererek bulabiliriz, ancak verilen ifadede 0 değeri tanımsızlık yaratacağı için farklı bir yol izlemeliyiz.
Bu ifadenin açılımındaki sabit terim her iki terimden gelen \( x \)'li çarpanlar birbirini götürdüğünde ve \( A \cdot x^0 \) şeklinde bir terim oluştuğunda oluşur.
\( (x + y)^n \) formundaki bir ifadenin açılımındaki \( (k + 1) \). terim aşağıdaki formülle bulunur.
\( T_{k + 1} = \binom{n}{k} x^{n - k}y^k \)
Sabit terimin oluştuğu terime \( ( k + 1) \). terim diyelim.
\( T_{k + 1} = \binom{5}{k}(\dfrac{x^3}{3})^{5 - k}(\dfrac{-9}{x^2})^k \)
\( = \binom{5}{k}\dfrac{x^{15 - 3k}}{3^{5 - k}}\dfrac{(-1)^k \cdot 3^{2k}}{x^{2k}} \)
\( = \binom{5}{k}x^{15 - 5k}3^{3k - 5}(-1)^3 \)
\( x \)'in üssünün 0 olması için \( k \)'nın alması gereken değeri bulalım.
\( 15 - 5k = 0 \)
\( k = 3 \)
\( k = 3 \) vererek açılımın 4. terimini bulalım.
\( T_4 = \binom{5}{3}x^{15 - 5(3)}3^{3(3) - 5}(-1)^3 \)
\( = 10x^03^4(-1) \)
\( = -810 \)
Buna göre verilen ifadenin açılımının sabit terimi -810'dur.
\( m \in \mathbb{Z^+} \) olmak üzere,
\( (\sqrt{x} + \dfrac{1}{\sqrt[5]{x}})^m \) açılımında sabit terimin var olabilmesi için \( m \) en az kaç olmalıdır?
Çözümü GösterBinom açılımının \( (k + 1) \). terimini yazalım.
\( T_{k + 1} = \binom{m}{k} (x^{\frac{1}{2}})^{m - k} (x^{-\frac{1}{5}})^k \)
\( = \binom{m}{k} x^{\frac{m - k}{2}} x^{-\frac{k}{5}} \)
\( = \binom{m}{k} x^{\frac{5m - 7k}{10}} \)
\( x \)'in üssünün 0 olması için \( k \)'nın alması gereken değeri bulalım.
\( 5m - 7k = 0 \)
\( m \) pozitif tam sayı, \( k \) doğal sayı ve \( k \le m \) olduğu için, \( m \) en küçük değerini \( k = 5 \) ve \( m = 7 \) olduğu durumda alır.
Buna göre açılımda sabit terim var olabilmesi için \( m \) en az 7 olmalıdır.
\( k \gt 0 \) olmak üzere,
\( (5 + kx^2)^4 = 625 + Ax^2 + \dfrac{200}{3}x^4 + \ldots \)
olduğuna göre, \( \frac{A}{k} \) ifadesi kaça eşittir?
Çözümü GösterVerilen ifadenin binom açılımından yararlanarak \( A \) ve \( k \)'yı bulalım.
\( (5 + kx^2)^4 = \binom{4}{0} \cdot 5^4 \cdot (kx^2)^0 + \binom{4}{1} \cdot 5^3 \cdot (kx^2)^1 + \binom{4}{2} \cdot 5^2 \cdot (kx^2)^2 + \ldots \)
\( = 625 + 4 \cdot 125 \cdot kx^2 + 6 \cdot 25 \cdot k^2x^4 + \ldots \)
\( = 625 + 500kx^2 + 150k^2x^4 + \ldots \)
3. terimleri birbirine eşitleyelim.
\( \dfrac{200}{3}x^4 = 150k^2x^4 \)
\( \dfrac{4}{9} = k^2 \)
\( k \) pozitif olarak verilmiştir.
\( k = \dfrac{2}{3} \)
2. terimleri birbirine eşitleyelim.
\( Ax^2 = 500kx^2 \)
\( A = 500 \cdot \dfrac{2}{3} \)
\( A = \dfrac{1000}{3} \)
\( \frac{A}{k} \) oranını bulalım.
\( \dfrac{A}{k} = \dfrac{\frac{1000}{3}}{\frac{2}{3}} \)
\( = 500 \) olarak bulunur.
\( (a^5 + 9b^8)^{29} \) ifadesinin açılımındaki terimler \( a \)'nın artan kuvvetlerine göre sıralandığında \( b^{24} \)'lü terim sondan kaçıncı terimdir?
Çözümü GösterBinom ifadelerin açılımında terimler birinci terimin azalan kuvvetlerine göre sıralandığında \( (k + 1) \). terim aşağıdaki formülle bulunur.
\( T_{k + 1} = \binom{n}{k} x^{n - k}y^k \)
\( (a^5 + 9b^8)^{29} \) ifadesinde terimlerin yerini aralarında değiştirirsek açılımdaki sıralama \( a \)'nın artan kuvvetlerine göre olur.
Buna göre önce \( (9b^8 + a^5)^{29} \) ifadesinin açılımında \( b^{24} \)'lü terimin baştan kaçıncı terim olduğunu bulalım.
\( T_{k + 1} = \binom{29}{k} (9b^8)^{29 - k}(a^5)^k \)
\( b^{24} \)'lü terim için \( k = 26 \) olmalıdır.
\( T_{27} = \binom{29}{26} (9b^8)^{29 - 26}(a^5)^{26} \)
Buna göre \( b^{24} \)'lü terim açılımda baştan 27., sondan \( 29 + 2 - 27 = 4 \). terimdir.
\( a + b = 1 \) olmak üzere,
\( (x + y)^8 \) binom ifadesinin açılımında \( x = a \) ve \( y = b \) değerleri verildiğinde ilk iki terimin değeri birbirine eşit oluyor.
Buna göre \( a \) kaçtır?
Çözümü Göster\( (x + y)^n \) ifadesinin açılımındaki \( (k + 1) \). terim aşağıdaki formülle bulunur.
\( T_{k+1} = \binom{n}{k} x^{n - k}y^k \)
Birinci terim için \( k = 0 \) verelim.
\( T_1 = \binom{8}{0} x^8y^0 \)
\( = x^8 \)
İkinci terim için \( k = 1 \) verelim.
\( T_2 = \binom{8}{1} x^7y^1 \)
\( = 8x^7y \)
\( x = a \) ve \( y = b \) değerleri verildiğinde ilk iki terimin değeri birbirine eşit oluyor.
\( a^8 = 8a^7b \)
\( a = 8b \)
\( a + b = 1 \) olduğu biliniyor.
\( a + b = 8b + b = 1 \)
\( b = \dfrac{1}{9} \)
\( a = 8b = \dfrac{8}{9} \) bulunur.
\( (3x - y)^5 \) ifadesinin açılımındaki terimlerin katsayılarından kaç tanesi 15 ile tam bölünür?
Çözümü GösterKatsayının 15 ile tam bölünmesi için katsayı 3 ve 5 çarpanlarını içermelidir.
İfadenin açılımında \( n + 1 = 6 \) terim vardır.
Bu 6 terimin binom katsayıları sırasıyla aşağıdaki gibidir.
\( 1 - 5 - 10 - 10 - 5 - 1 \)
Her terimde birinci terimin katsayısından aşağıdaki değerler gelir.
\( 3^5 - 3^4 - 3^3 - 3^2 - 3^1 - 3^0 \)
Bu sayıların çarpımını aldığımızda ilk ve son terimler hariç diğer 4 terim 3 ve 5 çarpanlarını içerir, dolayısıyla 15 ile tam bölünür.
Buna göre terimlerin katsayılarından 4'ü 15 ile tam bölünür.
\( (x^3 + \dfrac{2}{x^4})^n \) açılımında 4. ve 9. terimlerin binom katsayıları eşit olduğuna göre, \( x^{19} \) teriminin katsayısı kaçtır?
Çözümü GösterBir binom açılımında iki farklı terimin binom katsayıları aşağıdaki durumda eşit olur.
\( \binom{n}{k} = \binom{n}{n - k} \)
4. terimde \( k = 3 \), 9. terimde \( k = 8 \) olur.
\( \binom{n}{3} = \binom{n}{8} \)
Buna göre \( n = 3 + 8 = 11 \) olur.
İfadenin açılımındaki \( (k + 1). \) terimi bulalım.
\( T_{k + 1} = \binom{11}{k} (x^3)^{11 - k}(\dfrac{2}{x^4})^{k} \)
\( = \binom{11}{k} x^{33 - 3k} \dfrac{2^k}{x^{4k}} \)
\( = \binom{11}{k} 2^k x^{33 - 7k} \)
\( x \)'in üssünün 19 olması için \( k \)'nın alması gereken değeri bulalım.
\( 33 - 7k = 19 \Longrightarrow k = 2 \)
\( k = 2 \) vererek açılımın 3. terimini bulalım.
\( T_3 = \binom{11}{2} 2^2 x^{33 - 7(2)} \)
\( = 220 x^{19} \)
Buna göre \( x^{19} \) teriminin katsayısı 220 olarak bulunur.
\( ( \sqrt[3]{x} + \dfrac{1}{ \sqrt[4]{x}} )^6 \) açılımında \( x \)'in her doğal sayı değeri için tanımlı olan kaç terim vardır?
Çözümü GösterPaydada \( x \) değişkeninin bulunduğu terimler \( x = 0 \) olduğunda tanımlı olmayacağı için, istenen terimler paydasında \( x \) bulunmayan terimlerdir.
İfadenin açılımındaki \( (k + 1). \) terimi bulalım.
\( \binom{6}{k} (x^{\frac{1}{3}})^{6 - k} (x^{-\frac{1}{4}})^k \)
\( = \binom{6}{k} x^{\frac{6 - k}{3}} x^{-\frac{k}{4}} \)
\( = \binom{6}{k} x^{\frac{24 - 4k}{12} - \frac{3k}{12}} \)
\( = \binom{6}{k} x^{\frac{24 - 7k}{12}} \)
Paydada \( x \) değişkeni bulunmaması için yukarıdaki ifadede \( x \)'in üssünün negatif olmaması gerekir.
\( 24 - 7k \ge 0 \)
Buna göre, \( k = \{ 0, 1, 2, 3 \} \) olan 4 terimde paydada \( x \) değişkeni bulunmaz, dolayısıyla bu terimler \( x = 0 \) için de tanımlı olurlar.
\( (\sqrt[3]{x} + \dfrac{m}{x})^{12} \) ifadesinin açılımındaki değişken içermeyen terimin katsayısı 1760 olduğuna göre, \( m \) kaçtır?
Çözümü Göster\( (x + y)^n \) formundaki bir ifadenin açılımındaki \( (k + 1) \). terim aşağıdaki formülle bulunur.
\( T_{k + 1} = \binom{n}{k} x^{n - k}y^k \)
Değişken içermeyen terimi \( (k + 1). \) terim olarak kabul edelim.
\( T_{k + 1} = \binom{12}{k} \cdot (\sqrt[3]{x})^{12 - k} \cdot (\dfrac{m}{x})^k \)
\( = \binom{12}{k} \cdot x^{\frac{12 - k}{3}} \cdot \dfrac{m^k}{x^k} \)
\( = \binom{12}{k} \cdot x^{\frac{12 - k}{3} - k} \cdot m^k \)
\( = \binom{12}{k} \cdot x^{\frac{12 - 4k}{3}} \cdot m^k \)
\( x \) değişkeninin üssünü sıfır yapan \( k \) değerini bulalım.
\( \dfrac{12 - 4k}{3} = 0 \Longrightarrow k = 3 \)
\( k = 3 \) vererek açılımın 4. terimini bulalım.
Bu terim aynı zamanda 1760 sayısına eşittir.
\( T_4 = \binom{12}{3} \cdot x^{\frac{12 - 4(3)}{3}} \cdot m^3 \)
\( = \binom{12}{3} \cdot m^3 = 1760 \)
\( 220 \cdot m^3 = 1760 \)
\( m^3 = 8 \)
\( m = 2 \) bulunur.
\( (\sqrt[3]{y} + \sqrt[4]{x})^{48} \) ifadesinin açılımındaki kaç terim köklü ifade içermez?
Çözümü Göster\( (x + y)^n \) formundaki bir ifadenin açılımındaki \( (k + 1) \). terim aşağıdaki formülle bulunur.
\( T_{k + 1} = \binom{n}{k} x^{n - k}y^k \)
Köklü ifade içermeyen terimleri \( (k + 1). \) terim olarak kabul edelim.
\( T_{k + 1} = \binom{48}{k} \cdot (y^{\frac{1}{3}})^{48 - k} \cdot (x^{\frac{1}{4}})^k \)
\( = \binom{48}{k} \cdot y^{\frac{48 - k}{3}} \cdot x^{\frac{k}{4}} \)
Köklü bir ifadenin kökten kurtulması için ifadenin kuvveti kökün derecesinin bir tam sayı katı olmalıdır.
Buna göre \( 48 - k \) 3'ün bir tam sayı katı olmalıdır.
\( k \in \{0, 3, 6, \ldots, 48\} \)
Ayrıca \( k \) 4'ün bir tam sayı katı olmalıdır.
\( k \in \{0, 4, 8, \ldots 48 \} \)
\( k \)'nın hem 3'ün hem 4'ün katı olduğu değerler 12'nin tam sayı katlarıdır.
\( k \in \{0, 12, 24, 36, 48 \} \)
Buna göre ifadenin açılımındaki 5 terim köklü ifade içermez.
\( (\sqrt[5]{3} + \sqrt{7})^{105} \) ifadesinin açılımındaki kaç terim köklü ifade içermez?
Çözümü Göster\( (x + y)^n \) formundaki bir ifadenin açılımındaki \( (k + 1) \). terim aşağıdaki formülle bulunur.
\( T_{k + 1} = \binom{n}{k} x^{n - k}y^k \)
Köklü ifade içermeyen terimleri \( (k + 1). \) terim olarak kabul edelim.
\( T_{k + 1} = \binom{105}{k}(3^{\frac{1}{5}})^{105 - k}(7^{\frac{1}{2}})^k \)
\( = \binom{105}{k} 3^{21 - \frac{k}{5}} 7^{\frac{k}{2}} \)
Kök içindeki bir ifadenin kökten kurtulması için ifadenin kuvveti kökün derecesinin bir tam sayı katı olmalıdır.
Buna göre \( (105 - k) \) 5'in bir tam sayı katı olmalıdır.
\( k = \{0, 5, 10, \ldots 105\} \)
Ayrıca \( k \) 2'nin bir tam sayı katı olmalıdır.
\( k = \{0, 2, 4, 6, 8, \ldots 104\} \)
\( k \)'nın hem 5'in hem 2'nin katı olduğu değerler 10'un tam sayı katlarıdır.
\( k = \{0, 10, 20, 30, \ldots, 100\} \)
Buna göre açılımda 11 terim köklü ifade içermez.
\( (\sqrt{3} + \dfrac{1}{\sqrt{2}})^8 \) ifadesinin kaç terimi tam sayıdır?
Çözümü Göster\( (x + y)^n \) formundaki bir ifadenin açılımındaki \( (k + 1) \). terim aşağıdaki formülle bulunur.
\( T_{k + 1} = \binom{n}{k} x^{n - k}y^k \)
Tam sayı olan terimleri \( (k + 1) \). terim olarak kabul edelim.
\( T_{k + 1} = \binom{8}{k} (\sqrt{3})^{8 - k}(\dfrac{1}{\sqrt{2}})^k \)
\( = \binom{8}{k} (3^{\frac{1}{2}})^{8 - k}(2^{-\frac{1}{2}})^k \)
\( = \binom{8}{k} 3^{\frac{8 - k}{2}}2^{-\frac{k}{2}} \)
Köklü bir ifadenin kökten kurtulması için ifadenin kuvveti kökün derecesinin bir tam sayı katı olmalıdır.
Buna göre açılımda köklü ifade olmaması için \( k \) çift sayı olmalı ve 2 ve 3'ün üsleri birer tam sayı olmalıdır.
\( k \in \{0, 2, 4, 6, 8\} \)
Bu \( k \) değerlerinde terimler köklü ifade içermezler, ancak terimlerin tam sayı olup olmadığını bulmak için bu terimleri bulalım.
\( T_1 = \binom{8}{0} \cdot 3^{\frac{8 - 0}{2}} \cdot 2^{-\frac{0}{2}} \)
\( = 1 \cdot 3^4 \cdot 2^0 = 81 \)
\( T_3 = \binom{8}{2} \cdot 3^{\frac{8 - 2}{2}} \cdot 2^{-\frac{2}{2}} \)
\( = 28 \cdot 3^3 \cdot 2^{-1} = 378 \)
\( T_5 = \binom{8}{4} \cdot 3^{\frac{8 - 4}{2}} \cdot 2^{-\frac{4}{2}} \)
\( = 70 \cdot 3^2 \cdot 2^{-2} = \dfrac{315}{2} \)
\( T_7 = \binom{8}{6} \cdot 3^{\frac{8 - 6}{2}} \cdot 2^{-\frac{6}{2}} \)
\( = 28 \cdot 3^1 \cdot 2^{-3} = \dfrac{21}{2} \)
\( T_9 = \binom{8}{8} \cdot 3^{\frac{8 - 8}{2}} \cdot 2^{-\frac{8}{2}} \)
\( = 1 \cdot 3^0 \cdot 2^{-4} = \dfrac{1}{16} \)
Buna göre açılımdaki 1. ve 3. terimler olmak üzere 2 terim tam sayıdır.
\( (5x + 1)^n \) ifadesindeki \( x^2 \)'li terimin katsayısı 375 olduğuna göre, \( n \) kaçtır?
Çözümü Göster\( (x + y)^n \) formundaki bir ifadenin açılımındaki \( (k + 1) \). terim aşağıdaki formülle bulunur.
\( T_{k + 1} = \binom{n}{k} x^{n - k}y^k \)
Bu formülü verilen ifadeye uygulayalım.
\( T_{k + 1} = \binom{n}{k} (5x)^{n - k}(1)^k = 375x^2 \)
Açılımda \( x^2 \)'li terim \( n - k = 2 \) olduğunda oluşur.
\( \binom{n}{k} (5x)^2 = 375x^2 \)
\( \binom{n}{k} = \binom{n}{n - k} \) özdeşliğini kullanalım.
\( \binom{n}{n - k} 25x^2 = 375x^2 \)
\( \binom{n}{2} 25x^2 = 375x^2 \)
\( \binom{n}{2} = 15 \)
\( \dfrac{n(n - 1)}{2 \cdot 1} = 15 \)
\( n^2 - n - 30 = 0 \)
\( (n - 6)(n + 5) = 0 \)
\( n \) doğal sayı değer alabilir.
\( n = 6 \) olarak bulunur.
\( k \in \mathbb{R^+} \) olmak üzere,
\( (3 + kx)^5 \) ifadesinde bulunan \( x^2 \)'li terimin katsayısı \( x^4 \)'lü terimin katsayısının 8 katı olduğuna göre, \( k \) kaçtır?
Çözümü Göster\( (x + y)^n \) formundaki bir ifadenin açılımındaki \( (k + 1) \). terim aşağıdaki formülle bulunur.
\( T_{k + 1} = \binom{n}{k} x^{n - k}y^k \)
Binom ifadenin birinci terimi sabit olduğu için \( x^2 \)'li terim \( k = 2 \) olduğunda, \( x^4 \)'li terim \( k = 4 \) olduğunda elde edilir.
\( k = 2 \) vererek açılımın 3. terimini bulalım.
\( T_3 = \binom{5}{2} \cdot 3^{5-2} \cdot (kx)^2 \)
\( = 10 \cdot 27 \cdot k^2x^2 \)
\( k = 4 \) vererek açılımın 5. terimini bulalım.
\( T_5 = \binom{5}{4} \cdot 3^{5-4} \cdot (kx)^4 \)
\( = 5 \cdot 3 \cdot k^4x^4 \)
\( x^2 \)'li terimin katsayısı \( x^4 \)'lü terimin katsayısının 8 katıdır.
\( 10 \cdot 27 \cdot k^2 = 8 \cdot 5 \cdot 3 \cdot k^4 \)
\( k^2 = \dfrac{9}{4} \)
\( k \) pozitif reel sayı olarak verilmiştir.
\( k = \dfrac{3}{2} \) olarak bulunur.
\( t \ne 0 \) olmak üzere,
\( (5x + t)^4 \) ifadesinin açılımında \( x^2 \)'li terimin katsayısı \( x^3 \)'lü terimin katsayısının %60'ı olduğuna göre, \( t \) kaçtır?
Çözümü GösterVerilen ifadenin açılımındaki \( x^2 \) ve \( x^3 \)'lü terimleri bulalım.
\( (5x + t)^4 = \binom{4}{0} \cdot (5x)^4 \cdot t^0 + \binom{4}{1} \cdot (5x)^3 \cdot t^1 + \binom{4}{2} \cdot (5x)^2 \cdot t^2 + \binom{4}{3} \cdot (5x)^1 \cdot t^3 + \binom{4}{4} \cdot (5x)^0 \cdot t^4 \)
\( x^3 \)'lü terim olan 2. terimin katsayısını bulalım.
\( 4 \cdot 125 \cdot t = 500t \)
\( x^2 \)'li terim olan 3. terimin katsayısını bulalım.
\( 6 \cdot 25 \cdot t^2 = 150t^2 \)
\( x^2 \)'li terimin katsayısı \( x^3 \)'lü terimin katsayısının %60'ıdır.
\( \dfrac{60}{100} \cdot 500t = 150t^2 \)
\( 30t = 15t^2 \)
\( t = 2 \) olarak bulunur.
\( (6 - x)^3 + (6 + x)^3 = 540 \)
eşitliğini sağlayan \( x \) reel sayılarını bulunuz.
Çözümü GösterVerilen binom ifadelerin açılımı aynı terimlerden oluşur, sadece 2. ve 4. terimlerin işaretleri birbirinin tersi olur, dolayısıyla iki açılımın toplamında bu terimler birbirini götürür.
Buna göre iki açılımın toplamı, 1. ve 3. terimlerin toplamının iki katına eşittir.
\( 2(\binom{3}{0} \cdot 6^3 \cdot x^0 + \binom{3}{2} \cdot 6^1 \cdot x^2) = 540 \)
\( 1 \cdot 216 \cdot 1 + 3 \cdot 6 \cdot x^2 = 270 \)
\( 18x^2 = 54 \)
\( x^2 = 3 \)
Çözüm kümesi: \( x \in \{-\sqrt{3}, \sqrt{3}\} \)
\( (\dfrac{x^3}{y} + \dfrac{y^2}{x^2})^{12} \) açılımındaki \( Ax^my^n \) şeklindeki terimlerden \( m + 7n = 0 \) eşitliğini sağlayan terimi bulunuz.
Çözümü Göster\( (x + y)^n \) formundaki bir ifadenin açılımındaki \( (k + 1) \). terim aşağıdaki formülle bulunur.
\( T_{k + 1} = \binom{n}{k} x^{n - k}y^k \)
\( m + 7n = 0 \) eşitliğini sağlayan terimi \( (k + 1) \). terim olarak kabul edelim.
\( T_{k+1} = \binom{12}{k} \cdot (\dfrac{x^3}{y})^{12 - k} \cdot (\dfrac{y^2}{x^2})^k \)
\( = \binom{12}{k} \cdot \dfrac{x^{36 - 3k}}{y^{12 - k}} \cdot \dfrac{y^{2k}}{x^{2k}} \)
\( = \binom{12}{k} \cdot x^{36 - 5k} \cdot y^{3k - 12} \)
Çarpanların kuvvetleri arasında soruda verilen eşitliği sağlayan \( k \) değerini bulalım.
\( m + 7n = 0 \)
\( (36 - 5k) + 7(3k - 12) = 0 \)
\( 16k - 48 = 0 \)
\( k = 3 \)
\( k = 3 \) vererek açılımın 4. terimini bulalım.
\( T_4 = \binom{12}{3} \cdot x^{36 - 5(3)} \cdot y^{3(3) - 12} \)
\( = \binom{12}{3} \cdot x^{21} \cdot y^{-3} \)
\( = 220x^{21}y^{-3} \) olarak bulunur.
\( (x - \dfrac{3}{x})^3 \cdot (2x + \dfrac{2}{x})^5 \) çarpımındaki \( x^8 \)'li terimin katsayısı kaçtır?
Çözümü Gösterİki binom ifadenin açılımındaki terimlerin çarpımları sonucunda \( x^8 \)'li terimi nasıl elde edebileceğimizi bulalım.
Birinci binom ifadenin açılımındaki terimlerde \( x \)'in en yüksek derecesi \( x^3 \) olabilir, bu terim açılımın birinci terimidir.
İkinci binom ifadenin açılımındaki terimlerde \( x \)'in en yüksek derecesi \( x^5 \) olabilir, bu terim açılımın birinci terimidir.
Dolayısıyla her iki açılımdan sadece bu iki terimin çarpımı \( x^8 \)'li terimi verir.
Birinci binom ifadenin birinci terimini bulalım.
\( \binom{3}{0} \cdot x^{3-0} \cdot (-\dfrac{3}{x})^0 \)
\( = 1 \cdot x^3 \cdot 1^0 = x^3 \)
İkinci binom ifadenin birinci terimini bulalım.
\( \binom{5}{0} \cdot (2x)^{5-0} \cdot (\dfrac{2}{x})^0 \)
\( = 1 \cdot 32x^5 \cdot 1 = 32x^5 \)
İki terimin çarpımını bulalım.
\( x^3 \cdot 32x^5 = 32x^8 \)
\( x^8 \)'li terimin katsayısı 32 olarak bulunur.
\( (1 + x)^7 \cdot (2 + x^2)^5 \) çarpımındaki \( x^4 \)'lü terimin katsayısı kaçtır?
Çözümü Göster\( x^4 \)'lü terim her bir binom ifadenin aşağıdaki terimlerinin çarpımı ile elde edilebilir.
2. binom ifadenin açılımındaki tüm terimlerde \( x \)'in derecesi çift sayıdır, dolayısıyla 1. binom ifadenin açılımında çift dereceli terimleri dikkate almamız yeterlidir.
\( x^4 = x^0 \cdot x^4 = x^2 \cdot x^2 = x^4 \cdot x^0 \)
Bu çarpanları ifadelerin binom açılımlarından elde etmeye çalışalım.
Her bir açılımda yukarıdaki koşullara uygun terimleri listeleyelim.
\( (1 + x)^7 = \binom{7}{0} \cdot 1^7 \cdot x^0 + \ldots + \binom{7}{2} \cdot 1^5 \cdot x^2 + \ldots + \binom{7}{4} \cdot 1^3 \cdot x^4 + \ldots \)
\( (2 + x^2)^5 = \binom{5}{0} \cdot 2^5 \cdot (x^2)^0 + \binom{5}{1} \cdot 2^4 \cdot (x^2)^1 + \binom{5}{2} \cdot 2^3 \cdot (x^2)^2 + \ldots \)
Bu açılımlardaki terimleri çarpımları \( x^4 \)'lü terim olacak şekilde çarpalım.
1. açılımın 1. terimi ile 2. açılımın 3. terimi:
\( \binom{7}{0} \cdot 1^7 \cdot x^0 \cdot \binom{5}{2} \cdot 2^3 \cdot (x^2)^2 = 80x^4 \)
1. açılımın 3. terimi ile 2. açılımın 2. terimi:
\( \binom{7}{2} \cdot 1^5 \cdot x^2 \cdot \binom{5}{1} \cdot 2^4 \cdot (x^2)^1 = 1680x^4 \)
1. açılımın 5. terimi ile 2. açılımın 1. terimi:
\( \binom{7}{4} \cdot 1^3 \cdot x^4 \cdot \binom{5}{0} \cdot 2^5 \cdot (x^2)^0 = 1120x^4 \)
Bu üç terimin katsayıları toplamı \( x^4 \)'lü terimin katsayısını verir.
\( 1680 + 1120 + 80 = 2280 \) olarak bulunur.
\( (1 - x)^6 \cdot (3 + x)^4 \) çarpımındaki \( x \)'li terimin katsayısı kaçtır?
Çözümü Göster\( x \)'li terim her bir binom ifadenin aşağıdaki terimlerinin çarpımı ile elde edilebilir.
\( x = x^1 \cdot x^0 = x^0 \cdot x^1 \)
Her bir açılımda yukarıdaki koşullara uygun terimleri listeleyelim.
\( (1 - x)^6 = \binom{6}{0} \cdot 1^6 \cdot (-x)^0 + \binom{6}{1} \cdot 1^5 \cdot (-x)^1 + \ldots \)
\( (3 + x)^4 = \binom{4}{0} \cdot 3^4 \cdot x^0 + \binom{4}{1} \cdot 3^3 \cdot x^1 + \ldots \)
Bu açılımlardaki terimleri çarpımları \( x \)'li terim olacak şekilde çarpalım.
1. açılımın 1. terimi ile 2. açılımın 2. terimi:
\( \binom{6}{0} \cdot 1^6 \cdot (-x)^0 \cdot \binom{4}{1} \cdot 3^3 \cdot x^1 = 108x \)
1. açılımın 2. terimi ile 2. açılımın 1. terimi:
\( \binom{6}{1} \cdot 1^5 \cdot (-x)^1 \cdot \binom{4}{0} \cdot 3^4 \cdot x^1 = -486x \)
Bu iki terimin katsayıları toplamı \( x \)'li terimin katsayısını verir.
\( 108 + (-486) = -378 \) olarak bulunur.
\( (2 - x)^3 \cdot (2 + x)^5 \) çarpımındaki \( x^3 \)'lü terimin katsayısı kaçtır?
Çözümü GösterSoruda verilen ifadeyi aşağıdaki şekilde düzenleyelim.
\( (2 - x)^3 \cdot (2 + x)^5 = (2 - x)^3 \cdot (2 + x)^3 \cdot (2 + x)^2 \)
\( = (4 - x^2)^3 \cdot (2 + x)^2 \)
Bu çarpımın açılımındaki \( x^3 \)'lü terim sadece birinci çarpandan gelen \( x^2 \)'li terim ile ikinci çarpandan gelen \( x \)'li terimin çarpımı ile elde edilir.
\( (4 - x^2)^3 \) açılımının 2. terimi:
\( \binom{3}{1} \cdot 4^{3 - 1} \cdot (-x^2)^1 \)
\( = 3 \cdot 16 \cdot (-x^2) = -48x^2 \)
\( (2 + x)^2 \) açılımının 2. terimi:
\( \binom{2}{1} \cdot 2^{2 - 1} \cdot x^1 \)
\( = 2 \cdot 2 \cdot x = 4x \)
İki terimin çarpımını bulalım.
\( -48x^2 \cdot 4x = -192x^3 \)
\( x^3 \)'lü terimin katsayısı -192 olarak bulunur.
\( (1 - x^3)^3 \cdot (1 + x^2)^5 \) ifadesinin açılımdaki \( x^7 \)'li terimin katsayısı kaçtır?
Çözümü Gösterİki açılımın terimleri arasındaki çarpma işlemi sonucunda \( x^7 \)'li terimlerin nasıl oluşabileceğini bulalım.
\( (1 - x^3)^3 \) ifadesinin açılımındaki \( x \)'in kuvvetleri 3'ün katı olur.
\( (1 + x^2)^5 \) ifadesinin açılımındaki \( x \)'in kuvvetleri 2'nin katı olur.
Buna göre \( x^7 \)'li terim sadece ilk açılımdan gelen \( x^3 \)'lü terim ile ikinci açılımdan gelen \( x^4 \)'lü terimin çarpımı ile oluşur.
\( k = 1 \) vererek birinci açılımın 2. terimini bulalım.
\( T_2 = \binom{3}{1} 1^{3 - 1}(-x^3)^1 \)
\( = -3x^3 \)
\( k = 2 \) vererek ikinci açılımın 3. terimini bulalım.
\( T_3 = \binom{5}{2} 1^{5 - 2}(x^2)^2 \)
\( = 10x^4 \)
İki terimin çarpımı bize \( x^7 \)'li terimi verir.
\( (-3x^3) \cdot 10x^4 = -30x^7 \)
Buna göre \( x^7 \)'li terimin katsayısı -30 olarak bulunur.
\( (x + a)^8 \) ve \( (x^2 + a)^4 \) ifadelerinin açılımda ortadaki terimler birbirine eşit olduğuna göre, \( a \) kaçtır?
Çözümü Göster\( n \) çift sayı olmak üzere \( n \). dereceden bir binom ifadenin \( (\frac{n}{2} + 1) \). terimi ortadaki terimdir.
Verilen ifadelerin açılımında ortadaki terimlerini bulalım.
\( (x + a)^8 \) için ortadaki terim \( \frac{8}{2} + 1 = 5 \). terimdir.
\( T_5 = \binom{8}{4} x^{8 - 4}a^4 \)
\( = 70 x^4a^4 \)
\( (x^2 + a)^4 \) için ortadaki terim \( \frac{4}{2} + 1 = 3 \). terimdir.
\( T_3 = \binom{4}{2} (x^2)^{4 - 2}a^2 \)
\( = 6 x^4a^2 \)
Bulduğumuz iki terim birbirine eşittir.
\( 70x^4a^4 = 6x^4a^2 \)
\( 35a^4 = 3a^2 \)
\( 35a^2 = 3 \)
\( a = \sqrt{\dfrac{3}{35}} = \dfrac{\sqrt{105}}{35} \) bulunur.
\( (-1 - 2x + x^2 + 2x^3)^7 \) ifadesinin açılımındaki \( x^2 \)'li terimin katsayısı kaçtır?
Çözümü GösterParantez içindeki ifadeyi çarpanlarına ayıralım.
\( (-1 - 2x + x^2 + 2x^3)^7 = (-(1 + 2x) + x^2(1 + 2x))^7 \)
\( = ((1 + 2x)(x^2 - 1))^7 \)
\( = (1 + 2x)^7(x^2 - 1)^7 \)
\( x^2 \)'li terim bu iki açılımdan gelecek aşağıdaki terimlerin çarpımı ile elde edilir. İkinci açılımda \( x \)'li bir terim bulunmayacağı için \( x^2 \)'li terim \( x \cdot x \) çarpımı ile oluşmaz.
\( x^2 = x^0 \cdot x^2 = x^2 \cdot x^0 \)
Birinci açılımın 1. terimi ile ikinci açılımın 7. terimini bulalım.
\( T_1 = \binom{7}{0} 1^{7 - 0}(2x)^0 \)
\( = 1 \)
\( T_7 = \binom{7}{6} (x^2)^{7 - 6}(-1)^6 \)
\( = 7x^2 \)
Bu iki terimin çarpımını bulalım.
\( 1 \cdot 7x^2 = 7x^2 \)
Birinci açılımın 3. terimi ile ikinci açılımın 8. terimini bulalım.
\( T_3 = \binom{7}{2} 1^{7 - 2}(2x)^2 \)
\( = 84x^2 \)
\( T_8 = \binom{7}{7} (x^2)^{7 - 7}(-1)^7 \)
\( = -1 \)
Bu iki terimin çarpımını bulalım.
\( 84x^2 \cdot (-1) = -84x^2 \)
\( x^2 \)'li terimin katsayısı bu iki terimin toplanması ile elde edilen terimin katsayısıdır.
\( 7 + (-84) = -77 \) bulunur.
\( (x^2 + 3x - 4)^6 \) ifadesinin açılımındaki \( x^{10} \)'lu terimin katsayısı kaçtır?
Çözümü GösterParantez içindeki ifadeyi çarpanlarına ayıralım.
\( (x^2 + 3x - 4)^6 = ((x + 4)(x - 1))^6 \)
\( = (x + 4)^6(x - 1)^6 \)
\( x^{10} \)'lu terim bu iki açılımdan gelecek aşağıdaki terimlerin çarpımı ile elde edilir.
\( x^{10} = x^6 \cdot x^4 = x^5 \cdot x^5 = x^4 \cdot x^6 \)
Birinci açılımın 1. terimi ile ikinci açılımın 3. terimini bulalım.
\( T_1 = \binom{6}{0} x^{6 - 0}4^0 \)
\( = x^6 \)
\( T_3 = \binom{6}{2} x^{6 - 2}(-1)^2 \)
\( = 15x^4 \)
Bu iki terimin çarpımını bulalım.
\( x^6 \cdot 15x^4 = 15x^{10} \)
Birinci açılımın 2. terimi ile ikinci açılımın 2. terimini bulalım.
\( T_2 = \binom{6}{1} x^{6 - 1}4^1 \)
\( = 24x^5 \)
\( T_2 = \binom{6}{1} x^{6 - 1}(-1)^1 \)
\( = -6x^5 \)
Bu iki terimin çarpımını bulalım.
\( 24x^5 \cdot (-6x^5) = -144x^{10} \)
Birinci açılımın 3. terimi ile ikinci açılımın 1. terimini bulalım.
\( T_3 = \binom{6}{2} x^{6 - 2}4^2 \)
\( = 240x^4 \)
\( T_1 = \binom{6}{0} x^{6 - 0}(-1)^0 \)
\( = x^6 \)
Bu iki terimin çarpımını bulalım.
\( 240x^4 \cdot x^6 = 240x^{10} \)
\( x^{10} \)'lu terimin katsayısı bu üç terimin toplanması ile elde edilen terimin katsayısıdır.
\( 15 + (-144) + 240 = 111 \) olarak buluunur.
\( P(x) = 1 + x + (x + 1)^2 + (x + 1)^3 \) \( + (x + 1)^4 + (x + 1)^5 \) \( + (x + 1)^6 \)
\( P(x) \) polinomunun açılımında ortadaki terim nedir?
Çözümü Göster\( n \) çift sayı olmak üzere \( n \). dereceden bir binom ifadenin \( (\frac{n}{2} + 1) \). terimi ortadaki terimdir.
Verilen polinomda en yüksek dereceli ifade \( (x + 1)^6 \) olduğuna göre tüm ifadelerin açılımında en yüksek dereceli terim \( x^6 \) olur.
\( P(x) = a_0x^0 + a_1x^1 + \ldots + a_6x^6 \)
Buna göre ortadaki terim \( x^{\frac{6 + 0}{2}} = x^3 \)'lü bir terim olmalıdır.
Verilen polinom tanımdaki ifadelerin açılımlarındaki \( x^3 \)'lü terimleri bulalım.
\( (x + 1)^3 \) için:
\( T_1 = \binom{3}{0} x^{3 - 0} 1^0 = x^3 \)
\( (x + 1)^4 \) için:
\( T_2 = \binom{4}{1} x^{4 - 1} 1^1 = 4x^3 \)
\( (x + 1)^5 \) için:
\( T_3 = \binom{5}{2} x^{5 - 2} 1^2 = 10x^3 \)
\( (x + 1)^6 \) için:
\( T_4 = \binom{6}{3} x^{6 - 3} 1^3 = 20x^3 \)
Bulduğumuz terimlerin toplamı \( P(x) \) polinomunun açılımında ortadaki terim olan \( x^3 \)'lü terimi verir.
\( x^3 + 4x^3 + 10x^3 + 20x^3 = 35x^3 \) bulunur.
\( P(x) = (x - 2)^2 + (x - 2)^3 \) \( + (x - 2)^4 \) \( + (x - 2)^5 \)
\( P(x) \) polinomunun açılımındaki terimler \( x \)'in azalan kuvvetlerine göre dizildiğinde baştan 4. terim kaçtır?
Çözümü GösterVerilen polinomda en yüksek dereceli ifade \( (x - 2)^5 \) olduğuna göre tüm ifadelerin açılımında en yüksek dereceli terim \( x^5 \) olur.
Polinomun açılımdaki terimler \( x \)'in azalan kuvvetlerine göre dizildiğinde baştan 4. terim \( x^2 \)'li terim olur.
\( P(x) = a_5x^5 + a_4x^4 + \ldots + a_0x^0 \)
Verilen polinom tanımdaki ifadelerin açılımlarındaki \( x^2 \)'li terimleri bulalım.
\( (x - 2)^2 \) için:
\( T_0 = \binom{2}{0} x^{2 - 0} (-2)^0 = x^2 \)
\( (x - 2)^3 \) için:
\( T_1 = \binom{3}{1} x^{3 - 1} (-2)^1 = -6x^2 \)
\( (x - 2)^4 \) için:
\( T_2 = \binom{4}{2} x^{4 - 2} (-2)^2 = 24x^2 \)
\( (x - 2)^5 \) için:
\( T_3 = \binom{5}{3} x^{5 - 3} (-2)^3 = -80x^2 \)
Bulduğumuz terimlerin toplamı \( P(x) \) polinomunun açılımındaki 4. terim olan \( x^2 \)'li terimi verir.
\( x^2 - 6x^2 + 24x^2 - 80x^2 = -61x^2 \) bulunur.
\( (1 + \dfrac{x}{3})^{25} \) ifadesinin açılımında katsayısı en büyük olan terim kaçıncı terimdir?
Çözümü Göster\( (x + y)^n \) formundaki bir ifadenin açılımındaki \( (k + 1) \). terim aşağıdaki formülle bulunur.
\( T_{k + 1} = \binom{n}{k} x^{n - k}y^k \)
\( = \binom{25}{k} 1^{25 - k}(\dfrac{x}{3})^k \)
\( = \binom{25}{k} \dfrac{x^k}{3^k} \)
Buna göre \( (k + 1) \). terimin katsayısı aşağıdaki gibi olur.
\( \dfrac{\binom{25}{k}}{3^k} \)
Kombinasyon formülü ile binom katsayısının açılımını yazalım.
\( = \dfrac{25!}{k! \cdot (25 - k)! \cdot 3^k} \)
Soruda bu katsayının en büyük değeri sorulmaktadır.
Bu katsayıyı bir sayı dizisi olarak tanımlayalım.
\( (c_k) = \dfrac{25!}{k! \cdot (25 - k)! \cdot 3^k} \)
Sayı dizisindeki \( (k + 1) \). terimin formülünü yazalım.
\( (c_{k+1}) = \dfrac{25!}{(k + 1)! \cdot (25 - (k + 1))! \cdot 3^{k+1}} \)
\( = \dfrac{25!}{(k + 1)! \cdot (24 - k)! \cdot 3^{k+1}} \)
\( c_{k+1} \gt c_k \) olduğu sürece dizinin terimleri büyümektedir. Bir diğer ifadeyle dizinin terimlerinin büyüğü aralıkta \( (k + 1) \). terimin \( k \). terime oranı 1'den büyük olur.
\( \dfrac{c_{k+1}}{c_k} = \dfrac{\frac{25!}{(k + 1)! \cdot (24 - k)! \cdot 3^{k+1}}}{\frac{25!}{k! \cdot (25 - k)! \cdot 3^k}} \)
\( = \dfrac{25 - k}{3 \cdot (k + 1)} \gt 1 \)
\( 25 - k \gt 3k + 3 \)
\( 4k \lt 22 \)
Buna göre \( k \le 5 \) aralığında açılımın katsayıları büyür, \( k \gt 5 \) aralığında küçülür.
Buna göre katsayı en büyük değerini \( k = 5 \) olduğunda alır, yani binom açılımının katsayısı en büyük terimi \( (k + 1) = 6 \). terim olur.