Kutupsal Denklem Tanımı
Bir kartezyen denkleminde \( x \) değişkeninin belirli bir değeri için \( y \) değişkeninin değeri hesaplanır, daha sonra elde edilen \( (x, y) \) ikilisi denklemin grafiğinde bir nokta olarak işaretlenir.
Bir kutupsal denklemde ise \( \theta \) değişkeninin belirli bir değeri için \( r \) değişkeninin değeri hesaplanır, daha sonra elde edilen \( (r, \theta) \) ikilisi denklemin grafiğinde bir nokta olarak işaretlenir.
\( r = r(\theta) \)
\( r(\theta) = 1 + 2\sin{\theta} \) olmak üzere,
\( r(0) = 1 + 2\sin{0} = 1 \)
\( r(\frac{\pi}{6}) = 1 + 2\sin{\frac{\pi}{6}} = 2 \)
\( r(\frac{3\pi}{2}) = 1 + 2\sin{\frac{3\pi}{2}} = -1 \)
\( (1, 0) \), \( (2, \frac{\pi}{6}) \) ve \( (-1, \frac{3\pi}{2}) \) kutupsal eğri üzerinde üç noktadır.
\( (x, y) \) şeklindeki kartezyen koordinatlarında bağımsız değişken olan \( x \) değişkeni sıralı ikilinin ilk bileşeni iken \( (r, \theta) \) şeklindeki kutupsal koordinatlarda bağımsız değişken olan \( \theta \) değişkeni sıralı ikilinin ikinci bileşenidir.
Özellikle belirli bir noktayı referans alan ya da bir nokta etrafında simetrik olan eğriler kutupsal koordinat sistemi ve denklemlerle daha kolay modellebilir.
Aşağıdaki kutupsal denklem için bir değer tablosu oluşturup daha sonra bu değerleri kullanarak kutupsal denklemin grafiğini çizelim.
\( \theta \in [0, \pi) \) olmak üzere,
\( r(\theta) = \sin(3\theta) \)
Farklı \( \theta \) değerleri için kutupsal koordinat değerlerini hesapladığımız bir değer tablosu oluşturalım.
| \( \theta \) | \( r(\theta) = \sin(3\theta) \) | \( (r(\theta), \theta) \) |
|---|---|---|
| \( 0 \) | \( \sin(3(0)) = 0 \) | \( (0, 0) \) |
| \( \frac{\pi}{12} \) | \( \sin(3(\frac{\pi}{12})) = \frac{\sqrt{2}}{2} \) | \( (\frac{\sqrt{2}}{2}, \frac{\pi}{12}) \) |
| \( \frac{\pi}{6} \) | \( \sin(3(\frac{\pi}{6})) = 1 \) | \( (1, \frac{\pi}{6}) \) |
| \( \frac{\pi}{4} \) | \( \sin(3(\frac{\pi}{4})) = \frac{\sqrt{2}}{2} \) | \( (\frac{\sqrt{2}}{2}, \frac{\pi}{4}) \) |
| \( \frac{\pi}{3} \) | \( \sin(3(\frac{\pi}{3})) = 0 \) | \( (0, \frac{\pi}{3}) \) |
| \( \frac{5\pi}{12} \) | \( \sin(3(\frac{5\pi}{12})) = -\frac{\sqrt{2}}{2} \) | \( (-\frac{\sqrt{2}}{2}, \frac{5\pi}{12}) \) |
| \( \frac{\pi}{2} \) | \( \sin(3(\frac{\pi}{2})) = -1 \) | \( (-1, \frac{\pi}{2}) \) |
| \( \frac{7\pi}{12} \) | \( \sin(3(\frac{7\pi}{12})) = -\frac{\sqrt{2}}{2} \) | \( (-\frac{\sqrt{2}}{2}, \frac{7\pi}{12}) \) |
| \( \frac{2\pi}{3} \) | \( \sin(3(\frac{2\pi}{3})) = 0 \) | \( (0, \frac{2\pi}{3}) \) |
| \( \frac{3\pi}{4} \) | \( \sin(3(\frac{3\pi}{4})) = \frac{\sqrt{2}}{2} \) | \( (\frac{\sqrt{2}}{2}, \frac{3\pi}{4}) \) |
| \( \frac{5\pi}{6} \) | \( \sin(3(\frac{5\pi}{6})) = 1 \) | \( (1, \frac{5\pi}{6}) \) |
| \( \frac{11\pi}{12} \) | \( \sin(3(\frac{11\pi}{12})) = \frac{\sqrt{2}}{2} \) | \( (\frac{\sqrt{2}}{2}, \frac{11\pi}{12}) \) |
Elde ettiğimiz \( (r(\theta), \theta) \) ikililerini analitik düzlemde işaretlediğimizde aşağıdaki grafiği elde ederiz.
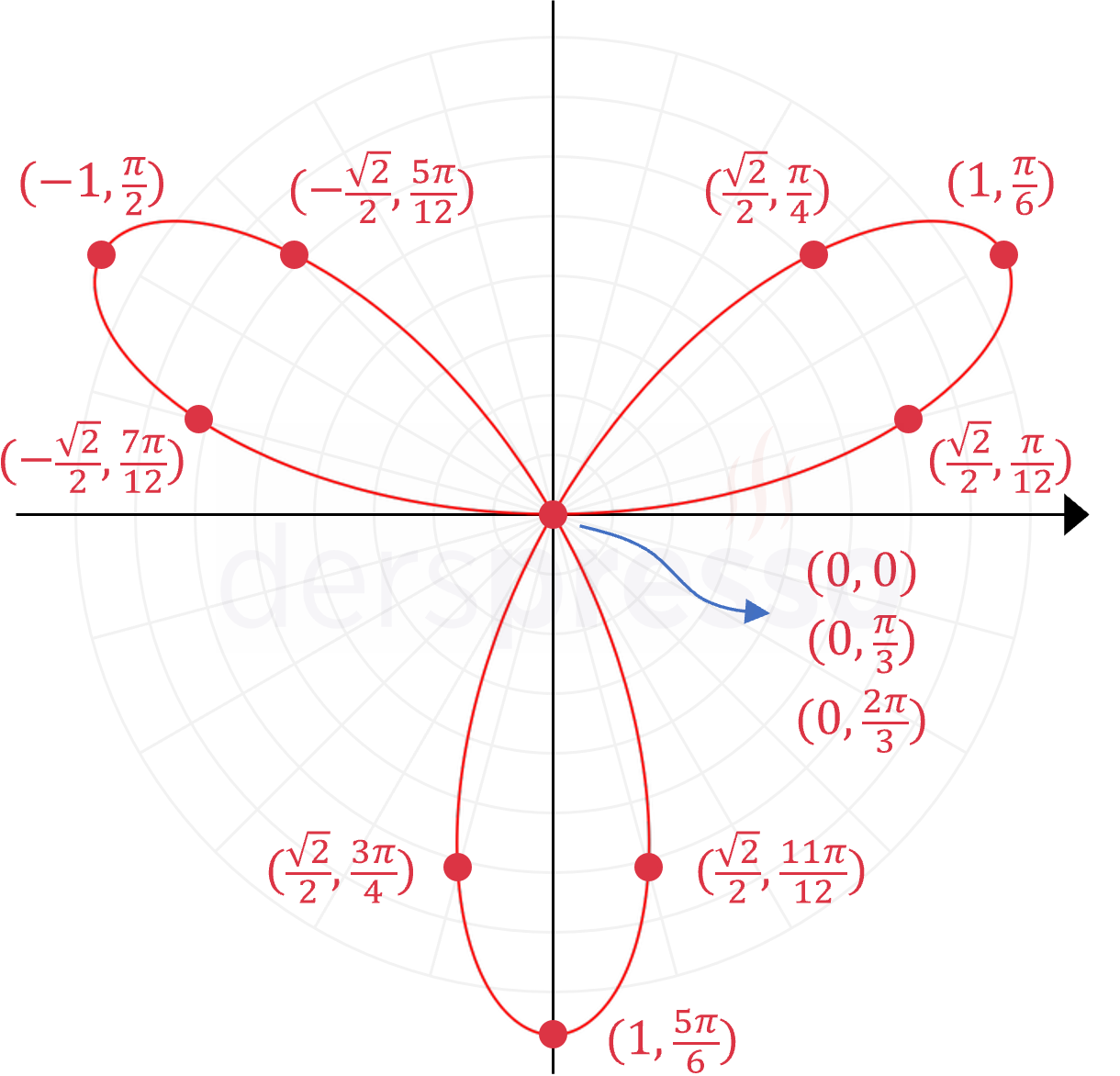
Kutupsal Eğrilerde Simetri
Kutupsal eğriler çoğu zaman bir eksene ya da orijine göre simetrik olabilmektedir. Kutupsal denklemlerin grafiklerini çizerken bu simetrileri belirlemek önem taşımaktadır.
Kutupsal eğrilerin üç farklı simetrisi olabilir.
Kutup Eksenine Göre Simetri
Eğer bir kutupsal denklemde \( (r, \theta) \) yerine \( (r, -\theta) \) ya da \( (-r, \pi - \theta) \) yazıldığında eşitlik sağlanmaya devam ediyorsa bu eğri kutup eksenine (\( x \) eksenine) göre simetriktir.
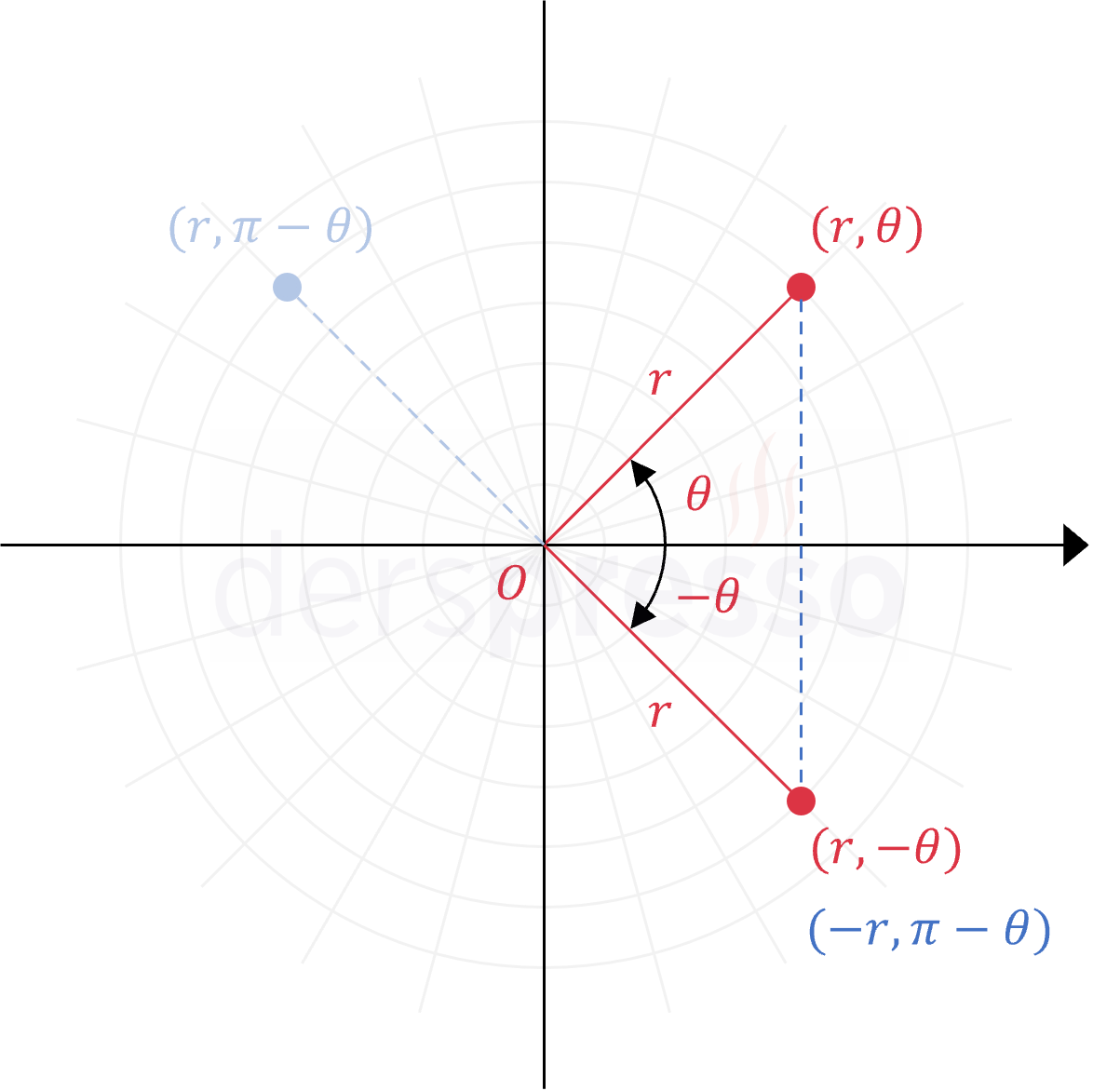
Sadece kosinüs fonksiyonunu içeren \( a + b\cos(k\theta) \) formundaki denklemler kutup eksenine göre simetriktir.
\( \theta = \frac{\pi}{2} \) Doğrusuna Göre Simetri
Eğer bir kutupsal denklemde \( (r, \theta) \) yerine \( (r, \pi - \theta) \) ya da \( (-r, -\theta) \) yazıldığında eşitlik sağlanmaya devam ediyorsa bu eğri \( \theta = \frac{\pi}{2} \) doğrusuna (\( y \) eksenine) göre simetriktir.
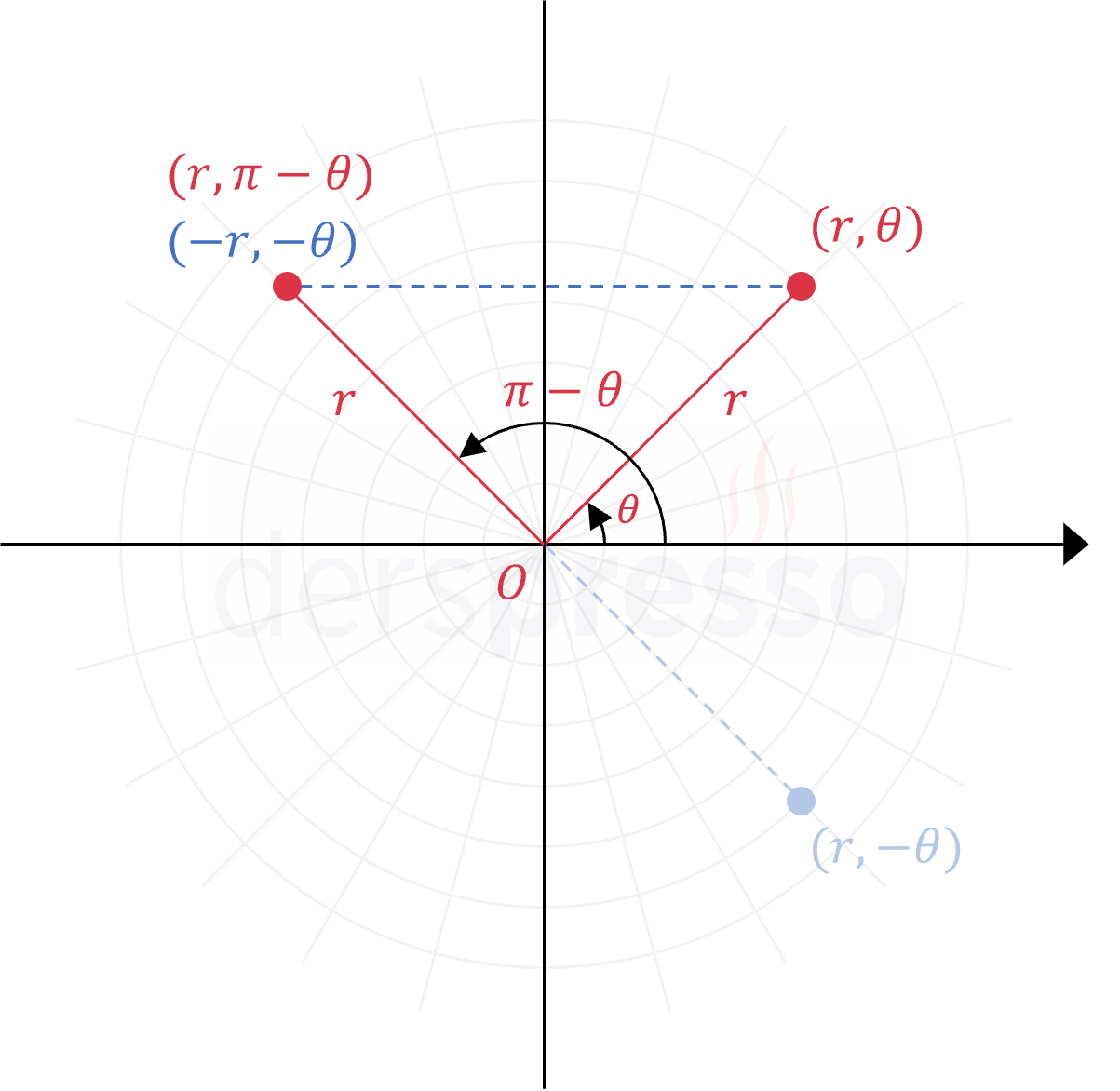
Sadece sinüs fonksiyonunu içeren \( a + b\sin(k\theta) \) formundaki denklemler \( \theta = \frac{\pi}{2} \) doğrusuna göre simetriktir.
Kutup Noktasına Göre Simetri
Eğer bir kutupsal denklemde \( (r, \theta) \) yerine \( (r, \theta + \pi) \) ya da \( (-r, \theta) \) yazıldığında eşitlik sağlanmaya devam ediyorsa bu eğri kutup noktasına (orijine) göre simetriktir.

Bir kutupsal denklem yukarıdaki koşulları sağlamasa da grafiği bu simetrilerden bazılarını içerebilir.
Yukarıda grafiğini çizdiğimiz kutupsal eğrinin eksenlere ve orijine göre simetri durumunu inceleyelim.
\( r(\theta) = \sin(3\theta) \)
Kutup eksenine göre simetri
\( (r, \theta) \longmapsto (r, -\theta) \) kontrolü:
\( \quad r \stackrel{?}{=} \sin(3(-\theta)) \)
\( \quad r \stackrel{?}{=} -\sin(3\theta) \)
\( \quad r \ne -r \)
\( (r, \theta) \longmapsto (-r, \pi - \theta) \) kontrolü:
\( \quad -r \stackrel{?}{=} \sin(3(\pi - \theta)) \)
\( \quad -r \stackrel{?}{=} \sin(3\pi - 3\theta) \)
\( \quad -r \stackrel{?}{=} \sin(3\theta) \)
\( \quad -r \ne r \)
İki koşul da sağlanmadığı için eğrinin kutup eksenine göre simetrik olduğunu söyleyemeyiz.
\( \theta = \frac{\pi}{2} \) doğrusuna göre simetri
\( (r, \theta) \longmapsto (r, \pi - \theta) \) kontrolü:
\( \quad r \stackrel{?}{=} \sin(3(\pi - \theta)) \)
\( \quad r \stackrel{?}{=} \sin(3\pi - 3\theta) \)
\( \quad r \stackrel{?}{=} \sin(3\theta) \)
\( \quad r = r \)
Birinci koşul sağlandığı için eğri \( \theta = \frac{\pi}{2} \) doğrusuna göre simetriktir.
Kutup noktasına göre simetri
\( (r, \theta) \longmapsto (r, \theta + \pi) \) kontrolü:
\( \quad r \stackrel{?}{=} \sin(3(\theta + \pi)) \)
\( \quad r \stackrel{?}{=} \sin(3\theta + 3\pi) \)
\( \quad r \stackrel{?}{=} -\sin(3\theta) \)
\( \quad r \ne -r \)
\( (r, \theta) \longmapsto (-r, \theta) \) kontrolü:
\( \quad -r \stackrel{?}{=} \sin(3\theta) \)
\( \quad -r \ne r \)
İki koşul da sağlanmadığı için eğrinin kutup noktasına göre simetrik olduğunu söyleyemeyiz.
Yukarıdaki örnekte çizdiğimiz grafiği incelediğimizde eğrinin gerçekten de \( \theta = \frac{\pi}{2} \) doğrusuna göre simetrik olduğunu görebiliriz.