Kutupsal Denklemlerin Türevi
Kutupsal denklemler \( \theta \) parametresine bağlı birer parametrik denklem oldukları için türevlerini parametrik denklemlerin türev formülüne dayanan aşağıdaki formül ile alabiliriz.
\( r = r(\theta) \) olmak üzere,
\( \dfrac{dy}{dx} = \dfrac{r'(\theta)\sin{\theta} + r\cos{\theta}}{r'(\theta)\cos{\theta} - r\sin{\theta}} \)
\( r(\theta) = 2\theta \) olmak üzere,
\( r'(\theta) = 2 \)
\( \dfrac{dy}{dx} = \dfrac{2\sin{\theta} + 2\theta\cos{\theta}}{2(\theta)\cos{\theta} - 2\theta\sin{\theta}} \)
\( = \dfrac{\sin{\theta} + \theta\cos{\theta}}{\cos{\theta} - \theta\sin{\theta}} \)
İSPATI GÖSTER
Bir kutupsal denklemin kartezyen denklemine dönüşüm formüllerini yazalım.
\( x = r\cos{\theta} \)
\( y = r\sin{\theta} \)
\( r \) değişkeni \( \theta \) parametresine bağlı olarak değiştiği için \( r = r(\theta) \) şeklinde yazabiliriz.
\( x = r(\theta)\cos{\theta} \)
\( y = r(\theta)\sin{\theta} \)
Parametresi \( \theta \) olan parametrik denklemin türev formülünü yazalım.
\( \dfrac{dy}{dx} = \dfrac{\frac{dy}{d\theta}}{\frac{dx}{d\theta}} \)
\( x \) ve \( y \) değişkenlerinin \( \theta \) parametresine göre türevlerini çarpma kuralını kullanarak alalım.
\( \dfrac{dx}{d\theta} = (r(\theta)\cos{\theta})' \)
\( = r'(\theta)\cos{\theta} - r(\theta)\sin{\theta} \)
\( \dfrac{dy}{d\theta} = (r(\theta)\sin{\theta})' \)
\( = r'(\theta)\sin{\theta} + r(\theta)\cos{\theta} \)
Bu ifadeleri türev formülünde yerine koyduğumuzda \( r = r(\theta) \) kutupsal denklemi için türev formülünü elde ederiz.
\( \dfrac{dy}{dx} = \dfrac{r'(\theta)\sin{\theta} + r(\theta)\cos{\theta}}{r'(\theta)\cos{\theta} - r(\theta)\sin{\theta}} \)
Bir kutupsal denklem orijinden geçiyorsa bu noktadaki türevini yukarıdaki formülde \( r = 0 \) koyarak aşağıdaki şekilde bulabiliriz.
Bir kutupsal denklemin \( (0, \theta) \) noktasındaki türevi:
\( \dfrac{dy}{dx} = \dfrac{r'(\theta)\sin{\theta} + 0\cos{\theta}}{r'(\theta)\cos{\theta} - 0\sin{\theta}} \)
\( = \dfrac{r'(\theta)\sin{\theta}}{r'(\theta)\cos{\theta}} = \tan{\theta} \)
\( r(\theta) = 1 + 2\sin{\theta} \) eğrisinin orijindeki türev değerlerini bulalım.
\( r = 0 \) yapan \( \theta \) değerleri:
\( \sin{\theta} = -\frac{1}{2} \)
\( \theta \in \{\frac{\pi}{6}, \frac{5\pi}{6}\} \)
\( \dfrac{dy}{dx}|_{\theta = \frac{\pi}{6}} = \tan{\frac{\pi}{6}} = \dfrac{\sqrt{3}}{3} \)
\( \dfrac{dy}{dx}|_{\theta = \frac{5\pi}{6}} = \tan{\frac{5\pi}{6}} = -\dfrac{\sqrt{3}}{3} \)
Türev Uygulamaları
Türevin kutupsal denklemlerdeki bazı uygulamaları aşağıdaki gibidir.
Eğim Bulma
Türevin eğim anlamı kutupsal denklemler için de geçerlidir. Buna göre \( \theta \) parametresine bağlı bir kutupsal eğriye \( \theta = a \) açısının karşılık geldiği \( (r(a), a) \) noktasında çizilen teğetin eğimi, denklemin birinci türevinin \( \theta = a \) için değerine eşittir.
Aşağıda denklemi verilen kutupsal eğriye \( \theta = \frac{5\pi}{2} \) noktasında çizilen teğet doğrunun eğimini bulalım.
\( r(\theta) = 2\theta \)
Kutupsal denklem türev formülünü yazalım.
\( \dfrac{dy}{dx} = \dfrac{r'(\theta)\sin{\theta} + r\cos{\theta}}{r'(\theta)\cos{\theta} - r\sin{\theta}} \)
\( r'(\theta) = (2\theta)' = 2 \)
\( = \dfrac{2\sin{\theta} + 2\theta\cos{\theta}}{2\cos{\theta} - 2\theta\sin{\theta}} \)
\( = \dfrac{\sin{\theta} + \theta\cos{\theta}}{\cos{\theta} - \theta\sin{\theta}} \)
Türev ifadesinde \( \theta = \frac{5\pi}{2} \) koyarak eğrinin bu noktadaki eğimini bulalım.
\( \dfrac{dy}{dx}|_{\theta = \frac{5\pi}{2}} = \dfrac{\sin{\frac{5\pi}{2}} + \frac{5\pi}{2}\cos{\frac{5\pi}{2}}}{\cos{\frac{5\pi}{2}} - \frac{5\pi}{2}\sin{\frac{5\pi}{2}}} \)
\( = \dfrac{1 + \frac{5\pi}{2}(0)}{0 - \frac{5\pi}{2}(1)} = -\dfrac{2}{5\pi} \)
\( \theta = \frac{5\pi}{2} \) değerinin karşılık geldiği \( (r(\theta), \theta) \) noktasını bulalım.
\( r(\theta) = 2\theta = 5\pi \)
Buna göre \( \theta = \frac{5\pi}{2} \) değeri kutupsal eğride \( (5\pi, \frac{5\pi}{2}) \) noktasına karşılık gelir ve eğriye bu noktada çizilen teğetin eğimi \( -\frac{2}{5\pi} \) olur.
Kutupsal eğrinin grafiği ve bu noktadaki teğeti aşağıdaki şekilde gösterilmiştir.
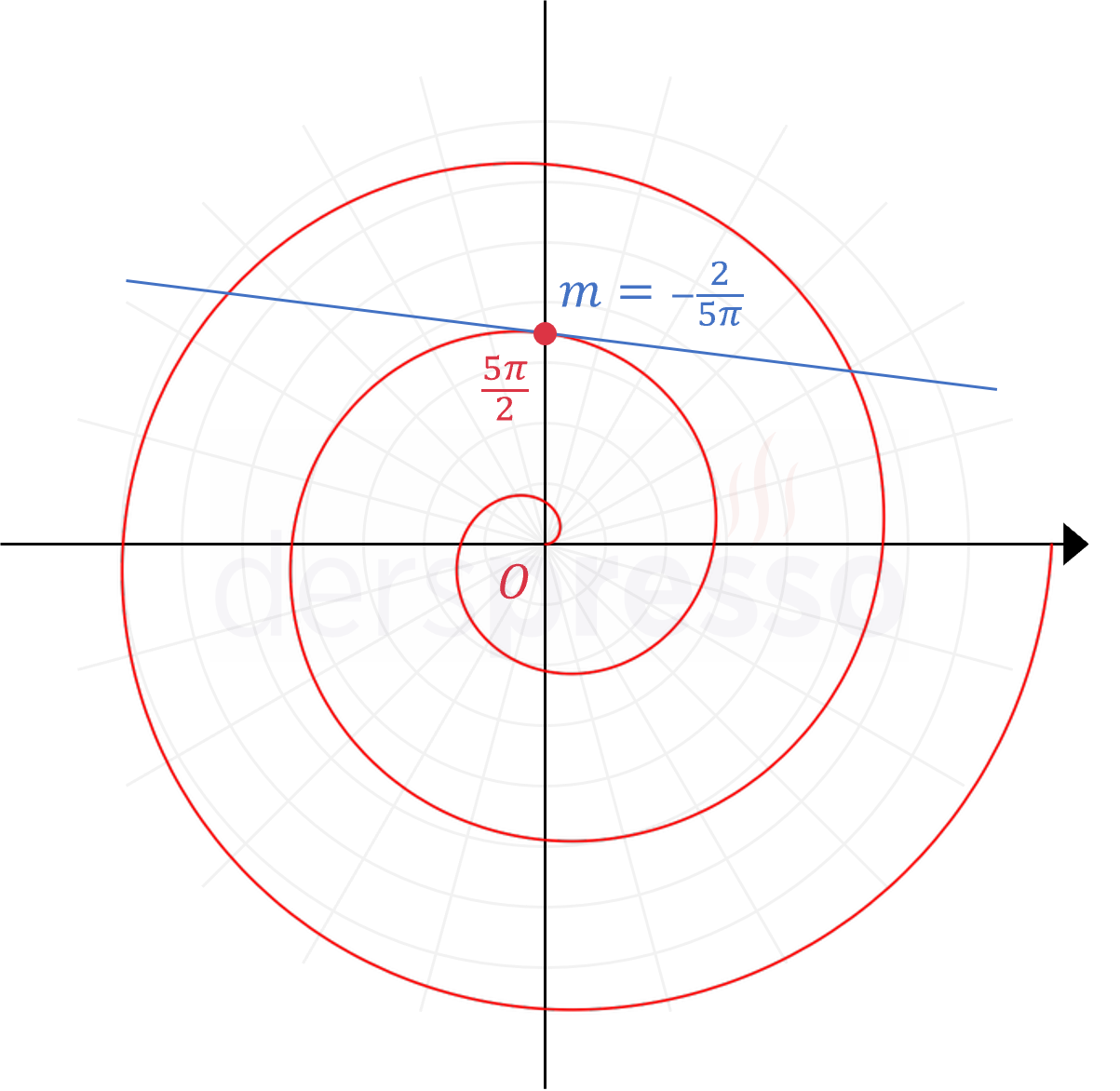
Durağan Noktaları Bulma
Bir fonksiyonun birinci türevinin tanımlı ve sıfır olduğu noktalara durağan nokta denir. Bir durağan nokta yerel minimum/maksimum nokta olmak zorunda değildir, bir yatay büküm noktası da olabilir.
Bir kutupsal denklemin durağan noktaları kartezyen denklemlerinde olduğu gibi \( y \) değişkeninin \( x \) değişkenine göre türevinin sıfır olduğu noktalarda oluşur.
\( \dfrac{dy}{dx} = 0 \)
Kutupsal denklemin türev formülü düşünüldüğünde, durağan noktalar türev formülünde payın sıfır olduğu, ama paydanın sıfır olmadığı noktalardır.
\( \dfrac{dy}{dx} = \dfrac{r'(\theta)\sin{\theta} + r\cos{\theta}}{r'(\theta)\cos{\theta} - r\sin{\theta}} = 0 \)
\( \Longrightarrow r'(\theta)\sin{\theta} + r\cos{\theta} = 0 \)
\( \Longrightarrow r'(\theta)\cos{\theta} - r\sin{\theta} \ne 0 \)
Aşağıdaki kutupsal denklemin durağan noktalarını bulalım.
\( \theta \in [0, 2\pi) \) olmak üzere,
\( r(\theta) = \sqrt{3} + \sin{\theta} \)
Kutupsal denklem türev formülünü yazalım.
\( \dfrac{dy}{dx} = \dfrac{r'(\theta)\sin{\theta} + r\cos{\theta}}{r'(\theta)\cos{\theta} - r\sin{\theta}} \)
\( r'(\theta) = (\sqrt{3} + \sin{\theta})' = \cos{\theta} \)
\( = \dfrac{\cos{\theta}\sin{\theta} + (\sqrt{3} + \sin{\theta})\cos{\theta}}{\cos{\theta}\cos{\theta} - (\sqrt{3} + \sin{\theta})\sin{\theta}} \)
\( = \dfrac{\cos{\theta}(2\sin{\theta} + \sqrt{3})}{\cos^2{\theta} - \sin^2{\theta} - \sqrt{3}\sin{\theta}} \)
Eğrinin durağan noktaları birinci türev sıfır olduğunda oluşur.
Payı \( \theta \in [0, 2\pi) \) aralığında sıfır yapan değerleri bulalım.
\( \cos{\theta}(2\sin{\theta} + \sqrt{3}) = 0 \)
\( \cos{\theta} = 0 \) ise:
\( \theta \in \{\frac{\pi}{2}, \frac{3\pi}{2}\} \)
\( 2\sin{\theta} + \sqrt{3} = 0 \) ise:
\( \sin{\theta} = -\frac{\sqrt{3}}{2} \)
\( \theta \in \{\frac{4\pi}{3}, \frac{5\pi}{3}\} \)
Bulduğumuz dört \( \theta \) değeri paydada yerine koyduğumuzda hiçbirinin paydayı da sıfır yapmadığını görebiliriz.
Buna göre eğrinin \( \theta \in \{\frac{\pi}{2}, \frac{3\pi}{2}, \frac{4\pi}{3}, \frac{5\pi}{3}\} \) noktalarında durağan noktaları vardır.
Bu \( \theta \) değerlerinde oluşan \( (r, \theta) \) noktalarını bulalım.
\( r(\frac{\pi}{2}) = \sqrt{3} + \sin{\frac{\pi}{2}} = \sqrt{3} + 1 \)
\( r(\frac{3\pi}{2}) = \sqrt{3} + \sin{\frac{3\pi}{2}} = \sqrt{3} - 1 \)
\( r(\frac{4\pi}{3}) = \sqrt{3} + \sin{\frac{4\pi}{3}} = \frac{\sqrt{3}}{2} \)
\( r(\frac{5\pi}{3}) = \sqrt{3} + \sin{\frac{5\pi}{3}} = \frac{\sqrt{3}}{2} \)
Buna göre kutupsal koordinatları \( (\sqrt{3} + 1, \frac{\pi}{2}) \), \( (\sqrt{3} - 1, \frac{3\pi}{2}) \), \( (\frac{\sqrt{3}}{2}, \frac{4\pi}{3}) \) ve \( (\frac{\sqrt{3}}{2}, \frac{5\pi}{3}) \) olan noktalar eğrinin durağan noktalarıdır.
Kutupsal eğrinin grafiği ve durağan noktaları aşağıdaki şekilde gösterilmiştir.
