Bir Sayının Çarpmaya Göre Tersi
Aritmetikte bir sayının çarpmaya göre tersini aşağıdaki şekilde tanımlamıştık.
\( a \ne 0 \) olmak üzere,
\( a \cdot a^{-1} = 1 \)
eşitliğini sağlayan \( a^{-1} \) sayısına \( a \)'nın çarpmaya göre tersi denir.
\( a^{-1} = \dfrac{1}{a} \)
\( 2^{-1} = \frac{1}{2} \)
Benzer bir tanımlamayı modüler aritmetikte aşağıdaki şekilde yapabiliriz.
\( a \cdot x \equiv 1 \pmod{n} \)
eşitliğini sağlayan \( x \) sayısına \( a \)'nın \( n \) modülünde çarpmaya göre tersi denir.
Modüler aritmetikte bölme işlemini standart aritmetikte olduğu gibi \( x = \frac{1}{a} \) şeklinde yapamadığımız için, çarpmaya göre tersi bulmak için farklı yöntemler kullanmamız gerekir. Bu yöntemlerden biri, bir sayının çarpmaya göre tersini deneyerek bulmaktır.
Deneme Yöntemiyle Çarpmaya Göre Tersi Bulma
Örnek olarak 3 sayısının 7 modülünde çarpmaya göre tersini bulmaya çalışalım. Bunun için, 3'ü 7 modülündeki tüm kalanlarla sırayla çarpalım.
\( 3 \cdot 0 \equiv 0 \pmod{7} \)
\( 3 \cdot 1 \equiv 3 \pmod{7} \)
\( 3 \cdot 2 \equiv 6 \pmod{7} \)
\( 3 \cdot 3 \equiv 9 \equiv 2 \pmod{7} \)
\( 3 \cdot 4 \equiv 12 \equiv 5 \pmod{7} \)
\( 3 \cdot 5 \equiv 15 \equiv 1 \pmod{7} \)
\( 3 \cdot 6 \equiv 18 \equiv 4 \pmod{7} \)
Sonuçlara baktığımızda \( 3 \cdot 5 \equiv 1 \pmod{7} \) olduğunu görüyoruz, dolayısıyla 3'ün 7 modülünde çarpmaya göre tersinin 5 olduğunu söyleyebiliriz.
Şimdi de 3'ü 5'in 7 modülünde denk olduğu diğer bazı sayılarla çarparak sonucun kaç olduğuna bakalım.
\( 3 \cdot 5 \equiv 15 \equiv 1 \pmod{7} \)
\( 3 \cdot 12 \equiv 36 \equiv 1 \pmod{7} \)
\( 3 \cdot 19 \equiv 57 \equiv 1 \pmod{7} \)
\( 3 \cdot (-2) \equiv -6 \equiv 1 \pmod{7} \)
\( 3 \cdot (-9) \equiv 15 \equiv 1 \pmod{7} \)
Görüyoruz ki, bir sayıyı belirli bir modüldeki çarpmaya göre tersinin denk olduğu diğer sayılarla çarptığımızda yine 1 sonucunu elde ediyoruz.
İkinci bir örnek olarak 4 sayısının 6 modülünde çarpmaya göre tersini bulmaya çalışalım.
\( 4 \cdot 0 \equiv 0 \pmod{6} \)
\( 4 \cdot 1 \equiv 4 \pmod{6} \)
\( 4 \cdot 2 \equiv 8 \equiv 2 \pmod{6} \)
\( 4 \cdot 3 \equiv 12 \equiv 0 \pmod{6} \)
\( 4 \cdot 4 \equiv 16 \equiv 4 \pmod{6} \)
\( 4 \cdot 5 \equiv 20 \equiv 2 \pmod{6} \)
Sonuçlara baktığımızda, 4'ün hiçbir sayı ile çarpımının 1'e denk olmadığını görüyoruz, buna göre 4'ün 6 modülünde çarpmaya göre tersinin olmadığı sonucuna varabiliriz.
Bu doğrultuda bir sayının çarpmaya göre tersi ile ilgili şu çıkarımlarda bulunabiliriz.
- Modüler aritmetikte bir \( a \) sayısının \( n \) modülünde çarpmaya göre tersi, o sayı ile çarpımı \( n \) modülünde 1'e denk olan sayıdır.
- Her sayının \( n \) modülünde çarpmaya göre tersi olmayabilir.
- Bir \( a \) sayısının \( n \) modülünde çarpmaya göre tersi varsa sadece bir tanedir.
- \( a \) sayısının \( n \) modülünde çarpmaya göre tersi \( x \) ise \( n \) modülünde \( a \)'nın denk olduğu herhangi bir sayı ile \( x \)'in denk olduğu herhangi bir sayının çarpımı da yine 1 sonucunu verir.
- 0 tüm modüllerde 0'a eşit olduğu ve diğer bir sayıyla çarpımı yine 0 olduğu için, hiçbir modülde çarpmaya göre tersi yoktur.
Bir Sayının Çarpmaya Göre Tersi Olma Koşulu
Kural olarak, bir \( a \) sayısının \( n \) modülünde çarpmaya göre tersi ancak ve ancak \( a \) ve \( n \) sayıları aralarında asalsa vardır. Buna göre, \( n \) modülünde sadece \( n \) ile aralarında asal olan sayıların çarpmaya göre tersi vardır, \( n \) ile aralarında asal olmayan sayıların çarpmaya göre tersi yoktur.
\( a \cdot x \equiv 1 \pmod{n} \)
\( EBOB(a, n) = 1 \iff \) \( a \) sayısının \( n \) modülünde çarpmaya göre tersi vardır ve bu sayı \( x \)'tir.
\( 3 \) ve \( 7 \) aralarında asal oldukları için \( 3 \)'ün \( 7 \) modülünde çarpmaya göre tersi olmalıdır, nitekim yukarıda verdiğimiz birinci örnekte \( 3 \)'ün \( 7 \) modülünde tersini \( 5 \) olarak bulmuştuk.
\( 4 \) ve \( 6 \) aralarında asal olmadığı için \( 4 \)'ün \( 6 \) modülünde çarpmaya göre tersi olmamalıdır, nitekim yukarıda verdiğimiz ikinci örnekte \( 4 \)'ün \( 6 \) modülünde tersinin olmadığını görmüştük.
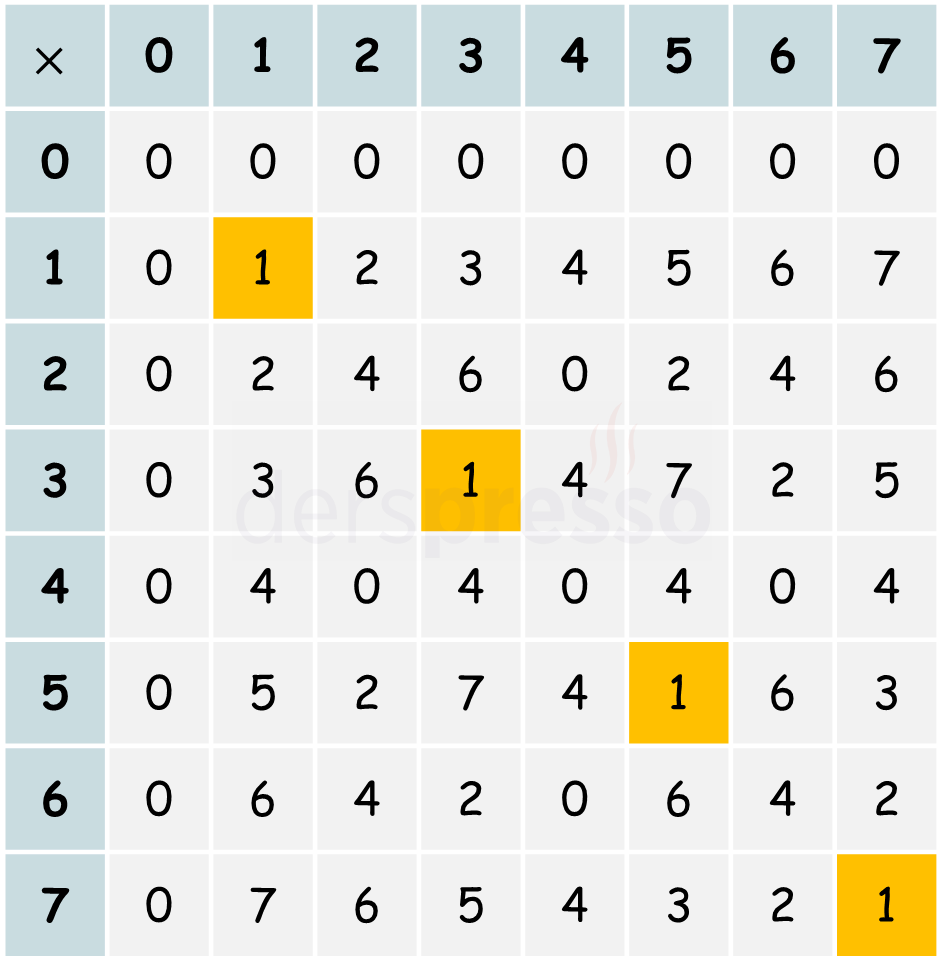
Buna göre, örneğin \( 8 \) modülünde çarpmaya göre tersi olan sayıları \( 8 \) ile aralarında asal olan sayılar kümesi olarak aşağıdaki şekilde tanımlayabiliriz.
\( 8 \) modülünde çarpmaya göre tersi olan sayılar \( = \{ 1, 3, 5, 7 \} \)
Aşağıdaki \( 8 \) modülü için çarpma tablosunu incelediğimizde, sadece \( 8 \) ile aralarında asal olan sayıların diğer bir sayı ile çarpımının \( 1 \) sonucunu verdiğini, diğer sayıların ise vermediğini görebiliriz.
Fermat'ın Küçük Teoremi
İşlem yaptığımız modül bir asal sayı ise ve \( a \) ve \( n \) sayıları aralarında asalsa bir sayının çarpmaya göre tersini bulmakta kullanabileceğimiz yöntemlerden biri Fermat'ın küçük teoremi'dir.
\( n \) bir asal sayı olmak üzere,
\( a^n \equiv a \pmod{n} \)
\( a \) ve \( n \) sayıları aralarında asal ise Fermat'ın küçük teoremini çarpmanın tersi problemine uygulayarak bir sayının \( n \) modülünde çarpmaya göre tersini aşağıdaki ifadeyle bulabiliriz.
\( n \) bir asal sayı ve \( EBOB(a, n) = 1 \) olmak üzere,
\( a \)'nın \( n \) modülünde çarpmaya göre tersi: \( a^{n - 2} \)
\( 4 \) sayısının aralarında asal olduğu \( 7 \) modülünde çarpmaya göre tersi:
\( 4^{7 - 2} \equiv 4^5 \equiv 1024 \equiv 2 \pmod{7}\)
Buna göre, \( 4 \)'ün \( 7 \) modülünde çarpmaya göre tersi 2'dir.
\( 4 \) ve \( 2 \)'nin çarpımının \( 7 \) modülünde \( 1 \) olup olmadığını kontrol edelim.
\( 4 \cdot 2 \equiv 8 \equiv 1 \pmod{7}\)
İSPATI GÖSTER
Fermat'ın küçük teoremini yazarak başlayalım.
\( n \) bir asal sayı olmak üzere,
\( a^n \equiv a \pmod{n} \)
Fermat'ın küçük teoremini çarpmaya göre ters bulmada kullanabilmemiz için gerekli ek koşulu da varsayımlarımıza ekleyelim.
\( EBOB(a, n) = 1 \)
Denkliğin sol tarafını iki çarpana ayıralım.
\( a^{n - 1} \cdot a \equiv a \pmod{n} \)
Önceki bölümde bir denkliğin iki tarafını \( n \) ile aralarında asal olan bir sayıya bölebileceğimizi görmüştük. \( a \) ve \( n \)'nin aralarında asal olduğu varsaydığımız için, denkliğin iki tarafını \( a \)'ya bölebiliriz.
\( a^{n - 1} \equiv 1 \pmod{n} \)
Denkliğin sol tarafını yine iki çarpana ayıralım.
\( a \cdot a^{n - 2} \equiv 1 \pmod{n} \)
Elde ettiğimiz bu denklikte iki ifadenin çarpımı 1 olduğu için, \( a^{n - 2} \)'nin \( n \) modülünde \( a \)'nın çarpmaya göre tersi olduğu sonucuna varabiliriz.
Doğrusal Denklik
Aşağıdaki gibi bir denklemi sağlayan \( x \) değerini bulmak için, \( a \)'nın \( n \) modülündeki çarpmaya göre tersini kullanabiliriz.
\( a \cdot x \equiv b \pmod{n} \)
\( EBOB(a, n) = 1 \) ise yani sayılar aralarında asal ise,
\( x \equiv a^{-1} \cdot b \pmod{n} \)
Eğer \( a \) ve \( n \) sayıları aralarında asal ise yani \( a \)'nın \( n \) modülünde çarpmaya göre tersi varsa bu doğrusal denkliğin tek çözümü vardır ve bu çözümü yukarıdaki \( x \) için denkliği çözerek bulabiliriz.