Modüler Aritmetikte İşlemler
Modüler aritmetikte sayılar arasında toplama, çıkarma ve çarpma işlemlerini standart aritmetiğe benzer şekilde yapabiliriz, aradaki temel fark elde ettiğimiz işlem sonucunu \( n \) modülündeki kalanına çevirmektir.
Toplama İşlemi
İki sayının \( n \) modülünde toplamının sonucu, sayıların aritmetik toplamının \( n \) modülünde kalanına eşittir.
\( 7 + 4 \equiv 11 \equiv 2 \pmod{9} \)
\( 9 + 6 \equiv 15 \equiv 5 \pmod{10} \)
Toplama İşlem Tablosu
İki sayının belirli bir modüldeki tüm kalanlarının aralarındaki toplama işlemlerinin sonucunu bir tablo halinde gösterebiliriz. Bu tabloda satır ve sütun başlıkları toplama işleminin terimleri, ilgili satır ve sütunun kesişimindeki hücredeki sayı da işlem sonucudur. Aşağıda \( 7 \) modülü için toplama işlem tablosu verilmiştir.
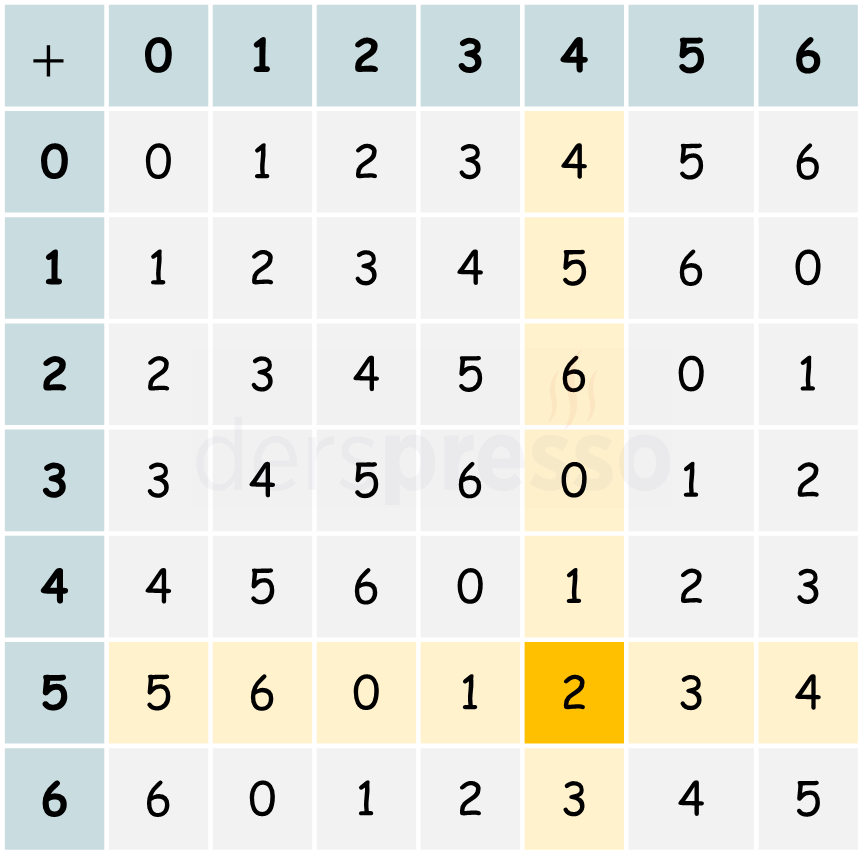
Yukarıdaki tabloya göre \( 7 \) modülünde bir toplama işlemi aşağıdaki gibidir.
\( 5 + 4 \equiv 2 \pmod{7} \)
Toplama İşlem Özellikleri
Toplama işleminin modüler aritmetikte değişme özelliği vardır.
\( a + b \equiv b + a \pmod{n} \)
Toplama işleminin modüler aritmetikte birleşme özelliği vardır.
\( (a + b) + c \equiv a + (b + c) \pmod{n} \)
Bir Sayının Toplamaya Göre Tersi
Bir \( a \) sayısının \( n \) modülünde toplamaya göre tersi aşağıdaki koşulu sağlayan sayıdır. Bu sayı aynı zamanda toplama işlem tablosunda \( a \) sayısı ile işlem sonucu \( 0 \) olan sayıdır.
\( a + b \equiv 0 \pmod{n} \)
5 sayısının 7 modülünde toplamaya göre tersi:
\( 5 + b \equiv 0 \pmod{7} \)
\( b = 2 \)
Toplama İşlem Kuralları
Bir denkliğin iki tarafını aynı tam sayı ile toplamamız denkliği bozmaz.
\( a \equiv b \pmod{n} \) ise,
\( a + c \equiv b + c \pmod{n} \)
\( 12 \equiv 42 \pmod{10} \)
Denkliğin iki tarafına +3 ekleyelim.
\( 15 \equiv 45 \pmod{10} \)
İSPATI GÖSTER
İki sayı \( n \) modülünde denk ise, \( n \) bu iki sayının farkını böler.
\( a \equiv b \pmod{n} \Longrightarrow n \mid (a - b) \)
Denkliğin iki tarafını aynı sayı ile toplarsak, tarafların farkı değişmez.
\( (a + c) - (b + c) = a - b \)
Bu yüzden \( n \) bu iki sayının farkını da böler.
\( n \mid (a - b) \Longrightarrow n \mid (a + c) - (b + c) \)
\( n \) iki sayının farkını bölüyorsa, bu iki sayı \( n \) modülünde denktir.
\( a + c \equiv b + c \pmod{n} \)
İki denkliği taraf tarafa toplamamız denkliği bozmaz.
\( a \equiv b \pmod{n} \)
\( c \equiv d \pmod{n} \) ise,
\( a + c \equiv b + d \pmod{n} \)
\( 17 \equiv 47 \pmod{10} \)
\( 24 \equiv 34 \pmod{10} \)
İki denkliği taraf tarafa toplayalım.
\( 41 \equiv 81 \pmod{10} \)
İSPATI GÖSTER
\( a \equiv b \pmod{n} \Longrightarrow a - b = k \cdot n \)
\( c \equiv d \pmod{n} \Longrightarrow c - d = l \cdot n \)
İki eşitliği taraf tarafa toplayalım ve terimleri düzenleyelim.
\( (a - b) + (c - d) = k\cdot n + l\cdot n \)
\( (a + c) - (b + d) = (k + l)\cdot n \)
Sol taraftaki fark ifadesini \( n \)'nin bir tam sayı katı şeklinde yazabildiğimiz için, \( n \) bu farkı böler, dolayısıyla bu farkın terimleri \( n \) modülünde denktir.
\( a + c \equiv b + d \pmod{n} \)
Çıkarma İşlemi
İki sayı arasında \( n \) modülünde çıkarma işleminin sonucu, sayıların aritmetik farkının \( n \) modülünde kalanına eşittir.
\( 3 - 6 \equiv -3 \equiv 5 \pmod{8} \)
\( 8 - 9 \equiv -1 \equiv 9 \pmod{10} \)
Çıkarma İşlem Özellikleri
Çıkarma işleminin modüler aritmetikte değişme özelliği yoktur.
\( a - b \not\equiv b - a \pmod{n} \)
Çıkarma İşlem Kuralları
Bir denkliğin iki tarafından aynı tam sayıyı çıkarmamız denkliği bozmaz.
\( a \equiv b \pmod{n} \) ise,
\( a - c \equiv b - c \pmod{n} \)
\( 28 \equiv 68 \pmod{8} \)
Denkliğin iki tarafından 10 çıkaralım.
\( 18 \equiv 58 \pmod{8} \)
İki denkliği taraf tarafa çıkarmamız denkliği bozmaz.
\( a \equiv b \pmod{n} \)
\( c \equiv d \pmod{n} \) ise,
\( a - c \equiv b - d \pmod{n} \)
\( 27 \equiv 52 \pmod{5} \)
\( 8 \equiv 23 \pmod{5} \)
İki denkliği taraf tarafa çıkaralım.
\( 19 \equiv 29 \pmod{5} \)
Çarpma İşlemi
İki sayının \( n \) modülünde çarpımının sonucu, sayıların aritmetik çarpımının \( n \) modülünde kalanına eşittir.
\( 5 \cdot 4 \equiv 20 \equiv 2 \pmod{6} \)
\( 6 \cdot 9 \equiv 54 \equiv 4 \pmod{10} \)
Çarpma İşlem Tablosu
İki sayının belirli bir modüldeki tüm kalanlarının aralarındaki çarpma işlemlerinin sonucunu bir tablo halinde gösterebiliriz. Bu tabloda satır ve sütun başlıkları çarpma işleminin terimleri, ilgili satır ve sütunun kesişimindeki hücredeki sayı da işlem sonucudur. Aşağıda \( 7 \) modülü için çarpma işlem tablosu verilmiştir.
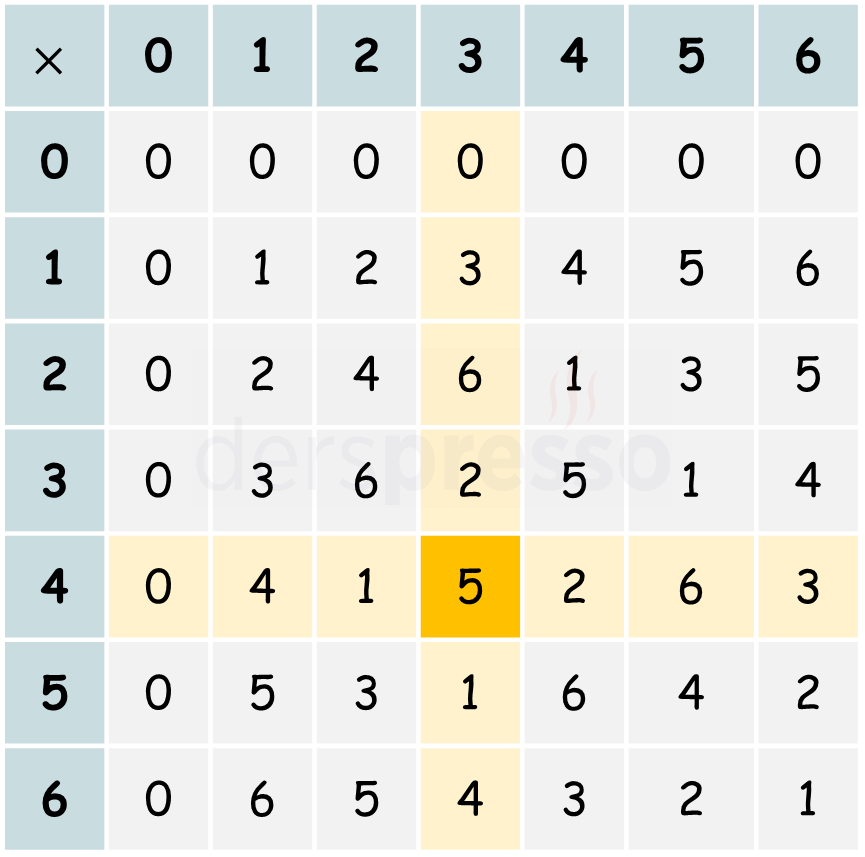
Yukarıdaki tabloya göre \( 7 \) modülünde bir çarpma işlemi aşağıdaki gibidir.
\( 4 \cdot 3 \equiv 5 \pmod{7} \)
Çarpma İşlem Özellikleri
Çarpma işleminin modüler aritmetikte değişme özelliği vardır.
\( a \cdot b \equiv b \cdot a \pmod{n} \)
Çarpma işleminin modüler aritmetikte birleşme özelliği vardır.
\( (a \cdot b) \cdot c \equiv a \cdot (b \cdot c) \pmod{n} \)
Çarpma İşlem Kuralları
Bir denkliğin iki tarafını aynı tam sayı ile çarpmamız denkliği bozmaz.
\( a \equiv b \pmod{n} \) ise,
\( c \cdot a \equiv c \cdot b \pmod{n} \)
\( 16 \equiv 27 \pmod{11} \)
Denkliğin iki tarafını 3 ile çarpalım.
\( 48 \equiv 81 \pmod{11} \)
İSPATI GÖSTER
İki sayı \( n \) modülünde denk ise, \( n \) bu iki sayının farkını böler.
\( a \equiv b \pmod{n} \Longrightarrow n \mid (a - b) \)
Denkliğin iki tarafını aynı sayı ile çarparsak, denkliğin taraflarının farkı aşağıdaki gibi olur.
\( c \cdot a \equiv c \cdot b \pmod{n} \)
\( c \cdot a - c \cdot b = c \cdot (a - b) \)
\( n \) sayısı iki sayının farkını bölüyorsa (bu farkın bir çarpanı ise), bu farkın bir tam sayı katını da böler (bu çarpım sonucunun da bir çarpanıdır).
\( n \mid (a - b) \Longrightarrow n \mid c \cdot (a - b) \)
\( n \) iki sayının farkını bölüyorsa, bu iki sayı \( n \) modülünde denktir.
\( n \mid (c \cdot a - c \cdot b) \Longrightarrow c \cdot a \equiv c \cdot b \pmod{n} \)
İki denkliği taraf tarafa çarpmamız denkliği bozmaz.
\( a \equiv b \pmod{n} \)
\( c \equiv d \pmod{n} \)
\( a \cdot c \equiv b \cdot d \pmod{n} \)
\( 8 \equiv 11 \pmod{3} \)
\( 15 \equiv 30 \pmod{3} \)
İki denkliği taraf tarafa çarpalım.
\( 120 \equiv 330 \pmod{3} \)
Bölme İşlemi
Modüler aritmetikte bir denkliğin iki tarafını bir sayıya, sadece bu sayı işlemin modülü ile aralarında asal ise bölebiliriz.
\( c \) ve \( n \) aralarında asal sayılar olmak üzere,
\( c \cdot a \equiv c \cdot b \pmod{n} \) ise,
\( a \equiv b \pmod{n} \)
\( 36 \equiv 51 \pmod{5} \)
3 ve 5 aralarında asal sayılar olduğu için, iki tarafı 3'e bölebiliriz.
\( 12 \cdot 3 \equiv 17 \cdot 3 \pmod{5} \)
\( 12 \equiv 17 \pmod{5} \)
\( 26 \equiv 50 \pmod{8} \)
2 ve 8 aralarında asal olmadığı için, iki tarafı 2'ye bölersek denklik sağlanmaya devam etmez.
\( 13 \not\equiv 25 \pmod{8} \)
İSPATI GÖSTER
İki sayı denk ise, \( n \) iki sayının farkını böler.
\( n \mid (c \cdot a - c \cdot b) \)
\( n \mid c \cdot (a - b) \)
\( c \) ve \( n \)'nın aralarında asal olduğunu kabul ettiğimiz için, \( n \) \( c \)'yi bölemez, dolayısıyla \( (a - b) \)'yi bölüyor olmak zorundadır (\( (a - b) \) içinde \( n \) çarpanı bulunmak zorundadır).
\( n \mid (a - b) \)
\( n \), \( a \) ve \( b \) farkını böldüğü için, bu iki sayı \( n \) modülünde denktir.
\( a \equiv b \pmod{n} \)
Üs İşlemi
Bir denkliğin iki tarafının aynı pozitif tam sayı kuvvetini almamız denkliği bozmaz.
\( k \in \mathbb{Z^+} \) olmak üzere,
\( a \equiv b \pmod{n} \) ise,
\( a^k \equiv b^k \pmod{n} \)
\( 4 \equiv 7 \pmod{3} \)
\( 4^3 \equiv 7^3 \pmod{3} \)
\( 64 \equiv 343 \pmod{3} \)
Üs işleminin tekrarlı çarpma olduğunu düşünürsek bu kuralın iki denkliğin taraf tarafa çarpımı kuralının bir uzantısı olduğunu görebiliriz.