Mutlak Değer Eşitsizlikleri
\( a, b \in \mathbb{R^+} \) ve \( m \in \mathbb{R} \) olmak üzere, farklı mutlak değer eşitsizlikleri için çözüm kümeleri aşağıdaki tabloda özetlenmiştir. Her bir durum için çözüm kümelerinin nasıl bulunduğu sayfanın geri kalanında detaylandırılmıştır.
| Mutlak Değerli İfade | Çözüm Kümesi |
|---|---|
| \( \abs{x} \ge 0 \) | \( x \in \mathbb{R} \) |
| \( \abs{x} \ge -a \) | \( x \in \mathbb{R} \) |
| \( \abs{x} \lt 0 \) | \( x = \{ \} \) |
| \( \abs{x} \le -a \) | \( x = \{ \} \) |
| \( \abs{x} \le 0 \) | \( x = 0 \) |
| \( \abs{x} \le a \) | \( -a \le x \le a \) |
| \( \abs{x - m} \le a \) | \( -a + m \le x \le a + m \) |
| \( a \le \abs{x} \) | \( x \le -a \quad \) ya da \( \quad a \le x \) |
| \( a \le \abs{x - m} \) | \( x \le -a + m \quad \) ya da \( \quad a + m \le x \) |
| \( a \le \abs{x} \le b \) | \( -b \le x \le -a \quad \) ya da \( \quad a \le x \le b \) |
| \( a \le \abs{x - m} \le b \) | \( -b + m \le x \le -a + m \quad \) ya da \( \quad a + m \le x \le b + m \) |
Sıfır ve Negatif Sınır Değerleri
Mutlak değerli bir ifadenin sonucu her zaman sıfır ya da pozitiftir, dolayısıyla mutlak değerli bir ifadenin negatif bir sayıdan büyük olduğu eşitsizliklerin çözüm kümesi tüm reel sayılar kümesidir.
\( a \in \mathbb{R^+} \) olmak üzere,
\( \abs{x} \ge 0 \) ya da \( \abs{x} \gt -a \) ise,
Çözüm kümesi: \( x \in \mathbb{R} \)
Benzer şekilde, mutlak değerli bir ifadenin sıfırdan küçük olduğu eşitsizliklerin çözüm kümesi boş kümedir.
\( a \in \mathbb{R^+} \) olmak üzere,
\( \abs{x} \lt 0 \) ya da \( \abs{x} \le -a \) ise,
Çözüm kümesi: \( x = \emptyset \)
Mutlak değerli bir ifadenin sonucu sıfıra eşitse ya da sıfırdan küçükse çözüm kümesi sadece sıfır olabilir.
\( \abs{x} \le 0 \) ise,
Çözüm kümesi: \( x = 0 \)
Üst Sınırlı Eşitsizlikler
\( \abs{x} \le a \) formundaki eşitsizlikler, orijine uzaklığı \( a \)'dan küçük ya da \( a \)'ya eşit olan noktaların kümesini verir.
\( \abs{x} \lt a \) formundaki eşitsizlikler, orijine uzaklığı \( a \)'dan küçük olan noktaların kümesini verir.

\( a \in \mathbb{R^+} \) olmak üzere,
\( \abs{x} \le a \) ise,
\( -a \le x \le a \)
Aralık gösterimi: \( [-a, a] \)
\( \abs{x} \le 4 \) ise,
Çözüm kümesi: \( -4 \le x \le 4 \)
İSPATI GÖSTER
\( \abs{x} \le a \)
Mutlak değer içinin pozitif ve negatif olduğu durumlar için eşitsizliği çözelim.
Durum 1: \( x \ge 0 \)
\( x \le a \)
\( 0 \le x \le a \)
Durum 2: \( x \lt 0 \)
\( -x \le a \)
\( -a \le x \lt 0 \)
Eşitsizliğin çözüm kümesi yukarıdaki iki durumun çözüm kümelerinin birleşim kümesidir.
\( -a \le x \le a \)
\( \abs{x - m} \le a \) formundaki eşitsizlikler, \( m \) noktasına uzaklığı \( a \)'dan küçük ya da \( a \)'ya eşit olan noktaların kümesini verir.
\( \abs{x - m} \lt a \) formundaki eşitsizlikler, \( m \) noktasına uzaklığı \( a \)'dan küçük olan noktaların kümesini verir.

\( a \in \mathbb{R^+}, m \in \mathbb{R} \) olmak üzere,
\( \abs{x - m} \le a \) ise,
\( -a + m \le x \le a + m \)
Aralık gösterimi: \( [-a + m, a + m] \)
\( \abs{x - 2} \le 4 \) ise,
\( -4 + 2 \le x \le 4 + 2 \)
Çözüm kümesi: \( -2 \le x \le 6 \)
İSPATI GÖSTER
\( \abs{x - m} \le a \)
Mutlak değer içinin pozitif ve negatif olduğu durumlar için eşitsizliği çözelim.
Durum 1: \( x - m \ge 0 \)
\( 0 \le x - m \le a \)
\( m \le x \le a + m \)
Durum 2: \( x - m \lt 0 \)
\( -(x - m) \le a \)
\( -a \le x - m \lt 0 \)
\( -a + m \le x \lt m \)
Eşitsizliğin çözüm kümesi yukarıdaki iki durumun çözüm kümelerinin birleşim kümesidir.
\( -a + m \le x \le a + m \)
Alt Sınırlı Eşitsizlikler
\( a \le \abs{x} \) formundaki eşitsizlikler, orijine uzaklığı \( a \)'dan büyük ya da \( a \)'ya eşit olan noktaların kümesini verir.
\( a \lt \abs{x} \) formundaki eşitsizlikler, orijine uzaklığı \( a \)'dan büyük olan noktaların kümesini verir.

\( a \in \mathbb{R^+} \) olmak üzere,
\( a \le \abs{x} \) ise,
\( x \le -a \quad \) ya da \( \quad a \le x \)
Aralık gösterimi: \( (-\infty, -a] \cup [a, \infty) \)
\( 4 \le \abs{x} \) ise,
Çözüm kümesi: \( x \le -4 \) ya da \( 4 \le x \)
İSPATI GÖSTER
\( a \le \abs{x} \) ise,
Mutlak değer içinin pozitif ve negatif olduğu durumlar için eşitsizliği çözelim.
Durum 1: \( x \ge 0 \)
\( 0 \lt a \le x \)
Durum 2: \( x \lt 0 \)
\( a \le -x \)
\( x \le -a \lt 0 \)
Eşitsizliğin çözüm kümesi yukarıdaki iki durumun çözüm kümelerinin birleşim kümesidir.
\( x \le -a \quad \) ya da \( \quad a \le x \)
\( a \le \abs{x - m} \) formundaki eşitsizlikler, \( m \) noktasına uzaklığı \( a \)'dan büyük ya da \( a \)'ya eşit olan noktaların kümesini verir.
\( a \lt \abs{x - m} \) formundaki eşitsizlikler, \( m \) noktasına uzaklığı \( a \)'dan büyük olan noktaların kümesini verir.

\( a \in \mathbb{R^+}, m \in \mathbb{R} \) olmak üzere,
\( a \le \abs{x - m} \) ise,
\( x \le -a + m \quad \) ya da \( \quad a + m \le x \)
Aralık gösterimi: \( (-\infty, -a + m] \cup [a + m, \infty) \)
\( 4 \le \abs{x - 2} \) ise,
\( x \le -4 + 2 \) ya da \( 4 + 2 \le x \)
Çözüm kümesi: \( x \le -2 \) ya da \( 6 \le x \)
İSPATI GÖSTER
\( a \le \abs{x - m} \)
Mutlak değer içinin pozitif ve negatif olduğu durumlar için eşitsizliği çözelim.
Durum 1: \( x - m \ge 0 \)
\( 0 \lt a \le x - m \)
\( m \lt a + m \le x \)
Durum 2: \( x - m \lt 0 \)
\( a \le -(x - m) \)
\( x - m \le -a \lt 0 \)
\( x \le -a + m \lt m \)
Eşitsizliğin çözüm kümesi yukarıdaki iki durumun çözüm kümelerinin birleşim kümesidir.
\( x \le -a + m \quad \) ya da \( \quad a + m \le x \)
Alt ve Üst Sınırlı Eşitsizlikler
\( a \le \abs{x} \le b \) formundaki eşitsizlikler, orijine uzaklığı \( a \) ve \( b \) kapalı aralığında olan noktaların kümesini verir.
\( a \lt \abs{x} \lt b \) formundaki eşitsizlikler, orijine uzaklığı \( a \) ve \( b \) açık aralığında olan noktaların kümesini verir.

\( a, b \in \mathbb{R^+} \) olmak üzere,
\( a \le \abs{x} \le b \) ise,
\( -b \le x \le -a \quad \) ya da \( \quad a \le x \le b \)
Aralık gösterimi: \( [-b, -a] \cup [a, b] \)
\( 2 \le \abs{x} \le 4 \) ise,
Çözüm kümesi: \( -4 \le x \le -2 \) ya da \( 2 \le x \le 4 \)
İSPATI GÖSTER
\( a \le \abs{x} \le b \)
Mutlak değer içinin pozitif ve negatif olduğu durumlar için eşitsizliği çözelim.
Durum 1: \( x \ge 0 \)
\( 0 \lt a \le x \le b \)
Durum 2: \( x \lt 0 \)
\( a \le -x \le b \)
\( -b \le x \le -a \lt 0 \)
Eşitsizliğin çözüm kümesi yukarıdaki iki durumun çözüm kümelerinin birleşim kümesidir.
\( -b \le x \le -a \quad \) ya da \( \quad a \le x \le b \)
\( a \le \abs{x - m} \le b \) formundaki eşitsizlikler, \( m \) noktasına uzaklığı \( a \) ve \( b \) kapalı aralığında olan noktaların kümesini verir.
\( a \lt \abs{x - m} \lt b \) formundaki eşitsizlikler, \( m \) noktasına uzaklığı \( a \) ve \( b \) açık aralığında olan noktaların kümesini verir.
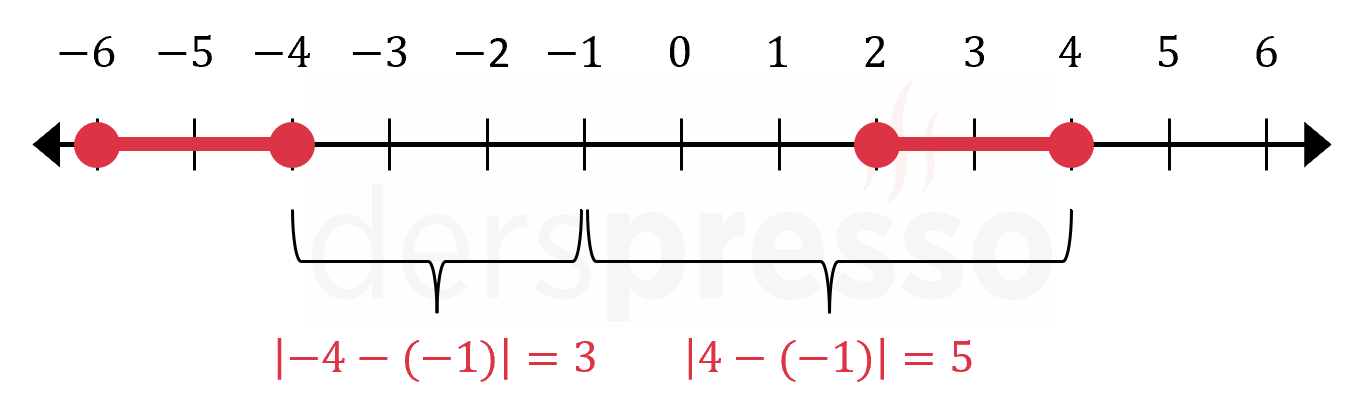
\( a, b \in \mathbb{R^+}, m \in \mathbb{R} \) olmak üzere,
\( a \le \abs{x - m} \le b \) ise,
\( -b + m \le x \le -a + m \quad \) ya da \( \quad a + m \le x \le b + m \)
\( [-b + m, -a + m] \cup [a + m, b + m] \)
\( 5 \le \abs{x - 2} \le 8 \) ise,
Çözüm kümesi: \( -6 \le x \le -3 \) ya da \( 7 \le x \le 10 \)
İSPATI GÖSTER
\( a \le \abs{x - m} \le b \) ise,
Mutlak değer içinin pozitif ve negatif olduğu durumlar için eşitsizliği çözelim.
Durum 1: \( x - m \ge 0 \)
\( 0 \lt a \le x - m \le b \)
\( m \lt a + m \le x \le b + m \)
Durum 2: \( x - m \lt 0 \)
\( a \le -(x - m) \le b \)
\( -b \le x - m \le -a \lt 0 \)
\( -b + m \le x \le -a + m \lt m \)
Eşitsizliğin çözüm kümesi yukarıdaki iki durumun çözüm kümelerinin birleşim kümesidir.
\( -b + m \le x \le -a + m \quad \) ya da \( \quad a + m \le x \le b + m \)
İki Mutlak Değerli İfade Arasındaki Eşitsizlikler
\( \abs{x} \le \abs{y} \) formundaki eşitsizlikler, denklemler bölümünde uyguladığımız yönteme benzer şekilde eşitsizliğin iki tarafının karesi alınarak çözülebilir. Mutlak değerli ifadeler her zaman sıfır ya da pozitif oldukları için, bu şekildeki eşitsizliklerin her iki tarafının karesi alındığında eşitsizlik bozulmaz ya da yön değiştirmez.
\( \abs{x} \le \abs{y} \) ise,
\( {\abs{x}}^2 \le {\abs{y}}^2 \)
\( \abs{x + 6} \gt \abs{x - 2} \) eşitsizliğini çözelim.
İki tarafın karesini alalım. İki taraf da negatif olamayacağı için, tarafların karesini almak eşitsizliği bozmaz ya da yönünü değiştirmez.
\( {\abs{x + 6}}^2 \gt {\abs{x - 2}}^2 \)
\( x^2 + 12x + 36 \gt x^2 - 4x + 4 \)
\( x \)'li terimleri eşitsizliğin bir tarafına, sabit terimleri diğer tarafına alalım.
\( 16x \gt -32 \)
\( x \gt -2 \)
Eşitsizliğin çözüm kümesini bulmuş olduk.
Çözüm kümesi: \( x \gt -2 \)
Aşağıdaki eşitsizliklerin çözüm kümelerini bulunuz.
(a) \( \abs{2x + 5} \lt 9 \)
(b) \( \abs{1 - 7x} \le 64 \)
(c) \( \abs{180 - 15x} \lt 210 \)
Çözümü Göster(a) seçeneği:
\( \abs{2x + 5} \lt 9 \)
Eşitsizlikte mutlak değer ifadesini kaldırdığımızda aşağıdaki şekilde tek bir eşitsizlik oluşur.
\( -9 \lt 2x + 5 \lt 9 \)
\( -14 \lt 2x \lt 4 \)
\( -7 \lt x \lt 2 \)
Çözüm kümesi: \( x \in (-7, 2) \)
(b) seçeneği:
\( \abs{1 - 7x} \le 64 \)
Eşitsizlikte mutlak değer ifadesini kaldırdığımızda aşağıdaki şekilde tek bir eşitsizlik oluşur.
\( -64 \le 1 - 7x \le 64 \)
\( -65 \le -7x \le 63 \)
\( -\dfrac{65}{7} \le -x \le 9 \)
\( -9 \le x \le \dfrac{65}{7} \)
Çözüm kümesi: \( x \in [-9, \frac{65}{7}] \)
(c) seçeneği:
\( \abs{180 - 15x} \lt 210 \)
Eşitsizlikte mutlak değer ifadesini kaldırdığımızda aşağıdaki şekilde tek bir eşitsizlik oluşur.
\( -210 \lt 180 - 15x \lt 210 \)
\( -390 \lt -15x \lt 30 \)
\( -26 \lt -x \lt 2 \)
\( -2 \lt x \lt 26 \)
Çözüm kümesi: \( x \in (-2, 26) \)
Aşağıdaki eşitsizliklerin çözüm kümelerini bulunuz.
(a) \( 2 \lt \abs{x - 3} \le 12 \)
(b) \( 3 \le \abs{10x + 7} \lt 23 \)
(c) \( 0 \lt \abs{x - 1} \lt 7 \)
Çözümü Göster(a) seçeneği:
\( 2 \lt \abs{x - 3} \le 12 \)
Verilen eşitsizlikte mutlak değer ifadesini kaldırdığımızda \( x - 3 \) için iki aralık oluşur.
Eşitsizlik 1:
\( 2 \lt x - 3 \le 12 \)
\( 5 \lt x \le 15 \)
Eşitsizlik 2:
\( -12 \le x - 3 \lt -2 \)
\( -9 \le x \lt 1 \)
Bulduğumuz çözüm aralıklarının birleşimi eşitsizliğin çözüm kümesini verir.
Çözüm kümesi: \( x \in [-9, 1) \cup (5, 15] \)
(b) seçeneği:
\( 3 \le \abs{10x + 7} \lt 23 \)
Verilen eşitsizlikte mutlak değer ifadesini kaldırdığımızda \( 10x + 7 \) için iki aralık oluşur.
Eşitsizlik 1:
\( 3 \le 10x + 7 \lt 23 \)
\( -4 \le 10x \lt 16 \)
\( -\dfrac{2}{5} \le x \lt \dfrac{8}{5} \)
Eşitsizlik 2:
\( -23 \lt 10x + 7 \le -3 \)
\( -30 \lt 10x \le -10 \)
\( -3 \lt x \le -1 \)
Bulduğumuz çözüm aralıklarının birleşimi eşitsizliğin çözüm kümesini verir.
Çözüm kümesi: \( x \in (-3, -1] \cup [-\frac{2}{5}, \frac{8}{5}) \)
(c) seçeneği:
\( 0 \lt \abs{x - 1} \lt 7 \)
Verilen eşitsizlikte mutlak değer ifadesini kaldırdığımızda \( x - 1 \) için iki aralık oluşur.
Eşitsizlik 1:
\( 0 \lt x - 1 \lt 7 \)
\( 1 \lt x \lt 8 \)
Eşitsizlik 2:
\( -7 \lt x - 1 \lt 0 \)
\( -6 \lt x \lt 1 \)
Bulduğumuz çözüm aralıklarının birleşimi eşitsizliğin çözüm kümesini verir.
Çözüm kümesi: \( x \in (-6, 1) \cup (1, 8) \)
Aşağıdaki eşitsizliklerin çözüm kümelerini bulunuz.
(a) \( \abs{12 - 15x} \gt 42 \)
(b) \( \abs{\dfrac{52 - x}{4}} \ge 7 \)
(c) \( \abs{7x - 11} \gt 0 \)
Çözümü Göster(a) seçeneği:
\( \abs{12 - 15x} \gt 42 \)
Eşitsizlikte mutlak değer ifadesini kaldırdığımızda \( 12 - 15x \gt 42 \) ve \( 12 - 15x \lt -42 \) şeklinde iki eşitsizlik oluşur.
Eşitsizlik 1:
\( 12 - 15x \gt 42 \)
\( -15x \gt 30 \)
\( x \lt -2 \)
Eşitsizlik 2:
\( 12 - 15x \lt -42 \)
\( 15x \gt 54 \)
\( x \gt \dfrac{18}{5} \)
Bulduğumuz çözüm aralıklarının birleşimi eşitsizliğin çözüm kümesini verir.
Çözüm kümesi: \( x \in (-\infty, -2) \cup (\frac{18}{5}, \infty) \)
(b) seçeneği:
\( \abs{\dfrac{52 - x}{4}} \ge 7 \)
Eşitsizlikte mutlak değer ifadesini kaldırdığımızda \( \frac{52 - x}{4} \ge 7 \) ve \( \frac{52 - x}{4} \le -7 \) şeklinde iki eşitsizlik oluşur.
Eşitsizlik 1:
\( \dfrac{52 - x}{4} \ge 7 \)
\( 52 - x \ge 28 \)
\( x \le 24 \)
Eşitsizlik 2:
\( \dfrac{52 - x}{4} \le -7 \)
\( 52 - x \le -28 \)
\( x \ge 80 \)
Bulduğumuz çözüm aralıklarının birleşimi eşitsizliğin çözüm kümesini verir.
Çözüm kümesi: \( x \in (-\infty, 24] \cup [80, \infty) \)
(c) seçeneği:
\( \abs{7x - 11} \gt 0 \)
Eşitsizlikte mutlak değer ifadesini kaldırdığımızda \( 7x - 11 \gt 0 \) ve \( 7x - 11 \lt 0 \) şeklinde iki eşitsizlik oluşur.
Eşitsizlik 1:
\( 7x - 11 \gt 0 \)
\( 7x \gt 11 \)
\( x \gt \dfrac{11}{7} \)
Eşitsizlik 2:
\( 7x - 11 \lt 0 \)
\( 7x \lt 11 \)
\( x \lt \dfrac{11}{7} \)
Bulduğumuz çözüm aralıklarının birleşimi eşitsizliğin çözüm kümesini verir.
Çözüm kümesi: \( x \in \mathbb{R} - \{\frac{11}{7}\} \)
Aşağıdaki eşitsizliklerin çözüm kümelerini bulunuz.
(a) \( \abs{\dfrac{3x - 6}{4}} \ge 9 \)
(b) \( \abs{\dfrac{6x - 12}{5}} \gt 48 \)
(c) \( \abs{\dfrac{x + 39}{8}} \ge 2 \)
Çözümü Göster(a) seçeneği:
\( \abs{\dfrac{3x - 6}{4}} \ge 9 \)
Eşitsizlikte mutlak değer ifadesini kaldırdığımızda \( \frac{3x - 6}{4} \ge 9 \) ve \( \frac{3x - 6}{4} \le -9 \) şeklinde iki eşitsizlik oluşur.
Eşitsizlik 1:
\( \dfrac{3x - 6}{4} \ge 9 \)
\( 3x - 6 \ge 36 \)
\( 3x \ge 42 \)
\( x \ge 14 \)
Eşitsizlik 2:
\( \dfrac{3x - 6}{4} \le -9 \)
\( 3x - 6 \le -36 \)
\( 3x \le -30 \)
\( x \le -10 \)
Bulduğumuz çözüm aralıklarının birleşimi eşitsizliğin çözüm kümesini verir.
Çözüm kümesi: \( x \in (-\infty, -10] \cup [14, \infty) \)
(b) seçeneği:
\( \abs{\dfrac{6x - 12}{5}} \gt 48 \)
Eşitsizlikte mutlak değer ifadesini kaldırdığımızda \( \frac{6x - 12}{5} \gt 48 \) ve \( \frac{6x - 12}{5} \lt -48 \) şeklinde iki eşitsizlik oluşur.
Eşitsizlik 1:
\( \dfrac{6x - 12}{5} \gt 48 \)
\( 6x - 12 \gt 240 \)
\( 6x \gt 252 \)
\( x \gt 42 \)
Eşitsizlik 2:
\( \dfrac{6x - 12}{5} \lt -48 \)
\( 6x - 12 \lt -240 \)
\( 6x \lt -228 \)
\( x \lt -38 \)
Bulduğumuz çözüm aralıklarının birleşimi eşitsizliğin çözüm kümesini verir.
Çözüm kümesi: \( x \in (-\infty, -38) \cup (42, \infty) \)
(c) seçeneği:
\( \abs{\dfrac{x + 39}{8}} \ge 2 \)
Eşitsizlikte mutlak değer ifadesini kaldırdığımızda \( \frac{x + 39}{8} \ge 2 \) ve \( \frac{x + 39}{8} \le -2 \) şeklinde iki eşitsizlik oluşur.
Eşitsizlik 1:
\( \dfrac{x + 39}{8} \ge 2 \)
\( x + 39 \ge 16 \)
\( x \ge -23 \)
Eşitsizlik 2:
\( \dfrac{x + 39}{8} \le -2 \)
\( x + 39 \le -16 \)
\( x \le -55 \)
Bulduğumuz çözüm aralıklarının birleşimi eşitsizliğin çözüm kümesini verir.
Çözüm kümesi: \( x \in (-\infty, -55] \cup [-23, \infty) \)
Aşağıdaki eşitsizliklerin çözüm kümelerini bulunuz.
(a) \( -5 \lt \abs{4x - 6} \le 10 \)
(b) \( -10 \le \abs{12 - 4x} \lt 44 \)
(c) \( -8 \le \abs{16x - 8} \le 0 \)
Çözümü Göster(a) seçeneği:
\( -5 \lt \abs{4x - 6} \le 10 \)
Bir mutlak değerli ifade hiçbir zaman negatif değer alamayacağı için verilen eşitsizlik aşağıdaki eşitsizliğe denktir.
\( 0 \le \abs{4x - 6} \le 10 \)
Verilen eşitsizlikte mutlak değer ifadesini kaldırdığımızda aşağıdaki şekilde tek bir eşitsizlik oluşur.
\( -10 \le 4x - 6 \le 10 \)
\( -4 \le 4x \le 16 \)
\( -1 \le x \le 4 \)
Çözüm kümesi: \( x \in [-1, 4] \)
(b) seçeneği:
\( -10 \le \abs{12 - 4x} \lt 44 \)
Bir mutlak değerli ifade hiçbir zaman negatif değer alamayacağı için verilen eşitsizlik aşağıdaki eşitsizliğe denktir.
\( 0 \le \abs{12 - 4x} \lt 44 \)
Verilen eşitsizlikte mutlak değer ifadesini kaldırdığımızda aşağıdaki şekilde tek bir eşitsizlik oluşur.
\( -44 \lt 12 - 4x \lt 44 \)
\( -56 \lt -4x \lt 32 \)
\( -14 \lt -x \lt 8 \)
\( -8 \lt x \lt 14 \)
Çözüm kümesi: \( x \in (-8, 14) \)
(c) seçeneği:
\( -8 \le \abs{16x - 8} \le 0 \)
Bir mutlak değerli ifade hiçbir zaman negatif değer alamayacağı için verilen eşitsizlik aşağıdaki eşitliğe denktir.
\( \abs{16x - 8} = 0 \)
Bir ifadenin mutlak değeri sıfıra eşitse kendisi de sıfırdır.
\( 16x - 8 = 0 \)
\( x = \dfrac{1}{2} \)
Çözüm kümesi: \( x \in \{\frac{1}{2}\} \)
\( \abs{x - 7} \ge 6 \) ve \( \abs{x - 3} \lt 13 \)
eşitsizlik sisteminin çözüm kümesi nedir?
Çözümü GösterEşitsizliklerin ayrı ayrı çözüm kümelerini bulalım.
Eşitsizlik 1:
\( \abs{x - 7} \ge 6 \)
\( x - 7 \ge 6 \) ya da \( x - 7 \le -6 \)
\( x \ge 13 \) ya da \( x \le 1 \)
Çözüm kümesi: \( x \in (-\infty, 1] \cup [13, \infty) \)
Eşitsizlik 2:
\( \abs{x - 3} \lt 13 \)
\( -13 \lt x - 3 \lt 13 \)
\( -10 \lt x \lt 16 \)
Çözüm kümesi: \( x \in (-10, 16) \)
Sorudaki eşitsizlik sisteminin çözüm kümesi iki eşitsizliğin çözüm kümelerinin kesişim kümesidir.
Çözüm kümesi: \( x \in (-10, 1] \cup [13, 16) \)
Aşağıdaki eşitsizliklerin çözüm kümelerini bulunuz.
(a) \( \abs{1 - x} \lt 9x - 4 \)
(b) \( \abs{5x + 2} \ge 6 - 11x \)
(c) \( \abs{x - 2} \gt 3x + 4 \)
Çözümü Göster(a) seçeneği:
\( \abs{1 - x} \lt 9x - 4 \)
Mutlak değer içini sıfır yapan \( x = 1 \) değerinin oluşturduğu \( x \le 1 \) ve \( x \gt 1 \) aralıklarını ayrı ayrı inceleyelim ve her durumda oluşan eşitsizliği çözelim.
Durum 1: \( x \le 1 \)
Bu aralıkta \( 1 - x \) ifadesi sıfır ya da pozitif olur ve mutlak değer dışına olduğu gibi çıkar.
\( 1 - x \lt 9x - 4 \)
\( 5 \lt 10x \)
\( x \gt \dfrac{1}{2} \)
Bu aralık ile incelediğimiz \( x \le 1 \) aralığının kesişimi bu durumun çözüm kümesini verir.
\( x \in (\frac{1}{2}, 1] \)
Durum 2: \( x \gt 1 \)
Bu aralıkta \( 1 - x \) ifadesi negatif olur ve mutlak değer dışına negatif işaretli çıkar.
\( -(1 - x) \lt 9x - 4 \)
\( x - 1 \lt 9x - 4 \)
\( 8x \gt 3 \)
\( x \gt \dfrac{3}{8} \)
Bu aralık ile incelediğimiz \( x \gt 1 \) aralığının kesişimi bu durumun çözüm kümesini verir.
\( x \in (1, \infty) \)
Bulduğumuz çözüm aralıklarının birleşimi eşitsizliğin çözüm kümesini verir.
Çözüm kümesi: \( x \in (\frac{1}{2}, \infty) \)
(b) seçeneği:
\( \abs{5x + 2} \ge 6 - 11x \)
Mutlak değer içini sıfır yapan \( x = -\frac{2}{5} \) değerinin oluşturduğu \( x \lt -\frac{2}{5} \) ve \( x \ge -\frac{2}{5} \) aralıklarını ayrı ayrı inceleyelim ve her durumda oluşan eşitsizliği çözelim.
Durum 1: \( x \lt -\frac{2}{5} \)
Bu aralıkta \( 5x + 2 \) ifadesi negatif olur ve mutlak değer dışına negatif işaretli çıkar.
\( -(5x + 2) \ge 6 - 11x \)
\( -5x - 2 \ge 6 - 11x \)
\( 6x \ge 8 \)
\( x \ge \dfrac{4}{3} \)
Bu aralık ile incelediğimiz \( x \lt -\frac{2}{5} \) aralığının kesişimi bu durumun çözüm kümesini verir.
\( x \in \emptyset \)
Durum 2: \( x \ge -\frac{2}{5} \)
Bu aralıkta \( 5x + 2 \) ifadesi sıfır ya da pozitif olur ve mutlak değer dışına olduğu gibi çıkar.
\( 5x + 2 \ge 6 - 11x \)
\( 16x \ge 4 \)
\( x \ge \dfrac{1}{4} \)
Bu aralık ile incelediğimiz \( x \ge -\frac{2}{5} \) aralığının kesişimi bu durumun çözüm kümesini verir.
\( x \in [\frac{1}{4}, \infty) \)
Bulduğumuz çözüm aralıklarının birleşimi eşitsizliğin çözüm kümesini verir.
Çözüm kümesi: \( x \in [\frac{1}{4}, \infty) \)
(c) seçeneği:
\( \abs{x - 2} \gt 3x + 4 \)
Mutlak değer içini sıfır yapan \( x = 2 \) değerinin oluşturduğu \( x \lt 2 \) ve \( x \ge 2 \) aralıklarını ayrı ayrı inceleyelim ve her durumda oluşan eşitsizliği çözelim.
Durum 1: \( x \lt 2 \)
Bu aralıkta \( x - 2 \) ifadesi negatif olur ve mutlak değer dışına negatif işaretli çıkar.
\( -(x - 2) \gt 3x + 4 \)
\( -x + 2 \gt 3x + 4 \)
\( 4x \lt -2 \)
\( x \lt -\dfrac{1}{2} \)
Bu aralık ile incelediğimiz \( x \lt 2 \) aralığının kesişimi bu durumun çözüm kümesini verir.
\( x \in (-\infty, -\frac{1}{2}) \)
Durum 2: \( x \ge 2 \)
Bu aralıkta \( x - 2 \) ifadesi sıfır ya da pozitif olur ve mutlak değer dışına olduğu gibi çıkar.
\( x - 2 \gt 3x + 4 \)
\( 2x \lt -6 \)
\( x \lt -3 \)
Bu aralık ile incelediğimiz \( x \ge 2 \) aralığının kesişimi bu durumun çözüm kümesini verir.
\( x \in \emptyset \)
Bulduğumuz çözüm aralıklarının birleşimi eşitsizliğin çözüm kümesini verir.
Çözüm kümesi: \( x \in (-\infty, -\frac{1}{2}) \)
\( x \lt \abs{x} \) eşitsizliği aşağıdaki aralıkların hangilerinin tümünde sağlanır?
I. \( x \lt -2 \)
II. \( -5 \le x \lt 0 \)
III. \( x \gt 3 \)
IV. \( -3 \le x \lt 2 \)
Çözümü GösterBir sayının mutlak değeri kendisinden büyükse bu sayı negatiftir.
Çözüm kümesi: \( x \lt 0 \)
I. ve II. aralıkların tümü çözüm kümesinin içindedir.
III. aralığın tümü çözüm kümesinin dışındadır.
IV. aralık kısmen çözüm kümesinin içinde kısmen dışındadır.
Buna göre verilen eşitsizlik I. ve II. aralıkların tümünde sağlanır.
\( \dfrac{x}{\abs{\abs{x} + x}} \gt 0 \)
eşitsizliğinin çözüm kümesi nedir?
Çözümü GösterEşitsizliği \( x \)'in negatif, pozitif ve sıfır olduğu durumlar için ayrı ayrı inceleyelim.
Durum 1: \( x \lt 0 \)
\( \abs{x} = -x \)
\( \dfrac{x}{\abs{\abs{x} + x}} \gt 0 \)
\( \dfrac{x}{\abs{-x + x}} \gt 0 \)
\( \dfrac{x}{0} \gt 0 \)
Eşitsizliğin sol tarafı tanımsızdır, dolayısıyla eşitsizlik hiçbir \( x \lt 0 \) için sağlanmaz.
Durum 2: \( x \gt 0 \)
\( \abs{x} = x \)
\( \dfrac{x}{\abs{x + x}} \gt 0 \)
\( \dfrac{x}{\abs{2x}} \gt 0 \)
\( \dfrac{x}{2x} \gt 0 \)
\( \dfrac{1}{2} \gt 0 \)
Eşitsizlik her durumda sağlandığı için her \( x \gt 0 \) değeri verilen eşitsizliği sağlar.
Durum 3: \( x = 0 \)
\( \dfrac{0}{\abs{\abs{0} + 0}} \gt 0 \)
\( \dfrac{0}{0} \gt 0 \)
Eşitsizliğin sol tarafı tanımsızdır, dolayısıyla eşitsizlik \( x = 0 \) için sağlanmaz.
Eşitsizliğin çözüm kümesi 2. durumda bulduğumuz aralıktır.
Çözüm kümesi: \( x \in (0, \infty) \)
\( x, k, m \in \mathbb{R} \) olmak üzere,
\( \abs{3x - k} \lt m \) eşitsizliğinin çözüm kümesi \( (-3, 7) \) aralığı olduğuna göre,
\( k \cdot m \) çarpımı kaçtır?
Çözümü GösterVerilen eşitsizliği kullanarak \( x \) değer aralığını bulalım.
\( -m \lt 3x - k \lt m \)
\(-m + k \lt 3x \lt m + k \)
\( \dfrac{k - m}{3} \lt x \lt \dfrac{k + m}{3} \)
Eşitsizliğin çözüm kümesi \( (-3, 7) \) aralığıdır, buna göre \( x \) için bulduğumuz değer aralığının sınır değerlerini bu değerlere eşitleyelim.
\( \dfrac{k - m}{3} = -3 \Longrightarrow k - m = -9 \)
\( \dfrac{k + m}{3} = 7 \Longrightarrow k + m = 21 \)
Elde ettiğimiz iki bilinmeyenli iki denklemi ortak çözerek \( k \) ve \( m \) değerlerini bulalım.
\( 2k = 12 \Longrightarrow k = 6 \)
\( 6 - m = -9 \Longrightarrow m = 15 \)
Buna göre \( k \cdot m = 6 \cdot 15 = 90 \) bulunur.
\( \abs{x - 4} \lt 20 \)
\( \dfrac{x}{2} + 4y = 4 \)
olduğuna göre, \( y \)'nin alabileceği kaç farklı tam sayı değeri vardır?
Çözümü GösterVerilen eşitsizliğin çözüm kümesini yazalım.
\( -20 \lt x - 4 \lt 20 \)
\( -16 \lt x \lt 24 \)
Verilen eşitlikte \( y \)'yi yalnız bırakalım.
\( 4y = 4 - \dfrac{x}{2} \)
\( y = 1 - \dfrac{x}{8} \)
Aritmetik işlemlerle eşitsizlikte bu \( x \)'li ifadeyi elde etmeye çalışalım.
Eşitsizliğin taraflarını 8'e bölelim.
\( -2 \lt \dfrac{x}{8} \lt 3 \)
Eşitsizliğin taraflarını -1 ile çarpalım. Bir eşitsizliğin tarafları negatif bir sayı ile çarpıldığında eşitsizlik yön değiştirir.
\( 2 \gt -\dfrac{x}{8} \gt -3 \)
Eşitsizliğin taraflarına 1 ekleyelim.
\( 3 \gt 1 - \dfrac{x}{8} \gt -2 \)
Eşitsizlikte ortadaki ifade \( y \)'ye eşittir.
\( 3 \gt y \gt -2 \)
Buna göre \( y \)'nin alabileceği tam sayı değerleri \( \{-1, 0, 1, 2\} \) olmak üzere 4 tanedir.
\( \abs{k - 3m} + \abs{3k + 2m - 55} \le 0 \) olduğuna göre, \( m \) kaçtır?
Çözümü GösterBir mutlak değer ifadesinin sonucu sıfır ya da pozitif olabilir, negatif olamaz.
Verilen iki mutlak değer ifadesinin toplamı negatif olamayacağı için ifadelerin toplamları, dolayısıyla kendileri sıfır olmalıdır
İfade 1: \( \abs{k - 3m} \)
\( k - 3m = 0 \)
\( k = 3m \)
İfade 2: \( \abs{3k + 2m - 55} \)
\( 3k + 2m - 55 = 0 \)
\( k = 3m \) yazalım.
\( 3(3m) + 2m - 55 = 0 \)
\( m = 5 \) bulunur.
\( \abs{x - 9} \lt \abs{x - 5} + 4 \) eşitsizliğinin en geniş çözüm kümesini bulunuz.
Çözümü GösterMutlak değerli ifadeleri sıfır yapan noktalar eşitsizliğin kritik noktalarıdır.
Buna göre eşitsizliğin kritik noktaları \( x \in \{5, 9\} \) noktalarıdır.
Bu iki kritik noktanın oluşturduğu üç aralığı ayrı ayrı inceleyelim ve her aralıkta mutlak değer içindeki ifadeleri o aralıktaki işaretlerine göre mutlak değerden çıkaralım.
Durum 1: \( x \lt 5 \)
Bu aralıkta her iki mutlak değerli ifade de negatif olur, dolayısıyla mutlak değerden negatif işaretli çıkar.
\( -(x - 9) \lt -(x - 5) + 4 \)
\( -x + 9 \lt -x + 5 + 4 \)
\( -x \lt -x \)
Bu eşitsizliğin çözümü olmadığı için bu aralıkta geçerli bir çözüm yoktur.
Durum 2: \( 5 \le x \lt 9 \)
Bu aralıkta \( x - 5 \) ifadesi pozitif, \( x - 9 \) ifadesi negatif olur, dolayısıyla birinci ifade mutlak değerden olduğu gibi, ikinci ifade negatif işaretli çıkar.
\( -(x - 9) \lt (x - 5) + 4 \)
\( -x + 9 \lt x - 5 + 4 \)
\( x \gt 5 \)
Bu aralık ile \( 5 \le x \lt 9 \) aralığının kesişimi bu aralığın çözüm kümesidir.
\( x \in (5, 9) \)
Durum 3: \( 9 \le x \)
Bu aralıkta her iki mutlak değerli ifade de pozitif olur, dolayısıyla mutlak değerden pozitif işaretli çıkar.
\( (x - 9) \lt (x - 5) + 4 \)
\( -9 \lt -1 \)
Bu eşitsizlik her zaman sağlandığı için eşitsizliği çözdüğümüz tüm aralık bu aralığın çözüm kümesidir.
\( x \in [9, \infty) \)
Eşitsizliğin çözüm kümesi yukarıdaki üç aralık için bulduğumuz çözüm aralıklarının birleşim kümesidir.
Çözüm kümesi: \( x \in (5, \infty) \)
\( x \) bir reel sayı ve \( \abs{x} \le 8 \) olmak üzere,
\( 4x + 3y = -2 \) eşitliğini sağlayan \( y \) tam sayıları toplamı kaçtır?
Çözümü GösterBu soruyu iki farklı yöntemle çözebiliriz.
1. yöntem:
Verilen denklemde \( y \) değişkenini yalnız bırakalım.
\( 3y = -2 - 4x \)
\( y = \dfrac{-2 - 4x}{3} \)
Verilen eşitsizlikte \( x \) değişkenini bu eşitlikteki ifadeye benzetelim.
\( \abs{x} \le 8 \)
\( -8 \le x \le 8 \)
Eşitsizliğin taraflarını -4 ile çarpalım. Bir eşitsizliğin tarafları negatif bir sayı ile çarpıldığında eşitsizlik yön değiştirir.
\( 32 \ge -4x \ge -32 \)
Eşitsizliğin taraflarına -2 ekleyelim.
\( 30 \ge -2 - 4x \ge -34 \)
Eşitsizliğin taraflarını 3'e bölelim.
\( 10 \ge \dfrac{-2 - 4x}{3} \ge \dfrac{-34}{3} \)
Eşitsizlikte ortadaki ifade \( y \)'ye eşittir.
\( 10 \ge y \ge \dfrac{-34}{3} \)
Bu aralıktaki tam sayı \( y \) değerlerinin toplamı aşağıdaki gibidir.
\( -11 + (-10) + \ldots + 10 = -11 \)
2. yöntem:
Alternatif olarak soruyu grafik yardımıyla çözebiliriz.
Aşağıda soruda verilen eşitliğin karşılık geldiği \( y = \dfrac{-2 - 4x}{3} \) doğrusunun grafiği verilmiştir.
Ayrıca \( \abs{x} \le 8 \) eşitsizliği \( x = -8 \) ve \( x = 8 \) doğruları arasında kalan bölgeyi ifade eder.
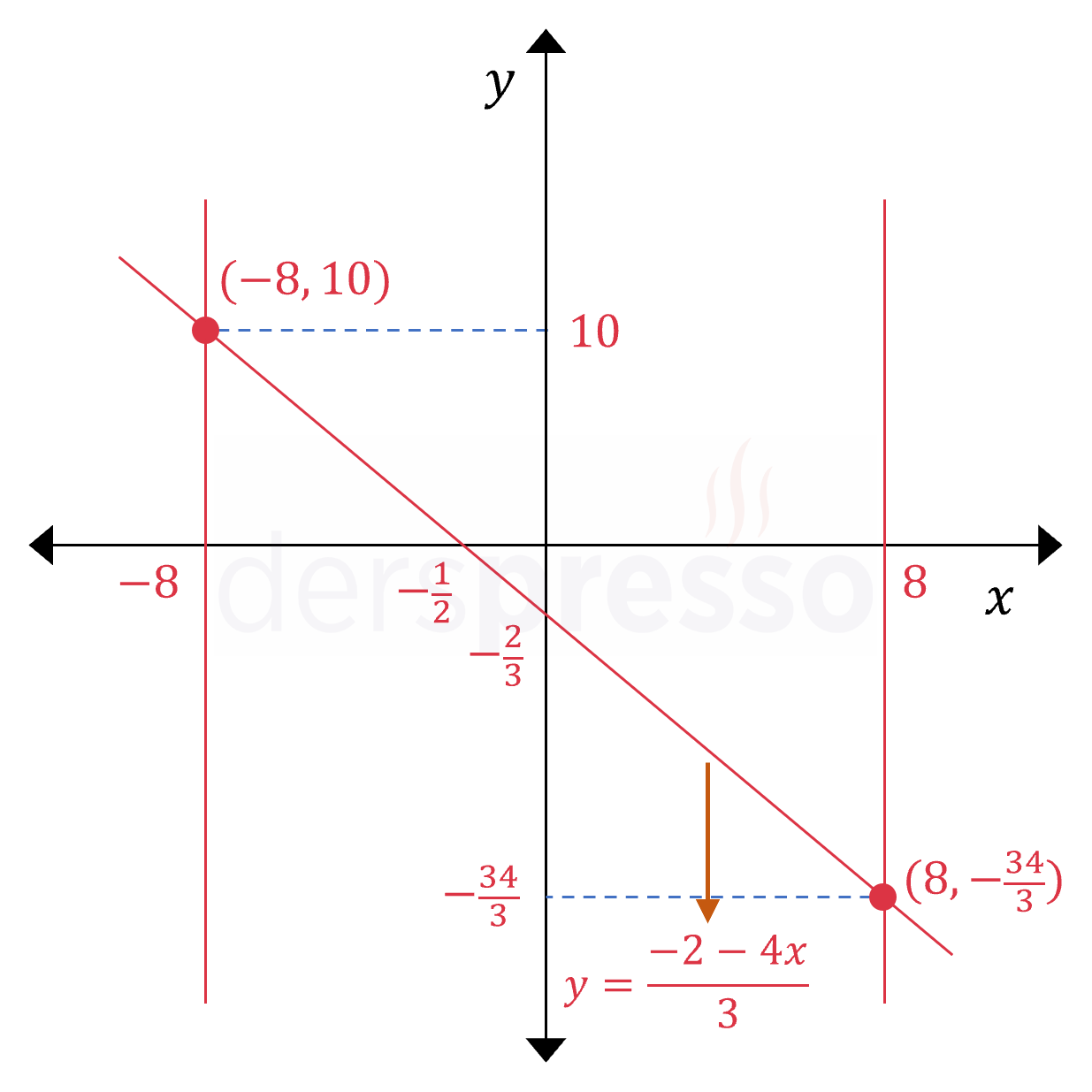
Bu eşitliği ve eşitsizliği birlikte sağlayan noktalar doğru üzerinde taralı alanda bulunan noktalardır.
Bu aralıktaki tam sayı \( y \) değerlerinin toplamı aşağıdaki gibidir.
\( -11 + (-10) + \ldots + 10 = -11 \)
\( \dfrac{10 - \abs{2x - 18}}{\abs{9 - x} + 4} \gt 0 \)
eşitsizliğini sağlayan tam sayı \( x \) değerlerinin toplamı kaçtır?
Çözümü GösterPayda mutlak değerli bir ifade ile 4'ün toplamından oluştuğu için hiçbir zaman sıfır olamaz, dolayısıyla ifadeyi tanımsız yapan \( x \) değeri yoktur.
Kesirli ifadenin paydası her zaman pozitif olduğu için, tüm ifade pay sıfırdan büyük olduğunda sıfırdan büyük olur.
\( 10 - \abs{2x - 18} \gt 0 \)
\( \abs{2x - 18} \lt 10 \)
\( -10 \lt 2x - 18 \lt 10 \)
\( 8 \lt 2x \lt 28 \)
\( 4 \lt x \lt 14 \)
Eşitsizliği sağlayan tam sayı \( x \) değerlerini bulmak için 1-13 arası ardışık tam sayıların toplamından 1-4 arası ardışık tam sayıların toplamını çıkaralım.
Her iki sayı da dahil olmak üzere, \( 1-n \) arası tam sayıların toplamı \( \frac{n(n + 1)}{2} \) formülü ile bulunur.
\( \dfrac{13 \cdot 14}{2} - \dfrac{4 \cdot 5}{2} \)
\( = 91 - 10 = 81 \) bulunur.
\( \abs{x - 1} \lt \abs{x + 5} \)
eşitsizliğinin çözüm kümesi nedir?
Çözümü GösterSoruyu grafik yöntemiyle çözelim.
İfadeyi düzenleyelim.
\( \abs{x - 1} - \abs{x + 5} \lt 0 \)
Önce bu eşitsizliğin sol tarafını bir fonksiyon gibi düşünerek grafiğini çizelim.
\( y = \abs{x - 1} - \abs{x + 5} \)
Mutlak değerli ifadeleri sıfır yapan noktalar fonksiyonun kritik noktalarıdır.
Buna göre fonksiyonun kritik noktaları \( x \in \{-5, 1\} \) noktalarıdır.
Bu iki kritik noktanın oluşturduğu üç aralığı ayrı ayrı inceleyelim ve her aralıkta mutlak değer içindeki ifadeleri o aralıktaki işaretlerine göre mutlak değerden çıkaralım.
Durum 1: \( x \lt -5 \)
\( y = -(x - 1) + (x + 5) \)
\( y = 6 \)
Durum 2: \( -5 \lt x \lt 1 \)
\( y = -(x - 1) - (x + 5) \)
\( y = -2x - 4 \)
Durum 3: \( 1 \lt x \)
\( y = (x - 1) - (x + 5) \)
\( y = -6 \)
Fonksiyonun bu üç aralıktaki grafiğini çizersek aşağıdaki grafiği elde ederiz.
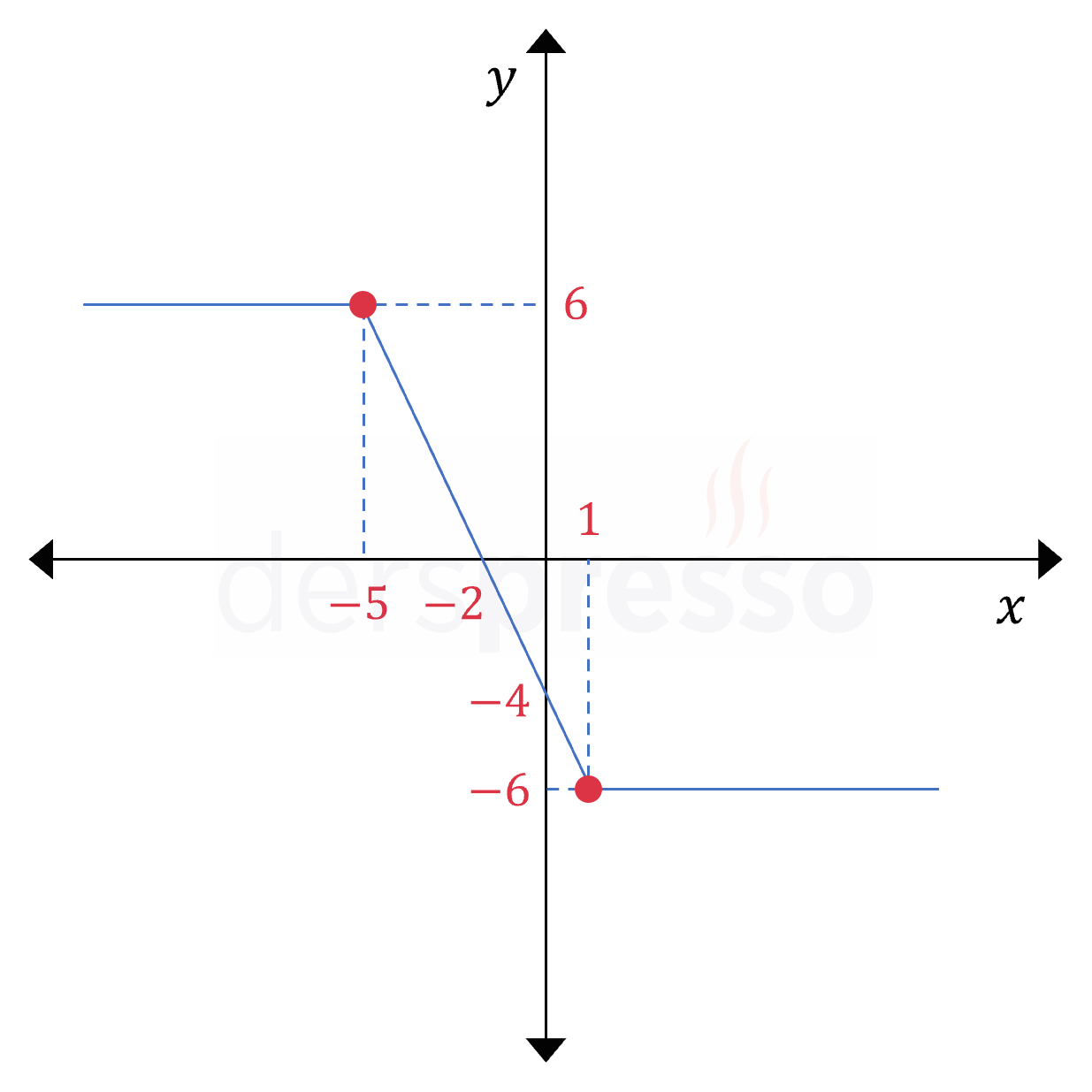
Soruda grafiği bulduğumuz fonksiyonun sıfırdan küçük olduğu \( x \) aralığı istenmiş.
Grafikten de görebileceğimiz gibi, fonksiyonun negatif değer aldığı \( x \) değer aralığı \( x \in (-2, \infty) \) aralığıdır.
\( (7 - x)(7 - \abs{x}) \lt 49 \) eşitsizliğinin çözüm kümesi nedir?
Çözümü GösterMutlak değer içini sıfır yapan noktalar mutlak değer ifadesinin kritik noktalarıdır.
\( x = 0 \)
Kritik noktanın oluşturduğu iki aralık için eşitsizliği ayrı ayrı çözelim.
Durum 1: \( x \lt 0 \)
Bu durumda mutlak değer içindeki ifade negatif olur ve mutlak değer dışına negatif işaretli çıkar.
\( (7 - x)(7 + x) \lt 49 \)
\( -x^2 + 49 \lt 49 \)
\( x^2 \gt 0 \)
\( x \in \mathbb{R} - \{0\} \)
Bu aralık ile \( x \lt 0 \) aralığının kesişimi 1. durumun çözüm kümesi olur.
\( x \in (-\infty, 0) \)
Durum 2: \( x \ge 0 \)
Bu durumda mutlak değer içindeki ifade sıfır ya da pozitif olur ve mutlak değer dışına olduğu gibi çıkar.
\( (7 - x)(7 - x) \lt 49 \)
\( (x - 7)^2 \lt 7^2 \)
\( \abs{x - 7} \lt 7 \)
\( -7 \lt x - 7 \lt 7 \)
\( 0 \lt x \lt 14 \)
Bu aralık ile \( x \ge 0 \) aralığının kesişimi 2. durumun çözüm kümesi olur.
\( x \in (0, 14) \)
Eşitsizliğin çözüm kümesi yukarıdaki iki durum için bulduğumuz çözüm aralıklarının birleşim kümesidir.
Çözüm kümesi: \( x \in (-\infty, 0) \cup (0, 14) \)
\( \abs{6 - 3x^2} \le 6 - 2x^2 \) eşitsizliğinin çözüm kümesi nedir?
Çözümü GösterMutlak değer içini sıfır yapan \( x \) değerini bulalım.
\( 6 - 3x^2 = 0 \)
\( x = \pm \sqrt{2} \)
Eşitsizliği bu değerin oluşturduğu iki durum için ayrı ayrı çözelim.
Durum 1: \( -\sqrt{2} \le x \le \sqrt{2} \)
Bu durumda mutlak değer içi pozitif olur ve ifade dışarıya olduğu gibi çıkar.
\( 6 - 3x^2 \le 6 - 2x^2 \)
\( x^2 \ge 0 \)
\( x \in \mathbb{R} \)
Bulduğumuz aralık ile bu durumun ön koşulu olan aralığın kesişimi bu durumun çözümü kümesi olur.
\( x \in [-\sqrt{2}, \sqrt{2}] \)
Durum 2: \( x \lt -\sqrt{2} \) ve \( x \gt \sqrt{2} \)
Bu durumda mutlak değer içi negatif olur ve ifade dışarıya negatif işaretli çıkar.
\( 3x^2 - 6 \le 6 - 2x^2 \)
\( 5x^2 \le 12 \)
\( -\dfrac{2\sqrt{15}}{5} \le x \le \dfrac{2\sqrt{15}}{5} \)
Bulduğumuz aralık ile bu durumun ön koşulu olan aralığın kesişimi bu durumun çözümü kümesi olur.
\( x \in [-\frac{2\sqrt{15}}{5}, -\sqrt{2}) \cup (\sqrt{2}, \frac{2\sqrt{15}}{5}] \)
Her iki durum için bulduğumuz çözüm kümelerinin birleşimi sorudaki ifadenin çözüm kümesi olur.
\( x \in [-\frac{2\sqrt{15}}{5}, \frac{2\sqrt{15}}{5}] \)
Aşağıdaki ifadelerin belirtilen aralıktaki görüntü kümelerini bulunuz.
(a) \( \abs{4x} \) ifadesinin \( -1 \lt x \lt 6 \) aralığında
(b) \( \abs{x - 9} \) ifadesinin \( -15 \le x \lt -5 \) aralığında
(c) \( 2\abs{x} + 1 \) ifadesinin \( -8 \lt x \le 2 \) aralığında
Çözümü Göster(a) seçeneği:
\( -1 \lt x \lt 6 \)
Eşitsizliğin taraflarını 4 ile çarpalım.
\( -4 \lt 4x \lt 24 \)
Eşitsizliğin taraflarının mutlak değerini alalım.
\( 0 \le \abs{4x} \lt 24 \)
(b) seçeneği:
\( -15 \le x \lt -5 \)
Eşitsizliğin taraflarından 9 çıkaralım.
\( -24 \le x - 9 \lt -14 \)
Eşitsizliğin taraflarının mutlak değerini alalım.
\( 14 \lt \abs{x - 9} \le 24 \)
(c) seçeneği:
\( -8 \lt x \le 2 \)
Eşitsizliğin taraflarının mutlak değerini alalım.
\( 0 \le \abs{x} \lt 8 \)
Eşitsizliğin taraflarını 2 ile çarpalım.
\( 0 \le 2\abs{x} \lt 16 \)
Eşitsizliğin taraflarına 1 ekleyelim.
\( 1 \le 2\abs{x} + 1 \lt 17 \)
\( x, y \in \mathbb{R} \) olmak üzere,
\( \abs{4x - 8} \lt 4 \)
\( \abs{-2y + 3} \le 9 \)
olduğuna göre, \( 5x - 2y + 4 \) ifadesinin alabileceği kaç farklı tam sayı değeri vardır?
Çözümü GösterBirinci eşitsizliği mutlak değersiz şekilde yazalım.
\( \abs{4x - 8} \lt 4 \)
\( -4 \lt 4x - 8 \lt 4 \)
\( 4 \lt 4x \lt 12 \)
\( 1 \lt x \lt 3 \)
\( 5 \lt 5x \lt 15 \)
İkinci eşitsizliği mutlak değersiz şekilde yazalım.
\( \abs{-2y + 3} \le 9 \)
\( -9 \le -2y + 3 \le 9 \)
\( -12 \le -2y \le 6 \)
Bulduğumuz iki eşitsizliği taraf tarafa toplayalım.
\( 5 \lt 5x \lt 15 \)
\( -12 \le -2y \le 6 \)
\( -7 \lt 5x - 2y \lt 21 \)
Eşitsizliğin taraflarına 4 ekleyelim.
\( -3 \lt 5x - y + 4 \lt 25 \)
\( 5x - y + 4 \) ifadesinin alabileceği tam sayı değerleri aşağıdaki gibidir.
\( -2, -1, 0, 1, \ldots, 24 \)
İfadenin bu aralıkta alabileceği \( 24 - (-2) + 1 = 27 \) farklı tam sayı değeri vardır.
\( \dfrac{\abs{2x - 3} - 11}{\abs{-6x - \frac{1}{2}} + 42} \lt 0 \)
olduğuna göre, \( x \)'in alabileceği tam sayı değerlerin toplamı kaçtır?
Çözümü GösterRasyonel ifadenin paydasındaki \( \abs{-6x - \frac{1}{2}} \) ifadesi her zaman sıfır ya da pozitif olacağından \( \abs{-6x - \frac{1}{2}} + 42 \) ifadesi her zaman pozitif olur.
Buna göre eşitsizlik rasyonel ifadenin payı negatif olduğunda sağlanır.
\( \abs{2x - 3} - 11 \lt 0 \)
\( \abs{2x - 3} \lt 11 \)
Eşitsizliği mutlak değersiz şekilde yazalım.
\( -11 \lt 2x - 3 \lt 11 \)
\( -8 \lt 2x \lt 14 \)
\( -4 \lt x \lt 7 \)
\( x \)'in alabileceği tam sayı değerlerinin toplamını bulalım.
\( (-3) + (-2) + (-1) + \ldots + 6 = 15 \) bulunur.
\( \abs{2x - 3} \ge \abs{3 + x} \) eşitsizliğinin çözüm kümesi nedir?
Çözümü GösterMutlak değerin karekök tanımını yazalım.
\( \sqrt{(2x - 3)^2} \ge \sqrt{(3 + x)^2} \)
Eşitsizliğin taraflarının karesini alalım.
Eşitsizliğin iki tarafında da karekök ifadesi olduğu için her iki taraf da pozitiftir, dolayısıyla tarafların karesini almamız eşitsizliğin çözüm kümesini değiştirmez (eşitsizliğe yeni çözümler eklemez).
\( (2x - 3)^2 \ge (3 + x)^2 \)
\( 4x^2 - 12x + 9 \ge 9 + 6x + x^2 \)
Tüm terimleri eşitsizliğin aynı tarafında toplayalım.
\( 3x^2 - 18x \ge 0 \)
\( x^2 - 6x \ge 0 \)
\( x(x - 6) \ge 0 \)
Pozitif başkatsayılı ve birbirinden farklı iki reel kökü olan ikinci dereceden bir ifade kök değerlerinde sıfır, köklerin arasındaki aralıkta negatif, dışındaki aralıkta pozitif olur.
Verilen eşitsizlikte \( \ge \) sembolü kullanıldığı için ikinci dereceden ifadenin pozitif ya da sıfır olduğu aralıklar eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in (-\infty, 0] \cup [6, \infty) \)
\( \abs{x} + \abs{y} \le 8 \)
eşitsizliğini sağlayan kaç farklı \( (x, y) \) tam sayı ikilisi vardır?
Çözümü Göster\( \abs{x} + \abs{y} \le 8 \) eşitsizliğini analitik düzlemdeki her bölge için ayrı ayrı inceleyelim.
I. bölge:
Bu bölgede hem \( x \) hem de \( y \) pozitiftir.
\( x + y \le 8 \)
\( y \le -x + 8 \)
II. bölge:
Bu bölgede \( x \) negatif, \( y \) pozitiftir.
\( -x + y \le 8 \)
\( y \le x + 8 \)
III. bölge:
Bu bölgede hem \( x \) hem de \( y \) negatiftir.
\( -x - y \le 8 \)
\( y \ge -x + 8 \)
IV. bölge:
Bu bölgede \( x \) pozitif, \( y \) negatiftir.
\( x - y \le 8 \)
\( y \ge x - 8 \)
Bu eşitsizliklerin tümünü çizdiğimizde aşağıdaki grafiği ve eşitsizliği sağlayan taralı alanı elde ederiz.
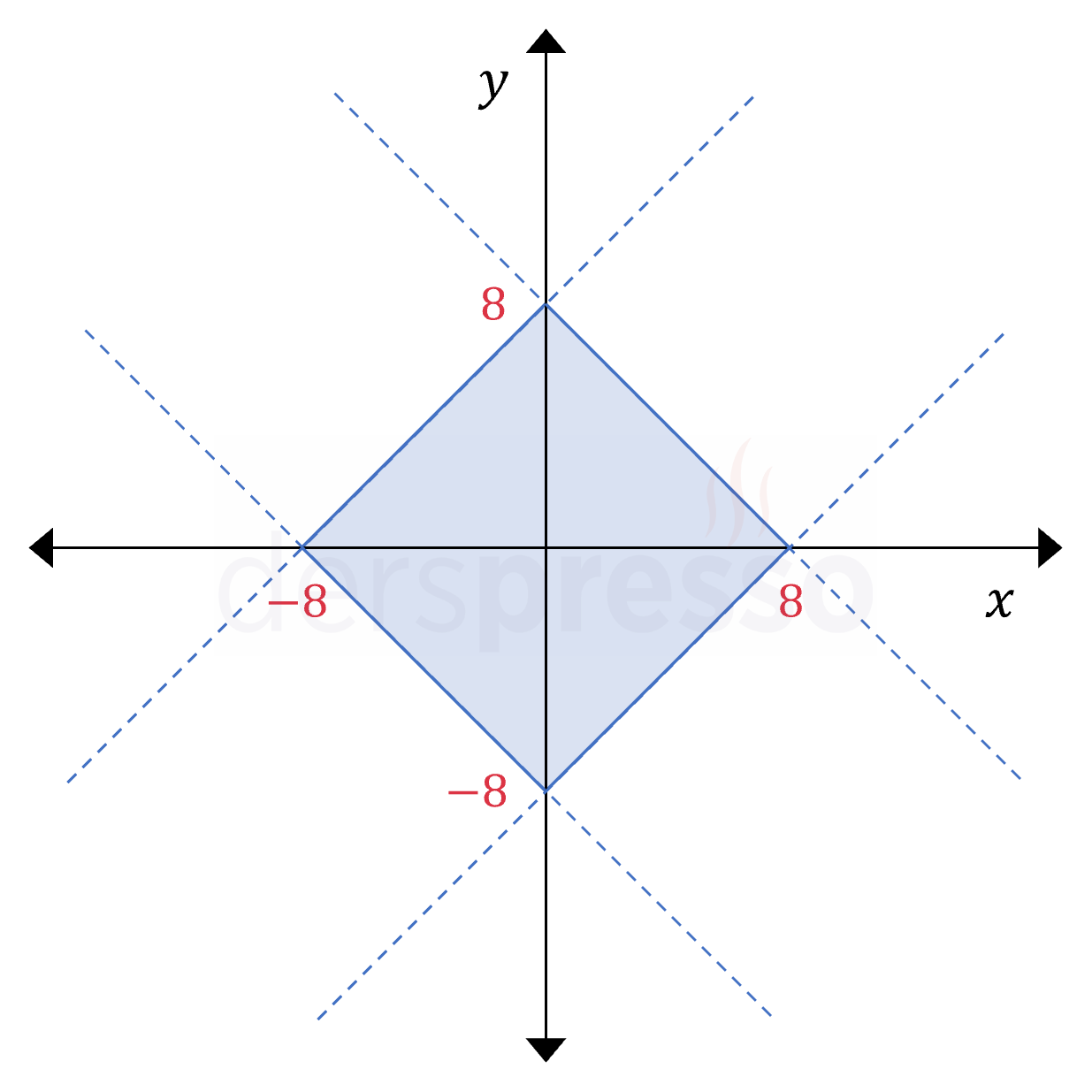
Görebileceğimiz gibi bu bölgeler eksenlere göre simetriktir ve her bölgedeki eşitsizliği sağlayan sıralı ikili sayısının eşit olmasını bekleyebiliriz.
Bu kapalı bölgedeki tam sayı \( (x, y) \) sıralı ikililerinin sayısını bulmak için önce (eksenler hariç) I. bölgeyi inceleyelim.
\( x = 1 \) olduğunda verilen eşitsizliği 7 \( y \) değeri sağlar.
\( y \in \{ 1, 2, 3, 4, 5, 6, 7 \} \)
\( x = 1 \) olduğunda verilen eşitsizliği 6 \( y \) değeri sağlar.
\( y \in \{ 1, 2, 3, 4, 5, 6 \} \)
\( x = 2 \) olduğunda verilen eşitsizliği 5 \( y \) değeri sağlar.
\( y \in \{ 1, 2, 3, 4, 5 \} \)
\( \vdots \)
\( x = 7 \) olduğunda verilen eşitsizliği 1 \( y \) değeri sağlar.
\( y \in \{1\} \)
Buna göre I. bölgede toplam \( 7 + 6 + 5 + \ldots + 1 = 28 \) nokta eşitsizliği sağlar.
Bu noktaların tümünün diğer üç bölgede birer simetriği vardır.
\( x \) ekseni üzerinde bu eşitsizliği sağlayan \( 8 - (-8) + 1 = 17 \) nokta vardır.
\( y \) ekseni üzerinde bu eşitsizliği sağlayan \( 8 - (-8) + 1 = 17 \) nokta vardır.
Eksenler üzerindeki bu noktalardan orijin iki eksen için ortaktır, dolayısıyla çift saymanın önüne geçmek için toplamdan 1 çıkarmalıyız.
Buna göre verilen eşitsizliği sağlayan nokta sayısını aşağıdaki şekilde bulabiliriz.
\( 4 \cdot 28 + 2 \cdot 17 - 1 = 145 \) bulunur.
\( \abs{x + 4} + \abs{y + 2} + \abs{z - 6} = 18 \) olduğuna göre,
\( \abs{x + y + z} \) ifadesinin alabileceği kaç farklı pozitif tam sayı değeri vardır?
Çözümü GösterMutlak değerli bir ifade için aşağıdaki eşitsizlik yazılabilir.
\( -\abs{a} \le a \le \abs{a} \)
Sorudaki üç mutlak değerli ifadeyi bu formda yazalım.
\( -\abs{x + 4} \le x + 4 \le \abs{x + 4} \)
\( -\abs{y + 2} \le y + 2 \le \abs{y + 2} \)
\( -\abs{z - 6} \le z - 6 \le \abs{z - 6} \)
Bu eşitsizlikleri taraf tarafa toplayalım.
\( -(\abs{x + 4} + \abs{y + 2} + \abs{z - 6}) \le x + y + z \le \abs{x + 4} + \abs{y + 2} + \abs{z - 6} \)
Soruda verilen eşitliği kullanarak eşitsizliği düzenleyelim.
\( -18 \le x + y + z \le 18 \)
\( 0 \le \abs{x + y + z} \le 18 \)
Buna göre, \( \abs{x + y + z} \) ifadesinin alabileceği pozitif tam sayı değerleri 18 tanedir.
\( \abs{\abs{x - 2} - 11} + \abs{22 - \abs{4 - 2x}} \lt 42 \)
eşitsizliğini sağlayan kaç \( x \) tam sayısı vardır?
Çözümü GösterMutlak değer içindeki pozitif çarpan mutlak değer dışına çıkarılabilir.
\( \abs{\abs{x - 2} - 11} + \abs{22 - 2\abs{2 - x}} \lt 42 \)
\( \abs{\abs{x - 2} - 11} + 2\abs{11 - \abs{2 - x}} \lt 42 \)
\( \abs{\abs{x - 2} - 11} + 2\abs{11 - \abs{x - 2}} \lt 42 \)
Mutlak değer içi \( -1 \) ile çarpılarak terimlerin yeri değiştirilebilir.
\( \abs{\abs{x - 2} - 11} + 2\abs{\abs{x - 2} - 11} \lt 42 \)
\( 3\abs{\abs{x - 2} - 11} \lt 42 \)
\( \abs{\abs{x - 2} - 11} \lt 14 \)
\( -14 \lt \abs{x - 2} - 11 \lt 14 \)
\( -3 \lt \abs{x - 2} \lt 25 \)
Bir mutlak değer ifadesi hiçbir zaman negatif olamayacağı için eşitsizliğin sol tarafı her zaman sağlanır, dolayısıyla eşitsizliğin sol tarafını dikkate almamıza gerek yoktur.
\( \abs{x - 2} \lt 25 \)
\( -25 \lt x - 2 \lt 25 \)
\( -23 \lt x \lt 27 \)
Ardışık sayı terim sayısı formülünü kullanalım.
Bu aralıkta \( 26 - (-22) + 1 = 49 \) tam sayı \( x \) değeri bulunur.
\( x \in \mathbb{Z} \) olmak üzere,
\( \abs{x - 80} \lt \abs{x - 30} \lt \abs{x - 110} \) eşitsizliğini sağlayan kaç \( x \) değeri vardır?
Çözümü GösterSorudaki eşitsizliği iki ayrı eşitsizliğe bölüp ayrı ayrı inceleyelim.
Eşitsizlik 1:
\( \abs{x - 80} \lt \abs{x - 30} \)
Bu eşitsizliğin çözüm kümesi, sayı doğrusu üzerinde 80'e olan uzaklığı 30'a olan uzaklığından küçük olan noktalar kümesidir.
İki sayıya eşit uzaklıkta olan sayıyı bulalım.
\( \dfrac{80 + 30}{2} = 55 \)
\( x = 55 \) noktasının sağındaki noktaların 80'e olan uzaklığı 30'a olan uzaklığından küçük olduğu için bu eşitsizliğin çözüm kümesi aşağıdaki gibi olur.
\( x \gt 55 \)
Eşitsizlik 2:
\( \abs{x - 30} \lt \abs{x - 110} \)
Bu eşitsizliğin çözüm kümesi, sayı doğrusu üzerinde 30'a olan uzaklığı 110'a olan uzaklığından küçük olan noktalar kümesidir.
İki sayıya eşit uzaklıkta olan sayıyı bulalım.
\( \dfrac{30 + 110}{2} = 70 \)
\( x = 70 \) noktasının solundaki noktaların 30'a olan uzaklığı 110'a olan uzaklığından küçük olduğu için bu eşitsizliğin çözüm kümesi aşağıdaki gibi olur.
\( x \lt 70 \)
Bulduğumuz iki aralığın kesişimi verilen eşitsizliğin çözüm kümesini verir.
\( 55 \lt x \lt 70 \)
Bu aralıkta \( 69 - 56 + 1 = 14 \) tam sayı değeri vardır.
\( \dfrac{3}{\abs{x - 2}} \gt \dfrac{1}{2} \) eşitsizliğinin çözüm kümesi nedir?
Çözümü GösterMutlak değer içini sıfır yapan \( x = 2 \) değerinin oluşturduğu \( x \lt 2 \) ve \( x \ge 2 \) aralıklarını ayrı ayrı inceleyelim ve her durumda oluşan denklemi çözelim.
Durum 1: \( x \lt 2 \)
Bu aralıkta \( x - 2 \) ifadesi negatif olur ve mutlak değer dışına negatif işaretli çıkar.
\( \dfrac{3}{-(x - 2)} \gt \dfrac{1}{2} \)
\( \dfrac{3}{2 - x} - \dfrac{1}{2} \gt 0 \)
\( \dfrac{6}{2(2 - x)} - \dfrac{2 - x}{2(2 - x)} \gt 0 \)
\( \dfrac{4 + x}{2(2 - x)} \gt 0 \)
\( \dfrac{4 + x}{2 - x} \gt 0 \)
Bu eşitsizliğin çözüm kümesini bulmak için bir işaret tablosu hazırlayalım. Rasyonel eşitsizliklerin işaret tablosu ile çözümü için rasyonel eşitsizlikler sayfasını inceleyebilirsiniz.

Verilen eşitsizlikte \( \gt \) sembolü kullanıldığı için rasyonel ifadenin pozitif olduğu aralık ve değerler eşitsizliğin çözüm kümesi olur.
\( -4 \lt x \lt 2 \)
Bu aralık ile incelediğimiz \( x \lt 2 \) aralığının kesişimi bu durumun çözüm kümesini verir.
\( x \in (-4, 2) \)
Durum 2: \( x \ge 2 \)
Bu aralıkta \( x - 2 \) ifadesi sıfır ya da pozitif olur ve mutlak değer dışına olduğu gibi çıkar.
\( \dfrac{3}{x - 2} \gt \dfrac{1}{2} \)
\( \dfrac{3}{x - 2} - \dfrac{1}{2} \gt 0 \)
\( \dfrac{6}{2(x - 2)} - \dfrac{x - 2}{2(x - 2)} \gt 0 \)
\( \dfrac{8 - x}{2(x - 2)} \gt 0 \)
\( \dfrac{8 - x}{x - 2} \gt 0 \)
Bu eşitsizliğin çözüm kümesini bulmak için bir işaret tablosu hazırlayalım. Rasyonel eşitsizliklerin işaret tablosu ile çözümü için rasyonel eşitsizlikler sayfasını inceleyebilirsiniz.

Verilen eşitsizlikte \( \gt \) sembolü kullanıldığı için rasyonel ifadenin pozitif olduğu aralık ve değerler eşitsizliğin çözüm kümesi olur.
\( 2 \lt x \lt 8 \)
Bu aralık ile incelediğimiz \( x \ge 2 \) aralığının kesişimi bu durumun çözüm kümesini verir.
\( x \in (2, 8) \)
Bulduğumuz çözüm aralıklarının birleşimi eşitsizliğin çözüm kümesini verir.
Çözüm kümesi: \( x \in (-4, 2) \cup (2, 8) \)
\( \dfrac{1}{\abs{x + 2}} \ge \dfrac{1}{10} \) eşitsizliğinin çözüm kümesi nedir?
Çözümü GösterMutlak değer içini sıfır yapan \( x = -2 \) değerinin oluşturduğu \( x \lt -2 \) ve \( x \ge -2 \) aralıklarını ayrı ayrı inceleyelim ve her durumda oluşan denklemi çözelim.
Durum 1: \( x \lt -2 \)
Bu aralıkta \( x + 2 \) ifadesi negatif olur ve mutlak değer dışına negatif işaretli çıkar.
\( \dfrac{1}{-(x + 2)} \ge \dfrac{1}{10} \)
\( \dfrac{1}{-(x + 2)} - \dfrac{1}{10} \ge 0 \)
\( \dfrac{-10}{10(x + 2)} - \dfrac{x + 2}{10(x + 2)} \ge 0 \)
\( \dfrac{-x - 12}{10(x + 2)} \ge 0 \)
\( \dfrac{-x - 12}{x + 2} \ge 0 \)
Bu eşitsizliğin çözüm kümesini bulmak için bir işaret tablosu hazırlayalım. Rasyonel eşitsizliklerin işaret tablosu ile çözümü için rasyonel eşitsizlikler sayfasını inceleyebilirsiniz.

Verilen eşitsizlikte \( \ge \) sembolü kullanıldığı için rasyonel ifadenin sıfır ya da pozitif olduğu aralık ve değerler eşitsizliğin çözüm kümesi olur.
\( -12 \le x \lt -2 \)
Bu aralık ile incelediğimiz \( x \lt -2 \) aralığının kesişimi bu durumun çözüm kümesini verir.
\( x \in [-12, -2) \)
Durum 2: \( x \ge -2 \)
Bu aralıkta \( x + 2 \) ifadesi sıfır ya da pozitif olur ve mutlak değer dışına olduğu gibi çıkar.
\( \dfrac{1}{x + 2} \ge \dfrac{1}{10} \)
\( \dfrac{1}{x + 2} - \dfrac{1}{10} \ge 0 \)
\( \dfrac{10}{10(x + 2)} - \dfrac{x + 2}{10(x + 2)} \ge 0 \)
\( \dfrac{8 - x}{10(x + 2)} \ge 0 \)
\( \dfrac{8 - x}{x + 2} \ge 0 \)
Bu eşitsizliğin çözüm kümesini bulmak için bir işaret tablosu hazırlayalım. Rasyonel eşitsizliklerin işaret tablosu ile çözümü için rasyonel eşitsizlikler sayfasını inceleyebilirsiniz.

Verilen eşitsizlikte \( \ge \) sembolü kullanıldığı için rasyonel ifadenin sıfır ya da pozitif olduğu aralık ve değerler eşitsizliğin çözüm kümesi olur.
\( -2 \lt x \le 8 \)
Bu aralık ile incelediğimiz \( x \ge -2 \) aralığının kesişimi bu durumun çözüm kümesini verir.
\( x \in (-2, 8] \)
Bulduğumuz çözüm aralıklarının birleşimi eşitsizliğin çözüm kümesini verir.
Çözüm kümesi: \( x \in [-12, -2) \cup (-2, 8] \)
\( \abs{\dfrac{2x - 5}{2 + x}} \le 2 \) eşitsizliğinin çözüm kümesi nedir?
Çözümü GösterEşitsizlikte mutlak değer ifadesini kaldırdığımızda aşağıdaki şekilde tek bir eşitsizlik oluşur.
\( -2 \le \dfrac{2x - 5}{2 + x} \le 2 \)
\( \frac{2x - 5}{2 + x} \ge -2 \) ve \( \frac{2x - 5}{2 + x} \le 2 \) eşitsizliklerini ayrı ayrı çözelim.
Eşitsizlik 1:
\( \dfrac{2x - 5}{2 + x} \ge -2 \)
Tüm terimleri eşitsizliğin sol tarafında toplayalım.
\( \dfrac{2x - 5}{2 + x} + 2 \ge 0 \)
\( \dfrac{2x - 5 + 2(2 + x)}{2 + x} \ge 0 \)
\( \dfrac{4x - 1}{2 + x} \ge 0 \)
Bu eşitsizliğin çözüm kümesini bulmak için bir işaret tablosu hazırlayalım. Rasyonel eşitsizliklerin işaret tablosu ile çözümü için rasyonel eşitsizlikler sayfasını inceleyebilirsiniz.

Verilen eşitsizlikte \( \ge \) sembolü kullanıldığı için rasyonel ifadenin sıfır ya da pozitif olduğu aralık ve değerler eşitsizliğin çözüm kümesi olur.
\( x \in (-\infty, -2) \cup [\frac{1}{4}, \infty) \)
Eşitsizlik 2:
\( \dfrac{2x - 5}{2 + x} \le 2 \)
Tüm terimleri eşitsizliğin sol tarafında toplayalım.
\( \dfrac{2x - 5}{2 + x} - 2 \le 0 \)
\( \dfrac{2x - 5 - 2(2 + x)}{2 + x} \le 0 \)
\( \dfrac{-9}{2 + x} \le 0 \)
Bu eşitsizlik paydadaki ifade pozitif olduğunda sağlanır.
\( 2 + x \gt 0 \)
\( x \gt -2 \)
Bulduğumuz çözüm aralıklarının kesişimi eşitsizliğin çözüm kümesini verir.
Çözüm kümesi: \( x \in [\frac{1}{4}, \infty) \)