Ters Trigonometrik Fonksiyon Tanımı
Konu tekrarı için: Ters Fonksiyon
Fonksiyonlar konusunda birebir ve örten olan fonksiyonların ters fonksiyonlarının da tanımlı olduğunu belirtmiştik. Kısaca hatırlamak gerekirse, ters fonksiyonlar bir fonksiyonun \( (a, b) \) şeklindeki tüm eşlemelerini \( (b, a) \) şeklinde tersine çeviren fonksiyonlardır.
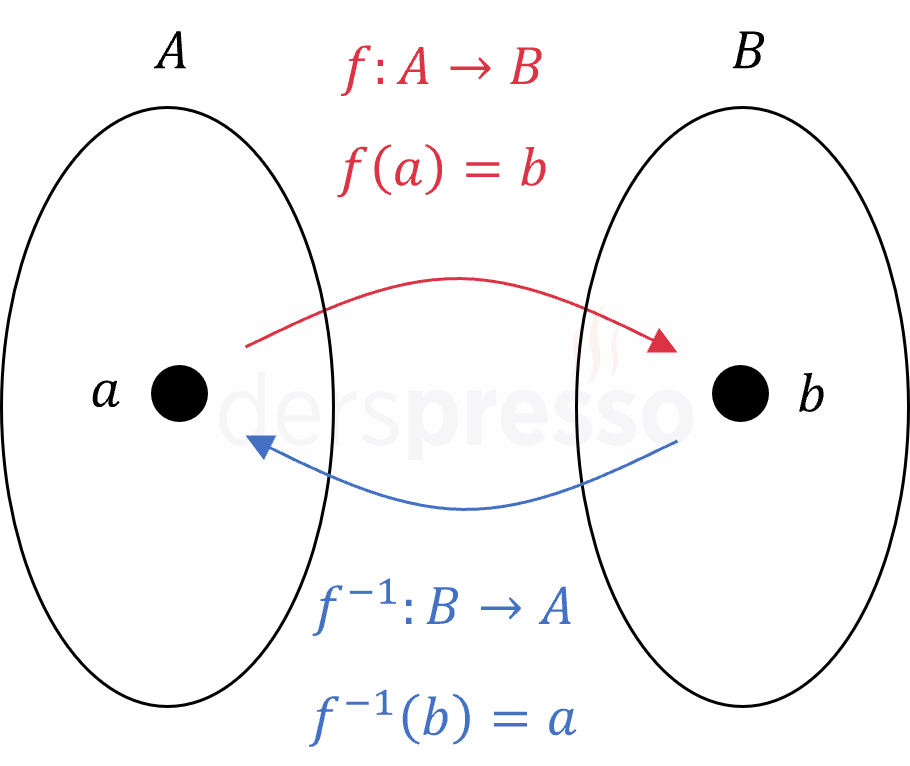
Ters Trigonometrik Fonksiyonlar
Trigonometrik fonksiyonlar bir açı ölçüsünü o açının karşılık geldiği trigonometrik oranla eşleyen fonksiyonlardır. Ters trigonometrik fonksiyonlar da bu eşlemeleri tersine çeviren, yani trigonometrik oranları açı ölçüleri ile eşleyen fonksiyonlardır.
Altı trigonometrik fonksiyonun her biri için tanımlı birer ters trigonometrik fonksiyon vardır. Ters fonksiyonlar genellikle \( f^{-1} \) şeklinde gösteriliyor olsa da, ters trigonometrik fonksiyonların kendilerine özel isimleri vardır.
| Trigonometrik Fonksiyon | Ters Trigonometrik Fonksiyon |
|---|---|
| \( y = \sin{x} \) | \( x = \arcsin{y} \) |
| \( y = \cos{x} \) | \( x = \arccos{y} \) |
| \( y = \tan{x} \) | \( x = \arctan{y} \) |
| \( y = \cot{x} \) | \( x = \arccot{y} \) |
| \( y = \sec{x} \) | \( x = \arcsec{y} \) |
| \( y = \csc{x} \) | \( x = \arccsc{y} \) |
Fonksiyonlarda kullandığımız makine benzetmesi üzerinden bir örnek vermek gerekirse, sinüs fonksiyonu \( \frac{\pi}{6} \) açı değeri için \( \frac{1}{2} \) oranını verirken, sinüs fonksiyonunun ters trigonometrik fonksiyonu olan \( \arcsin \) fonksiyonu bu eşlemeyi tersine çevirerek \( \frac{1}{2} \) oranı için \( \frac{\pi}{6} \) açı değerini verir.
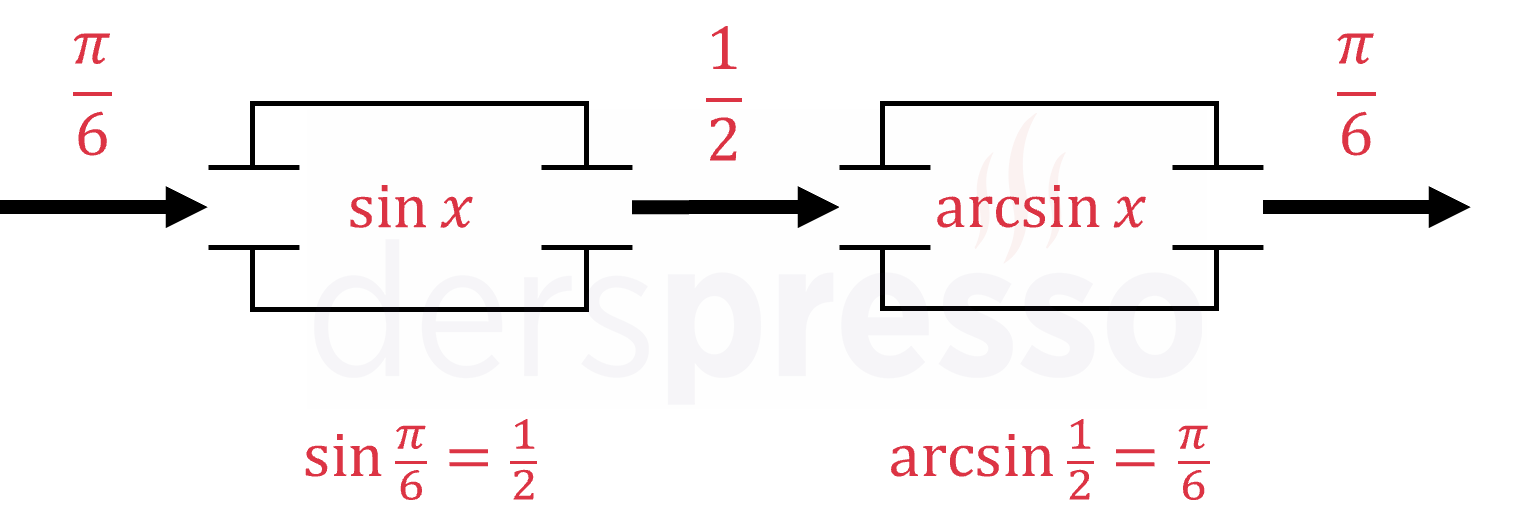
\( \arcsin{1} = \frac{\pi}{2} \)
\( \arccos(-1) = \pi \)
\( \arctan{1} = \frac{\pi}{4} \)
\( \arccot{\sqrt{3}} = \frac{\pi}{6} \)
\( \arcsec(-\sqrt{2}) = \frac{3\pi}{4} \)
\( \arccsc{\sqrt{2}} = \frac{\pi}{4} \)

Yukarıdaki dik üçgenin \( x \) açısını altı ters trigonometrik fonksiyon cinsinden yazalım.
\( x \) sinüs değeri \( \frac{3}{5} \) olan açıdır.
\( x = \arcsin{\frac{3}{5}} \)
\( x \) kosinüs değeri \( \frac{4}{5} \) olan açıdır.
\( x = \arccos{\frac{4}{5}} \)
\( x \) tanjant değeri \( \frac{3}{4} \) olan açıdır.
\( x = \arctan{\frac{3}{4}} \)
\( x \) kotanjant değeri \( \frac{4}{3} \) olan açıdır.
\( x = \arccot{\frac{4}{3}} \)
\( x \) sekant değeri \( \frac{5}{4} \) olan açıdır.
\( x = \arcsec{\frac{5}{4}} \)
\( x \) kosekant değeri \( \frac{5}{3} \) olan açıdır.
\( x = \arccsc{\frac{5}{3}} \)
Aşağıdaki ifadelerin değerini bulunuz.
(a) \( \arcsin{\frac{1}{2}} \)
(b) \( \arccos{0} \)
(c) \( \arccot{1} \)
(d) \( \arcsec{2} \)
Çözümü Göster(a) seçeneği:
\( \arcsin{\frac{1}{2}} = x \) diyelim.
Arc sinüs, sinüsün ters fonksiyonudur.
\( \sin{x} = \dfrac{1}{2} \)
\( x \) sinüs değeri \( \frac{1}{2} \) olan açıdır.
\( x = 30° \)
(b) seçeneği:
\( \arccos{0} = x \) diyelim.
Arc kosinüs, kosinüsün ters fonksiyonudur.
\( \cos{x} = 0 \)
\( x = 90° \)
(c) seçeneği:
\( \arccot{1} = x \) diyelim.
Arc kotanjant, kotanjantın ters fonksiyonudur.
\( \cot{x} = 1 \)
\( x \) kotanjant değeri 1 olan açıdır.
\( x = 45° \)
(d) seçeneği:
\( \arcsec{2} = x \) diyelim.
Arc sekant, sekantın ters fonksiyonudur.
\( \sec{x} = 2 \)
\( x \) sekant değeri 2 olan açıdır.
\( x = 60° \)
\( \dfrac{\arccos(-1)}{\sin(\arctan{\frac{1}{\sqrt{3}}})} \) işleminin sonucu kaçtır?
Çözümü GösterSorudaki trigonometrik ifadelerin değerlerini yazalım.
\( \arccos(-1) = \pi \)
\( \arctan{\frac{1}{\sqrt{3}}} = \dfrac{\pi}{6} \)
\( \sin{\dfrac{\pi}{6}} = \dfrac{1}{2} \)
Bulduğumuz değerleri yerlerine yazalım.
\( \dfrac{\arccos(-1)}{\sin(\arctan{\frac{1}{\sqrt{3}}})} = \dfrac{\pi}{\frac{1}{2}} \)
\( = 2\pi \) bulunur.
\( f(x) = -4 + 2\tan{\dfrac{x}{2}} \) fonksiyonunun tersini bulunuz.
Çözümü GösterFonksiyonun tersini bulmak için ifadeyi \( y \)'ye eşitleyip \( x \)'i yalnız bırakalım.
\( y = -4 + 2\tan{\dfrac{x}{2}} \)
\( y + 4 = 2\tan{\dfrac{x}{2}} \)
\( \tan{\dfrac{x}{2}} = \dfrac{y}{2} + 2 \)
Eşitliğin iki tarafın arctanjantını alalım.
\( \dfrac{x}{2} = \arctan(\dfrac{y}{2} + 2) \)
\( x = 2\arctan(\dfrac{y}{2} + 2) \)
\( x \) ve \( y \) değişkenleri aralarında yer değiştirdiğinde \( y = f^{-1}(x) \) fonksiyonunu elde ederiz.
\( f^{-1}(x) = y = 2\arctan(\dfrac{x}{2} + 2) \)
\( 0 \lt x \lt 1 \) olmak üzere,
\( f(x) = 2\arccos(\sqrt{1 - x^2}) \)
fonksiyonu için, \( f^{-1}(2x) \) ifadesinin eşitini bulunuz.
Çözümü Göster\( y = 2\arccos(\sqrt{1 - x^2}) \)
\( \dfrac{y}{2} = \arccos(\sqrt{1 - x^2}) \)
\( \cos{\dfrac{y}{2}} = \sqrt{1 - x^2} \)
\( \cos^2{\dfrac{y}{2}} = 1 - x^2 \)
\( x^2 = 1 - \cos^2{\dfrac{y}{2}} \)
\( x^2 = \sin^2{\dfrac{y}{2}} \)
\( x = \sin{\dfrac{y}{2}} \)
Elde ettiğimiz ifade \( f \)'in ters fonksiyonudur.
\( f^{-1}(x) = \sin{\dfrac{x}{2}} \)
\( f^{-1}(2x) \) için \( x \) yerine \( 2x \) yazalım.
\( f^{-1}(2x) = \sin{\dfrac{2x}{2}} = \sin{x} \) bulunur.
\( -\dfrac{\pi}{2} \lt x \lt \dfrac{\pi}{2} \) olmak üzere,
\( f(x) = 5\sin{x} \)
\( g(x) = 15 - 10x^2 \)
olduğuna göre, \( (f^{-1} \circ g)(x) \) nedir?
Çözümü Göster\( f \) fonksiyonunun tersini bulmak için ifadeyi \( y \)'ye eşitleyip \( x \)'i yalnız bırakalım.
\( y = 5\sin{x} \)
\( \dfrac{y}{5} = \sin{x} \)
\( x = \arcsin{\dfrac{y}{5}} \)
\( x \) ve \( y \) değişkenleri aralarında yer değiştirdiğinde \( y = f^{-1}(x) \) fonksiyonunu elde ederiz.
\( y = f^{-1}(x) = \arcsin{\dfrac{x}{5}} \)
Bileşke fonksiyonu bulmak için \( (f^{-1} \) fonksiyonunda \( x \) yerine \( g(x) \) yazalım.
\( (f^{-1} \circ g)(x) = f^{-1}(g(x)) \)
\( = \arcsin{\dfrac{15 - 10x^2}{5}} \)
\( = \arcsin(3 - 2x^2) \) bulunur.
\( f(\cos{x}) = \tan^2{x} \) veriliyor.
\( f(x) \) fonksiyonunu bulunuz.
Çözümü GösterTanjant fonksiyonunu kosinüs cinsinden yazalım.
\( f(\cos{x}) = \dfrac{\sin^2{x}}{\cos^2{x}} \)
Pisagor özdeşliğini kullanalım.
\( = \dfrac{1 - \cos^2{x}}{\cos^2{x}} \)
Tüm \( \cos{x} \) ifadeleri yerine \( x \) yazalım.
\( f(x) = \dfrac{1 - x^2}{x^2} \) bulunur.
\( f(x) = \arccot{x} \) ve \( g(x) = \sin{x} \) fonksiyonları veriliyor.
\( (f^{-1} \circ g^{-1})(\frac{1}{\sqrt{2}}) \) ifadesinin değeri nedir?
Çözümü Göster\( (f^{-1} \circ g^{-1})(\frac{1}{\sqrt{2}}) = f^{-1}(g^{-1}(\frac{1}{\sqrt{2}})) \)
\( g \) fonksiyonunun ters fonksiyonunu bulalım.
\( g^{-1}(x) = \arcsin{x} \)
\( g^{-1}(\frac{1}{\sqrt{2}}) = \arcsin{\frac{1}{\sqrt{2}}} \)
\( = \dfrac{\pi}{4} \)
\( f^{-1}(g^{-1}(\frac{1}{\sqrt{2}})) = f^{-1}(\frac{\pi}{4}) \)
\( f \) fonksiyonunun ters fonksiyonunu bulalım.
\( f^{-1}(x) = \cot{x} \)
\( f^{-1}(\frac{\pi}{4}) = \cot{\frac{\pi}{4}} = 1 \)
\( f^{-1}(\frac{\pi}{4}) = 1 \) olarak bulunur.