Çokgenlerde Benzerlik
Birbirine karşılık gelen açıları eş, birbirine karşılık gelen kenar uzunlukları orantılı olan çokgenlere benzer çokgenler denir. Benzer çokgenlerin şekilleri aynı, boyutları farklıdır.

\( ABCDE \) ve \( KLMNO \) çokgenlerinin benzerliği \( ABCDE \sim KLMNO \) şeklinde gösterilir. Bu gösterimde köşelerin yazım sırası önemli olup açı ölçüleri aynı olan köşeler her iki çokgenin yazılışında aynı konumda bulunmalıdır.

Benzer iki çokgende birbirine karşılık gelen açılar eştir.
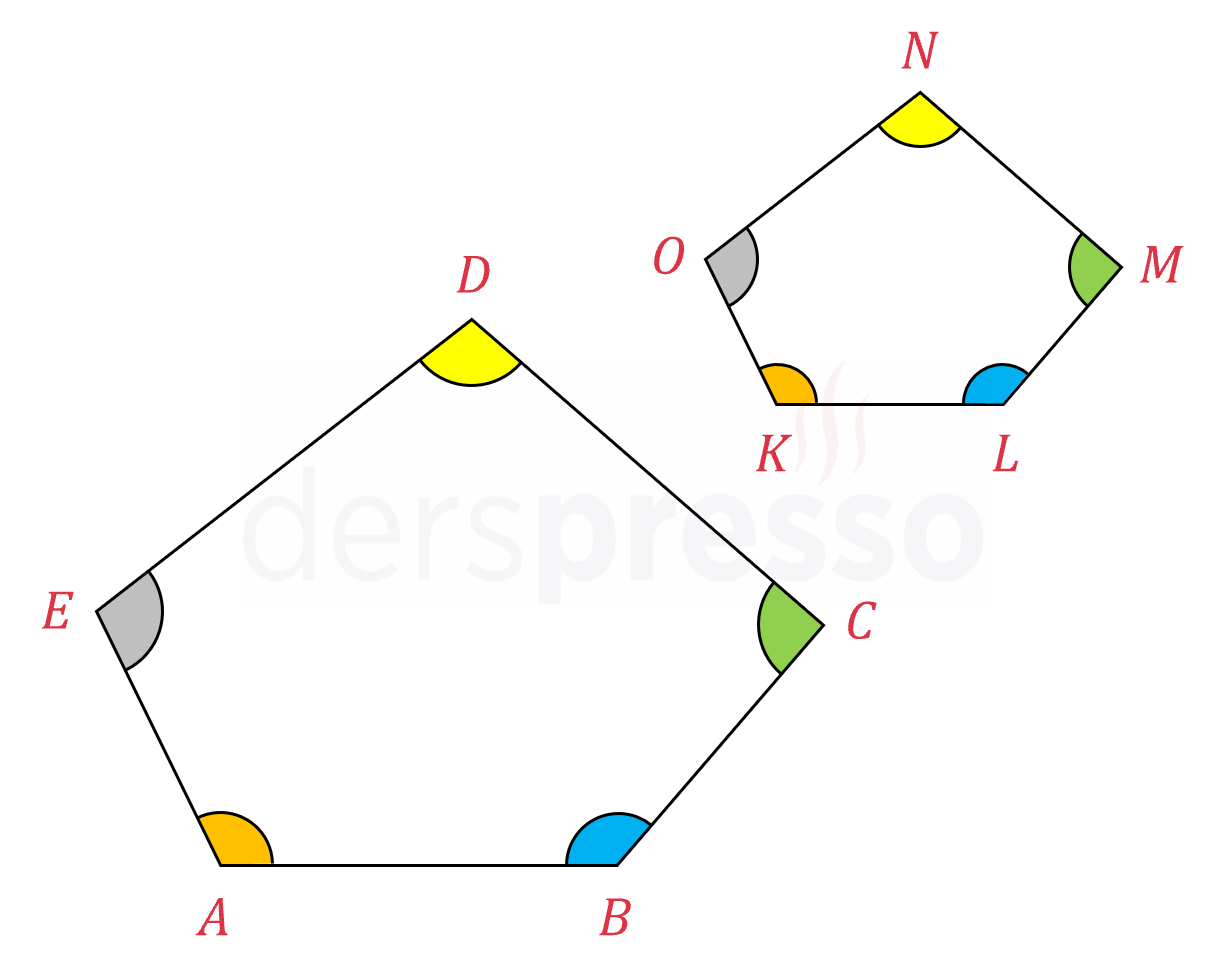
\( ABCDE \sim KLMNO \) ise,
\( m(\widehat{A}) = m(\widehat{K}) \)
\( m(\widehat{B}) = m(\widehat{L}) \)
\( m(\widehat{C}) = m(\widehat{M}) \)
\( m(\widehat{D}) = m(\widehat{N}) \)
\( m(\widehat{E}) = m(\widehat{O}) \)
Benzer iki çokgende birbirine karşılık gelen kenarların uzunlukları oranı sabittir ve bu orana benzerlik oranı denir.
\( ABCDE \sim KLMNO \) ise,
\( k \) iki çokgen arasındaki benzerlik oranı olmak üzere,
\( \dfrac{\abs{AB}}{\abs{KL}} = \dfrac{\abs{BC}}{\abs{LM}} = \dfrac{\abs{CD}}{\abs{MN}} = \dfrac{\abs{DE}}{\abs{NO}} = \dfrac{\abs{EA}}{\abs{OK}} = k \)
Benzer iki çokgenin birbirine karşılık gelen köşe ve kenarları arasında çizilen köşegenler, açıortaylar ve kenarortaylar arasında ve ayrıca benzer iki çokgenin çevreleri arasında aynı \( k \) benzerlik oranı vardır.
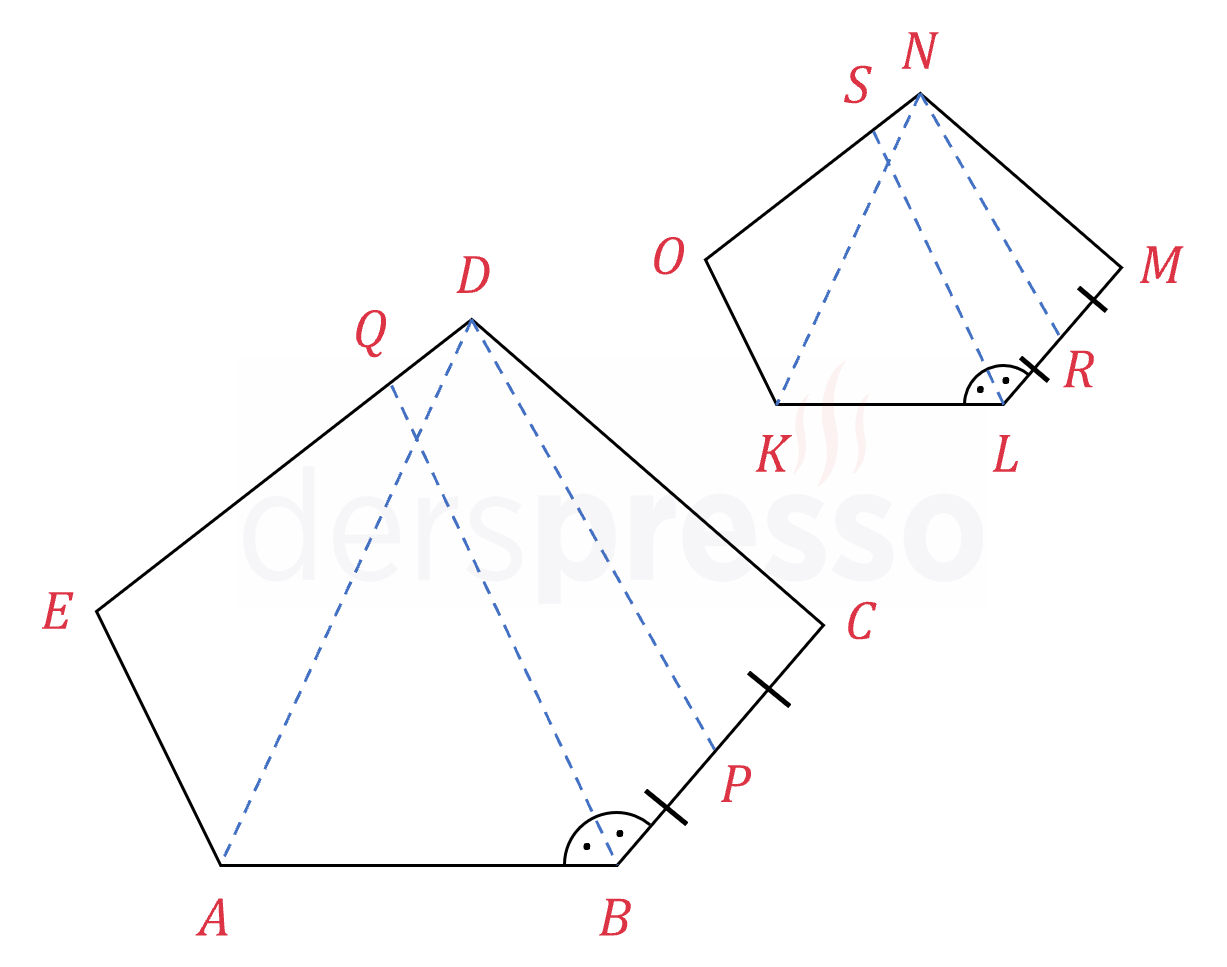
\( \dfrac{\abs{AD}}{\abs{KN}} = \dfrac{\abs{DP}}{\abs{NR}} = \dfrac{\abs{BQ}}{\abs{LS}} = k \)
\( \dfrac{Ç(ABCDE)}{Ç(KLMNO)} = k \)
Benzer iki çokgenin alanları arasındaki benzerlik oranı \( k^2 \)'dir.
\( \dfrac{A(ABCDE)}{A(KLMNO)} = k^2 \)
Kenar sayıları aynı olan tüm düzgün çokgenler (eşkenar üçgen, kare, düzgün beşgen vb.) birbirine benzerdir.
Çokgenlerde Eşlik
Birbirine karşılık gelen tüm iç açıları eş ve kenar uzunlukları birbirine eşit olan, diğer bir deyişle benzerlik oranı 1 olan benzer çokgenlere eş çokgenler denir.