Çokgenlerin Kenar ve Köşegen Özellikleri
Bir çokgenin kenar ve köşe sayıları birbirine eşittir.
Çokgenin bir köşesinden kendisine ve komşu iki köşeye köşegen çizilemeyeceği için, \( n \) kenarlı bir çokgenin bir köşesinden diğer köşelere \( n - 3 \) köşegen çizilebilir.
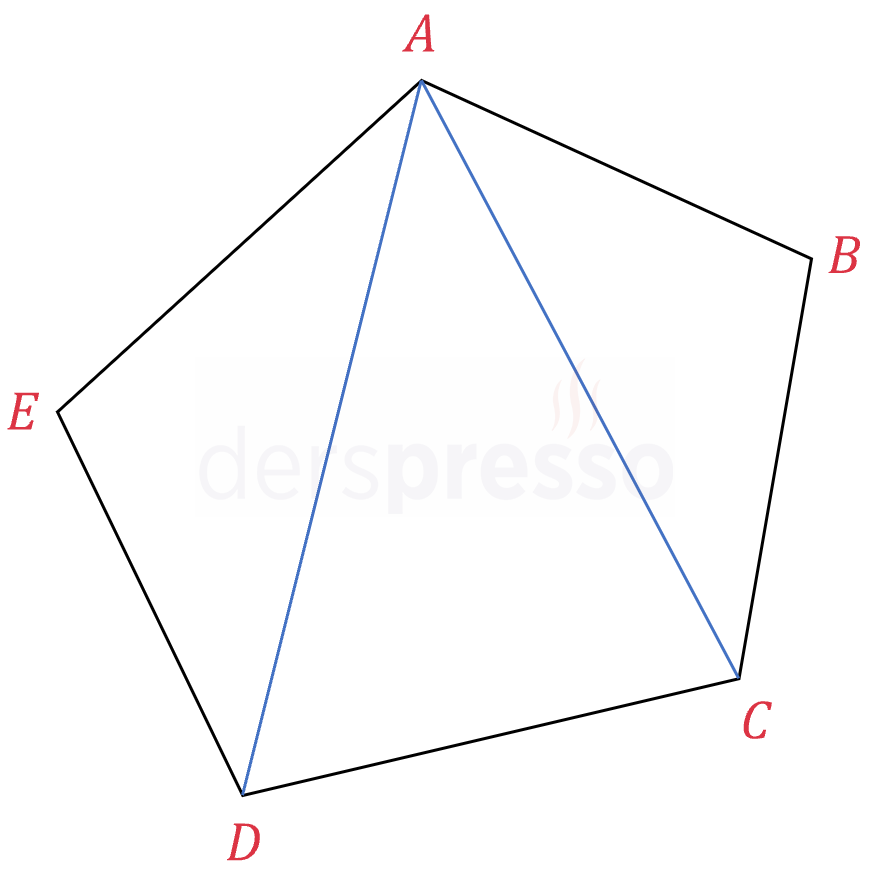
\( \text{Bir köşeden çizilebilen köşegen sayısı}: n - 3 \)
Bir çokgenin toplam köşegen sayısı, yukarıdaki sayının köşe sayısı ile çarpımının yarısıdır. Çarpımı ikiye bölmemizin sebebi, herhangi iki köşeden birbirine çizilen köşegenlerin aynı köşegen olmasıdır.
\( \text{Toplam köşegen sayısı} = \dfrac{n(n - 3)}{2} \)
İSPATI GÖSTER
Köşegenler bir çokgenin köşe noktalarını birleştiren doğru parçalarıdır, ancak bu doğru parçaları şeklin kenarları olmamalıdır.
Buna göre, \( n \) kenarlı bir çokgende \( n \) köşe içinden aynı kenar üzerindeki iki köşe olmamak üzere seçebileceğimiz 2 farklı köşe sayısı kadar köşegen çizebiliriz. Bunun için de \( n \) köşe içinden yapabileceğimiz ikili seçim sayısından kenar sayısını çıkarmamız gerekir.
Toplam köşegen sayısı \( = C(n, 2) - n \)
\( = \dfrac{n!}{2!(n - 2)!} - n \)
\( = \dfrac{n(n - 1)}{2} - n \)
\( = \dfrac{n^2 - n - 2n}{2} \)
\( = \dfrac{n(n - 3)}{2} \)
Herhangi bir köşeden çizilen \( n - 3 \) köşegen çokgeni \( n - 2 \) üçgene ayırır.