Çokgen Tanımı
Bir düzlem üzerinde bulunan ve sonlu sayıda doğru parçasının biraraya gelmesiyle oluşan kapalı şekle çokgen denir. Doğru parçalarının bir çokgen oluşturması için en az üç doğru parçası gereklidir.

Aşağıdaki iki şekilden soldaki bir eğri içerdiği, sağdaki de kapalı bir şekil olmadığı için çokgen değildir.

Bir çokgeni oluşturan doğru parçalarına kenar, çokgenin kenarlarının buluşma noktalarına köşe denir.
Çokgenler sahip oldukları kenar sayısına göre isimlendirilirler (üçgen, dörtgen, beşgen, altıgen, sekizgen vb).
Bir çokgenin komşu olmayan herhangi iki köşesini birleştiren doğru parçasına köşegen denir.
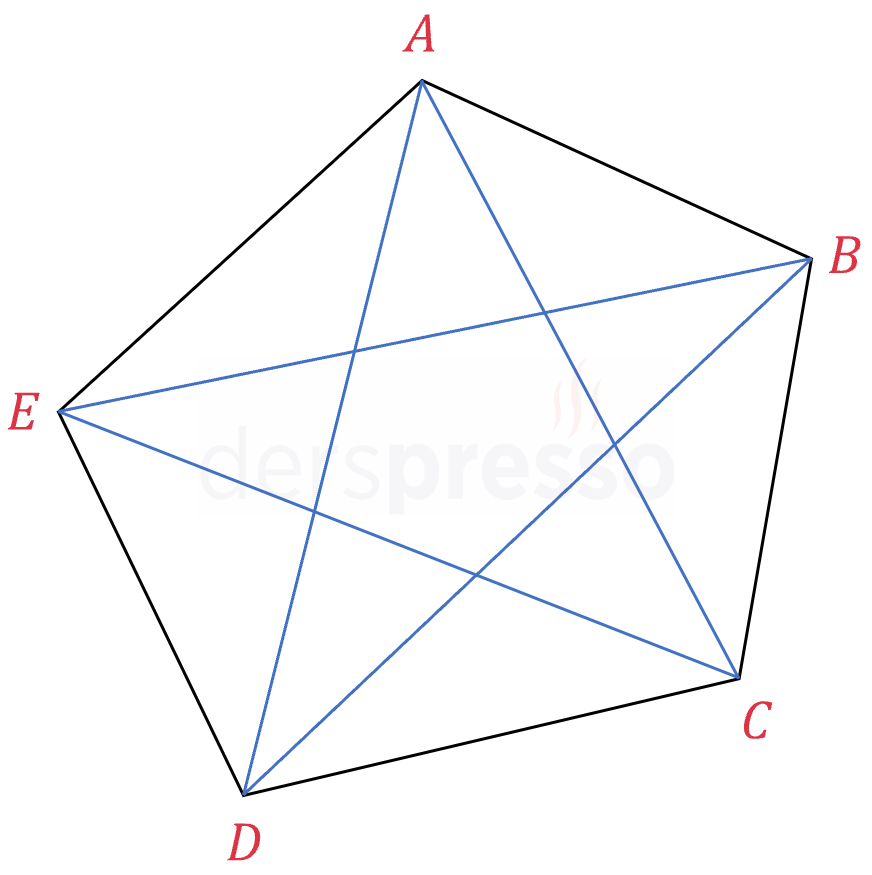
Yukarıda verilen beşgenin köşe, kenar ve köşegenleri aşağıda listelenmiştir.
Köşeler: \( A, B, C, D, E \)
Kenarlar: \( \left[ AB \right], \left[ BC \right], \left[ CD \right], \left[ DE \right], \left[ EA \right] \)
Köşegenler: \( \left[ AC \right], \left[ AD \right], \left[ BD \right], \left[ BE \right], \left[ CE \right] \)
Çokgen Tipleri
Çokgenleri kenar sayıları dışında aşağıdaki üç şekilde sınıflandırabiliriz.
Konveks ve Konkav Çokgenler
İç açılarının tümü 180°'den küçük olan çokgenler konveks ya da dışbükey olarak adlandırılırlar. Bir konveks çokgenin iç bölgesinden seçilecek herhangi iki noktayı birleştiren doğru parçası her zaman çokgenin iç bölgesinde kalır.

Konveks olmayan çokgenler konkav ya da içbükey olarak adlandırılırlar. Buna göre, bir konkav çokgenin en az bir iç açısı 180°'den büyüktür. Bir konkav çokgenin iç bölgesinden seçilecek herhangi iki noktayı birleştiren doğru parçasının tümü çokgenin iç bölgesinde kalmayabilir. Ayrıca konkav çokgenlerin en az bir kenarının uzantısı şekli keser.

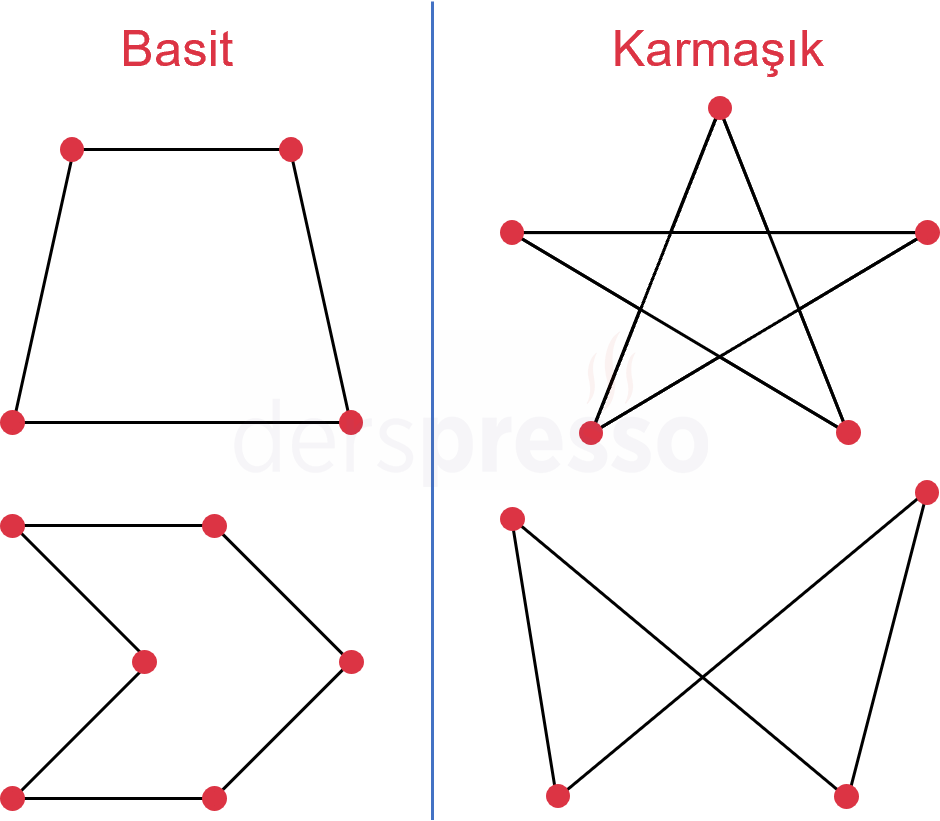
Basit ve Karmaşık Çokgenler
Kenarları uç noktalar dışında kesişmeyen, düzlemi çokgenin içi ve dışı olarak iki bölgeye ayıran çokgenlere basit çokgen denir. Basit çokgenlerde kenar ve köşe sayıları birbirine eşittir.
Kenarları uç noktalar dışında da kesişen ve düzlemi net bir şekilde çokgenin içi ve dışı olarak iki bölgeye ayırmayan çokgenlere karmaşık çokgen denir.
Karmaşık bir çokgende sadece kenarların uç noktalarındaki kesişim noktaları çokgenin köşeleridir.
Aşağıda basit ve karmaşık çokgenlere bazı örnekler verilmiştir. Çokgenlerin köşe noktaları her şekil üzerinde işaretlenmiştir.
Eşkenar, Eş Açılı ve Düzgün Çokgenler
Tüm kenar uzunlukları eşit olan çokgenlere eşkenar çokgen denir. Eşkenar çokgenler konveks ya da konkav, basit ya da karmaşık olabilir.

Tüm açıları eşit olan çokgenlere eş açılı çokgen denir.

Hem eşkenar, hem de eş açılı olan çokgenlere düzgün çokgen denir. Düzgün çokgenleri önümüzdeki bölümlerde daha detaylı şekilde inceleyeceğiz.

Bir çokgenin eşkenar olması eş açılı olmasını, eş açılı olması da eşkenar olmasını gerektirmez. Örneğin dikdörtgen eş açılı olan, ama eşkenar olmayan bir dörtgen iken, eşkenar dörtgen eşkenar olan, ama eş açılı olmayan bir dörtgendir. Kare ve eşkenar üçgen ise hem eşkenar hem de eş açılı olduğu için birer düzgün çokgendir.
Bu konu anlatımında bahsedeceğimiz tüm özellikler aksi belirtilmediği sürece konveks ve basit çokgenler için geçerli olacaktır.

Yukarıdaki şekildeki çokgenin alanı kaç birimkaredir?
Çözümü GösterÇokgenin köşelerinden geçen bir dörtgen çizelim ve çokgenin alanını bulmak için dikdörtgenin alanından şekildeki gibi numaralandırılmış üçgen ve dörtgenlerin alanlarını çıkaralım.
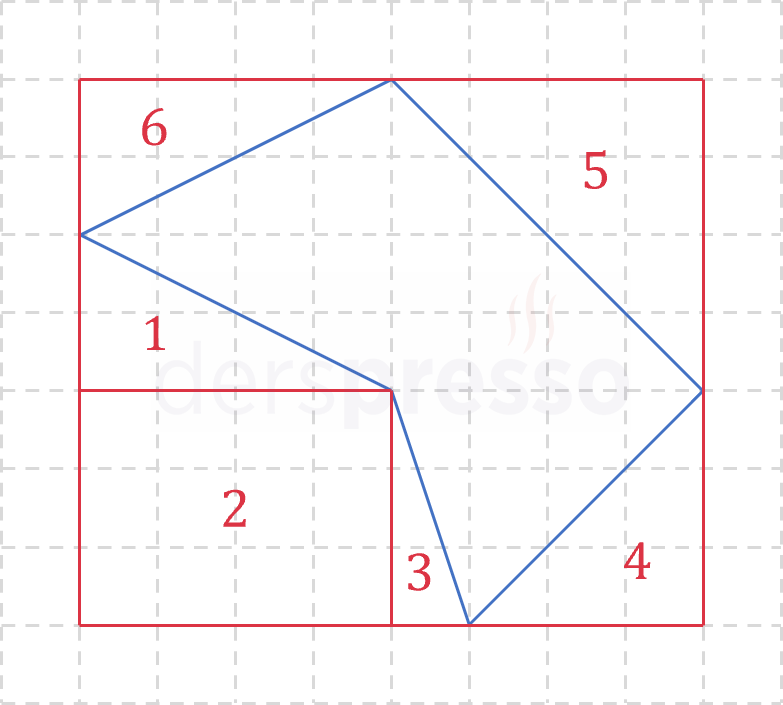
Dikdörtgenin alanı:
\( = 8 \cdot 7 = 56 \)
1 numaralı alan:
\( = \dfrac{2 \cdot 4}{2} = 4 \)
2 numaralı alan:
\( = 4 \cdot 3 = 12 \)
3 numaralı alan:
\( = \dfrac{1 \cdot 3}{2} = \dfrac{3}{2} \)
4 numaralı alan:
\( = \dfrac{3 \cdot 3}{2} = \dfrac{9}{2} \)
5 numaralı alan:
\( = \dfrac{4 \cdot 4}{2} = 8 \)
6 numaralı alan:
\( = \dfrac{2 \cdot 4}{2} = 4 \)
İstenen bölgenin alanı:
\( = 56 - 4 - 12 - \dfrac{3}{2} - \dfrac{9}{2} - 8 - 4 \)
\( = 22 \) bulunur.