Deltoid
Bir köşegenine göre yansıma simetrisine sahip olan dörtgene deltoid denir.
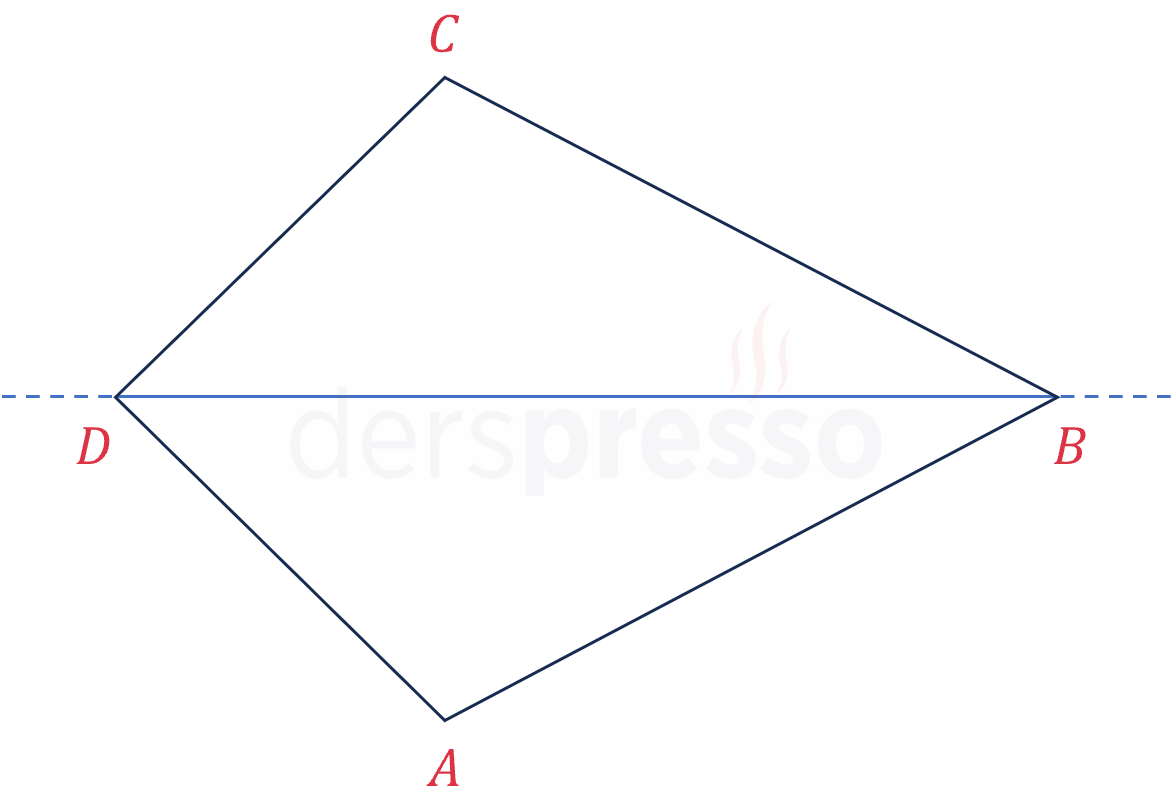
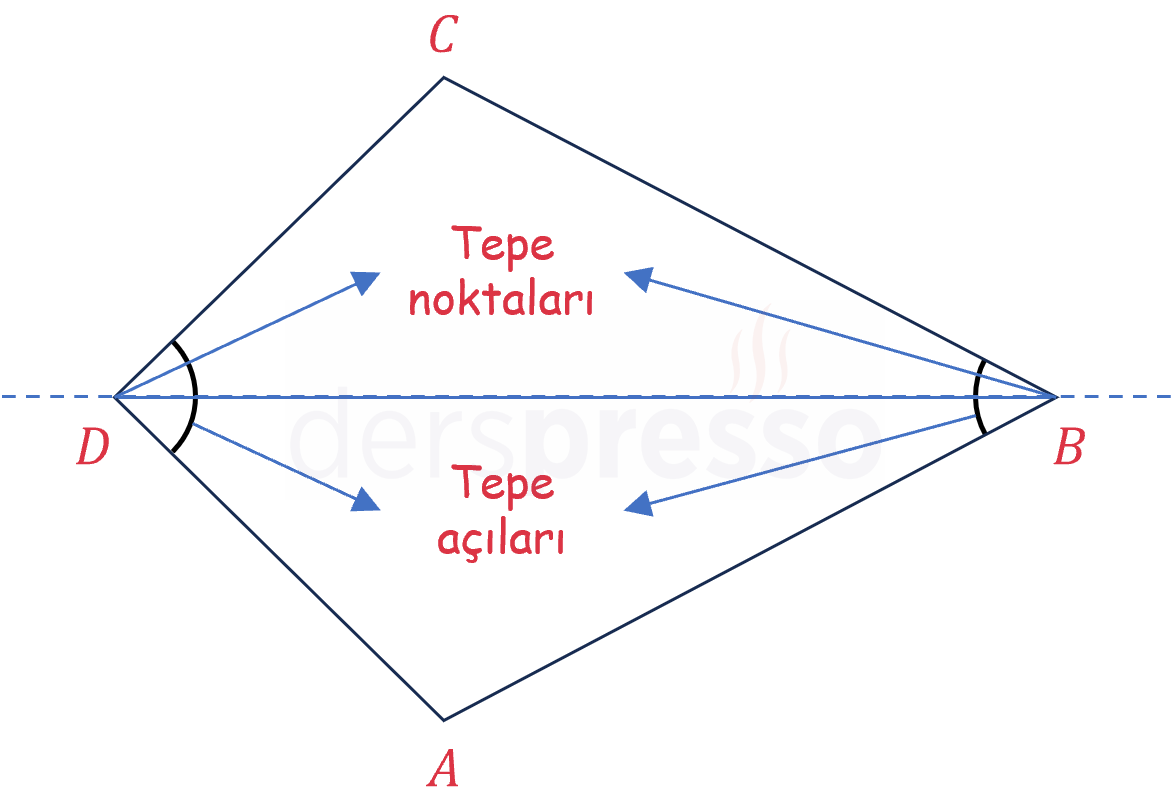
Deltoidin simetri ekseninin geçtiği köşeler deltoidin tepe noktaları, bu köşelere ait açılar da tepe açılarıdır.
Bir dörtgenin aşağıdaki özelliklerden en az birini taşıdığı biliniyorsa bu dörtgen bir deltoiddir ve diğer özellikleri de taşır.
- Köşegenlerden biri diğer köşegeni dik kesiyor ve ortalıyor.
- Köşegenlerden biri açıortay
- İki farklı komşu kenar ikilisinin uzunlukları eşit
- Köşegenlerden birine göre yansıma simetrisine sahip
Deltoid bir dörtgen olduğu için, dörtgenler bölümünde bahsettiğimiz tüm özellikler deltoid için de geçerlidir.
Giriş bölümünde paylaştığımız dörtgen hiyerarşisine göre; eşkenar dörtgen ve kare deltoidin ek özelliklere sahip özel birer durumu olarak düşünülebilir.
Deltoidin Kenar ve Köşegen Özellikleri
Deltoidin köşegenleri birbirini dik keser ve tepe noktalarını birleştiren köşegen diğer köşegeni ortalar.
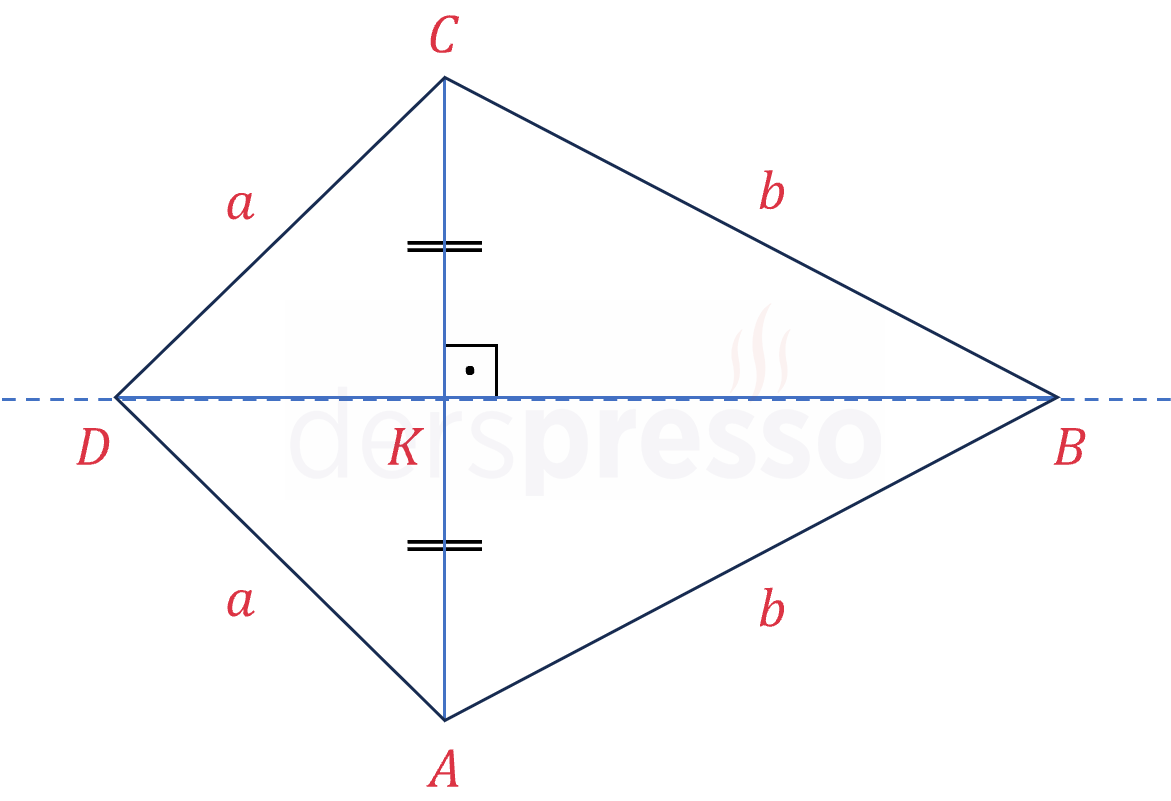
\( [DB] \perp [AC] \)
\( \abs{AK} = \abs{KC} \)
Deltoidin tepe noktalarına komşu olan ikişer kenar eşit uzunluktadır. Bunun bir sonucu olarak, deltoid tabanları ortak iki ikizkenar üçgenden oluşur.
\( \abs{DA} = \abs{DC} = a \)
\( \abs{BA} = \abs{BC} = b \)
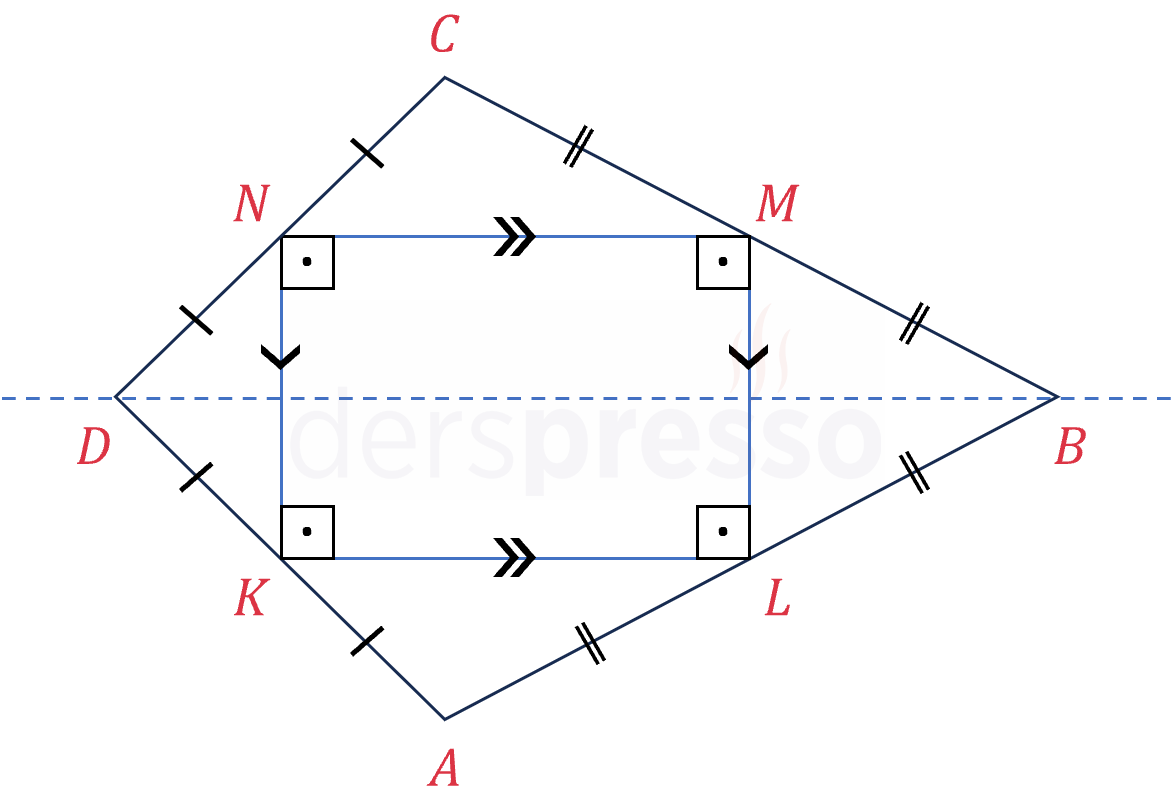
Tüm dörtgenlerde kenar orta noktalarının birleştirilmesiyle oluşan dörtgen bir paralelkenardır, köşegenleri birbirine dik olan deltoidde bu dörtgen bir dikdörtgendir. Varignon paralelkenarı adı verilen bu dörtgenle ilgili daha fazla bilgi ve deltoidde de geçerli olan özellikleri için dörtgenler sayfasını inceleyebilirsiniz.
Deltoidin Açı Özellikleri
Tüm dörtgenlerde olduğu gibi, deltoidin hem iç açıları hem de dış açıları toplamı 360°'dir.
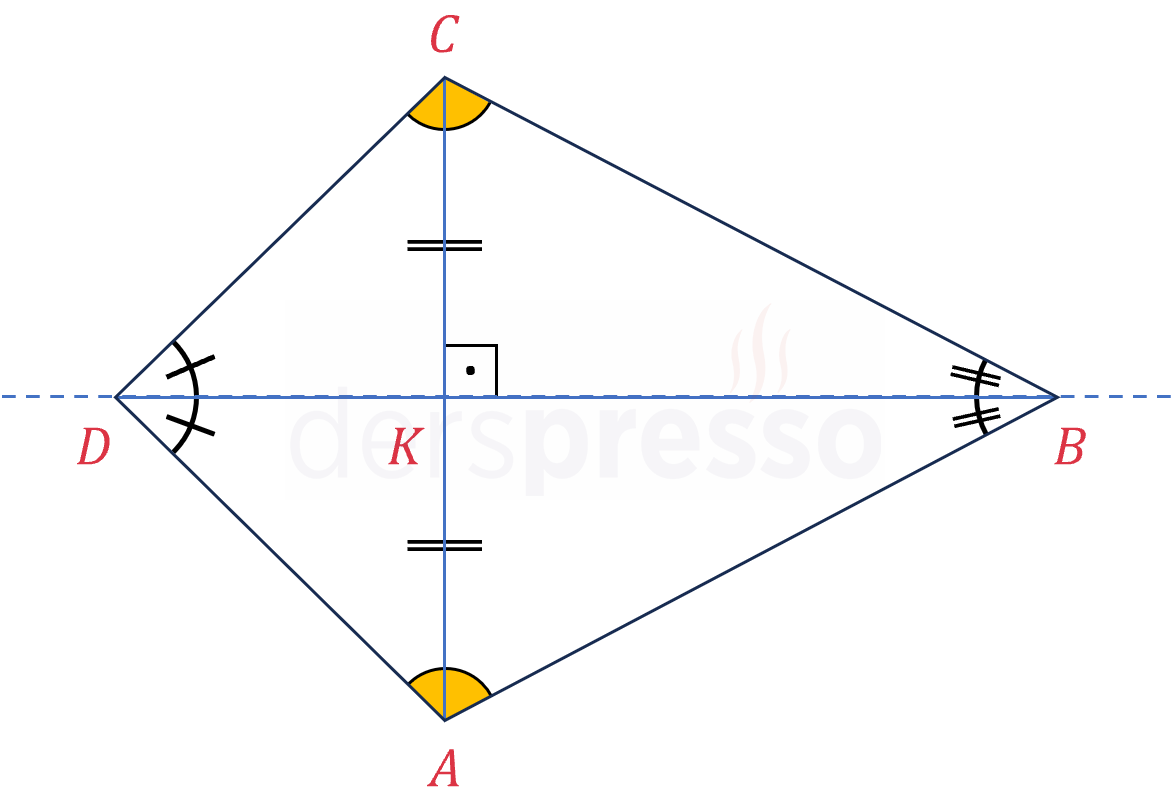
Deltoidin tepe açısı olmayan açılarının ölçüleri birbirine eşittir.
\( m(\widehat{A}) = m(\widehat{C}) \)
Deltoidin tepe noktalarını birleştiren köşegen tepe açılarının açıortayıdır.
\( m(\widehat{ADK}) = m(\widehat{CDK}) \)
\( m(\widehat{ABK}) = m(\widehat{CBK}) \)
Tüm iç açıları ve birer kenarı ortak olduğu için, tepe noktalarını birleştiren köşegenin deltoidi böldüğü iki üçgen eş üçgenlerdir.
\( \overset{\triangle}{DAB} \cong \overset{\triangle}{DCB} \)
Deltoidin Çevresi ve Alanı
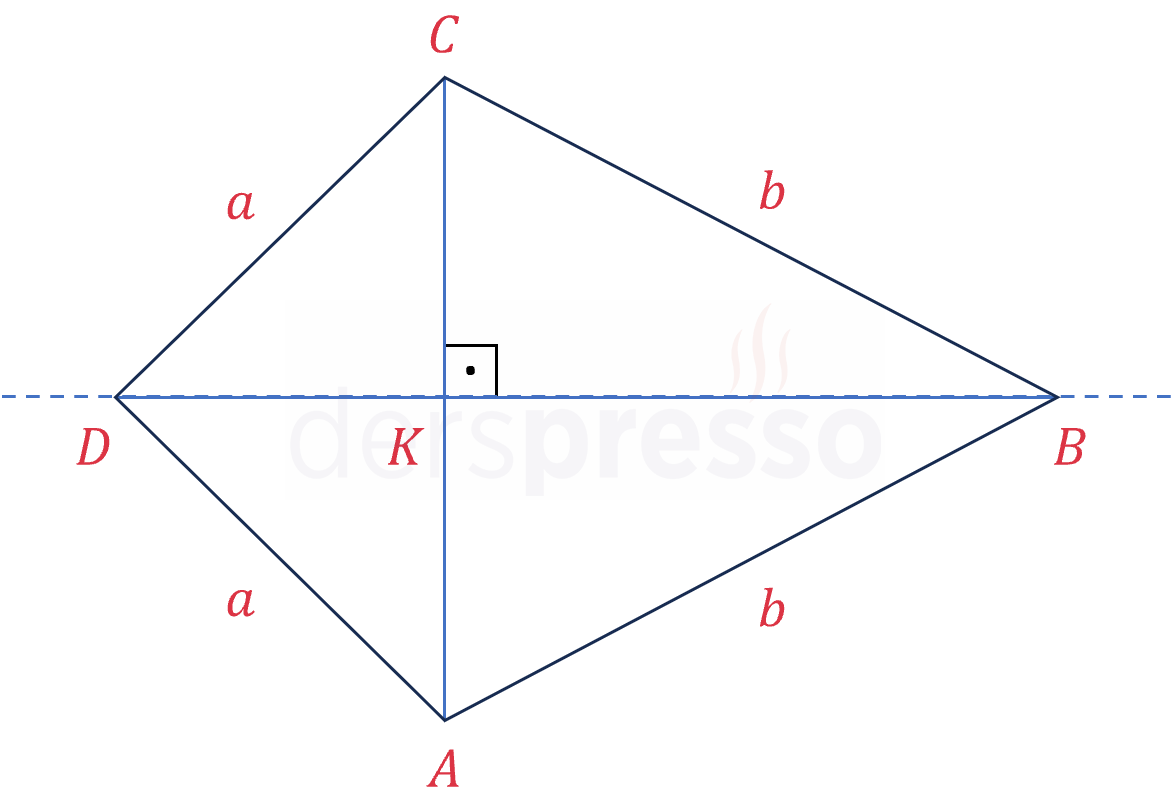
Deltoidin çevresi dört kenar uzunluğunun toplamına eşittir.
\( \text{Ç}(ABCD) = 2(a + b) \)
Deltoidin köşegenleri birbirini dik kestiği için, alanı köşegenlerin uzunlukları çarpımının yarısına eşittir. Aşağıda bu formülün köşegenleri dik kesişen tüm dörtgenler için geçerli olan ispatı verilmiştir.
\( A(ABCD) = \frac{1}{2} \abs{AC} \cdot \abs{DB} \)
İSPATI GÖSTER
İspat 1:
Bir dörtgenin alanı, köşegenlerin uzunlukları ile aralarındaki açının sinüs değerinin çarpımının yarısına eşittir.
\( A(ABCD) = \dfrac{1}{2} \cdot \abs{AC} \cdot \abs{BD} \cdot \sin{x} \)
Köşegenleri dik kesişen dörtgenlerde bu açı 90° olur.
\( A(ABCD) = \dfrac{1}{2} \cdot \abs{AC} \cdot \abs{BD} \cdot \sin{90°} \)
\( \sin{90°} = 1 \)
\( A(ABCD) = \frac{1}{2} \abs{AC} \cdot \abs{BD} \)
İspat 2:
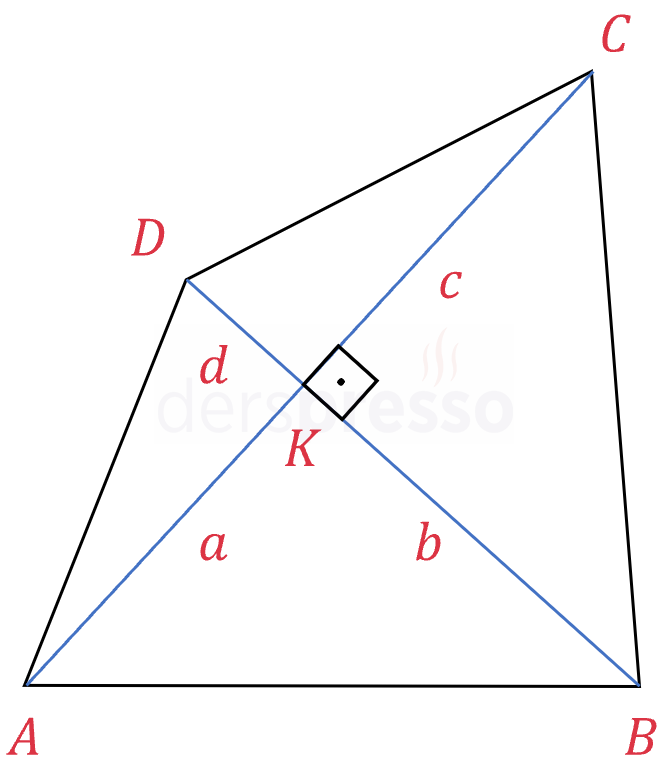
Köşegenlerin oluşturduğu dört üçgenin alanını ayrı ayrı hesaplayalım.
\( A(\overset{\triangle}{AKB}) = \dfrac{a \cdot b}{2} \)
\( A(\overset{\triangle}{BKC}) = \dfrac{b \cdot c}{2} \)
\( A(\overset{\triangle}{CKD}) = \dfrac{c \cdot d}{2} \)
\( A(\overset{\triangle}{DKA}) = \dfrac{d \cdot a}{2} \)
Dörtgenin alanını bulmak için bu dört üçgenin alanlarını toplayalım.
\( A(ABCD) = \dfrac{a \cdot b + b \cdot c + c \cdot d + d \cdot a}{2} \)
\( = \dfrac{b(a + c) + d(a + c)}{2} \)
\( = \dfrac{(a + c)(b + d)}{2} \)
Parantez içindeki toplamlar köşegen uzunluklarına eşittir.
\( A(ABCD) = \frac{1}{2} \abs{AC} \cdot \abs{BD} \)
\( A \) ve \( C \) köşeleri deltoidin tepe noktası olmayan köşeleri olmak üzere, deltoidin bir diğer alan formülü aşağıdaki gibidir.
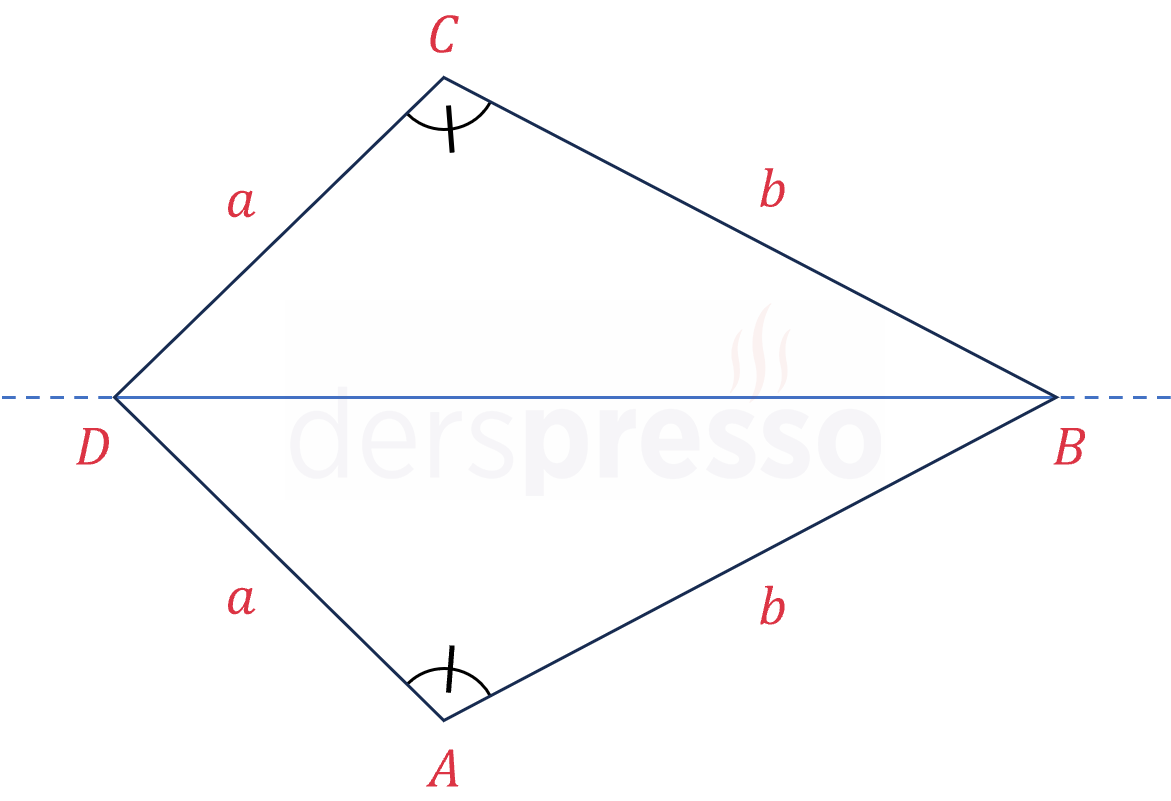
\( A(ABCD) = a \cdot b \cdot \sin{\widehat{A}} \)
\( A(ABCD) = a \cdot b \cdot \sin{\widehat{C}} \)
İSPATI GÖSTER
Sinüs alan formülünü kullanarak \( \overset{\triangle}{ABD} \) üçgeninin alanını hesaplayalım.
\( A(\overset{\triangle}{ABD}) = \dfrac{1}{2} \cdot a \cdot b \cdot \sin{\widehat{A}} \)
Sinüs alan formülünü kullanarak \( \overset{\triangle}{CBD} \) üçgeninin alanını hesaplayalım.
\( A(\overset{\triangle}{CBD}) = \dfrac{1}{2} \cdot a \cdot b \cdot \sin{\widehat{C}} \)
Deltoidin tepe noktası olmayan köşelerinin açı ölçüleri eşittir.
\( m(\widehat{A}) = m(\widehat{C}) \)
\( \sin{\widehat{A}} = \sin{\widehat{C}} \)
Buna göre deltoidin alanı, alanını hesapladığımız üçgenlerden birinin alanının iki katına eşit olur.
\( A(ABCD) = a \cdot b \cdot \sin{\widehat{A}} \)
\( A(ABCD) = a \cdot b \cdot \sin{\widehat{C}} \)
Köşegenler deltoidi alanları ikişerli eşit dört üçgene böler.
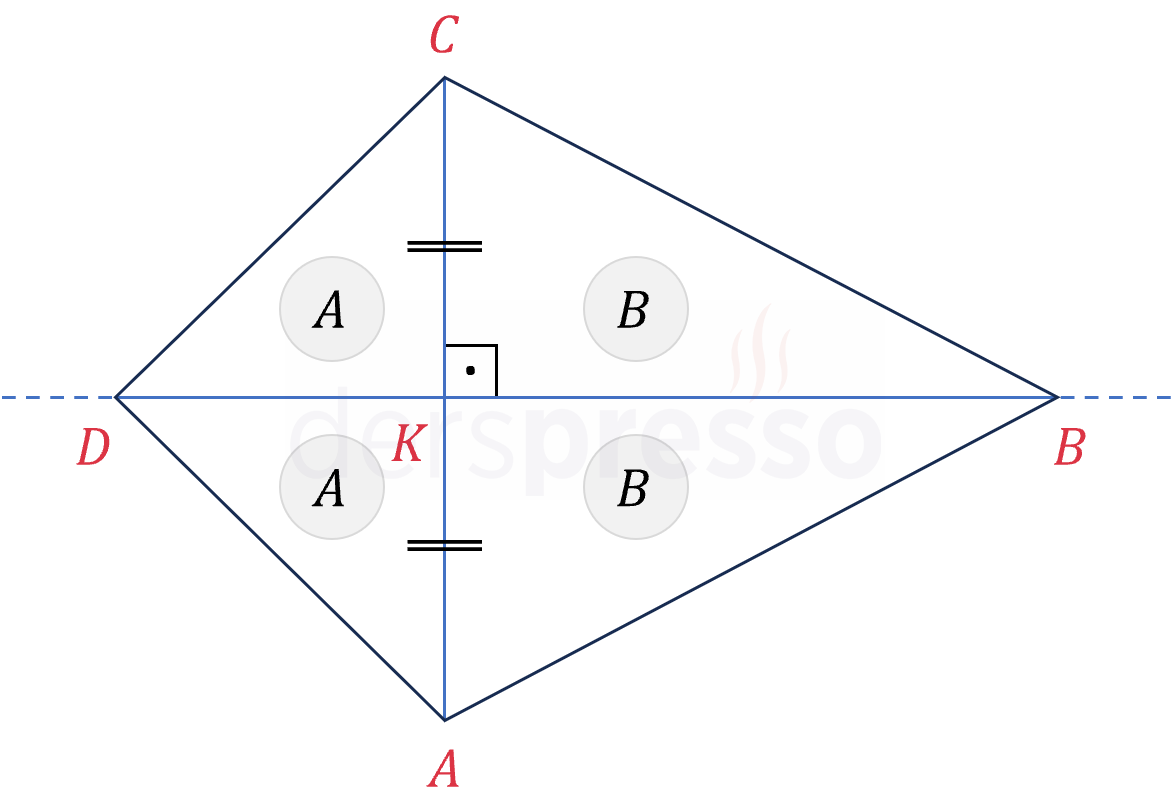
\( A(DAK) = A(DCK) \)
\( A(BAK) = A(BCK) \)