Paralelkenar
Karşılıklı kenarları paralel olan dörtgene paralelkenar denir.

Bir dörtgenin aşağıdaki özelliklerden en az birini taşıdığı biliniyorsa bu dörtgen bir paralelkenardır ve diğer özellikleri de taşır.
- Karşılıklı kenarlar paralel (paralelkenar tanımı)
- Karşılıklı kenar uzunlukları eşit
- Karşılıklı iki kenar paralel ve uzunlukları eşit
- Karşılıklı açı ölçüleri eşit
- Köşegenler birbirini ortalıyor.
- Komşu köşe açıları bütünler
- Her bir köşegen dörtgeni iki eş üçgene ayırıyor.
Paralelkenar bir dörtgen olduğu için, dörtgenler bölümünde bahsettiğimiz tüm özellikler paralelkenar için de geçerlidir.
Giriş bölümünde paylaştığımız dörtgen hiyerarşisine göre; eşkenar dörtgen, dikdörtgen ve kare paralelkenarın ek özelliklere sahip özel birer durumu olarak düşünülebilir.
Paralelkenarın Kenar ve Köşegen Özellikleri
Paralelkenarda karşılıklı kenarlar birbirine paraleldir ve uzunlukları birbirine eşittir.

\( [AB] \parallel [DC], \quad [AD] \parallel [BC] \)
\( \abs{AB} = \abs{DC}, \quad \abs{AD} = \abs{BC} \)
Paralelkenarın köşegenleri birbirini ortalar. Bunun karşıtı da doğrudur, bir dörtgenin köşegenleri birbirini ortalıyorsa o dörtgenin karşılıklı kenarları paraleldir.
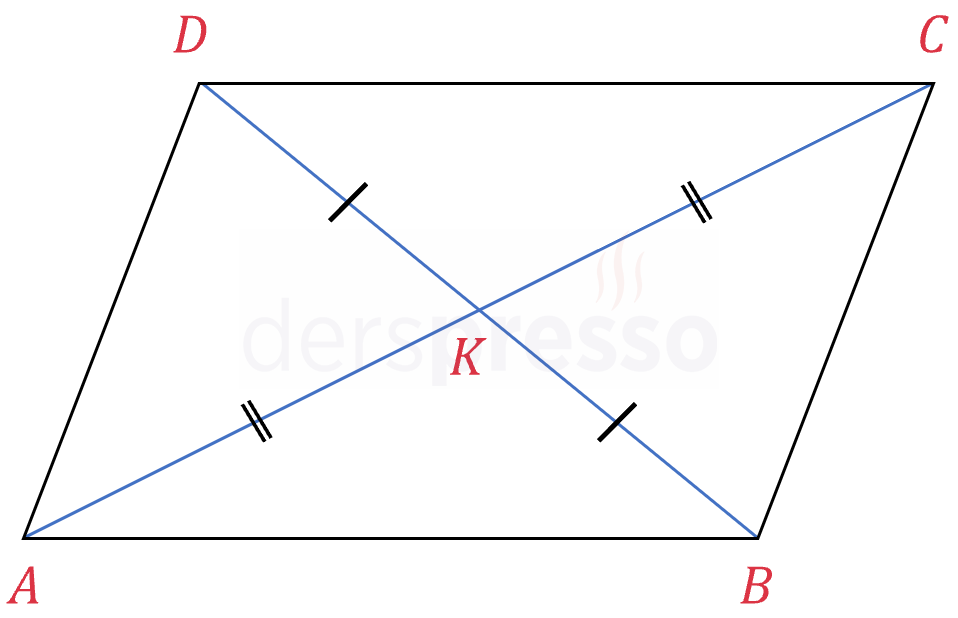
\( \abs{AK} = \abs{KC} \)
\( \abs{BK} = \abs{KD} \)
İSPATI GÖSTER
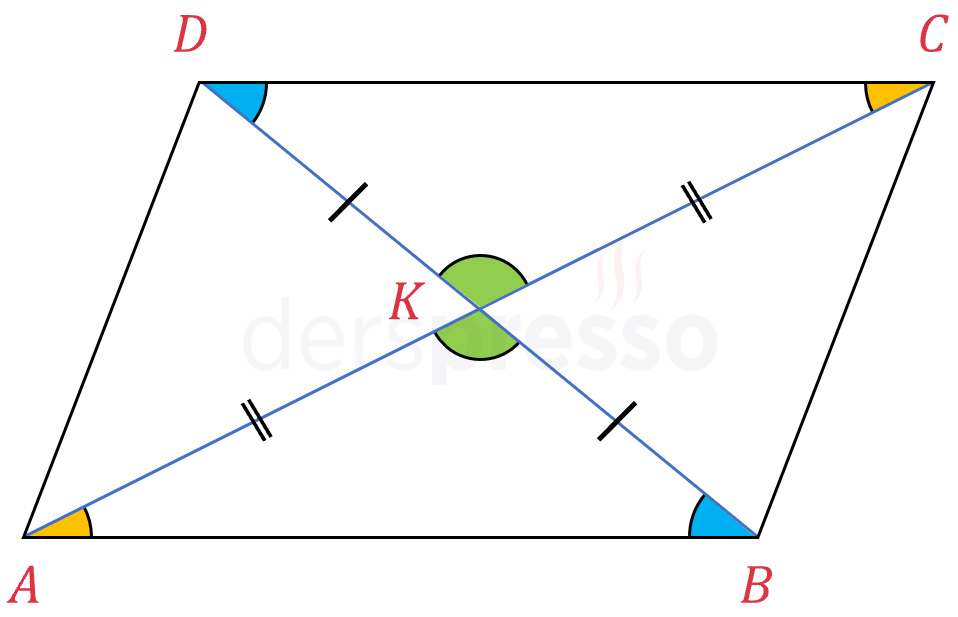
\( [AB] \parallel [DC] \) olduğu için aşağıdaki iç ters açı ikililerinin ölçüleri birbirine eşittir.
\( m(\widehat{KAB}) = m(\widehat{KCD}) \)
\( m(\widehat{KBA}) = m(\widehat{KDC}) \)
Ters açıların ölçüleri birbirine eşittir.
\( m(\widehat{AKB}) = m(\widehat{CKD}) \)
Paralelkenarın karşılıklı kenar uzunlukları eşittir.
\( \abs{AB} = \abs{CD} \)
İç açıları ve birer kenarı eş olan iki üçgen eş üçgenlerdir.
\( \overset{\triangle}{ABK} \cong \overset{\triangle}{CDK} \)
Eş üçgenlerin birbirine karşılık gelen kenar uzunlukları birbirine eşittir.
\( \abs{AK} = \abs{CK} \)
\( \abs{BK} = \abs{DK} \)
Buna göre karşılıklı kenarları paralel olan bir dörtgende köşegenler birbirini ortalar.
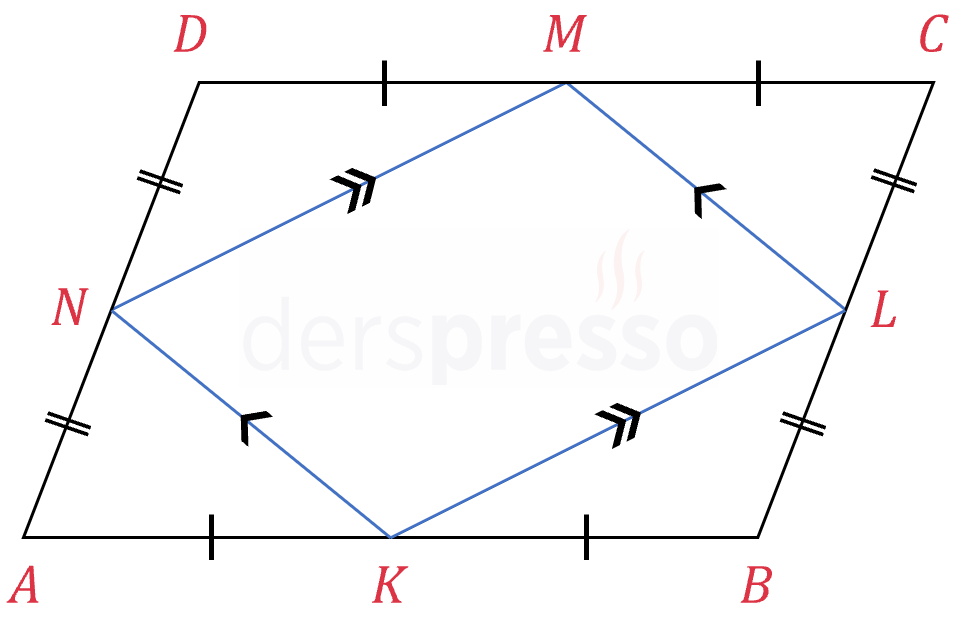
Tüm dörtgenlerde olduğu gibi, paralelkenarın kenar orta noktalarının birleştirilmesiyle oluşan dörtgen bir paralelkenardır. Varignon paralelkenarı adı verilen bu dörtgenle ilgili daha fazla bilgi ve paralelkenarda da geçerli olan özellikleri için dörtgenler sayfasını inceleyebilirsiniz.
Paralelkenarda geniş açılar uzun köşegeni, dar açılar kısa köşegeni görür. Bu kuralın ispatı üçgenler konusunda gördüğümüz Hinge teoremi ile yapılabilir. Bu teoreme göre, iki üçgenin ikişer kenar uzunluğu eşitse bu iki kenarın arasındaki açısı daha büyük olan üçgenin üçüncü kenar uzunluğu daha büyüktür.
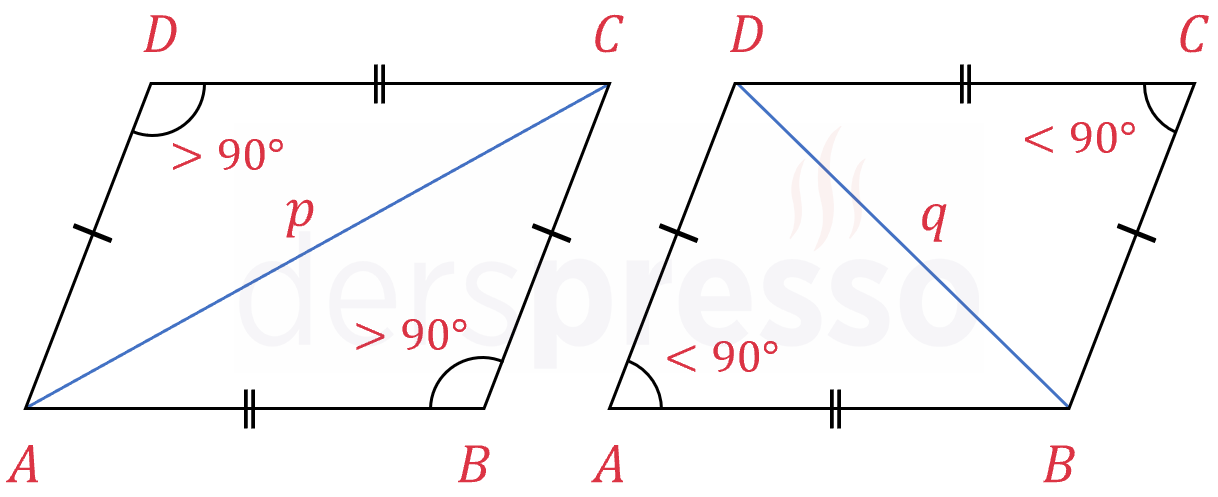
\( p \gt q \)
Paralelkenarın köşegen uzunluklarının kareleri toplamı, kenar uzunluklarının kareleri toplamının iki katına eşittir.
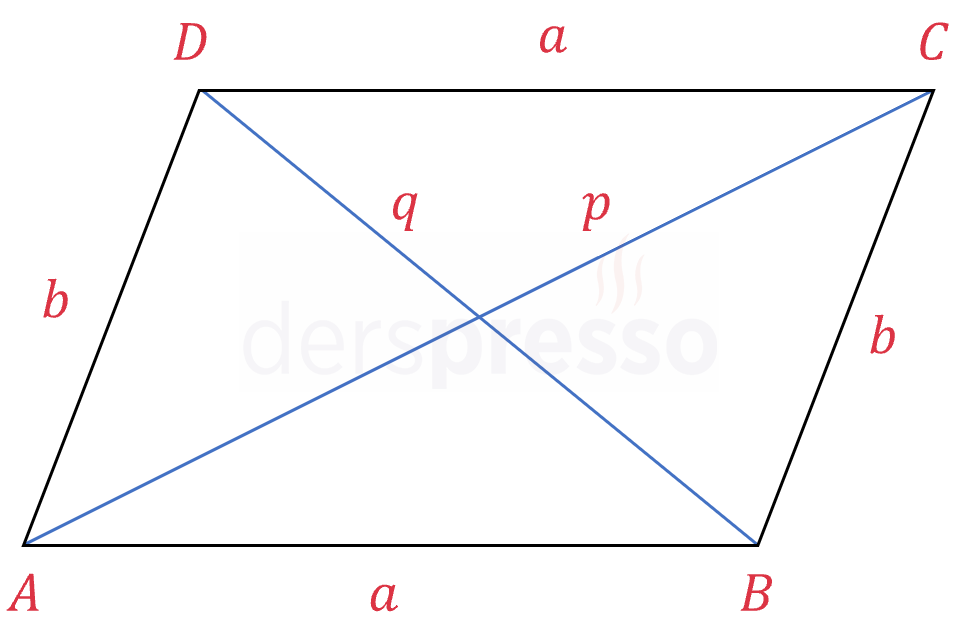
\( p^2 + q^2 = 2(a^2 + b^2) \)
İSPATI GÖSTER
\( \overset{\triangle}{ABC} \) üçgenine kosinüs teoremi uygulayalım.
\( p^2 = a^2 + b^2 - 2ab \cdot \cos{\hat{B}} \)
Şimdi de \( \overset{\triangle}{ABD} \) üçgenine kosinüs teoremi uygulayalım.
\( q^2 = a^2 + b^2 - 2ab \cdot \cos{\hat{A}} \)
\( A \) ve \( B \) açıları bütünler açılar oldukları için, aralarında aşağıdaki ilişki vardır.
\( \cos{\hat{A}} = \cos(180° - \hat{B}) = -\cos{\hat{B}} \)
Bu dönüşümü kullanarak yukarıdaki ilk denklemi \( A \) açısı cinsinden yazalım.
\( p^2 = a^2 + b^2 + 2ab \cdot \cos{\hat{A}} \)
İki denklemi taraf tarafa toplayalım.
\( p^2 + q^2 = 2(a^2 + b^2) \)
Paralelkenarın bir köşesinden karşı iki kenarın orta noktalarına çizilen doğru parçaları, paralelkenarın köşegenini üç eşit parçaya böler.
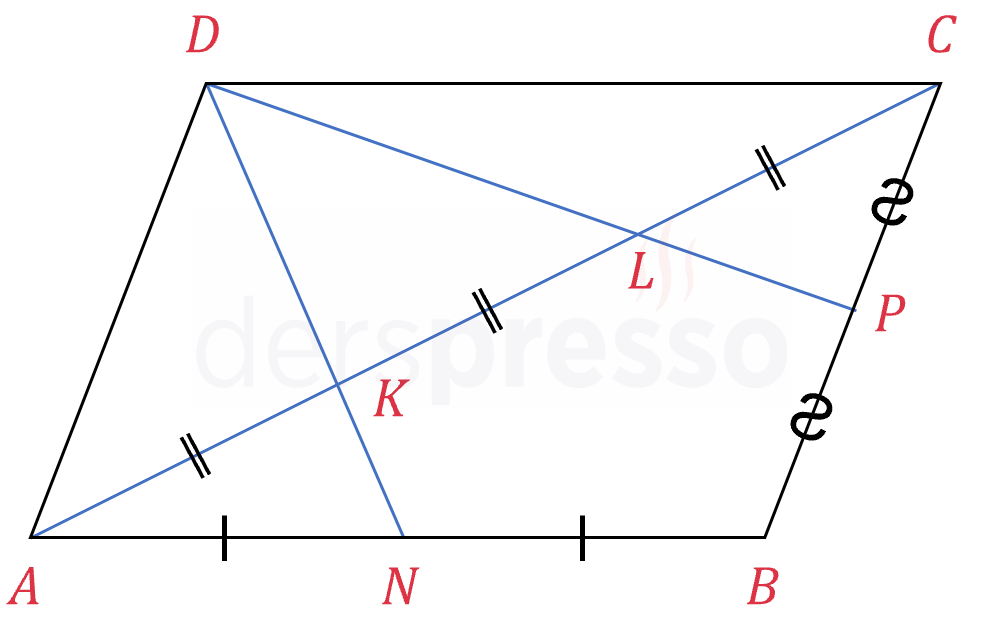
\( \abs{AK} = \abs{KL} = \abs{LC} \)
İSPATI GÖSTER
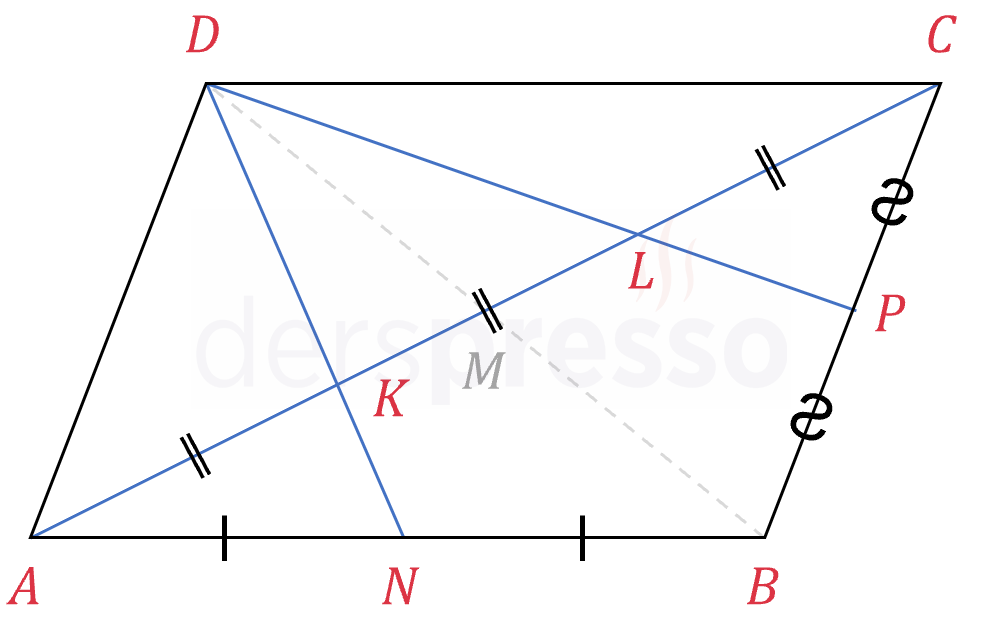
Paralelkenarın diğer köşegenini de çizelim (kesikli gri doğru). \( [DN] \) \( \overset{\triangle}{ABD} \) üçgeninin bir kenarortayıdır. Paralelkenarın köşegenleri birbirini ortaladığı için, \( [AM] \) de \( \overset{\triangle}{ABD} \) üçgeninin bir kenarortayıdır. Buna göre, iki kenarortayın kesişim noktası olan \( K \) noktası \( \overset{\triangle}{ABD} \) üçgeninin ağırlık merkezidir ve \( [AM] \) doğru parçasını 2:1 oranında böler.
Aynı yöntemi \( \overset{\triangle}{BCD} \) üçgenine uygularsak, \( L \) noktasının \( \overset{\triangle}{BCD} \) üçgeninin ağırlık merkezi olduğunu buluruz. Dolayısıyla, \( [AC] \) köşegeninin 2:2:2 oranında, yani eşit üç parçaya bölündüğünü buluruz.
Yukarıdaki eşitliğin bir diğer uygulamasında; paralelkenarın karşılıklı iki köşesinden karşı kenarların orta noktalarına çizilen doğru parçaları, paralelkenarın köşegenini üç eşit parçaya böler.

\( \abs{AK} = \abs{KL} = \abs{LC} \)
İSPATI GÖSTER
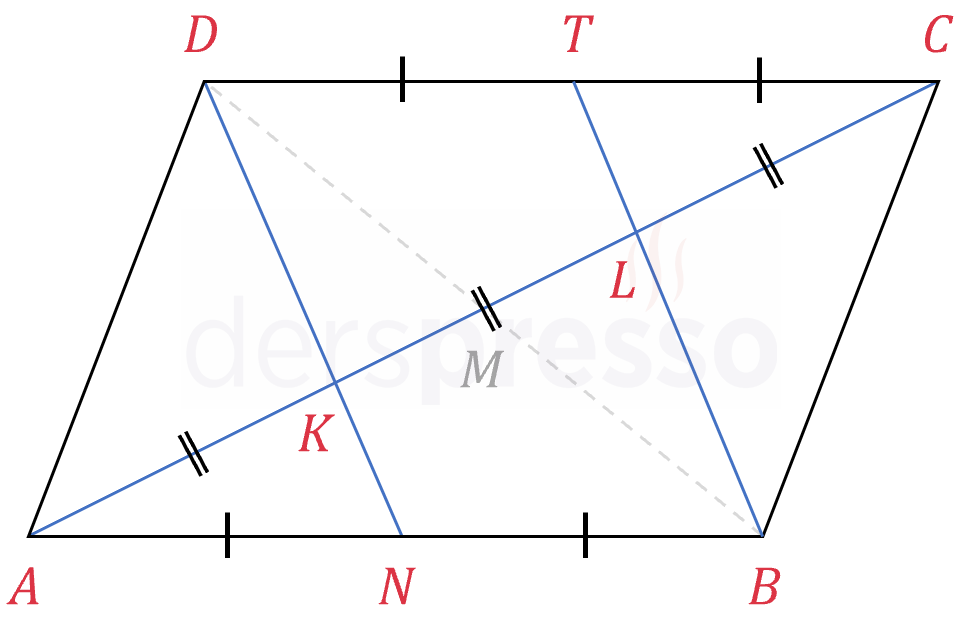
Bu kuralın yukarıdaki kuraldan farkı, \( \overset{\triangle}{BCD} \) üçgeninde \( [DP] \) kenarortayı yerine \( [BT] \) kenarortayının çizilmiş olmasıdır. \( L \) noktasının \( \overset{\triangle}{BCD} \) üçgeninin ağırlık merkezi (kenarortayların kesişim noktası) olduğunu bildiğimiz için, \( L \) noktasının konumu, dolayısıyla \( [AC] \) köşegeninin bölünme oranı değişmeyecektir.
Paralelkenarın bir köşegenini şekildeki gibi kesen doğru üzerinde oluşan doğru parçalarının uzunlukları arasında aşağıdaki ilişki vardır.
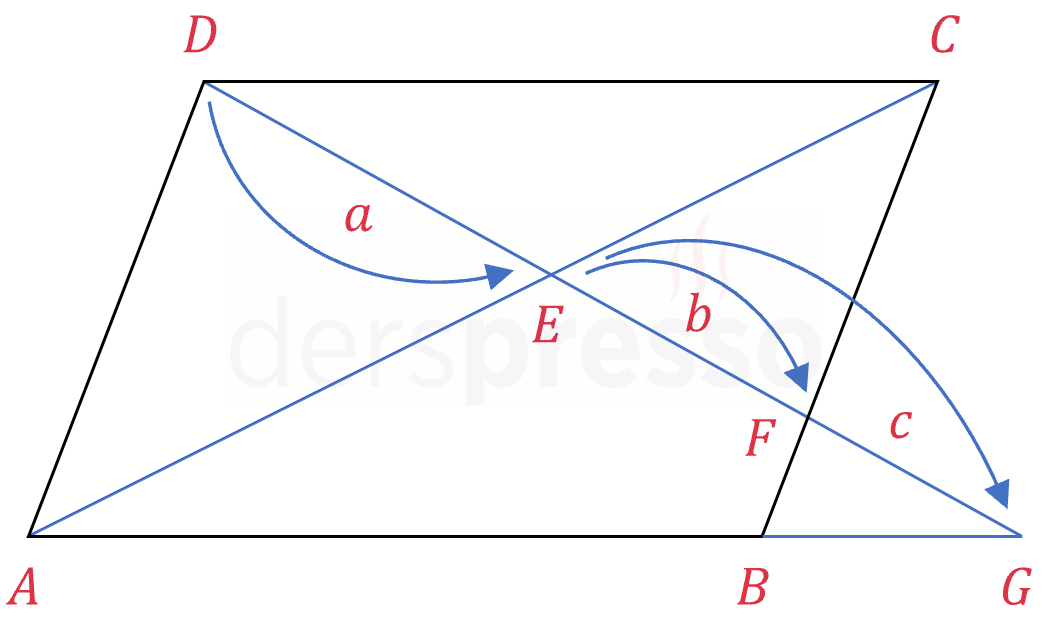
\( a^2 = b(b + c) \)
İSPATI GÖSTER
Paralelkenarın alt ve üst kenar uzunluklarına \( m \), \( [GB] \) uzunluğuna \( n \) diyelim.
\( \abs{AB} = \abs{DC} = m \)
\( \abs{GB} = n \)
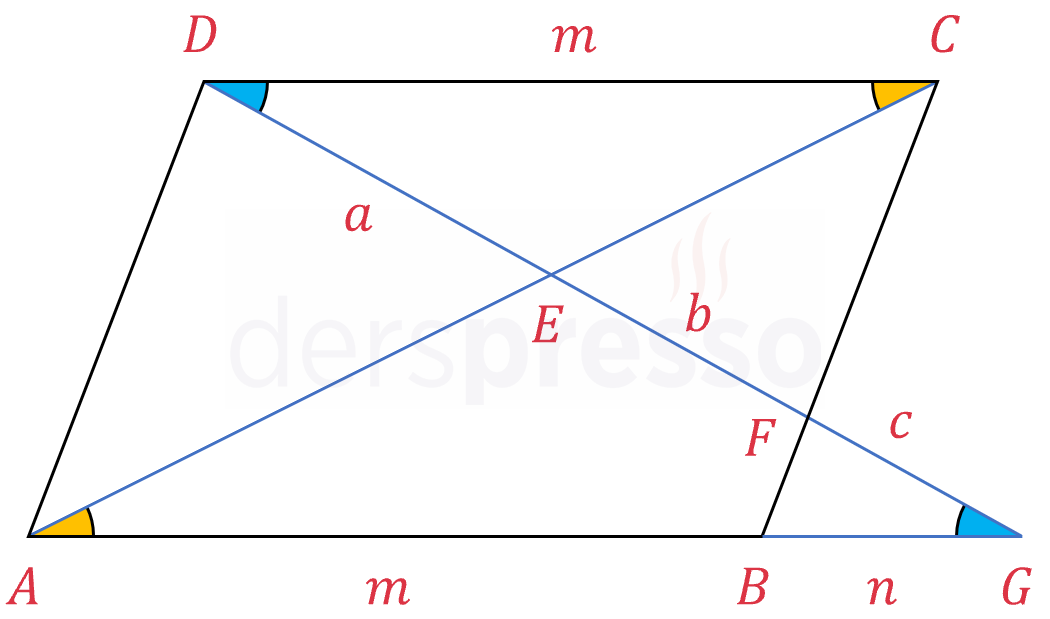
\( [AG] \parallel [DC] \) olduğu için aşağıdaki açılar iç ters açılardır ve ölçüleri eşittir.
\( m(\widehat{CAG}) = m(\widehat{ACD}) \)
\( m(\widehat{DGA}) = m(\widehat{GDC}) \)
İkişer açısı eş olan aşağıdaki iki üçgenin üçüncü açıları da eştir, dolayısıyla iki üçgen benzerdir.
\( \overset{\triangle}{AGE} \sim \overset{\triangle}{CDE} \)
Benzer iki üçgenin kenar uzunlukları arasında orantı kuralım.
\( \dfrac{\abs{CD}}{\abs{AG}} = \dfrac{\abs{DE}}{\abs{GE}} \)
\( \dfrac{m}{m + n} = \dfrac{a}{b + c} \)
\( [AD] \parallel [BC] \) olduğu için, temel orantı teoreminden aşağıdaki iki üçgen de benzerdir.
\( \overset{\triangle}{GBF} \sim \overset{\triangle}{GAD} \)
Benzer iki üçgenin kenar uzunlukları arasında orantı kuralım.
\( \dfrac{\abs{GB}}{\abs{GA}} = \dfrac{\abs{GF}}{\abs{GD}} \)
\( \dfrac{n}{m + n} = \dfrac{c}{a + b + c} \)
Elde ettiğimiz iki eşitliği taraf tarafa toplayalım.
\( \dfrac{m}{m + n} + \dfrac{n}{m + n} = \dfrac{a}{b + c} + \dfrac{c}{a + b + c} \)
\( \dfrac{m + n}{m + n} = \dfrac{a(a + b + c)}{(b + c)(a + b + c)} + \dfrac{c(b + c)}{(a + b + c)(b + c)} \)
\( 1 = \dfrac{a^2 + ab + ac + bc + c^2}{(b + c)(a + b + c)} \)
İçler - dışlar çarpımı yapalım.
\( a^2 + ab + ac + bc + c^2 = ab + b^2 + bc + ac + bc + c^2 \)
\( a^2 = b^2 + bc \)
\( a^2 = b(b + c) \)
Paralelkenarın Açı Özellikleri
Tüm dörtgenlerde olduğu gibi, paralelkenarın hem iç açıları hem de dış açıları toplamı 360°'dir.
Paralelkenarda karşılıklı köşelerin açıları birbirine eşittir.

\( m(\widehat{A}) = m(\widehat{C}) = x \)
\( m(\widehat{B}) = m(\widehat{D}) = y \)
İSPATI GÖSTER
\( ABCD \) paralelkenarının üst ve yan kenarlarını uzatalım (mavi kesikli çizgiler).
\( A \) köşesinin açı ölçüsüne \( x \), \( B \) köşesinin açı ölçüsüne \( y \) diyelim.

\( D \) köşesinin dış açısı \( A \) köşesinin iç açısı ile iç ters açılardır. \( [AB] \parallel [DC] \) olduğu için bu açının ölçüsü de \( x \) olur.
\( x + y = 180° \)
\( B \) köşesinin dış açısı \( A \) köşesinin iç açısı ile iç ters açılardır. \( [AD] \parallel [BC] \) olduğu için bu açının ölçüsü \( x \) olur.
\( x + y = 180° \)
\( C \) köşesinin dış açısı \( B \) köşesinin iç açısı ile iç ters açılardır. \( [AB] \parallel [DC] \) olduğu için bu açının ölçüsü \( y \) olur.
\( x + y = 180° \)
Buna göre paralelkenarda karşılıklı köşelerin açıları birbirine eşittir ve komşu köşe açıları bütünler açılardır.
Paralelkenarda komşu köşe açıları bütünler açılardır. Yukarıda karşılıklı köşe açılarının eşliğini göstermek için yaptığımız ispat bu kuralın ispatını da içermektedir.
\( x + y = 180° \)
Paralelkenarda komşu iki köşenin açıortayları birbirini orta taban üzerinde ve dik keser.
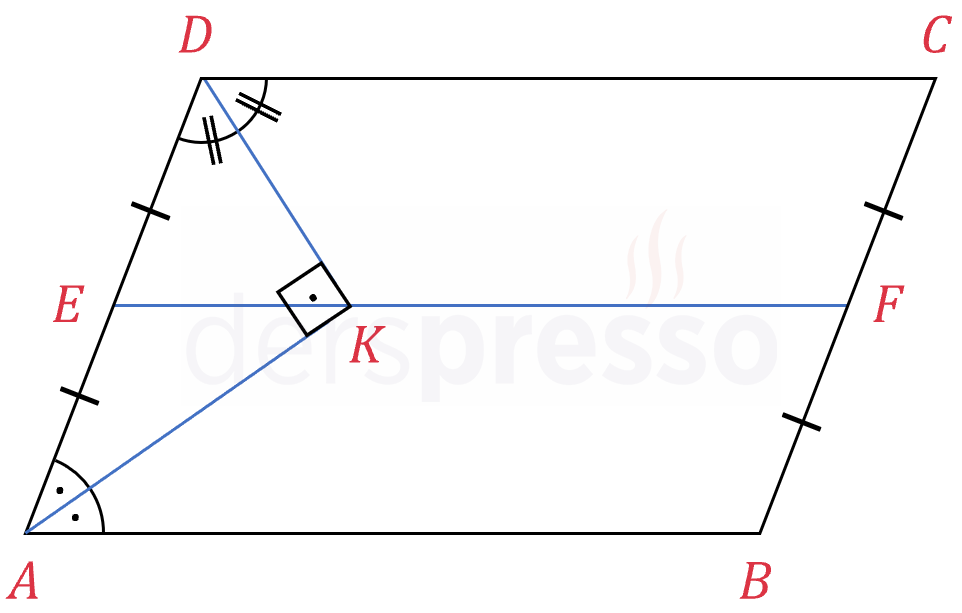
\( [AK] \) ve \( [DK] \) açıortay, \( [EF] \) orta taban olmak üzere,
\( K \in [EF] \) ve
\( m(\widehat{AKD}) = 90° \)
İSPATI GÖSTER
Paralelkenarın bir kenarı üzerindeki iki açıya \( x \) ve \( y \) diyelim.
\( m(\widehat{A}) = x \)
\( m(\widehat{B}) = y \)
\( [AK] \) ve \( [DK] \) sırasıyla \( \widehat{A} \) ve \( \widehat{D} \) açılarının açıortaylarıdır.
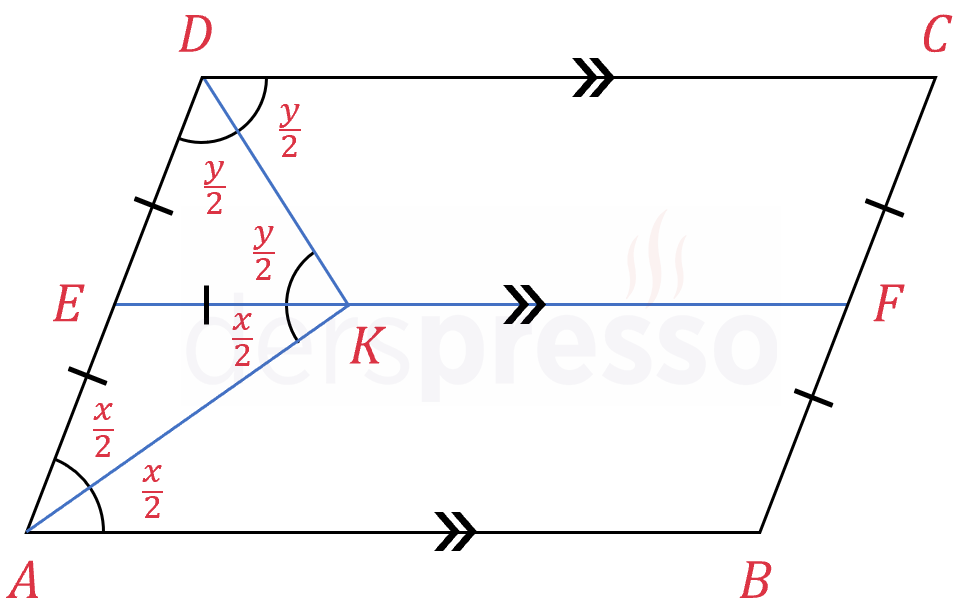
\( m(\widehat{EAK}) = m(\widehat{KAB}) = \dfrac{x}{2} \)
\( m(\widehat{EDK}) = m(\widehat{KDC}) = \dfrac{y}{2} \)
\( K \) noktasından geçen, \( [AD] \) ve \( [BC] \) kenarlarını birleştiren, \( [AB] \) ve \( [DC] \) kenarlarına paralel \( [EF] \) doğru parçasını çizelim.
\( \widehat{BAK} \) ve \( \widehat{EKA} \) açıları iç ters açılar oldukları için eş açılardır.
\( m(\widehat{EKA}) = \dfrac{x}{2} \)
\( \widehat{CDK} \) ve \( \widehat{DKE} \) açıları iç ters açılar oldukları için eş açılardır.
\( m(\widehat{DKE}) = \dfrac{y}{2} \)
Buna göre \( AEK \) ve \( DEK \) üçgenleri ikizkenardır.
\( \abs{AE} = \abs{EK} \)
\( \abs{DE} = \abs{EK} \)
Buna göre \( [EF] \) doğru parçası \( [AD] \) kenarını ortalar.
\( [EF] \) doğru parçası aynı zamanda \( [AB] \) ve \( [DC] \) kenarlarına paralel olduğu için \( [BC] \) kenarını da ortalar, dolayısıyla paralelkenarın bir orta tabanıdır.
Paralelkenarda bir kenar üzerindeki iki açı bütünlerdir.
\( \widehat{A} + \widehat{D} = 180° \)
\( x + y = 180° \)
\( \widehat{AKD} \) açısının ölçüsünü bulalım.
\( \dfrac{x}{2} + \dfrac{x}{2} = \dfrac{180°}{2} = 90° \)
Paralelkenarın karşılıklı kenarları paralel olduğu için, iç ya da dış bölgesine çizilen doğrularla farklı benzer üçgenler oluşturulabilir, bu durumlarda üçgenler konusunda gördüğümüz kelebek ve Thales kuralları sıklıkla kullanılır.
Aşağıdaki şekilde paralelkenarda kelebek kuralının kullanımına bir örnek verilmiştir.
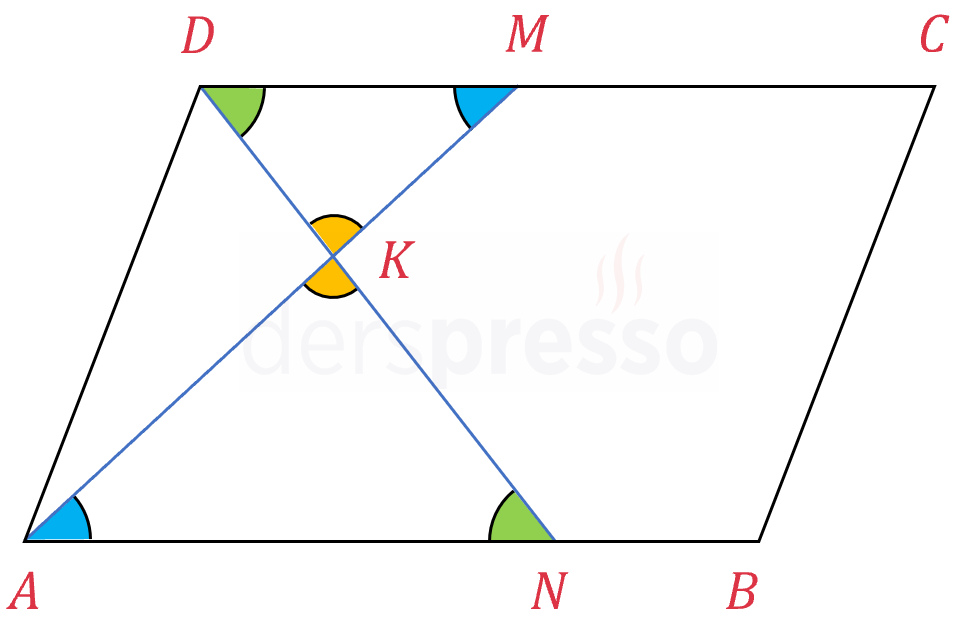
\( \overset{\triangle}{DMK} \sim \overset{\triangle}{NAK} \)
\( \dfrac{\abs{DM}}{\abs{NA}} = \dfrac{\abs{DK}}{\abs{NK}} = \dfrac{\abs{MK}}{\abs{AK}} \)
Aşağıdaki şekilde paralelkenarda Thales kuralının kullanımına bir örnek verilmiştir.
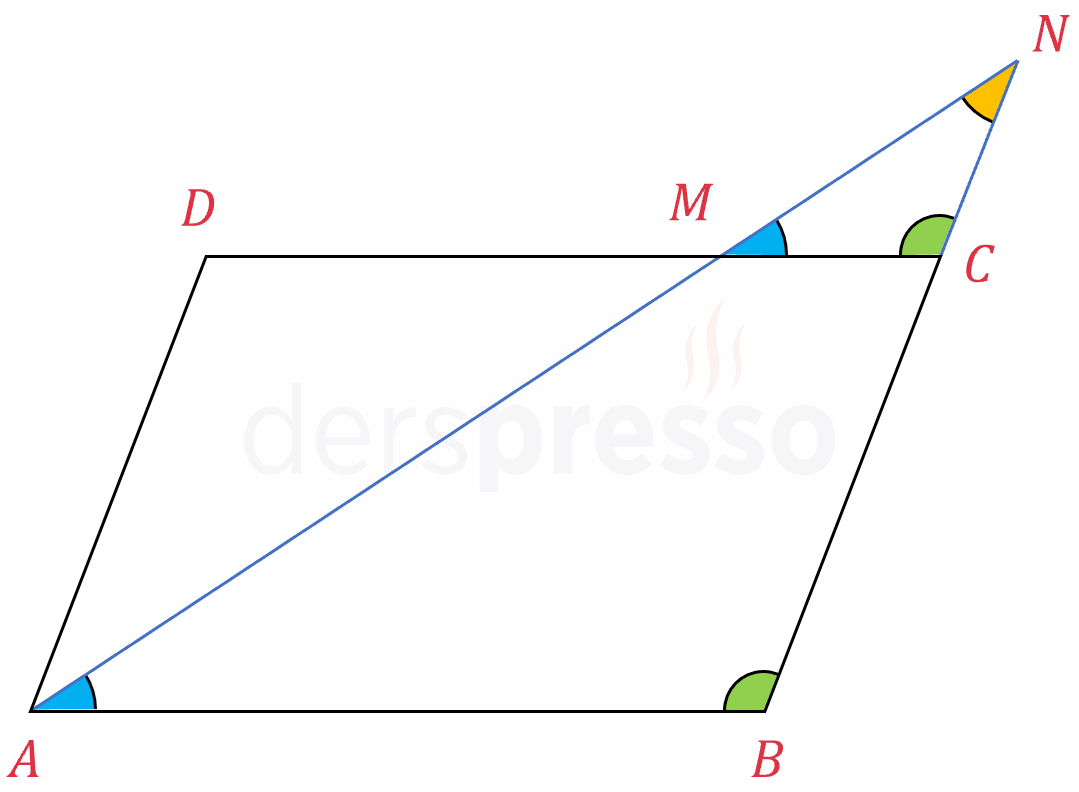
\( \overset{\triangle}{NMC} \sim \overset{\triangle}{NAB} \)
\( \dfrac{\abs{NM}}{\abs{NA}} = \dfrac{\abs{NC}}{\abs{NB}} = \dfrac{\abs{MC}}{\abs{AB}} \)
Paralelkenarın Çevresi ve Alanı

Paralelkenarın çevresi, komşu iki kenarın uzunlukları toplamının iki katına eşittir.
\( Ç(ABCD) = 2(a + b) \)
Paralelkenarın alanı, bir kenar uzunluğu ile o kenara ait yüksekliğin çarpımına eşittir.
\( A(ABCD) = a \cdot h_a = b \cdot h_b \)
İSPATI GÖSTER

\( D \) ve \( B \) köşelerini birleştiren bir köşegen çizelim.
Oluşan \( \overset{\triangle}{ABD} \) ve \( \overset{\triangle}{CDB} \) üçgenlerinin alan formüllerini yazalım.
\( A(\overset{\triangle}{ABD}) = \dfrac{a \cdot h_a}{2} \)
\( A(\overset{\triangle}{CDB}) = \dfrac{b \cdot h_b}{2} \)
Bu iki üçgenin tüm kenar uzunlukları ve karşı durumlu \( \hat{A} \) ve \( \hat{C} \) açıları eşit olduğu için eş üçgenlerdir ve alanları eşittir.
\( \overset{\triangle}{ABD} \cong \overset{\triangle}{CDB} \)
\( A(\overset{\triangle}{ABD}) = A(\overset{\triangle}{CDB}) \)
Paralelkenarın alanı bu iki üçgenin alanları toplamına ve aynı zamanda her birinin alanının iki katına eşittir.
\( A(ABCD) = a \cdot h_a = b \cdot h_b \)
Tüm dörtgenlerde olduğu gibi; paralelkenarın alanı, köşegenlerin uzunlukları ile aralarındaki açının sinüs değerinin çarpımının yarısına eşittir. Birbirini 180°'ye tamamlayan açıların sinüs değerleri eşit olduğu için, köşegenlerin arasında oluşan bütünler açıların ikisi de aynı sonucu verir. Aşağıda bu formülün tüm dörtgenler için geçerli olan ispatı verilmiştir.
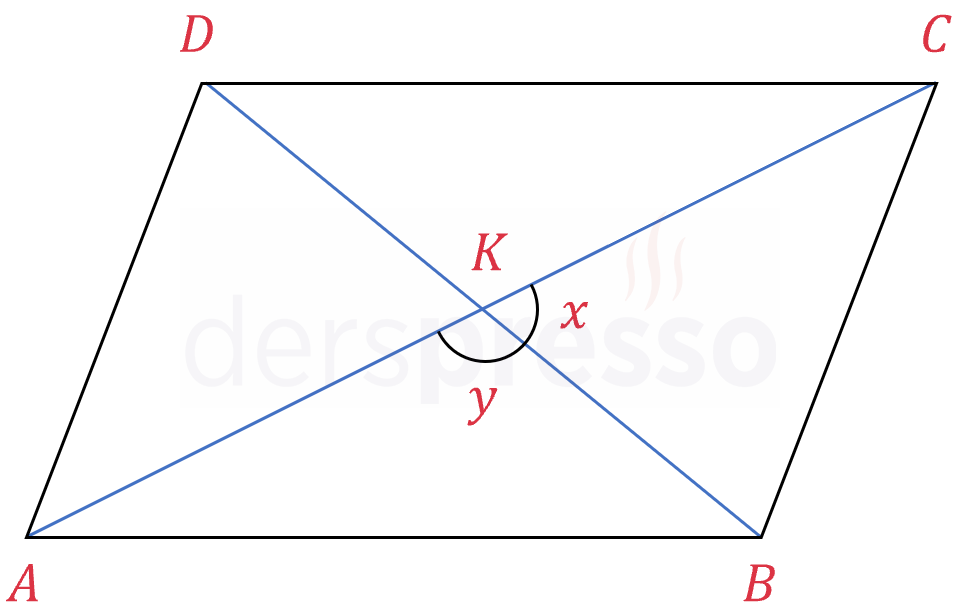
\( A(ABCD) = \dfrac{1}{2} \abs{AC} \cdot \abs{BD} \cdot \sin{x} \)
\( A(ABCD) = \dfrac{1}{2} \abs{AC} \cdot \abs{BD} \cdot \sin{y} \)
İSPATI GÖSTER
KONVEKS DÖRTGEN:
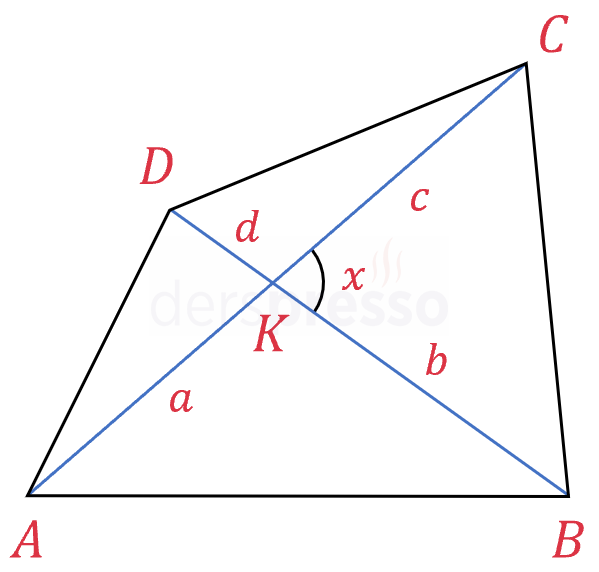
Köşegenlerin ayırdığı dört üçgenin alanlarını sinüs alan formülünü kullanarak hesaplayalım.
\( A(\overset{\triangle}{KAB}) = \dfrac{1}{2} \cdot a \cdot b \cdot \sin(180° - x) \)
\( A(\overset{\triangle}{KBC}) = \dfrac{1}{2} \cdot b \cdot c \cdot \sin{x} \)
\( A(\overset{\triangle}{KCD}) = \dfrac{1}{2} \cdot c \cdot d \cdot \sin(180° - x) \)
\( A(\overset{\triangle}{KDA}) = \dfrac{1}{2} \cdot d \cdot a \cdot \sin{x} \)
Bütünler açıların sinüs değerleri eşittir.
\( \sin{x} = \sin(180° - x) \)
Dört üçgenin alanlarını toplayarak dörtgenin alanını bulalım.
\( A(ABCD) = \dfrac{1}{2} \cdot \sin{x} \cdot (a \cdot b + b \cdot c \) \( + c \cdot d + d \cdot a) \)
\( = \dfrac{1}{2} \cdot \sin{x} \cdot [b \cdot (a + c) + d \cdot (a + c)] \)
\( = \dfrac{1}{2} \cdot \sin{x} \cdot (a + c) \cdot (b + d) \)
\( = \dfrac{1}{2} \cdot \abs{AC} \cdot \abs{BD} \cdot \sin{x} \)
KONKAV DÖRTGEN:
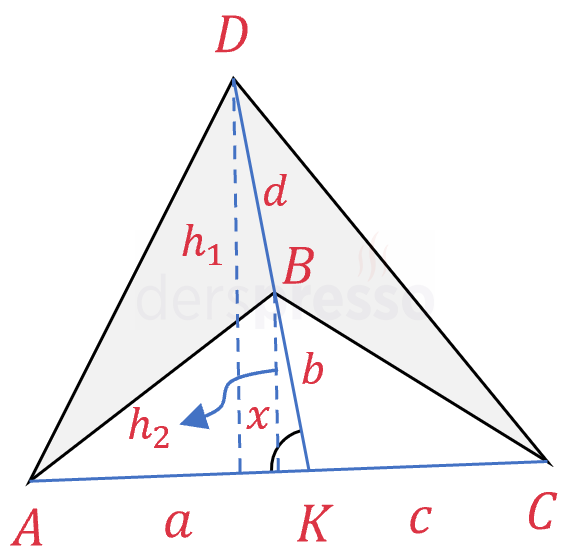
Şekilde oluşan iki üçgenin alanlarını bulalım:
Büyük üçgenin alanı:
\( A(\overset{\triangle}{ACD}) = \dfrac{(a + c) \cdot h_1}{2} \)
\( = \dfrac{(a + c) \cdot (b + d) \cdot \sin{x}}{2} \)
Küçük üçgenin alanı:
\( A(\overset{\triangle}{ACB}) = \dfrac{(a + c) \cdot h_2}{2} \)
\( = \dfrac{(a + c) \cdot b \cdot \sin{x}}{2} \)
Gri renk ile işaretlenmiş konkav dörtgenin alanını, büyük ve küçük üçgenler cinsinden yazalım.
\( A(ABCD) = A(\overset{\triangle}{ACD}) - A(\overset{\triangle}{ACB}) \)
\( = \dfrac{(a + c) \cdot (b + d) \cdot \sin{x}}{2} \) \( - \dfrac{(a + c) \cdot b \cdot \sin{x}}{2}\)
\( = \dfrac{(a + c) \cdot d \cdot \sin{x}}{2} \)
\( = \dfrac{1}{2} \cdot \abs{AC} \cdot \abs{BD} \cdot \sin{x} \)
Bir diğer formüle göre; paralelkenarın alanı, komşu iki kenarın uzunlukları ile aralarındaki açının sinüs değerinin çarpımına eşittir. Birbirini 180°'ye tamamlayan açıların sinüs değerleri eşit olduğu için, hangi iki komşu kenar seçilirse seçilsin aynı sonuç elde edilir.

\( A(ABCD) = a \cdot b \cdot \sin{x} \)
\( A(ABCD) = a \cdot b \cdot \sin{y} \)
İSPATI GÖSTER
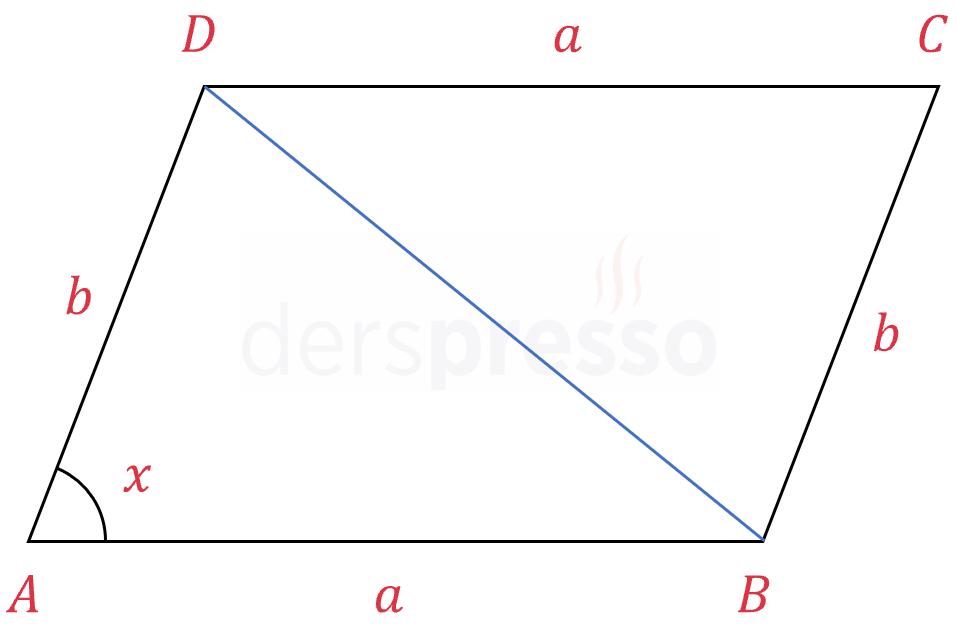
Paralelkenarın \( [BD] \) köşegenini çizelim.
Sinüs alan formülünü kullanarak \( ABD \) üçgeninin alanını bulalım.
\( A(ABD) = \dfrac{1}{2} a \cdot b \cdot \sin{x} \)
Aynı formülü kullanarak \( CBD \) üçgeninin alanını bulalım.
\( A(CBD) = \dfrac{1}{2} a \cdot b \cdot \sin{x} \)
Paralelkenarın alanı bu iki üçgenin alanları toplamına eşittir.
\( A(ABCD) = A(ABD) + A(CBD) \)
\( = a \cdot b \cdot \sin{x} \)
Paralelkenarın her bir köşegeni paralelkenarı iki eş üçgene ayırır.

\( \overset{\triangle}{ABC} \cong \overset{\triangle}{CDA} \)
\( A(ABC) = A(CDA) \)
\( \overset{\triangle}{KLN} \cong \overset{\triangle}{MNL} \)
\( A(KLN) = A(MNL) \)
İSPATI GÖSTER
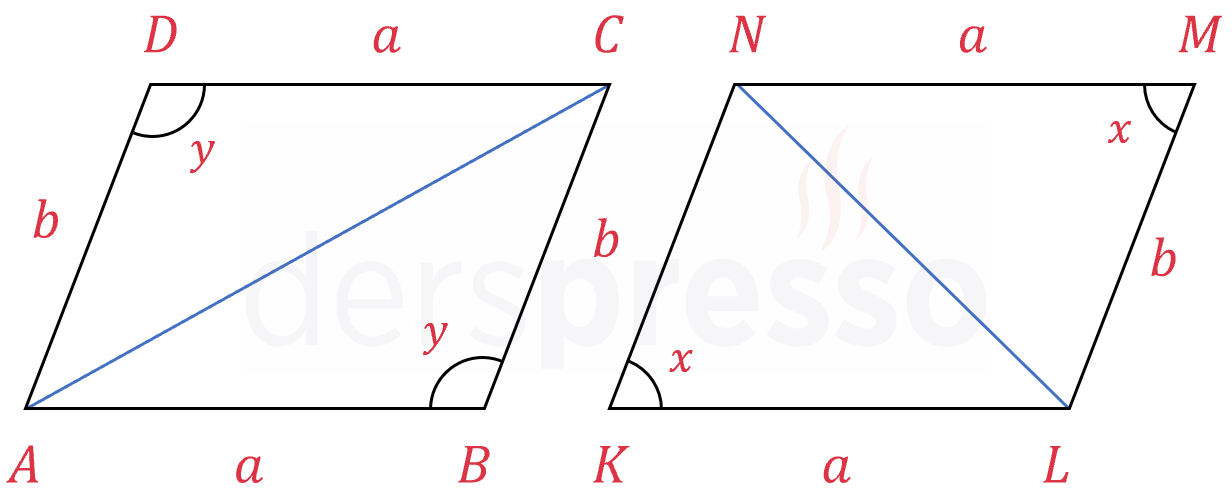
\( ABCD \) Dörtgeni:
\( [AC] \) köşegeninin ayırdığı iki üçgenin alanını sinüs alan formülü ile ayrı ayrı bulalım.
\( A(ABC) = \dfrac{1}{2} \cdot a \cdot b \cdot \sin{y} \)
\( A(ADC) = \dfrac{1}{2} \cdot a \cdot b \cdot \sin{y} \)
Buna göre köşegeninin ayırdığı iki üçgenin alanı birbirine eşittir.
\( KLMN \) Dörtgeni:
\( [LN] \) köşegeninin ayırdığı iki üçgenin alanını sinüs alan formülü ile ayrı ayrı bulalım.
\( A(KLN) = \dfrac{1}{2} \cdot a \cdot b \cdot \sin{x} \)
\( A(LMN) = \dfrac{1}{2} \cdot a \cdot b \cdot \sin{x} \)
Buna göre köşegeninin ayırdığı iki üçgenin alanı birbirine eşittir.
Paralelkenarın köşegenleri birbirini ortaladığı için, aynı zamanda paralelkenarın alanını dört eşit parçaya bölerler.

\( A(ABK) = A(BCK) = A(CDK) \) \( = A(ADK) \)
İSPATI GÖSTER
\( ABC \) üçgeni paralelkenarla aynı tabana ve yüksekliğe sahip olduğu için, alanı paralelkenarın alanının yarısıdır.
\( A(ABC) = A(ADC) = \frac{1}{2} A(ABCD) \)
Paralelkenarda köşegenler birbirini ortaladığı için, \( ABK \) ve \( BCK \) üçgenlerinin \( [AC] \) köşegeni üzerindeki taban uzunlukları eşittir.
\( \abs{AK} = \abs{KC} \)
Bu iki üçgenin tepe noktaları aynı (\( B \) noktası) ve yükseklikleri eşit olduğu için, alanları da eşittir.
\( A(ABK) = A(BCK) = \frac{1}{2} A(ABC) \)
Paralelkenarın köşegenlerinin oluşturduğu aşağıdaki üçgenler, tüm kenar uzunlukları ve açı ölçüleri eşit olduğu için eş üçgenlerdir.
\( \overset{\triangle}{ABK} \cong \overset{\triangle}{CDK} \), \( \quad \overset{\triangle}{BCK} \cong \overset{\triangle}{DAK} \)
\( \overset{\triangle}{ABC} \cong \overset{\triangle}{CDA} \), \( \quad \overset{\triangle}{ABD} \cong \overset{\triangle}{CDB} \)
Paralelkenarın bir köşegeni üzerindeki herhangi bir noktadan (\( K \) noktası) kenarlara paralel çizilen doğru parçalarının oluşturduğu altı bölgeden karşılıklı bölgelerin alanları birbirine eşittir.
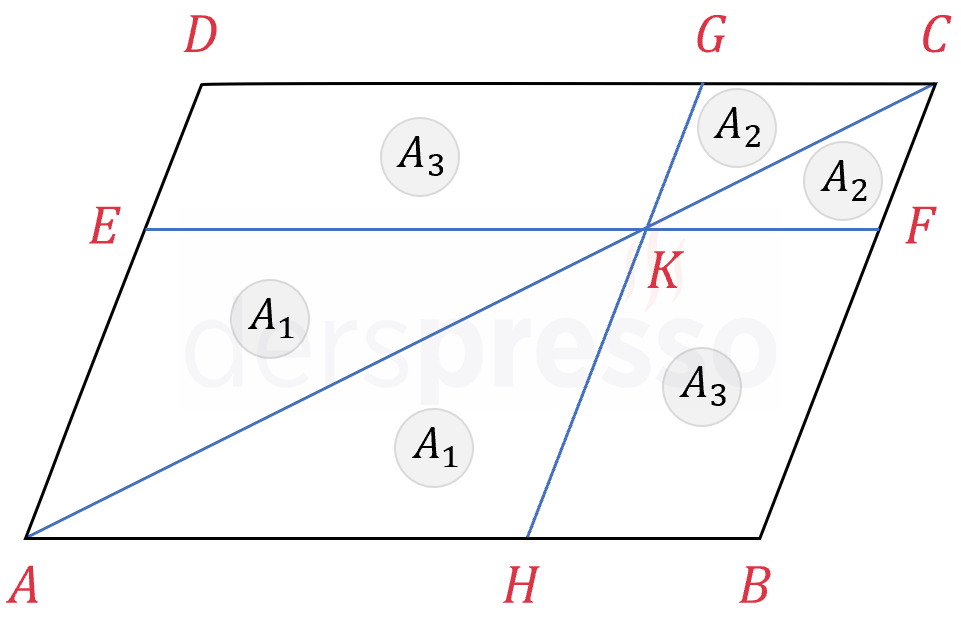
\( A(AHK) = A(AEK) \)
\( A(KFC) = A(KGC) \)
\( A(HBFK) = A(EKGD) \)
İSPATI GÖSTER
\( [EF] \parallel [DC] \) ve \( [HG] \parallel [AD] \) olduğu için oluşan \( AHKE \), \( KFCG \), \( HBFK \) ve \( EKGD \) dörtgenleri de birer paralelkenardır.
\( [AK] \) doğru parçası \( AHKE \) paralelkenarının köşegeni olduğu için paralelkenarın alanını iki eşit parçaya böler.
\( A(AHK) = A(AEK) = A_1 \)
\( [KC] \) doğru parçası \( KFCG \) paralelkenarının köşegeni olduğu için paralelkenarın alanını iki eşit parçaya böler.
\( A(KFC) = A(KGC) = A_2 \)
\( [AC] \) doğru parçası \( ABCD \) paralelkenarının köşegeni olduğu için paralelkenarın alanını iki eşit parçaya böler.
\( A(ABC) = A(ADC) \)
\( A(AHK) + A(HBFK) + A(KFC) = A(AEK) + A(EDGK) + A(KGC) \)
\( A_1 + A(HBFK) + A_2 = A_1 + A(EDGK) + A_2 \)
\( A(HBFK) = A(EDGK) = A_3 \)
Paralelkenarın bir köşegeni üzerindeki herhangi bir noktaya (\( K \) noktası) diğer iki köşeden çizilen doğru parçalarının oluşturduğu dört bölgeden karşılıklı bölgelerin alanları birbirine eşittir.
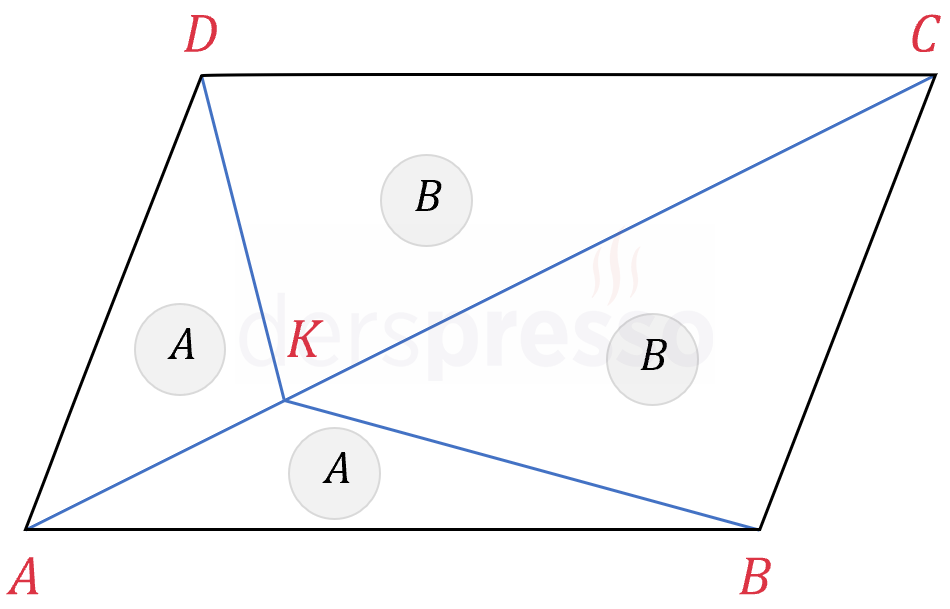
\( A(ABK) = A(ADK) \)
\( A(CBK) = A(CDK) \)
İSPATI GÖSTER
Yukarıda ispatını verdiğimiz üzere, paralelkenarın her bir köşegeni paralelkenarı iki eş üçgene ayırır.
\( A(ABC) = A(ADC) \)
Alanları eşit bu iki üçgende \( [AC] \) kenarı ortak olduğu için bu kenara ait yükseklikler de eşittir.
\( h_b = h_d \)

Buna göre taban uzunlukları (\( \abs{AK} \) ve \( \abs{KC} \)) ve yükseklikleri (\( h_b \) ve \( h_d \)) eşit olan aşağıdaki üçgenlerin alanları eşit olur.
\( A(ABK) = A(ADK) \)
\( A(CBK) = A(CDK) \)
Paralelkenarın içindeki herhangi bir noktadan (\( K \) noktası) köşelere çizilen doğru parçalarının oluşturduğu dört bölgeden karşılıklı bölgelerin alanları toplamı birbirine eşittir.
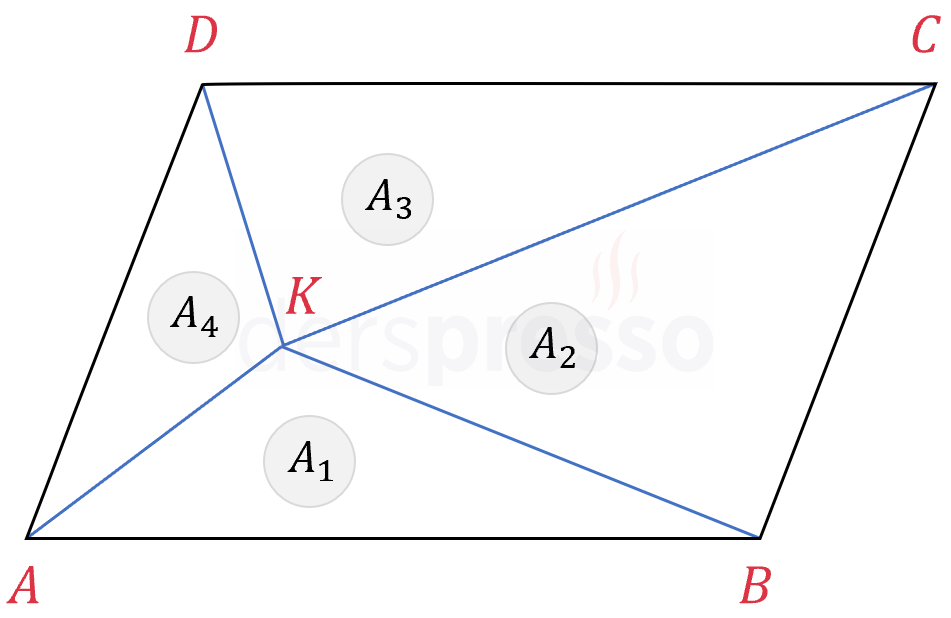
\( A_1 + A_3 = A_2 + A_4 \)
İSPATI GÖSTER
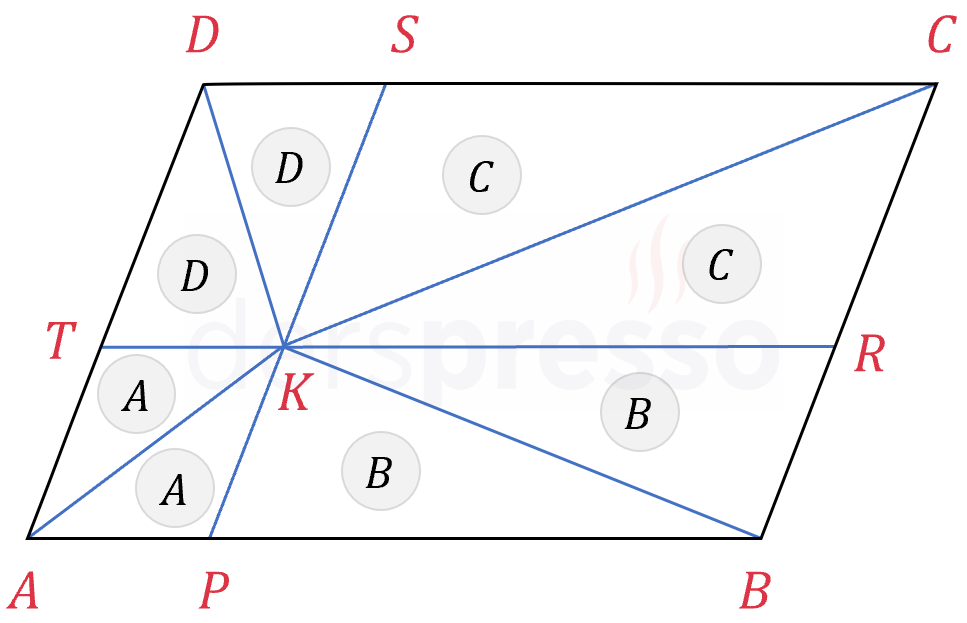
\( K \) noktasından kenarlara paralel doğrular çizelim.
Oluşan şekilde büyük paralelkenar dört küçük paralelkenara bölünmüş olur ve \( K \) noktasından köşelere çizilen doğru parçaları küçük paralelkenarların köşegeni olur ve her paralelkenarın alanını iki eşit parçaya böler.
\( A(\overset{\triangle}{APK}) = A(\overset{\triangle}{ATK}) = A \)
\( A(\overset{\triangle}{BPK}) = A(\overset{\triangle}{BRK}) = B \)
\( A(\overset{\triangle}{CRK}) = A(\overset{\triangle}{CSK}) = C \)
\( A(\overset{\triangle}{DSK}) = A(\overset{\triangle}{DTK}) = D \)
\( A_1 \), \( A_2 \), \( A_3 \) ve \( A_4 \) bölgelerinin alanlarını yukarıdaki alanlar cinsiden yazarsak karşılıklı bölgelerin alanları toplamının eşit olduğunu görebiliriz.
\( A_1 = A + B \)
\( A_2 = B + C \)
\( A_3 = C + D \)
\( A_4 = D + A \)
\( A_1 + A_3 = A + B + C + D \)
\( A_2 + A_4 = A + B + C + D \)
\( A_1 + A_3 = A_2 + A_4 \)
Komşu iki köşeden karşı paralel kenar üzerindeki herhangi bir noktaya çizilen doğru parçalarının oluşturduğu üçgenin alanı, paralelkenarın alanının yarısına eşittir.
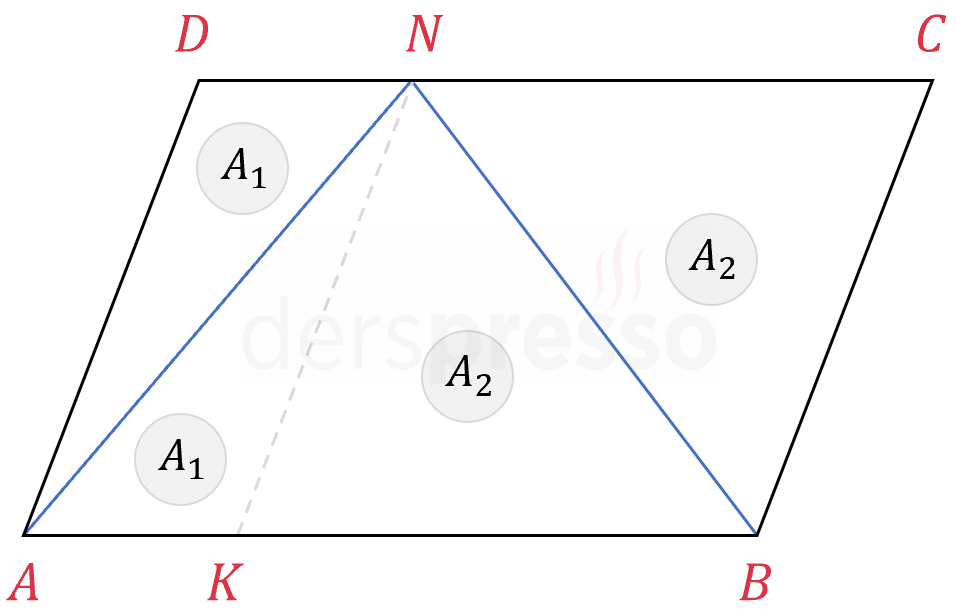
\( A(ABN) = \frac{1}{2} A(ABCD) \)
İSPATI GÖSTER
Doğru parçalarının karşı kenarda kestiği nokta olan \( N \)'den yan kenarlara paralel bir doğru çizersek (kesikli gri doğru), oluşan dört üçgenin alanları arasında aşağıdaki gibi eşitlik olduğunu görürüz.
\( A(\overset{\triangle}{AKN}) = A(\overset{\triangle}{ADN}) = A_1 \)
\( A(\overset{\triangle}{BKN}) = A(\overset{\triangle}{BCN}) = A_2 \)
Yukarıda \( [AC] \) köşegenini üç eşit parçaya böldüğünü gösterdiğimiz \( [DN] \) ve \( [DP] \) doğru parçaları, paralelkenarın alanını aşağıda belirtilen oranlarda böler.
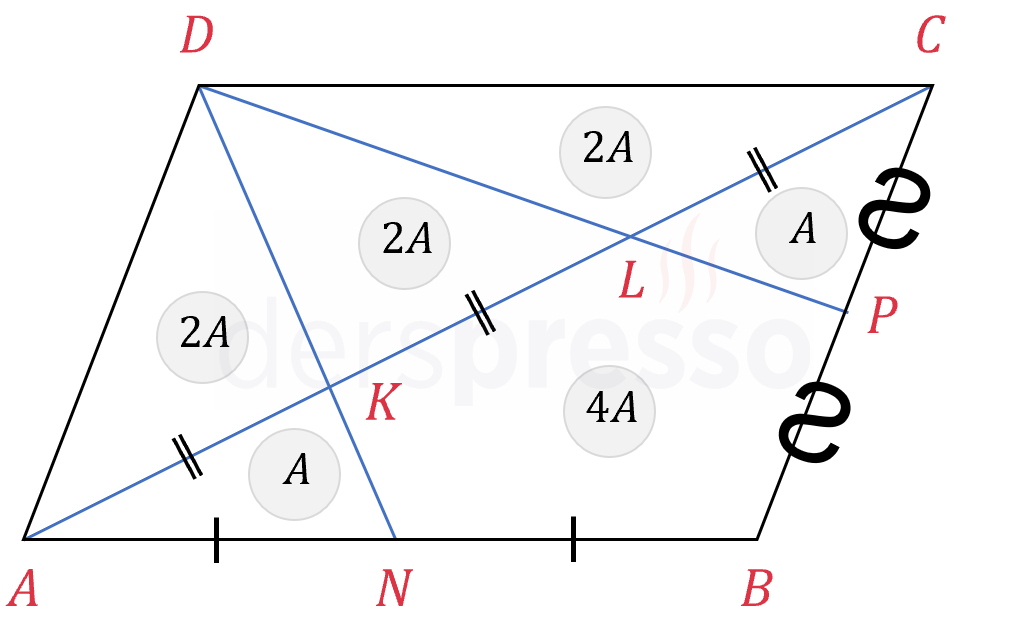
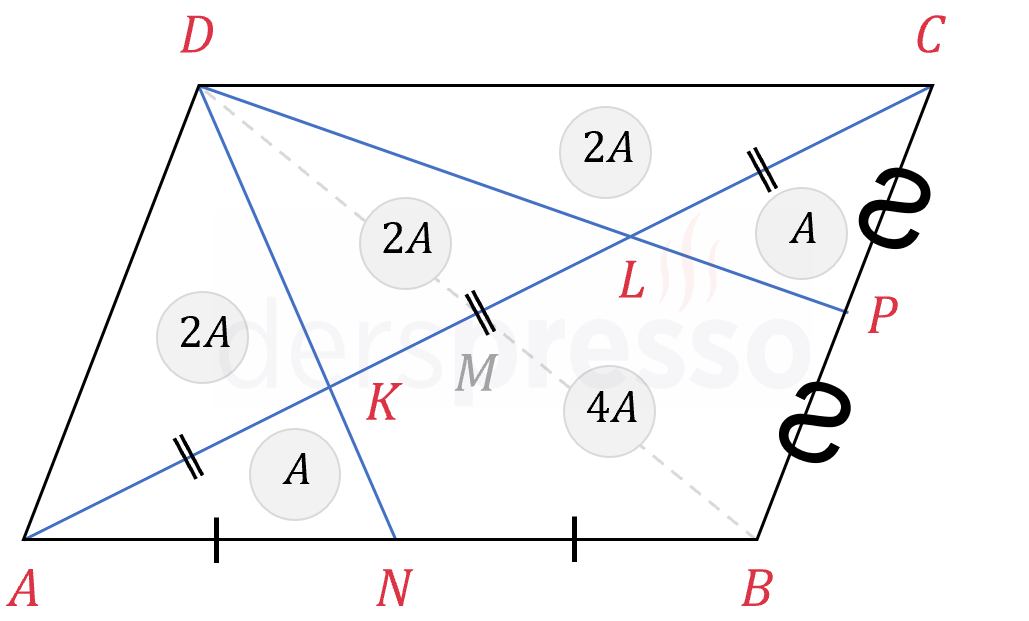
Paralelkenarın diğer köşegenini de çizelim (kesikli gri doğru).
\( A(\overset{\triangle}{AKN}) = A \) diyelim.
\( \overset{\triangle}{ABD} \) üçgeninin ağırlık merkezi olan \( K \) noktası, \( \overset{\triangle}{ADN} \) üçgeninin bir tabanı olan \( [DN] \) doğru parçasını 2:1 oranında böler.
\( A(\overset{\triangle}{ADK}) = 2A \)
\( K \) ve \( L \) noktaları \( [AC] \) köşegenini üç eşit parçaya böler, dolayısıyla tabanları ve yükseklikleri eşit üç üçgen oluşur.
\( A(\overset{\triangle}{DKL}) = 2A \)
\( A(\overset{\triangle}{CDL}) = 2A \)
\( \overset{\triangle}{BCD} \) üçgeninin ağırlık merkezi olan \( L \) noktası \( [DP] \) doğru parçasını 2:1 oranında böler.
\( A(\overset{\triangle}{CLP}) = A \)
\( [AC] \) köşegeni paralelkenarın alanını iki eşit parçaya böldüğü için, beşgen şekil için kalan alan 4A'dır.
\( A(KLPBN) = 6A - A - A = 4A \)
Yukarıda \( [AC] \) köşegenini üç eşit parçaya böldüğünü gösterdiğimiz \( [DN] \) ve \( [BT] \) doğru parçaları, paralelkenarın alanını aşağıda belirtilen oranlarda böler.
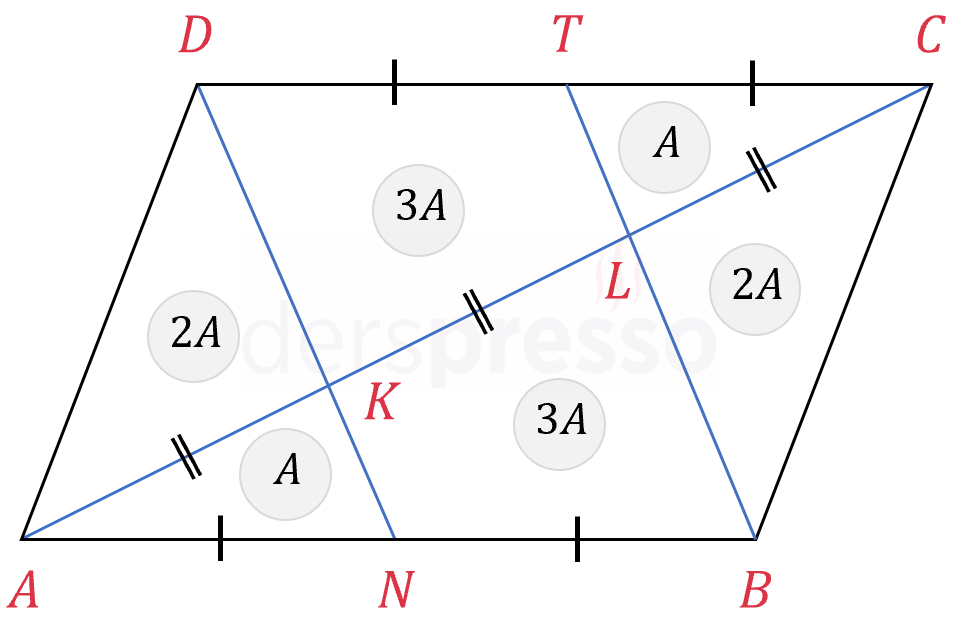
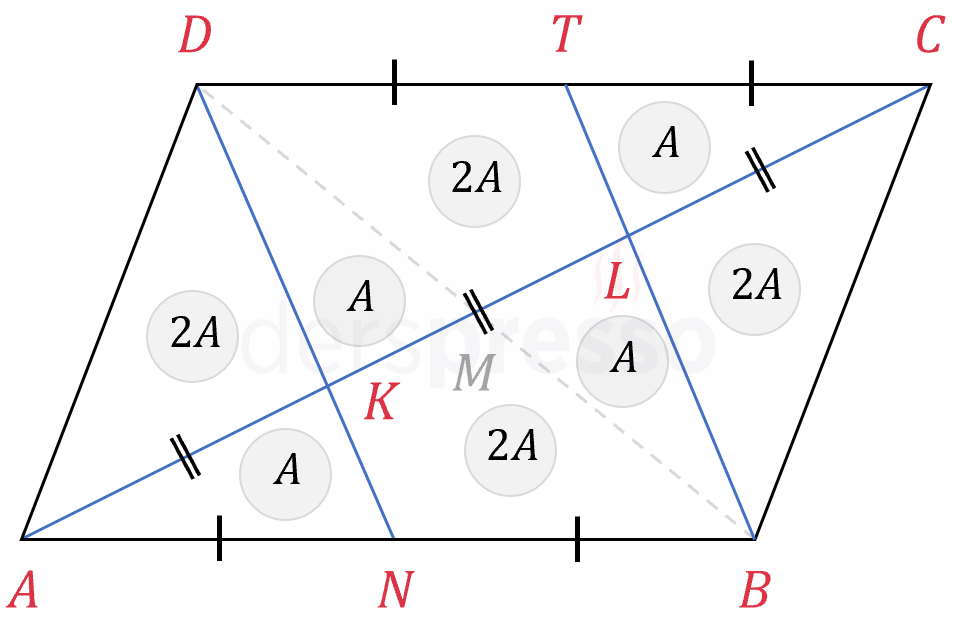
Paralelkenarın diğer köşegenini de çizelim (kesikli gri doğru).
\( A(\overset{\triangle}{AKN}) = A \) diyelim.
\( \overset{\triangle}{ABD} \) üçgeninin ağırlık merkezi olan \( K \) noktası, \( \overset{\triangle}{ADN} \) üçgeninin bir tabanı olan \( [DN] \) doğru parçasını 2:1 oranında böler.
\( A(\overset{\triangle}{ADK}) = 2A \)
\( \overset{\triangle}{ABD} \) üçgeninin ağırlık merkezi olan \( K \) noktası, \( \overset{\triangle}{ADM} \) üçgeninin bir tabanı olan \( [AM] \) doğru parçasını 2:1 oranında böler.
\( A(\overset{\triangle}{DKM}) = A \)
\( \overset{\triangle}{AKN} \) ve \( \overset{\triangle}{CLT} \) üçgenleri eş üçgenlerdir (iki kenar uzunluğu ve aralarındaki açı eşit).
\( A(\overset{\triangle}{CLT}) = A \)
Paralelkenarın köşegenleri birbirini ortaladığı için, \( \overset{\triangle}{ADM} \) ve \( \overset{\triangle}{CDM} \) üçgenlerinin alanları eşittir.
\( A(DMLT) = 2A \)
\( \overset{\triangle}{BCD} \) üçgeninin ağırlık merkezi olan \( L \) noktası, \( \overset{\triangle}{BCT} \) üçgeninin bir tabanı olan \( [BT] \) doğru parçasını 2:1 oranında böler.
\( A(\overset{\triangle}{BCL}) = 2A \)
\( \overset{\triangle}{BCD} \) üçgeninin ağırlık merkezi olan \( L \) noktası, \( \overset{\triangle}{BCM} \) üçgeninin bir tabanı olan \( [CM] \) doğru parçasını 2:1 oranında böler.
\( A(\overset{\triangle}{BLM}) = A \)
\( [AC] \) köşegeni paralelkenarın alanını iki eşit parçaya böldüğü için, dörtgen şekil için kalan alan 4A'dır.
\( A(BNKM) = 6A - 2A - A - A = 2A \)
Bir paralelkenarın köşe ve kenarları arasında şekildeki gibi çizilen doğru parçaları, paralelkenarın alanını aşağıda belirtilen oranlarda böler.

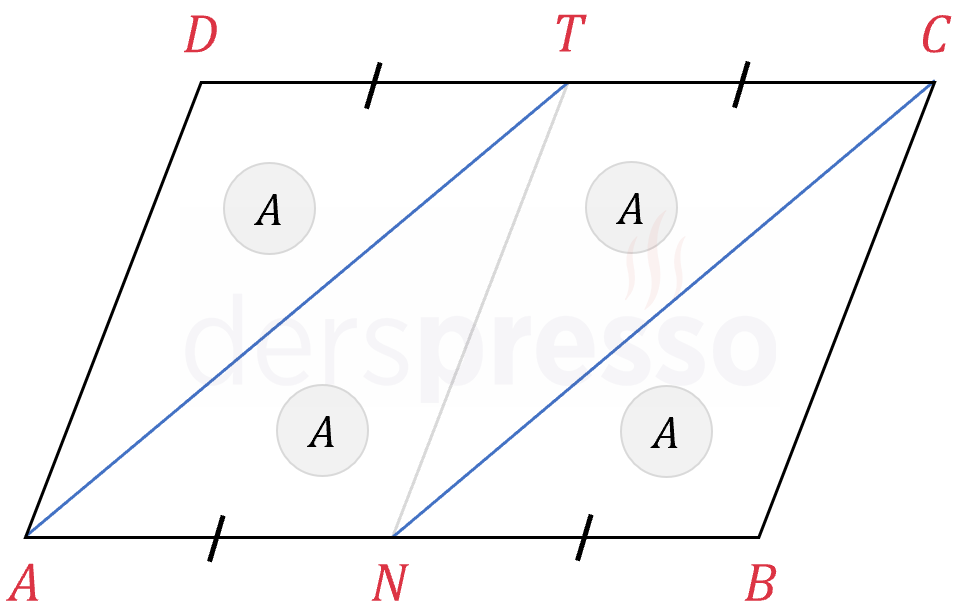
\( N \) ve \( T \) noktalarını bir doğru parçası ile birleştirelim.
\( ANTD \) ve \( NBCT \) tabanları ve yükseklikleri eşit iki eş paralelkenar olur.
\( A(ANTD) = A(NBCT) \)
\( [AT] \) ve \( [NC] \) doğru parçaları bu iki paralelkenarın köşegenleri olduğu için ilgili paralelkenarların alanlarını iki eşit parçaya böler.
\( A(\overset{\triangle}{ADT}) = A(\overset{\triangle}{ANT}) = A \)
\( A(\overset{\triangle}{NBC}) = A(\overset{\triangle}{NTC}) = A \)
Buna göre \( ANCT \) paralelkenarının alanı \( 2A \) olur.
\( A(ANCT) = A + A = 2A \)
Bir paralelkenarın birer köşesini köşe kabul eden üçgenlerin alanları bu köşelere komşu kenar uzunluklarının çarpımı ile doğru orantılıdır.
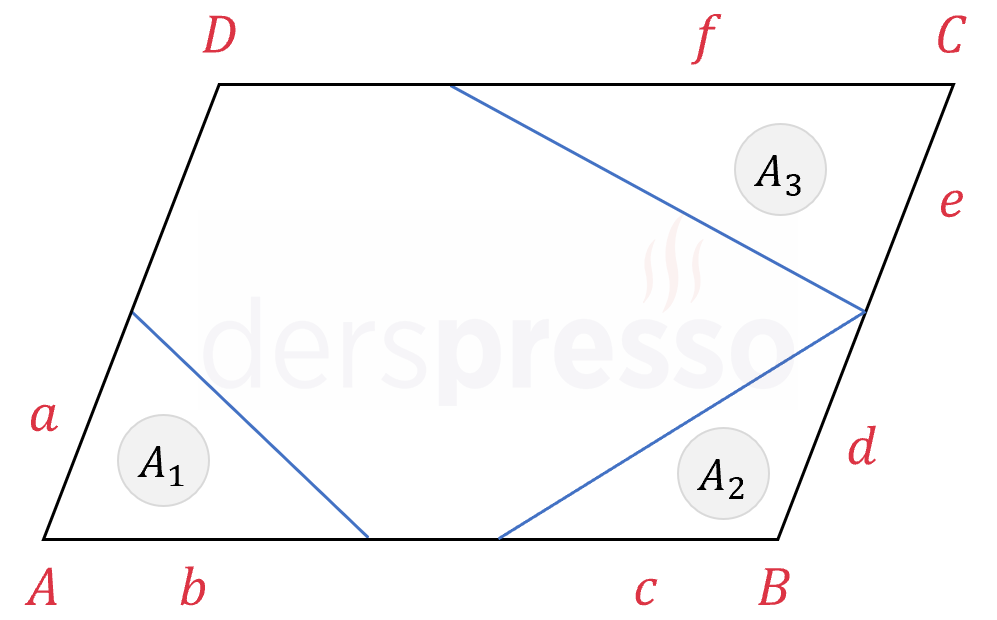
\( \dfrac{A_1}{a \cdot b} = \dfrac{A_2}{c \cdot d} = \dfrac{A_3}{e \cdot f} \)
İSPATI GÖSTER
Sinüs alan formülü ile \( A_1 \), \( A_2 \) ve \( A_3 \) alanlarını yazalım.
\( A_1 = \frac{1}{2} a \cdot b \cdot \sin{\widehat{A}} \)
\( A_2 = \frac{1}{2} c \cdot d \cdot \sin{\widehat{B}} \)
\( A_3 = \frac{1}{2} e \cdot f \cdot \sin{\widehat{C}} \)
Paralelkenarda karşılıklı köşelerin açıları eş, komşu köşelerin açıları bütünlerdir.
\( m(\widehat{A}) = m(\widehat{C}) \)
\( m(\widehat{B}) = m(\widehat{D}) \)
Bütünler açıların sinüs değerleri eşittir.
Buna göre paralelkenarın tüm köşelerinin sinüs değerleri eşittir.
\( \sin{\widehat{A}} = \sin{\widehat{B}} = \sin{\widehat{C}} = \sin{\widehat{D}} \)
\( A_1 = \frac{1}{2} a \cdot b \cdot \sin{\widehat{A}} \)
\( A_2 = \frac{1}{2} c \cdot d \cdot \sin{\widehat{A}} \)
\( A_3 = \frac{1}{2} e \cdot f \cdot \sin{\widehat{A}} \)
Üç eşitlikte de \( \sin{\widehat{A}} \) ifadesini yalnız bıraktığımızda alanlarla kenar uzunluklarının çarpımı arasındaki orantıyı elde ederiz.
\( \dfrac{A_1}{a \cdot b} = \dfrac{A_2}{c \cdot d} = \dfrac{A_3}{e \cdot f} = \dfrac{\sin{\widehat{A}}}{2} \)