Yamuk
Karşılıklı iki kenarı birbirine paralel olan dörtgene yamuk denir.

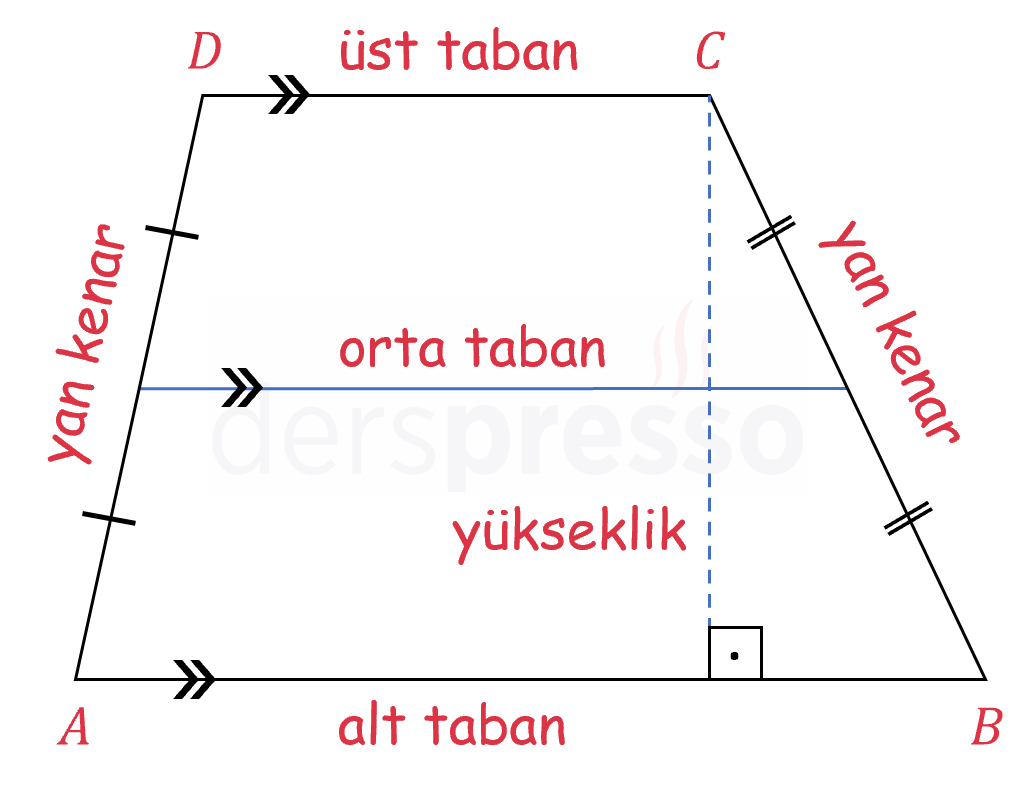
Bir yamuğun paralel kenarlarına üst taban ve alt taban, paralel olmayan kenarlarına yan kenar, yan kenarların orta noktalarını birleştiren doğru parçasına orta taban, tabanları birleştiren dikmeye yükseklik denir.
Bir dörtgenin aşağıdaki özelliklerden en az birini taşıdığı biliniyorsa bu dörtgen bir yamuktur ve diğer özellikleri de taşır.
- Karşılıklı iki kenar paralel (yamuk tanımı)
- Komşu iki köşenin açıları bütünler
Yamuk bir dörtgen olduğu için, dörtgenler bölümünde bahsettiğimiz tüm özellikler yamuk için de geçerlidir.
Giriş bölümünde paylaştığımız dörtgen hiyerarşisine göre; paralelkenar, eşkenar dörtgen, dikdörtgen ve kare yamuğun ek özelliklere sahip özel birer durumu olarak düşünülebilir.
Yamuğun Kenar ve Köşegen Özellikleri
Yamuğun alt ve üst tabanları birbirine paraleldir.
\( [AB] \parallel [DC] \)
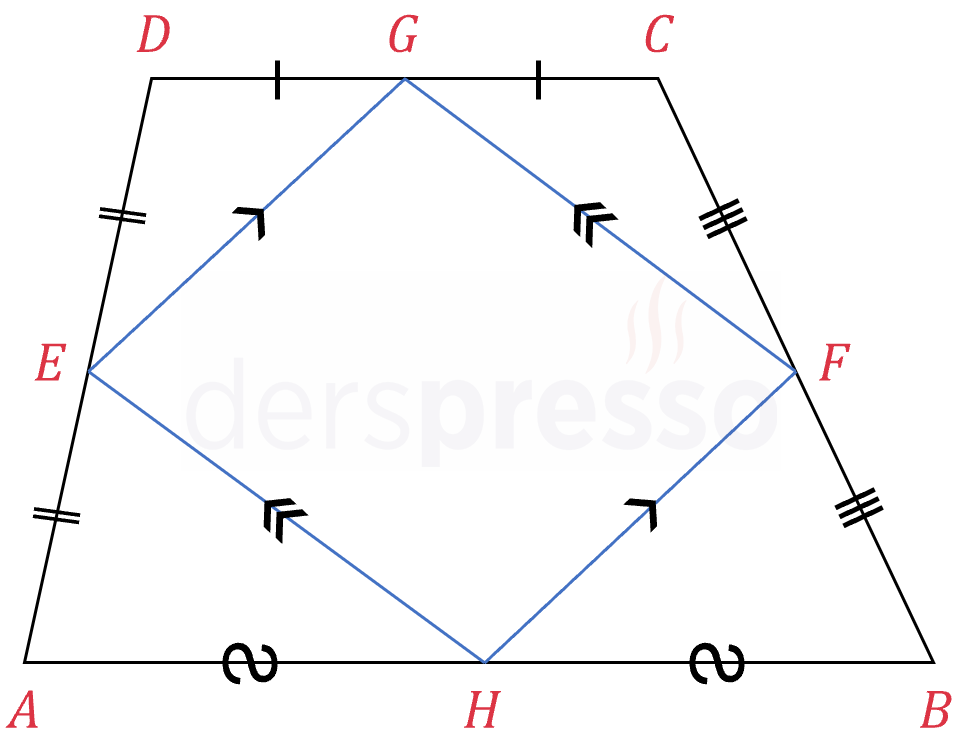
Tüm dörtgenlerde olduğu gibi, yamuğun kenar orta noktalarının birleştirilmesiyle oluşan dörtgen bir paralelkenardır. Varignon paralelkenarı adı verilen bu dörtgenle ilgili daha fazla bilgi ve yamukta da geçerli olan özellikleri için dörtgenler sayfasını inceleyebilirsiniz.
Yamuğun yan kenarlarının orta noktalarını birleştiren orta tabanın uzunluğu alt ve üst taban uzunluklarının yarısına eşittir.
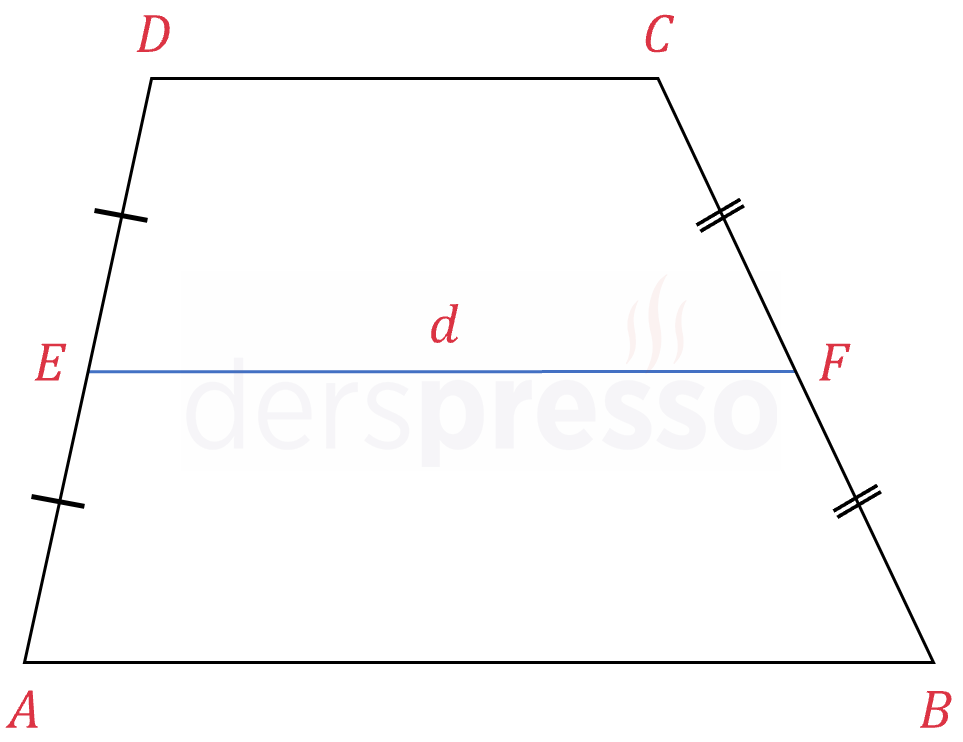
\( [EF] \) orta taban olmak üzere,
\( d = \dfrac{\abs{AB} + \abs{DC}}{2} \)
İSPATI GÖSTER
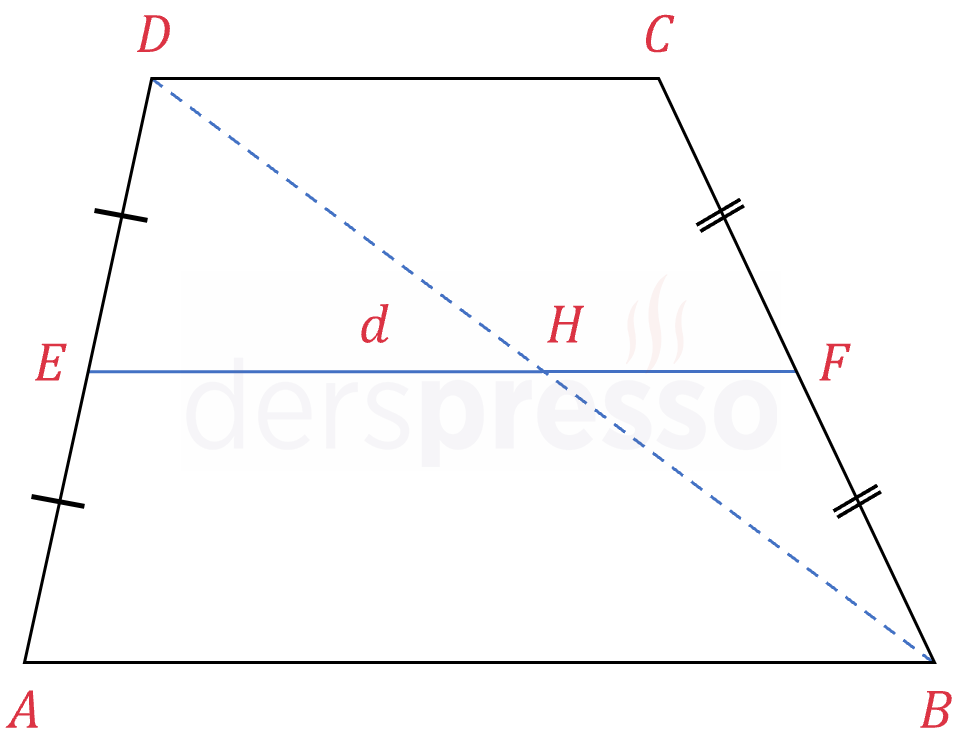
\( \dfrac{[DE]}{[EA]} = \dfrac{[CF]}{[FB]} \) olduğundan,
\( [DC] \parallel [EF] \parallel [AB] \) olur.
\( ABCD \) yamuğunun \( DB \) köşegenini çizelim (mavi kesikli çizgi).
\( ABD \) üçgenine temel orantı teoremini uygulayalım.
\( \dfrac{\abs{DE}}{\abs{DA}} = \dfrac{\abs{EH}}{\abs{AB}} = \dfrac{1}{2} \)
\( \abs{EH} = \dfrac{\abs{AB}}{2} \)
\( BCD \) üçgenine temel orantı teoremini uygulayalım.
\( \dfrac{\abs{BF}}{\abs{BC}} = \dfrac{\abs{HF}}{\abs{DC}} = \dfrac{1}{2} \)
\( \abs{HF} = \dfrac{\abs{DC}}{2} \)
Orta taban uzunluğunu yazalım.
\( \abs{EF} = d = \abs{EH} + \abs{HF} \)
\( = \dfrac{\abs{AB}}{2} + \dfrac{\abs{DC}}{2} = \dfrac{\abs{AB} + \abs{DC}}{2} \)
Orta taban yamuğun yükseklik ve köşegenlerini de ortalar.
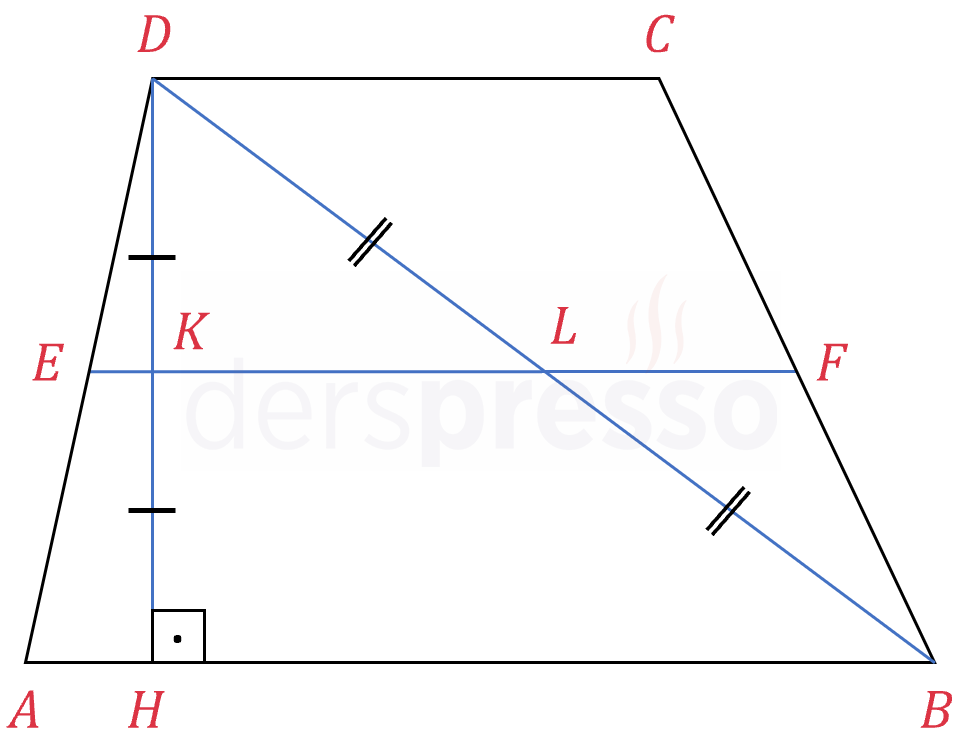
\( [EF] \) orta taban olmak üzere,
\( \abs{DL} = \abs{LB} \)
\( \abs{DK} = \abs{KH} \)
İSPATI GÖSTER
\( [EF] \) yamuğun orta tabanı olduğu için alt ve üst tabana paraleldir.
\( [EF] \parallel [AB] \parallel [DC] \)
\( [EF] \) yamuğun orta tabanı olduğu için yan kenarları ortalar.
\( \abs{DE} = \abs{EA} \)
\( \abs{CF} = \abs{FB} \)
Önce \( ADB \) üçgenini inceleyelim.
\( [EL] \) doğru parçasının üçgenin tabanına paralel olduğunu ve \( [DA] \) kenarını ortaladığını gösterdik.
Üçgenler konusunda gördüğümüz orta taban teoremine göre, bir üçgenin bir yan kenarının orta noktasından tabana paralel çizilen doğru parçası üçgenin orta tabanı olur ve diğer yan kenarı ortalar.
\( \abs{DL} = \abs{LB} \)
Şimdi \( DAH \) üçgenini inceleyelim.
\( [EK] \) doğru parçasının üçgenin tabanına paralel olduğunu ve \( [DA] \) kenarını ortaladığını gösterdik.
Orta taban teoremine göre, bir üçgenin bir yan kenarının orta noktasından tabana paralel çizilen doğru parçası üçgenin orta tabanı olur ve diğer yan kenarı ortalar.
\( \abs{DK} = \abs{KH} \)
Bir yamuğun köşegenlerinin orta tabanı kestiği noktalar arasındaki uzaklık aşağıdaki formülle bulunur.
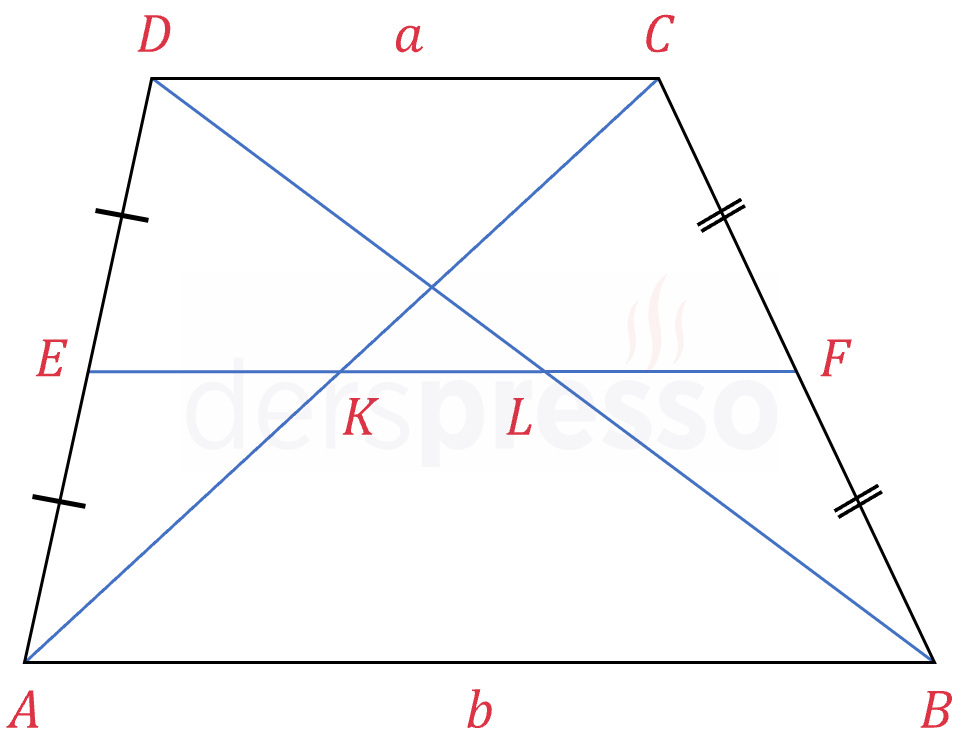
\( [EF] \) orta taban olmak üzere,
\( \abs{KL} = \dfrac{b - a}{2} \)
İSPATI GÖSTER
\( [EL] \) doğru parçası \( DAB \) üçgeninin orta tabanı olduğu için uzunluğu taban uzunluğunun yarısıdır.
\( \abs{EL} = \dfrac{b}{2} \)
\( [EK] \) doğru parçası \( DAC \) üçgeninin orta tabanı olduğu için uzunluğu taban uzunluğunun yarısıdır.
\( \abs{EK} = \dfrac{a}{2} \)
Köşegenlerin orta tabanı kestiği noktalar arasındaki doğru parçasının uzunluğunu yazalım.
\( \abs{KL} = \abs{EL} - \abs{EK} \)
\( = \dfrac{b}{2} - \dfrac{a}{2} \)
\( = \dfrac{b - a}{2} \)
Yamuğun Açı Özellikleri
Tüm dörtgenlerde olduğu gibi, yamuğun hem iç açıları hem de dış açıları toplamı 360°'dir.

Yamuğun yan kenarları üzerindeki komşu köşe açıları bütünler açılardır.
\( a + d = 180° \)
\( b + c = 180° \)
İSPATI GÖSTER
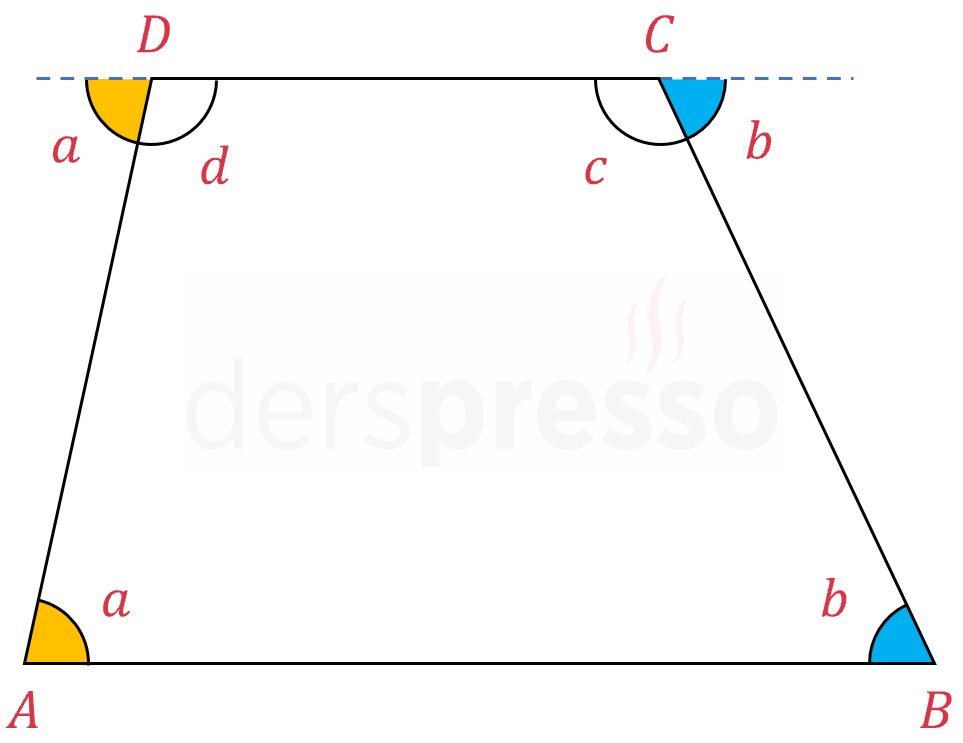
\( ABCD \) yamuğunun üst kenarını uzatalım (mavi kesikli çizgi).
\( D \) köşesinin komşu bütünler açısı ve \( A \) köşesinin açısı iç ters açılar olduğu için ölçüleri birbirine eşittir ve \( a \)'dır.
\( C \) köşesinin komşu bütünler açısı ve \( B \) köşesinin açısı iç ters açılar olduğu için ölçüleri birbirine eşittir ve \( b \)'dir.
Buna göre yamuğun yan kenarları üzerindeki karşı durumlu açılarının toplamı 180° olur.
\( a + d = 180° \)
\( b + c = 180° \)
Yamuğun yan kenarları üzerindeki komşu köşelerin açıortayları birbirini orta taban üzerinde ve dik keser.
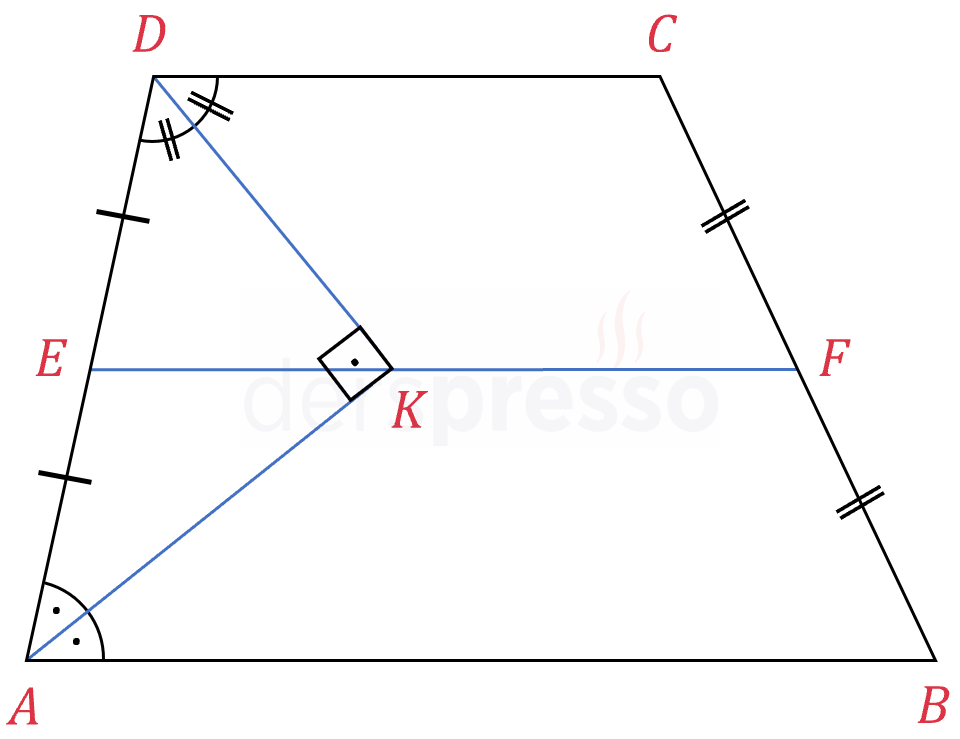
\( [AK] \) ve \( [DK] \) açıortay, \( [EF] \) orta taban olmak üzere,
\( K \in [EF] \) ve
\( m(\widehat{AKD}) = 90° \)
İSPATI GÖSTER
Yamuğun bir yan kenarı üzerindeki iki açıya \( x \) ve \( y \) diyelim.
\( m(\widehat{A}) = x \)
\( m(\widehat{D}) = y \)
\( [AK] \) ve \( [DK] \) sırasıyla \( \widehat{A} \) ve \( \widehat{B} \) açılarının açıortaylarıdır.
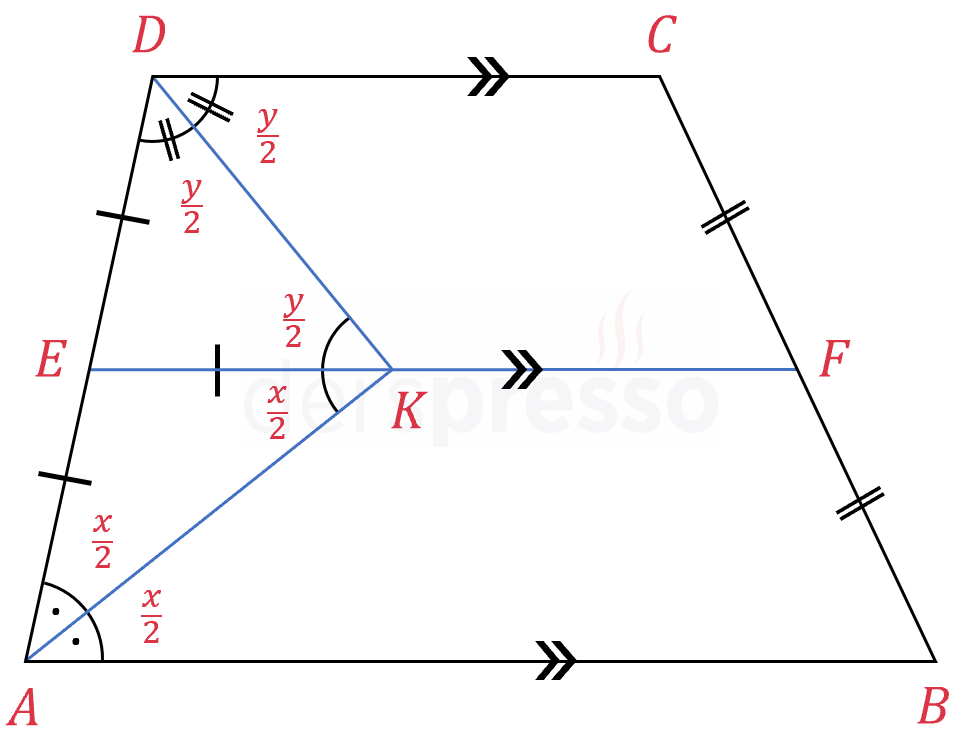
\( m(\widehat{EAK}) = m(\widehat{KAB}) = \dfrac{x}{2} \)
\( m(\widehat{EDK}) = m(\widehat{KDC}) = \dfrac{y}{2} \)
\( K \) noktasından geçen, \( [AD] \) ve \( [BC] \) kenarlarını birleştiren, \( [AB] \) ve \( [DC] \) kenarlarına paralel \( [EF] \) doğru parçasını çizelim.
\( \widehat{BAK} \) ve \( \widehat{EKA} \) açıları iç ters açılar oldukları için eş açılardır.
\( m(\widehat{EKA}) = \dfrac{x}{2} \)
\( \widehat{CDK} \) ve \( \widehat{DKE} \) açıları iç ters açılar oldukları için eş açılardır.
\( m(\widehat{DKE}) = \dfrac{y}{2} \)
Buna göre \( AEK \) ve \( DEK \) üçgenleri ikizkenardır.
\( \abs{AE} = \abs{EK} \)
\( \abs{DE} = \abs{EK} \)
Buna göre \( [EF] \) doğru parçası \( [AD] \) kenarını ortalar.
\( [EF] \) doğru parçası aynı zamanda \( [AB] \) ve \( [DC] \) kenarlarına paralel olduğu için \( [BC] \) kenarını da ortalar, dolayısıyla yamuğun bir orta tabanıdır.
Yamukta bir yan kenar üzerindeki iki açı bütünlerdir.
\( \widehat{A} + \widehat{D} = 180° \)
\( x + y = 180° \)
\( \widehat{AKD} \) açısının ölçüsünü bulalım.
\( \dfrac{x}{2} + \dfrac{y}{2} = \dfrac{180°}{2} = 90° \)
Yamuğun Çevresi ve Alanı
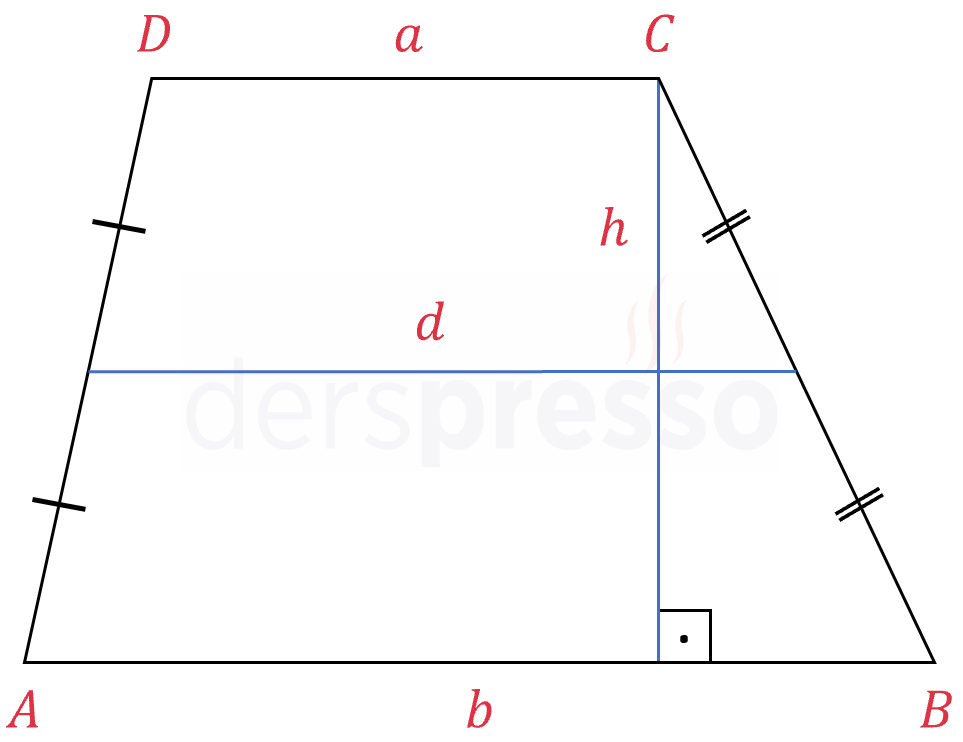
Yamuğun çevresi, dört kenar uzunluğunun toplamına eşittir.
\( Ç(ABCD) = \abs{AB} + \abs{BC} + \abs{CD} \) \( + \abs{DA} \)
Yamuğun alanı, alt ve üst taban uzunlukları toplamının yarısı ile yüksekliğin çarpımına eşittir. Orta taban alt ve üst taban uzunlukları toplamının yarısına eşit olduğu için, yamuğun alanını orta taban uzunluğu ile yüksekliğin çarpımı şeklinde de yazabiliriz.
\( A(ABCD) = \dfrac{a + b}{2} \cdot h \)
\( A(ABCD) = d \cdot h \)
İSPATI GÖSTER
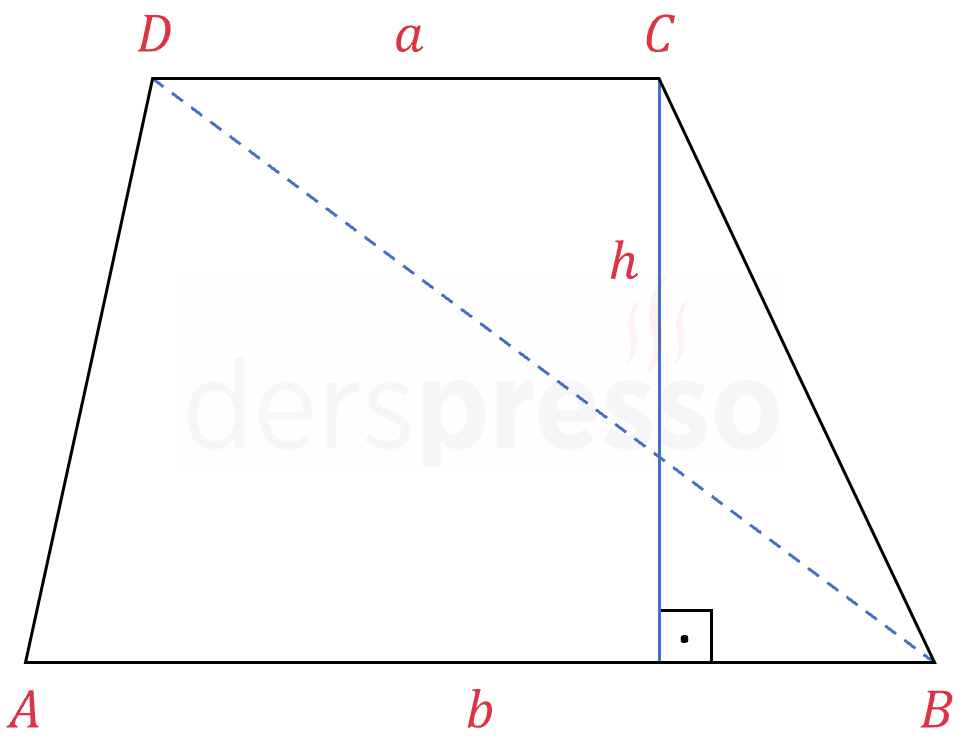
\( ABCD \) yamuğunun \( DB \) köşegenini çizelim (mavi kesikli çizgi).
\( ABCD \) yamuğunun alanı köşegenin ayırdığı iki üçgenin alanları toplamına eşittir.
\( A(ABCD) = A(\overset{\triangle}{ABD}) + A(\overset{\triangle}{BCD}) \)
\( A(\overset{\triangle}{ABD}) = \dfrac{b \cdot h}{2} \)
\( A(\overset{\triangle}{BCD}) = \dfrac{a \cdot h}{2} \)
\( A(ABCD) = \dfrac{b \cdot h}{2} + \dfrac{a \cdot h}{2} \)
\( = \dfrac{(a + b)}{2} \cdot h \)
Tüm dörtgenlerde olduğu gibi; yamuğun alanı, köşegenlerin uzunlukları ile aralarındaki açının sinüs değerinin çarpımının yarısına eşittir. Birbirini 180°'ye tamamlayan açıların sinüs değerleri eşit olduğu için, köşegenlerin arasında oluşan bütünler açıların ikisi de aynı sonucu verir. Aşağıda bu formülün tüm dörtgenler için geçerli olan ispatı verilmiştir.
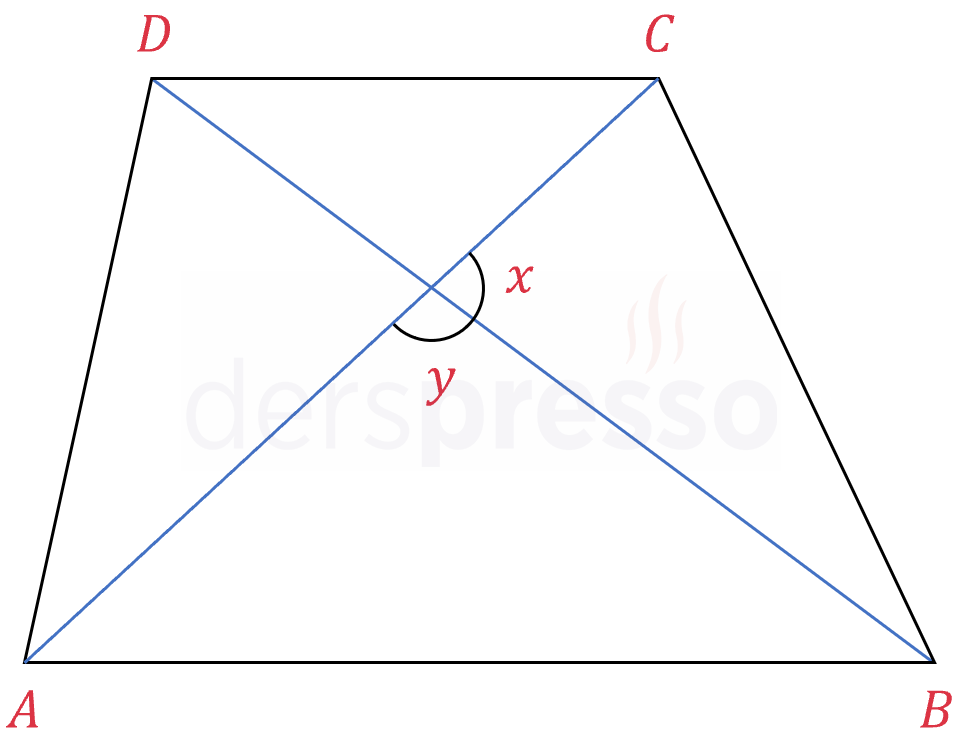
\( A(ABCD) = \dfrac{1}{2} \abs{AC} \cdot \abs{BD} \cdot \sin{x} \)
\( A(ABCD) = \dfrac{1}{2} \abs{AC} \cdot \abs{BD} \cdot \sin{y} \)
İSPATI GÖSTER
KONVEKS DÖRTGEN:
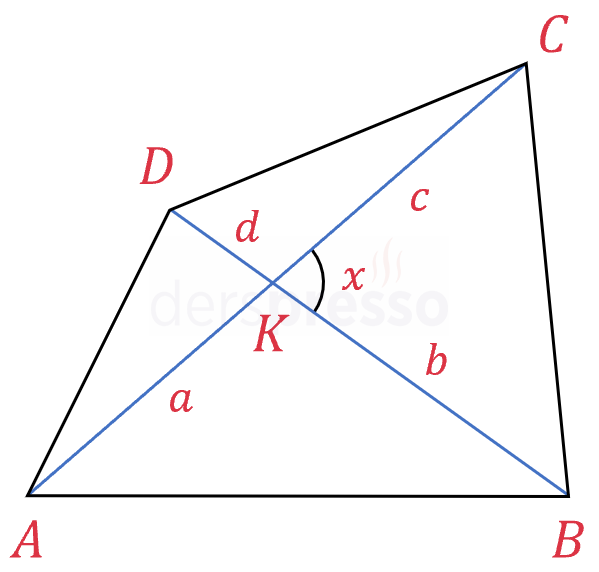
Köşegenlerin ayırdığı dört üçgenin alanlarını sinüs alan formülünü kullanarak hesaplayalım.
\( A(\overset{\triangle}{KAB}) = \dfrac{1}{2} \cdot a \cdot b \cdot \sin(180° - x) \)
\( A(\overset{\triangle}{KBC}) = \dfrac{1}{2} \cdot b \cdot c \cdot \sin{x} \)
\( A(\overset{\triangle}{KCD}) = \dfrac{1}{2} \cdot c \cdot d \cdot \sin(180° - x) \)
\( A(\overset{\triangle}{KDA}) = \dfrac{1}{2} \cdot d \cdot a \cdot \sin{x} \)
Bütünler açıların sinüs değerleri eşittir.
\( \sin{x} = \sin(180° - x) \)
Dört üçgenin alanlarını toplayarak dörtgenin alanını bulalım.
\( A(ABCD) = \dfrac{1}{2} \cdot \sin{x} \cdot (a \cdot b + b \cdot c \) \( + c \cdot d + d \cdot a) \)
\( = \dfrac{1}{2} \cdot \sin{x} \cdot [b \cdot (a + c) + d \cdot (a + c)] \)
\( = \dfrac{1}{2} \cdot \sin{x} \cdot (a + c) \cdot (b + d) \)
\( = \dfrac{1}{2} \cdot \abs{AC} \cdot \abs{BD} \cdot \sin{x} \)
KONKAV DÖRTGEN:
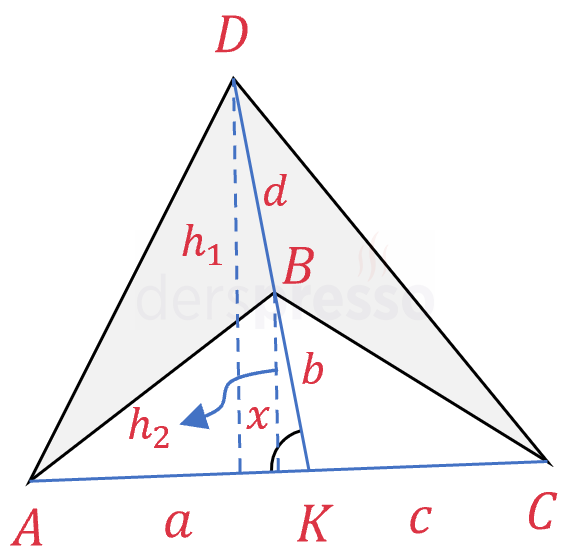
Şekilde oluşan iki üçgenin alanlarını bulalım:
Büyük üçgenin alanı:
\( A(\overset{\triangle}{ACD}) = \dfrac{(a + c) \cdot h_1}{2} \)
\( = \dfrac{(a + c) \cdot (b + d) \cdot \sin{x}}{2} \)
Küçük üçgenin alanı:
\( A(\overset{\triangle}{ACB}) = \dfrac{(a + c) \cdot h_2}{2} \)
\( = \dfrac{(a + c) \cdot b \cdot \sin{x}}{2} \)
Gri renk ile işaretlenmiş konkav dörtgenin alanını, büyük ve küçük üçgenler cinsinden yazalım.
\( A(ABCD) = A(\overset{\triangle}{ACD}) - A(\overset{\triangle}{ACB}) \)
\( = \dfrac{(a + c) \cdot (b + d) \cdot \sin{x}}{2} \) \( - \dfrac{(a + c) \cdot b \cdot \sin{x}}{2}\)
\( = \dfrac{(a + c) \cdot d \cdot \sin{x}}{2} \)
\( = \dfrac{1}{2} \cdot \abs{AC} \cdot \abs{BD} \cdot \sin{x} \)
Yamukta köşegenlerin oluşturduğu dört üçgenden yan kenarlara bakan alanlar birbirine eşittir.
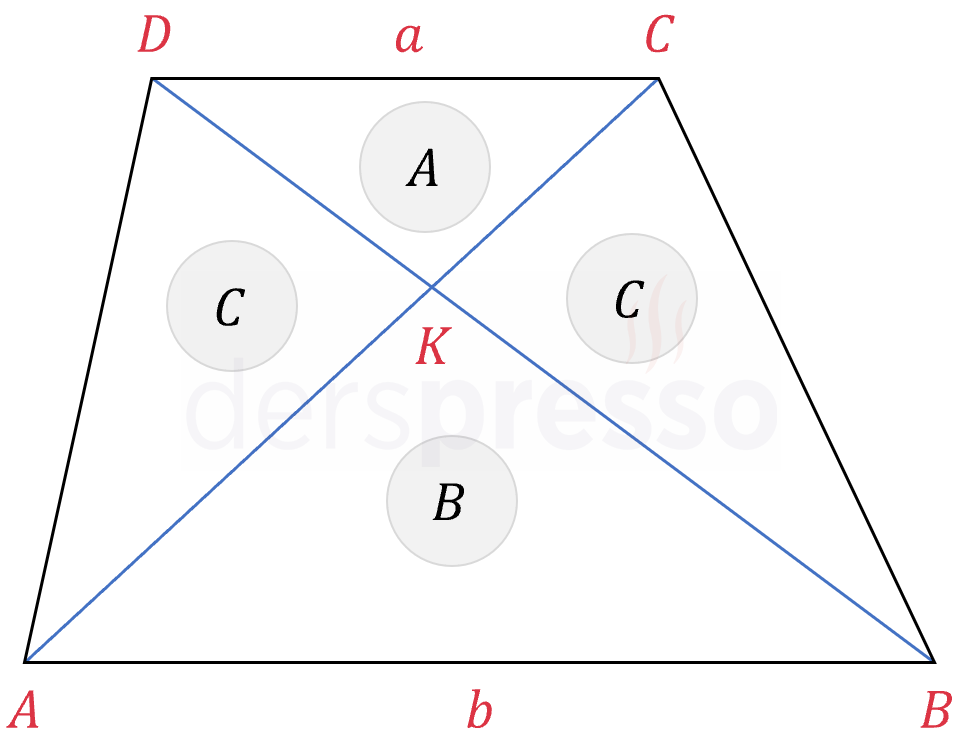
\( A(AKD) = A(BKC) \)
İSPATI GÖSTER
Yamuğun yüksekliğini çizelim.
\( \abs{EC} = h \)
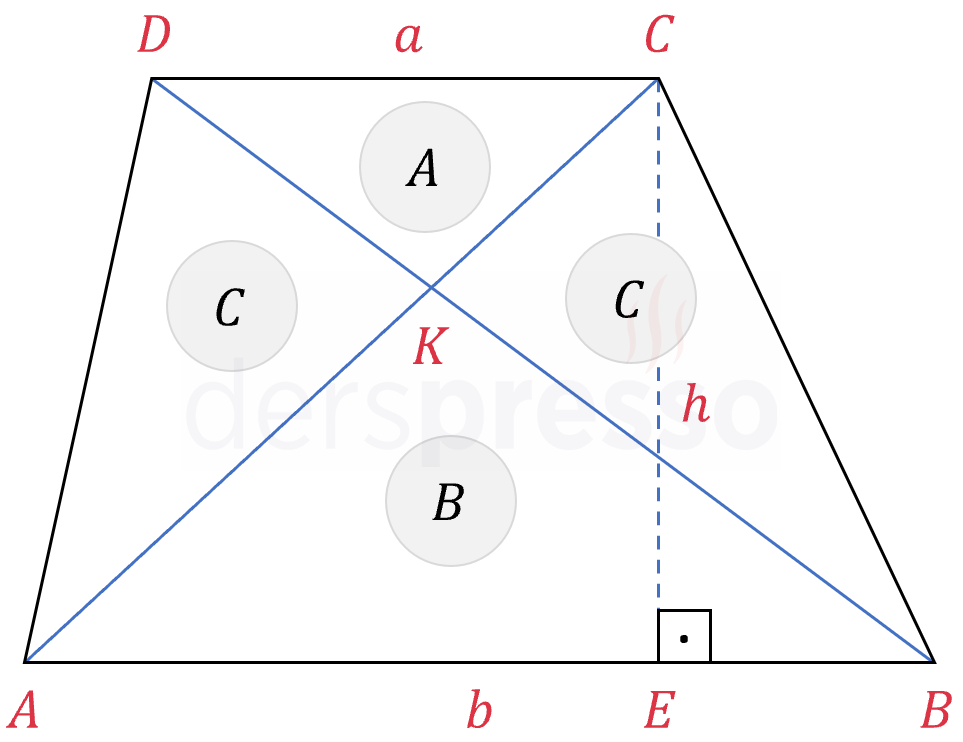
\( ABD \) üçgeninin alanını hesaplayalım.
\( A(ABD) = \dfrac{b \cdot h}{2} \)
Bu alan \( AKB \) ve \( AKD \) üçgenlerinin alanları toplamına eşittir.
\( A(AKB) + A(AKD) = \dfrac{b \cdot h}{2} \)
\( ABC \) üçgeninin alanını hesaplayalım.
\( A(ABC) = \dfrac{b \cdot h}{2} \)
Bu alan \( AKB \) ve \( BKC \) üçgenlerinin alanları toplamına eşittir.
\( A(AKB) + A(BKC) = \dfrac{b \cdot h}{2} \)
İki alan birbirine eşittir.
\( A(AKB) + A(AKD) = A(AKB) + A(BKC) = \dfrac{b \cdot h}{2} \)
Yan kenarlara bakan alanlar birbirine eşit olarak bulunur.
\( A(AKD) = A(BKC) \)
Tüm dörtgenlerde olduğu gibi, yamuğun köşegenlerinin oluşturduğu dört üçgenden karşılıklı olanların alanları çarpımı birbirine eşittir. Aşağıda bu formülün tüm dörtgenler için geçerli olan ispatı verilmiştir.
\( C^2 = A \cdot B \)
İSPATI GÖSTER
İspat 1:
\( ABD \) ve \( CBD \) üçgenlerinin yüksekliklerini çizelim.
\( h_1 \): \( ABD \) üçgeninin yüksekliği
\( h_2 \): \( CBD \) üçgeninin yüksekliği
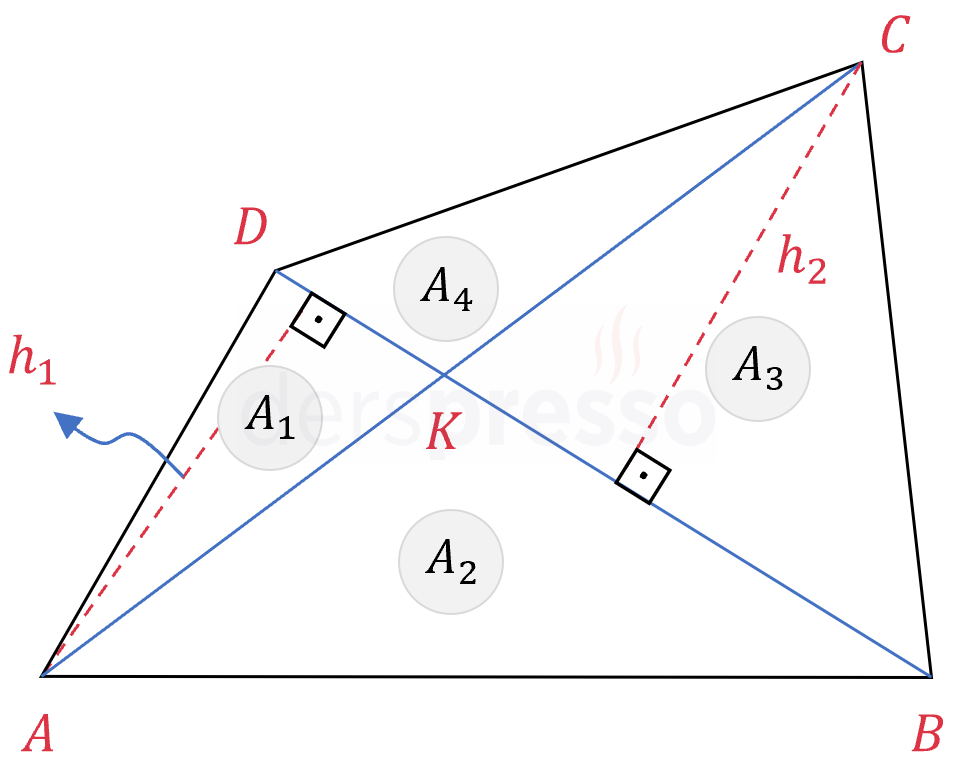
Dört üçgenin alanlarını ayrı ayrı bulalım.
\( A_1 = \dfrac{\abs{DK} \cdot h_1}{2} \)
\( A_2 = \dfrac{\abs{BK} \cdot h_1}{2} \)
\( A_3 = \dfrac{\abs{BK} \cdot h_2}{2} \)
\( A_4 = \dfrac{\abs{DK} \cdot h_2}{2} \)
Formülleri incelediğimizde, aşağıdaki iki ifadenin çarpımının eşit olduğunu görebiliriz.
\( A_1 \cdot A_3 = A_2 \cdot A_4 \)
İspat 2:
Köşegenlerin birbiriyle kesişimi sonucunda oluşan doğru parçalarının uzunluklarına \( x \), \( y \), \( z \) ve \( t \) diyelim.
Köşegenlerin birbiriyle kesişim noktasında oluşan açılara \( \alpha \) ve \( \beta \) diyelim.
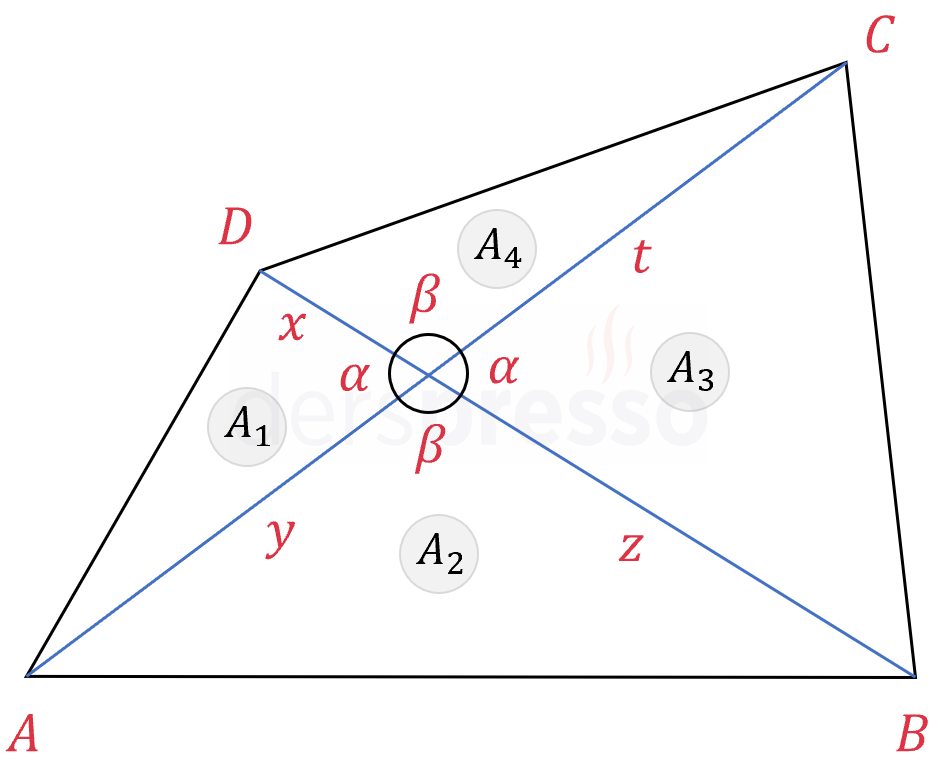
Sinüs alan formülünü kullanarak dört üçgenin alanlarını ayrı ayrı bulalım.
\( A_1 = \dfrac{1}{2} x \cdot y \cdot \sin{\alpha} \)
\( A_2 = \dfrac{1}{2} y \cdot z \cdot \sin{\beta} \)
\( A_3 = \dfrac{1}{2} z \cdot t \cdot \sin{\alpha} \)
\( A_4 = \dfrac{1}{2} t \cdot x \cdot \sin{\beta} \)
\( A_1 \cdot A_3 \) çarpımını bulalım.
\( A_1 \cdot A_3 = \dfrac{1}{2} x \cdot y \cdot \sin{\alpha} \cdot \dfrac{1}{2} z \cdot t \cdot \sin{\alpha} \)
\( = \dfrac{1}{4} x \cdot y \cdot z \cdot t \cdot \sin^2{\alpha} \)
\( A_2 \cdot A_4 \) çarpımını bulalım.
\( A_2 \cdot A_4 = \dfrac{1}{2} y \cdot z \cdot \sin{\beta} \cdot \dfrac{1}{2} t \cdot x \cdot \sin{\beta} \)
\( = \dfrac{1}{4} x \cdot y \cdot z \cdot t \cdot \sin^2{\beta} \)
\( \alpha \) ve \( \beta \) bütünler açılar oldukları için sinüs değerleri birbirine eşittir.
\( \sin{\beta} = \sin(180° - \alpha) = \sin{\alpha} \)
\( = \dfrac{1}{4} x \cdot y \cdot z \cdot t \cdot \sin^2{\alpha} \)
Bulduğumuz iki çarpım birbirine eşittir.
\( A_1 \cdot A_3 = A_2 \cdot A_4 \)
Yamuğun bir yan kenarı üzerindeki iki komşu köşeden diğer yan kenarın orta noktasına çizilen doğru parçalarının oluşturduğu üçgenin alanı, yamuğun alanının yarısına eşittir.
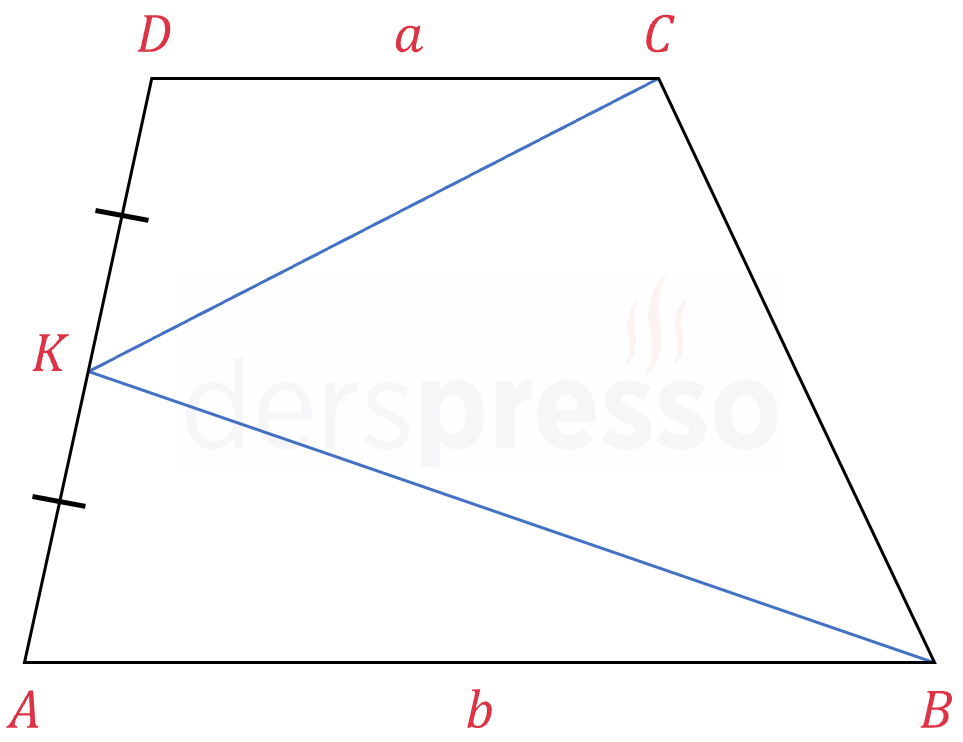
\( A(BKC) = \dfrac{A(ABCD)}{2} \)
İSPATI GÖSTER
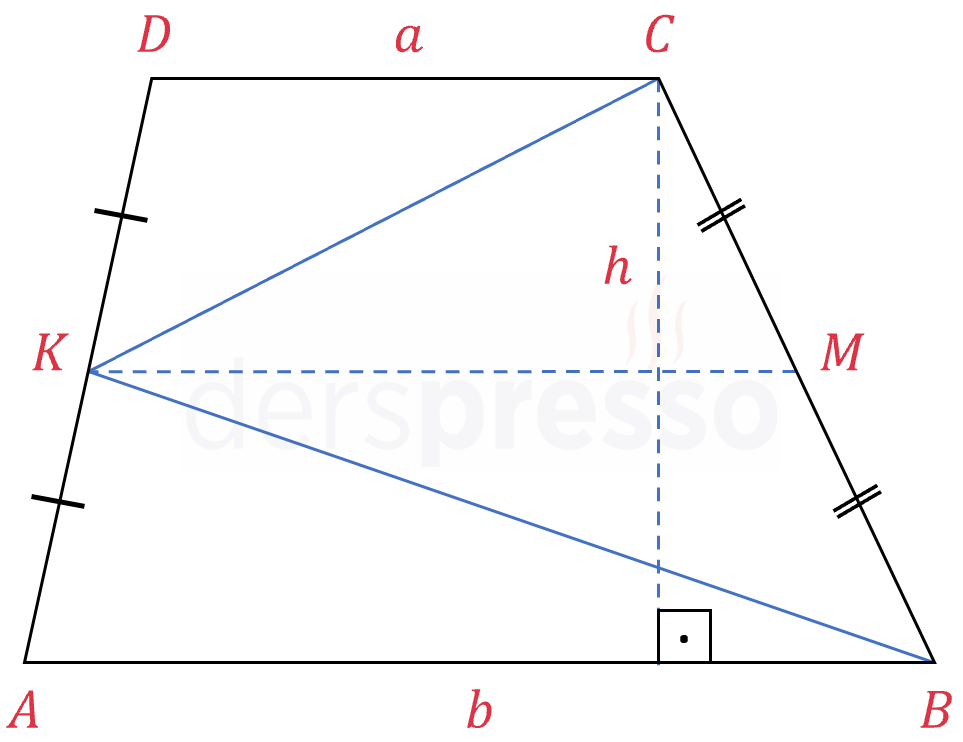
Yamuğun orta tabanını ve yüksekliğini çizelim (mavi kesikli çizgiler).
\( A(ABCD) = \dfrac{a + b}{2} \cdot h \)
\( KBC \) üçgeninin alanı \( KMB \) ve \( KMC \) üçgenlerinin alanları toplamına eşittir.
\( A(\overset{\triangle}{KBC}) = A(\overset{\triangle}{KMB}) + A(\overset{\triangle}{KMC}) \)
\( A(\overset{\triangle}{KMB}) = \dfrac{\abs{KM} \cdot \frac{h}{2}}{2} \)
\( A(\overset{\triangle}{KMC}) = \dfrac{\abs{KM} \cdot \frac{h}{2}}{2} \)
\( A(\overset{\triangle}{KBC}) = \dfrac{\abs{KM} \cdot \frac{h}{2}}{2} + \dfrac{\abs{KM} \cdot \frac{h}{2}}{2} \)
\( = \dfrac{\abs{KM} \cdot h}{2} \)
\( \abs{KM} \) orta taban olduğu için, uzunluğu alt ve üst taban uzunluk toplamlarının yarısına eşittir.
\( \abs{KM} = \dfrac{a + b}{2} \)
Alan formülünde yerine koyalım.
\( A(\overset{\triangle}{KBC}) = \dfrac{\frac{a + b}{2} \cdot h}{2} \)
\( = \dfrac{(a + b) \cdot h}{4} \)
Bu formülü yamuk alan formülü ile karşılaştırırsak üçgenin alanının yamuğun alanının yarısı olduğu görürüz.
\( A(\overset{\triangle}{KBC}) = \dfrac{A(ABCD)}{2} \)
İkizkenar Yamuk
Yan kenar uzunlukları eşit olan ve paralel kenarlarını ortalayan bir doğruya göre simetrik olan yamuğa ikizkenar yamuk denir.
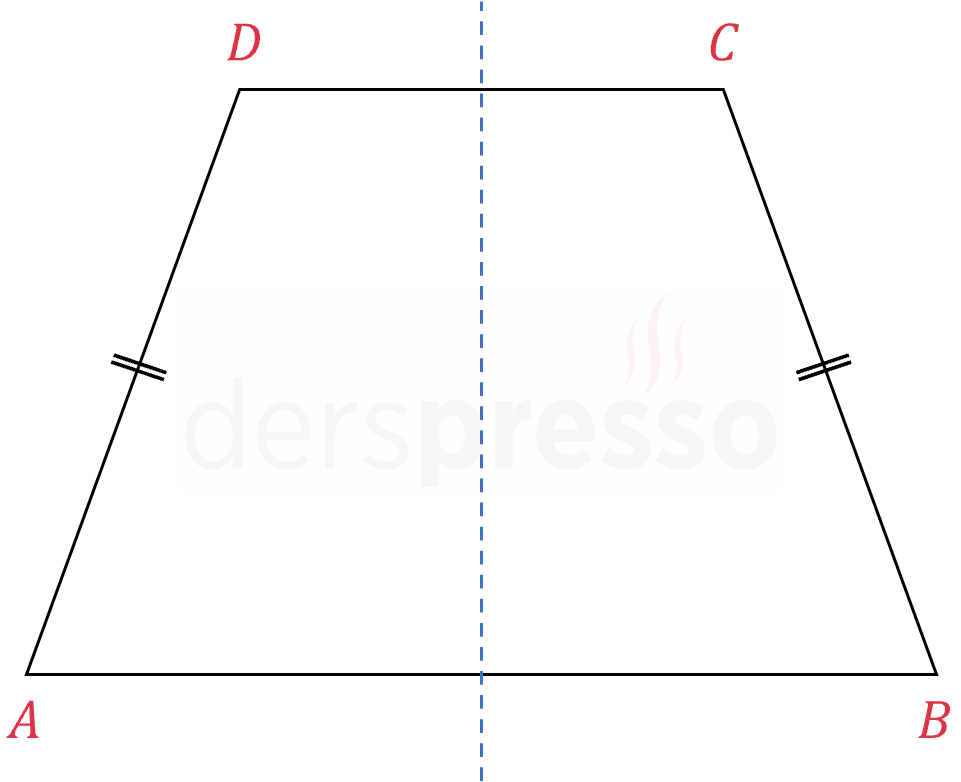
İkizkenar yamuk normal yamuğun sahip olduğu tüm özelliklere sahiptir.
Bir yamuğun aşağıdaki özelliklerden en az birini taşıdığı biliniyorsa bu yamuk bir ikizkenar yamuktur ve diğer özellikleri de taşır.
- Paralel olmayan iki kenar uzunluğu eşit (ikizkenar yamuk tanımı)
- Alt taban açı ölçüleri birbirine eşit
- Üst taban açı ölçüleri birbirine eşit
- Köşegen uzunlukları birbirine eşit
İkizkenar yamukta köşegenlerin uzunlukları birbirine eşittir ve köşegenler birbirini eşit oranlarda böler. Benzer şekilde, bir yamuğun köşegen uzunlukları eşitse bu yamuk ikizkenardır.
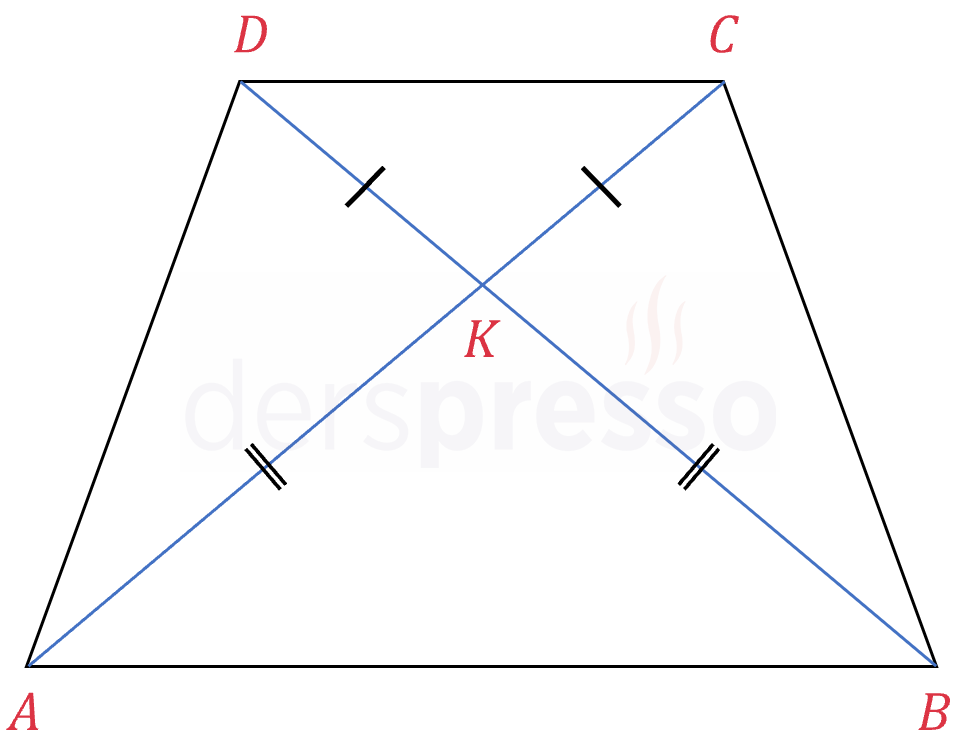
\( \abs{AK} = \abs{BK} \)
\( \abs{CK} = \abs{DK} \)
İkizkenar yamukta alt taban ve üst taban açı ölçüleri ayrı ayrı birbirine eşittir. Benzer şekilde, bir yamuğun alt taban ya da üst taban açı ölçüleri birbirine eşitse bu yamuk ikizkenardır.

\( m(\widehat{A}) = m(\widehat{B}) \)
\( m(\widehat{C}) = m(\widehat{D}) \)
İkizkenar yamukta üst tabanın iki ucundaki köşelerden alt tabana indirilen dikmeler solda ve sağda eş üçgenler oluşturur.
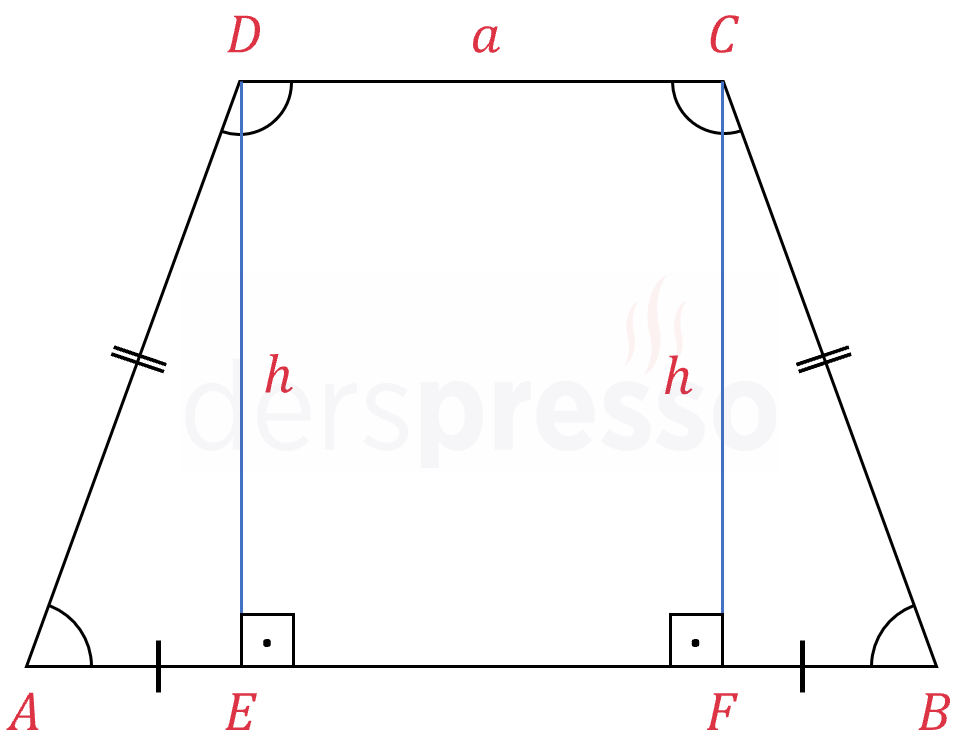
\( \overset{\triangle}{AED} \cong \overset{\triangle}{BFC} \)
\( \abs{AE} = \abs{BF} \)
Dik Yamuk
Yan kenarlarından biri alt ve üst tabana dik olan yamuğa dik yamuk denir.

Dik yamuk normal yamuğun sahip olduğu tüm özelliklere sahiptir.

Şekilde verilenlere göre \( ABCD \) dik yamuğunun alanı kaç \( \text{ br}^2 \) olur?
Çözümü Göster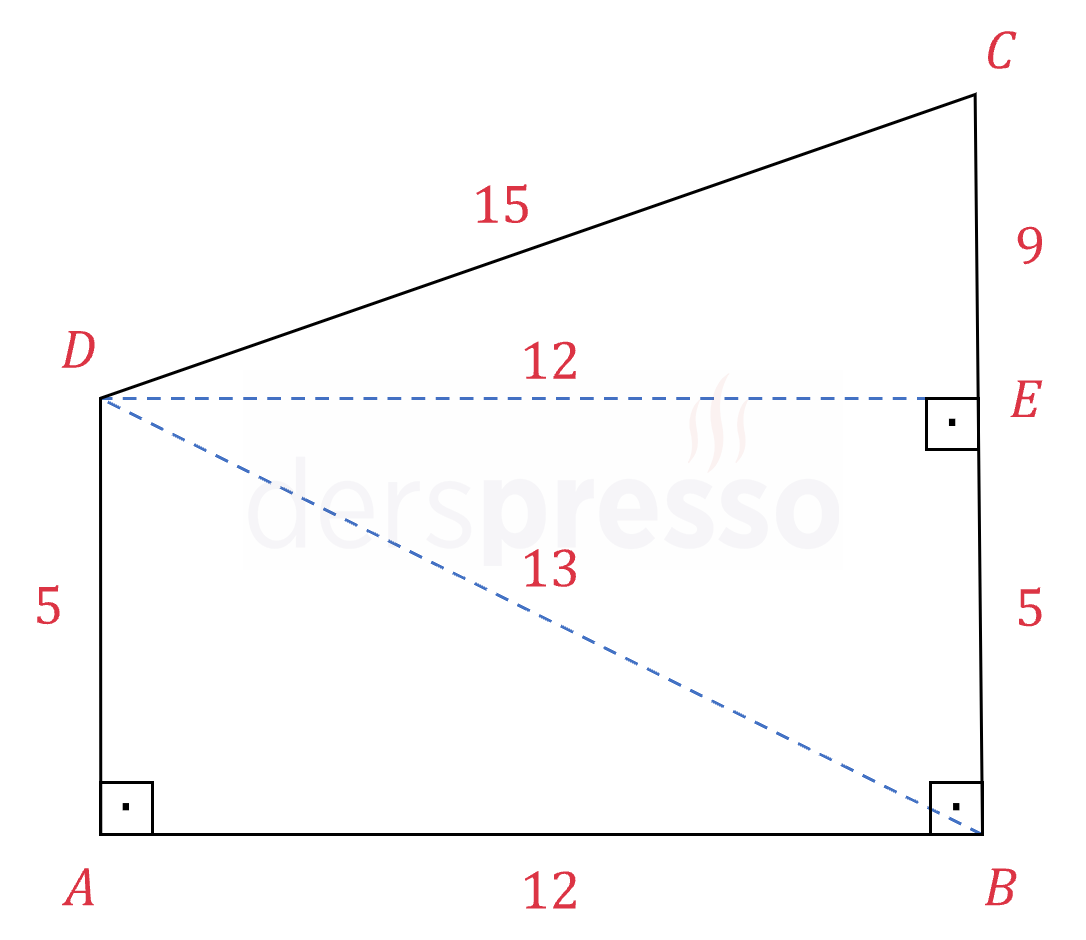
Dik yamuğun \( B \) ve \( D \) köşelerini birleştirelim ve \( D \) köşesinden \( [BC] \) kenarına bir dik indirelim (mavi kesikli çizgiler).
Pisagor teoremini kullanarak \( \abs{BD} \) uzunluğunu bulalım.
\( \abs{BD}^2 = 5^2 + 12^2 \)
\( \abs{BD} = 13 \) br
\( ABED \) bir dikdörtgen olduğu için karşılıklı kenar uzunlukları birbirine eşittir.
\( \abs{DE} = \abs{AB} = 12 \) br
\( \abs{BE} = \abs{AD} = 5 \) br
Pisagor teoremini kullanarak \( \abs{EC} \) uzunluğunu bulalım.
\(15^2 = 12^2 + \abs{EC}^2 \)
\( \abs{EC} = 9 \) br
Bu noktada dik yamuğun alanını \( [BD] \) doğru parçasının oluşturduğu iki üçgenin alanlarını toplayarak bulabiliriz.
\( A(ABCD) = A(\overset{\triangle}{ABD}) + A(\overset{\triangle}{BCD}) \)
\( = \dfrac{5 \cdot 12}{2} + \dfrac{(9 + 5) \cdot 12}{2} \)
\( = 30 + 84 = 114 \text{ br}^2 \) bulunur.
Alternatif olarak alanı yamuk alan formülü ile de bulabiliriz.
\( A(ABCD) = \dfrac{(5 + 5 + 9) \cdot 12}{2} \)
\( = 114 \text{ br}^2 \) bulunur.