Geometrik Kombinasyon
Noktalardan Geçen Doğrular
İki farklı noktadan geçen tek bir doğru çizilebilir.

Doğrusal üç ya da daha fazla farklı noktadan geçen tek bir doğru çizilebilir.

Herhangi üçü doğrusal olmayan \( n \) tane farklı nokta içinden seçilecek her nokta ikilisinden geçen benzersiz bir doğru çizilebilir, dolayısıyla bu şekilde çizilebilecek toplam doğru sayısı \( C(n, 2) \) olur.
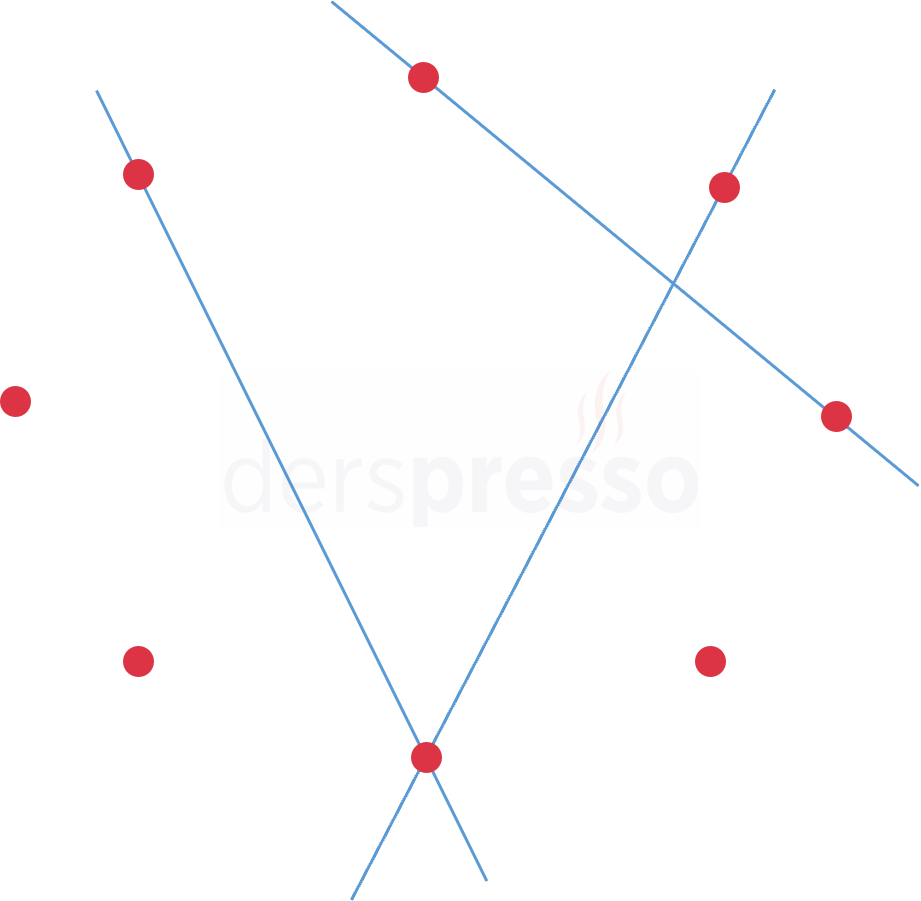
Herhangi üçü doğrusal olmayan 10 farklı noktadan geçen toplam doğru sayısı:
\( = C(10, 2) = 45 \)
Çizilebilecek toplam doğru sayısını \( m \) tanesi doğrusal olan, \( n \) tanesi doğrusal olmayan \( m + n \) farklı nokta için bulalım. Noktalardan hiçbirinin doğrusal olmadığı durumda bu noktalardan geçen \( C(m + n, 2) \) doğru çizilebilir. Doğrusal olan \( m \) tane nokta doğrusal olmasaydı bu noktalardan geçen \( C(m, 2) \) doğru çizilebilirdi, ancak doğrusal oldukları için sadece bir doğru çizilebilir.
Buna göre, \( m \) tanesi doğrusal olan, \( n \) tanesi doğrusal olmayan \( m + n \) farklı noktadan geçen toplam doğru sayısı \( C(m + n, 2) - C(m, 2) + 1 \) olur.

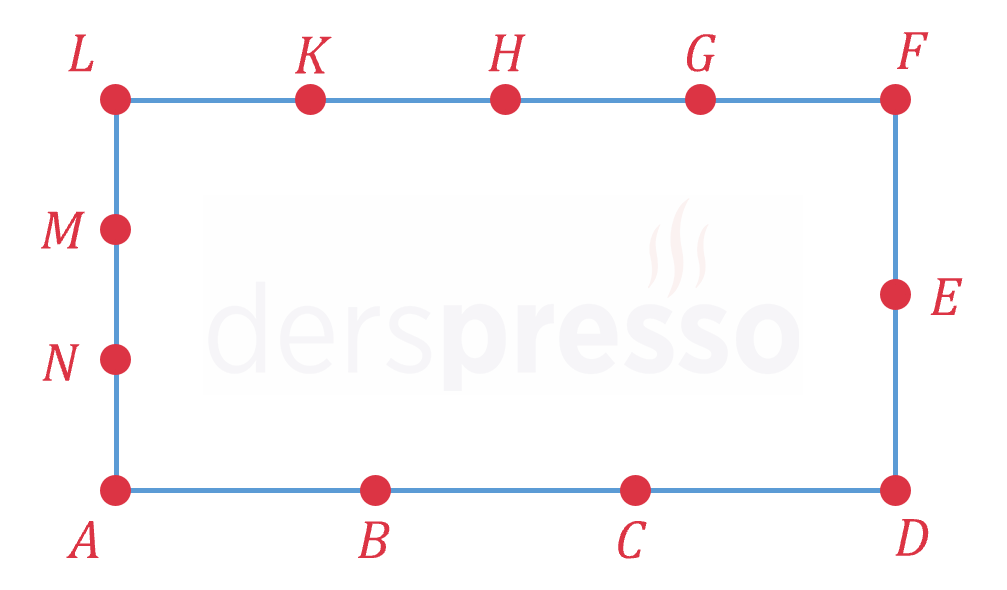
Yukarıdaki şekilde verilen 12 noktadan geçen en çok kaç farklı doğru çizilebilir?
Çözümü Göster12 nokta arasından seçilebilecek her nokta ikilisi bir doğru belirtir, ancak dikdörtgenin kenarları üzerindeki noktalar doğrusal oldukları için her kenar üzerindeki noktalar sadece bir doğru belirtir.
\( C(12, 2) \): 12 nokta içinde herhangi üç noktanın doğrusal olmadığı durumda çizilebilecek doğru sayısı
\( C(4, 2) \): \( [AD] \) kenarı üzerindeki noktalar doğrusal olduğu için çizilemeyecek doğru sayısı
\( C(3, 2) \): \( [DF] \) kenarı üzerindeki noktalar doğrusal olduğu için çizilemeyecek doğru sayısı
\( C(5, 2) \): \( [FL] \) kenarı üzerindeki noktalar doğrusal olduğu için çizilemeyecek doğru sayısı
\( C(4, 2) \): \( [LA] \) kenarı üzerindeki noktalar doğrusal olduğu için çizilemeyecek doğru sayısı
Tüm durumlardan doğrusal olan noktaların oluşturduğu tüm nokta ikililerinin sayısını çıkaralım.
\( C(12, 2) - C(4, 2) - C(3, 2) - C(5, 2) - C(4, 2) \)
\( = 66 - 6 - 3 - 10 - 6 \)
\( = 41 \)
Dikdörtgenin kenarları üzerindeki noktalar doğrusal olsalar da her bir kenar üzerindeki noktalar tek bir doğru oluşturur, dolayısıyla bu dört doğruyu yukarıda bulduğumuz sayıya ekleriz.
\( 41 + 4 = 45 \) tane doğru çizilebilir.
Noktaların Oluşturduğu Üçgenler
Doğrusal olmayan üç farklı nokta tek bir üçgen oluşturur.
Doğrusal üç farklı nokta bir üçgen oluşturmaz.
Herhangi üçü doğrusal olmayan \( n \) tane farklı nokta içinden seçilecek her nokta üçlüsü benzersiz bir üçgen oluşturur, dolayısıyla bu noktaların oluşturduğu toplam üçgen sayısı \( C(n, 3) \) olur.
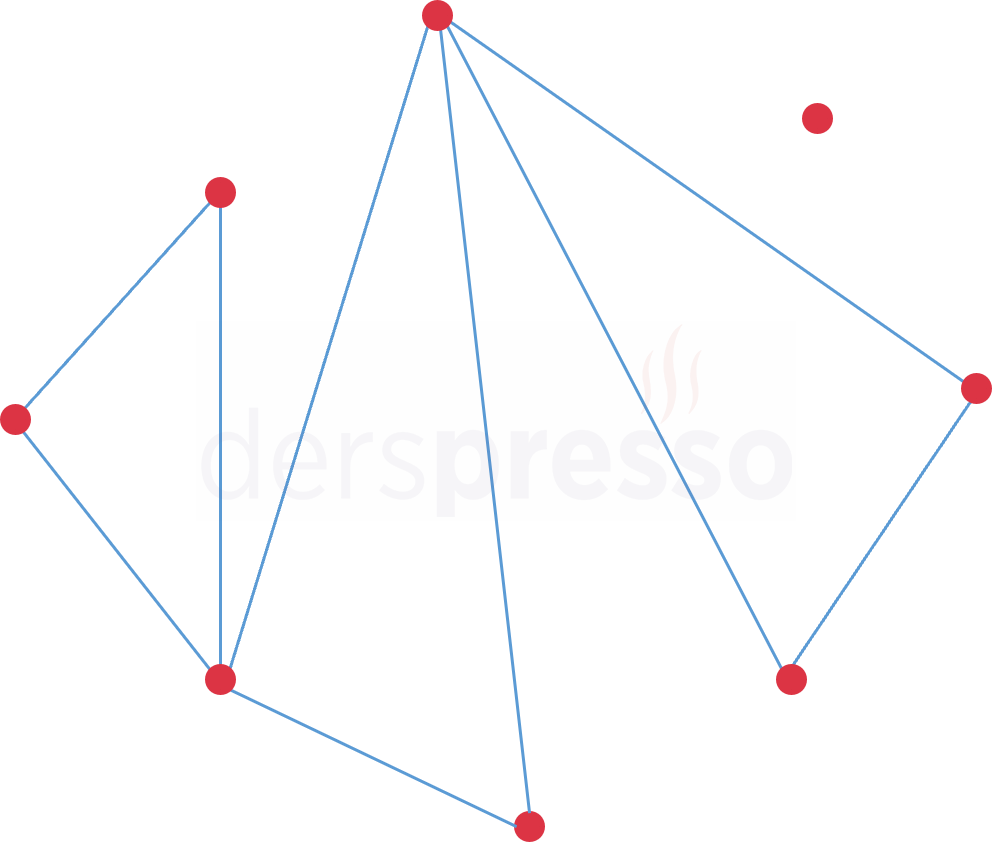
\( m \) tanesi doğrusal olan, \( n \) tanesi doğrusal olmayan \( (m + n) \) noktanın oluşturduğu üçgen sayısını bulmak için önce tüm noktaların doğrusal olmadığı durumda oluşacak üçgen sayısını \( C(m + n, 3) \) olarak buluruz. Doğrusal olan \( m \) tane nokta doğrusal olmasalardı bu noktalar \( C(m, 3) \) üçgen oluşturabilirlerdi, ancak doğrusal oldukları için bu doğrular hiçbir üçgen oluşturmazlar (\( n \) tane doğrusal noktadan bir doğru geçer, ama bu noktalar bir üçgen oluşturmazlasr).
Buna göre, \( m \) tanesi doğrusal olan, \( n \) tanesi doğrusal olmayan \( (m + n) \) noktanın oluşturduğu üçgen sayısı \( C(m + n, 3) - C(m, 3) \) olur.
Herhangi üçü doğrusal olmayan 8 noktayı köşe kabul eden kaç farklı üçgen çizilebilir?
Çözümü GösterDoğrusal olmayan üç farklı nokta tek bir üçgen oluşturur. Herhangi üçü doğrusal olmayan \( n \) tane farklı nokta içinden seçilecek her nokta üçlüsü benzersiz bir üçgen oluşturur, dolayısıyla bu noktaların oluşturduğu toplam üçgen sayısı \( C(n, 3) \) olur.
Buna göre, herhangi üçü doğrusal olmayan bu 8 noktayı köşe kabul eden üçgen sayısı:
\( C(8, 3) = \dfrac{8 \cdot 7 \cdot 6}{3 \cdot 2 \cdot 1} = 56 \) olur.
Aynı düzlemde bulunan 10 noktadan 6 tanesi doğrusaldır. Köşeleri bu noktalar olan en çok kaç tane üçgen çizilebilir?
Çözümü Göster10 nokta arasından 3 nokta \( C(10, 3) \) farklı şekilde seçilebilir. Ancak 6 nokta doğrusal olduğu için bu seçimlerden \( C(6, 3) \) kadarı üçgen belirtmez. Tüm durumlardan üçgen belirtmeyen durumları çıkarırsak çizilebilecek üçgen sayısını buluruz.
\( C(10, 3) - C(6, 3) \)
\( = \dfrac{10 \cdot 9 \cdot 8}{3 \cdot 2 \cdot 1} - \dfrac{6 \cdot 5 \cdot 4}{3 \cdot 2 \cdot 1} \)
\( 120 - 20 = 100 \) tane üçgen çizilebilir.
Herhangi üçü doğrusal olmayan 9 noktadan biri \( A \) noktasıdır. Köşeleri bu noktalar olan üçgenlerden kaç tanesinin bir köşesi \( A \) noktasıdır?
Çözümü GösterÇizilecek üçgenlerin bir köşesi \( A \) olduğundan, diğer iki köşesi kalan 8 nokta arasından seçilmelidir. Dolayısıyla 8 nokta içinden seçilebilecek her nokta ikilisi kadar bir köşesi \( A \) olan üçgen çizilebilir.
Buna göre, bir köşesi \( A \) olan üçgen sayısı:
\( C(8, 2) = \dfrac{8 \cdot 7}{2 \cdot 1} = 28 \) olur.
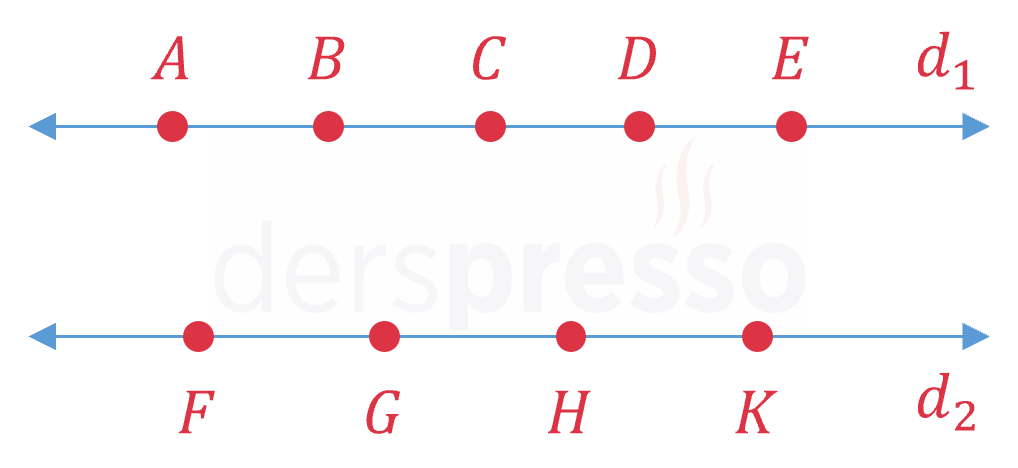
Yukarıdaki şekilde \( d_1 \parallel d_2 \) olmak üzere, \( d_1 \) doğrusu üzerinde 5, \( d_2 \) doğrusu üzerinde 4 farklı nokta bulunmaktadır.
Köşeleri bu noktalar olan kaç farklı üçgen çizilebilir?
Çözümü Göster1. yöntem:
9 nokta içinde herhangi üç noktanın doğrusal olmadığı durumda çizilebilecek üçgen sayısından \( d_1 \) ve \( d_2 \) doğruları üzerindeki noktaların doğrusallığı dolayısıyla çizilemeyecek üçgenlerin sayısını çıkarırsak verilen noktalarla çizilebilecek toplam üçgen sayısını buluruz.
\( C(9, 3) \): 9 nokta içinde herhangi üç noktanın doğrusal olmadığı durumda çizilebilecek üçgen sayısı
\( C(5, 3) \): \( d_1 \) doğrusu üzerindeki noktaların doğrusallığı dolayısıyla çizilemeyecek üçgen sayısı
\( C(4, 3) \): \( d_2 \) doğrusu üzerindeki noktaların doğrusallığı dolayısıyla çizilemeyecek üçgen sayısı
\( C(9, 3) - C(5, 3) - C(4, 3) \)
\( = 84 - 10 - 4 = 70 \) bulunur.
2. yöntem:
Çizilebilecek üçgenlerin ya bir köşesi \( d_1 \) doğrusu üzerinde ve iki köşesi \( d_2 \) doğrusu üzerinde olur, ya da iki köşesi \( d_1 \) doğrusu üzerinde ve bir köşesi \( d_2 \) doğrusu üzerinde olur.
Durum 1: İki köşe \( d_2 \) doğrusu üzerinde
\( d_1 \) doğrusu üzerinden bir ve \( d_2 \) doğrusu üzerinden iki noktanın farklı seçim sayısı: \( C(5, 1) \cdot C(4, 2) = 5 \cdot 6 = 30 \)
Durum 2: İki köşe \( d_1 \) doğrusu üzerinde
\( d_1 \) doğrusu üzerinden iki ve \( d_2 \) doğrusu üzerinden bir noktanın farklı seçim sayısı: \( C(5, 2) \cdot C(4, 1) = 10 \cdot 4 = 40 \)
Toplam farklı seçim sayısı bu iki durumun toplamına eşittir.
\( 30 + 40 = 70 \) bulunur.
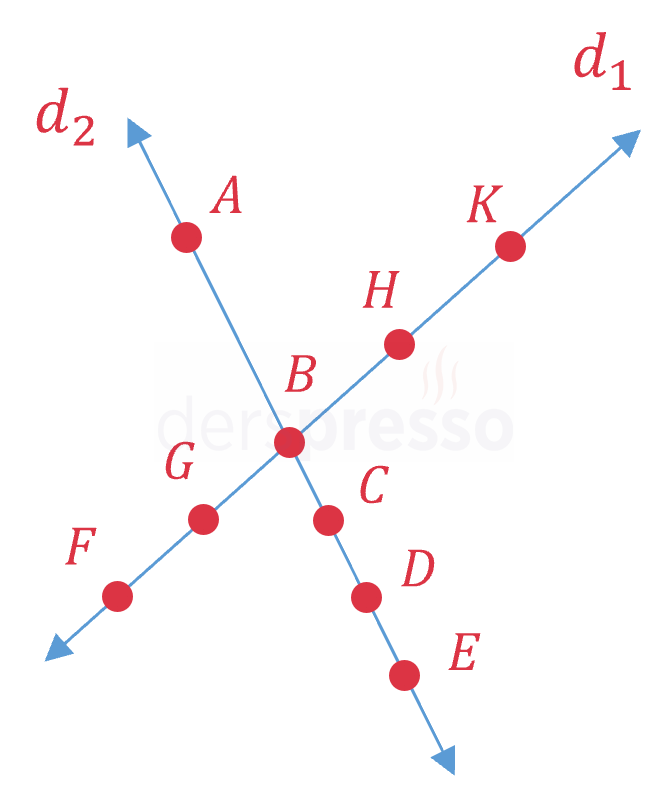
Yukarıdaki şekilde \( B \) noktasında kesişen iki doğru üzerindeki noktalar verilmiştir.
Köşeleri bu 9 noktadan herhangi üçü olan kaç tane üçgen çizilebilir?
Çözümü Göster9 nokta içinde herhangi üç noktanın doğrusal olmadığı durumda çizilebilecek üçgen sayısından, \( d_1 \) ve \( d_2 \) doğruları üzerindeki noktaların doğrusallığı dolayısıyla çizilemeyecek üçgenlerin sayısını çıkarırsak verilen noktalarla çizilebilecek toplam üçgen sayısını buluruz.
\( C(9, 3) \): 9 nokta içinde herhangi üç noktanın doğrusal olmadığı durumda çizilebilecek üçgen sayısı
\( C(5, 3) \): \( d_1 \) doğrusu üzerindeki noktaların doğrusallığı dolayısıyla çizilemeyecek üçgen sayısı
\( C(5, 3) \): \( d_2 \) doğrusu üzerindeki noktaların doğrusallığı dolayısıyla çizilemeyecek üçgen sayısı
\( C(9, 3) - C(5, 3) - C(5, 3) \)
\( = 84 - 10 - 10 = 64 \) tane üçgen çizilebilir.
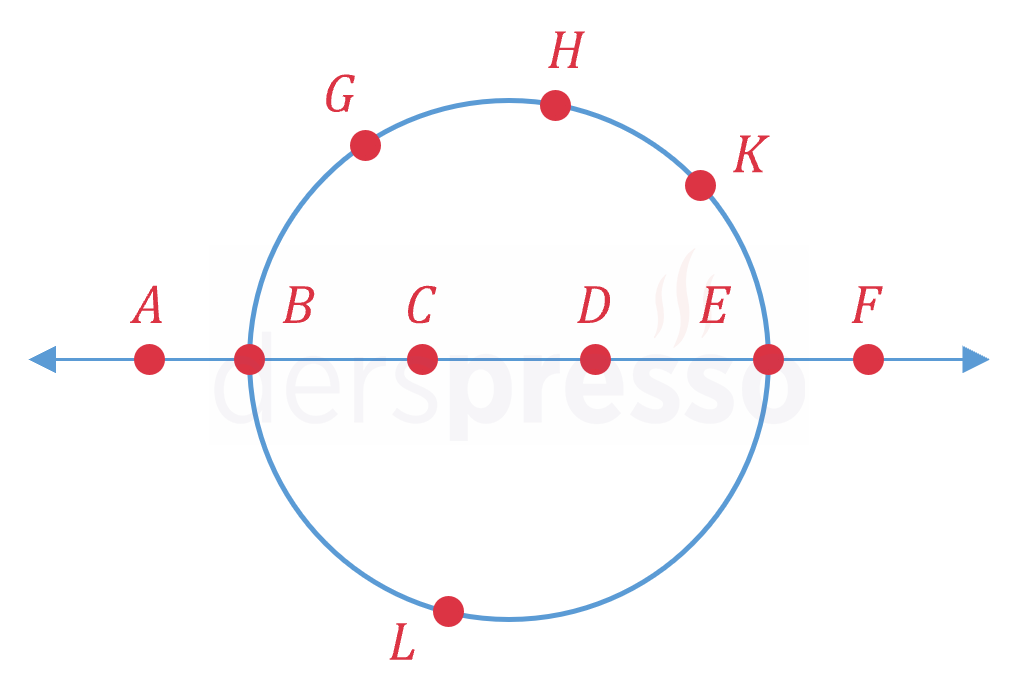
Yukarıdaki şekilde verilen 10 noktayı köşe kabul eden kaç tane üçgen çizilebilir?
Çözümü Göster10 nokta arasından 3 nokta \( C(10, 3) \) farklı şekilde seçilebilir. Ancak bu noktalardan 6'sı (\( A, B, C, D, E, F \) noktaları) doğrusal olduğu için bu seçimlerden \( C(6, 3) \) kadarı üçgen belirtmez. Tüm durumlardan üçgen belirtmeyen durumları çıkarırsak çizilebilecek üçgen sayısını buluruz.
\( C(10, 3) - C(6, 3) \)
\( = \dfrac{10 \cdot 9 \cdot 8}{3 \cdot 2 \cdot 1} - \dfrac{6 \cdot 5 \cdot 4}{3 \cdot 2 \cdot 1} \)
\( 120 - 20 = 100 \) tane üçgen çizilebilir.

Köşeleri yukarıdaki şekildeki 10 noktadan 3'ü olacak şekilde kaç farklı üçgen çizilebilir?
Çözümü GösterHerhangi üçü doğrusal olmayan 10 nokta \( C(10, 3) = 120 \) farklı üçgen oluşturur, ancak bu sayıdan doğrusal olan noktalarla oluşturulamayacak üçgenlerin sayısı çıkarılmalıdır.
Üzerinde 3 nokta bulunan kenar üzerindeki noktalar doğrusal olmasalardı \( C(3, 3) = 1 \) üçgen oluşturulabilirdi.
Üzerinde 4 nokta bulunan kenar üzerindeki noktalar doğrusal olmasalardı \( C(4, 3) = 4 \) üçgen oluşturulabilirdi.
Üzerinde 6 nokta bulunan kenar üzerindeki noktalar doğrusal olmasalardı \( C(6, 3) = 20 \) üçgen oluşturulabilirdi.
Buna göre şekildeki noktalar ile oluşturulabilecek üçgen sayısı \( 120 - 1 - 4 - 20 = 95 \) olarak bulunur.

Köşeleri şekildeki 9 noktanın 3'ü olan kaç farklı üçgen çizilebilir?
Çözümü GösterHerhangi üçü doğrusal olmayan 9 nokta \( C(9, 3) \) farklı üçgen oluşturur.
Bu noktalardan \( d_1 \) doğrusu üzerindeki 3 nokta doğrusal oldukları için \( C(3, 3) \) üçgen eksik oluşmuş olur.
Buna göre şekildeki noktalar \( C(9, 3) - C(3, 3) = 84 - 1 = 83 \) üçgen oluşturur.
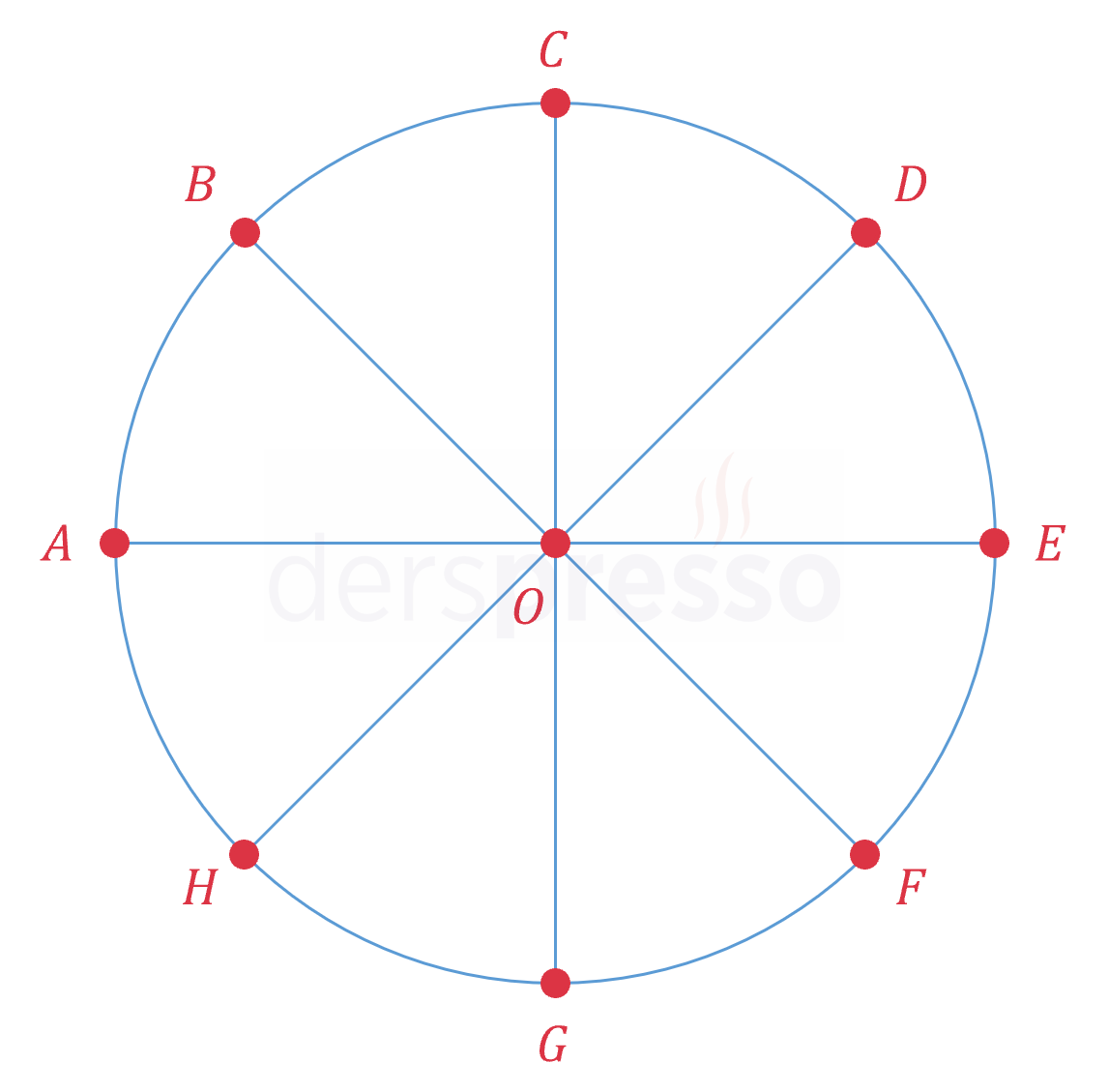
Şekilde \( O \) merkezli çember ve çemberin 4 çapı verilmiştir. Bu çapların çemberi kestiği 8 nokta ve çemberin merkezi arasından 3 nokta, bir üçgen oluşturacak şekilde kaç farklı şekilde seçilebilir?
Çözümü GösterDoğrusal olmayan üç farklı nokta tek bir üçgen oluşturur. Doğrusal üç farklı nokta bir üçgen oluşturmaz.
Şekildeki 9 nokta arasından 3 nokta \( C(9, 3) = 84 \) farklı şekilde seçilebilir.
Bu kombinasyonlar içinden AOE, BOF, COG ve DOH nokta üçlüleri doğrusal oldukları için bir üçgen oluşturmaz.
Buna göre verilen 9 nokta arasından 3 nokta bir üçgen oluşturacak şekilde \( 84 - 4 = 80 \) farklı şekilde seçilebilir.
Noktaların Oluşturduğu Dörtgenler
Herhangi üçü doğrusal olmayan dört farklı nokta tek bir dörtgen oluşturur.
Herhangi üçü doğrusal dört farklı nokta bir dörtgen oluşturmaz.
Herhangi üçü doğrusal olmayan \( n \) tane farklı nokta içinden seçilecek herhangi dört nokta benzersiz bir dörtgen oluşturur, dolayısıyla bu noktaların oluşturduğu toplam dörtgen sayısı \( C(n, 4) \) olur.
\( m \) tanesi doğrusal olan, \( n \) tanesi doğrusal olmayan \( m + n \) noktanın oluşturduğu dörtgen sayısını bulmak için önce tüm noktaların doğrusal olmadığı durumda oluşacak dörtgen sayısı \( C(m + n, 4) \) olarak bulunur. Bu sayıdan aşağıdaki iki farklı durum çıkarılır.
- \( m \) tane doğrusal nokta doğrusal olmasalardı \( C(m, 4) \) farklı dörtgen oluştururdu, ancak doğrusal oldukları için bu noktalar hiçbir dörtgen oluşturmaz. Bu yüzden \( C(m, 4) \) sayısı yukarıdaki sayıdan çıkarılır.
- Bir dörtgenin herhangi üç köşesi de doğrusal olamayacağı için, 3 köşesi \( m \) tane doğrusal noktadan, 1 köşesi \( n \) tane doğrusal olmayan noktalardan seçilen 4 nokta da bir dörtgen oluşturmaz. Bu yüzden doğrusal noktalardan 3, doğrusal olmayan noktalardan 1 farklı seçim sayısı olan \( C(m, 3) \cdot C(n, 1) \) sayısı yukarıdaki sayıdan çıkarılır.
Buna göre, \( m \) tanesi doğrusal olan, \( n \) tanesi doğrusal olmayan \( m + n \) noktanın oluşturduğu dörtgen sayısı \( C(m + n, 4) - C(m, 4) - C(m, 3) \cdot C(n, 1) \) olur.
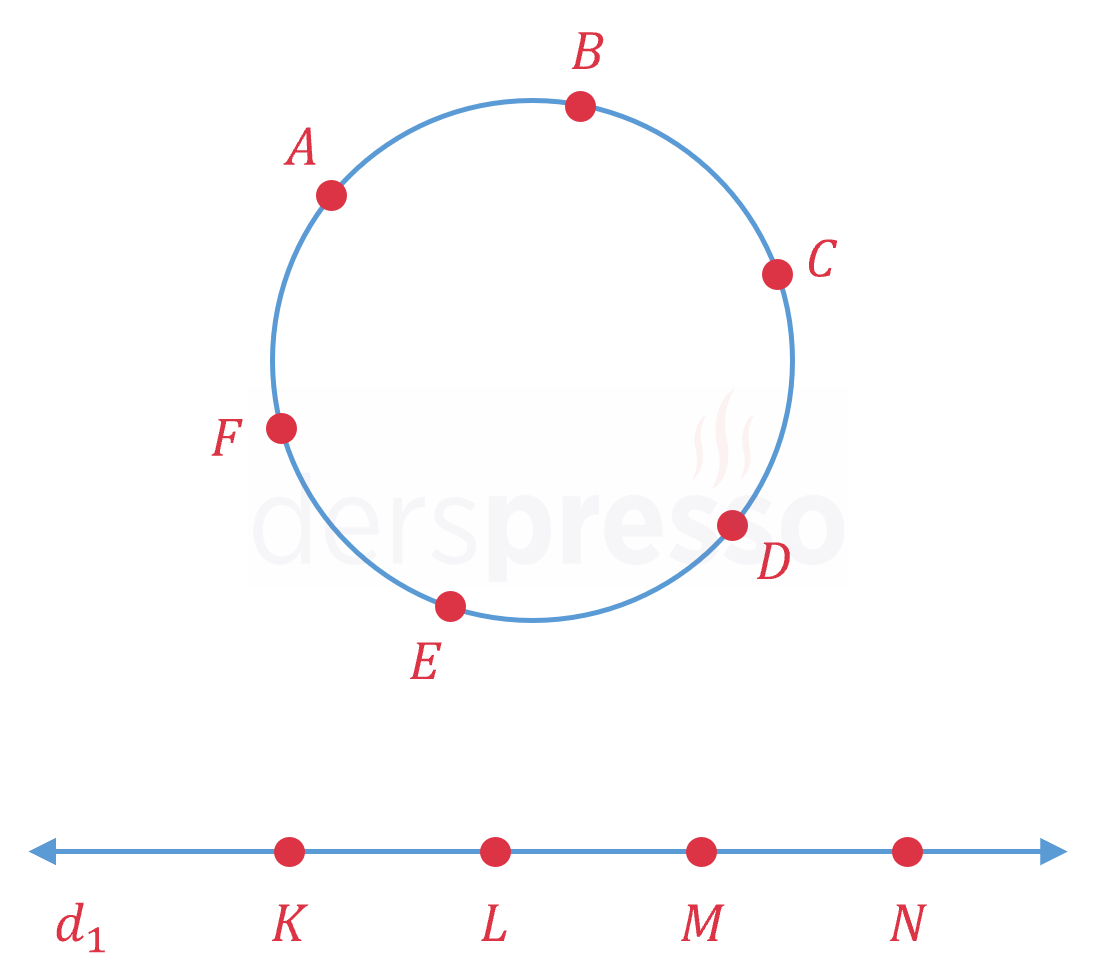
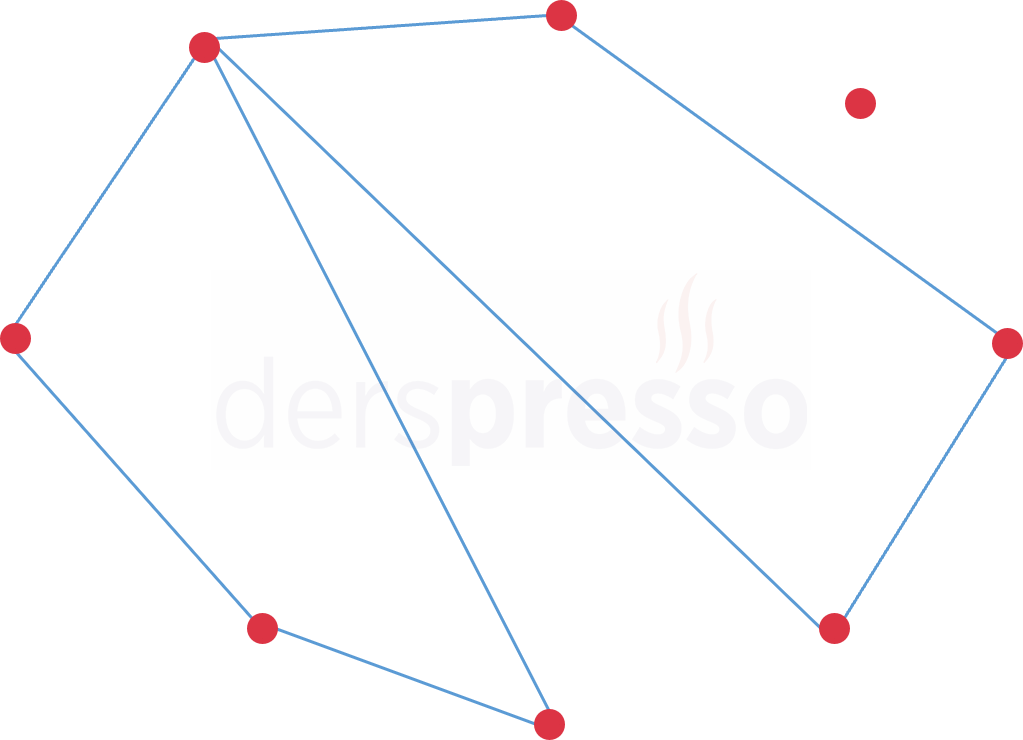
Şekilde verilen noktalardan her biri dörtgenin bir köşesi olacak şekilde, bu noktalar en fazla kaç farklı dörtgen oluşturur?
Çözümü Göster\( A, B, C, D, E, F \) noktaları doğrusal olmadıkları için bu noktalarla \( C(6, 4) = 15 \) farklı dörtgen elde edilebilir.
\( d_1 \) doğrusu üzerindeki noktalar doğrusal oldukları için bu noktalar bir dörtgen oluşturmaz.
\( A, B, C, D, E, F \) noktaları ile \( K, L, M, N \) noktaları birlikte 2 farklı şekilde dörtgen oluşturur.
Durum 1: 3 köşesi \( A, B, C, D, E, F \) noktalarından, 1 köşesi \( K, L, M, N \) noktalarından olacak şekilde en fazla \( C(6, 3) \cdot C(4, 1) = 80 \) farklı dörtgen elde edilebilir.
Durum 2: 2 köşesi \( A, B, C, D, E, F \) noktalarından, 2 köşesi \( K, L, M, N \) noktalarından olacak şekilde en fazla \( C(6, 2) \cdot C(4, 2) = 90 \) farklı dörtgen elde edilebilir.
\( K, L, M, N \) noktaları doğrusal oldukları için 3 köşesi bu noktalardan seçilen bir dörtgen çizilemez.
Buna göre şekilde verilen noktalar \( 15 + 80 + 90 = 185 \) farklı dörtgen oluşturur.
Doğruların Kesişimi
Çakışık iki doğrunun kesişimi sonsuz noktadan oluşur. Çakışık olmayan paralel iki doğru hiçbir noktada kesişmez. Paralel ya da çakışık olmayan ve aynı düzlem üzerinde bulunan iki doğru tek bir noktada kesişir.
Aynı düzlemde bulunan ve farklı (çakışık olmayan) \( n \) tane doğrunun kesişebileceği nokta sayısı en çok \( C(n, 2) \) olabilir. Doğruların kesişim noktaları çakıştığı ya da doğrular birbirine paralel olduğu ölçüde bu sayı azalacaktır.
\( m \) tanesi paralel olan \( m + n \) farklı doğrunun kesişebileceği en çok nokta sayısını bulmak için önce tüm doğruların paralel olmadığı durumda kesişebileceği en çok nokta sayısı \( C(m + n, 2) \) ile bulunur. Paralel \( m \) tane doğru paralel olmasalardı bu doğrular \( C(m, 2) \) farklı noktada kesişebilirlerdi, ancak paralel oldukları için hiçbir noktada kesişmezler.
Buna göre, \( m \) tanesi paralel olan \( m + n \) farklı doğrunun kesişebileceği en çok nokta sayısı \( C(m + n, 2) - C(m, 2) \) olabilir. Burada kesin bir sayı hesaplamak mümkün değildir, çünkü doğruların kaçının paralel kaçının kesişen doğrular olduğu bilinse de doğruların kesişim noktalarının ne ölçüde çakıştıkları doğruların denklemleri olmadan bilinemez.
Aynı düzlemde bulunan 7 farklı doğru en fazla kaç noktada kesişebilir?
Çözümü GösterAynı düzlemde bulunan ve farklı (çakışık olmayan) \( n \) tane doğrunun kesişebileceği nokta sayısı en çok \( C(n, 2) \) olabilir. Doğruların kesişim noktaları çakıştığı ya da doğrular birbirine paralel olduğu ölçüde bu sayı azalacaktır.
Buna göre, aynı düzlemde bulunan bu 7 farklı doğrunun kesişebileceği en fazla nokta sayısı:
\( C(7, 2) = \dfrac{7 \cdot 6}{2 \cdot 1} = 21 \) olur.
Bir düzlem üzerindeki 12 doğrudan 3'ü \( A \) noktasından, geri kalanlardan 5'i de \( B \) noktasından geçmektedir.
Herhangi ikisi paralel olmayan bu doğruların \( A \) ve \( B \) noktaları ile birlikte en çok kaç kesişim noktası vardır?
Çözümü Göster12 farklı doğru en fazla \( C(12, 2) \) farklı noktada kesişir. Ancak bu noktalardan 3'ü tek bir \( A \) noktasında, 5'i de tek bir \( B \) noktasında kesiştikleri için sırasıyla \( C(3, 2) \) ve \( C(5, 2) \) kesişim noktası yerine sadece birer kesişim noktası olmuş olur.
\( C(12, 2) \): 12 farklı doğrunun kesişebileceği en fazla nokta sayısı
\( C(3, 2) \): 3 farklı doğrunun kesişebileceği en fazla nokta sayısı
\( C(5, 2) \): 5 farklı doğrunun kesişebileceği en fazla nokta sayısı
Bu doğruların toplam kesişim nokta sayısını aşağıdaki şekilde hesaplayabiliriz.
\( C(12, 2) - C(3, 2) - C(5, 2) \)
\( = 66 - 3 - 10 \)
\( = 53 \)
Bu sonuca çıkardığımız doğruların kesiştikleri \( A \) ve \( B \) noktalarını eklersek sonucu buluruz.
\( = 53 + 2 = 55 \) kesişim noktası vardır.
Birbirinden farklı 11 doğrudan 5'i \( A \) noktasından geçmektedir, diğer 6 doğru ise birbirine paraleldir.
Buna göre bu doğrular en çok kaç noktada kesişebilir?
Çözümü Göster11 doğru en çok \( C(11, 2) = 55 \) noktada kesişebilir.
Verilen 11 doğrunun 6'sı birbirine paralel olduğu için hiçbir noktada kesişmez, dolayısıyla hesapladığımız en çok kesişme durumundan \( C(6, 2) = 15 \) sayısını çıkarmamız gerekir.
Diğer 5 doğru sadece tek bir \( A \) noktasında kesiştikleri için kesişebilecekleri en çok \( C(5, 2) = 10 \) noktası yerine tek bir noktada kesişmiş olurlar, dolayısıyla en çok kesişme durumundan bu sayıyı da çıkarmamız ve kesiştikleri bir noktayı eklememiz gerekir.
Buna göre, 11 doğru belirtilen şekilde en çok \( 55 - 15 - 10 + 1 = 31 \) noktada kesişebilir.
Üçgenlerin Kesişimi
İki üçgen hiç kesişmeyebilir ya da kesişimi sonsuz noktadan oluşacak şekilde çakışık olabilir. Bu iki durum dışında iki üçgen 1-6 arası farklı noktada kesişebilir. Bu farklı kesişim durumlarının bazıları aşağıdaki şekilde gösterilmiştir.
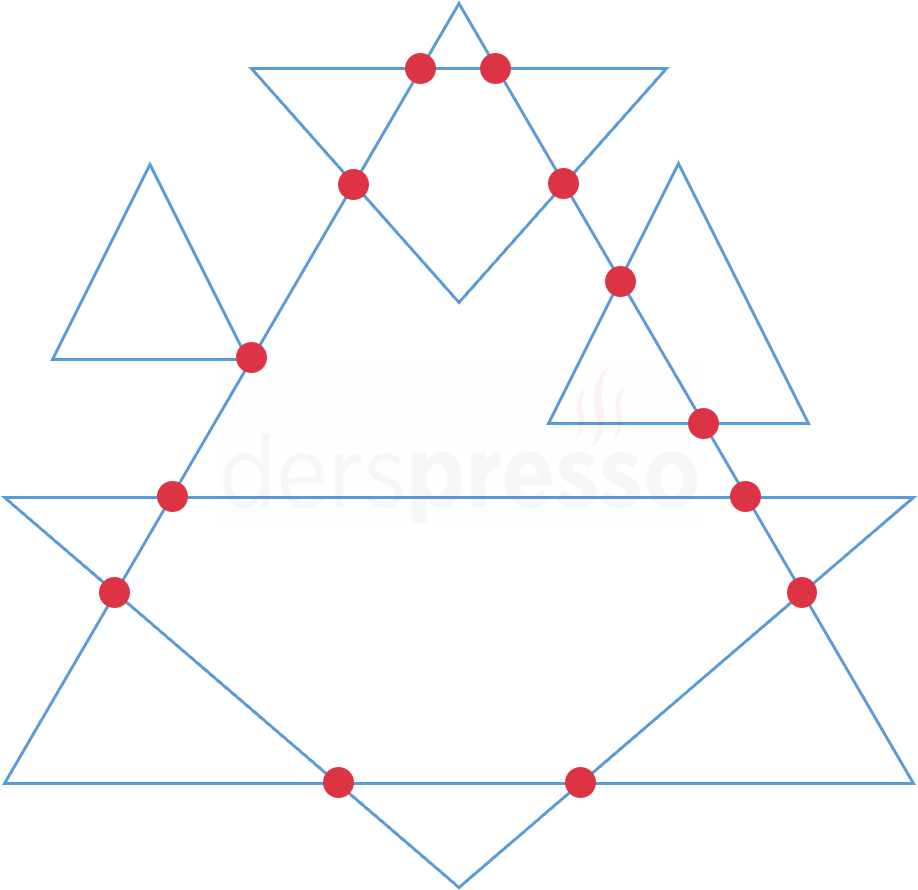
Buna göre, birbiriyle çakışık olmayan \( n \) tane üçgen en çok \( 6 \cdot C(n, 2) \) noktada kesişebilir. Üçgenler 6 yerine daha az sayıda noktada kesiştiği ve kesişim noktaları çakıştığı ölçüde toplam kesişim sayısı bu sayıdan daha az olacaktır.

Çemberlerin Kesişimi
İki çember hiç kesişmeyebilir ya da sonsuz noktada kesişim noktası olacak şekilde çakışık olabilir. Bu iki durum dışında iki çember bir ya da iki noktada kesişebilir. Bu iki kesişim durumu aşağıdaki şekilde gösterilmiştir.

Buna göre, birbiriyle çakışık olmayan \( n \) tane çember en çok \( 2 \cdot C(n, 2) \) noktada kesişebilir. Çemberler 2 yerine daha az sayıda noktada kesiştiği ve kesişim noktaları çakıştığı ölçüde toplam kesişim sayısı bu sayıdan daha az olacaktır.

8 farklı çemberin kesişimi sonucunda en çok kaç kesişim noktası oluşur?
Çözümü Göster
Birbiriyle çakışık olmayan \( n \) tane çember en çok \( 2 \cdot C(n, 2) \) noktada kesişir.
Buna göre 8 farklı çemberin kesişebileceği en fazla nokta sayısı:
\( 2 \cdot C(8, 2) = 2 \cdot \dfrac{8 \cdot 7}{2 \cdot 1} = 56 \) kesişim noktası olur.
Elipslerin Kesişimi
İki elips hiç kesişmeyebilir ya da sonsuz noktada kesişim noktası olacak şekilde çakışık olabilir. Bu iki durum dışında iki elips 1-4 arası noktada kesişebilir. Bu farklı kesişim durumlarının bazıları aşağıdaki şekilde gösterilmiştir.

Buna göre, hiçbiri birbiriyle çakışık olmayan \( n \) tane elips en fazla \( 4 \cdot C(n, 2) \) noktada kesişebilir. Elipsler ve kesişim noktaları çakıştığı ölçüde toplam kesişim sayısı bu sayıdan daha az olacaktır.

Paralel Doğruların Oluşturduğu Dörtgenler
Tümü aynı düzlemde bulunan 2 paralel doğru ile bu 2 doğruya paralel olmayan farklı 2 paralel doğrunun kesişimleri arasında kalan bölge bir dörtgen oluşturur.
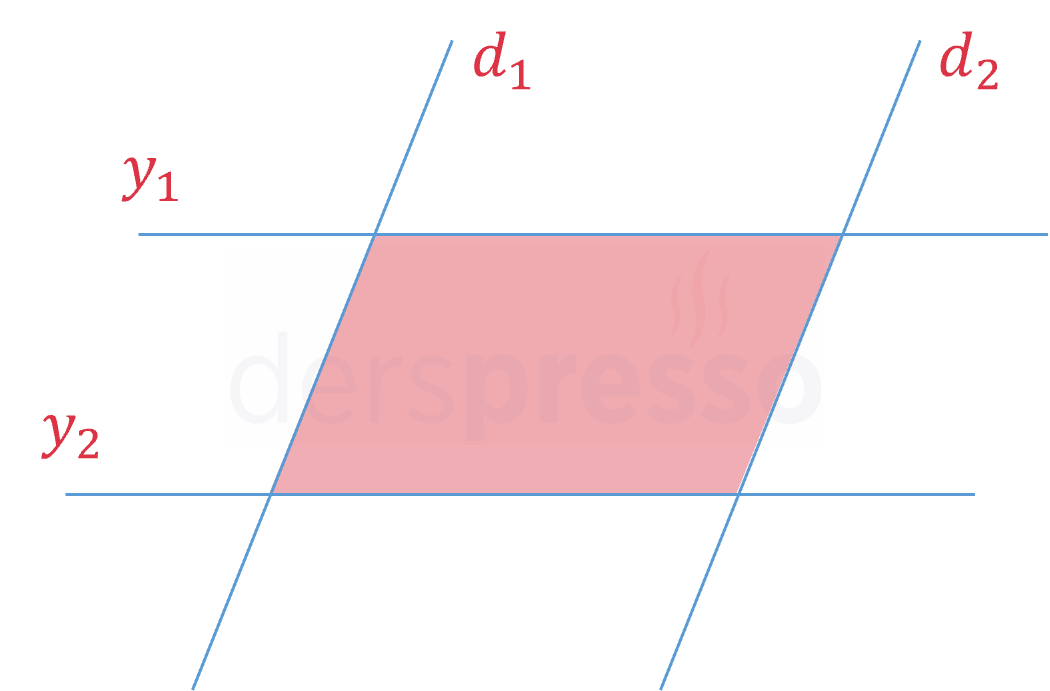
Tümü aynı düzlemde bulunan \( m \) tane paralel doğru arasından seçilen 2 doğru ile bu doğrulara paralel olmayan \( n \) tane farklı paralel doğru arasından seçilen 2 doğrunun kesişimleri de bir dörtgen oluşturur. Buna göre, bu doğruların oluşturduğu tüm dörtgenlerin sayısı paralel doğrular arasından yapılabilecek ikili seçimlerin çarpımı olan \( C(m, 2) \cdot C(n, 2) \) olur.
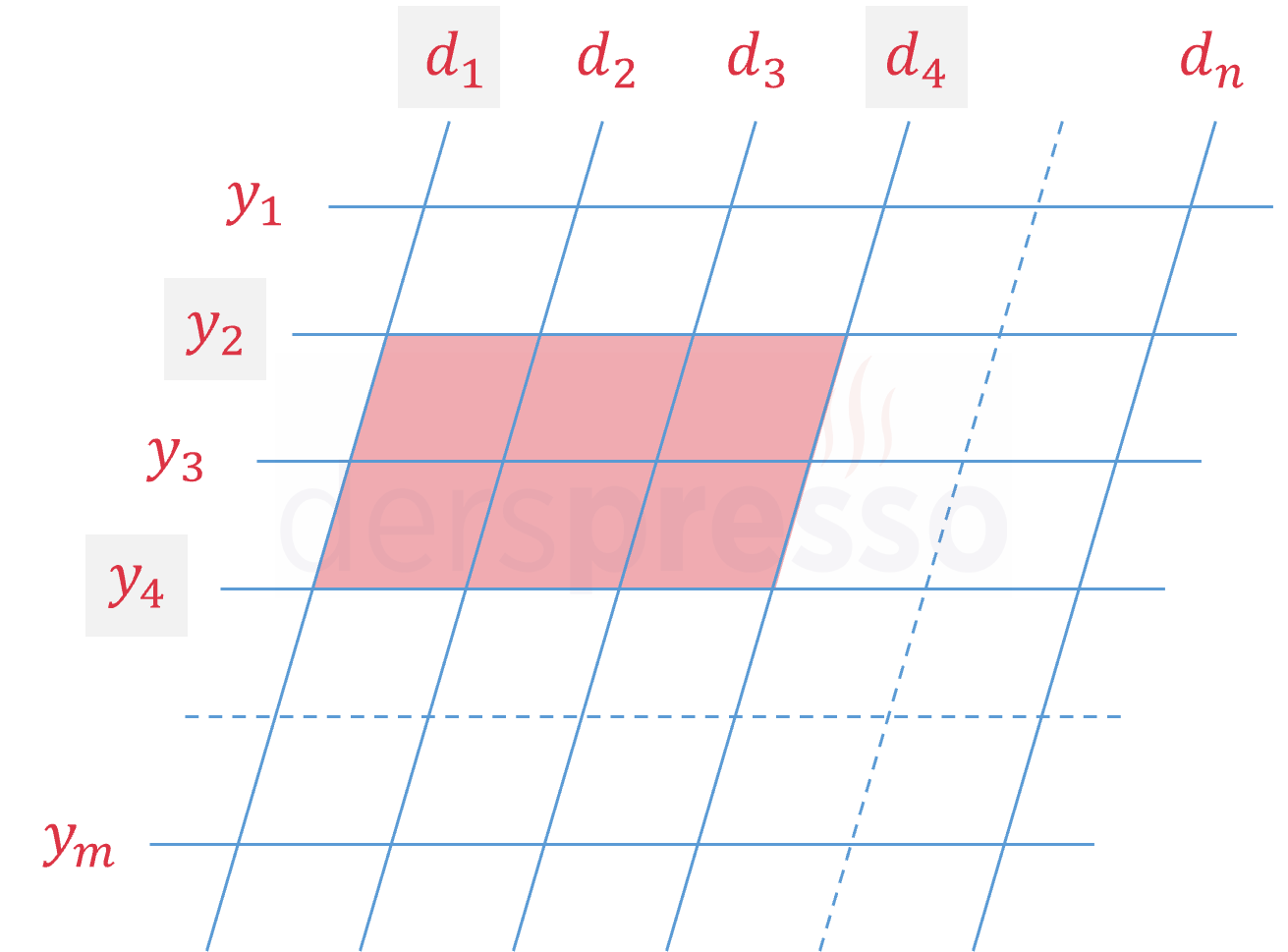
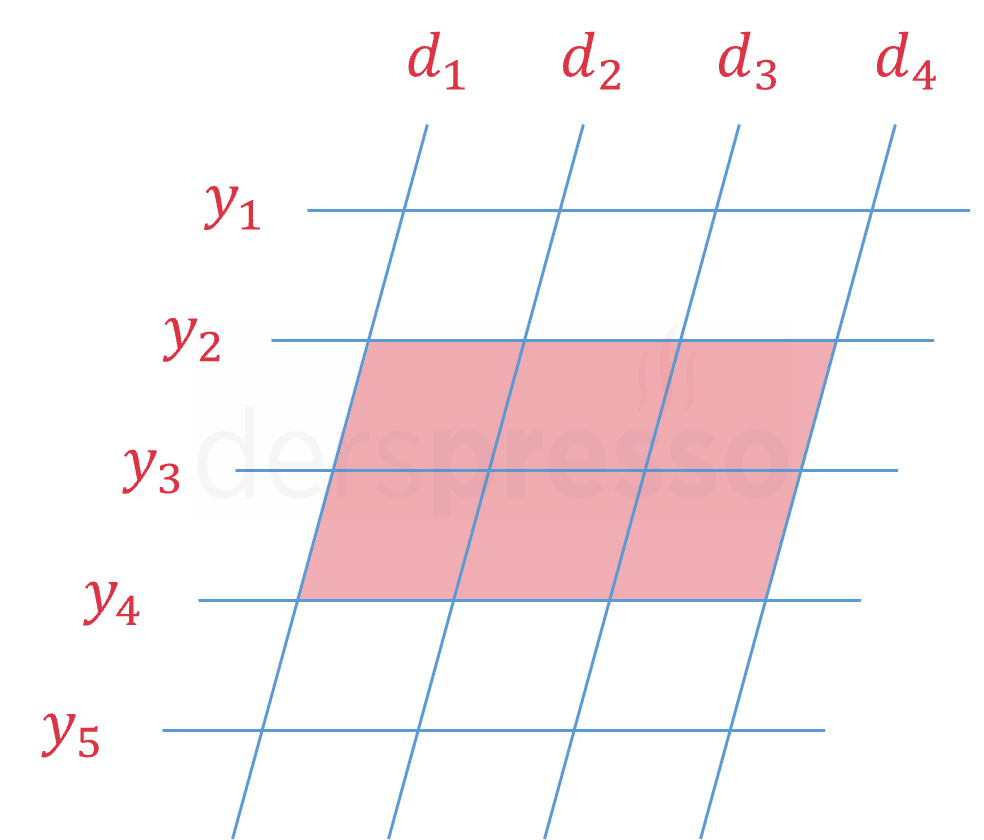
\( y_1 \parallel y_2 \parallel y_3 \parallel y_4 \parallel y_5 \) ve \(d_1 \parallel d_2 \parallel d_3 \parallel d_4 \) olduğuna göre, bu doğruların oluşturduğu kaç tane paralelkenar vardır?
Çözümü GösterYatay paralel doğrular arasından seçeceğimiz her 2 farklı doğru ve düşey paralel doğrular arasından seçeceğimiz her 2 farklı doğru arasında kalan alan bir paralelkenar oluşturur.
Buna göre, yatay ve paralel doğrular arasından yapabileceğimiz 2'şer farklı doğru seçim sayısı:
\( C(5, 2) \cdot C(4, 2) = 10 \cdot 6 = 60 \) tane paralelkenar vardır.
Bir kenarı 1 birim olan kare şeklindeki levhaya 25 adet kare sığdırılmıştır.
Buna göre, levha kaç farklı dikdörtgen barındırır?
Çözümü GösterLevhada 6 yatay, 6 düşey doğru parçası vardır. Yatay doğru parçaları arasından seçilecek herhangi iki doğru parçası ve düşey doğru parçaları arasından seçilecek herhangi iki doğru parçası bir dikdörtgen oluşturur.
Buna göre oluşan dikdörtgenlerin sayısı:
\( = C(6, 2) \cdot C(6, 2) \)
\( = 15 \cdot 15 = 225 \) tane dikdörtgen oluşur.
Paralel Doğruların Oluşturduğu Kareler
\( m \lt n \) olmak üzere, tümü aynı düzlemde bulunan, aralarındaki mesafe eşit \( m \) tane paralel doğru ve bu doğrulara dik ve aralarındaki mesafe eşit \( n \) tane paralel doğrunun kesişimlerinin oluşturduğu kare sayısı \( \sum_{i = 1}^m{(m - i + 1)(n - i + 1)} \) olur.
5 farklı kare en çok kaç noktada kesişir?
Çözümü Göster2 kare en çok 8 noktada kesişir.

\( n \) tane kare en çok \( 8 \cdot C(n, 2) \) noktada kesişir.
Buna göre 5 farklı karenin kesişebileceği en fazla nokta sayısı:
\( 8 \cdot C(5, 2) = 8 \cdot \dfrac{5 \cdot 4}{2 \cdot 1} = 80 \) kesişim noktası olur.
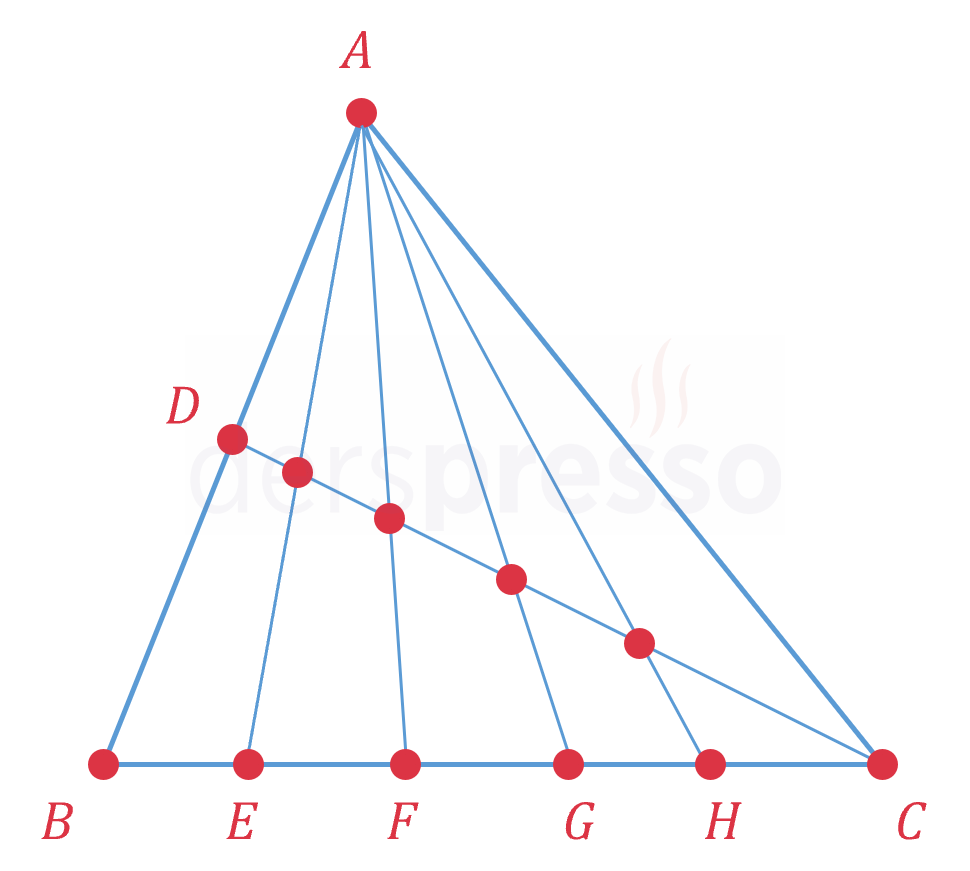
Yukarıdaki şekilde kaç üçgen vardır?
Çözümü GösterÜçgenin bir köşesi \( A \) ise diğer iki köşesi \( [CB] \) ve \( [CD] \) kenarları üzerinden seçilmelidir. \( [CB] \) üzerindeki 6 noktadan iki nokta \( C(6, 2) = 15 \) farklı şekilde seçilir. Aynı şekilde \( [CD] \) üzerindeki 6 noktadan iki nokta da 15 farklı şekilde seçilir. O halde, bir köşesi \( A \) olan \( 15 + 15 = 30 \) tane üçgen vardır.
Üçgenin bir köşesi \( C \), ikinci köşesi \( [HB] \) üzerindeki 5 noktadan biri, üçüncü köşesi de \( [CD] \) üzerinde bir nokta olan 5 farklı üçgen vardır.
Buna göre şekilde toplam \( 30 + 5 = 35 \) tane üçgen vardır.
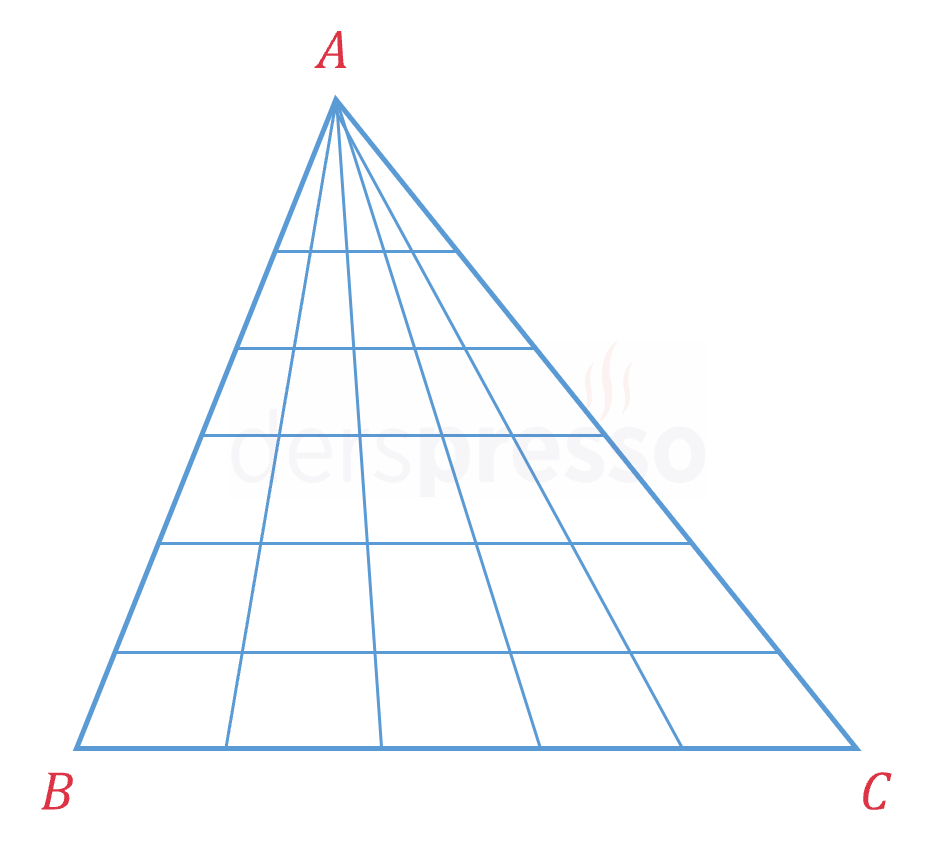
Yukarıdaki şekilde kaç üçgen vardır?
Çözümü GösterBu şekildeki üçgenlerin tümünün tepe köşesi ortak ve \( A \) noktasıdır.
\( A \) noktasında birleşen 6 doğru içinden seçilecek herhangi 2 doğru üçgenin yan kenarlarını oluşturur.
Buna göre bir üçgenin yan kenarları \( C(6, 2) = 15 \) farklı şekilde seçilebilir.
Birbirine paralel 6 doğru içinden seçilecek bir doğru üçgenin tabanını oluşturur.
Buna göre bir üçgenin tabanı \( C(6, 1) = 6 \) farklı şekilde seçilebilir.
Buna göre verilen şekilde seçilebilecek 2 yan kenar ve 1 taban ile oluşan \( 15 \cdot 6 = 90 \) üçgen vardır.
Bir çember üzerinde seçilen 6 noktayı köşe kabul eden kaç farklı çokgen çizilebilir?
Çözümü GösterÇember üzerinde seçilecek noktalar doğrusal değildir.
Bu 6 noktadan üçü ile \( C(6, 3) = 20 \) farklı üçgen çizilebilir.
Bu 6 noktadan dördü ile \( C(6, 4) = 15 \) farklı dörtgen çizilebilir.
Bu 6 noktadan beşi ile \( C(6, 5) = 6 \) farklı beşgen çizilebilir.
Bu 6 noktadan altısı ile \( C(6, 6) = 1 \) farklı altıgen çizilebilir.
Buna göre bu 6 nokta ile \( 20 + 15 + 6 + 1 = 42 \) farklı çokgen çizilebilir.
\( \mathbb{R}^3 \) kümesinde (3 boyutlu uzayda) birbirinden farklı 10 noktadan en fazla kaç düzlem geçer?
Çözümü GösterDoğrusal olmayan 3 nokta uzayda tek bir düzlem belirtir. Buna göre herhangi üçünün doğrusal olmadığı durumda 10 nokta arasından seçilecek her 3 nokta bir düzlem belirtir.
Buna göre 10 noktadan en fazla \( C(10, 3) = 120 \) düzlem geçer.

Şekilde \( O \) merkezli ve \( [AB] \) çaplı yarım daire verilmiştir.
Buna göre şekildeki noktaları kullanarak kaç daire dilimi elde edilebilir?
Çözümü Göster\( O \) noktasına ek olarak çember üzerindeki 9 noktadan herhangi 2'si seçilerek bir daire dilimi çizilebilir.
Buna göre verilen şekildeki noktalar ile \( C(9, 2) = 36 \) farklı daire dilimi elde edilebilir.

Şekildeki gibi bir düzgün altıgen prizmada birbirine paralel kaç farklı kenar ikilisi vardır?
Çözümü GösterBir düzgün altıgen prizmada kenarlar arasındaki paralellik iki şekilde olur.
Öncelikle, bir düzgün altıgen prizmada 6 yan kenar kendi aralarında paraleldir.
Buna göre, 6 yan kenar arasından seçilebilecek her kenar ikilisi kadar birbirine paralel kenar ikilisi vardır.
\( C(6, 2) = 15 \)
İkinci olarak, prizmanın alt ve üst tabanlarındaki karşılıklı kenarlar birbirine paraleldir. Örneğin alt tabandan seçilen bir kenar; alt tabanda karşısındaki 1 kenarla, üst tabanda aynı hizadaki 1 kenarla ve onun karşısındaki 1 kenarla olmak üzere toplam 3 kenarla paraleldir.
Alt ve üst tabandaki toplam 12 kenarı aralarında paralellik gösteren, her biri 4 kenardan oluşan 3 gruba ayırabiliriz.
Buna göre, her gruptaki 4 kenar arasından seçilebilecek her kenar ikilisi kadar paralel kenar ikilisi vardır.
\( C(4, 2) = 6 \)
Alt ve üst tabanda bu şekilde 3 kenar dörtlüsü vardır, dolayısıyla alt ve üst tabandaki kenarlar arasında birbirine paralel \( 3 \cdot 6 = 18 \) kenar ikilisi vardır.
Yan kenarlar arasındaki paralel kenar ikilileri ile alt ve üst taban kenarları arasındaki paralel kenar ikililerini toplayalım.
\( 15 + 18 = 33 \) bulunur.
\( i, j \in \{8, 9, 10, 11, 12\} \) olmak üzere,
Koordinat düzleminde köşeleri \( (i, j) \) noktalarında olan kaç üçgen çizilebilir?
Çözümü GösterVerilen \( (i, j) \) tanım kümesine göre üçgenin köşelerinin bulunabileceği \( 5 \cdot 5 = 25 \) tane nokta vardır.
25 nokta arasından 3 nokta \( C(25, 3) = 2300 \) farklı şekilde seçilebilir.
Bu 2300 farklı seçimden, seçilen 3 noktanın doğrusal olduğu durumları çıkarmamız gerekir.
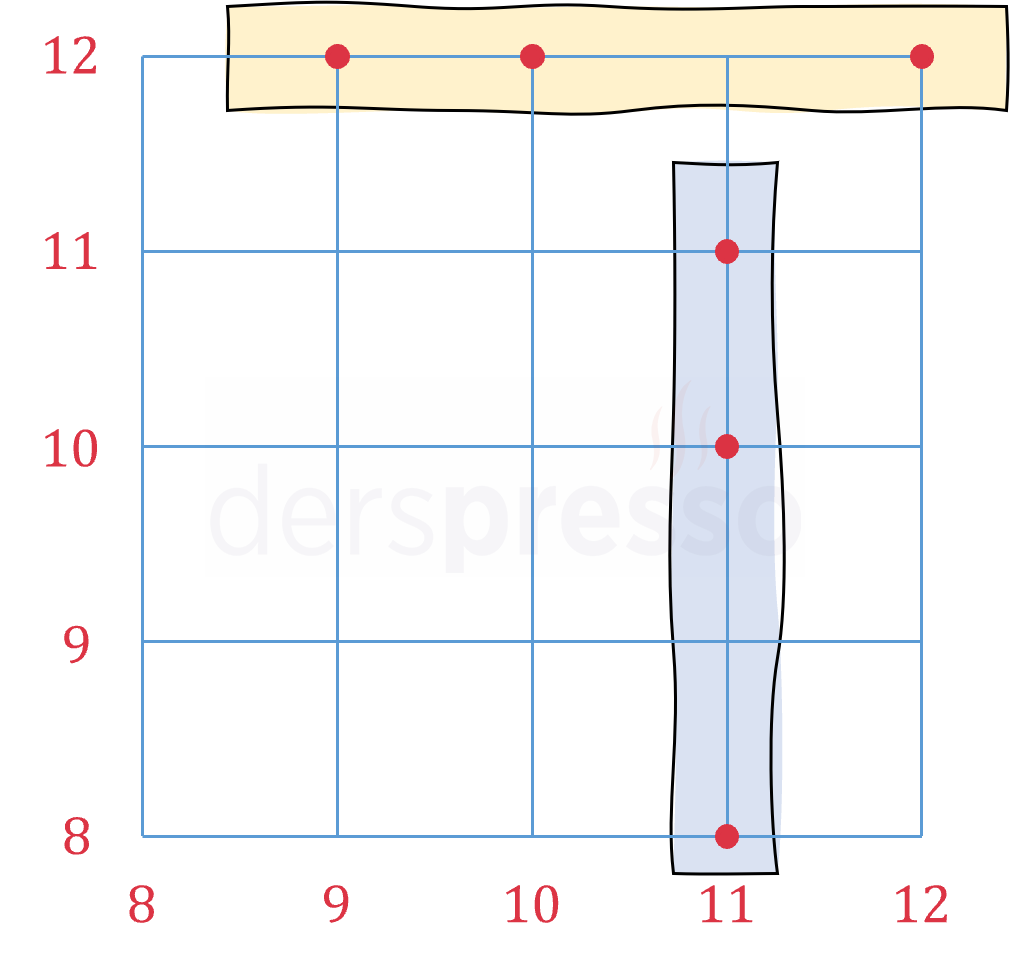
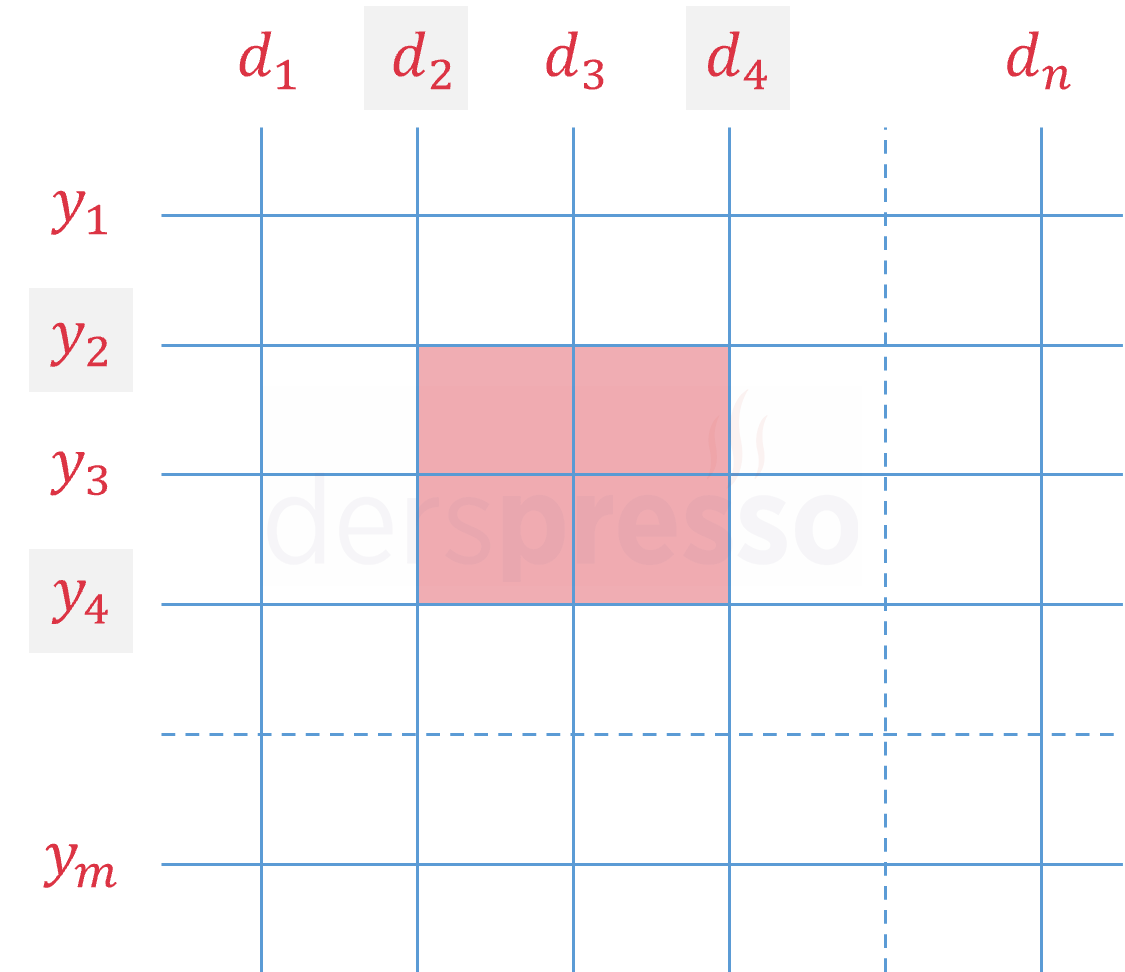
Yukarıdaki şekildeki turuncu kutuda olduğu gibi, aynı yatay doğru üzerinde seçilecek 3 nokta doğrusal olur. Bu şekilde seçilebilecek \( 5 \cdot C(5, 3) = 50 \) farklı nokta üçlüsü vardır.
Yukarıdaki şekildeki mavi kutuda olduğu gibi, aynı dikey doğru üzerinde seçilecek 3 nokta doğrusal olur. Bu şekilde seçilebilecek \( 5 \cdot C(5, 3) = 50 \) farklı nokta üçlüsü vardır.
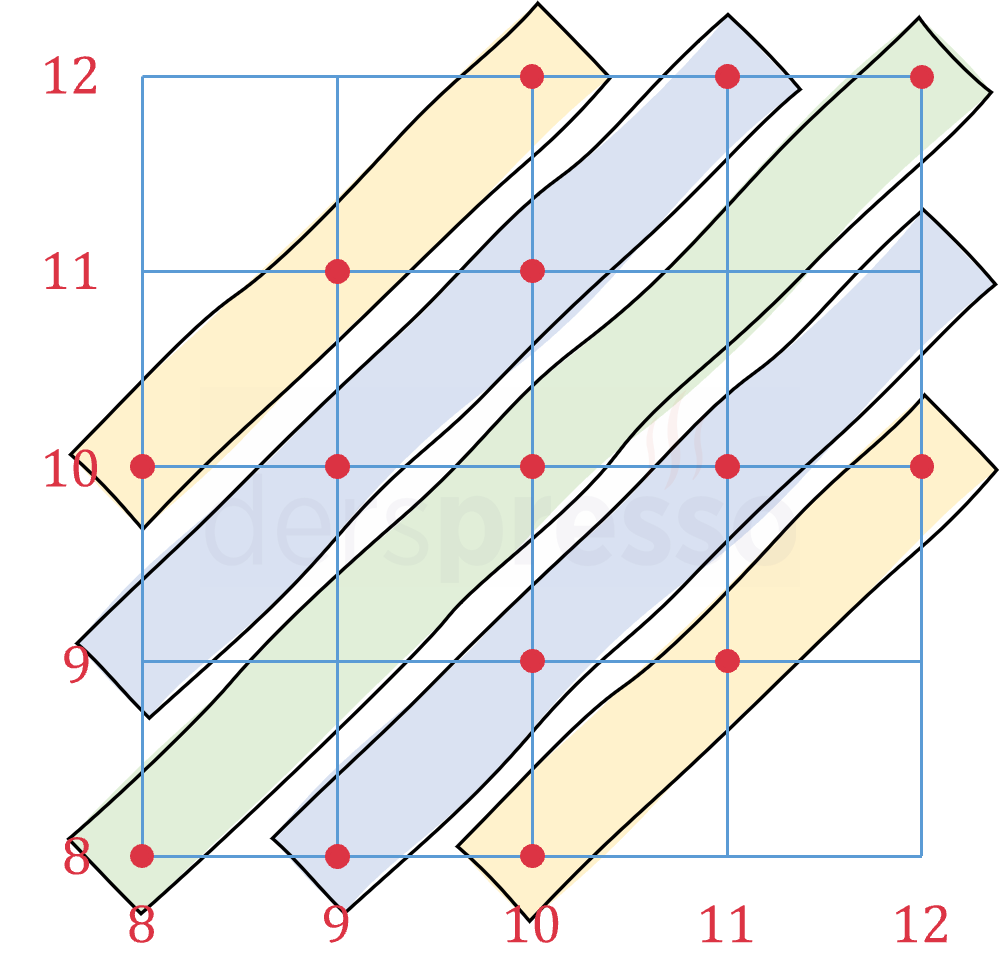
Yukarıdaki şekildeki turuncu kutularda olduğu gibi, 3 nokta içeren aynı çapraz doğru üzerinde seçilecek 3 nokta doğrusal olur. Bu kutuların yatay simetriklerini de sayarsak bu şekilde seçilebilecek \( 4 \cdot C(3, 3) = 4 \) farklı nokta üçlüsü vardır.
Yukarıdaki şekildeki mavi kutularda olduğu gibi, 4 nokta içeren aynı çapraz doğru üzerinde seçilecek 3 nokta doğrusal olur. Bu kutuların yatay simetriklerini de sayarsak bu şekilde seçilebilecek \( 4 \cdot C(4, 3) = 16 \) farklı nokta üçlüsü vardır.
Yukarıdaki şekildeki yeşil kutuda olduğu gibi, 5 nokta içeren aynı çapraz doğru üzerinde seçilecek 3 nokta doğrusal olur. Bu kutunun yatay simetriğini de sayarsak bu şekilde seçilebilecek \( 2 \cdot C(5, 3) = 20 \) farklı nokta üçlüsü vardır.
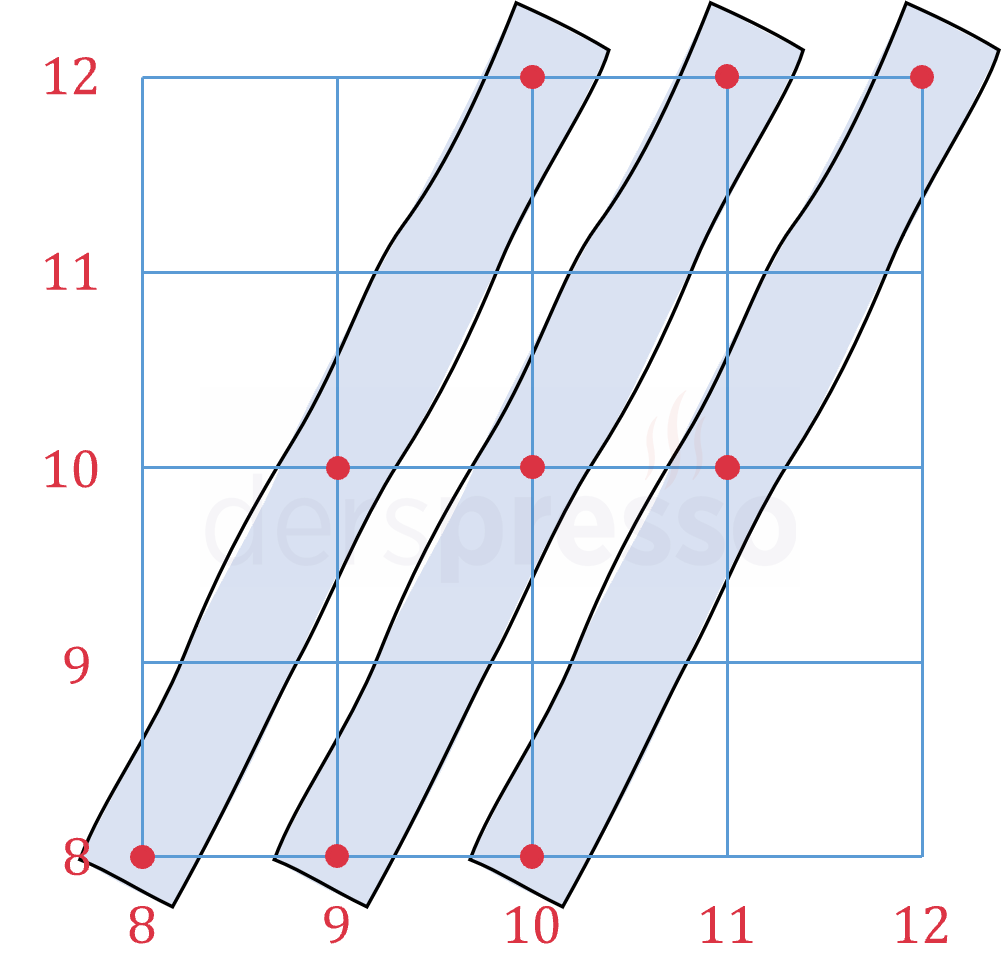
Yukarıdaki şekildeki mavi kutularda olduğu gibi, eğimleri 2 olacak şekilde 3 nokta içeren aynı çapraz doğru üzerinde seçilecek 3 nokta doğrusal olur. Bu kutuların eğimleri \( -2 \), \( \frac{1}{2} \) ve \( -\frac{1}{2} \) olacak şekilde yatay ve dikey simetriklerini de sayarsak bu şekilde seçilebilecek \( 4 \cdot 3 \cdot C(3, 3) = 12 \) farklı nokta üçlüsü vardır.
Doğrusal nokta üçlülerinin toplam sayısı \( 50 + 50 + 4 + 16 + 20 + 12 = 152 \) olur.
Buna göre köşeleri verilen noktalarda olan \( 2300 - 152 = 2148 \) tane üçgen çizilebilir.