Kombinasyon Tanımı
\( n \) elemanlı bir \( A \) kümesinin elemanları arasından bir sıra gözetmeksizin \( r \) elemanın seçim işlemine kombinasyon denir. Permütasyon işleminde elemanların dizilişi önemliyken kombinasyonda diziliş önemli değildir.
\( n \) elemanlı bir kümenin \( r \) elemanlı kombinasyonu \( C(n, r) \) ya da \( \binom{n}{r} \) ile gösterilir ve aşağıdaki formülle hesaplanır.
\( n, r \in \mathbb{N}, \quad r \le n \) olmak üzere,
\( C(n, r) = \binom{n}{r} = \dfrac{n!}{r!\ (n - r)!} \)
\( A = \{ \text{Eda}, \text{Ela}, \text{Can}, \text{Cem} \} \) olmak üzere,
\( A \) kümesinin 2'li kombinasyonları:
\( C(4, 2) = \dfrac{4!}{2!\ (4 - 2)!} = 6 \)
\( \{\text{Eda}, \text{Ela}\}, \{\text{Eda}, \text{Can}\} \)
\( \{\text{Eda}, \text{Cem}\}, \{\text{Ela}, \text{Can}\} \)
\( \{\text{Ela}, \text{Cem}\}, \{\text{Can}, \text{Cem}\} \)
\( A \) kümesinin 3'lü kombinasyonları:
\( C(4, 3) = \dfrac{4!}{3!\ (4 - 3)!} = 4 \)
\( \{\text{Eda}, \text{Ela}, \text{Can}\}, \{\text{Eda}, \text{Ela}, \text{Cem}\} \)
\( \{\text{Eda}, \text{Can}, \text{Cem}\}, \{\text{Ela}, \text{Can}, \text{Cem}\} \)
Kombinasyonda seçilen elemanların sırası önemli olmadığı için, yukarıdaki 2'li kombinasyonlarda \( \{\text{Eda}, \text{Ela}\} \) seçimine ek olarak \( \{\text{Ela}, \text{Eda}\} \) kümesinin seçime dahil edilmesine gerek yoktur.
Pratik bir yol olarak, \( n \)'nin \( r \)'li kombinasyonunu hesaplamak için paya \( n \)'den başlayarak ve birer eksilterek \( r \) sayının çarpımı yazılır (son sayının faktöriyeli alınmaz), paydaya da \( r \) faktöriyelin açılımı yazılır.
\( C(12, 4) = \dfrac{\overbrace{12 \cdot 11 \cdot 10 \cdot 9}^\text{4 kez}}{\underbrace{4 \cdot 3 \cdot 2 \cdot 1}_\text{4!}} = 495 \)
\( C(6, 2) - C(5, 3) + C(4, 1) \) işleminin sonucu kaçtır?
Çözümü Göster\( n \gt 0 \) olmak üzere,
\( \binom{n}{2} + \binom{n}{1} = 3(n + 1) \) olduğuna göre \( n \) kaçtır?
Çözümü GösterKombinasyon İşlem Kuralları
Hatırlatma olarak, 0 ve 1'in faktöriyel değerleri 1'dir.
\( 0! = 1! = 1 \)
\( n \lt r \) olmak üzere, \( n \) elemanlı bir kümenin \( r \) elemanlı kombinasyonu 0'dır. Bunu 3 kişi arasından 5 kişi 0 farklı şekilde seçilebilir şeklinde yorumlayabiliriz.
\( n \lt r \) olmak üzere,
\( C(n, r) = 0 \)
\( C(3, 5) = 0 \)
\( r \gt 0 \) olmak üzere, boş kümenin \( r \) elemanlı kombinasyonu 0'dır. Bunu boş kümenin 3 elemanlı alt kümelerinin sayısı sıfırdır şeklinde yorumlayabiliriz.
\( r \gt 0 \) olmak üzere,
\( C(0, r) = 0 \)
\( C(0, 3) = 0 \)
Boş kümenin boş küme olan alt küme sayısı 1'dir.
\( C(0, 0) = 1 \)
\( n \) elemanlı bir kümenin \( 0 \)'lı ve \( n \)'li kombinasyonları 1'e eşittir. \( n \) elemanlı bir küme içinden seçilebilecek 0 elemanlı tek alt küme boş kümedir. \( n \) elemanlı bir küme içinden seçilebilecek \( n \) elemanlı tek alt küme kümenin kendisidir.
\( C(n, 0) = C(n, n) = \dfrac{n!}{0!\ n!} = 1 \)
\( A = \{ a, b, c, d, e \} \) olmak üzere,
\( C(5, 0) = \dfrac{5!}{0!\ (5 - 0)!} \) \( = 1 \)
\( A \)'nın 0'lı kombinasyonu: \( \emptyset \)
\( C(5, 5) = \dfrac{5!}{5!\ (5 - 5)!} \) \( = 1 \)
\( A \)'nın 5'li kombinasyonu: \( \{a, b, c, d, e\} \)
\( n \) elemanlı bir kümenin \( 1 \)'li ve \( (n - 1) \)'li kombinasyonları \( n \)'ye eşittir. \( n \) elemanlı bir küme içinden seçilebilecek 1 elemanlı alt kümelerin her biri kümenin bir elemanını içerir. \( n \) elemanlı bir küme içinden seçilebilecek \( (n - 1) \) elemanlı alt kümeler kümenin kendisinden sırayla bir elemanın çıkartıldığı alt kümelerdir.
\( C(n, 1) = C(n, n - 1) \) \( = \dfrac{n!}{1!\ (n - 1)!} = n \)
\( C(5, 1) = \dfrac{5!}{1!\ (5 - 1)!} \) \( = \dfrac{5!}{1!\ 4!} = 5 \)
\( A \)'nın 1'li kombinasyonları: \( \{a\}, \{b\}, \{c\}, \{d\}, \{e\} \)
\( C(5, 4) = \dfrac{5!}{4!\ (5 - 4)!} \) \( = \dfrac{5!}{4!\ 1!} = 5 \)
\( A \)'nın 4'lü kombinasyonları: \( \{a, b, c, d\}, \{a, b, c, e\}, \) \( \{a, b, d, e\}, \{a, c, d, e\}, \) \( \{b, c, d, e\} \)
Yukarıdaki iki kuralın bir uzantısı olarak, \( n \) elemanlı bir kümenin \( r \)'li ve \( (n - r) \)'li kombinasyonları birbirine eşittir.
\( C(n, r) = C(n, n - r) \) \( = \dfrac{n!}{r!\ (n - r)!} \)
\( C(100, 60) = C(100, 40) \)
\( C(1000, 5) = C(1000, 995) \)
Bu kuralı şu şekilde de ifade edebiliriz: \( n \) elemanlı bir kümenin \( r \)'li ve \( k \)'lı kombinasyonları birbirine eşitse bu sayılar ya birbirine eşittir ya da toplamları \( n \)'ye eşittir.
\( r \le n, \quad k \le n \) olmak üzere,
\( C(n, r) = C(n, k) \) ise,
\( r = k \) veya \( r + k = n \)
\( C(8, 3) = C(8, k) \) ise,
\( k = 3 \) ya da \( k = 5 \)
Pascal Formülü
Pascal Üçgeni konusunda görsel olarak da göreceğimiz aşağıdaki kuralı burada formül olarak paylaşıyoruz.
\( C(n, r) + C(n, r + 1) = C(n + 1, r + 1) \)
\( C(8, 3) + C(8, 4) = C(9, 4) \)
İSPATI GÖSTER
\( C(n, n - 1) + 2C(n, n - 2) = 100 \) eşitliğini sağlayan \( n \) doğal sayısı kaçtır?
Çözümü Göster\( \binom{10}{x + 3} = \binom{10}{2x - 2} \) denklemini sağlayan \( x \) değerlerinin toplamı kaçtır?
Çözümü Göster\( \binom{79}{r^2 + 1} - \binom{79}{r + 6} = \binom{79}{r + 7} - \binom{79}{r^2} \) olduğuna göre,
\( r \)'nin alabileceği tam sayı değerlerin toplamı kaçtır?
Çözümü GösterKombinasyon - Permütasyon İlişkisi
Permütasyon ve kombinasyon formülleri arasında aşağıdaki ilişkiyi kurabiliriz.
\( 0 \le r \le n \) olmak üzere,
\( P(n, r) = C(n, r) \cdot r! \)
\( P(5, 3) = 5 \cdot 4 \cdot 3 = 60 \)
\( C(5, 3) = 10 \)
\( P(5, 3) = C(5, 3) \cdot 3! \)
\( 60 = 10 \cdot 6 \)
İSPATI GÖSTER
Buna göre \( n \)'nin \( r \)'li permütasyonunu aşağıdaki iki işlemin arka arkaya gerçekleştirildiği bir işlem olarak düşünülebilir.
- \( n \) elemanlı bir küme içinden \( r \) elemanın seçilmesi (\( C(n, r) \))
- Seçilen bu \( r \) elemanın farklı permütasyonları/dizilişleri (\( r! \))
5 kişinin katıldığı bir yarışmada 1., 2. ve 3. kaç farklı şekilde belirlenebilir?
Çözümü GösterKombinasyonun Kullanım Alanları
Kombinasyonun bazı kullanım alanları aşağıdaki gibidir.
Alt Küme Sayısı
\( n \) elemanlı bir kümenin \( r \)'li kombinasyonu aynı zamanda o kümenin \( r \) elemanlı alt küme sayısını verir.
\( n \) elemanlı bir kümenin \( r \) elemanlı alt kümelerinin sayısı \( = C(n, r) \)
6 elemanlı bir kümenin 2 elemanlı alt kümelerinin sayısı:
\( C(6, 2) = \dfrac{6!}{2!\ (6 - 2)!} = 15 \)
\( 0 \le r \le n \) olmak koşuluyla, \( n \) elemanlı bir kümenin tüm \( r \) elemanlı alt kümelerinin toplamı \( 2^n \)'e, yani kümeler konusunda gördüğümüz toplam alt küme sayı formülüne eşittir.
\( C(n, 0) + C(n, 1) + C(n, 2) + \ldots \) \( + C(n, n - 1) + C(n, n) \) \( = 2^n \)
Pascal Üçgeni
Binom açılımı konusunda göreceğimiz Pascal Üçgeni'nin her kutusundaki değerler o kutunun karşılık geldiği satır (\( n \)) ve sütun (\( r \)) için \( C(n, r) \) değerini verir. Ayrıca bir satırdaki tüm değerlerin toplamı bize yine \( 2^n \) değerini verir.
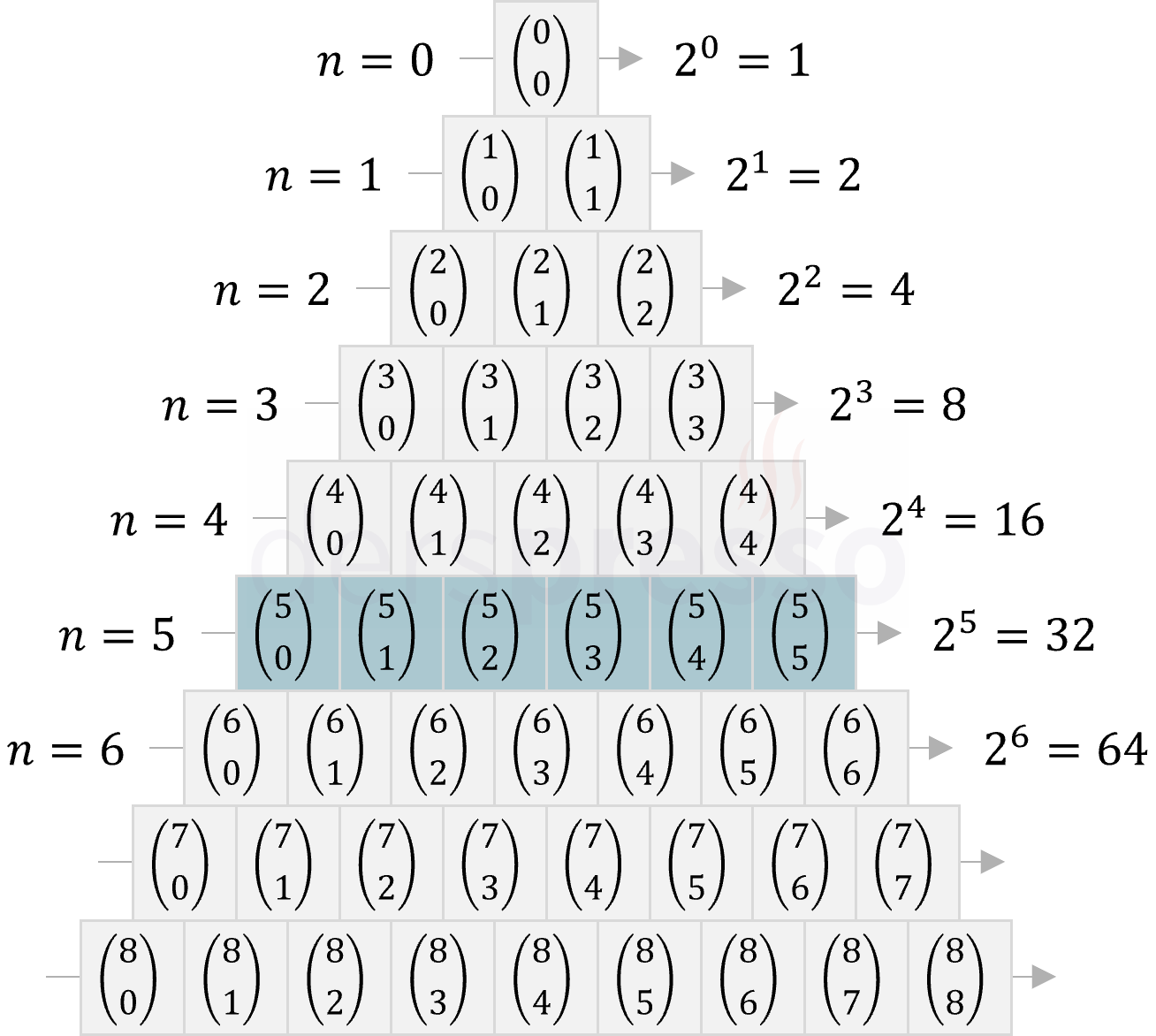
Belirli bir \( n \) sayısının çift sayı kombinasyonlarının toplamı tek sayı kombinasyonlarının toplamına eşittir.
\( C(n, 0) + C(n, 2) + C(n, 4) + \ldots = 2^{n - 1} \)
\( C(n, 1) + C(n, 3) + C(n, 5) + \ldots = 2^{n - 1} \)
Binom Katsayıları
Binom açılımı konusunda göreceğimiz iki terimli ifadelerin kuvvetlerinin açılımındaki katsayılar da kombinasyon formülleri ile hesaplanabilir. Bir binom ifadenin açılımını aşağıdaki şekilde ifade edebiliriz.
\( (x + y)^n = \binom{n}{0} x^{n - 0}y^0 \) \( + \binom{n}{1} x^{n - 1}y \) \( + \binom{n}{2} x^{n - 2}y^2 + \ldots \) \( + \binom{n}{k} x^{n - k}y^k + \ldots \) \( + \binom{n}{n} x^{n - n}y^{n - 0} \)
\( \binom{10}{3} + \binom{10}{4} + \ldots + \binom{10}{9} + \binom{10}{10} \) işleminin sonucu kaçtır?
Çözümü Göster\( \binom{9}{0} + \binom{9}{1} + \binom{9}{2} + \binom{9}{3} + \binom{9}{4} \) toplamının sonucu kaçtır?
Çözümü Göster