Durağan ve Kritik Noktalar
Bir fonksiyonun grafiğinde incelenmesi gereken önemli noktalardan ikisi durağan ve kritik noktalardır.
Durağan Noktalar
Bir fonksiyonun birinci türevinin tanımlı ve sıfır olduğu iç noktalara durağan nokta denir.
\( f'(a) = 0 \) ise,
\( x = a \) noktası \( f \) fonksiyonunun bir durağan noktasıdır.
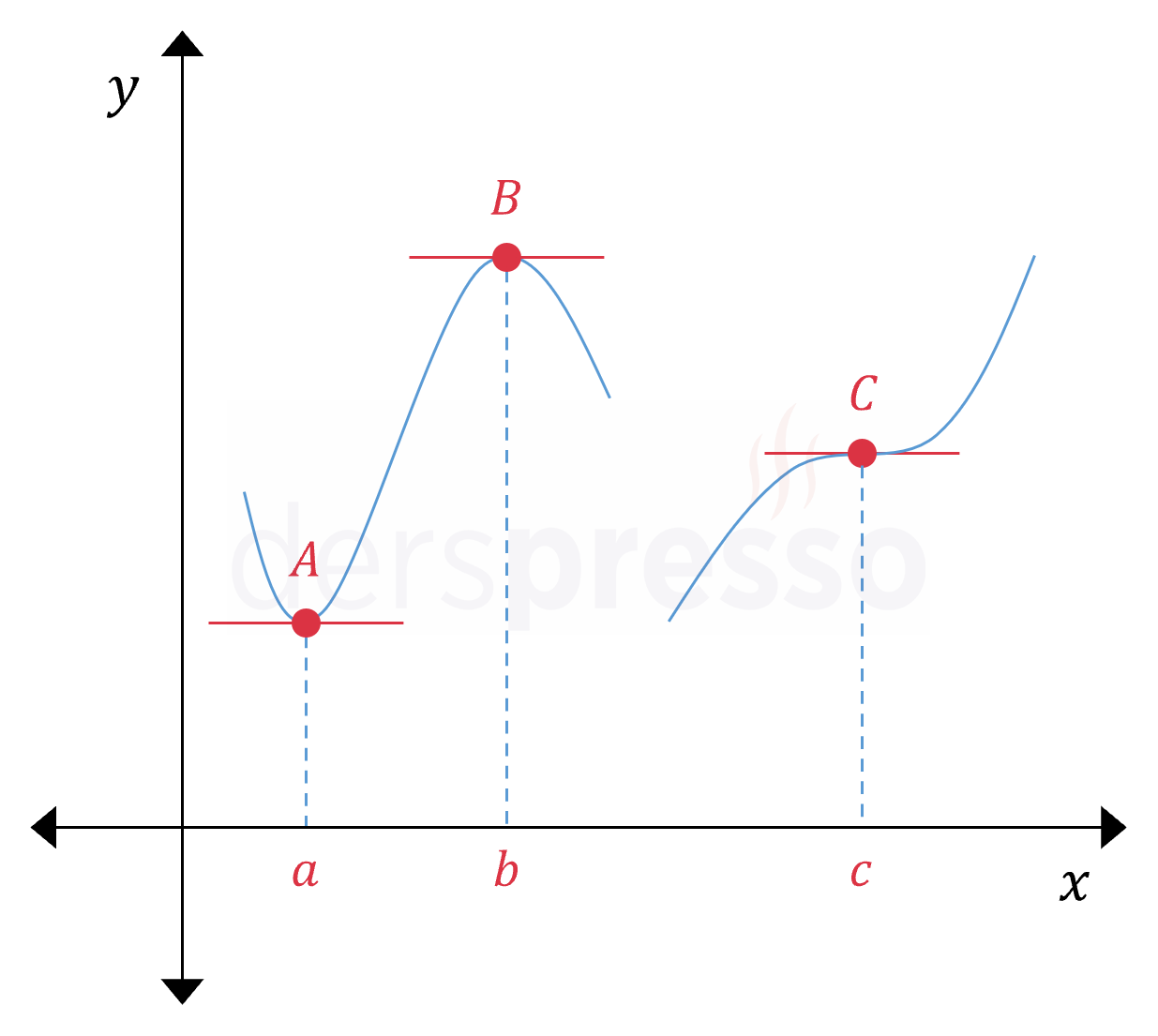
Durağan noktalar iki tipte olabilir.
- Türevlenebilir ekstremum noktaları: Bu noktalarda fonksiyonun grafiğinde bir yerel minimum ya da maksimum oluşur, fonksiyonun artış/azalış yönü değişir ve fonksiyonun birinci türevi (eğimi) işaret değiştirir. Şekildeki \( A \) ve \( B \) noktaları bu tipte noktalardır.
- Yatay büküm noktası: Bu noktalarda fonksiyonun grafiğinde bir yerel minimum ya da maksimum oluşmaz, fonksiyonun artış/azalış yönü ve birinci türevinin işareti değişmez. Şekildeki \( C \) noktası bu tipte bir noktadır.
\( f(x) = 4x^3 + 6mx^2 + 3x + 7 \) fonksiyonunun durağan noktasının olmaması için \( m \) değer aralığı ne olmalıdır?
Bir fonksiyonun birinci türevinin tanımlı ve sıfır olduğu iç noktalar fonksiyonun durağan noktalarıdır.
Bir fonksiyonun durağan noktasının olmaması için fonksiyonun birinci türevini sıfır yapan bir reel sayı \( x \) değeri bulunmamalıdır.
\( f'(x) = 12x^2 + 12mx + 3 \)
Bu ikinci dereceden fonksiyonun sıfır değerini almaması için grafiği \( x \) eksenini kesmemelidir, dolayısıyla deltası sıfırdan küçük olmalıdır.
\( \Delta = b^2 - 4ac \lt 0 \)
\( (12m)^2 - 4(12)(3) \lt 0 \)
\( 144(m - 1)(m + 1) \lt 0 \)
\( -1 \lt m \lt 1 \) bulunur.
Bir fonksiyonun herhangi bir sayıda (sıfır ve sonsuz dahil) durağan noktası olabilir. Örneğin aşağıda soldaki fonksiyonun hiçbir durağan noktası yokken sağdaki periyodik fonksiyonun sonsuz sayıda durağan noktası vardır.
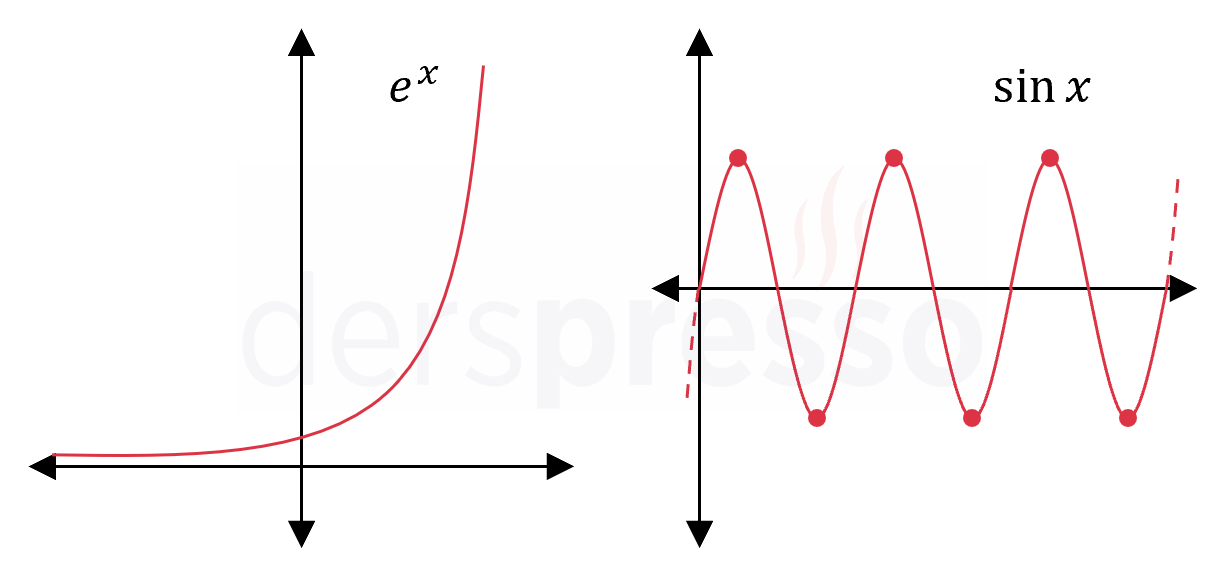
Kritik Noktalar
Bir fonksiyonun tanımlı olduğu aralıkta birinci türevinin sıfır ya da tanımsız olduğu iç noktalara kritik nokta denir. Bu tanıma göre her durağan nokta aynı zamanda bir kritik noktadır, ancak her kritik nokta bir durağan nokta değildir.
\( f(a) \) tanımlı ve
\( f'(a) = 0 \) ya da \( f'(a) \) tanımsız ise,
\( x = a \) noktası \( f \) fonksiyonunun bir kritik noktasıdır.
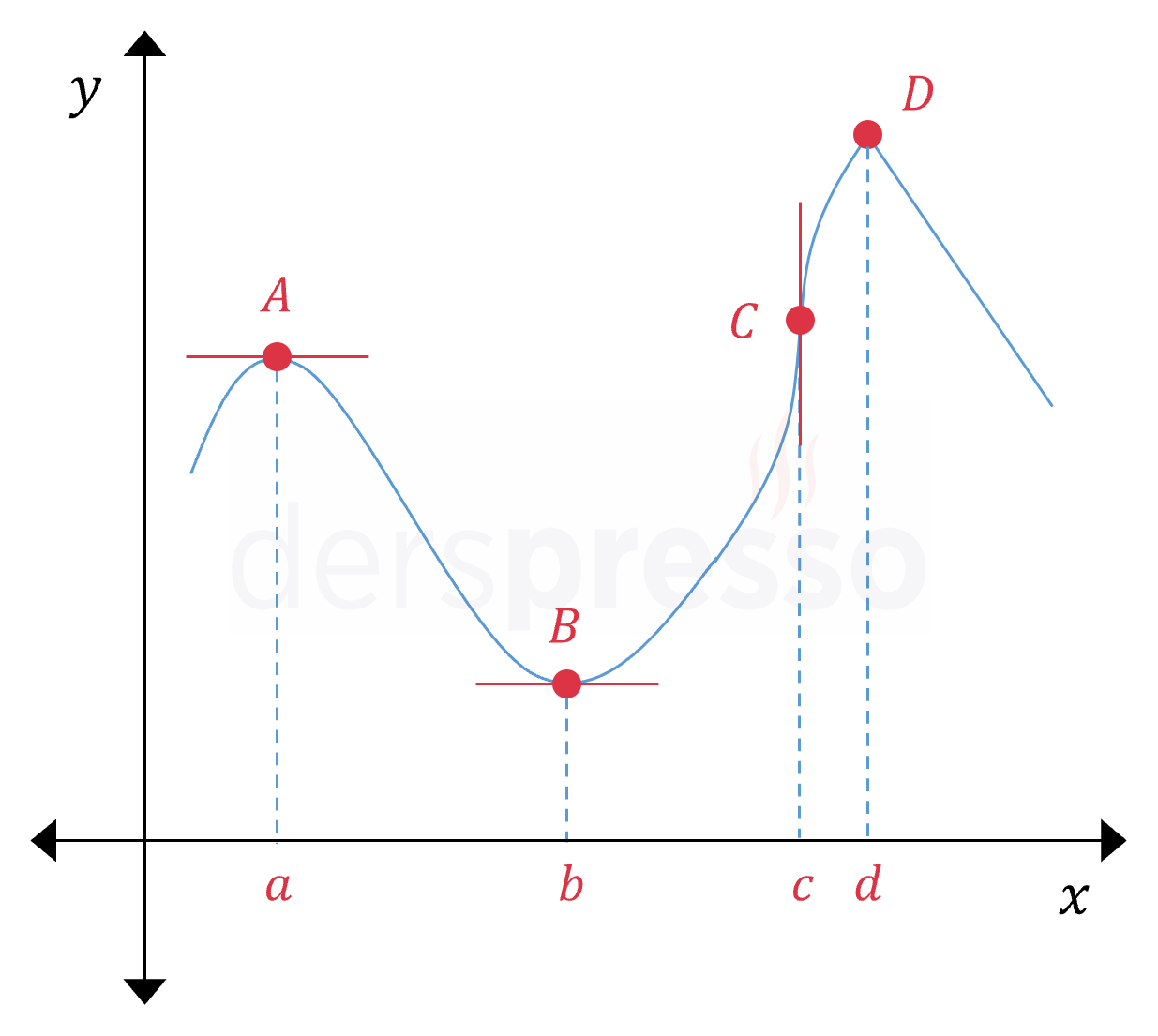
Yukarıdaki şekilde farklı tipteki kritik noktalar gösterilmiştir.
- \( A \), \( B \) ve \( C \) noktalarında birinci türev sıfırdır, dolayısıyla bu noktalar birer kritik (ve aynı zamanda durağan) noktadır.
- \( D \) noktasındaki teğet doğru dikeydir ve birinci türev (eğim) tanımsızdır, dolayısıyla bu nokta bir kritik noktadır.
- \( E \) noktasında soldan ve sağdan türevler birbirine eşit olmadığı için birinci türev tanımsızdır, dolayısıyla bu nokta bir kritik noktadır.
- \( F \) noktası sürekli olmadığı için birinci türev tanımsızdır, dolayısıyla bu nokta bir kritik noktadır.
Bir fonksiyonun herhangi bir sayıda (sıfır ve sonsuz dahil) kritik noktası olabilir. Yukarıda durağan noktalar için paylaştığımız örneklere ek olarak, aşağıda soldaki fonksiyonun hiçbir kritik noktası yokken sağdaki periyodik fonksiyonun sonsuz sayıda kritik noktası vardır.
Bir fonksiyonun kritik noktalarının bulunması, fonksiyonun grafiğinin çiziminde ve maksimum - minimum (optimizasyon) problemlerinin çözümünde önemli bir adımdır.
NOT: Farklı kaynaklarda durağan ve kritik noktaların fonksiyonun iç ya da sınır noktası olabilecek şekilde tanımlandığı görülebilir. Biz burada her iki nokta tipi için de tanımı iç noktalarla sınırlı tutuyoruz.
Aşağıdaki fonksiyonların tanımlı oldukları en geniş aralıktaki durağan noktalarını bulunuz.
(a) \( f(x) = \dfrac{x^2 - 1}{x} \)
(b) \( g(x) = \dfrac{x^2}{x - 1} \)
(c) \( h(x) = \dfrac{x^2 + x + 1}{x} \)
Çözümü GösterBir fonksiyonun birinci türevinin tanımlı ve sıfır olduğu noktalara durağan nokta denir.
(a) seçeneği:
\( f: \mathbb{R} - \{0\} \to \mathbb{R} \)
\( f(x) = \dfrac{x^2 - 1}{x} \)
\( = x - \dfrac{1}{x} \)
Fonksiyonun birinci türevini alalım.
\( f'(x) = 1 + \dfrac{1}{x^2} \)
Birinci türevi sıfıra eşitleyelim.
\( 1 + \dfrac{1}{x^2} = 0 \)
\( \dfrac{1}{x^2} \) asla negatif olamayacağı için bu eşitliğin çözümü yoktur. Dolayısıyla, bu fonksiyonun durağan noktası yoktur.
(b) seçeneği:
\( g: \mathbb{R} - \{1\} \to \mathbb{R} \)
\( g(x) = \dfrac{x^2}{x - 1} \)
Fonksiyonun birinci türevini alalım.
\( g'(x) = \dfrac{2x(x - 1) - x^2}{(x - 1)^2} \)
\( = \dfrac{x(x - 2)}{(x - 1)^2} \)
Birinci türevi sıfıra eşitleyelim.
\( \dfrac{x(x - 2)}{(x - 1)^2} = 0 \)
\( x \in \{ 0, 2 \} \)
Buna göre \( x = 0 \) ve \( x = 2 \) noktaları fonksiyonun durağan noktalarıdır.
(c) seçeneği:
\( h: \mathbb{R} - \{0\} \to \mathbb{R} \)
\( h(x) = \dfrac{x^2 + x + 1}{x} \)
\( = x + 1 + \dfrac{1}{x} \)
Fonksiyonun birinci türevini alalım.
\( h'(x) = 1 - \dfrac{1}{x^2} \)
Birinci türevi sıfıra eşitleyelim.
\( 1 - \dfrac{1}{x^2} = 0 \)
\( \dfrac{(x - 1)(x + 1)}{x^2} = 0 \)
\( x \in \{ -1, 1 \} \)
Buna göre \( x = -1 \) ve \( x = 1 \) noktaları fonksiyonun durağan noktalarıdır.
Aşağıdaki fonksiyonların tanımlı oldukları en geniş aralıktaki kritik noktalarını bulunuz.
(a) \( f(x) = 2x^2 - 8x + 7 \)
(b) \( g(x) = x^2 + \dfrac{16}{x} \)
(c) \( h(x) = x(2 - x)^3 \)
Çözümü GösterBir fonksiyonun tanım kümesi içinde birinci türevi sıfır ya da tanımsız olan noktalara kritik nokta denir.
(a) seçeneği:
\( f: \mathbb{R} \to \mathbb{R} \)
\( f(x) = 2x^2 - 8x + 7 \)
Fonksiyonun birinci türevini alalım.
\( f'(x) = 4x - 8 \)
Birinci türevi sıfıra eşitleyelim.
\( 4x - 8 = 0 \)
\( x = 2 \)
\( x = 2 \) noktasında fonksiyon tanımlı ve \( f'(2) = 0 \) olduğundan bu nokta fonksiyonun bir kritik noktasıdır.
(b) seçeneği:
\( g: \mathbb{R} - \{0\} \to \mathbb{R} \)
\( g(x) = x^2 + \dfrac{16}{x} \)
Fonksiyonun birinci türevini alalım.
\( g'(x) = 2x - \dfrac{16}{x^2} \)
Birinci türevi sıfıra eşitleyelim.
\( 2x - \dfrac{16}{x^2} = 0 \)
\( \dfrac{2x^3 - 16}{x^2} = 0 \)
\( \dfrac{2(x - 2)(x^2 + 2x + 4)}{x^2} = 0 \)
\( x = 2 \)
\( x = 2 \) noktasında fonksiyon tanımlı ve \( f'(2) = 0 \) olduğundan bu nokta fonksiyonun bir kritik noktasıdır.
\( x = 0 \) noktasında birinci türev tanımsızdır, ancak bu noktada fonksiyon da tanımsız olduğu için bu nokta fonksiyonun bir kritik noktası değildir.
(c) seçeneği:
\( h: \mathbb{R} \to \mathbb{R} \)
\( h(x) = x(2 - x)^3 \)
Fonksiyonun birinci türevini alalım.
\( h'(x) = (2 - x)^3 - 3x(2 - x)^2 \)
\( = (2 - x)^2(2 - 4x) \)
Birinci türevi sıfıra eşitleyelim.
\( (2 - x)^2(2 - 4x) = 0 \)
\( x \in \{ \dfrac{1}{2}, 2 \} \)
\( x = \frac{1}{2} \) noktasında fonksiyon tanımlı ve \( f'(\frac{1}{2}) = 0 \) olduğundan bu nokta fonksiyonun bir kritik noktasıdır.
\( x = 2 \) noktasında fonksiyon tanımlı ve \( f'(2) = 0 \) olduğundan bu nokta fonksiyonun bir kritik noktasıdır.
\( f: \mathbb{R} \to \mathbb{R} \) olmak üzere,
\( f(x) = x^{\frac{1}{3}}(x - 2) \) fonksiyonunun durağan ve kritik noktalarını bulunuz.
Çözümü GösterBir fonksiyonun birinci türevinin tanımlı ve sıfır olduğu noktalara durağan nokta denir.
Fonksiyonun birinci türevini alalım.
\( f'(x) = \dfrac{1}{3}x^{-\frac{2}{3}}(x - 2) + x^{\frac{1}{3}} \)
\( = \dfrac{4x - 2}{3x^{\frac{2}{3}}} \)
Durağan noktaları bulmak için birinci türevi sıfıra eşitleyelim.
\( \dfrac{4x - 2}{3x^{\frac{2}{3}}} = 0 \)
\( 4x - 2 = 0 \)
\( x = \dfrac{1}{2} \)
\( x = \frac{1}{2} \) noktasında birinci türev tanımlı ve \( f'(\frac{1}{2}) = 0 \) olduğundan bu nokta fonksiyonun bir durağan noktasıdır.
Bir fonksiyonun tanım kümesi içinde birinci türevi sıfır ya da tanımsız olan noktalara kritik nokta denir.
Buna göre \( x = \frac{1}{2} \) noktası aynı zamanda kritik noktadır.
\( x = 0 \) noktasında fonksiyon tanımlı ve birinci türev tanımsız olduğundan bu nokta fonksiyonun bir kritik noktasıdır.
Durağan noktalar: \( x = \dfrac{1}{2} \)
Kritik noktalar: \( x \in \{ 0, \dfrac{1}{2} \} \)
\( f: \mathbb{R} - \{1\} \to \mathbb{R} \) olmak üzere,
\( f(x) = \dfrac{x^2 + x - 6}{x - 1} \) fonksiyonunun durağan ve kritik noktalarını bulunuz.
Çözümü GösterBir fonksiyonun birinci türevinin tanımlı ve sıfır olduğu noktalara durağan nokta denir.
Fonksiyonun birinci türevini alalım.
\( f'(x) = \dfrac{(2x + 1)(x - 1) - (x^2 + x - 6)}{(x - 1)^2} \)
\( = \dfrac{x^2 - 2x + 5}{(x - 1)^2} \)
Durağan noktaları bulmak için birinci türevi sıfıra eşitleyelim.
\( \dfrac{x^2 - 2x + 5}{(x - 1)^2} = 0 \)
\( x^2 - 2x + 5 = 0 \)
Denklemin deltasını hesaplayalım.
\( \Delta = b^2 - 4ac \)
\( = (-2)^2 - 4(1)(5) \)
\( = 4 - 20 = -16 \lt 0 \)
\( \Delta \lt 0 \) olduğundan denklemin reel kökü yoktur, yani birinci türevi sıfır yapan bir \( x \) değeri yoktur, dolayısıyla fonksiyonun durağan noktası yoktur.
Bir fonksiyonun tanım kümesi içinde birinci türevi sıfır ya da tanımsız olan noktalara kritik nokta denir.
\( x = 1 \) noktasında birinci türev tanımsızdır, ancak bu noktada fonksiyon da tanımsız olduğu için bu nokta fonksiyonun bir kritik noktası değildir.
Durağan noktalar: \( x \in \emptyset \)
Kritik noktalar: \( x \in \emptyset \)
\( f: \mathbb{R} \to \mathbb{R} \) olmak üzere,
\( f(x) = \sqrt[3]{x^2 - 9} \) fonksiyonunun durağan ve kritik noktalarını bulunuz.
Çözümü GösterBir fonksiyonun birinci türevinin tanımlı ve sıfır olduğu noktalara durağan nokta denir.
Fonksiyonun birinci türevini alalım.
\( f'(x) = \dfrac{1}{3}(x^2 - 9)^{-\frac{2}{3}}2x \)
\( = \dfrac{2x}{3\sqrt[3]{(x^2 - 9)^2}} \)
Durağan noktaları bulmak için birinci türevi sıfıra eşitleyelim.
\( \dfrac{2x}{3\sqrt[3]{(x^2 - 9)^2}} = 0 \)
\( x = 0 \)
\( x = 0 \) noktasında birinci türev tanımlı ve \( f'(0) = 0 \) olduğundan bu nokta fonksiyonun bir durağan noktasıdır.
Bir fonksiyonun tanım kümesi içinde birinci türevi sıfır ya da tanımsız olan noktalara kritik nokta denir.
Buna göre \( x = 0 \) noktası aynı zamanda kritik noktadır.
Türev fonksiyonunu tanımsız yapan değerleri bulmak için paydayı sıfıra eşitleyelim.
\( 3\sqrt[3]{(x^2 - 9)^2} = 0 \)
\( x \in \{ -3, 3 \} \)
\( x = -3 \) noktasında fonksiyon tanımlı ve birinci türev tanımsız olduğundan bu nokta fonksiyonun bir kritik noktasıdır.
\( x = 3 \) noktasında fonksiyon tanımlı ve birinci türev tanımsız olduğundan bu nokta fonksiyonun bir kritik noktasıdır.
Durağan noktalar: \( x = 0 \)
Kritik noktalar: \( x \in \{ -3, 0, 3 \} \)