Lineer Denklem Sistemlerinin Çözüm Durumları
Lineer denklem sistemlerinin çözüm kümesi üç şekilde olabilir.
- Tek çözümlü: Denklem sistemini sağlayan tek bir \( (s_1, s_2, \ldots, s_n) \) sıralı \( n \)'lisi vardır. Bu denklem sistemlerinde satır eşelon formu her sütunda bir pivot içerir. Pivotu olan bu sütunların karşılık geldiği değişkenleri temel değişken olarak isimlendireceğiz.
- Çözümsüz: Denklem sistemini sağlayan hiçbir \( (s_1, s_2, \ldots, s_n) \) sıralı \( n \)'lisi yoktur. Bu denklem sistemlerinde satır eşelon formu \( b \ne 0 \) olmak üzere \( [\ 0\ 0\ \ldots\ 0\ |\ b\ ] \) formunda bir satır içerir.
- Sonsuz sayıda çözümlü: Denklem sistemini sağlayan sonsuz sayıda \( (s_1, s_2, \ldots, s_n) \) sıralı \( n \)'lisi vardır. Bu denklem sistemlerinde satır eşelon formu pivotu olmayan sütun(lar) içerir. Pivotu olmayan bu sütunların karşılık geldiği değişkenleri serbest değişken olarak isimlendireceğiz.
Şimdi bu üç durumu daha detaylı inceleyelim.
Tek Çözümlü Sistem
Aşağıdaki denklem sisteminin çözümünü bulalım.
\( \begin{array}{rrrrcl} & x_2 & −2x_3 & +7x_4 & = & 11 \\ x_1 & +2x_2 & +4x_3 & +4x_4 & = & 10 \\ x_1 & -2x_2 & -3x_3 & -4x_4 & = & -9 \\ -3x_1 & +3x_2 & +x_3 & +5x_4 & = & 8 \end{array} \)
Denklem sistemini artırılmış matris formunda yazalım ve Gauss eliminasyon yöntemiyle satır eşelon formuna getirelim.
Orijinal denklem sistemi:
\( \left[ \begin{array}{cccc|c} 0 & 1 & -2 & 7 & 11 \\ 1 & 2 & 4 & 4 & 10 \\ 1 & -2 & -3 & -4 & -9 \\ -3 & 3 & 1 & 5 & 8 \end{array} \right] \)
Satır eşelon formu:
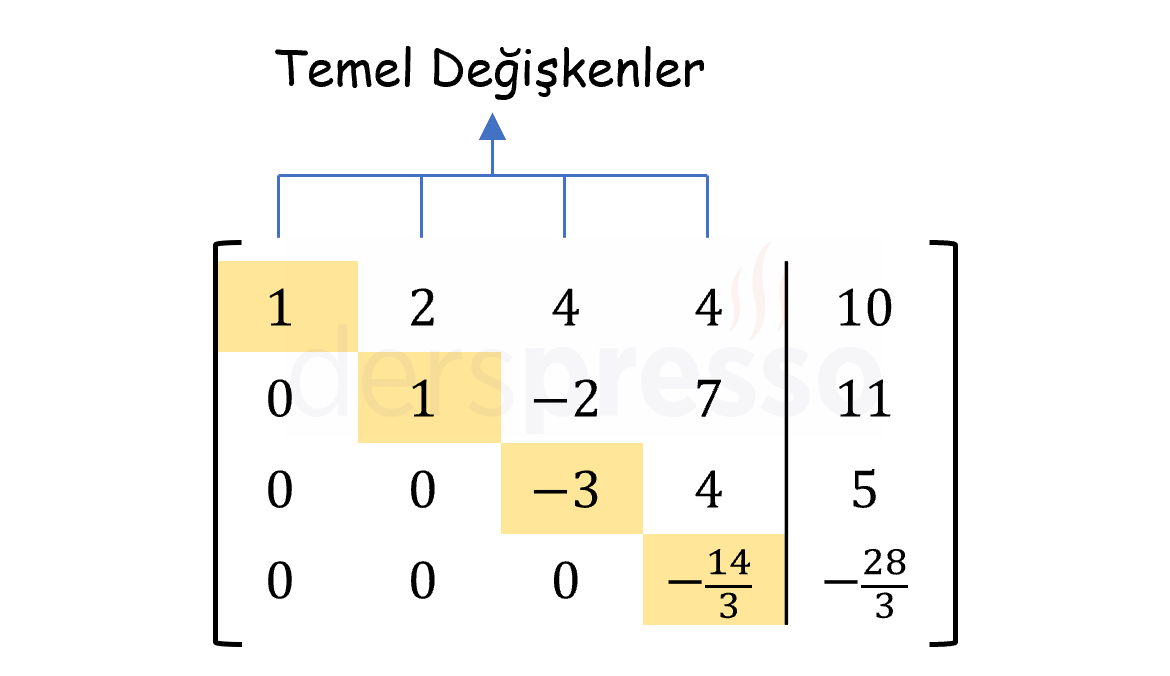
\( \left[ \begin{array}{cccc|c} \color{red}{1} & 2 & 4 & 4 & 10 \\ 0 & \color{red}{1} & -2 & 7 & 11 \\ 0 & 0 & \color{red}{-3} & 4 & 5 \\ 0 & 0 & 0 & \color{red}{-\frac{14}{3}} & -\frac{28}{3} \end{array} \right] \)
Dikkat edilirse elde ettiğimiz satır eşelon formu her sütunda bir pivot içermektedir, bu da lineer denklem sisteminin tek çözümünün olduğuna işaret etmektedir. Satır eşelon formunda pivotu olan değişkenlere temel değişken adı verilir. Buna göre \( x_1 \), \( x_2 \), \( x_3 \) ve \( x_4 \) birer temel değişkendir.
Elde ettiğimiz satır eşelon formundaki denklem sistemini, en son denklemden başlayarak geriye doğru yerine koyma yöntemi ile çözelim.
Dördüncü denklemi kullanarak \( x_4 \) değerini bulalım.
\( -\dfrac{14}{3}x_4 = -\dfrac{28}{3} \)
\( x_4 = 2 \)
Üçüncü denklemi ve \( x_4 \) değerini kullanarak \( x_3 \) değerini bulalım.
\( -3x_3 + 4x_4 = 5 \)
\( -3x_3 + 4(2) = 5 \)
\( x_3 = 1 \)
İkinci denklemi ve \( x_3, x_4 \) değerlerini kullanarak \( x_2 \) değerini bulalım.
\( x_2 - 2x_3 + 7x_4 = 11 \)
\( x_2 - 2(1) + 7(2) = 11 \)
\( x_2 = -1 \)
Birinci denklemi ve \( x_2, x_3, x_4 \) değerlerini kullanarak \( x_1 \) değerini bulalım.
\( x_1 + 2x_2 + 4x_3 + 4x_4 = 10 \)
\( x_1 + 2(-1) + 4(1) + 4(2) = 10 \)
\( x_1 = 0 \)
Buna göre lineer denklem sisteminin tek çözümü \( (x_1, x_2, x_3, x_4) = (0, -1, 1, 2) \) olarak bulunur.
Çözümsüz Sistem
Aşağıdaki denklem sisteminin çözümünü bulalım.
\( \begin{array}{rrrcl} x_1 & -3x_2 & +x_3 & = & 4 \\ 3x_1 & +2x_2 & +x_3 & = & 3 \\ -6x_1 & -4x_2 & -2x_3 & = & 1 \end{array} \)
Denklem sistemini artırılmış matris formunda yazalım ve Gauss eliminasyon yöntemiyle satır eşelon formuna getirelim.
Orijinal denklem sistemi:
\( \left[ \begin{array}{ccc|c} 1 & -3 & 1 & 4 \\ 3 & 2 & 1 & 3 \\ -6 & -4 & -2 & 1 \end{array} \right] \)
Satır eşelon formu:
\( \left[ \begin{array}{ccc|c} \color{red}{1} & -3 & 1 & 4 \\ 0 & \color{red}{11} & -2 & -9 \\ 0 & 0 & 0 & 7 \end{array} \right] \)
Elde ettiğimiz satır eşelon formundaki denklem sisteminde üçüncü satırın \( 0 = 7 \) olduğunu görüyoruz. Bu eşitlik hiçbir \( (x_1, x_2, x_3) \) üçlüsü için sağlanmayacağı için bu denklem sisteminin bir çözümü yoktur. Temel satır işlemleri ile satırca denk ve aynı çözüm kümesine sahip denklem sistemleri elde ettiğimiz için, orijinal denklem sisteminin de bir çözümü olmadığını söyleyebiliriz.
Sonsuz Çözümlü Sistem
1 Serbest Değişken
Aşağıdaki denklem sisteminin çözümünü bulalım.
\( \begin{array}{rrrrcl} x_1 & +4x_2 & +5x_3 & -9x_4 & = & 11 \\ -x_1 & -2x_2 & -x_3 & +3x_4 & = & -5 \\ -2x_1 & -3x_2 & & +3x_4 & = & -7 \\ & -3x_2 & -6x_3 & +4x_4 & = & 1 \end{array} \)
Denklem sistemini artırılmış matris formunda yazalım ve Gauss eliminasyon yöntemiyle satır eşelon formuna getirelim.
Orijinal denklem sistemi:
\( \left[ \begin{array}{cccc|c} 1 & 4 & 5 & -9 & 11 \\ -1 & -2 & -1 & 3 & -5 \\ -2 & -3 & 0 & 3 & -7 \\ 0 & -3 & -6 & 4 & 1 \end{array} \right] \)
Satır eşelon formu:
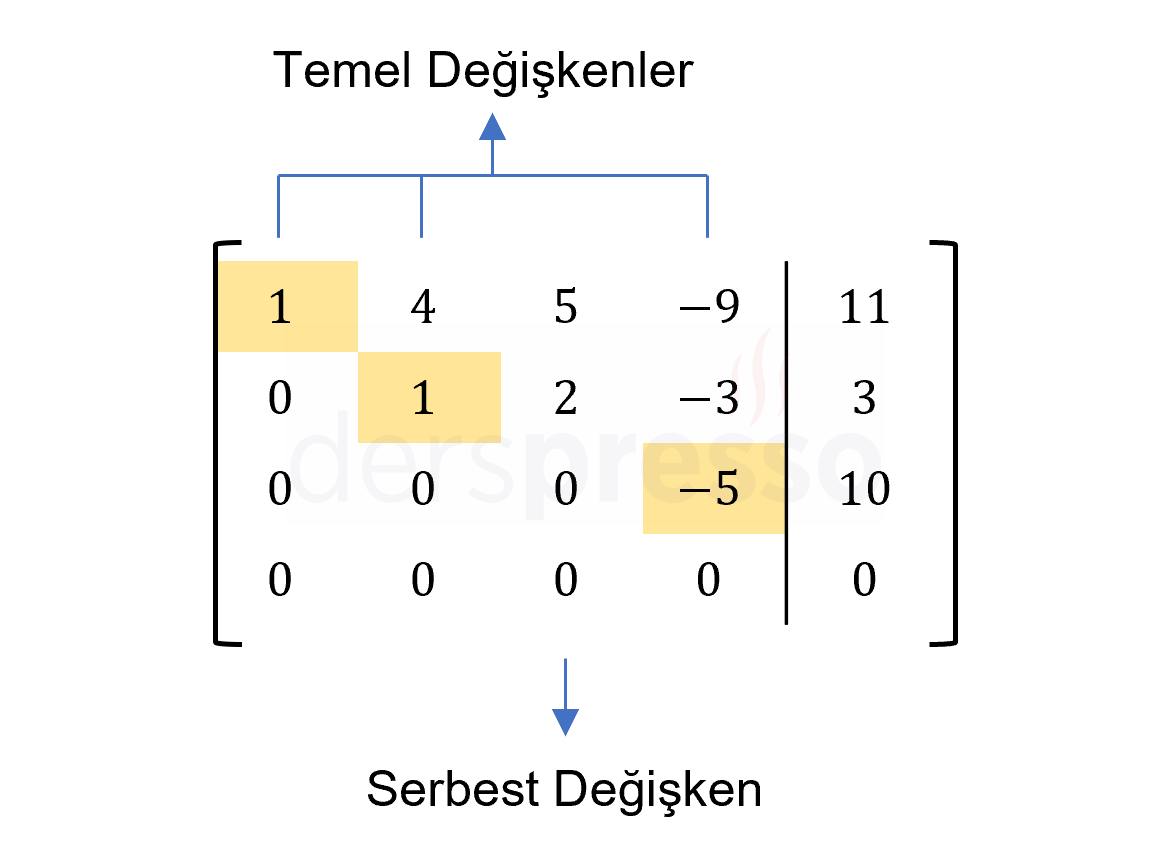
\( \left[ \begin{array}{cccc|c} \color{red}{1} & 4 & 5 & -9 & 11 \\ 0 & \color{red}{1} & 2 & -3 & 3 \\ 0 & 0 & 0 & \color{red}{-5} & 10 \\ 0 & 0 & 0 & 0 & 0 \end{array} \right] \)
Dikkat edilirse elde ettiğimiz satır eşelon formu üçüncü sütunda bir pivot içermemektedir, bu da lineer denklem sisteminin sonsuz çözümünün olduğuna işaret etmektedir. Satır eşelon formunda pivotu olmayan değişkenlere serbest değişken adı verilir. Buna göre birer pivotu olan \( x_1 \), \( x_2 \) ve \( x_4 \) değişkenleri birer temel değişkendir, pivotu olmayan \( x_3 \) değişkeni ise bir serbest değişkendir.
Elde ettiğimiz satır eşelon formundaki denklem sistemini, en son denklemden başlayarak geriye doğru yerine koyma yöntemi ile çözelim.
Üçüncü denklemi kullanarak \( x_4 \) değerini bulalım.
\( -5x_4 = 10 \)
\( x_4 = -2 \)
Satır eşelon formundaki denklem sisteminde \( x_4 \) değerini kullanarak \( x_3 \) değerini bulabileceğimiz bir denklem olmadığını görüyoruz. Bu yüzden \( x_3 \) değişkenini olduğu gibi bırakalım.
\( x_3 = x_3 \)
İkinci denklemi ve \( x_3, x_4 \) değerlerini kullanarak \( x_2 \) değerini bulalım.
\( x_2 + 2x_3 - 3x_4 = 3 \)
\( x_2 + 2x_3 - 3(-2) = 3 \)
\( x_2 = -3 - 2x_3 \)
Birinci denklemi ve \( x_2, x_3, x_4 \) değerlerini kullanarak \( x_1 \) değerini bulalım.
\( x_1 + 4x_2 + 5x_3 - 9x_4 = 11 \)
\( x_1 + 4(-3 - 2x_3) + 5x_3 - 9(-2) = 11 \)
\( x_1 - 12 - 8x_3 + 5x_3 + 18 = 11 \)
\( x_1 = 5 + 3x_3 \)
Buna göre lineer denklem sisteminin çözüm kümesi \( x_3 \) değişkenine bağlı olarak \( (x_1, x_2, x_3, x_4) = (5 + 3x_3, -3 - 2x_3, x_3, -2) \) olarak bulunur.
Bulduğumuz sonuç \( x_3 \) değişkeninin farklı değerleri için denklem sisteminin farklı çözümleri olabileceğini söylemektedir. Örneğin \( x_3 = 0 \) değeri için oluşan çözümün denklem sistemini sağlayıp sağlamadığını kontrol edelim.
\( (x_1, x_2, x_3, x_4) = (5 + 3x_3, -3 - 2x_3, x_3, -2) \)
\( = (5 + 3(0), -3 - 2(0), 0, -2) \)
\( = (5, -3, 0, -2) \)
\( 5 + 4(-3) + 5(0) - 9(-2) = 11 \)
\( -5 - 2(-3) - 0 + 3(-2) = -5 \)
\( -2(5) - 3(-3) + 3(-2) = -7 \)
\( -3(-3) - 6(0) + 4(-2) = 1 \)
Tüm denklemler sağlandığı için \( (5, -3, 0, -2) \) denklem sisteminin bir çözümüdür. Şimdi de \( x_3 = -2 \) değeri için oluşan çözümün denklem sistemini sağlayıp sağlamadığını kontrol edelim.
\( (x_1, x_2, x_3, x_4) = (5 + 3x_3, -3 - 2x_3, x_3, -2) \)
\( = (5 + 3(-2), -3 - 2(-2), -2, -2) \)
\( = (-1, 1, -2, -2) \)
\( -1 + 4(1) + 5(-2) - 9(-2) = 11 \)
\( -(-1) - 2(1) - (-2) + 3(-2) = -5 \)
\( -2(-1) - 3(1) + 3(-2) = -7 \)
\( -3(1) - 6(-2) + 4(-2) = 1 \)
Tüm denklemler sağlandığı için \( (-1, 1, -2, -2) \) de denklem sisteminin bir çözümüdür.
\( x_3 \) değişkenine herhangi bir değer verebileceğimiz için denklem sisteminin sonsuz sayıda çözümü olur.
Serbest değişkenler \( s \), \( t \) gibi değişkenler yardımıyla parametrik şekilde de ifade edilebilir. Örneğin bu örnekte \( x_3 = s \) dersek çözüm kümesini \( s \) cinsinden parametrik şekilde de ifade edebiliriz.
\( x_3 = s \) olmak üzere,
\( (x_1, x_2, x_3, x_4) = (5 + 3s, -3 - 2s, s, -2) \)
2 Serbest Değişken
Aşağıdaki denklem sisteminin çözümünü bulalım.
\( \begin{array}{rrrrrcl} x_1 & +x_2 & -2x_3 & +x_4 & +3x_5 & = & 12 \\ x_1 & -x_2 & +2x_3 & +2x_4 & +6x_5 & = & 23 \\ 3x_1 & +5x_2 & -10x_3 & -5x_4 & -15x_5 & = & 18 \\ -4x_1 & +x_2 & -2x_3 & -3x_4 & -9x_5 & = & -72 \end{array} \)
Denklem sistemini artırılmış matris formunda yazalım ve Gauss eliminasyon yöntemiyle satır eşelon formuna getirelim.
Orijinal denklem sistemi:
\( \left[ \begin{array}{ccccc|c} 1 & 1 & -2 & 1 & 3 & 12 \\ 1 & -1 & 2 & 2 & 6 & 23 \\ 3 & 5 & -10 & -5 & -15 & 18 \\ -4 & 1 & -2 & -3 & -9 & -72 \end{array} \right] \)
Satır eşelon formu:
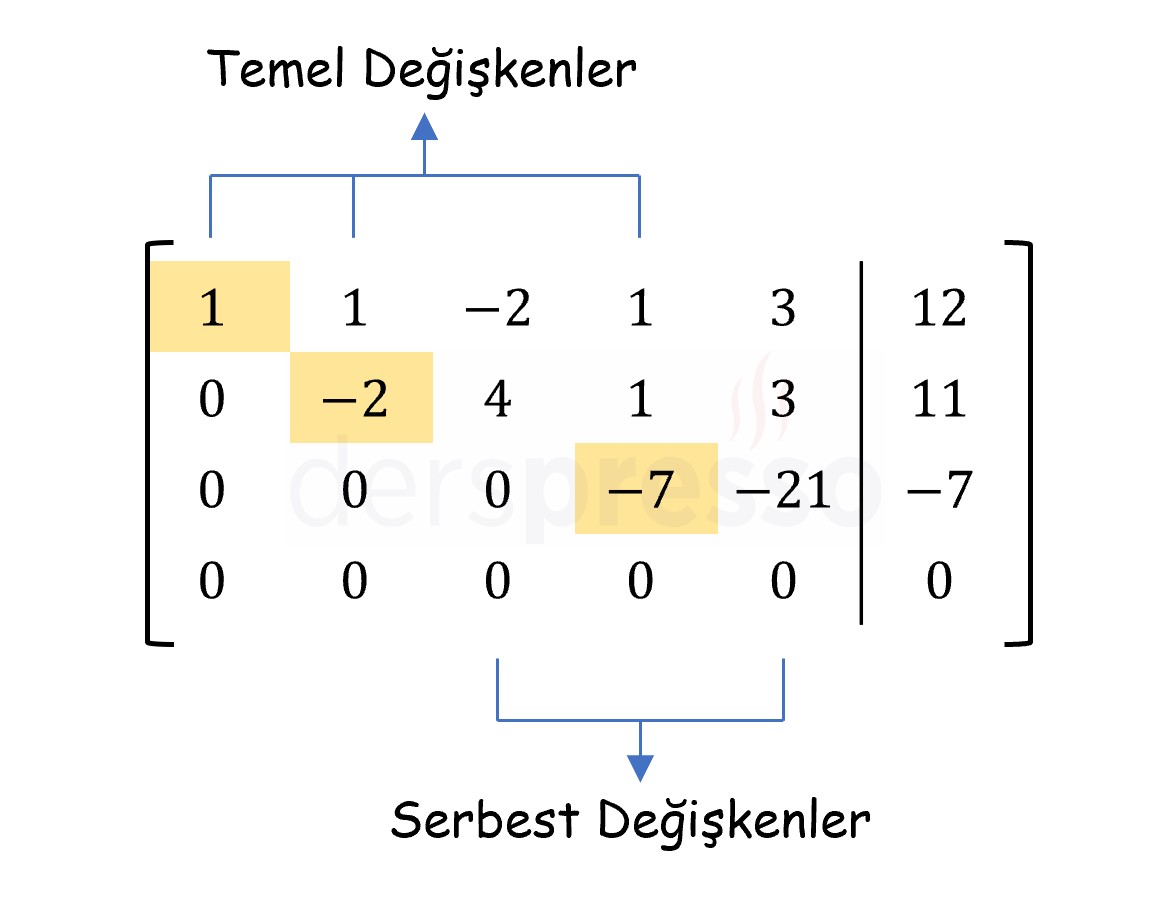
\( \left[ \begin{array}{ccccc|c} \color{red}{1} & 1 & -2 & 1 & 3 & 12 \\ 0 & \color{red}{-2} & 4 & 1 & 3 & 11 \\ 0 & 0 & 0 & \color{red}{-7} & -21 & -7 \\ 0 & 0 & 0 & 0 & 0 & 0 \end{array} \right] \)
Dikkat edilirse elde ettiğimiz satır eşelon formu üçüncü ve beşinci sütunlarda bir pivot içermemektedir, bu da lineer denklem sisteminin sonsuz çözümünün olduğuna işaret etmektedir. Birer pivotu olan \( x_1 \), \( x_2 \) ve \( x_4 \) değişkenleri birer temel değişkendir, pivotu olmayan \( x_3 \) ve \( x_5 \) değişkenleri ise birer serbest değişkendir.
Elde ettiğimiz satır eşelon formundaki denklem sistemini, en son denklemden başlayarak geriye doğru yerine koyma yöntemi ile çözelim.
Satır eşelon formundaki denklem sisteminde sadece \( x_5 \) değerini içeren bir denklem olmadığını görüyoruz. Bu yüzden \( x_5 \) değişkenini olduğu gibi bırakalım.
\( x_5 = x_5 \)
Üçüncü denklemi kullanarak \( x_4 \) değerini bulalım.
\( -7x_4 - 21x_5 = -7 \)
\( x_4 = 1 - 3x_5 \)
Satır eşelon formundaki denklem sisteminde \( x_4 \) ve \( x_5 \) değerlerini kullanarak \( x_3 \) değerini bulabileceğimiz bir denklem olmadığını görüyoruz. Bu yüzden \( x_3 \) değişkenini olduğu gibi bırakalım.
\( x_3 = x_3 \)
İkinci denklemi ve \( x_3, x_4, x_5 \) değerlerini kullanarak \( x_2 \) değerini bulalım.
\( -2x_2 + 4x_3 + x_4 + 3x_5 = 11 \)
\( -2x_2 + 4x_3 + (1 - 3x_5) + 3x_5 = 11 \)
\( -2x_2 + 4x_3 + 1 - 3x_5 + 3x_5 = 11 \)
\( x_2 = -5 + 2x_3 \)
Birinci denklemi ve \( x_2, x_3, x_4, x_5 \) değerlerini kullanarak \( x_1 \) değerini bulalım.
\( x_1 + x_2 - 2x_3 + x_4 + 3x_5 = 12 \)
\( x_1 + (-5 + 2x_3) - 2x_3 + (1 - 3x_5) + 3x_5 = 12 \)
\( x_1 + -5 + 2x_3 - 2x_3 + 1 - 3x_5 + 3x_5 = 12 \)
\( x_1 = 16 \)
Buna göre lineer denklem sisteminin çözüm kümesi \( x_3 \) ve \( x_5 \) değişkenlerine bağlı olarak \( (x_1, x_2, x_3, x_4, x_5) = (16, -5 + 2x_3, x_3, 1 - 3x_5, x_5) \) olarak bulunur.
Bulduğumuz sonuç \( x_3 \) ve \( x_5 \) değişkenlerinin farklı değerleri için denklem sisteminin farklı çözümleri olabileceğini söylemektedir. Örneğin \( (x_3, x_5) = (0, 0) \) ikilisi için oluşan çözümün denklem sistemini sağlayıp sağlamadığını kontrol edelim.
\( (x_1, x_2, x_3, x_4, x_5) = (16, -5 + 2x_3, x_3, 1 - 3x_5, x_5) \)
\( = (16, -5 + 2(0), 0, 1 - 3(0), 0) \)
\( = (16, -5, 0, 1, 0) \)
\( 16 + (-5) − 2(0) + 1 + 3(0) = 12 \)
\( 16 − (-5) + 2(0) + 2(1) + 6(0) = 23 \)
\( 3(16) + 5(-5) − 10(0) − 5(1) − 15(0) = 18 \)
\( -4(16) + (-5) - 2(0) - 3(1) - 9(0) = -72 \)
Tüm denklemler sağlandığı için \( (16, -5, 0, 1, 0) \) denklem sisteminin bir çözümüdür. Şimdi de \( (x_3, x_5) = (2, 1) \) ikilisi için oluşan çözümün denklem sistemini sağlayıp sağlamadığını kontrol edelim.
\( (x_1, x_2, x_3, x_4, x_5) = (16, -5 + 2x_3, x_3, 1 - 3x_5, x_5) \)
\( = (16, -5 + 2(2), 2, 1 - 3(1), 1) \)
\( = (16, -1, 2, -2, 1) \)
\( 16 + (-1) − 2(2) + (-2) + 3(1) = 12 \)
\( 16 − (-1) + 2(2) + 2(-2) + 6(1) = 23 \)
\( 3(16) + 5(-1) − 10(2) − 5(-2) − 15(1) = 18 \)
\( -4(16) + (-1) - 2(2) - 3(-2) - 9(1) = -72 \)
Tüm denklemler sağlandığı için \( (16, -1, 2, -2, 1) \) de denklem sisteminin bir çözümüdür.
\( x_3 \) ve \( x_5 \) değişkenlerine herhangi bir değer verebileceğimiz için denklem sisteminin sonsuz sayıda çözümü olur.
\( x_3 = s \) ve \( x_5 = t \) dersek çözüm kümesini \( s \) ve \( t \) cinsinden parametrik şekilde de ifade edebiliriz.
\( x_3 = s \) ve \( x_5 = t \) olmak üzere,
\( (x_1, x_2, x_3, x_4, x_5) = (16, -5 + 2s, s, 1 - 3t, t) \)