Gauss - Jordan Eliminasyon Yöntemi
Önceki bölümde gördüğümüz Gauss eliminasyon yönteminin ilk adımında artırılmış matrisi satır eşelon formuna getirmiş, ikinci adımda geriye doğru yerine koyma yöntemi ile sadeleştirilmiş lineer denklem sistemini cebirsel olarak çözmüştük.
Bu bölümde göreceğimiz Gauss - Jordan eliminasyon yöntemi, Gauss eliminasyon yönteminin (iki yöntemin isim benzerliğine dikkat ediniz!!!) ikinci adımı olan geriye doğru yerine koyma adımı yerine kullanabileceğimiz ve bu cebirsel adım yerine denklem çözümünü matris üzerinden tamamlayabileceğimiz bir yöntemdir.
Gauss - Jordan eliminasyon yönteminin amacı matrisi satır eşelon formundan indirgenmiş satır eşelon formuna getirmektir. İndirgenmiş satır eşelon formundaki bir matris ek bir işlem gerektirmeden bir lineer denklem sisteminin çözümünü verir.
İndirgenmiş Satır Eşelon Formu
İndirgenmiş satır eşelon formundaki bir matris satır eşelon formu koşullarına ek olarak aşağıdaki iki koşulu sağlar.
- Matrisin tüm pivotları 1'dir.
- Bir sütunda pivot varsa o sütunda pivot dışındaki tüm elemanlar sıfırdır.
Aşağıda indirgenmiş satır eşelon formunda bir matris satır eşelon formu ile karşılaştırmalı olarak verilmiştir. Görülebileceği gibi, indirgenmiş satır eşelon formundaki bir matriste tüm pivotlar 1'dir ve sadece pivotların altındaki elemanlar değil, üstündeki elemanlar da sıfırdır.
NOT: Bazı kaynaklarda pivotların 1 olma koşulu indirgenmiş satır eşelon formunun değil, satır eşelon formunun bir koşulu olarak geçmektedir. Koşulların bu şekilde kabul edilmesi elde edeceğimiz nihai çözüm kümesini değiştirmeyecektir.
İndirgenmiş satır eşelon formundaki bir denklem sisteminin cebirsel yazılışına baktığımızda hiçbir ek işleme gerek kalmadan değişkenlerin çözüm değerlerini verdiği görülebilir.
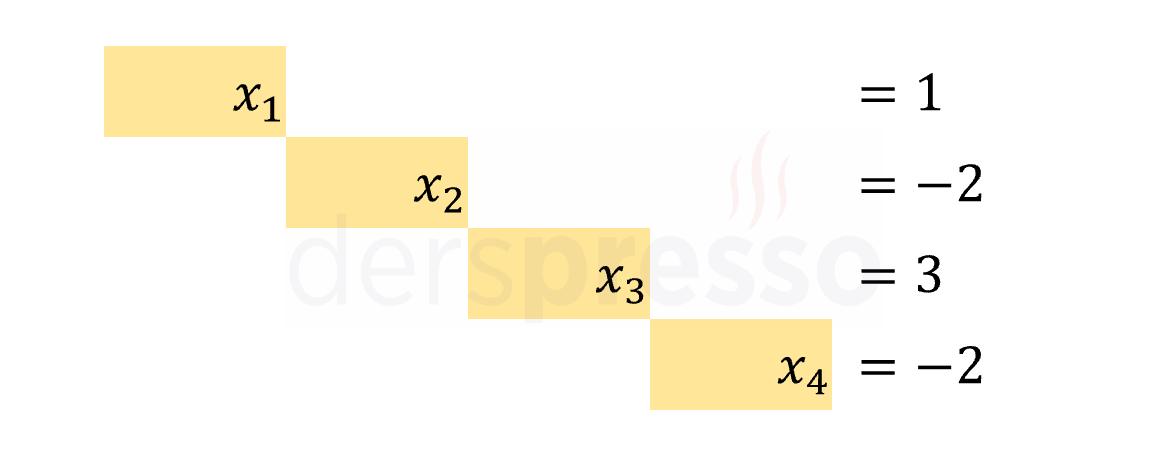
Matrisi İndirgenmiş Satır Eşelon Formuna Getirme
Gauss eliminasyon yöntemi ile elde ettiğimiz satır eşelon formundaki bir matris indirgenmiş satır eşelon formuna aşağıdaki adımlar takip edilerek getirilebilir.
- Tüm pivotlar çarpma satır işlemi ile 1'e eşitlenir.
- Matriste en sağdaki sütundaki pivot seçilir.
- Seçilen pivotun aynı sütunda ve üstünde bulunan elemanlar toplama satır işlemi ile sıfıra eşitlenir.
- Yukarıdaki 2. ve 3. adımlar sola doğru pivotu olan her sütun için tekrarlanır.
Şimdi bu yöntemi Gauss eliminasyon yöntemi konusundaki örnekte elde ettiğimiz satır eşelon formundaki matrise uygulayalım.
| İşlem | Denklem Sistemi |
|---|---|
|
Gauss eliminasyon yöntemi ile elde ettiğimiz satır eşelon formundaki matrisi yazalım. |
|
|
Tüm pivotları 1'e eşitleyelim. \( -R_1 \rightarrow R_1 \) \( \dfrac{1}{8}R_2 \rightarrow R_2 \) \( -\dfrac{1}{3}R_3 \rightarrow R_3 \) \( \dfrac{2}{9}R_4 \rightarrow R_4 \) |
|
|
4. sütunun pivotuyla (\( a_{44} \)) aynı sütunda ve üstündeki elemanları toplama satır işlemi ile sıfıra eşitleyelim. \( 2R_4 + R_1 \rightarrow R_1 \) \( \dfrac{11}{8}R_4 + R_2 \rightarrow R_2 \) \( \dfrac{1}{3}R_4 + R_3 \rightarrow R_3 \) Bu işlemler sonucunda matrisin 4. sütunu istediğimiz forma gelmiş olur. |
|
|
3. sütunun pivotuyla (\( a_{33} \)) aynı sütunda ve üstündeki elemanları toplama satır işlemi ile sıfıra eşitleyelim. \( -4R_3 + R_1 \rightarrow R_1 \) \( -\dfrac{9}{4}R_3 + R_2 \rightarrow R_2 \) Bu işlemler sonucunda matrisin 3. sütunu istediğimiz forma gelmiş olur. |
|
|
2. sütunun pivotuyla (\( a_{22} \)) aynı sütunda ve üstündeki elemanları toplama satır işlemi ile sıfıra eşitleyelim. \( -2R_2 + R_1 \rightarrow R_1 \) Bu işlemler sonucunda matrisin 2. sütunu istediğimiz forma gelmiş olur. Bu işlemler sonucunda matris istediğimiz indirgenmiş satış eşelon formuna gelmiş olur. |
|
|
Elde ettiğimiz indirgenmiş satır eşelon formundaki denklem sistemini cebirsel olarak yazalım. |
|
Çözüm Kümesini Bulma
Satır eşelon formundan farklı olarak, indirgenmiş eşelon formundaki bir matris ek bir işleme gerek kalmadan denklem sisteminin çözüm kümesini verir. En son adımda elde ettiğimiz matrisi bir denklem sistemi şeklinde yazdığımızda her satırın ayrı bir değişken değerini verdiğini görebiliriz.
\( x_1 = -5 \)
\( x_2 = 4 \)
\( x_3 = -7 \)
\( x_4 = 2 \)
Buna göre lineer denklem sisteminin tek çözümü Gauss eliminasyon yöntemi ile bulduğumuz çözümle aynı şekilde \( (x_1, x_2, x_3, x_4) = (-5, 4, -7, 2) \) olarak bulunur.