Olasılık Problemleri

Örnek uzaya \( S \) diyelim.

Örnek uzay Ali'nin yarışta elde edebileceği tüm derecelerden oluşur.

\( S = \{1, 2, 3, \ldots, 10\} \)

\( s(S) = 10 \)

Her sonucun gerçekleşme olasılığı eşittir.

Ali'nin madalya kazanma olayına \( A \) diyelim.

\( A \) olayı ilk 3 dereceden oluşur.

\( A = \{1, 2, 3\} \)

\( s(A) = 3 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{3}{10} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay sınıftaki tüm öğrencilerden oluşur.

\( s(S) = 15 + 12 = 27 \)

Her sonucun gerçekleşme olasılığı eşittir.

Seçilecek öğrencinin fenden zayıf not almış olma olayına \( A \) diyelim.

Kız öğrencilerin beşte biri yani 3'ü, erkek öğrencilerin üçte biri yani 4'ü fenden zayıf not almıştır.

\( s(A) = 3 + 4 = 7 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{7}{27} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay 2 zar atışının tüm farklı sonuçlarından oluşur.

\( S = \{11, 12, 13, \ldots, 66\} \)

\( s(S) = 6^2 = 36 \)

İlk zarın ikinciden büyük gelme olayına \( A \) diyelim.

Sonuçların 6'sında iki zar eşit gelir.

\( \{(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)\} \)

Kalan sonuçların yarısında ilk zar, diğer yarısında ikinci zar büyük gelir.

Buna göre ilk zarın ikinci zardan büyük geldiği sonuçlar \( \frac{36 - 6}{2} = 15 \) tanedir.

\( s(A) = 15 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{15}{36} = \dfrac{5}{12} \) bulunur.

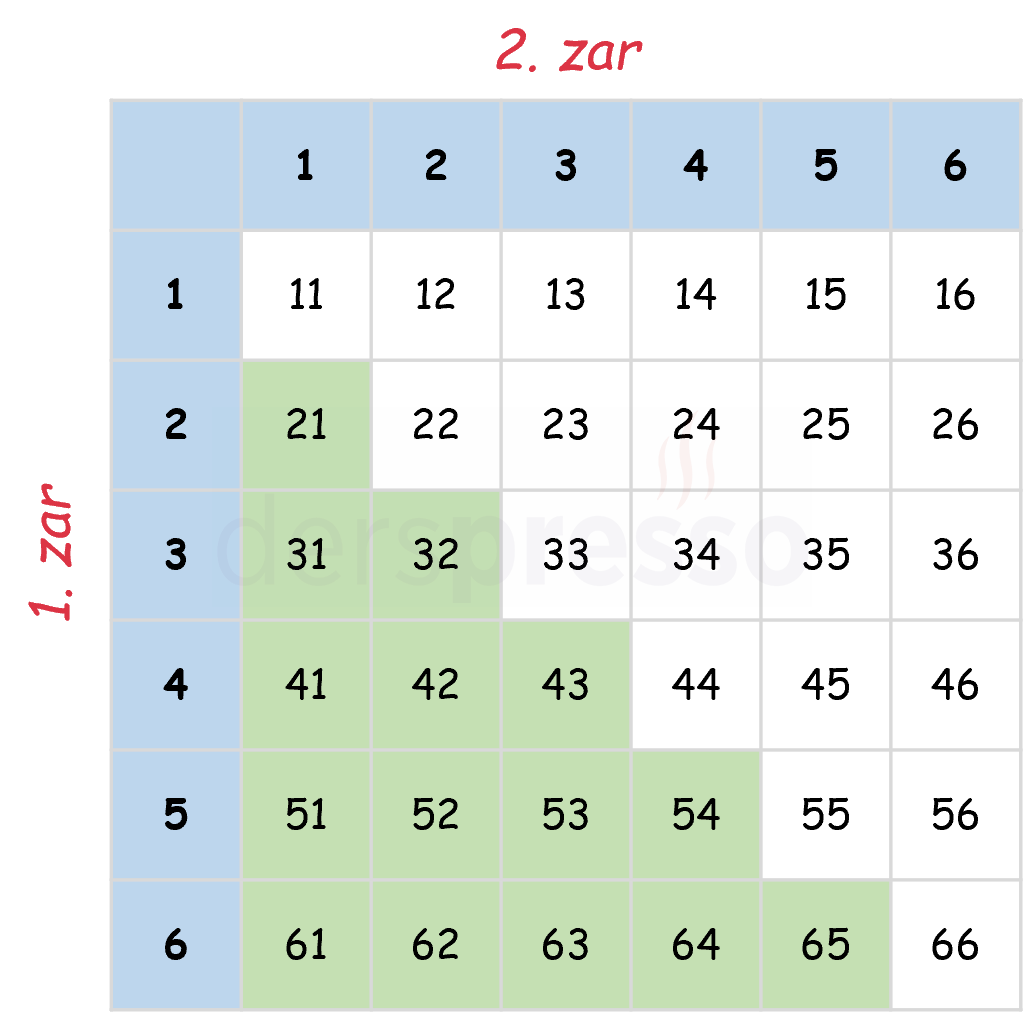
Örnek uzaydaki tüm sonuçlar aşağıdaki tabloda gösterilmiştir ve \( A \) olayına ait 15 sonuç yeşil ile işaretlenmiştir.

Örnek uzaya \( S \) diyelim.

Örnek uzay 2 zar atışının tüm farklı sonuçlarından oluşur. Zarlar üzerinde bazı rakamlar tekrar etse de bu yüzleri örnek uzay açısından ayrı sonuçlar olarak düşünelim.

\( s(S) = 6^2 = 36 \)

Zarların aynı gelme olayına \( A \) diyelim.

\( A \) olayını ayrık 3 olayın birleşimi şeklinde tanımlayalım.

\( A_1 \): İki zarın da 1 gelme olayı (\( \{11\} \))

\( A_2 \): İki zarın da 2 gelme olayı (\( \{22\} \))

\( A_3 \): İki zarın da 3 gelme olayı (\( \{33\} \))

\( A = A_1 \cup A_2 \cup A_3 \)

Zarlarda birer tane 1 bulunduğu için \( A_1 \) olayı \( 1 \cdot 1 = 1 \) tane \( \{11\} \) sonucundan oluşur.

\( s(A_1) = 1 \)

Zarlarda ikişer tane 2 bulunduğu için \( A_2 \) olayı \( 2 \cdot 2 = 4 \) tane \( \{22\} \) sonucundan oluşur.

\( s(A_2) = 4 \)

Zarlarda üçer tane 3 bulunduğu için \( A_3 \) olayı \( 3 \cdot 3 = 9 \) tane \( \{33\} \) sonucundan oluşur.

\( s(A_3) = 9 \)

\( A \) olayının eleman sayısını bulalım.

\( s(A) = s(A_1) + s(A_2) + s(A_3) \)

\( = 1 + 4 + 9 = 14 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{14}{36} = \dfrac{7}{18} \) bulunur.

Mete'nin hedefi vurma olasılığı \( \frac{5}{8} \) ise hedefi vuramama olasılığı \( 1 - \frac{5}{8} = \frac{3}{8} \) olur.

Ezgi'nin hedefi vurma olasılığı \( \frac{7}{9} \) ise hedefi vuramama olasılığı \( 1 - \frac{7}{9} = \frac{2}{9} \) olur.

(a) seçeneği:

İkisinin de hedefi vurma olasılığı, ayrı ayrı hedefi vurma olasılıklarının çarpımına eşittir.

\( P = \dfrac{5}{8} \cdot \dfrac{7}{9} = \dfrac{35}{72} \)

(b) seçeneği:

İkisinin de hedefi vuramama olasılığı, ayrı ayrı hedefi vuramama olasılıklarının çarpımına eşittir.

\( P = \dfrac{3}{8} \cdot \dfrac{2}{9} = \dfrac{1}{12} \)

(c) seçeneği:

Mete'nin hedefi vurup Ezgi'nin vuramama olasılığı, Mete'nin hedefi vurma olasılığı ile Ezgi'nin hedefi vuramama olasılıklarının çarpımına eşittir.

\( P = \dfrac{5}{8} \cdot \dfrac{2}{9} = \dfrac{5}{36} \)

(d) seçeneği:

Sadece birinin hedefi vurma olasılığı, sadece Mete'nin hedefi vurma olasılığı ile sadece Ezgi'nin hedefi vurma olasılığının toplamına eşittir.

\( P = \dfrac{5}{8} \cdot \dfrac{2}{9} + \dfrac{3}{8} \cdot \dfrac{7}{9} \)

\( = \dfrac{10 + 21}{72} = \dfrac{31}{72} \)

Emre'nin bir problemi çözme olasılığı \( \frac{3}{4} \) ise çözememe olasılığı \( 1 - \frac{3}{4} = \frac{1}{4} \) olur.

Özgür'ün bir problemi çözme olasılığı \( \frac{2}{3} \) ise çözememe olasılığı \( 1 - \frac{2}{3} = \frac{1}{3} \) olur.

Murat'ın bir problemi çözme olasılığı \( \frac{3}{5} \) ise çözememe olasılığı \( 1 - \frac{3}{5} = \frac{2}{5} \) olur.

(a) seçeneği:

Üçünün de problemi çözme olasılığı, ayrı ayrı problemi çözme olasılıklarının çarpımına eşittir.

\( P = \dfrac{3}{4} \cdot \dfrac{2}{3} \cdot \dfrac{3}{5} = \dfrac{3}{10} \)

(b) seçeneği:

Üçünün de problemi çözememe olasılığı, ayrı ayrı problemi çözememe olasılıklarının çarpımına eşittir.

\( P = \dfrac{1}{4} \cdot \dfrac{1}{3} \cdot \dfrac{2}{5} = \dfrac{1}{30} \)

(c) seçeneği:

Murat'ın problemi çözüp diğer ikisinin çözememe olasılığı, Murat'ın problemi çözme olasılığı ile diğer ikisinin ayrı ayrı çözememe olasılıklarının çarpımına eşittir.

\( P = \dfrac{1}{4} \cdot \dfrac{1}{3} \cdot \dfrac{3}{5} = \dfrac{1}{20} \)

(d) seçeneği:

En az birinin problemi çözme olasılığı, (b) seçeneğinde hesapladığımız üçünün de problemi çözememe olasılığının tümleyenine eşittir.

\( P = 1 - \dfrac{1}{30} = \dfrac{29}{30} \)

(e) seçeneği:

En az birinin problemi çözememe olasılığı, (a) seçeneğinde hesapladığımız üçünün de problemi çözme olasılığının tümleyenine eşittir.

\( P = 1 - \dfrac{3}{10} = \dfrac{7}{10} \)

(f) seçeneği:

Sadece birinin problemi çözme olasılığı, ayrı ayrı sadece Emre'nin, sadece Özgür'ün ve sadece Murat'ın problemi çözme olasılıklarının toplamına eşittir.

\( P = \dfrac{3}{4} \cdot \dfrac{1}{3} \cdot \dfrac{2}{5} \)

\( + \dfrac{1}{4} \cdot \dfrac{2}{3} \cdot \dfrac{2}{5} \)

\( + \dfrac{1}{4} \cdot \dfrac{1}{3} \cdot \dfrac{3}{5} \)

\( = \dfrac{6}{60} + \dfrac{4}{60} + \dfrac{3}{60} \)

\( = \dfrac{13}{60} \)

(g) seçeneği:

Sadece ikisinin problemi çözme olasılığı, ayrı ayrı sadece Emre ve Özgür'ün, sadece Emre ve Murat'ın ve sadece Özgür ve Murat'ın problemi çözme olasılıklarının toplamına eşittir.

\( P = \dfrac{3}{4} \cdot \dfrac{2}{3} \cdot \dfrac{2}{5} \)

\( + \dfrac{3}{4} \cdot \dfrac{1}{3} \cdot \dfrac{3}{5} \)

\( + \dfrac{1}{4} \cdot \dfrac{2}{3} \cdot \dfrac{3}{5} \)

\( = \dfrac{12}{60} + \dfrac{9}{60} + \dfrac{6}{60} \)

\( = \dfrac{9}{20} \)

1. avcının hedefi vurma olasılığı \( \frac{7}{10} \) ise hedefi vuramama olasılığı \( 1 - \frac{7}{10} = \frac{3}{10} \) olur.

2. avcının hedefi vurma olasılığı \( \frac{3}{4} \) ise hedefi vuramama olasılığı \( 1 - \frac{3}{4} = \frac{1}{4} \) olur.

3. avcının hedefi vurma olasılığı \( \frac{4}{5} \) ise hedefi vuramama olasılığı \( 1 - \frac{4}{5} = \frac{1}{5} \) olur.

Hedefi yalnızca bir avcının vurma olayına \( A \) diyelim.

\( A \) olayını aşağıdaki üç ayrık olayın birleşimi olarak düşünebiliriz.

\( A_1 \): Hedefi sadece 1. avcının vurma olayı

\( A_2 \): Hedefi sadece 2. avcının vurma olayı

\( A_3 \): Hedefi sadece 3. avcının vurma olayı

\( A = A_1 \cup A_2 \cup A_3 \)

\( A_1 \) olayının olasılığı 1. avcının hedefi vurma, 2. ve 3. avcıların hedefi vuramama olasılıklarının çarpımına eşittir.

\( P(A_1) = \dfrac{7}{10} \cdot \dfrac{1}{4} \cdot \dfrac{1}{5} = \dfrac{7}{200} \)

\( A_2 \) olayının olasılığı 2. avcının hedefi vurma, 1. ve 3. avcıların hedefi vuramama olasılıklarının çarpımına eşittir.

\( P(A_2) = \dfrac{3}{10} \cdot \dfrac{3}{4} \cdot \dfrac{1}{5} = \dfrac{9}{200} \)

\( A_3 \) olayının olasılığı 3. avcının hedefi vurma, 1. ve 2. avcıların hedefi vuramama olasılıklarının çarpımına eşittir.

\( P(A_3) = \dfrac{3}{10} \cdot \dfrac{1}{4} \cdot \dfrac{4}{5} = \dfrac{12}{200} \)

Üç olay ayrık olaylar olduğu için \( A \) olayının olasılığı bu üç olayın olasılıkları toplamına eşittir.

\( P(A) = P(A_1) + P(A_2) + P(A_3) \)

\( = \dfrac{7}{200} + \dfrac{9}{200} + \dfrac{12}{200} \)

\( = \dfrac{28}{200} = \%14 \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay zarın masaya bakan yüzündeki sayılardan oluşur.

\( S = \{1, 2, 3, 4, 5, 6\} \)

Her sonucun gerçekleşme olasılığı eşittir.

Görünen 5 yüzdeki sayıların çarpımının 9'a tam bölünme olayına \( A \) diyelim.

Görünen 5 yüzdeki sayıların çarpımının 9'a tam bölünmesi için içinde iki tane 3 çarpanı bulunması, yani 3 ve 6'yı içermesi gerekir.

\( A \) olayı 3 ve 6'nın birlikte görünür olduğu, dolayısıyla görünmeyen yüzde bu iki sayıdan birinin olmadığı sonuçlardan oluşur.

\( A = \{1, 2, 4, 5\} \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{4}{6} = \dfrac{2}{3} \) bulunur.

İlk zarda tek sayı gelme olasılığı \( \frac{4}{6} = \frac{2}{3} \), çift sayı gelme olasılığı \( \frac{2}{6} = \frac{1}{3} \) olur.

İkinci zarda tek sayı gelme olasılığı \( \frac{2}{6} = \frac{1}{3} \), çift sayı gelme olasılığı \( \frac{4}{6} = \frac{2}{3} \) olur.

Gelen sayıların toplamın çift sayı olması için zarların ikisi de ya tek sayı ya da çift sayı gelmelidir.

İki zarın da tek sayı gelme olasılığı \( = \dfrac{2}{3} \cdot \dfrac{1}{3} = \dfrac{2}{9} \)

İki zarın da çift sayı gelme olasılığı \( = \dfrac{1}{3} \cdot \dfrac{2}{3} = \dfrac{2}{9} \)

Gelen sayıların toplamının çift sayı olma olasılığı bulduğumuz iki duruma ait olasılıkların toplamına eşittir.

\( \dfrac{2}{9} + \dfrac{2}{9} = \dfrac{4}{9} \) bulunur.

Topların aynı olma olayı üç top da futbol topu ya da üç top da basketbol topu olduğu durumda gerçekleşir.

Durum 1: Üç top da basketbol topu

\( \dfrac{6}{10} \cdot \dfrac{6}{10} \cdot \dfrac{6}{10} = \dfrac{27}{125} \)

Durum 2: Üç top da futbol topu

\( \dfrac{4}{10} \cdot \dfrac{4}{10} \cdot \dfrac{4}{10} = \dfrac{8}{125} \)

Topların aynı olma olasılığı bu iki duruma ait olasılıkların toplamına eşittir.

\( \dfrac{27}{125} + \dfrac{8}{125} = \dfrac{35}{125} = \dfrac{7}{25} \) bulunur.

Hileli zarın tek sayı gelme olasılığına \( p \), çift sayı gelme olasılığına \( 2p \) diyelim.

Tek ya da çift gelme olasılıkları toplamı 1 olmalıdır.

\( p + 2p = 1 \)

\( p = \dfrac{1}{3} \)

Buna göre tek sayı gelme olasılığı \( \frac{1}{3} \), çift sayı gelme olasılığı \( \frac{2}{3} \) olur.

Atılan iki zarın toplamı iki durumda tek olur.

Durum 1: İlk zar tek, ikinci zar çift

Bu durumda zarların toplamının tek sayı olma olasılığı:

\( = \dfrac{1}{3} \cdot \dfrac{2}{3} = \dfrac{2}{9} \)

Durum 2: İlk zar çift, ikinci zar tek

Bu durumda zarların toplamının tek sayı olma olasılığı:

\( = \dfrac{2}{3} \cdot \dfrac{1}{3} = \dfrac{2}{9} \)

İki zarın toplamının tek sayı olma olasılığı, iki duruma ait olasılıkların toplamına eşittir.

\( \dfrac{2}{9} + \dfrac{2}{9} = \dfrac{4}{9} \) bulunur.

İstenen durum iki farklı şekilde gerçekleşebilir.

Durum 1: 1. bilye beyaz, 2. bilye kırmızı

\( \dfrac{7}{10} \cdot \dfrac{3}{9} = \dfrac{7}{30} \)

Durum 2: 1. bilye kırmızı, 2. bilye beyaz

\( \dfrac{3}{10} \cdot \dfrac{7}{9} = \dfrac{7}{30} \)

Bilyelerin farklı renkte olma olasılığı bu iki duruma ait olasılıkların toplamına eşittir.

\( \dfrac{7}{30} + \dfrac{7}{30} = \dfrac{7}{15} \) bulunur.

Torbada en başta 5'i tek sayı 5'i çift sayı olmak üzere 10 top vardır.

Belirtilen durum iki farklı şekilde gerçekleşebilir.

Durum 1: 1. top tek sayı

Bu durumda 1. top dışarıda bırakılacağı için 2. çekilişte torbada 4'ü tek sayı olmak üzere 9 top bulunur.

2. çekilişte tek sayı gelme olasılığı:

\( \dfrac{5}{10} \cdot \dfrac{4}{9} = \dfrac{2}{9} \)

Durum 2: 1. top çift sayı

Bu durumda 1. top torbaya geri atılacağı için 2. çekilişte torbada 5'i tek sayı olmak üzere 10 top bulunur.

2. çekilişte tek sayı gelme olasılığı:

\( \dfrac{5}{10} \cdot \dfrac{5}{10} = \dfrac{1}{4} \)

Bu iki durum ayrık olaylar olduğu için, 2. çekilişte tek sayı gelme olasılığı bu iki duruma ait olasılıkların toplamına eşittir.

\( \dfrac{2}{9} + \dfrac{1}{4} = \dfrac{17}{36}\) bulunur.

Ege'nin metro kartını 3. denemede çekmesi için ilk iki denemede farklı kart, üçüncü denemede metro kartını çekmesi gerekmektedir.

İlk 2 denemede yanlış kartı, 3. denemede doğru kartı çekme olasılığını bulalım.

\( \dfrac{4}{5} \cdot \dfrac{3}{4} \cdot \dfrac{1}{3} = \dfrac{1}{5} \) bulunur.

Verilen oranları kullandığımızda atılan bir zarın 1, 2, 3, 4, 5, 6 gelme olasılıkları sırasıyla aşağıdaki gibi olur.

\( \dfrac{3}{12}, \dfrac{3}{12}, \dfrac{2}{12}, \dfrac{2}{12}, \dfrac{1}{12}, \dfrac{1}{12} \)

\( \dfrac{1}{4}, \dfrac{1}{4}, \dfrac{1}{6}, \dfrac{1}{6}, \dfrac{1}{12}, \dfrac{1}{12} \)

Gelen sayıların toplamının 6 olduğu 5 durum vardır.

\( (1, 5), (2, 4), (3, 3), (4, 2), (5, 1) \)

\( (1, 5) \) gelme olasılığını bulalım.

\( \dfrac{1}{4} \cdot \dfrac{1}{12} = \dfrac{1}{48} \)

\( (2, 4) \) gelme olasılığını bulalım.

\( \dfrac{1}{4} \cdot \dfrac{1}{6} = \dfrac{1}{24} \)

\( (3, 3) \) gelme olasığını bulalım.

\( \dfrac{1}{6} \cdot \dfrac{1}{6} = \dfrac{1}{36} \)

\( (5, 1) \) gelme olasılığı \( (1, 5) \) gelme olasılığına, \( (4, 2) \) gelme olasılığı \( (2, 4) \) gelme olasılığına eşittir.

İki zarın toplamının 6 gelme olasılığı bu 5 duruma ait olasılıkların toplamına eşittir.

\( 2 \cdot \dfrac{1}{48} + 2 \cdot \dfrac{1}{24} + \dfrac{1}{36} = \dfrac{3}{72} + \dfrac{6}{72} + \dfrac{2}{72} \)

\( = \dfrac{11}{72} \) bulunur.

İlk çekilen kağıtta \( \frac{6}{10} \) olasılıkla "evet", \( \frac{4}{10} \) olasılıkla "hayır" yazar.

İkinci çekilişte "hayır" gelme olasılığını birinci çekilişin iki farklı sonucuna göre ayrı ayrı hesaplayalım.

Durum 1: Birinci çekilişte "evet" gelir.

Birinci çekilişte \( \frac{6}{10} \) olasılıkla "evet" yazan kağıt çekilip kutuya zıt anlamlısı konduğunda kutuda 5 "evet" ve 5 "hayır" yazan kağıt olur.

Bu durumda ikinci çekilişte "hayır" çekme olasılığını hesaplayalım.

\( \dfrac{6}{10} \cdot \dfrac{5}{10} = \dfrac{3}{10} \)

Durum 2: Birinci çekilişte "hayır" gelir.

Birinci çekilişte \( \frac{4}{10} \) olasılıkla "hayır" yazan kağıt çekilip kutuya zıt anlamlısı konduğunda kutuda 7 "evet" ve 3 "hayır" yazan kağıt olur.

Bu durumda ikinci çekilişte "hayır" çekme olasılığını hesaplayalım.

\( \dfrac{4}{10} \cdot \dfrac{3}{10} = \dfrac{3}{25} \)

İkinci çekilişte kağıtta "hayır" yazma olasılığı bu iki duruma ait olasılıkların toplamına eşittir.

\( \dfrac{3}{10} + \dfrac{3}{25} = \dfrac{21}{50} \) bulunur.

Sepetten ilk seçilen mandalın mor ve kırmızı olduğu iki durumu ayrı ayrı inceleyelim.

Durum 1: İlk mandal mor

Bu durumda sepete 3 mor mandal daha eklenir ve sepette toplam 10 mor, 6 kırmızı mandal olur.

İlk mandalın mor olduğu durumda, seçilen ikinci mandalın da mor renkte olma olasılığını bulalım.

\( \dfrac{7}{13} \cdot \dfrac{10}{16} = \dfrac{70}{208} \)

Durum 2: İlk mandal kırmızı

Bu durumda sepete 3 kırmızı mandal daha eklenir ve sepette toplam 7 mor, 9 kırmızı mandal olur.

İlk mandalın kırmızı olduğu durumda, seçilen ikinci mandalın mor renkte olma olasılığını bulalım.

\( \dfrac{6}{13} \cdot \dfrac{7}{16} = \dfrac{42}{208} \)

İstenen durumun gerçekleşme olasılığı bulduğumuz iki durumun olasılıkları toplamına eşittir.

\( \dfrac{70}{208} + \dfrac{42}{208} = \dfrac{112}{208} \)

\( = \dfrac{7}{13} \) olarak bulunur.

Bir seti kazanma olasılıkları eşit olduğuna göre, bu olasılıklar ikisi için ayrı ayrı \( \frac{1}{2} \)'dir.

Kadir'in oynayacakları ilk seti kazanıp maçı beraberliğe getirme olasılığı \( \frac{1}{2} \) olur.

Maçta durum eşitlenince ikisinin de maçı kazanma olasılıkları ayrı ayrı \( \frac{1}{2} \) olur (herhangi birinin maçı kazanma olasılığının daha yüksek olmasını gerektirecek bir sebep yoktur.).

Buna göre, Cenk 1 set öndeyken Kadir'in maçı kazanma olasılığı \( \frac{1}{2} \cdot \frac{1}{2} = \frac{1}{4} \) olur.

Arkadaşlarının problemi çözme olasılıklarına sırasıyla \( P_1, P_2, P_3 \) diyelim.

Problemin çözülme olayına \( A \) diyelim.

Bir olay ile tümleyeninin olasılıkları toplamı 1'dir.

\( 1 = A + A' \)

\( A = 1 - A' \)

Problem çözülmediği \( A' \) olayı, üç arkadaşın da problemi çözemediği durumda gerçekleşir.

\( A = 1 - P_1' \cdot P_2' \cdot P_3' \)

Üç arkadaşın problemi çözememe olasılıkları sırasıyla \( \frac{1}{2}, \frac{2}{3}, \frac{3}{5} \) olur.

\( A = 1 - \dfrac{1}{2} \cdot \dfrac{2}{3} \cdot \dfrac{3}{5} \)

\( = \dfrac{4}{5} \) bulunur.

Torbada tek bir sarı top olduğu için ilk iki çekilişte mavi ya da kırmızı toplar gelebilir.

İstenen durum dört şekilde gerçekleşebilir.

Çekilen topları renklerinin baş harfleriyle adlandıralım.

Durum 1: MMS

\( \dfrac{3}{6} \cdot \dfrac{2}{5} \cdot \dfrac{1}{4} = \dfrac{1}{20} \)

Durum 2: KKS

\( \dfrac{2}{6} \cdot \dfrac{1}{5} \cdot \dfrac{1}{4} = \dfrac{1}{60} \)

Durum 3: MKS

\( \dfrac{3}{6} \cdot \dfrac{2}{5} \cdot \dfrac{1}{4} = \dfrac{1}{20} \)

Durum 4: KMS

\( \dfrac{2}{6} \cdot \dfrac{3}{5} \cdot \dfrac{1}{4} = \dfrac{1}{20} \)

İstenen olasılık bu dört durumun olasılıklarının toplamıdır.

\( \dfrac{1}{20} + \dfrac{1}{60} + \dfrac{1}{20} + \dfrac{1}{20} = \dfrac{1}{6} \) bulunur.

İlk tanığın yanlış ifade verme olasılığı \( \frac{7}{10} \), ikinci tanığın yanlış ifade verme olasılığı \( \frac{3}{8} \) olur.

İstenen durum iki şekilde gerçekleşebilir.

Durum 1:

Bu durumda birinci tanık doğru, ikinci tanık yanlış ifade verir.

\( \dfrac{3}{10} \cdot \dfrac{3}{8} = \dfrac{9}{80} \)

Durum 2:

Bu durumda birinci tanık yanlış, ikinci tanık doğru ifade verir.

\( \dfrac{7}{10} \cdot \dfrac{5}{8} = \dfrac{35}{80} \)

İstenen olasılık bu iki durumun olasılıklarının toplamıdır.

\( \dfrac{9}{80} + \dfrac{35}{80} = \dfrac{44}{80} \)

\( = \dfrac{11}{20} \) bulunur.

İstenen olasılığı aşağıdaki gibi ifade edebiliriz.

\( P(S_1 \cup (S_2 \cap S_3)) \)

\( S_1 \) ve \( S_2 \cap S_3 \) kümeleri arasında toplama kuralını uygulayalım.

\( = P(S_1) + P(S_2 \cap S_3) - P(S_1 \cap (S_2 \cap S_3)) \)

\( = P(S_1) + P(S_2 \cap S_3) - P(S_1 \cap S_2 \cap S_3) \)

\( S_2 \cap S_3 \) olayı iki anahtarın aynı anda kapalı olma, \( S_1 \cap S_2 \cap S_3 \) olayı üç anahtarın aynı anda kapalı olma olayına karşılık gelir.

\( = \dfrac{1}{2} + \dfrac{1}{3} \cdot \dfrac{2}{3} - \dfrac{1}{2} \cdot \dfrac{1}{3} \cdot \dfrac{2}{3} \)

\( = \dfrac{11}{18} \) bulunur.

Derin'e \( n \) kez yazı gelme olasılığına \( A(n) \), Beril'e \( n \) kez yazı gelme olasılığına \( B(n) \) diyelim.

Her para atışında yazı ve tura gelme olasılıkları birbirine eşit ve \( \frac{1}{2} \) olur.

\( A(0) \) "TT" gelme olasılığına eşittir.

\( A(0) = \dfrac{1}{2} \cdot \dfrac{1}{2} = \dfrac{1}{4} \)

\( A(1) \) "TY" ya da "YT" gelme olasılıklarının toplamına eşittir.

\( A(1) = \dfrac{1}{2} \cdot \dfrac{1}{2} \cdot 2 = \dfrac{1}{2} \)

\( A(2) \) "YY" gelme olasılığına eşittir.

\( A(2) = \dfrac{1}{2} \cdot \dfrac{1}{2} = \dfrac{1}{4} \)

\( B(0) \) "TT" gelme olasılığına eşittir.

\( B(0) = \dfrac{1}{2} \cdot \dfrac{1}{2} = \dfrac{1}{4} \)

\( B(1) \) "TY" ya da "YT" gelme olasılıklarının toplamına eşittir.

\( B(1) = \dfrac{1}{2} \cdot \dfrac{1}{2} \cdot 2 = \dfrac{1}{2} \)

\( B(2) \) "YY" gelme olasılığına eşittir.

\( B(2) = \dfrac{1}{2} \cdot \dfrac{1}{2} = \dfrac{1}{4} \)

İki arkadaşa aynı sayıda yazı gelme olasılığı, ikisine aynı anda 0, 1, 2 yazı gelme olasılıklarının toplamına eşittir.

\( A(0) \cdot B(0) + A(1) \cdot B(1) + A(2) \cdot B(2) \)

\( = \dfrac{1}{4} \cdot \dfrac{1}{4} + \dfrac{1}{2} \cdot \dfrac{1}{2} + \dfrac{1}{4} \cdot \dfrac{1}{4} \)

\( = \dfrac{1}{16} + \dfrac{1}{4} + \dfrac{1}{16} \)

\( = \dfrac{3}{8} \) bulunur.

Eleştirmenlerin bir filmi beğenmeme olasılıkları sırasıyla \( \frac{3}{5} \), \( \frac{2}{5} \) ve \( \frac{1}{5} \) olur.

İstenen durum eleştirmenlerin en az ikisinin filmi beğenmesi ile oluşur.

İstenen durum dört farklı şekilde oluşabilir.

Durum 1:

Bu durumda birinci ve ikinci eleştirmenler filmi beğenir, üçüncü eleştirmen beğenmez.

\( \dfrac{2}{5} \cdot \dfrac{3}{5} \cdot \dfrac{1}{5} = \dfrac{6}{125} \)

Durum 2:

Bu durumda birinci ve üçüncü eleştirmenler filmi beğenir, ikinci eleştirmen beğenmez.

\( \dfrac{2}{5} \cdot \dfrac{2}{5} \cdot \dfrac{4}{5} = \dfrac{16}{125} \)

Durum 3:

Bu durumda ikinci ve üçüncü eleştirmenler filmi beğenir, birinci eleştirmen beğenmez.

\( \dfrac{3}{5} \cdot \dfrac{3}{5} \cdot \dfrac{4}{5} = \dfrac{36}{125} \)

Durum 4:

Bu durumda üç eleştirmen de filmi beğenir.

\( \dfrac{2}{5} \cdot \dfrac{3}{5} \cdot \dfrac{4}{5} = \dfrac{24}{125} \)

İstenen olasılık birbirinden bağımsız bu dört durumun olasılıklarının toplamına eşittir.

\( P = \dfrac{6}{125} + \dfrac{16}{125} + \dfrac{36}{125} + \dfrac{24}{125} \)

\( = \dfrac{82}{125} \) bulunur.

Bir \( x \) sayısının sadece 3 pozitif böleni olması için bu sayının tek bir asal çarpanı olmalı ve bu çarpanın kuvveti 2 olmalıdır.

\( x = p^2 \)

\( [1,1000] \) aralığındaki bu şartı sağlayan en büyük sayı \( 31^2 = 961 \)'dir.

31'e kadar olan asal sayıları yazalım.

\( \{2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31\} \)

Bu 11 sayının karelerinin sadece 3 pozitif böleni vardır.

İstenen olasılık 1001 sayı içerisinden bu 11 sayıdan birinin seçilme olasılığıdır.

\( P = \dfrac{11}{1001} = \dfrac{1}{91} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay 5 elemanlı bir kümeden sırasıyla iki elemanın tüm farklı seçimlerinden oluşur.

\( s(S) = P(5, 2) = 5 \cdot 4 = 20 \)

Denklemin köklerinin karmaşık sayı olma olayına \( A \) diyelim.

İkinci dereceden bir denklemin kökleri karmaşık sayı ise deltası (diskriminantı) sıfırdan küçüktür.

\( \Delta = b^2 - 4ac \lt 0 \)

Verilen denklemde \( a \) katsayısı 1'dir.

\( b^2 \lt 4c \)

Buna göre \( A \) olayı için aşağıdaki üç koşul sağlanmalıdır.

\( b, c \in \{1, 2, 3, 4, 5\} \)

\( b \neq c \)

\( b^2 \lt 4c \)

Bu koşulları sağlayan her \( b \) değeri için geçerli \( c \) değerlerini bulalım.

\( b = 1 \) için:

\( c \in \{2, 3, 4, 5 \} \)

\( b = 2 \) için:

\( c \in \{ 3, 4, 5 \} \)

\( b = 3 \) için:

\( c \in \{ 4, 5 \} \)

\( b = 4 \) için:

\( c = 5 \)

\( b = 5 \) için:

\( c \) için geçerli bir değer yoktur.

Buna göre istenen durumu sağlayan 10 sonuç vardır.

\( s(A) = 10 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{10}{20} = \dfrac{1}{2} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay \( [0, 150] \) aralığındaki tam sayılardan oluşur.

Verilen aralıkta \( 150 - 0 + 1 = 151 \) tane tam sayı vardır.

\( s(S) = 151 \)

Seçilen sayının verilen eşitsizliği sağlama olayına \( A \) diyelim.

Verilen eşitsizliği düzenleyelim.

\( x + 5 - \dfrac{50}{x} \lt 0 \)

\( \dfrac{x(x + 5) - 50}{x} \lt 0 \)

\( \dfrac{x^2 + 5x - 50}{x} \lt 0 \)

\( \dfrac{(x + 10)(x - 5)}{x} \lt 0 \)

Pay ve paydadaki her bir çarpanı sıfır yapan \( \{-10, 0, 5\} \) değerleri eşitsizliğin kritik noktalarıdır.

Bu kritik noktalar reel sayı doğrusunda \( (-\infty, -10) \), \( (-10, 0) \), \( (0, 5) \) ve \( (5, \infty) \) aralıklarını oluşturur.

Bir işaret tablosu hazırlayalım.

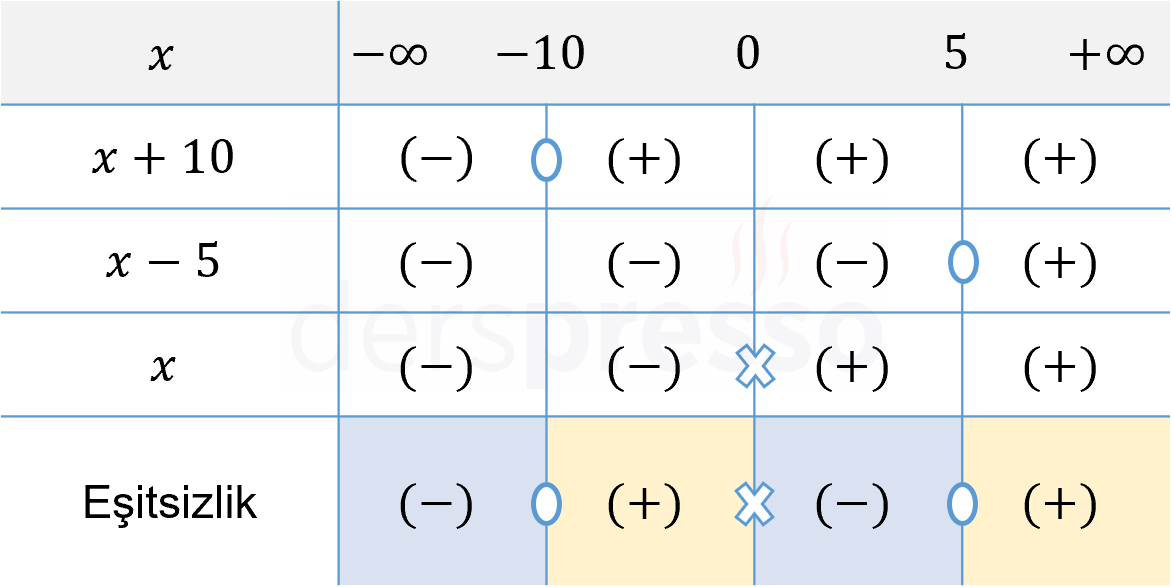
Rasyonel ifade paydayı sıfır yapan \( x = 0 \) değerinde tanımsız, payı sıfır yapan \( \{-10, 5\} \) değerlerinde sıfır olur.

Verilen eşitsizlikte \( \lt \) sembolü kullanıldığı için rasyonel ifadenin negatif olduğu aralık ve değerler eşitsizliğin çözüm kümesi olur.

Çözüm kümesi: \( x \in (-\infty, 0) \cup (0, 5) \)

Buna göre eşitsizlik \( [0, 150] \) aralığında dört tam sayı değeri için sağlanır.

\( A = \{ 1, 2, 3, 4 \} \)

\( s(A) = 4 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{4}{151} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay üç zar atışının tüm farklı sonuçlarından oluşur.

\( s(S) = 6^3 = 256 \)

Gelen sayılara \( x, y, z \) diyelim.

Gelen sayıların bir aritmetik dizi oluşturma olayına \( A \) diyelim.

Bir aritmetik dizide bir terim, kendisinden eşit uzaklıktaki iki terimin aritmetik ortalamasına (toplamlarının yarısına) eşittir.

Buna göre \( A \) olayı aşağıdaki eşitlik sağlandığında gerçekleşir.

\( 2y = x + z \)

\( y \) değişkeni 6 farklı değer alabilir. Her durum için oluşan \( (x, y, z) \) üçlülerini bulalım.

Durum 1: \( y = 1 \)

\( 2 = x + z \)

\( x = 1, z = 1 \)

\( (x, y, z) = (1, 1, 1) \)

Durum 2: \( y = 2 \)

\( 4 = x + z \)

\( x = 1, z = 3 \)

\( x = 2, z = 2 \)

\( x = 3, z = 1 \)

\( (x, y, z) \in \{(1, 2, 3), (2, 2, 2), (3, 2, 1)\} \)

Durum 3: \( y = 3 \)

\( 6 = x + z \)

\( x = 1, z = 5 \)

\( x = 2, z = 4 \)

\( x = 3, z = 3 \)

\( x = 4, z = 2 \)

\( x = 5, z = 1 \)

\( (x, y, z) \in \{(1, 3, 5), (2, 3, 4), (3, 3, 3), (4, 3, 2), (5, 3, 1)\} \)

Durum 4: \( y = 4 \)

\( 8 = x + z \)

\( x = 2, z = 6 \)

\( x = 3, z = 5 \)

\( x = 4, z = 4 \)

\( x = 5, z = 3 \)

\( x = 6, z = 2 \)

\( (x, y, z) \in \{(2, 4, 6), (3, 4, 5), (4, 4, 4), (5, 4, 3), (6, 4, 2)\} \)

Durum 5: \( y = 5 \)

\( 10 = x + z \)

\( x = 4, z = 6 \)

\( x = 5, z = 5 \)

\( x = 6, z = 4 \)

\( (x, y, z) \in \{(4, 5, 6), (5, 5, 5), (6, 5, 4)\} \)

Durum 6: \( y = 6 \)

\( 12 = x + z \)

\( x = 6, z = 6 \)

\( (x, y, z) = (6, 6, 6) \)

Buna göre 18 sonuçta gelen sayılar bir aritmetik dizi oluşturur.

\( s(A) = 18 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{18}{216} \)

\( = \dfrac{1}{12} \) bulunur.

Bir fonksiyon birinci türevinin pozitif olduğu aralıkta artandır.

Buna göre fonksiyon daima artan ise tüm tanım aralığında \( f'(x) \gt 0 \) olur.

Fonsiyonun birinci türevini alalım.

\( f'(x) = 3x^2 + 2ax + b \gt 0 \)

\( c \) ikinci türevde olmadığı için fonksiyonun artan/azalan olma durumuna etkisi olmaz, dolayısıyla üçüncü zarı olasılık hesabının dışında tutabiliriz.

Örnek uzaya \( S \) diyelim.

Örnek uzay iki zar atışının tüm farklı sonuçlarından oluşur

\( s(S) = 6^2 = 36 \)

\( f'(x) \) fonksiyonu pozitif başkatsayılı bir paraboldur ve daima pozitif olması için deltası sıfırdan küçük olmalıdır, yani grafik \( x \) eksenini kesmemelidir.

\( \Delta = b^2 - 4ac \lt 0 \)

\( (2a)^2 - 4(3)(b) \lt 0 \)

\( a^2 \lt 3b \)

Fonksiyonun daima artan olma olayına \( A \) diyelim.

\( A \) olayı için aşağıdaki iki koşul sağlanmalıdır.

\( a, b \in [1, 6] \)

\( a^2 \lt 3b \)

Aşağıdaki sayı ikilileri bu iki koşulu sağlar.

\( (a, b) \in \{(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6), (4, 6)\} \)

\( s(A) = 15 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{15}{36} = \dfrac{5}{12} \) bulunur.

Kardan adamın devrilmesi için isabet etmesi gereken kartopu sayısına \( n \) diyelim.

Bir kartopunun hedefe isabet etme olasılığı \( \frac{2}{3} \) olduğuna göre, isabet etmeme olasılığı \( \frac{1}{3} \) olur.

Kardan adamın devrilmesi için en az iki kartopu isabet etmelidir.

Atılan \( n \) kartopu arasından en az ikisininin isabet etme olayına \( A \) diyelim.

\( A \) olayının olasılığı, örnek uzayın olasılığından sıfır ve bir kartopunun isabet etme olasılığı çıkarılarak bulunur.

\( n \) kartopu arasından sıfır kartopu isabet etme olasılığını bulalım.

\( (\dfrac{1}{3})^n \)

\( n \) kartopu arasından sadece bir kartopu isabet etme olasılığını bulalım.

\( C(n, 1) \cdot \dfrac{2}{3} \cdot (\dfrac{1}{3})^{n-1} \)

\( = 2n \cdot (\dfrac{1}{3})^n \)

\( P(A) = 1 - (\dfrac{1}{3})^n - 2n \cdot (\dfrac{1}{3})^n \)

Bu olasılığın en az %99 olması için gerekli \( n \) değerini bulalım.

\( 1 - (\dfrac{1}{3})^n - 2n \cdot (\dfrac{1}{3})^n \ge \dfrac{99}{100} \)

\( (2n + 1) \cdot \dfrac{1}{3^n} \le \dfrac{1}{100} \)

\( 100(2n + 1) \le 3^n \)

Üstel bir fonksiyon doğrusal bir fonksiyondan daha hızlı büyüdüğü için, belirli bir \( n \) değerinden sonra eşitsizliğin sağ tarafı sol tarafından büyük olur.

Bu \( n \) değerini deneyerek bulalım.

\( n = 3 \) verelim.

\( 100(2(3) + 1) \stackrel{?}{\le} 3^3 \)

\( 700 \not\le 27 \)

\( n = 5 \) verelim.

\( 100(2(5) + 1) \stackrel{?}{\le} 3^5 \)

\( 1100 \not\le 243 \)

\( n = 6 \) verelim.

\( 100(2(6) + 1) \stackrel{?}{\le} 3^6 \)

\( 1300 \not\le 729 \)

\( n = 7 \) verelim.

\( 100(2(7) + 1) \stackrel{?}{\le} 3^7 \)

\( 1500 \le 2187 \)

Buna göre kardan adamı devirmek için en az 7 kartopu atılmalıdır.

Örnek uzaya \( S \) diyelim.

Örnek uzay üç sayının tüm farklı seçimlerinden oluşur.

\( s(S) = C(10, 3) = \dfrac{10 \cdot 9 \cdot 8}{3 \cdot 2 \cdot 1} = 120 \)

Seçilen sayılardan birinin diğer ikisinin ortalaması olma olayına \( A \) diyelim.

15 ve 42 herhangi iki sayının ortalaması olamaz.

Ortalamanın 18 olduğu tek bir durum vardır.

(15, 18, 21)

Ortalamanın 21 olduğu iki durum vardır.

(18, 21, 24), (15, 21, 27)

Ortalamanın 24 olduğu üç durum vardır.

(21, 24, 27), (18, 24, 30), (15, 24, 33)

Ortalamanın 27 olduğu dört durum vardır.

(24, 27, 30), (21, 27, 33), (18, 27, 36), (15, 27, 39)

Ortalamanın 30 olduğu (27'ye benzer şekilde) dört durum, 33 olduğu (24'e benzer şekilde) üç durum, 36 olduğu (21'e benzer şekilde) iki durum, 39 olduğu (18'e benzer şekilde) tek bir durum vardır.

\( s(A) = 2(1 + 2 + 3 + 4) = 20 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{20}{120} = \dfrac{1}{6} \) bulunur.

Başlangıçtaki durumun elde edilmesi için iki torbadan da aynı renkte top çekilmelidir.

Buna göre istenen durum aşağıdaki iki olaydan birinin gerçekleşmesi ile elde edilir.

Durum 1: İki torbadan da çekilen top sarı renkte

Bu durumda birinci torbadan ikinci torbaya atılan top sarı olur.

\( \dfrac{3}{5} \cdot \dfrac{5}{10} = \dfrac{15}{50} \)

Durum 2: İki torbadan da çekilen top kırmızı renkte

Bu durumda birinci torbadan ikinci torbaya atılan top kırmızı olur.

\( \dfrac{2}{5} \cdot \dfrac{6}{10} = \dfrac{12}{50} \)

Başlangıçtaki durumun elde edilme olasılığı bu iki olayın olasılıkları toplamına eşittir.

\( \dfrac{15}{50} + \dfrac{12}{50} = \dfrac{27}{50} \) bulunur.

504 sayısını asal çarpanlarına ayıralım.

\( 504 = 2^3 \cdot 3^2 \cdot 7 \)

Örnek uzaya \( S \) diyelim.

Örnek uzay 504'ün tüm pozitif bölenlerinden oluşur.

Bir sayının pozitif bölenlerinin sayısı, asal çarpanlarının kuvvetlerinin birer fazlasının çarpımına eşittir.

PBS \( = (3 + 1)(2 + 1)(1 + 1) = 24 \)

\( s(S) = 24 \)

Her sonucun gerçekleşme olasılığı eşittir.

Seçilen sayının 13'ten küçük olma olayına \( A \) diyelim.

\( A \) olayı 504'ün 13'ten küçük pozitif bölenlerinden oluşur.

\( A = \{1, 2, 3, 4 = 2^2, 6 = 2 \cdot 3, 7, 8 = 2^3, 9 = 3^2, 12 = 2^2 \cdot 3\} \)

\( s(A) = 9 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{9}{24} = \dfrac{3}{8} \) bulunur.

Fonksiyonlar konusunda gördüğümüz bazı formülleri hatırlayalım.

\( f: A \to B \)

\( s(A) = n, \quad s(B) = k \) olmak üzere,

Fonksiyon sayısı \( = k^n \)

Sabit fonksiyon sayısı \( = k \)

Birebir fonksiyon sayısı \( = P(k, n) \)

Örnek uzaya \( S \) diyelim.

Örnek uzay bu iki küme arasında yazılabilecek tüm fonksiyonlardan oluşur.

\( s(S) = 3^2 = 9 \)

Fonksiyon rastgele seçileceği için her sonucun gerçekleşme olasılığı eşittir.

(a) seçeneği:

Fonksiyonun sabit fonksiyon olma olayına \( C \) diyelim.

\( C \) olayı iki küme arasında yazılabilecek sabit fonksiyonlardan oluşur.

\( s(C) = 3 \)

\( C \) olayının gerçekleşme olasılığı, \( C \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(C) = \dfrac{s(C)}{s(S)} \)

\( = \dfrac{3}{9} = \dfrac{1}{3} \)

(b) seçeneği:

Fonksiyonun birebir fonksiyon olma olayına \( D \) diyelim.

\( D \) olayı iki küme arasında yazılabilecek birebir fonksiyonlardan oluşur.

\( s(D) = P(k, n) = 3 \cdot 2 = 6 \)

\( D \) olayının gerçekleşme olasılığı, \( D \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(D) = \dfrac{s(D)}{s(S)} \)

\( = \dfrac{6}{9} = \dfrac{2}{3} \)

Örnek uzaya \( S \) diyelim.

Örnek uzay iki basamaklı doğal sayılardan oluşur.

Toplam 90 adet iki basamaklı doğal sayı vardır.

\( s(S) = 90 \)

İşlem sonucunda dört basamaklı bir sayı elde etme olayına \( A \) diyelim.

İşlem sonucunda dört basamaklı bir sayı elde etmek için, seçilen sayının iki basamağındaki rakam da 3 ile çarpıldığında iki basamaklı sayı veren rakamlar olmalıdır.

\( 4, 5, 6, 7, 8, 9 \) rakamları 3 ile çarpıldığında iki basamaklı bir sayı oluşur.

İşlem sonucunda dört basamaklı bir sayı oluşması için seçilen sayının iki basamağı da bu 6 rakamdan biri olmalıdır, dolayısıyla işlem sonucu dört basamaklı olan \( 6 \cdot 6 = 36 \) farklı iki basamaklı sayı vardır.

\( s(A) = 36 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{36}{90} = \dfrac{2}{5} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay 1-100 aralığındaki tam sayılardan oluşur.

\( S = \{1, 2, 3, \ldots, 100\} \)

\( s(S) = 100 \)

Her sonucun gerçekleşme olasılığı eşittir.

Seçilen sayının 3'e ve 4'e tam bölünme olayına \( A \) diyelim.

\( A \) olayını aşağıdaki şekilde tanımlayabiliriz.

\( B_3 \): Sayının 3'e tam bölünme olayı

\( B_4 \): Sayının 4'e tam bölünme olayı

\( A = B_3 \cap B_4 \)

Bir sayının 3'e ve 4'e tam bölünmesi için gerekli ve yeterli koşul 12'ye tam bölünmesidir.

\( B_{12} \): Sayının 12'ye tam bölünme olayı

\( A = B_3 \cap B_4 = B_{12} \)

1-100 aralığındaki 12'ye tam bölünen sayıları taban (tam değer) fonksiyonu ile bulabiliriz.

\( s(B_{12}) = \floor{\dfrac{100}{12}} = 8 \)

\( s(A) = s(B_{12}) = 8 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{8}{100} = \dfrac{2}{25} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay 1-100 aralığındaki tam sayılardan oluşur.

\( S = \{1, 2, 3, \ldots, 100\} \)

\( s(S) = 100 \)

Her sonucun gerçekleşme olasılığı eşittir.

Seçilen sayının 3'e veya 4'e tam bölünme olayına \( A \) diyelim.

\( A \) olayını aşağıdaki şekilde tanımlayabiliriz.

\( B_3 \): Sayının 3'e tam bölünme olayı

\( B_4 \): Sayının 4'e tam bölünme olayı

\( A = B_3 \cup B_4 \)

Ayrık olmayan iki kümenin birleşim kümesinin eleman sayısı aşağıdaki formülle bulunur.

\( s(A) = s(B_3 \cup B_4) = s(B_3) + s(B_4) - s(B_3 \cap B_4) \)

1-100 aralığındaki 3'e (ve 4'e) tam bölünen sayıları taban (tam değer) fonksiyonu ile bulabiliriz.

\( s(B_3) = \floor{\dfrac{100}{3}} = 33 \)

\( s(B_4) = \floor{\dfrac{100}{4}} = 25 \)

Önceki soruda \( B_3 \cap B_4 = B_{12} \) olduğunu göstermiştik.

\( B_{12} \): Sayının 12'ye tam bölünme olayı

\( B_3 \cap B_4 = B_{12} \)

\( s(B_{12}) = \floor{\dfrac{100}{12}} = 8 \)

Bulduğumuz değerleri formülde yerine koyalım.

\( s(A) = s(B_3 \cup B_4) = s(B_3) + s(B_4) - s(B_3 \cap B_4) \)

\( = 33 + 25 - 8 = 50 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{50}{100} = \dfrac{1}{2} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay \( A \times B \) çarpımının elemanlarından oluşur.

\( S = \{(-4, -2), (-4, -1), \ldots, (4, 3)\} \)

\( A \times B \) çarpımının eleman sayısı iki kümenin eleman sayılarının çarpımına eşittir.

\( s(S) = s(A \times B) = s(A) \cdot s(B) \)

\( = 6 \cdot 5 = 30 \)

Kartezyen çarpımının bir elemanının bileşenleri toplamının sıfır olma olayına \( A \) diyelim.

Kartezyen çarpımının bu şekildeki elemanları aşağıdaki gibidir.

\( A = \{(-3, 3), (1, -1), (2, -2)\} \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{3}{30} = \dfrac{1}{10} \) bulunur.

\( 24 - \frac{12}{4} \) işleminin doğru sonucu 21'dir.

Verilen işlemde "4" rakamı iki kez bulunmaktadır. "4" tuşuna her basıldığında 3 farklı durum oluştuğu için toplamda \( 3^2 = 9 \) farklı durum oluşacaktır. Bu durumların her birinde doğru sonuç elde edilip edilmediğini kontrol edelim.

1. tuşlama "3", 2. tuşlama "3" algılanırsa:

\( 23 - \dfrac{12}{3} = 19 \)

1. tuşlama "3", 2. tuşlama "4" algılanırsa:

\( 23 - \dfrac{12}{4} = 20 \)

1. tuşlama "3", 2. tuşlama "6" algılanırsa:

\( 23 - \dfrac{12}{6} = 21 \)

1. tuşlama "4", 2. tuşlama "3" algılanırsa:

\( 24 - \dfrac{12}{3} = 20 \)

1. tuşlama "4", 2. tuşlama "4" algılanırsa:

\( 24 - \dfrac{12}{4} = 21 \)

1. tuşlama "4", 2. tuşlama "6" algılanırsa:

\( 24 - \dfrac{12}{6} = 22 \)

1. tuşlama "6", 2. tuşlama "3" algılanırsa:

\( 26 - \dfrac{12}{3} = 22 \)

1. tuşlama "6", 2. tuşlama "4" algılanırsa:

\( 26 - \dfrac{12}{4} = 23 \)

1. tuşlama "6", 2. tuşlama "6" algılanırsa:

\( 26 - \dfrac{12}{6} = 24 \)

Buna göre doğru cevap iki durumda elde edilir. Bu iki durumun oluşma olasılıklarını bulalım.

1. tuşlama "3", 2. tuşlama "6" algılanma olasılığı:

\( \dfrac{1}{3} \cdot \dfrac{1}{6} = \dfrac{1}{18} \)

1. tuşlama "4", 2. tuşlama "4" algılanma olasılığı:

\( \dfrac{1}{2} \cdot \dfrac{1}{2} = \dfrac{1}{4} \)

Bu iki durumun olasılıkları toplamı, doğru sonuç elde etme olasılığını verir.

\( \dfrac{1}{18} + \dfrac{1}{4} = \dfrac{11}{36} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay \( A \) kümesinin boş küme hariç tüm alt kümelerinden oluşur.

\( s(S) = 2^6 - 1 = 63 \)

Seçilen alt kümedeki elemanların çarpımının çift sayı olma olasılığı = 1 - Seçilen alt kümedeki elemanların çarpımının tek sayı olma olasılığı

Alt kümedeki elemanların çarpımının tek sayı olma olayına \( E \) diyelim.

Belirli sayıda sayının çarpımının tek sayı olması için sayıların tümü tek olmalıdır.

\( A \) kümesinde üç tek sayı bulunduğu için bu koşulu sağlayan alt kümeler \( \{1, 3, 5\} \) ve bu kümenin boş küme hariç alt kümeleridir.

\( s(E) = 2^3 - 1 = 7 \)

\( E \) olayının gerçekleşme olasılığı, \( E \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(E) = \dfrac{s(E)}{s(S)} \)

\( = \dfrac{7}{63} = \dfrac{1}{9} \)

Seçilen alt kümedeki elemanların çarpımının çift sayı olma olasılığı = 1 - Seçilen alt kümedeki elemanların çarpımının tek sayı olma olasılığı

\( = 1 - \dfrac{1}{9} = \dfrac{8}{9} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay altıgenin tüm kenar ve köşegenlerinden oluşur.

\( n \) köşeli konveks bir çokgenin köşegen sayısı \( = \dfrac{n(n - 3)}{2} \)

Buna göre konveks altıgenin \( \dfrac{6(6 - 3)}{2} = 9 \) köşegeni vardır.

\( s(S) = 6 + 9 = 15 \)

Seçilen doğru parçasının altıgenin bir kenarı olma olayına \( A \) diyelim.

\( s(A) = 6 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{6}{15} = \dfrac{2}{5} \) bulunur.

Rastgele seçilen üç basamaklı bir pozitif tam sayının birler basamağı, her biri eşit olasılıkla olmak üzere, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 olur.

Seçilen sayının karesi alındığında elde edilen sayının birler basamağı ise sırasıyla 0, 1, 4, 9, 6, 5, 6, 9, 4, 1 olur.

Buna göre seçilen sayının karesinin birler basamağı iki durumda (birler basamağı 2 ya da 8 olduğunda) 4 olur.

Üç basamaklı bir pozitif tam sayının karesinin birler basamağının 4 olma olasılığı:

\( = \dfrac{\text{İstenen durumların sayısı}}{\text{Tüm durumların sayısı}} = \dfrac{2}{10} = \dfrac{1}{5} \) bulunur.

İki sayının çarpımının tek sayı olması için iki sayı da tek olmalıdır.

İki sayının çarpımının çift sayı olması için sayılardan en az biri çift olmalıdır.

\( ad - bc \) işleminin sonucunun tek sayı olabilmesi için terimlerden biri tek, diğeri çift sayı olmalıdır.

Durum 1: \( ad \) tek, \( bc \) çift

\( ad \) ifadesinin tek olma olasılığı, iki sayının da ayrı ayrı tek olma olasılıklarının çarpımına eşittir.

Verilen aralıkta tek ve çift sayılar eşit sayıdadır.

\( P_1 = \dfrac{1}{2} \cdot \dfrac{1}{2} = \dfrac{1}{4} \)

\( bc \) ifadesinin çift olma olasılığı, tek olma olasılığının tümleyenine eşittir.

\( P_2 = 1 - \dfrac{1}{4} = \dfrac{3}{4} \)

\( ad \) ifadesinin tek ve \( bc \) ifadesinin çift olma olma olasılığı, bulduğumuz iki olasılığın çarpımına eşittir.

\( P_1 \cdot P_2 = \dfrac{1}{4} \cdot \dfrac{3}{4} = \dfrac{3}{16} \)

Durum 2: \( ad \) çift, \( bc \) tek

Benzer bir hesaplamayla 2. durumun olasılığının 1. durumla aynı olduğu görülebilir.

Buna göre istenen olasılık \( 2 \cdot \dfrac{3}{16} = \dfrac{3}{8} \) olarak bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay iki basamaklı pozitif tam sayılardan oluşur.

10-99 aralığında \( 99 - 10 + 1 = 90 \) tam sayı vardır.

\( s(S) = 90 \)

Basamakları toplamının bir tam sayının küpü olma olayına \( A \) diyelim.

Tam küp sayılar aşağıdaki gibidir.

1, 8, 27, 64, 125, ...

Basamakları toplamı 1 olan iki basamaklı sayı sadece 10'dur.

Basamakları toplamı 8 olan iki basamaklı sayılar 8 tanedir.

17, 26, 35, 44, 53, 62, 71, 80

İki basamaklı bir sayının basamakları toplamı en çok \( 9 + 9 = 18 \) olabileceği için bu toplam 27 ya da daha büyük bir tam küp sayı olamaz.

\( s(A) = 1 + 8 = 9 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{9}{90} = \dfrac{1}{10} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay verilen iki tarih arasındaki tüm günlerden oluşur.

Şubat ayı artık yıllarda 29, diğer yıllarda 28 gün çektiğinden öncelikle bu iki tarih arasında kaç artık yıl olduğunu bulalım.

Artık yıllar 4'ün katları olan yıllardır. Bu yüzden 2000 - 2009 yılları arasında 2000, 2004 ve 2008 olmak üzere 3 artık yıl vardır.

Verilen tarihler arasında bulunan 10 yılda şubat ayı 7 yılda 28 gün, 3 yılda 29 gün çeker.

10 yıldaki toplam gün sayısı \( 365 \cdot 10 + 3 \cdot 1 = 3653 \) olur.

\( s(S) = 3653 \)

İki tarih arasındaki bir günün şubat ayında olma olayına \( A \) diyelim.

\( A \) olayı verilen iki tarih arasında şubat ayında bulunan günlerden oluşur.

10 yılda şubat aylarındaki toplam gün sayısı \( 10 \cdot 28 + 3 \cdot 1 = 283 \) olur.

\( s(A) = 283 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{283}{3653} \) bulunur.

Her bir torbanın seçilme olasılığı \( \frac{1}{3} \) olur.

1. torbanın seçilme ve bu torbadan çekilen bilyenin beyaz olma olasılığı:

\( = \dfrac{1}{3} \cdot \dfrac{3}{9} = \dfrac{1}{9}\)

2. torbanın seçilme ve bu torbadan çekilen bilyenin beyaz olma olasılığı:

\( = \dfrac{1}{3} \cdot \dfrac{4}{6} = \dfrac{2}{9}\)

3. torbanın seçilme ve bu torbadan çekilen bilyenin beyaz olma olasılığı:

\( = \dfrac{1}{3} \cdot \dfrac{5}{6} = \dfrac{5}{18}\)

Her bir torbanın seçilmesi birbirinden ayrık olaylar olduğu için, toplam beyaz bilye çekilme olasılığı bu üç olasılığın toplamına eşittir.

\( \dfrac{1}{9} + \dfrac{2}{9} + \dfrac{5}{18} = \dfrac{11}{18} \) bulunur.

Mina'nın elindeki kutuda 4 farklı renkte 8 top, Leyla'nın elindeki kutuda 3 farklı renkte 6 top vardır.

Çekilen topların üç farklı durumda aynı renkte olur. Leyla'nın elindeki kutuda beyaz top bulunmadığı için ikisinin de beyaz çekme olasılığı sıfırdır.

Durum 1: İki top da mavi renkte

İki kutudan da mavi top çekilme olasılığı:

\( \dfrac{2}{8} \cdot \dfrac{3}{6} = \dfrac{1}{8} \)

Durum 2: İki top da turuncu renkte

İki kutudan da turuncu top seçilme olasılığı:

\( \dfrac{1}{8} \cdot \dfrac{2}{6} = \dfrac{1}{24} \)

Durum 3: İki top da yeşil renkte

İki kutudan da yeşil top seçilme olasılığı:

\( \dfrac{3}{8} \cdot \dfrac{1}{6} = \dfrac{1}{16} \)

İki kutudan da aynı renk top çekilme olasılığı bu üç duruma ait olasılıkların toplamına eşittir.

\( \dfrac{1}{8} + \dfrac{1}{24} + \dfrac{1}{16} = \dfrac{6}{48} + \dfrac{2}{48} + \dfrac{3}{48} \)

\( = \dfrac{11}{48} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay 3 zar atışının tüm farklı sonuçlarından oluşur.

\( s(S) = 6^3 = 216 \)

Doğan'ın oyunu kazanma olayına \( A \) diyelim.

\( A \) olayı Doğan'ın attığı tek zarın, Ilgın'ın attığı iki zarın toplamından büyük olduğu sonuçlardan oluşur.

Ilgın'ın attığı iki zar atışında ortaya çıkan 36 farklı sonuç ve her biri için zarların toplamını gösteren tablo aşağıdaki gibidir.

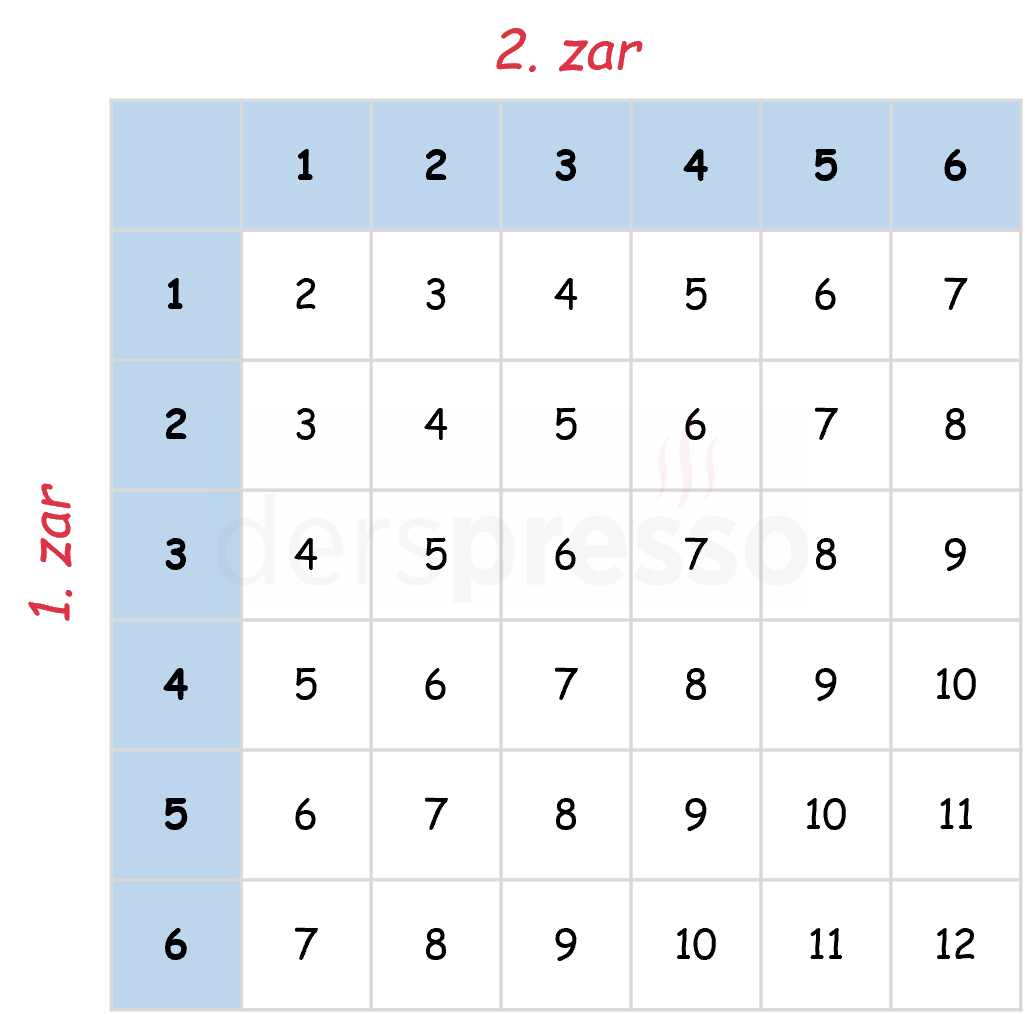
Ilgın'ın attığı 2 zarın toplamı en az 2 olacağı için Doğan 1 ya da 2 attığında oyunu kazanamaz.

Doğan 3 attığında Ilgın'ın sadece "11" attığı 1 durumda oyunu kazanır.

Doğan 4 attığında Ilgın'ın "11", "12" ve "21" attığı 3 durumda oyunu kazanır.

Doğan 5 attığında Ilgın'ın "11", "12", "21", "31", "13" ve "22" attığı 6 durumda oyunu kazanır.

Doğan 6 attığında Ilgın'ın "11", "12", "21", "31", "13", "22", "14", "41", "23", "32" attığı 10 durumda oyunu kazanır.

\( s(A) = 1 + 3 + 6 + 10 = 20 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{20}{216} = \dfrac{5}{54} \) bulunur.

Berke ve Berk'in ikisi de bir maçı unuttuklarında o maçı kaçırırlar.

İkisinin de bir maçı unutma olasılığı \( (1 - \frac{60}{100})(1 - \frac{70}{100}) = \frac{12}{100} \) olur.

Buna göre en az birinin maçı hatırlama ve o maça gitme olasılıkları \( 1 - \frac{12}{100} = \frac{88}{100} \) olur.

Hiçbirini unutmadan 10 maça da gitme olasılıkları bu durumda \( \underbrace{\frac{88}{100} \cdot \ldots \cdot \frac{88}{100}}_\text{10 adet} \) olur.

Hiçbirini unutmadan 10 maça da gitme olasılıkları:

\( = (\frac{88}{100})^{10} = (\frac{22}{25})^{10} \) bulunur.

Alp'e \( n \) kez tura gelme olasılığına \( A(n) \), Bora'ya \( n \) kez tura gelme olasılığına \( B(n) \) diyelim.

Her para atışında yazı ve tura gelme olasılıklarının eşit olduğunu varsayarak olasılıkları yazalım.

\( A(0) \) "YY" gelme olasılığına eşittir.

\( A(0) = \dfrac{1}{2} \cdot \dfrac{1}{2} = \dfrac{1}{4} \)

\( A(1) \) "TY" ya da "YT" gelme olasılığına eşittir.

\( A(1) = \dfrac{1}{2} \cdot \dfrac{1}{2} \cdot 2 = \dfrac{1}{2} \)

\( A(2) \) "TT" gelme olasılığına eşittir.

\( A(2) = \dfrac{1}{2} \cdot \dfrac{1}{2} = \dfrac{1}{4} \)

Alp parayı 2 kez attığı için 3 kez tura gelemez.

\( A(3) = 0 \)

\( B(0) \) "YYY" gelme olasılığına eşittir.

\( B(0) = \dfrac{1}{2} \cdot \dfrac{1}{2} \cdot \dfrac{1}{2} = \dfrac{1}{8} \)

\( B(1) \) "TYY", "YTY" ya da "YYT" gelme olasılığına eşittir.

\( B(1) = \dfrac{1}{2} \cdot \dfrac{1}{2} \cdot \dfrac{1}{2} \cdot 3 = \dfrac{3}{8} \)

\( B(2) \) "TTY", "TYT" ya da "YTT" gelme olasılığına eşittir.

\( B(2) = \dfrac{1}{2} \cdot \dfrac{1}{2} \cdot \dfrac{1}{2} \cdot 3 = \dfrac{3}{8} \)

\( B(3) \) "TTT" gelme olasılığına eşittir.

\( B(3) = \dfrac{1}{2} \cdot \dfrac{1}{2} \cdot \dfrac{1}{2} = \dfrac{1}{8} \)

İki arkadaşa aynı sayıda tura gelme olasılığı, ikisine aynı anda 0, 1, 2 ve 3 tura gelme olasılıklarının toplamına eşittir.

\( A(0) \cdot B(0) + A(1) \cdot B(1) + A(2) \cdot B(2) + A(3) \cdot B(3) \)

\( = \dfrac{1}{4} \cdot \dfrac{1}{8} + \dfrac{1}{2} \cdot \dfrac{3}{8} + \dfrac{1}{4} \cdot \dfrac{3}{8} + 0 \cdot \dfrac{1}{8} \)

\( = \dfrac{1}{32} + \dfrac{3}{16} + \dfrac{3}{32} \)

\( = \dfrac{5}{16} \) bulunur.

Hilesiz zarın herhangi bir sayı gelme olasılığı \( \frac{1}{6} \)'dır.

Hileli zarın herhangi bir çift sayı gelme olasılığı \( \frac{2}{9} \), herhangi bir tek sayı gelme olasılığı \( \frac{1}{9} \) olur.

\( 3 \cdot \dfrac{2}{9} + 3 \cdot \dfrac{1}{9} = 1 \)

Birinci zar hilesiz, ikinci zar hileli olmak üzere, iki zarın toplamı 5 farklı şekilde 6 gelebilir.

Durum 1: \( 1 + 5 = 6 \)

\( \dfrac{1}{6} \cdot \dfrac{1}{9} = \dfrac{1}{54} \)

Durum 2: \( 2 + 4 = 6 \)

\( \dfrac{1}{6} \cdot \dfrac{2}{9} = \dfrac{2}{54} \)

Durum 3: \( 3 + 3 = 6 \)

\( \dfrac{1}{6} \cdot \dfrac{1}{9} = \dfrac{1}{54} \)

Durum 4: \( 4 + 2 = 6 \)

\( \dfrac{1}{6} \cdot \dfrac{2}{9} = \dfrac{2}{54} \)

Durum 5: \( 5 + 1 = 6 \)

\( \dfrac{1}{6} \cdot \dfrac{1}{9} = \dfrac{1}{54} \)

İki zarın toplamının 6 olma olasılığı bu beş durumun toplamına eşittir.

\( \dfrac{1}{54} + \dfrac{2}{54} + \dfrac{1}{54} + \dfrac{2}{54} + \dfrac{1}{54} \)

\( = \dfrac{7}{54} \) bulunur.

Bir sayının rakamlarının toplamı 3'e tam bölünüyorsa o sayı 3'e tam bölünür. Rakamların dizilişinin 3'e bölünebilirliğe bir etkisi olmadığı için gelen zarların sırasının bir önemi yoktur.

Atılan ilk 2 zarın toplamını 3'e böldüğümüzde kalan 0, 1 ya da 2 olabilir. 2 zar atıldığında oluşan 36 farklı sonuçtan bu 3 kalandan her birinin oluştuğu durumlara sırasıyla \( a \), \( b \) ve \( c \) diyelim.

\( a + b + c = 36 \)

İlk 2 zar sonucunda elde edilen kalan 0 ise 3. zar 3 ve 6 geldiğinde rakamların toplamı 3'e tam bölünür.

İlk 2 zar sonucunda elde edilen kalan 1 ise 3. zar 2 ve 5 geldiğinde rakamların toplamı 3'e tam bölünür.

İlk 2 zar sonucunda elde edilen kalan 2 ise 3. zar 1 ve 4 geldiğinde rakamların toplamı 3'e tam bölünür.

Buna göre ilk 2 zar sonucunda elde edilen kalanı 3. zarda eşit sayıda sonuç 3'ün katına tamamlamaktadır.

Bu doğrultuda 3 zarın toplamının 3'ün bir katı olma olasılığını hesaplayalım.

\( \dfrac{a}{36} \cdot \dfrac{1}{3} + \dfrac{b}{36} \cdot \dfrac{1}{3} + \dfrac{c}{36} \cdot \dfrac{1}{3} \)

\( = \dfrac{a + b + c}{36} \cdot \dfrac{1}{3} \)

\( = \dfrac{36}{36} \cdot \dfrac{1}{3} = \dfrac{1}{3} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay iki basamaklı pozitif tam sayı ikililerinden oluşur.

10-99 aralığında 90 tane tam sayı vardır.

Bu sayılar arasından iki sayı \( 90 \cdot 90 \) farklı şekilde seçilebilir.

\( s(S) = 90 \cdot 90 \)

Seçilen iki sayının toplamının 65 olma olayına \( A \) diyelim.

\( A \) olayı toplamları 65 olan iki basamaklı sayı ikililerinden oluşur.

\( A = \{(10, 55), (11, 54), (12, 53), \ldots, (55, 10)\} \)

Sayı ikililerinin birinci bileşenini baz alırsak 10'dan 55'e kadar \( 55 - 10 + 1 = 46 \) tam sayı vardır, buna göre toplamları 65 olan 46 sayı ikilisi vardır.

\( s(A) = 46 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{46}{90 \cdot 90} \) bulunur.

Nisa ve Miray ikişer sayıyı \( C(3, 2) = 3 \) farklı şekilde seçebilir.

Nisa için bu üç farklı durumdaki toplamları bulalım.

\( 4 + 7 = 11 \)

\( 4 + 11 = 15 \)

\( 7 + 11 = 18 \)

Miray için bu üç farklı durumdaki çarpımları bulalım.

\( 2 \cdot 5 = 10 \)

\( 2 \cdot 7 = 14 \)

\( 5 \cdot 7 = 35 \)

Nisa ve Miray'ın her bir sonucu elde etme olasılıkları eşit ve \( \frac{1}{3} \) olur.

Nisa'nın bulduğu sonucun Miray'ın bulduğu sonuçtan büyük olduğu durumları bulalım.

Durum 1: Nisa'nın toplamı = 11

Bu durumda Nisa'nın toplamı Miray'ın çarpımından 1 durumda büyük olur.

\( 11 \gt 10 \)

\( \dfrac{1}{3} \cdot \dfrac{1}{3} = \dfrac{1}{9} \)

Durum 2: Nisa'nın toplamı = 15

Bu durumda Nisa'nın toplamı Miray'ın çarpımından 2 durumda büyük olur.

\( 15 \gt 14 \) ve \( 15 \gt 10 \)

\( \dfrac{1}{3} \cdot \dfrac{2}{3} = \dfrac{2}{9} \)

Durum 3: Nisa'nın toplamı = 18

Bu durumda Nisa'nın toplamı Miray'ın çarpımından 2 durumda büyük olur.

\( 18 \gt 10 \) ve \( 18 \gt 14 \)

\( \dfrac{1}{3} \cdot \dfrac{2}{3} = \dfrac{2}{9} \)

Nisa'nın bulduğu sonucun Miray'ın bulduğu sonuçtan büyük olma olasılığı her bir duruma ait olasılıkların toplamına eşittir.

\( \dfrac{1}{9} + \dfrac{2}{9} + \dfrac{2}{9} = \dfrac{5}{9} \) bulunur.

Gelen zarlara \( x \) ve \( y \) diyelim.

Örnek uzaya \( S \) diyelim.

Örnek uzay iki zar atışının tüm farklı sonuçlarından oluşur.

\( s(S) = 6^2 = 36 \)

\( \log_2(xy) \) ifadesinin tam sayı olma olayına \( A \) diyelim.

\( \log_2(xy) \) ifadesinin tam sayı olması için \( xy \) çarpımı 2'nin bir tam sayı kuvveti olmalıdır.

\( xy = 2^0 = 1 \) için:

\( (x, y) \in \{ (1, 1) \} \)

\( xy = 2^1 = 2 \) için:

\( (x, y) \in \{ (1, 2), (2, 1) \} \)

\( xy = 2^2 = 4 \) için:

\( (x, y) \in \{ (1, 4), (2, 2), (4, 1) \} \)

\( xy = 2^3 = 8 \) için:

\( (x, y) \in \{ (2, 4), (4, 2) \} \)

\( xy = 2^4 = 16 \) için:

\( (x, y) \in \{ (4, 4) \} \)

\( xy = 2^5 = 32 \) için:

\( (x, y) \in \emptyset \)

Buna göre 9 sonuç istenen koşulu sağlar.

\( s(A) = 9 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{9}{36} = \dfrac{1}{4} \) bulunur.

Soru mantık yürüterek de çözülebilecek olsa da biz matematiksel bir yol izleyelim.

Sınıftaki kız öğrencilerin toplam öğrenci sayısına oranına \( p \) diyelim.

Bu durumda rastgele seçilen bir öğrencinin kız öğrenci olma olasılığı \( p \) olur.

\( 0 \lt p \lt 1 \)

Birinci seçilen öğrencinin kız öğrenci olma olasılığı \( p \) olur.

\( P_1 = p \)

Seçilen üç öğrencinin de kız öğrenci olma olasılığı \( p \cdot p \cdot p = p^3 \) olur.

\( P_2 = p^3 \)

\( 0 \lt p \lt 1 \) olduğu için \( P_1 \gt P_2 \) olur.

En az bir öğrencinin kız öğrenci olma olasılığını tüm öğrencilerin erkek öğrenci olma olasılığını 1'den çıkararak bulabiliriz.

\( P_3 = 1 - (1 - p)^3 \)

\( = 1 - (1 - 3p + 3p^2 - p^3) \)

Bu ifadeyi iki şekilde sadeleştirebiliriz.

Aşağıdaki eşitliği \( P_3 \) değerini \( P_2 \) ile karşılaştırmakta kullanacağız.

\( = p^3 + 3p(1 - p) \)

Aşağıdaki eşitliği \( P_3 \) değerini \( P_1 \) ile karşılaştırmakta kullanacağız.

\( = p(3 - 3p + p^2) \)

\( P_2 \) ve \( P_3 \)'ü karşılaştıralım.

\( P_3 = p^3 + 3p(1 - p) \) ifadesi \( p^3 \) üzerine pozitif bir sayının eklenmesiyle elde edildiği için \( P_2 \)'den büyüktür.

\( P_3 \gt P_2 \)

\( P_1 \) ve \( P_3 \)'ü karşılaştıralım.

\( P_3 = p(3 - 3p + p^2) \) eşitliğindeki \( 3 - 3p + p^2 \) ifadesinin 1'den büyük olduğunu gösterebilirsek \( P_3 \gt P_1 \) olduğunu göstermiş oluruz.

\( 3 - 3p + p^2 \stackrel{?}{\gt} 1 \)

\( p^2 - 3p + 2 \stackrel{?}{\gt} 0 \)

\( (p - 1)(p - 2) \stackrel{?}{\gt} 0 \)

\( 0 \lt p \lt 1 \) aralığında bu ifade pozitiftir.

\( P_3 \gt P_1 \)

Buna göre üç olasılığın sıralaması aşağıdaki gibi bulunur.

\( P_2 \lt P_1 \lt P_3 \)

Örnek uzaya \( S \) diyelim.

Örnek uzay 1'den 10'a kadar olan tüm tam sayılardan oluşur.

\( s(S) = 10 \)

Üretilen sayıların üçgen oluşturma olayına \( A \) diyelim.

Üretilen sayıların bir üçgen oluşturabilmesi için bu sayıların üçgen eşitsizliğini sağlaması gerekir.

Üretilen üçüncü sayıya \( a \) diyelim.

\( 9 - 5 \lt a \lt 9 + 5 \)

\( 4 \lt a \lt 14 \)

\( a \) sayısı 10'dan büyük olamaz.

\( a \in \{ 5, 6, 7, 8, 9, 10 \} \)

\( s(A) = 6 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \) bulunur.

\( = \dfrac{6}{10} = \dfrac{3}{5} \) bulunur.

Derin'in bitter çikolata seçme olasılığı arkadaşlarının seçtiği çikolatalara göre değişir.

Arkadaşlarının seçtiği çikolatalara göre oluşan 4 durumu ayrı ayrı inceleyelim.

Poşette toplam 20 çikolata vardır.

Durum 1:

İki arkadaşı da beyaz çikolata seçer.

\( \dfrac{12}{20} \cdot \dfrac{11}{19} \cdot \dfrac{8}{18} = \dfrac{1056}{6840} \)

Durum 2:

İki arkadaşı da bitter çikolata seçer.

\( \dfrac{8}{20} \cdot \dfrac{7}{19} \cdot \dfrac{6}{18} = \dfrac{336}{6840} \)

Durum 3:

İlk arkadaşı beyaz, ikinci arkadaşı bitter çikolata seçer.

\( \dfrac{12}{20} \cdot \dfrac{8}{19} \cdot \dfrac{7}{18} = \dfrac{672}{6840} \)

Durum 4:

İlk arkadaşı bitter, ikinci arkadaşı beyaz çikolata seçer.

\( \dfrac{8}{20} \cdot \dfrac{12}{19} \cdot \dfrac{7}{18} = \dfrac{672}{6840} \)

İstenen olayın gerçekleşme olasılığı, birbirinden bağımsız bu dört olayın olasılıklarının toplamına eşittir.

\( \dfrac{1056}{6840} + \dfrac{336}{6840} + \dfrac{672}{6840} + \dfrac{672}{6840} \)

\( = \dfrac{2736}{6840} = \dfrac{2}{5} \) bulunur.

Ceren'in bir soruya yanlış cevap verme olasılığı \( \frac{1}{4} \) ise doğru cevap verme olasılığı \( \frac{3}{4} \)'tür.

Emre'nin bir soruya doğru cevap verme olasılığı \( \frac{2}{3} \) ise yanlış cevap verme olasılığı \( \frac{1}{3} \)'tür.

Ceren ve Emre'nin 6 sorudan 4'üne doğru cevap verdiği 3 durum vardır.

Durum 1:

Ceren 3 sorudan 3'üne, Emre 3 sorudan 1'ine doğru cevap verir.

Ceren: D-D-D, Emre: D-Y-Y

Ceren'in 3 sorudan 3'üne de doğru cevap verme olasılığını bulalım.

\( \dfrac{3}{4} \cdot \dfrac{3}{4} \cdot \dfrac{3}{4} = \dfrac{27}{64} \)

Emre'nin 3 soru içinden doğru cevapladığı 1 soru \( C(3, 1) = 3 \) farklı şekilde seçilebilir.

Emre'nin 3 sorudan 1'ine doğru cevap verme olasılığını bulalım.

\( \dfrac{2}{3} \cdot \dfrac{1}{3} \cdot \dfrac{1}{3} \cdot 3 = \dfrac{2}{9} \)

Ceren'in 3 sorudan 3'üne, Emre'nin 3 sorudan 1'ine doğru cevap verme olasılığı bulduğumuz iki olasılığın çarpımına eşittir.

\( \dfrac{27}{64} \cdot \dfrac{2}{9} = \dfrac{3}{32} \)

Durum 2:

Ceren 3 sorudan 1'ine, Emre 3 sorudan 3'üne doğru cevap verir.

Ceren: D-Y-Y, Emre: D-D-D

Ceren'in 3 soru içinden doğru cevapladığı 1 soru \( C(3, 1) = 3 \) farklı şekilde seçilebilir.

Ceren'in 3 sorudan 1'ine doğru cevap verme olasılığını bulalım.

\( \dfrac{3}{4} \cdot \dfrac{1}{4} \cdot \dfrac{1}{4} \cdot 3 = \dfrac{9}{64} \)

Emre'nin 3 sorudan 3'üne de doğru cevap verme olasılığını bulalım.

\( \dfrac{2}{3} \cdot \dfrac{2}{3} \cdot \dfrac{2}{3} = \dfrac{8}{27} \)

Ceren'in 3 sorudan 1'ine, Emre'nin 3 sorudan 3'üne doğru cevap verme olasılığı bulduğumuz iki olasılığın çarpımına eşittir.

\( \dfrac{9}{64} \cdot \dfrac{8}{27} = \dfrac{1}{24} \)

Durum 3:

Ceren 3 sorudan 2'sine, Emre 3 sorudan 2'sine doğru cevap verir.

Ceren: D-D-Y, Emre: D-D-Y

Ceren'in 3 soru içinden doğru cevapladığı 2 soru \( C(3, 2) = 3 \) farklı şekilde seçilebilir.

Ceren'in 3 sorudan 2'sine doğru cevap verme olasılığını bulalım.

\( \dfrac{3}{4} \cdot \dfrac{3}{4} \cdot \dfrac{1}{4} \cdot 3 = \dfrac{27}{64} \)

Emre'nin 3 soru içinden doğru cevapladığı 2 soru \( C(3, 2) = 3 \) farklı şekilde seçilebilir.

Emre'nin 3 sorudan 2'sine doğru cevap verme olasılığını bulalım.

\( \dfrac{2}{3} \cdot \dfrac{2}{3} \cdot \dfrac{1}{3} \cdot 3 = \dfrac{4}{9} \)

Ceren'in 3 sorudan 2'sine, Emre'nin 3 sorudan 2'sine doğru cevap verme olasılığı bulduğumuz iki olasılığın çarpımına eşittir.

\( \dfrac{27}{64} \cdot \dfrac{4}{9} = \dfrac{3}{16} \)

İstenen olasılık üç durum için bulduğumuz olasılıkların toplamına eşittir.

\( \dfrac{3}{32} + \dfrac{1}{24} + \dfrac{3}{16} = \dfrac{31}{96} \) bulunur.

Bir bölenin çift sayı olması için sayının içinde en az bir tane 2 çarpanı bulunmalıdır.

\( 61! \) sayısının içinde kaç tane 2 çarpanı olduğunu bulalım.

\( 61! \) sayısının içinde;

2'nin her katı için \( \floor{61 / 2} = 30 \) tane

4'ün her katı için \( \floor{30 / 2} = 15 \) tane daha

8'in her katı için \( \floor{15 / 2} = 7 \) tane daha

16'nın her katı için \( \floor{7 / 2} = 3 \) tane daha

32'nin her katı için \( \floor{3 / 2} = 1 \) tane daha

olmak üzere, toplamda \( 30 + 15 + 7 + 3 + 1 = 56 \) tane 2 çarpanı vardır.

\( 61! \) sayısının asal çarpanlarına aşağıdaki şekilde ayrıldığını varsayalım.

\( 61! = 2^{56} \cdot 3^a \cdot 5^b \cdot 7^c \cdot \ldots \)

\( 61! \) sayısının 2 çarpanı içermeyen tek sayı bölenlerinin sayısına \( n \) diyelim.

\( n = (a + 1)(b + 1)(c + 1)\ldots \)

Bu tek sayı bölenlerin her birini \( 2^0 \) ile \( 2^{56} \) arasındaki 57 çarpanla çarparak \( 61! \) sayısının tüm \( 57n \) tane pozitif böleni elde edilir. Bu \( 57n \) bölenden \( 56n \) tanesi \( 2^1 \) ile \( 2^{56} \) arasında çarpan içerdiği için çift sayıdır, \( n \) tanesi ise \( 2^0 \) ile çarpıldığı, dolayısıyla 2 çarpanı içermediği için tek sayıdır.

Buna göre \( 61! \) sayısının toplam \( 56n + n = 57n \) farklı pozitif böleni olup bunların \( 56n \) tanesi çift sayıdır.

\( \dfrac{56n}{57n} = \dfrac{56}{57} \) bulunur.

Soldan sağa ve sağdan sola okunuşları aynı olan sayılara palindromik sayı denir.

Yani 4 basamaklı bir \( (abcd) \) sayısının palindromik bir sayı olabilmesi için \( a = d \) ve \( b = c \) olmalıdır. Bu durumda bu 4 basamaklı sayı \( (abba) \) formatında olur.

Örnek uzaya \( S \) diyelim.

Örnek uzay 4 basamaklı tüm palindromik sayılardan oluşur.

Bir \( (abba) \) palindromik sayısında \( a \) yerine 0 hariç 9 rakam, \( b \) yerine ise 10 rakam gelebilir.

\( a \in \{1, 2, 3, \ldots, 9\} \)

\( b \in \{0, 1, 2, \ldots, 9\} \)

\( s(S) = 9 \cdot 10 = 90 \)

Bu sayılardan 9'a tam bölünme olayına \( A \) diyelim.

Bir \( (abba) \) palindromik sayısının 9'a tam bölünmesi için rakamları toplamı 9'un tam sayı katı olmalıdır.

\( k \in \mathbb{Z^+} \) olmak üzere,

\( a + b + b + a = 9k \)

\( 2(a + b) = 9k \)

\( a \) ve \( b \) birer rakam olduğu için, bu eşitliğin sağlanması için \( k \) sadece çift sayı değer alabilir.

\( k = 2 \) için:

\( 2(a + b) = 18 \Longrightarrow a + b = 9 \)

Bu durumda \( a \) 0 hariç 9 farklı değer alabilir, \( b \) ise \( a \)'nın her değeri için tek bir değer alabilir.

\( k = 4 \) için:

\( 2(a + b) = 36 \Longrightarrow a + b = 18 \)

Bu durumda \( a \) ve \( b \) sadece 9 değerini alabilir.

\( k \)'nın daha büyük değerleri \( a \) ve \( b \) için geçerli birer değer üretmez.

Buna göre istenen koşulu sağlayan \( 9 + 1 = 10 \) farklı durum vardır ve bu durumlarda aşağıdaki palindromik sayılar oluşur.

1881, 2772, 3663, 4554, 5445, 6336, 7227, 8118, 9009, 9999

\( s(A) = 10 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{10}{90} = \dfrac{1}{9} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay LED lamba üzerindeki 14 çubuğun tüm farklı yanma durumlarından oluşur.

14 çubuğun her biri eşit olasılıkla yanar ya da yanmaz.

\( s(S) = 2^{14} \)

Ekranda geçerli bir sayı gözükme olayına \( A \) diyelim.

\( A \) olayındaki sonuç sayısını üç durum altında inceleyelim.

Durum 1:

Bu durumda iki basamak da geçerli birer rakam gösterir.

Birinci ve ikinci basamakların geçerli birer rakam gösterdiği 10'ar durum vardır.

\( 10 \cdot 10 = 100 \) farklı sonuç

Durum 2:

Bu durumda birinci basamak geçerli bir rakam gösterir, ikinci basamak hiç yanmaz.

Birinci basamağın geçerli bir rakam gösterdiği 10 durum, ikinci basamağın hiç yanmadığı bir durum vardır.

\( 10 \cdot 1 = 10 \) farklı sonuç

Durum 3:

Bu durumda birinci basamak hiç yanmaz, ikinci basamak geçerli bir rakam gösterir.

Birinci basamağın hiç yanmadığı bir durum, ikinci basamağın geçerli bir rakam gösterdiği 10 durum vardır.

\( 1 \cdot 10 = 10 \) farklı sonuç

\( A \) olayındaki sonuç sayısı bu üç durumdaki sonuç sayılarının toplamına eşittir.

\( s(A) = 100 + 10 + 10 = 120 \) farklı sonuç

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{120}{2^{14}} \) bulunur.

Bir sayının 8'e tam bölünmesi için sayı en az üç tane 2 çarpanı içermelidir, 8'e tam bölünmemesi için ise en fazla iki tane 2 çarpanı içermelidir.

4 zar atıldığında gelen sayıların en fazla iki tane 2 çarpanı içerdiği durumların olasılığını bulup 1'den çıkaralım.

1 ve 6 arası sayılardan 2 ve 6 birer tane, 4 iki tane 2 çarpanı içerir.

Buna göre 4 zar atıldığında en fazla iki tane 2 çarpanı üç farklı şekilde gelebilir.

Durum 1: 0 tane 2 çarpanı

Bunun için 4 zar da 1, 3 ya da 5 gelmelidir.

\( \dfrac{3}{6} \cdot \dfrac{3}{6} \cdot \dfrac{3}{6} \cdot \dfrac{3}{6} = \dfrac{1}{16} \)

Durum 2: 1 tane 2 çarpanı

Bunun için 1 zar 2 ya da 6; 3 zar 1, 3 ya da 5 gelmelidir.

Ayrıca 4 zar atıldığında bunun gibi \( C(4, 1) = 4 \) farklı durum oluşur.

\( \dfrac{2}{6} \cdot \dfrac{3}{6} \cdot \dfrac{3}{6} \cdot \dfrac{3}{6} \cdot 4 = \dfrac{1}{6} \)

Durum 3: 2 tane 2 çarpanı

Bu durumu iki alt durum altında inceleyelim.

Durum 3.1: 2 tane 2 çarpanı (1'er tane 2 ve 6)

Bunun için iki zar 2 ya da 6; iki zar 1, 3 ya da 5 gelmelidir.

Ayrıca 4 zar atıldığında bunun gibi \( C(4, 2) = 6 \) farklı durum oluşur.

\( \dfrac{2}{6} \cdot \dfrac{2}{6} \cdot \dfrac{3}{6} \cdot \dfrac{3}{6} \cdot 6 = \dfrac{1}{6} \)

Durum 3.2: 2 tane 2 çarpanı (1 tane 4)

Bunun için 1 zar 4; 3 zar 1, 3 ya da 5 gelmelidir.

Ayrıca 4 zar atıldığında bunun gibi \( C(4, 1) = 4 \) farklı durum oluşur.

\( \dfrac{1}{6} \cdot \dfrac{3}{6} \cdot \dfrac{3}{6} \cdot \dfrac{3}{6} \cdot 4 = \dfrac{1}{12} \)

Bulduğumuz olasılıkların toplamı gelen 4 zarın çarpımının en fazla 2 tane 2 çarpanı içerme olasılığına eşittir.

\( \dfrac{1}{16} + \dfrac{1}{6} + \dfrac{1}{6} + \dfrac{1}{12} = \dfrac{23}{48} \)

4 zarın çarpımının 8'e bölünme, yani en az üç tane 2 çarpanı içerme olasılığını bulmak için bu olasılığı 1'den çıkaralım.

\( 1 - \dfrac{23}{48} = \dfrac{25}{48} \) bulunur.

İkinci kartın as çıkma olasılığı birinci karta göre değişir.

Buna göre iki farklı durum oluşur.

(1) Karo as - karo as dışında bir as

(2) As dışında bir karo - dört astan biri

Durum 1:

İlk kartın karo as, ikinci kartın karo as dışında bir as çıkma olasılığını bulalım.

\( P_1 = \dfrac{1}{52} \cdot \dfrac{3}{51} = \dfrac{3}{51 \cdot 52} \)

Durum 2:

İlk kartın as dışında bir karo, ikinci kartın dört astan biri çıkma olasılığını bulalım.

\( P_2 = \dfrac{12}{52} \cdot \dfrac{4}{51} = \dfrac{48}{51 \cdot 52} \)

İstenen olayın gerçekleşme olasılığı, birbirinden bağımsız bu iki olayın olasılıkları toplamına eşittir.

\( P = P_1 + P_2 \)

\( = \dfrac{3}{51 \cdot 52} + \dfrac{48}{51 \cdot 52} \)

\( = \dfrac{51}{51 \cdot 52} = \dfrac{1}{52} \) bulunur.

Belirli bir turda Efe'nin oyunu kazanma olasılığı; Efe'nin basketi atma, Ege'nin kaçırma olasılığına eşittir.

\( \dfrac{3}{4} \cdot \dfrac{1}{3} = \dfrac{1}{4} \)

Belirli bir turda Ege'nin oyunu kazanma olasılığı; Ege'nin basketi atma, Efe'nin kaçırma olasılığına eşittir.

\( \dfrac{2}{3} \cdot \dfrac{1}{4} = \dfrac{1}{6} \)

Belirli bir turda berabere kalma olasılığı bu iki durumun dışında kalan durumdur.

\( 1 - \dfrac{1}{4} - \dfrac{1}{6} = \dfrac{7}{12} \)

Buna göre oyun her turda \( \frac{7}{12} \) olasılıkla bir sonraki tura kalır.

Efe'nin bu oyunu kazanma olasılığına \( p \) diyelim.

Efe'nin oyunu kazanma olasılığı, oyunu ilk turda kazanma olasılığı ile oyun ikinci tura kalırsa ikinci turda kazanma olasılığının toplamına eşittir.

İkinci turda da benzer bir mantık olduğu için, \( p \) olasılığını sonsuza giden bir toplam şeklinde yazabiliriz.

\( p = \dfrac{1}{4} + \dfrac{7}{12}(\dfrac{1}{4} + \dfrac{7}{12}(\ldots)) \)

Eşitliğin sağ tarafı ile parantez içindeki ifadenin ikisi de sonsuza gittiği için parantez içindeki ifade de \( p \)'ye eşit olur.

\( p = \dfrac{1}{4} + \dfrac{7}{12}p \)

Bu denklemi \( p \) için çözelim.

\( \dfrac{5}{12}p = \dfrac{1}{4} \)

\( p = \dfrac{3}{5} \) olarak bulunur.

İskambilde maça ve sinek siyah yüzlü, kupa ve karo kırmızı yüzlü kartlardır.

İkinci kartın as çıkma olasılığı birinci karta göre, üçüncü kartın maça çıkma olasılığı birinci ve ikinci karta göre değişir.

Buna göre yedi farklı durum oluşur.

(1) Sinek as - maça as - as dışında bir maça

(2) Sinek as - maça ve sinek dışında bir as - 13 maçadan biri

(3) As dışında bir sinek - maça as - as dışında bir maça

(4) As dışında bir sinek - maça dışında bir as - 13 maçadan biri

(5) Maça as - maça dışında bir as - as dışında bir maça

(6) As dışında bir maça - maça as - as dışında bir maça

(7) As dışında bir maça - maça dışında bir as - 13 maçadan biri

Durum 1:

İlk kartın sinek as, ikinci kartın maça as, üçüncü kartın as dışında bir maça çıkma olasılığını bulalım.

\( P_1 = \dfrac{1}{52} \cdot \dfrac{1}{51} \cdot \dfrac{12}{50} \)

\( = \dfrac{12}{50 \cdot 51 \cdot 52} \)

Durum 2:

İlk kartın sinek as, ikinci kartın maça ve sinek dışında bir as, üçüncü kartın 13 maçadan biri çıkma olasılığını bulalım.

\( P_2 = \dfrac{1}{52} \cdot \dfrac{2}{51} \cdot \dfrac{13}{50} \)

\( = \dfrac{26}{50 \cdot 51 \cdot 52} \)

Durum 3:

İlk kartın as dışında bir sinek, ikinci kartın maça as, üçüncü kartın as dışında bir maça çıkma olasılığını bulalım.

\( P_3 = \dfrac{12}{52} \cdot \dfrac{1}{51} \cdot \dfrac{12}{50} \)

\( = \dfrac{144}{50 \cdot 51 \cdot 52} \)

Durum 4:

İlk kartın as dışında bir sinek, ikinci kartın maça dışında bir as, üçüncü kartın 13 maçadan biri çıkma olasılığını bulalım.

\( P_4 = \dfrac{12}{52} \cdot \dfrac{3}{51} \cdot \dfrac{13}{50} \)

\( = \dfrac{468}{50 \cdot 51 \cdot 52} \)

Durum 5:

İlk kartın maça as, ikinci kartın maça dışında bir as, üçüncü kartın as dışında bir maça çıkma olasılığını bulalım.

\( P_5 = \dfrac{1}{52} \cdot \dfrac{3}{51} \cdot \dfrac{12}{50} \)

\( = \dfrac{36}{50 \cdot 51 \cdot 52} \)

Durum 6:

İlk kartın as dışında bir maça, ikinci kartın maça as, üçüncü kartın as dışında bir maça çıkma olasılığını bulalım.

\( P_6 = \dfrac{12}{52} \cdot \dfrac{1}{51} \cdot \dfrac{11}{50} \)

\( = \dfrac{132}{50 \cdot 51 \cdot 52} \)

Durum 7:

İlk kartın as dışında bir maça, ikinci kartın maça dışında bir as, üçüncü kartın 13 maçadan biri çıkma olasılığını bulalım.

\( P_7 = \dfrac{12}{52} \cdot \dfrac{3}{51} \cdot \dfrac{12}{50} \)

\( = \dfrac{432}{50 \cdot 51 \cdot 52} \)

İstenen olayın gerçekleşme olasılığı, birbirinden bağımsız bu yedi olayın olasılıkları toplamına eşittir.

\( P = P_1 + P_2 + P_3 + P_4 + P_5 + P_6 + P_7 \)

\( = \dfrac{12 + 26 + 144 + 468 + 36 + 132 + 432}{50 \cdot 51 \cdot 52} \)

\( = \dfrac{1250}{50 \cdot 51 \cdot 52} = \dfrac{25}{2652} \) bulunur.