Sayma Yöntemleri ile Olasılık Problemleri

Örnek uzaya \( S \) diyelim.

Örnek uzay 12 öğrencinin yan yana farklı dizilişlerinden oluşur.

\( s(S) = 12! \)

Kızların yan yana gelme olayına \( A \) diyelim.

Kız öğrencilerin yan yana olduğu diziliş sayısını bulmak için 5 kız öğrenciyi tek bir grup olarak düşünelim. Bu durumda 7 erkek öğrenci ve 1 kız öğrenci grubu \( 8! \) farklı şekilde dizilebilirler.

Bir grup olarak düşündüğümüz 5 kız öğrenci kendi aralarında \( 5! \) farklı şekilde dizilebildikleri için kız öğrencilerin yan yana olduğu toplam diziliş sayısı \( 8! \cdot 5! \) olur.

\( s(A) = 8! \cdot 5! \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{8! \cdot 5!}{12!} = \dfrac{5 \cdot 4 \cdot 3 \cdot 2}{12 \cdot 11 \cdot 10 \cdot 9} \)

\( = \dfrac{1}{99} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay 8 elemanlı \( K \) kümesinin 3'lü permütasyonlarından oluşur.

\( s(S) = P(8, 3) = 8 \cdot 7 \cdot 6 = 336 \)

Bu permütasyonların 5'e tam bölünme olayına \( A \) diyelim.

\( A \) olayı örnek uzaydaki sayılar içinde 5'e tam bölünen sayılardan oluşur.

Bu sayılardan sadece son basamağı 5 olanlar 5'e tam bölünür.

\( K \) kümesinin 3'lü permütasyonları içinde son basamağı 5 olanları bulmak için önce son basamağa 5 yerleştirelim ve kalan 7 elemanın diğer iki basamak için 2'li permütasyonlarının sayısını bulalım.

\( s(A) = P(7, 2) = 7 \cdot 6 = 42 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{42}{336} = \dfrac{1}{8} \) bulunur.

Toplamları 7 ve herbiri birbirinden farklı dört rakam üçlüsü vardır.

\( 6 + 1 + 0 = 7 \)

\( 5 + 2 + 0 = 7 \)

\( 4 + 3 + 0 = 7 \)

\( 4 + 2 + 1 = 7 \)

Her bir durumdaki rakamlarla kaç farklı 3 basamaklı tek sayı yazılabileceğini bulalım.

6-1-0 rakamları ile \( 2 \cdot 2 \cdot 1 = 4 \) farklı sayı yazılabilir, bunlardan sadece 601 tek sayıdır.

5-2-0 rakamları ile \( 2 \cdot 2 \cdot 1 = 4 \) farklı sayı yazılabilir, bunlardan sadece 205 tek sayıdır.

4-3-0 rakamları ile \( 2 \cdot 2 \cdot 1 = 4 \) farklı sayı yazılabilir, bunlardan sadece 403 tek sayıdır.

4-2-1 rakamları ile \( 3! = 6 \) farklı sayı yazılabilir, bunlardan 241 ve 421 tek sayıdır.

Buna göre istenen koşulu sağlayan \( 4 + 4 + 4 + 6 = 18 \) farklı sayı yazılabilir ve bunlardan \( 1 + 1 + 1 + 2 = 5 \)'i tek sayıdır.

Belirtilen koşulları sağlayan bir sayının tek sayı olma olasılığını bulalım.

\( \dfrac{\text{İstenen durum sayısı}}{\text{Toplam durum sayısı}} = \dfrac{5}{18} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay 6 elemanlı \( K \) kümesinin 3 elemanlı permütasyonlarından oluşur.

\( s(S) = P(6, 3) = 6 \cdot 5 \cdot 4 = 120 \)

Bu sayılar arasından seçilen bir sayının 300'den büyük olma olayına \( A \) diyelim.

Bu sayılardan ilk basamağı \( \{3, 4, 5, 6\} \) rakamlarından biri olan sayılar 300'den büyük olur.

Bu sayıları oluşturmak için ilk basamak için 4 farklı seçenek, kalan iki basamak için sırasıyla 5 ve 4 farklı seçenek vardır.

\( s(A) = 4 \cdot 5 \cdot 4 = 80 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{80}{120} = \dfrac{2}{3} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay 5 zar atışının tüm farklı sonuçlarından oluşur.

\( S = \{11111, 11112, \ldots, 66666\} \)

\( s(S) = 6^5 \)

Her defasında farklı bir yüzün üstte gelme olayına \( A \) diyelim.

1-6 arası 5 rakam \( P(6, 5) = 6! \) farklı şekilde dizilebilir, dolayısıyla her defasında farklı bir yüzün üstte geldiği \( 6! \) farklı durum vardır.

\( A = \{12345, 12346, \ldots, 65432\} \)

\( s(A) = 6! \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{6!}{6^5} = \dfrac{5!}{6^4} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay boncukların ipe tüm farklı dizilişlerinden oluşur.

Farklı diziliş sayısını bulmak için tekrarlı permütasyon formülünü kullanalım.

\( s(S) = \dfrac{7!}{3! \cdot 4!} = 35 \)

Başta ve sonda yeşil boncuk bulunma olayına \( A \) diyelim.

Başa ve sona koymak için özdeş 3 yeşil boncuk içinden 2 boncuk 1 şekilde seçilebilir.

Kalan 1 yeşil ve 4 kırmızı boncuk uçlardaki iki boncuk arasında \( \frac{5!}{4!} \) farklı şekilde dizilebilir.

\( s(A) = 1 \cdot \dfrac{5!}{4!} = 5 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{5}{35} = \dfrac{1}{7} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay 6 kız, 4 erkek öğrenci arasından 2 öğrencinin tüm farklı seçimlerinden oluşur.

\( s(S) = C(10, 2) = 45 \)

(a) seçeneği:

Öğrencilerin ikisinin de erkek olma olayına \( A \) diyelim.

Bu olayın eleman sayısı 4 erkek öğrenci arasından 2 öğrencinin farklı seçim sayısı kadardır.

\( s(A) = C(4, 2) = 6 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{6}{45} = \dfrac{2}{15} \)

(b) seçeneği:

Bir öğrencinin kız diğerinin erkek olma olayına \( B \) diyelim.

Bu olayın eleman sayısı 6 kız, 4 erkek öğrenci arasından 1 kız 1 erkek öğrencinin farklı seçim sayısı kadardır.

\( s(B) = C(6, 1) \cdot C(4, 1) = 24 \)

\( B \) olayının gerçekleşme olasılığı, \( B \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(B) = \dfrac{s(B)}{s(S)} \)

\( = \dfrac{24}{45} = \dfrac{8}{15} \)

Örnek uzaya \( S \) diyelim.

Örnek uzay küpün üç kez atışının tüm farklı sonuçlarından oluşur.

\( s(S) = 6^3 = 216 \)

Her rengin bir defa gelme olayı \( A \) diyelim.

\( A \) olayı "YKM" şeklindeki sonuçların tüm farklı dizilişlerinden oluşur.

3 yeşil yüzeyden biri \( C(3, 1) = 3 \) farklı şekilde, 2 kırmızı yüzeyden biri \( C(2, 1) = 2 \) farklı şekilde, 1 mavi yüzeyden biri \( C(1, 1) = 1 \) farklı şekilde seçilebilir.

Seçilen her renge ait yüzeyler aralarında \( 3! \) farklı şekilde dizilebilir.

\( A \) olayının sonuç sayısını bulalım.

\( s(A) = 3 \cdot 2 \cdot 1 \cdot 3! = 36 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{36}{216} = \dfrac{1}{6} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay Zeynep'in hatırladığı rakamlarla oluşturulabilecek tüm şifrelerden oluşur.

3 tane 1 ve 4 tane 5 rakamı ile oluşturulabilecek 7 basamaklı şifre sayısını tekrarlı permütasyon formülü ile bulalım.

\( s(S) = \dfrac{7!}{3! \cdot 4!} = 35 \)

Zeynep'in doğru şifreyi bulma olayına \( A \) diyelim.

Doğru şifre sadece bir tanedir.

\( s(A) = 1 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{1}{35} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay 5 öğrencinin tüm farklı dizilişlerinden oluşur.

\( s(S) = 5! = 120 \)

En kısa ve en uzun boylu öğrencilerin sıranın iki ucunda olma olayına \( A \) diyelim.

Önce en kısa ve en uzun boylu öğrencileri sıranın iki ucuna yerleştirelim. Kalan 3 öğrenci \( 3! = 6 \) farklı şekilde dizilebilirler. Bu dizilişlerin herbirinde en uzun ve en kısa öğrenciler kendi aralarında \( 2! \) farklı şekilde yer değiştirebilir.

\( s(A) = 3! \cdot 2! = 12 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{12}{120} = \dfrac{1}{10} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay üç kişinin tüm farklı seçimlerinden oluşur.

\( s(S) = C(11, 3) = \dfrac{11!}{8! \cdot 3!} = 165 \)

Seçilen üç kişinin aynı ülkeden olma olayına \( A \) diyelim.

Grupta iki Türk bulunduğu için seçilen üç kişi ya Alman ya da İngiliz olabilir.

11 kişi arasından üç Alman \( C(4, 3) \), üç İngiliz \( C(5, 3) \) farklı şekilde seçilebilir.

\( s(A) = C(4, 3) + C(5, 3) = 14 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{14}{165} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay 9 elemanlı bir kümeden 5 elemanın tüm farklı seçimlerinden oluşur.

\( s(S) = C(9, 5) = 126 \)

Seçilen beş sayı arasında ikinci en küçük sayının 4 olma olayına \( A \) diyelim.

4 ikinci en küçük sayı ise diğer dört sayıdan biri 4'ten küçük, üçü 4'ten büyük olmalıdır.

\( \{ 1, 2, 3 \} \) sayıları arasından bir sayı \( C(3, 1) = 3 \) farklı şekilde seçilebilir.

\( \{ 5, 6, 7, 8, 9 \} \) sayıları arasından üç sayı \( C(5, 3) = 10 \) farklı şekilde seçilebilir.

4'ün seçilen beş sayı arasında en küçük ikinci sayı olduğu durum sayısı bu iki sayının çarpımına eşittir.

\( s(A) = 3 \cdot 10 = 30 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{30}{126} = \dfrac{5}{21} \) bulunur.

İki ailede toplamda 11 kişi vardır.

Örnek uzaya \( S \) diyelim.

Örnek uzay 11 kişi arasından 2 kişinin tüm farklı seçimlerinden oluşur.

\( s(S) = C(11, 2) = \dfrac{11!}{2! \cdot 9!} = 55 \)

Seçilen iki kişinin kardeş olma olayına \( A \) diyelim.

Yılmaz ailesindeki 4 kardeşten ikisi \( C(4, 2) = 6 \) farklı şekilde seçilebilir.

Demir ailesindeki 3 kardeşten ikisi \( C(3, 2) = 3 \) farklı şekilde seçilebilir.

Dolayısıyla yapılabilecek farklı seçimlerden \( 6 + 3 = 9 \)'unda seçilen kişiler kardeş olur.

\( s(A) = 9 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{9}{55} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay 6 kişi arasından 3 kişinin farklı seçimlerinden oluşur.

\( s(S) = C(6, 3) = \dfrac{6!}{3! \cdot 3!} = 20 \)

Seçilen kişiler arasında evli bir çiftin bulunma olayına \( A \) diyelim.

3 evli çift içinden bir çift \( C(3, 1) = 3 \) farklı şekilde seçilebilir. Seçilen evli çiftin yanına üçüncü kişi diğer 4 kişi arasından \( C(4, 1) = 4 \) farklı şekilde seçilebilir.

Buna göre ikisi evli bir çift olmak üzere üç kişi \( 3 \cdot 4 = 12 \) farklı şekilde seçilebilir.

\( s(A) = 12 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{12}{20} = \dfrac{3}{5} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay rakamları sıfırdan ve birbirinden farklı olan 5 basamaklı doğal sayılardan oluşur.

\( s(S) = P(9, 5) = 9 \cdot 8 \cdot 7 \cdot 6 \cdot 5 \)

Bu sayıların rakamlarından sadece birinin çift sayı olma olayına \( A \) diyelim.

Sıfır dışında çift sayı 4 rakam vardır (2, 4, 6, 8). Bu 4 rakamdan biri \( C(4, 1) = 4 \) farklı şekilde, diğer tek sayı 5 rakamdan 4'ü \( C(5, 4) = 5 \) farklı şekilde seçilebilir.

Seçilen bu 5 rakam aralarında \( 5! \) farklı şekilde dizilebilir.

\( s(A) = 4 \cdot 5 \cdot 5! \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{4 \cdot 5 \cdot 5!}{9 \cdot 8 \cdot 7 \cdot 6 \cdot 5} = \dfrac{10}{63} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay verilen 7 sayı arasından 3 sayının tüm farklı seçimlerinden oluşur.

\( s(S) = C(7, 3) = 35 \)

3 sayının çarpımının pozitif olma olayına \( A \) diyelim.

3 sayının çarpımının pozitif olması için, ya sayıların üçü de pozitif olmalıdır ya da biri pozitif diğer ikisi negatif olmalıdır.

Verilen 7 sayının 3'ü pozitif 4'ü negatiftir.

Pozitif sayılar arasından 3 sayı \( C(3, 3) = 1 \) farklı şekilde seçilebilir.

Pozitif sayılar arasından 1 sayı, negatif sayılar arasından 2 sayı toplamda \( C(3, 1) \cdot C(4, 2) = 3 \cdot 6 = 18 \) farklı şekilde seçilebilir.

\( A \) olayının eleman sayısı bu iki durumun toplamına eşittir.

\( s(A) = 1 + 18 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{19}{35} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay 3 zar atışının tüm farklı sonuçlarından oluşur.

\( S = \{ 111, 112, \ldots, 666 \} \)

\( s(S) = 6^3 = 216 \)

Her atışta bir önceki sayıdan daha büyük bir sayı gelme olayına \( A \) diyelim.

Her atışta bir önceki sayıdan daha büyük bir sayı geliyor ise sayılar birbirinden farklıdır.

Bu durum 6 sayı arasından seçilen herhangi 3 sayının küçükten büyüğe sıralanması ile gerçekleşir.

\( s(A) = C(6, 3) = 20 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{20}{216} = \dfrac{5}{54} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay 10 bilyenin tüm farklı dizilişlerinden oluşur.

Aynı renkteki bilyeler özdeş oldukları için diziliş sayısını tekrarlı permütasyon formülü ile bulabiliriz.

\( s(S) = \dfrac{10!}{5!\ 3!\ 2!} = 2520 \)

Bilyelerin 5 mavi, 3 pembe, 2 sarı sırası ile çekilme olayına \( A \) diyelim.

\( A \) olayı için tek bir diziliş vardır.

MMMMMPPSS

\( s(A) = 1 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{1}{2520} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay paranın 8 atıştaki tüm farklı sonuçlarından oluşur.

\( s(S) = 2^8 = 256 \)

Paranın sekizinci atışta dördüncü kez tura gelme olayına \( A \) diyelim.

Paranın sekizinci atışta dördüncü kez tura gelebilmesi için para ilk 7 atışta 3 kez tura gelmelidir.

Para ilk 7 atışta \( C(7, 3) \) farklı şekilde 3 kez tura gelebilir, sekizinci atışta da 1 şekilde tura gelebilir.

\( s(A) = C(7, 3) \cdot 1 = 35 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{35}{256} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay 15 top arasından 4 topun tüm farklı seçimlerinden oluşur.

\( s(S) = C(15, 4) = 1365 \)

Arkadaşının Ezgi ile tam olarak 3 tane topu aynı çekme olayına \( A \) diyelim.

\( A \) olayı Ezgi'nin çektiği 8 top arasından 3 topun ve Ezgi'nin çekmediği 7 top arasından 1 topun çekilmesi ile oluşur.

\( s(A) = C(8, 3) \cdot C(7, 1) = 392 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{392}{1365} = \dfrac{56}{195} \) bulunur.

Bir biberin acı olma olayına \( A \) diyelim.

\( P(A) = \dfrac{1}{3} \)

Bir biberin acı olmama olayı \( A' \) olur.

\( P(A') = \dfrac{2}{3} \)

İstenen durum altı biberin üçünün acı olduğu, üçünün acı olmadığı durumda gerçekleşir.

Mustafa'nın yediği ilk üç biberin acı olduğu, sonraki üç biberin acı olmadığı durumun olasılığını hesaplayalım.

\( P(\{AAAA'A'A'\}) = (\dfrac{1}{3})^3 \cdot (\dfrac{2}{3})^3 \)

\( = \dfrac{8}{729} \)

AAAA'A'A' harflerinin her farklı dizilişi, biberlerin üçünün acı olduğu, üçünün acı olmadığı bir duruma karşılık gelir.

AAAA'A'A' harflerinin farklı dizilişleri için tekrarlı permütasyon formülünü kullanalım.

\( \dfrac{6!}{3!\ 3!} = 20 \)

Her farklı diziliş için yukarıda hesapladığımız olasılık aynı olacağı için, bu iki sayının çarpımı Mustafa'nın yediği altı biberin üçünün acı olduğu, üçünün acı olmadığı durumların toplam olasılığını verir.

\( \dfrac{8}{729} \cdot 20 = \dfrac{160}{729} \) bulunur.

Her atışta iki zar atılıyor.

Her zar için 6 durum olmak üzere, aynı anda atılan her iki zar için 36 farklı durum vardır.

Örnek uzaya \( S \) diyelim.

Örnek uzay iki zarın 25 atıştaki tüm farklı sonuçlarından oluşur.

\( s(S) = 36^{25} \)

Her seferinde farklı sayı gelme olayına \( A \) diyelim.

Her zar atışında ikisinin de aynı sayıyı attığı 6 durum vardır.

\( \{(1, 1), (2, 2), \ldots, (6, 6) \} \)

Buna göre farklı sayı geldiği \( 36 - 6 = 30 \) durum vardır.

\( A \) olayı 25 zar atışında da bu 30 durumdan birinin gerçekleştiği sonuçlardan oluşur.

\( s(A) = 30^{25} \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{30^{25}}{36^{25}} = (\dfrac{5}{6})^{25} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay 10 farklı şekerin üç çocuğa tüm farklı dağıtımlarından oluşur.

Her şeker için çocuk sayısı kadar farklı seçenek vardır.

\( s(S) = 3^{10} \)

En küçük çocuğun 3 şeker alma olayına \( A \) diyelim.

Bunun için önce 10 farklı şeker arasından 3 şeker \( C(10, 3) \) farklı şekilde en küçük çocuğa verilir, sonra kalan 7 şeker \( 2^7 \) farklı şekilde diğer iki çocuğa paylaştırılır.

\( s(A) = C(10, 3) \cdot 2^7 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{C(10, 3) \cdot 2^7}{3^{10}} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay 52 kart arasından 12 kartın tüm farklı seçimlerinden oluşur.

\( s(S) = C(52, 12) \)

Papazın ilk kez 12. çekilen kartta çıkma olayına \( A \) diyelim.

İskambilde 4 tane papaz, \( 52 - 4 = 48 \) tane papaz dışında kart vardır.

Papazın ilk kez 12. çekilen kartta çıktığı durumda; ilk 11 kart \( C(48, 11) \) farklı şekilde papaz dışında, 12. kart \( C(4, 1) \) farklı şekilde papaz seçilebilir.

\( s(A) = C(48, 11) \cdot C(4, 1) \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{C(48, 11) \cdot C(4, 1)}{C(52, 12)} \) bulunur.

Oyuncak askerin 12 adım sonunda başlangıç noktasında olması için ileri ve geri adımları eşit sayıda olmalıdır.

Oyuncak askerin önce 6 adım ileri, sonra 6 adım geri gitme olasılığını bulalım.

İİİİİİGGGGGG

\( (\dfrac{2}{3})^6 \cdot (\dfrac{1}{3})^6 = \dfrac{64}{729^2} \)

"İ" ve "G" harflerinin her farklı dizilişinde oyuncak asker 6 ileri ve 6 geri adım atar ve sonuçta başlangıç noktasına döner.

Tekrarlı permütasyonu kullanarak ileri ve geri adım sırasının tüm farklı dizilişlerini bulalım.

\( \dfrac{12!}{6!\ 6!} = 924 \)

Buna göre oyuncak askerin 12 adımın sonunda başlangıç noktasına döndüğü 924 durum vardır. Her durumda yukarıda hesapladığımız olasılığın sadece çarpım sırası değişeceği için gerçekleşme olasılıkları aynı olur.

Oyuncak askerin 12 adım sonra başlangıç noktasına dönme olasılığı:

\( P = 924 \cdot \dfrac{64}{729^2} \) bulunur.

Örnek uzaya \( S \) diyelim

Örnek uzay 30 sayı arasından 3 sayının tüm farklı seçimlerinden oluşur.

\( s(S) = C(30, 3) \)

Sayıları 3'e bölümünden kalanlarına göre üç ayrık kümeye (denklik sınıfına) ayırabiliriz.

Bu kümelere sırasıyla \( \overline{0}, \overline{1}, \overline{2} \) diyelim.

\( \overline{0} = \{ 3, 6, 9, \ldots, 30 \} \)

\( \overline{1} = \{ 1, 4, 7, \ldots, 28 \} \)

\( \overline{2} = \{ 2, 5, 8, \ldots, 29 \} \)

Her kümenin 10'ar elemanı vardır.

\( s(\overline{0}) = s(\overline{1}) = s(\overline{2}) = 10 \)

Seçilen üç sayının toplamının 3'e tam bölünme olayına \( A \) diyelim.

Sayıların toplamı dört şekilde 3'e tam bölünür.

Durum 1:

Bu durumda üç sayı da \( \overline{0} \) kümesinden seçilir.

\( C(10, 3) = 120 \)

Durum 2:

Bu durumda üç sayı da \( \overline{1} \) kümesinden seçilir.

\( C(10, 3) = 120 \)

Durum 3:

Bu durumda üç sayı da \( \overline{2} \) kümesinden seçilir.

\( C(10, 3) = 120 \)

Durum 4:

Bu durumda her kümeden birer sayı seçilir.

\( C(10, 1) \cdot C(10, 1) \cdot C(10, 1) = 1000 \)

Dört durumdaki sonuç sayılarının toplamı \( A \) olayındaki toplam sonuç sayısını verir.

\( s(A) = 120 + 120 + 120 + 1000 = 1360 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} = \dfrac{1360}{4060} \)

\( = \dfrac{68}{203} \) bulunur.

Zar atışında her bir sayının gelme olasılığı \( \frac{1}{6} \)'dır.

İstenen olasılık için 6 durum vardır.

Durum 1: Zarın 1 gelmesi

10 öğrenci arasından seçilen 1 öğrencinin kız olma olasılığını bulalım.

\( \dfrac{C(6, 1)}{C(10, 1)} = \dfrac{3}{5} \)

Bu durumun olasılığı bu iki olasılığın çarpımıdır.

\( \dfrac{1}{6} \cdot \dfrac{3}{5} = \dfrac{1}{10} \)

Durum 2: Zarın 2 gelmesi

10 öğrenci arasından seçilen 2 öğrencinin de kız olma olasılığını bulalım.

\( \dfrac{C(6, 2)}{C(10, 2)} = \dfrac{1}{3} \)

Bu durumun olasılığı bu iki olasılığın çarpımıdır.

\( \dfrac{1}{6} \cdot \dfrac{1}{3} = \dfrac{1}{18} \)

Durum 3: Zarın 3 gelmesi

10 öğrenci arasından seçilen 3 öğrencinin de kız olma olasılığını bulalım.

\( \dfrac{C(6, 3)}{C(10, 3)} = \dfrac{1}{6} \)

Bu durumun olasılığı bu iki olasılığın çarpımıdır.

\( \dfrac{1}{6} \cdot \dfrac{1}{6} = \dfrac{1}{36} \)

Durum 4: Zarın 4 gelmesi

10 öğrenci arasından seçilen 4 öğrencinin de kız olma olasılığını bulalım.

\( \dfrac{C(6, 4)}{C(10, 4)} = \dfrac{1}{14} \)

Bu durumun olasılığı bu iki olasılığın çarpımıdır.

\( \dfrac{1}{6} \cdot \dfrac{1}{14} = \dfrac{1}{84} \)

Durum 5: Zarın 5 gelmesi

10 öğrenci arasından seçilen 5 öğrencinin de kız olma olasılığını bulalım.

\( \dfrac{C(6, 5)}{C(10, 5)} = \dfrac{1}{42} \)

Bu durumun olasılığı bu iki olasılığın çarpımıdır.

\( \dfrac{1}{6} \cdot \dfrac{1}{42} = \dfrac{1}{252} \)

Durum 6: Zarın 6 gelmesi

10 öğrenci arasından seçilen 6 öğrencinin de kız olma olasılığını bulalım.

\( \dfrac{C(6, 6)}{C(10, 6)} = \dfrac{1}{210} \)

Bu durumun olasılığı bu iki olasılığın çarpımıdır.

\( \dfrac{1}{6} \cdot \dfrac{1}{210} = \dfrac{1}{1260} \)

İstenen olayın gerçekleşme olasılığı, birbirinden bağımsız bu altı olayın olasılıklarının toplamına eşittir.

\( \dfrac{1}{10} + \dfrac{1}{18} + \dfrac{1}{36} + \dfrac{1}{84} + \dfrac{1}{252} + \dfrac{1}{1260} \)

\( = \dfrac{1}{5} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay \( K \) kümesinin elemanları arasından 3 sayının tüm farklı seçimlerinden oluşur.

\( s(S) = C(10, 3) = 120 \)

Seçilen sayılar arasında en küçük sayının 4 veya en büyük sayının 12 olma olayına \( A \) diyelim.

\( A \) olayını aşağıdaki şekilde tanımlayabiliriz.

\( E_4 \): Seçilen sayılar arasında en küçük sayının 4 olma olayı

\( E_{12} \): Seçilen sayılar arasında en büyük sayının 12 olma olayı

\( A = E_4 \cup E_{12} \)

Ayrık olmayan iki kümenin birleşim kümesinin eleman sayısı aşağıdaki formülle bulunur.

\( s(A) = s(E_4 \cup E_{12}) = s(E_4) + s(E_{12}) - s(E_4 \cap E_{12}) \)

\( E_4 \) olayının gerçekleşmesi için "4" elemanına ek olarak \( \{6, 8, 10, 12, 14, 16, 18, 20\} \) kümesinden iki eleman seçilmelidir.

\( s(E_4) = C(8, 2) = 28 \)

\( E_{12} \) olayının gerçekleşmesi için "12" elemanına ek olarak \( \{2, 4, 6, 8, 10\} \) kümesinden iki eleman seçilmelidir.

\( s(E_{12}) = C(5, 2) = 10 \)

\( E_4 \cup E_{12} \) olayının gerçekleşmesi için "4" ve "12" elemanlarına ek olarak \( \{6, 8, 10\} \) kümesinden bir eleman seçilmelidir.

\( s(E_4 \cap E_{12}) = C(3, 1) = 3 \)

Bulduğumuz değerleri formülde yerine koyalım.

\( s(A) = s(E_4 \cup E_{12}) = s(E_4) + s(E_{12}) - s(E_4 \cap E_{12}) \)

\( = 28 + 10 - 3 = 35 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{35}{120} = \dfrac{7}{24} \)bulunur.

Bir satranç tahtasında \( 8 \cdot 8 = 64 \) kare vardır.

Örnek uzaya \( S \) diyelim.

Örnek uzay 64 kare arasından 3 karenin tüm farklı seçimlerinden oluşur.

\( s(S) = C(64, 3) = 41664 \)

Seçilen üç karenin aynı satır, aynı sütun ya da aynı çapraz üzerinde olma olayına \( A \) diyelim.

\( A \) olayı 3 durumda oluşur.

Durum 1:

Bu durumda seçilen üç kare aynı satır üzerinde olur.

Satranç tahtasında 8 satır ve her satırda 8 kare vardır.

\( 8 \cdot C(8, 3) = 448 \)

Durum 2:

Bu durumda seçilen üç kare aynı sütun üzerinde olur.

Satranç tahtasında 8 sütun ve her sütunda 8 kare vardır.

\( 8 \cdot C(8, 3) = 448 \)

Durum 3:

Bu durumda seçilen üç kare aynı çapraz üzerinde olur.

Satranç tahtasında iki farklı tipte çapraz kareler vardır.

Durum 3.1: Sola yatık çaprazlar

Satranç tahtasını sola yatık bir köşegen çizerek iki eşit parçaya ayıralım ve köşegenin altında kalan çaprazlar (kırmızı çizgiler) üzerinde çalışalım.

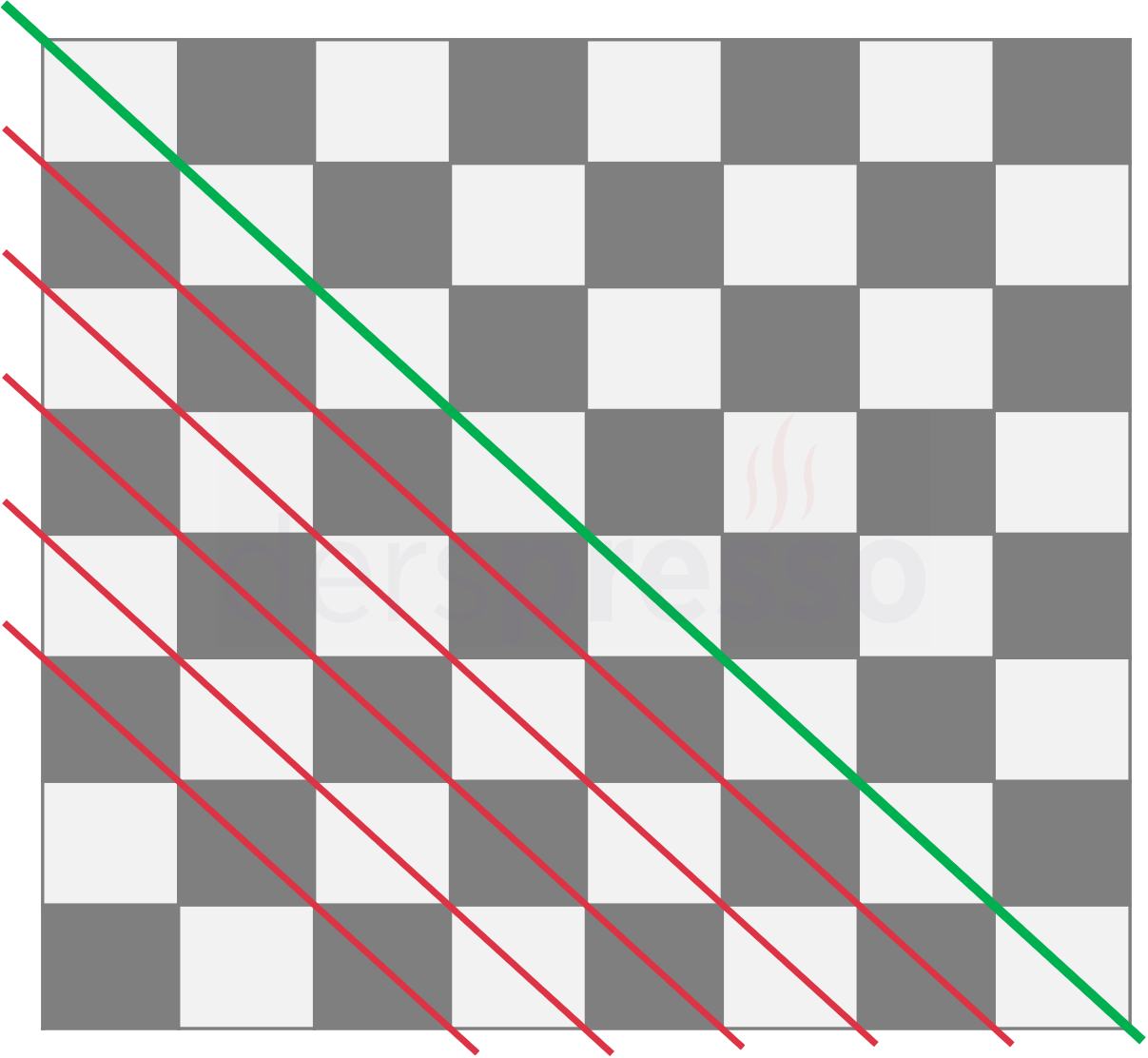
Aynı çaprazda 3 kare bulunabilmesi için çaprazlar en az 3 kareden oluşmalıdır.

Her çapraz için 3 karenin kaç farklı şekilde seçilebileceğini bulalım.

3 kareden oluşan çapraz: \( C(3, 3) = 1 \)

4 kareden oluşan çapraz: \( C(4, 3) = 4 \)

5 kareden oluşan çapraz: \( C(5, 3) = 10 \)

6 kareden oluşan çapraz: \( C(6, 3) = 20 \)

7 kareden oluşan çapraz: \( C(7, 3) = 35 \)

Köşegenin altında kalan çaprazlar için toplam farklı seçim sayısını bulalım.

\( 1 + 4 + 10 + 20 + 35 = 70 \)

Köşegenin üstünde bulunan çaprazlar için de seçim sayısı aynıdır.

Ana köşegen üzerinde 3 kare \( C(8, 3) = 56 \) farklı şekilde seçilebilir (yeşil çizgi).

Sağa yatık çaprazlar üzerinde yapılabilecek toplam farklı seçim sayısı, her çapraz için hesapladığımız değerlerin toplamıdır.

\( 70 + 70 + 56 = 196 \)

Durum 3.2: Sağa yatık çaprazlar

Sola yatık çaprazlar için yaptığımız hesaplama, sağa yatık çaprazlar için de geçerlidir.

Buna göre, seçilen 3 kare \( 196 + 196 = 392 \) farklı şekilde aynı çapraz üzerinde olabilir.

\( A \) olayındaki sonuç sayısı, birbirinden bağımsız bu 3 durumun eleman sayılarının toplamıdır.

\( s(A) = 448 + 448 + 392 \)

\( = 1288 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{1288}{41664} = \dfrac{23}{744} \) bulunur.

On dondurmanın her birinin çubuğunda D, A, N, C, E harflerinden biri yazmaktadır.

Örnek uzaya \( S \) diyelim.

On çubuğu dağıtılacak özdeş nesneler ve D, A, N, C, E harflerini bu çubukların dağıtılacağı farklı kutular olarak düşünelim.

Bu durumda örnek uzayı \( n \) özdeş nesnenin \( k \) farklı kutuya herhangi bir koşul olmaksızın dağıtım problemi olarak modelleyebiliriz.

Özdeş nesne sayısı \( n = 10 \) ve kutu sayısı \( k = 5 \) olacak şekilde ayraç yöntemi formülünü uygulayalım.

\( s(S) = C(n + k - 1, k - 1) \)

\( = C(10 + 5 - 1, 5 - 1) \)

\( = C(14, 4) = 1001 \)

(a) seçeneği:

On çubuktan tam olarak bir tane bedava dondurma kazanma olayına \( A \) diyelim.

\( A \) olayı her harften birer tane çıktığında, ama ikişer tane çıkmadığında gerçekleşir.

Önce beş çubuğu D, A, N, C, E harflerine birer tane olmak üzere dağıtalım.

Kalan beş çubuğu D, A, N, C, E harflerine kaç farklı şekilde dağıtabileceğimizi bulalım.

Özdeş nesne sayısı \( n = 5 \) ve kutu sayısı \( k = 5 \) olacak şekilde ayraç yöntemi formülünü uygulayalım.

Farklı dağıtım sayısı \( = C(n + k - 1, k - 1) \)

\( = C(5 + 5 - 1, 5 - 1) \)

\( = C(9, 4) = 126 \)

Bu 126 dağıtımdan sadece birinde 5 çubuk D, A, N, C, E harflere birer tane dağılır ve bu durum ek bir bedava dondurma daha (toplamda iki dondurma) kazanmasına neden olur.

Bu tek durumu çıkardığımızda tam olarak bir tane bedava dondurma kazanma olayının sonuç sayısını buluruz.

\( s(A) = 126 - 1 = 125 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{125}{1001} \)

(b) seçeneği:

On çubuktan iki tane bedava dondurma kazanma olayına \( B \) diyelim.

\( B \) olayı (a) seçeneğinde bulduğumuz tek bir duruma karşılık gelir.

\( P(B) = \dfrac{s(B)}{s(S)} \)

\( = \dfrac{1}{1001} \)

(c) seçeneği:

On çubuktan hiç bedava dondurma kazanamama olayına \( C \) diyelim.

\( A, B, C \) olayları bütünü kapsayıcı olaylar olduğu için olasılıkları toplamı 1'e eşittir.

\( P(A) + P(B) + P(C) = P(S) \)

\( P(C) = P(S) - P(A) - P(B) \)

\( = 1 - \dfrac{125}{1001} - \dfrac{1}{1001} \)

\( = \dfrac{875}{1001} = \dfrac{125}{143} \)

Genel bölünebilme kuralına göre, bir sayının 10'a bölünmesi için sayı hem 2'ye hem de 5'e bölünmelidir.

2'ye bölünen rakamlar 0, 2, 4, 6, 8 olmak üzere beş tanedir.

5'e bölünen rakamlar 0, 5 olmak üzere iki tanedir.

Buna göre seçilen 12 rakam, 2'ye bölünen rakamlardan en az bir tane ve 5'e bölünen rakamlardan en az bir tane içerdiği durumda çarpımları 10'a bölünür.

Seçilen 12 rakam en az bir tane 0 içerdiği durumda iki koşul da sağlandığı için çarpımları (yani 0) yine 10'a bölünür.

Örnek uzaya \( S \) diyelim.

Örnek uzay 12 rakamın tüm farklı seçimlerinden oluşur.

\( s(S) = 10^{12} \)

İstenen olasılığı 12 tane rakamın çarpımının 10'a bölünmeme olasılığı üzerinden hesaplayalım.

Seçilen 12 tane rakamın da 2'ye bölünmeyen rakamlar olma olayına \( A \) diyelim.

2'ye bölünmeyen rakamlar 1, 3, 5, 7, 9 olmak üzere beş tanedir.

\( s(A) = 5^{12} \)

Seçilen 12 tane rakamın da 5'e bölünmeyen rakamlar olma olayına \( B \) diyelim.

5'e bölünmeyen rakamlar 0 ve 5 dışındaki rakamlar olmak üzere 8 tanedir.

\( s(B) = 8^{12} \)

\( A \) ve \( B \) olaylarında hem 2'ye hem de 5'e bölünmeyen sonuçlar ortak olduğu için, bu sonuçları çift saymaya yol açmamak için toplamdan çıkarmamız gerekir.

Ne 2'ye ne de 5'e bölünmeyen rakamlar 1, 3, 7, 9 olmak üzere 4 tanedir.

\( s(A \cap B) = 4^{12} \)

İstenen olasılık aşağıdaki gibi bulunur.

\( P = 1 - \dfrac{s(A) + s(B) - s(A \cap B)}{s(S)} \)

\( = 1 - \dfrac{5^{12} + 8^{12} - 4^{12}}{10^{12}} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay üç zar atışının tüm farklı sonuçlarından oluşur.

\( s(S) = 6^3 = 216 \)

Gelen sayıların ortak farkı pozitif olan bir aritmetik dizi oluşturma olayına \( A \) diyelim.

1 ve 6 arası sayıların ortak farkı pozitif olan kaç farklı aritmetik dizi oluşturduğunu bulalım.

Ortak farkı 1 olan diziler:

\( (1, 2, 3), (2, 3, 4), (3, 4, 5), (4, 5, 6) \)

Ortak farkı 2 olan diziler:

\( (1, 3, 5), (2, 4, 6) \)

Her bir sayı üçlüsü üç zar atıldığında \( 3! = 6 \) farklı şekilde gelebilir.

\( s(A) = (4 + 2) \cdot 6 = 36 \) bulunur.

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{36}{216} = \dfrac{1}{6} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay 6 elemanlı \( K \) kümesinin elemanlarını tekrarlı kullanarak yazılabilecek tüm üç basamaklı sayılardan oluşur.

\( s(S) = 6^3 = 216 \)

Bu sayılar arasından seçilen bir sayının yalnız iki basamağının aynı olma olayına \( A \) diyelim.

Bu sayılardan yalnız iki basamağı aynı olan sayıları bulmak için tekrar eden rakam \( C(6, 1) = 6 \) farklı şekilde, diğer rakam da kalan 5 eleman içinden \( C(5, 1) = 5 \) farklı şekilde seçilebilir.

Bu iki rakam kullanılarak yalnız iki basamağı aynı olan "aab" formunda üç basamaklı bir sayı tekrarlı permütasyonla \( \frac{3!}{2!} = 3 \) farklı şekilde dizilebilir.

\( s(A) = 6 \cdot 5 \cdot 3 = 90 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{90}{216} = \dfrac{5}{12} \) bulunur.

Yılmaz'ın önce herhangi 4 sayı seçtiğini varsayalım.

Örnek uzaya \( S \) diyelim.

Örnek uzay Burak'ın 9 sayı arasından 4 sayı seçtiği tüm farklı sonuçlardan oluşur.

\( s(S) = C(9, 4) = 126 \)

Burak'ın seçtiği yalnız bir sayının Yılmaz'ın seçtiği sayılarla ortak olma olayına \( A \) diyelim.

Burak, Yılmaz'ın seçtiği 4 sayıdan birini \( C(4, 1) = 4 \) farklı şekilde, Yılmaz'ın seçmediği 5 sayıdan üçünü \( C(5, 3) = 10 \) farklı şekilde seçebilir.

\( s(A) = 4 \cdot 10 = 40 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{40}{126} = \dfrac{20}{63} \) bulunur.

7 harfli bu kelimede "A" harfi 4 kez, "D" harfi 2 kez yer almaktadır.

Örnek uzaya \( S \) diyelim.

Örnek uzay ADANADA kelimesinin harfleri ile oluşturulabilecek tüm farklı kelimelerden oluşur.

Tekrarlı permütasyon formülü ile oluşturulabilecek farklı kelime sayısını bulalım.

\( s(S) = \dfrac{7!}{4! \cdot 2!} = 105 \)

Oluşturulacak kelimenin palindrom olma olayına \( A \) diyelim.

Kelimenin palindrom olması için en ortadaki harf "N" olmalı, öncesinde de "A", "A" ve "D" harfleri herhangi bir sırada bulunmalıdır. Bu durumda geri kalan "A", "A" ve "D" harfleri kelimenin sonuna ilk 3 harf ile ters sırada yerleştirilerek bir palindrom kelime oluşturulur.

"A", "A" ve "D" harfleri ile oluşturulabilecek 3 harfli kelime sayısını tekrarlı permütasyon formülü ile bulalım.

\( s(A) = \dfrac{3!}{2!} = 3 \)

Buna göre ADANADA kelimesinin harfleri ile 3 farklı palindrom kelime yazılabilir: ADANADA, AADNDAA, DAANAAD.

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{3}{105} = \dfrac{1}{35} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay 6 madeni para atışının tüm farklı sonuçlarından oluşur.

\( s(S) = 2^6 = 64 \)

Kamil ve Berat'ın berabere kalması için 3 yazı ve 3 tura gelmelidir.

3 yazı ve 3 tura gelme olayına \( A \) diyelim.

Çoklu permütasyon formülü ile 3 yazı ve 3 turanın tüm farklı dizilişlerini bulalım.

\( s(A) = \dfrac{6!}{3!\ 3!} = 20 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{20}{64} = \dfrac{5}{16} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay MATEMATİK kelimesinin tüm farklı dizilişlerinden oluşur.

9 harfli MATEMATİK kelimesinde "M", "A" ve "T" harfleri ikişer kez, diğer harfler birer kez bulunur.

Örnek uzayın eleman sayısını tekrarlı permütasyon formülü ile bulalım.

\( s(S) = \dfrac{9!}{2!\ 2!\ 2!} = \dfrac{9!}{8} \)

Bir dizilişte tüm sessiz harflerin yan yana olma olayına \( A \) diyelim.

Tüm sessiz harfleri tek bir harf olarak düşünelim. Buna göre AAEİ harfleri ve "MMTTK" harf setinden oluşan 5 elemanın farklı dizilişlerinin sayısını bulalım. Bu dizilişte "A" harfi 2 kez bulunmaktadır.

\( \dfrac{5!}{2!} = 60 \)

Bu 60 dizilişin her birinde "MMTTK" harfleri kendi aralarında \( \dfrac{5!}{2!\ 2!} = 30 \) farklı şekilde dizilebilir.

Tüm sessiz harflerin yan yana geldiği toplam diziliş sayısı bulduğumuz iki sayının çarpımına eşittir.

\( s(A) = 60 \cdot 30 = 1800 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{1800}{\frac{9!}{8}} = \dfrac{5}{126} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay kitapların tüm farklı dizilişlerinden oluşur.

Tekrarlı permütasyon formülü ile kitapların farklı diziliş sayısını bulalım.

\( s(S) = \dfrac{7!}{2!} \)

Özdeş kimya kitaplarının yan yana gelme olayına \( A \) diyelim.

Kimya kitaplarının yan yana olduğu dizilişlerin sayısını bulmak için kimya kitaplarını bir grup olarak düşünelim.

Buna göre kimya kitaplarının yan yana olduğu diziliş sayısı 3 farklı fizik kitabı, 2 farklı matematik kitabı ve 1 kimya kitap grubunun farklı diziliş sayısına eşittir.

Kimya kitapları özdeş olduğu için kitapların aralarında yer değiştirmesi yeni diziliş oluşturmaz.

\( s(A) = 6! \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{6!}{\frac{7!}{2!}} = \dfrac{2}{7} \) bulunur.

1. yöntem:

Tekrarlı permütasyon formülüne göre dergiler \( \frac{5!}{3! \cdot 2!} = 10 \) farklı şekilde kutulara bırakılabilir. Bunlardan sadece birinde tüm dergiler doğru kutuya bırakılmış olur.

Tüm dergilerin doğru kutuya bırakılma olasılığı:

\( = \dfrac{\text{İstenen durumlar}}{\text{Tüm durumlar}} = \dfrac{1}{10} \)

2. yöntem:

Dergilerin posta kutularına doğru dağıtım sırasının "AAABB" olduğunu varsayalım.

Dergilerin kutulara bu sırada bırakılma olasılığı:

\( = \dfrac{3}{5} \cdot \dfrac{2}{4} \cdot \dfrac{1}{3} \cdot \dfrac{2}{2} \cdot \dfrac{1}{1} \)

\( = \dfrac{1}{10} \)

Avcının hedefi vurduğu atışa "O", kaçırdığı atışa "X" diyelim.

Avcının hedefi ilk iki atışta vurup son iki atışta kaçırdığı "OOXX" durumunun olasılığını bulalım.

\( \dfrac{3}{4} \cdot \dfrac{3}{4} \cdot \dfrac{1}{4} \cdot \dfrac{1}{4} = \dfrac{9}{256} \)

İki "O" ve iki "X" işaretinin farklı diziliş sayısını tekrarlı permütasyon formülü ile bulalım.

\( \dfrac{4!}{2! \cdot 2!} = 6 \)

Buna göre avcının dört atışının ikisinde hedefi vurduğu 6 durum daha vardır. Her durumda yukarıda hesapladığımız olasılığın sadece çarpım sırası değişeceği için gerçekleşme olasılıkları yine \( \frac{9}{256} \) olur.

Avcının 4 atış sonunda hedefi iki kez vurmuş olma olasılığı:

\( = 6 \cdot \dfrac{9}{256} = \dfrac{27}{128} \) bulunur.

Tek bir zarın en fazla 2 gelme olasılığı 1 ve 2 gelme olasılıklarının toplamına eşittir.

\( 2 \cdot \dfrac{1}{6} = \dfrac{1}{3}\)

İstenen durum 5 zar atışında en az dört kez iki şekilde gerçekleşebilir: 4 kez en fazla 2 gelmesi, 5 kez en fazla 2 gelmesi.

Bu iki durumun olasılıklarını ayrı ayrı bulalım.

Durum 1: 4 kez en fazla 2 gelme olasılığı

\( C(5, 4) \cdot (\dfrac{1}{3})^4 \cdot (\dfrac{2}{3})^1 \)

\( = 5 \cdot \dfrac{1}{81} \cdot \dfrac{2}{3} \)

\( = \dfrac{10}{243} \)

Durum 2: 5 kez en fazla 2 gelme olasılığı

\( C(5, 5) \cdot (\dfrac{1}{3})^5 \cdot (\dfrac{2}{3})^0 \)

\( = 1 \cdot \dfrac{1}{243} \cdot 1 \)

\( = \dfrac{1}{243} \)

Zarların en az 4 kez en fazla 2 gelme olasılığı bu iki durumun olasılıkları toplamına eşittir.

\( \dfrac{10}{243} + \dfrac{1}{243} = \dfrac{11}{243}\) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay verilen kümenin elemanları arasından 4 sayının tüm farklı seçimlerinden oluşur.

\( s(S) = C(8, 4) = \dfrac{8!}{4! \cdot 4!} = 70 \)

Seçilen 4 sayının toplamının tek sayı olma olayına \( A \) diyelim.

Verilen kümenin elemanlarının 5'i tek, 3'ü çift sayıdır.

4 sayının toplamının tek olması için ya sayıların 3'ü tek 1'i çift sayı ya da 1'i tek 3'ü çift sayı olmalıdır.

Her iki durum için farklı seçim sayılarını bulalım.

Durum 1: 3 tek, 1 çift sayı

\( C(5, 3) \cdot C(3, 1) = 10 \cdot 3 = 30 \)

Durum 2: 1 tek, 3 çift sayı

\( C(5, 1) \cdot C(3, 3) = 5 \cdot 1 = 5 \)

İki durumun toplamı \( A \) olayındaki toplam sonuç sayısını verir.

\( s(A) = 30 + 5 = 35 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{35}{70} = \dfrac{1}{2} \) bulunur.

İstenen olasılığı aşağıdaki şekilde hesaplayabiliriz.

İki renkten en az birer bilye olma olasılığı = 1 - 3 bilyenin de kırmızı olma olasılığı - 3 bilyenin de beyaz olma olasılığı

3 bilyenin de kırmızı olma olasılığı, 6 kırmızı bilye içinden 3 bilyenin farklı seçim sayısının 10 bilye içinden 3 bilyenin farklı seçim sayısına oranına eşittir.

\( \dfrac{C(6, 3)}{C(10, 3)} = \dfrac{\frac{6!}{3! \cdot 3!}}{\frac{10!}{3! \cdot 7!}} \)

\( = \dfrac{20}{120} = \dfrac{1}{6} \)

3 bilyenin de beyaz olma olasılığı, 4 beyaz bilye içinden 3 bilyenin farklı seçim sayısının 10 bilye içinden 3 bilyenin farklı seçim sayısına oranına eşittir.

\( \dfrac{C(4, 3)}{C(10, 3)} = \dfrac{\frac{4!}{3! \cdot 1!}}{\frac{10!}{3! \cdot 7!}} \)

\( = \dfrac{4}{120} = \dfrac{1}{30} \)

İki renkten en az birer bilye olma olasılığını hesaplayalım.

\( 1 - \dfrac{1}{6} - \dfrac{1}{30} = \dfrac{4}{5} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay 6 çift (12 tek) eldiven arasından 4 tek eldivenin tüm farklı seçimlerinden oluşur.

\( s(S) = C(12, 4) = 495 \)

Seçilen 4 tek eldivenin farklı renklerde olma olayına \( A \) diyelim.

Önce 6 renk arasından 4 renk \( C(6, 4) = 15 \) farklı şekilde seçilir.

Daha sonra seçilen 4 renkten birer tek eldiven \( 2^4 = 16 \) farklı şekilde seçilir.

\( s(A) = 15 \cdot 16 = 240 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{240}{495} = \dfrac{16}{33} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay iki kutudan birer saatin tüm farklı seçimlerinden oluşur.

Birinci kutuda 8, ikinci kutuda 7 saat vardır. İki kutudan birer saat \( C(8, 1) \cdot C(7, 1) \) farklı şekilde seçilebilir.

\( s(S) = 8 \cdot 7 = 56 \)

Seçilen saatlerin hata durumlarının aynı olma olayına \( A \) diyelim.

\( A \) olayındaki sonuç sayısı, iki kutudan da sağlam ve iki kutudan da bozuk saat seçilme durumlarının toplamına eşittir.

Durum 1: İki kutudan da sağlam saat

\( C(2, 1) \cdot C(3, 1) = 2 \cdot 3 = 6 \)

Durum 2: İki kutudan da bozuk saat

\( C(6, 1) \cdot C(4, 1) = 6 \cdot 4 = 24 \)

\( A \) olayındaki sonuç sayısı bu iki sayının toplamına eşittir.

\( s(A) = 6 + 24 = 30 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{30}{56} = \dfrac{15}{28} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay \( A \times A \) kartezyen çarpımının elemanlarından oluşur.

\( s(S) = 6 \cdot 6 = 36 \)

Seçilen sıralı ikilinin bileşenlerinin aralarında asal olma olayına \( E \) diyelim.

Bir sayı kendisiyle aralarında asal değildir (6 ikili).

4, 6, 8 ve 12 sayıları çift oldukları ve ortak 2 çarpanları olduğu için aralarında asal değildir (\( C(4, 2) \cdot 2! = 12 \) ikili).

Geriye kalan \( 36 - 6 - 12 = 18 \) ikili, 5 ve 11 sayılarından en az birini içeren ve bileşenlerin birbirine eşit olmadığı ikililerdir.

Bu 18 sayı ikilisi aralarında asaldır.

\( E = \{(4, 5), (5, 4), (4, 11), (11, 4), \ldots, (11, 12), (12, 11)\} \)

\( s(E) = 18 \)

\( E \) olayının gerçekleşme olasılığı, \( E \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(E) = \dfrac{s(E)}{s(S)} \)

\( = \dfrac{18}{36} = \dfrac{1}{2} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay 15 kart arasından 2 kartın farklı seçimlerinden oluşur.

\( s(S) = C(15, 2) = 105 \)

Çekilen iki kartın aynı renk olma ya da üzerlerinde aynı sayının yazıyor olma olayına \( A \) diyelim.

2 mor kart \( C(5, 2) = 10 \) farklı şekilde, 2 beyaz kart \( C(5, 2) = 10 \) farklı şekilde, 2 sarı kart \( C(5, 2) = 10 \) farklı şekilde seçilebilir.

Buna göre aynı renkte iki kart \( 3 \cdot 10 = 30 \) farklı şekilde seçilebilir.

Üzerinde "1" yazan 2 kart \( C(3, 2) = 3 \) farklı şekilde seçilebilir. Benzer şekilde, diğer sayıların her biri için de 3'er farklı seçim vardır.

Buna göre üzerinde aynı sayı yazan iki kart \( 5 \cdot 3 = 15 \) farklı şekilde seçilebilir.

Hem aynı renk olan hem de üzerinde aynı sayı yazan kart bulunmadığı için yukarıdaki kart gruplarının kesişim kümesi boş kümedir.

\( s(A) = 30 + 15 = 45 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{45}{105} = \dfrac{3}{7} \) bulunur.

Rastgele cevaplanan bir sorunun doğru olma olasılığı \( \frac{1}{4} \), yanlış olma olasılığı \( \frac{3}{4} \) olur.

Ali'nin ön elemeyi geçtiği 3 durum vardır.

Durum 1: 5 sorudan 3'ü doğru

D-D-D-Y-Y

\( \dfrac{1}{4} \cdot \dfrac{1}{4} \cdot \dfrac{1}{4} \cdot \dfrac{3}{4} \cdot \dfrac{3}{4} = \dfrac{9}{4^5} \)

5 soru içinden doğru cevaplanan 3 soru \( C(5, 3) = 10 \) farklı şekilde seçilebilir.

5 sorudan 3'ünü doğru cevaplama olasılığı:

\( = \dfrac{9}{4^5} \cdot 10 = \dfrac{90}{4^5} \)

Durum 2: 5 sorudan 4'ü doğru

D-D-D-D-Y

\( \dfrac{1}{4} \cdot \dfrac{1}{4} \cdot \dfrac{1}{4} \cdot \dfrac{1}{4} \cdot \dfrac{3}{4} = \dfrac{3}{4^5} \)

5 soru içinden doğru cevaplanan 4 soru \( C(5, 4) = 5 \) farklı şekilde seçilebilir.

5 sorudan 4'ünü doğru cevaplama olasılığı:

\( = \dfrac{3}{4^5} \cdot 5 = \dfrac{15}{4^5} \)

Durum 3: 5 sorunun tümü doğru

D-D-D-D-D

\( \dfrac{1}{4} \cdot \dfrac{1}{4} \cdot \dfrac{1}{4} \cdot \dfrac{1}{4} \cdot \dfrac{1}{4} = \dfrac{1}{4^5} \)

5 soru içinden doğru cevaplanan 3 soru \( C(5, 5) = 1 \) farklı şekilde seçilebilir.

5 sorunun tümünü doğru cevaplama olasılığı:

\( = \dfrac{1}{4^5} \cdot 1 = \dfrac{1}{4^5} \)

Ali'nin ön elemeyi geçme olasılığı bu üç duruma ait olasılıkların toplamına eşittir.

\( \dfrac{90}{4^5} + \dfrac{15}{4^5} + \dfrac{1}{4^5} = \dfrac{106}{4^5} \)

\( = \dfrac{53}{512} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay 5 zarın tüm farklı sonuçlarından oluşur.

\( s(S) = 6^5 \)

Gelen zarların toplamının 8 olma olayına \( A \) diyelim.

Gelen zarların toplamı 3 farklı şekilde 8 olabilir.

Durum 1: Zarlardan biri 4, diğerleri 1

4-1-1-1-1

Zarların bu şekilde geldiği durum sayısı tekrarlı permütasyon formülü ile \( \frac{5!}{4!} = 5 \) olur.

Durum 2: Zarlardan biri 3, biri 2, diğerleri 1

3-2-1-1-1

Zarların bu şekilde geldiği durum sayısı tekrarlı permütasyon formülü ile \( \frac{5!}{3!} = 20 \) olur.

Durum 3: Zarlardan üçü 2, diğerleri 1

2-2-2-1-1

Zarların bu şekilde geldiği durum sayısı tekrarlı permütasyon formülü ile \( \frac{5!}{3!2!} = 10 \) olur.

Zarların toplamının 8 olduğu durum sayısı bu üç durumun toplamına eşittir.

\( s(A) = 5 + 20 + 10 = 35 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{35}{6^5} \) bulunur.

Rastgele seçilen bir çiçeğin gül olma olasılığı \( \frac{16}{40} = \frac{2}{5} \), manolya olma olasılığı \( \frac{24}{40} = \frac{3}{5} \) olur.

Seçilen çiçek gül ise G, manolya ise M diyelim.

GGMMM sırasıyla iki gül, üç manolya seçilme olasılığını bulalım.

\( (\dfrac{3}{5})^2 \cdot (\dfrac{2}{5})^3 = \dfrac{72}{3125} \)

GGGMM harflerinin her farklı dizilişi kadar seçilen 5 çiçekten ikisi gül, üçü manolya olur.

GGGMM harflerinin farklı dizilişleri için tekrarlı permütasyon formülü kullanılır.

\( \dfrac{5!}{2!\ 3!} = 10 \)

Bu iki sayının çarpımı seçilen 5 çiçekten ikisinin gül, üçünün manolya olma olasılığını verir.

\( \dfrac{72}{3125} \cdot 10 = \dfrac{144}{625} \) bulunur.

B oyuncusunun bu seriyi 7. maçta kazanması için 6. maç sonunda durum 2-4 olmalıdır.

AABBBB sırasıyla oyuncuların maçları kazanma olasılığını bulalım.

\( (\dfrac{1}{3})^2 \cdot (\dfrac{2}{3})^4 = \dfrac{16}{729} \)

AABBBB harflerinin her farklı dizilişi kadar 6. maç sonunda durum 2-4 olur.

AABBBB harflerinin farklı dizilişleri için tekrarlı permütasyon formülü kullanılır.

\( \dfrac{6!}{2!\ 4!} = 15 \)

Bu iki sayının çarpımı B oyuncusunun bu seriyi 7. maçta kazanma olasılığını verir.

\( \dfrac{16}{729} \cdot 15 = \dfrac{80}{243} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay verilen noktalar kullanılarak çizilebilecek tüm üçgenlerden oluşur.

Aynı doğru üzerinde bulunan 3 nokta bir üçgen oluşturmaz, buna göre çizilecek üçgenin ya 2 köşesi üstteki, 1 köşesi alttaki doğru üzerinde olmalıdır, ya da 1 köşesi üstteki, 2 köşesi alttaki doğru üzerinde olmalıdır.

Üstteki doğru üzerinden 2, alttaki doğru üzerinden 1 nokta \( C(5, 2) \cdot C(3, 1) = 30 \) farklı şekilde seçilebilir.

Üstteki doğru üzerinden 1, alttaki doğru üzerinden 2 nokta \( C(5, 1) \cdot C(3, 2) = 15 \) farklı şekilde seçilebilir.

Buna göre verilen noktaları kullanarak çizilebilecek toplam üçgen sayısı \( 30 + 15 = 45 \) olur.

\( s(S) = 45 \)

Seçilen üçgenin bir köşesinin \( A \) noktası olma olayına \( E \) diyelim.

Bir köşesi \( A \) olan üçgen sayısını iki farklı yöntemle bulabiliriz.

1. yöntem:

Bir köşesi \( A \) olan üçgenin ya diğer 2 köşesi üstteki doğru üzerinde olur ya da 1 köşesi üstteki, 1 köşesi alttaki doğru üzerinde olur.

Üstteki doğru üzerinden 2 nokta \( C(5, 2) = 10 \) farklı şekilde seçilebilir.

Üstteki doğru üzerinden 1, alttaki doğru üzerinden 1 nokta \( C(5, 1) \cdot C(2, 1) = 10 \) farklı şekilde seçilebilir.

Buna göre bir köşesi \( A \) olan \( 10 + 10 = 20 \) farklı üçgen seçilebilir.

2. yöntem:

\( A \) noktası hariç diğer noktaları kullanarak çizilebilecek üçgen sayısını hesaplayalım.

Üstteki doğru üzerinden 2, alttaki doğru üzerinden \( A \) hariç 1 nokta \( C(5, 2) \cdot C(2, 1) = 20 \) farklı şekilde seçilebilir.

Üstteki doğru üzerinden 1, alttaki doğru üzerinden \( A \) hariç 2 nokta \( C(5, 1) \cdot C(2, 2) = 5 \) farklı şekilde seçilebilir.

Buna göre \( A \) dışındaki noktaları kullanarak çizilebilecek toplam üçgen sayısı \( 20 + 5 = 25 \) olur. Bu sayıyı yukarıda hesapladığımız \( A \) dahil çizilebilecek toplam üçgen sayısından çıkarırsak bir köşesi \( A \) olan üçgen sayısını buluruz.

\( 45 - 25 = 20 \)

\( s(E) = 20 \)

\( E \) olayının gerçekleşme olasılığı, \( E \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(E) = \dfrac{s(E)}{s(S)} \)

\( = \dfrac{20}{45} = \dfrac{4}{9} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay verilen 8 nokta arasından 3 noktanın farklı seçimlerinden oluşur.

\( s(S) = C(8, 3) = 56 \)

Seçilen üç noktanın bir üçgen oluşturma olayına \( A \) diyelim.

Aynı kenar üzerindeki (doğrusal) noktalar üçgen oluşturmaz, bu yüzden bu 56 sonuçtan aynı kenar üzerinden seçilebilecek 3 noktadan oluşan kombinasyonlar çıkarılır.

\( s(A) = 56 - [C(4, 3) + C(4, 3) + C(3, 3)] = 47 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{47}{56} \) bulunur.

Şekerleri özdeş nesneler, dağıtılacak arkadaşları da farklı kutular olarak düşünürsek problemi 12 özdeş nesnenin (\( n \)) 4 farklı kutuya (\( k \)) her kutuda en az bir nesne olacak şekilde dağıtım problemi olarak kurgulayabiliriz.

Bu tip problemlerin çözümünde ayraç yöntemini kullanabiliriz.

Farklı dağıtım sayısı \( = C(n - 1, k - 1) = C(11, 3) \)

\( = \dfrac{11!}{3! \cdot 8!} = 165 \)

Bu durumlardan sadece birinde tüm arkadaşlar eşit sayıda şeker alırlar.

Buna göre her arkadaşın eşit sayıda şeker alma olasılığı:

\( = \dfrac{1}{165} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay 9 bozuk para içinden 4 bozuk paranın tüm farklı seçimlerinden oluşur.

\( s(S) = C(9, 4) = \dfrac{9!}{4! \cdot 5!} = 126 \)

Düşen 4 paranın toplamının 2 TL olma olayına \( A \) diyelim.

Makinedeki paralar arasından toplamı 2 TL yapan para dörtlülerinin sayısı iki tanedir.

(1) 4 tane 50 Kr

(2) 1 tane 1 TL, 1 tane 50 Kr, 2 tane 25 Kr

1. durumda, 4 tane 50 Kr arasından 4'ü \( C(4, 4) = 1 \) farklı şekilde seçilebilir.

2. durumda, 3 tane 1 TL arasından 1'i, 4 tane 50 Kr arasından 1'i ve 2 tane 25 Kr arasından 2'si \( C(3, 1) \cdot C(4, 1) \cdot C(2, 2) = 3 \cdot 4 \cdot 1 = 12 \) farklı şekilde seçilebilir.

\( A \) olayının eleman sayısı bu durumların toplamına eşittir.

\( s(A) = 1 + 12 = 13 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{13}{126} \) bulunur.

Çekilen topların rengi ile ilgilendiğimiz için kırmızı ve siyah topların kendi aralarında özdeş ya da farklı olmaları sonucu değiştirmez.

1. yöntem: 5 farklı kırmızı ve 4 farklı siyah top

Örnek uzaya \( S \) diyelim.

Örnek uzay 9 farklı topun farklı dizilişlerinden oluşur.

\( s(S) = 9! \)

Topların dizilişinin bir kırmızı bir siyah olma olayına \( A \) diyelim.

Kırmızı toplar için \( K \), siyah toplar için \( S \) kullanalım. 5 kırmızı ve 4 siyah topun kırmızıdan başlayarak bir kırmızı bir siyah olarak dizilmesi \( K-S-K-S-K-S-K-S-K \) şeklinde olur.

5 kırmızı top \( K \) ile belirtilen yerlerde aralarında \( 5! \) farklı şekilde yer değiştirebilir.

4 siyah top \( S \) ile belirtilen yerlerde aralarında \( 4! \) farklı şekilde yer değiştirebilir.

Tüm topların bir kırmızı bir siyah olacak şekilde farklı diziliş sayısı \( 5! \cdot 4! \) olur.

\( s(A) = 5! \cdot 4! \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{5! \cdot 4!}{9!} \)

\( = \dfrac{4 \cdot 3 \cdot 2}{9 \cdot 8 \cdot 7 \cdot 6} \)

\( = \dfrac{1}{126} \)

2. yöntem: 5 özdeş kırmızı ve 4 özdeş siyah top

5 özdeş kırmızı ve 4 özdeş siyah topun farklı diziliş sayısını tekrarlı permütasyon formülü ile bulalım.

\( s(S) = \dfrac{9!}{5! \cdot 4!} \)

Bu dizilişlerin sadece biri \( K-S-K-S-K-S-K-S-K \) şeklinde olur.

\( s(A) = 1 \)

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{1}{126} \)

Örnek uzaya \( S \) diyelim.

Örnek uzay iki kardeşin hafta boyunca annelerini tüm farklı arama durumlarından oluşur.

Büyük kardeş annesini bir haftada \( C(7, 4) \) farklı şekilde, küçük kardeş de \( C(7, 3) \) farklı şekilde arayabilir.

\( s(S) = C(7, 4) \cdot C(7, 3) \)

Annelerinin haftanın her günü aranması için kardeşlerin haftanın farklı günlerinde aramaları gerekir.

Kardeşlerin haftanın farklı günlerinde annelerini aramaları olayına \( A \) diyelim.

Büyük kardeş annesini arayacağı 4 günü \( C(7, 4) \) farklı şekilde seçtikten sonra küçük kardeş kalan günler içinden 3 günü \( C(3, 3) \) farklı şekilde seçebilir.

\( s(A) = C(7, 4) \cdot C(3, 3) \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{C(7, 4) \cdot C(3, 3)}{C(7, 4) \cdot C(7, 3)} \)

\( = \dfrac{1}{35} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay 10 rakam arasından iki rakamın tüm farklı seçimlerinden oluşur.

\( s(S) = C(10, 2) = 45 \)

Rakamlardan büyük olanın küçük olana oranının tam sayı olma olayına \( A \) diyelim.

Toplama yoluyla sayma yöntemiyle bu koşulu sağlayan durum sayısını hesaplayalım.

Rakamlardan küçük olan 1 seçildiğinde istenen durumu sağlayan 8 sayı (2 - 9) vardır,

2 seçildiğinde 3 sayı (4, 6, 8) vardır,

3 seçildiğinde 2 sayı (6, 9) vardır,

4 seçildiğinde 1 sayı (8) vardır.

Küçük sayı olarak daha büyük sayılar seçildiğinde istenen durum sağlanmaz.

\( s(A) = 8 + 3 + 2 + 1 = 14 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{14}{45} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay 10 top arasından 3 topun tüm farklı seçimlerinden oluşur.

\( s(S) = C(10, 3) = 120 \)

Toplardan ikisinin üzerindeki rakamlar toplamının üçüncü topun üzerindeki rakama eşit olma olayına \( A \) diyelim.

En küçük rakamlı topun belirli bir değeri için ortanca rakamlı topun geçerli değerlerini belirleyelim.

Buna göre en küçük rakamlı topun üzerindeki sayı;

0 olamaz, çünkü 0 olması ortanca ve en büyük rakamlı topların aynı olmasını gerektirir.

1 olursa ortanca rakamlı top 2, 3, 4, 5, 6, 7, 8

2 olursa ortanca rakamlı top 3, 4, 5, 6, 7

3 olursa ortanca rakamlı top 4, 5, 6

4 olursa ortanca rakamlı top 5

olduğunda istenen durumu sağlayan en büyük rakamlı bir top mevcuttur.

Buna göre istenen koşulu sağlayan 16 durum vardır.

\( s(A) = 16 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{16}{120} = \dfrac{2}{15} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay 10 tane madeni paradan 6'sının tüm farklı seçimlerinden oluşur.

\( s(S) = C(10, 6) = \dfrac{10!}{6! \cdot 4!} = 210 \)

Seçilen 6 madeni paranın toplamının en az 1 TL olma olayına \( A \) diyelim.

\( A \) olayı dört durumda gerçekleşir.

Durum 1: 5 tane 25 kr ve herhangi diğer bir madeni para

\( C(5, 5) \cdot C(5, 1) = 1 \cdot 5 = 5 \)

Durum 2: 4 tane 25 kr ve herhangi diğer 2 madeni para

\( C(5, 4) \cdot C(5, 2) = 5 \cdot 10 = 50 \)

Durum 3: 3 tane 25 kr ve 3 tane 10 kr

\( C(5, 3) \cdot C(3, 3) = 10 \cdot 1 = 10 \)

Durum 4: 3 tane 25 kr, 2 tane 10 kr, 1 tane 5 kr

\( C(5, 3) \cdot C(3, 2) \cdot C(2, 1) = 10 \cdot 3 \cdot 2 = 60 \)

Geriye kalan tüm seçimlerde paraların toplamı 1 TL'den az olacaktır.

\( s(A) = 5 + 50 + 10 + 60 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{125}{210} = \dfrac{25}{42} \) bulunur.

Deneye ikizlerden \( 10 \cdot 2 = 20 \), üçüzlerden \( 4 \cdot 3 = 12 \) olmak üzere 32 kişi katılıyor.

Örnek uzaya \( S \) diyelim.

Örnek uzay 32 kişi arasından 2 kişinin tüm farklı seçimlerinden oluşur.

\( s(S) = C(32, 2) = 496 \)

Seçilen iki kişinin kardeş olmama olayına \( A \) diyelim.

Kardeş olmayan iki kişi üç farklı şekilde seçilebilir.

Durum 1: İkisi de ikizlerden

Önce 10 ikiz grubu arasından 2 grup \( C(10, 2) \) farklı şekilde seçilebilir, seçilen gruplardan birer kişi \( C(2, 1) \cdot C(2, 1) \) farklı şekilde seçilebilir.

Bu durumda farklı seçim sayısı \( C(10, 2) \cdot C(2, 1) \cdot C(2, 1) = 180 \) olur.

Durum 2: İkisi de üçüzlerden

Önce 4 üçüz grubu arasından 2 grup \( C(4, 2) \) farklı şekilde seçilebilir, seçilen gruplardan birer kişi \( C(3, 1) \cdot C(3, 1) \) farklı şekilde seçilebilir.

Bu durumda farklı seçim sayısı \( C(4, 2) \cdot C(3, 1) \cdot C(3, 1) = 54 \) olur.

Durum 3: Biri ikizlerden, diğeri üçüzlerden

Önce 10 ikiz grubu ve 4 üçüz grubu arasından 2 grup \( C(10, 1) \cdot C(4, 1) \) farklı şekilde seçilebilir, seçilen gruplardan birer kişi \( C(2, 1) \cdot C(3, 1) \) farklı şekilde seçilebilir.

Bu durumda farklı seçim sayısı \( C(10, 1) \cdot C(4, 1) \cdot C(2, 1) \cdot C(3, 1) = 240 \) olur.

\( A \) olayının eleman sayısı bu durumların toplamına eşittir.

\( s(A) = 180 + 54 + 240 = 474 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{474}{496} = \dfrac{237}{248} \) bulunur.

Örnek uzaya \( S \) diyelim.

Aynı değerdeki banknotların birbirinden farklı nesneler olduğunu varsayalım (birinci 5 TL'lik banknot, ikinci 5 TL'lik banknot).

Örnek uzay 8 banknot içinden 2'sinin tüm farklı seçimlerinden oluşur.

8 banknot içinden 2'si \( C(8, 2) = 28 \) farklı şekilde seçilebilir.

\( s(S) = 28 \)

Toplamları 100 TL ve üzeri olan iki banknot seçme olayına \( A \) diyelim.

Toplamı 100 TL'den az olan banknot ikililerini bulalım.

\( (5, 5), (5, 20), (5, 50), (20, 20), (20, 50) \)

\( (5, 5), (20, 20) \) banknot ikilileri 28 farklı seçim içinde \( C(2, 2) = 1 \)'er kez bulunur.

\( (5, 20), (5, 50), (20, 50) \) banknot ikililerinin her biri 28 farklı seçim içinde \( C(2, 1) \cdot C(2, 1) = 4 \) 'er kez bulunur.

Buna göre 28 farklı seçim içinde istenen koşulu sağlamayan seçim sayısı \( 2 \cdot 1 + 3 \cdot 4 = 14 \) adet olur.

\( s(A) = 28 - 14 = 14 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{14}{28} = \dfrac{1}{2} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay 9 bilyenin tüm farklı dizilişlerinden oluşur.

Mavi ve sarı bilyeler özdeş oldukları için diziliş sayısını tekrarlı permütasyon formülü ile bulabiliriz.

\( s(S) = \dfrac{9!}{5! \cdot 4!} = 126 \)

Dizilişteki son bilyenin sarı olma olayına \( A \) diyelim.

Bu dizilişlerden kaçında son bilyenin sarı olduğunu bulalım.

Son bilyenin sarı olduğunu varsayarsak geriye kalan 5 mavi bilye ve 3 sarı bilyenin farklı diziliş sayısını bulalım.

5 özdeş mavi ve 3 özdeş sarı bilyenin farklı diziliş sayısını tekrarlı permütasyon formülü ile bulalım.

\( s(A) = \dfrac{8!}{5! \cdot 3!} = 56 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{56}{126} = \dfrac{4}{9} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay çekilişi kazanacak iki kişinin tüm farklı kombinasyonlarından oluşur.

Çekilişe katılan toplam 174 müşteri vardır.

\( s(S) = C(174, 2) = 15051 \)

Çekilişi kazanan kişilerin ikisinin de kız çocuğu ya da ikisinin de erkek çocuğu olma olayına \( A \) diyelim.

Bu olayın eleman sayısı 15 kız çocuğunun tüm ikili kombinasyonları ile 34 erkek çocuğunun tüm ikili kombinasyonlarının toplamı kadardır.

\( s(A) = C(15, 2) + C(34, 2) \)

\( = 105 + 561 = 666 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{666}{15051} = \dfrac{222}{5017} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay 10 kart arasından 3 kartın tüm farklı seçimlerinden oluşur.

\( s(S) = C(10, 3) = 120 \)

Kartların üzerindeki sayıların 5'i tek, 5'i çifttir.

Seçilen 3 kartın üzerinde yazan sayıların toplamının tek sayı olma olayına \( A \) diyelim.

3 sayının toplamının tek olması için ya sayıların 3'ü de tek sayı olmalıdır ya da 2'si çift 1'i tek sayı olmalıdır.

Her iki durum için farklı seçim sayılarını bulalım.

Durum 1: 3 tek sayı

5 tek sayı arasından 3 sayının farklı seçim sayısını bulalım.

\( C(5, 3) = 10 \)

Durum 2: 2 çift sayı, 1 tek sayı

5 çift sayı arasından 2 sayının ve 5 tek sayı arasından 1 sayının farklı seçim sayısını bulalım.

\( C(5, 2) \cdot C(5, 1) = 10 \cdot 5 = 50 \)

İki durumun toplamı \( A \) olayındaki toplam sonuç sayısını verir.

\( s(A) = 10 + 50 = 60 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{60}{120} = \dfrac{1}{2} \) bulunur.

Yarışma sonucunda oluşan sıralamayı 12 kişinin yan yana dizilişleri olarak düşünebiliriz.

Örnek uzaya \( S \) diyelim.

Örnek uzay 12 kişinin yan yana tüm farklı dizilişlerinden oluşur.

\( s(S) = 12! \)

Selin, Eda ve Mehmet'in üçünün de madalya kazanma olayına \( A \) diyelim.

\( A \) olayının gerçekleşebilmesi için, üçünün yarışmayı herhangi bir sırada 1. 2. ve 3. olarak bitirmesi gerekir.

Bu durumda Selin, Eda ve Mehmet sıranın başında aralarında \( 3! \) farklı şekilde dizilebilir.

Kalan 9 kişi ise sıranın sonunda aralarında \( 9! \) farklı şekilde dizilebilir.

\( s(A) = 3! \cdot 9! \)

\( A \) olayının gerçekleşme olasılığı \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{3! \cdot 9!}{12!} = \dfrac{1}{220} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay 8 öğrencinin uygulayabileceği farklı işlemlerin tüm dizilişlerinden oluşur.

Her öğrenci iki işlemden birini uygulayacağı için toplam farklı işlem diziliş sayısı \( 2^8 \) olur.

Örneğin çarpma ve bölme işlemlerine sırayla "C" ve "B" dersek bir olası işlem sırası "CCBCBCCB" olur.

\( s(S) = 2^8 = 256 \)

Bu sıralamada "C" sayısı "B" sayısına eşit olursa işlem sonucu ilk sayıya eşit, "C" sayısı daha fazla olursa işlem sonucu ilk sayıdan büyük, "B" sayısı daha fazla olursa işlem sonucu ilk sayıdan küçük olur.

"B" sayısının "C" sayısından fazla olma olayına \( A \) diyelim.

"C" ve "B" işlemlerinin eşit sayıda olduğu durum sayısı "CCCCBBBB" harflerinin tekrarlı permütasyon formülü ile \( \frac{8!}{4! \cdot 4!} = 70 \) olarak bulunur.

"B" sayısının daha fazla olduğu durumların sayısını bulalım.

3 "C" ve 5 "B"nin farklı diziliş sayısı:

\( = \dfrac{8!}{3! \cdot 5!} = 56 \)

2 "C" ve 6 "B"nin farklı diziliş sayısı:

\( = \dfrac{8!}{2! \cdot 6!} = 28 \)

1 "C" ve 7 "B"nin farklı diziliş sayısı:

\( = \dfrac{8!}{1! \cdot 7!} = 8 \)

0 "C" ve 8 "B"nin farklı diziliş sayısı:

\( = \dfrac{8!}{0! \cdot 8!} = 1 \)

\( A \) olayının eleman sayısı bu durumların toplamına eşittir.

\( s(A) = 56 + 28 + 8 + 1 = 93 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{93}{256} \) bulunur.

Sayıları yazalım ve kesim yerlerini işaretleyelim.

1 | 3 | 5 | 7 9 | 11 | 13 15 | 17 | 19 21 | 23 25 27 | 29 | 31 33

Buna göre toplam 11 parça vardır.

Örnek uzaya \( S \) diyelim.

Örnek uzay 11 parça içinden 2 parçanın farklı seçimlerinden oluşur.

\( s(S) = C(11, 2) = 55 \)

Bir parçanın üzerindeki sayıların 8'e tam bölünme olayına \( A \) diyelim.

Her parçanın üzerindeki sayıların toplamını yazalım.

1 | 3 | 5 | 16 | 11 | 28 | 17 | 40 | 75 | 29 | 64

Her parçanın üzerindeki sayıların toplamı 8'e bölündüğünde elde edilen kalanları yazalım.

1 | 3 | 5 | 0 | 3 | 4 | 1 | 0 | 3 | 5 | 0

Seçilecek iki parçanın üzerindeki sayıların toplamının 8'e tam bölünmesi için ya parçaların üzerindeki sayıların toplamı ayrı ayrı 8'e tam bölünmelidir ya da parçalar ayrı ayrı bölünmeyip, toplamları 8'e tam bölünmelidir.

Durum 1: Toplamları ayrı ayrı 8'e tam bölünen parçalar

Toplamları ayrı ayrı 8'e tam bölünen 3 parça vardır (kalanı 0 olan parçalar).

Bu 3 parça arasından 2 parça \( C(3, 2) = 3 \) farklı şekilde seçilebilir.

Durum 2: Ayrı ayrı 8'e tam bölünmeyip, toplamları 8'e tam bölünen parçalar

Parçalardan birinin kalanı 3 diğerinin 5 olduğunda toplamları 8'e tam bölünür.

Kalanı 3 olan üç parça arasından 1 parça \( C(3, 1) = 3 \) farklı şekilde, kalanı 5 olan iki parça arasından 1 parça \( C(2, 1) = 2 \) farklı şekilde seçilebilir.

Bu iki seçim birlikte \( 3 \cdot 2 = 6 \) farklı şekilde yapılabilir.

Buna göre 55 farklı parça ikilisi arasından \( 3 + 6 = 9 \) ikilinin üzerindeki sayıların toplamı 8'e tam bölünür.

\( s(A) = 9 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{9}{55} \) bulunur.

Örnek uzaya \( S \) diyelim.

Örnek uzay \( A \) kümesinin boş kümeden farklı alt kümeleri arasından 3 alt kümenin farklı seçimlerinden oluşur.

4 elemanlı \( A \) kümesinin boş kümeden farklı \( 2^4 - 1 = 15 \) alt kümesi vardır.

Bu 15 alt küme içinden 3 küme \( C(15, 3) = 455 \) farklı şekilde seçilebilir.

\( s(S) = 455 \)

Seçilen 3 alt kümenin \( K \subset L \subset M \) koşulunu sağlama olayına \( E \) diyelim.

\( K \subset L \subset M \) koşulu alt kümelerin eleman sayılarına göre aşağıdaki 4 durumda sağlanır.

Durum 1: \( s(K) = 1, s(L) = 2, s(M) = 3 \)

\( A \) kümesinin 4 elemanı içinden \( M \) kümesinin 3 elemanı \( C(4, 3) = 4 \) farklı şekilde seçilebilir.

\( M \) kümesinin 3 elemanı içinden \( L \) kümesinin 2 elemanı \( C(3, 2) = 3 \) farklı şekilde seçilebilir.

\( L \) kümesinin 2 elemanı içinden \( K \) kümesinin 1 elemanı \( C(2, 1) = 2 \) farklı şekilde seçilebilir.

Buna göre bu duruma uygun \( 4 \cdot 3 \cdot 2 = 24 \) farklı alt küme seçilebilir.

Durum 2: \( s(K) = 1, s(L) = 2, s(M) = 4 \)

\( A \) kümesinin 4 elemanı içinden \( M \) kümesinin 4 elemanı \( C(4, 4) = 1 \) farklı şekilde seçilebilir.

\( M \) kümesinin 4 elemanı içinden \( L \) kümesinin 2 elemanı \( C(4, 2) = 6 \) farklı şekilde seçilebilir.

\( L \) kümesinin 2 elemanı içinden \( K \) kümesinin 1 elemanı \( C(2, 1) = 2 \) farklı şekilde seçilebilir.

Buna göre bu duruma uygun \( 1 \cdot 6 \cdot 2 = 12 \) farklı alt küme seçilebilir.

Durum 3: \( s(K) = 1, s(L) = 3, s(M) = 4 \)

\( A \) kümesinin 4 elemanı içinden \( M \) kümesinin 4 elemanı \( C(4, 4) = 1 \) farklı şekilde seçilebilir.

\( M \) kümesinin 4 elemanı içinden \( L \) kümesinin 3 elemanı \( C(4, 3) = 4 \) farklı şekilde seçilebilir.

\( L \) kümesinin 3 elemanı içinden \( K \) kümesinin 1 elemanı \( C(3, 1) = 3 \) farklı şekilde seçilebilir.

Buna göre bu duruma uygun \( 1 \cdot 4 \cdot 3 = 12 \) farklı alt küme seçilebilir.

Durum 4: \( s(K) = 2, s(L) = 3, s(M) = 4 \)

\( A \) kümesinin 4 elemanı içinden \( M \) kümesinin 4 elemanı \( C(4, 4) = 1 \) farklı şekilde seçilebilir.

\( M \) kümesinin 4 elemanı içinden \( L \) kümesinin 3 elemanı \( C(4, 3) = 4 \) farklı şekilde seçilebilir.

\( L \) kümesinin 3 elemanı içinden \( K \) kümesinin 2 elemanı \( C(3, 2) = 3 \) farklı şekilde seçilebilir.

Buna göre bu duruma uygun \( 1 \cdot 4 \cdot 3 = 12 \) farklı alt küme seçilebilir.

\( E \) olayının eleman sayısı bu durumların toplamından oluşur.

\( s(E) = 24 + 12 + 12 + 12 = 60 \)

\( E \) olayının gerçekleşme olasılığı, \( E \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(E) = \dfrac{s(E)}{s(S)} \)

\( = \dfrac{60}{455} = \dfrac{12}{91} \) bulunur.

Şirketteki çalışan sayısına \( n \) diyelim.

Örnek uzaya \( S \) diyelim.

Örnek uzay \( n \) kişi arasından 3 kişinin farklı seçimlerinden oluşur.

\( s(S) = C(n, 3) \)

Gamze'nin kazanıp Yaşar'ın kazanmama olayına \( A \) diyelim.

Gamze kazandıktan ve Yaşar kazanmadıktan sonra, kalan \( n - 2 \) kişi arasından bilgisayar kazanan 2 kişi \( C(n - 2, 2) \) farklı şekilde seçilebilir.

\( s(A) = C(n - 2, 2) \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

Bu olasılık \( \%25 \) olarak veriliyor.

\( \dfrac{C(n - 2, 2)}{C(n, 3)} = \dfrac{25}{100} \)

Kombinasyon ifadelerini açıp içler - dışlar çarpımı yapalım.

\( \dfrac{100(n - 2)(n - 3)}{2 \cdot 1} = \dfrac{25n(n - 1)(n - 2)}{3 \cdot 2 \cdot 1} \)

\( 12n - 36 = n^2 - n \)

\( n^2 - 13n + 36 = 0 \)

\( (n - 4)(n - 9) = 0 \)

Çalışan sayısı 4 ya da 9'dur.

Buna göre iş yerinde en çok 9 çalışan vardır.

İki basamaklı (10 - 99 aralığında) 90 sayı vardır.

Örnek uzaya \( S \) diyelim.

Örnek uzay iki basamaklı sayılar arasından iki sayının farklı seçimlerinden oluşur.

\( s(S) = C(90, 2) \)

İki sayının toplamının 100'den küçük olma olayına \( A \) diyelim.

Küçük sayının alabileceği her değer için büyük sayının kaç farklı değer alabileceğini bulalım.

Küçük sayı 10 ise büyük sayı 11-89 arasında \( \frac{89 - 11}{1} + 1 = 79 \) değer alabilir.

Küçük sayı 11 ise büyük sayı 12-88 arasında \( \frac{88 - 12}{1} + 1 = 77 \) değer alabilir.

Küçük sayı 12 ise büyük sayı 13-87 arasında \( \frac{87 - 13}{1} + 1 = 75 \) değer alabilir.

Görüldüğü üzere, küçük olan sayıyı 1 artırdığımızda büyük sayının alabileceği değer sayısı 2 azalmaktadır. Küçük sayı alabileceği en büyük değer olan 49'u aldığında ise büyük sayının alabileceği tek değer 50 olur.

\( A \) olayının eleman sayısını bulmak için ardışık sayıların toplam formülünü kullanalım.

\( s(A) = 79 + 77 + \ldots + 1 \)

\( = (\text{İlk terim} + \text{Son terim}) \cdot \dfrac{\text{Terim sayısı}}{2} \)

\( = (79 + 1) \cdot \dfrac{40}{2} = 1600 \)

\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(A) = \dfrac{s(A)}{s(S)} \)

\( = \dfrac{1600}{C(90, 2)} = \dfrac{320}{801} \) bulunur.

5 madeni paradan ikisi \( C(5, 2) = 10 \) farklı şekilde seçilebilir.

2 para ikisi de hileli olacak şekilde \( C(3, 2) = 3 \) farklı şekilde seçilebilir. Buna göre seçilen iki paranın ikisinin de hileli olma olasılığı \( \frac{3}{10} \) olur.

2 para ikisi de hilesiz olacak şekilde \( C(2, 2) = 1 \) farklı şekilde seçilebilir. Buna göre seçilen iki paranın ikisinin de hilesiz olma olasılığı \( \frac{1}{10} \) olur.

2 para biri hileli biri hilesiz olacak şekilde \( C(3, 1) \cdot C(2, 1) = 6 \) farklı şekilde seçilebilir. Buna göre seçilen iki paranın birinin hileli birinin hilesiz olma olasılığı \( \frac{6}{10} = \frac{3}{5} \) olur.

Paraların hileli/hilesiz olma durumlarına göre seçim olasılıkları ile her durumda paraların tura gelme olasılıklarını çarptığımızda toplamda iki paranın da tura gelme olasılığını buluruz.

Hileli paranın tura gelme olasılığı \( \frac{60}{100} = \frac{3}{5} \), hilesiz paranın tura gelme olasılığı \( \frac{1}{2} \)'dir.

Seçilen iki paranın tura gelme olasılığı:

\( = \dfrac{3}{10} \cdot \dfrac{3}{5} \cdot \dfrac{3}{5} + \dfrac{1}{10} \cdot \dfrac{1}{2} \cdot \dfrac{1}{2} + \dfrac{3}{5} \cdot \dfrac{3}{5} \cdot \dfrac{1}{2} \)

\( = \dfrac{27}{250} + \dfrac{1}{40} + \dfrac{9}{50} \)

\( = \dfrac{108}{1000} + \dfrac{25}{1000} + \dfrac{180}{1000} \)

\( = \dfrac{313}{1000} \) bulunur.

Her iki kümede de 4'er çift sayı, 5'er tek sayı vardır.

Örnek uzaya \( S \) diyelim.

Örnek uzay \( A \) kümesinin elemanları arasından 2 sayının ve \( B \) kümesinin elemanları arasından 2 sayının tüm farklı seçimlerinden oluşur.

\( s(S) = C(9, 2) \cdot C(9, 2) = 1296 \)

Seçilen 4 sayının toplamının çift sayı olma olayına \( E \) diyelim.

4 sayının toplamının çift olması için ya sayıların hepsi çift sayı ya hepsi tek sayı ya da 2'si çift 2'si tek sayı olmalıdır.

Her durum için farklı seçim sayılarını bulalım.

Durum 1:

Bu durumda seçilen sayıların hepsi çift sayıdır.

Bu durum \( A \) kümesinin elemanları arasından 2 çift sayının ve \( B \) kümesinin elemanları arasından 2 çift sayının tüm farklı seçimlerinden oluşur.

\( C(4, 2) \cdot C(4, 2) = 36 \)

Durum 2:

Bu durumda seçilen sayıların hepsi tek sayıdır.

Bu durum \( A \) kümesinin elemanları arasından 2 tek sayının ve \( B \) kümesinin elemanları arasından 2 tek sayının tüm farklı seçimlerinden oluşur.

\( C(5, 2) \cdot C(5, 2) = 100 \)

Durum 3:

Bu durumda \( A \) kutusundan seçilen 2 sayı tek sayı, \( B \) kutusundan seçilen 2 sayı çift sayıdır.

\( C(5, 2) \cdot C(4, 2) = 60 \)

Durum 4:

Bu durumda \( A \) kutusundan seçilen 2 sayı çift sayı, \( B \) kutusundan seçilen 2 sayı tek sayıdır.

\( C(4, 2) \cdot C(5, 2) = 60 \)

Durum 5:

Bu durumda iki kutudan da seçilen sayıların biri tek diğeri çift sayıdır.

\( C(5, 1) \cdot C(4, 1) \cdot C(5, 1) \cdot C(4, 1) = 400 \)

Bu durumların toplamı \( E \) olayındaki toplam sonuç sayısını verir.

\( s(E) = 36 + 100 + 60 + 60 + 400 = 656 \)

\( E \) olayının gerçekleşme olasılığı, \( E \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.

\( P(E) = \dfrac{s(E)}{s(S)} \)

\( = \dfrac{656}{1296} = \dfrac{41}{81} \) bulunur.