Özdeşliklerin Geometrik İspatı

Bu bölümde önceki bölümde bahsettiğimiz özdeşliklerden dördünün ispatını geometrik olarak göstereceğiz.

İki Sayının Toplamının Karesi

Aşağıda bir kenar uzunluğu birim olan ve kenarları ve birim olmak üzere iki parçaya ayrılmış bir kare verilmiştir. Bu karenin alan formülünü yazalım ve kareyi oluşturan dört küçük parçanın alanları toplamına eşitleyelim.

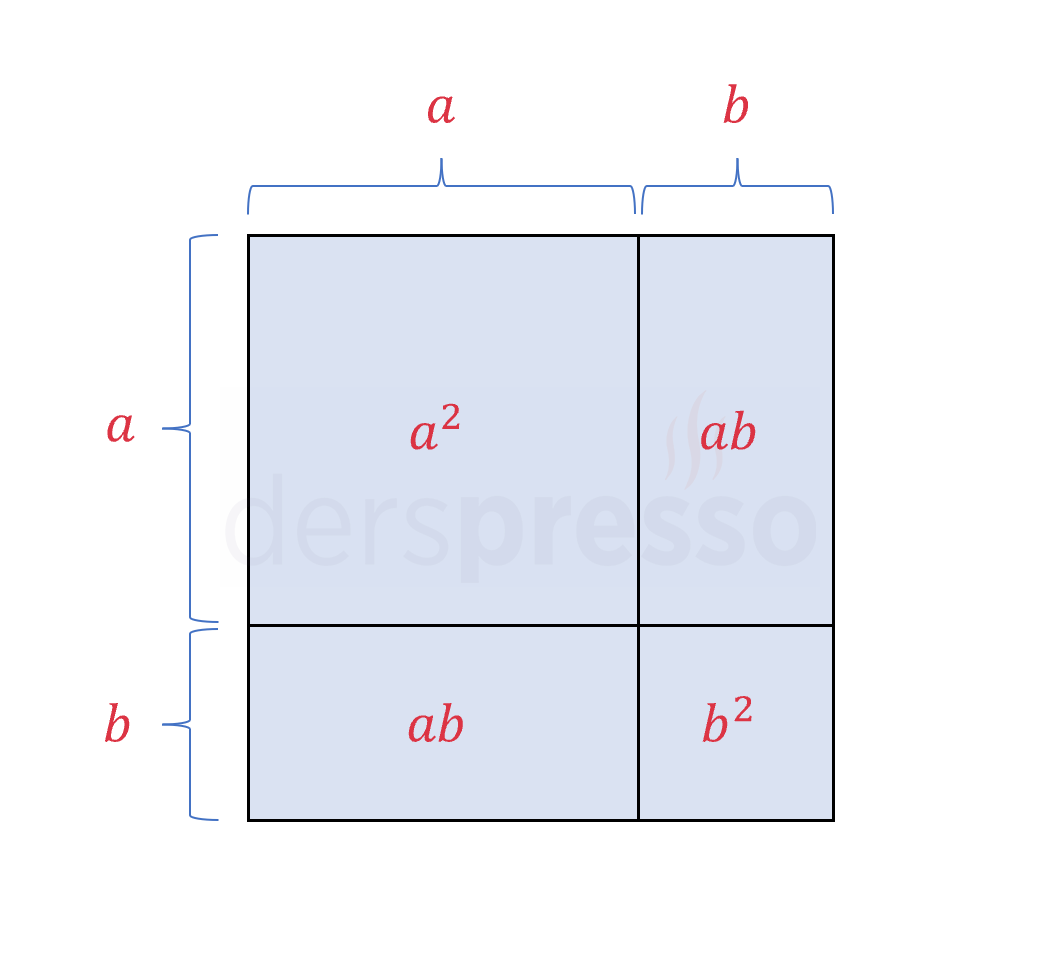
Büyük karenin alanı:

Dört küçük dörtgenin alanları toplamı:

Büyük karenin alanının küçük alanların toplamına eşitliği iki sayının toplamının karesi özdeşliğini verir.

İki Sayının Farkının Karesi

Aşağıda bir kenar uzunluğu birim olan bir büyük kare ve içinde bir kenar uzunluğu birim olan bir küçük kare verilmiştir. Renkli küçük karenin alan formülünü yazalım ve dıştaki büyük karenin alanı ile beyaz üç dörtgenin alanları farkına eşitleyelim.

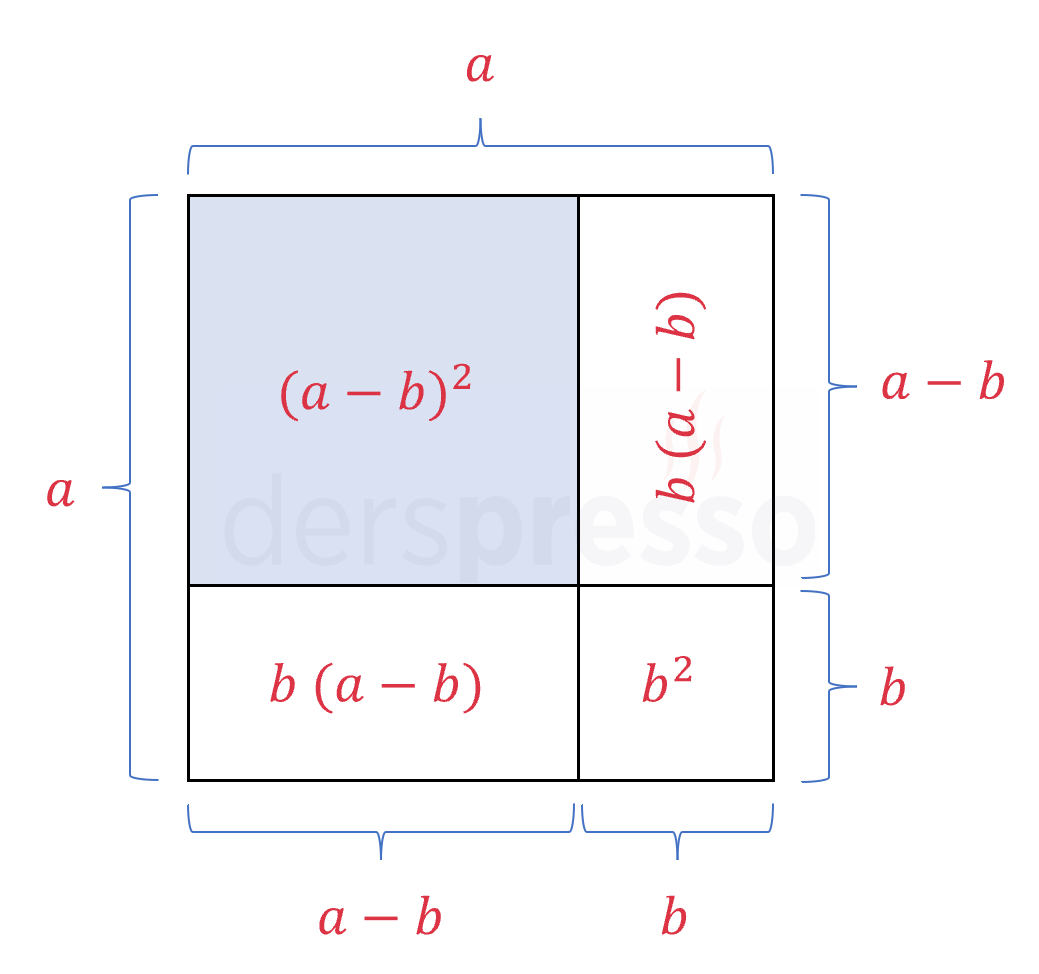
Renkli karenin alanı:

Büyük karenin alanı:

Beyaz üç dörtgenin alanları toplamı:

Büyük karenin alanının beyaz alanlardan farkının renkli karenin alanına eşitliği iki sayının farkının karesi özdeşliğini verir.

İki Sayının Karesinin Farkı

Aşağıda bir kenar uzunluğu birim olan bir büyük kare ve içinde bir kenar uzunluğu birim olan bir küçük kare verilmiştir. Renkli işaretlenmiş üç dörtgenin alan formülünü yazalım ve büyük kare ile küçük karenin alanları farkına eşitleyelim.

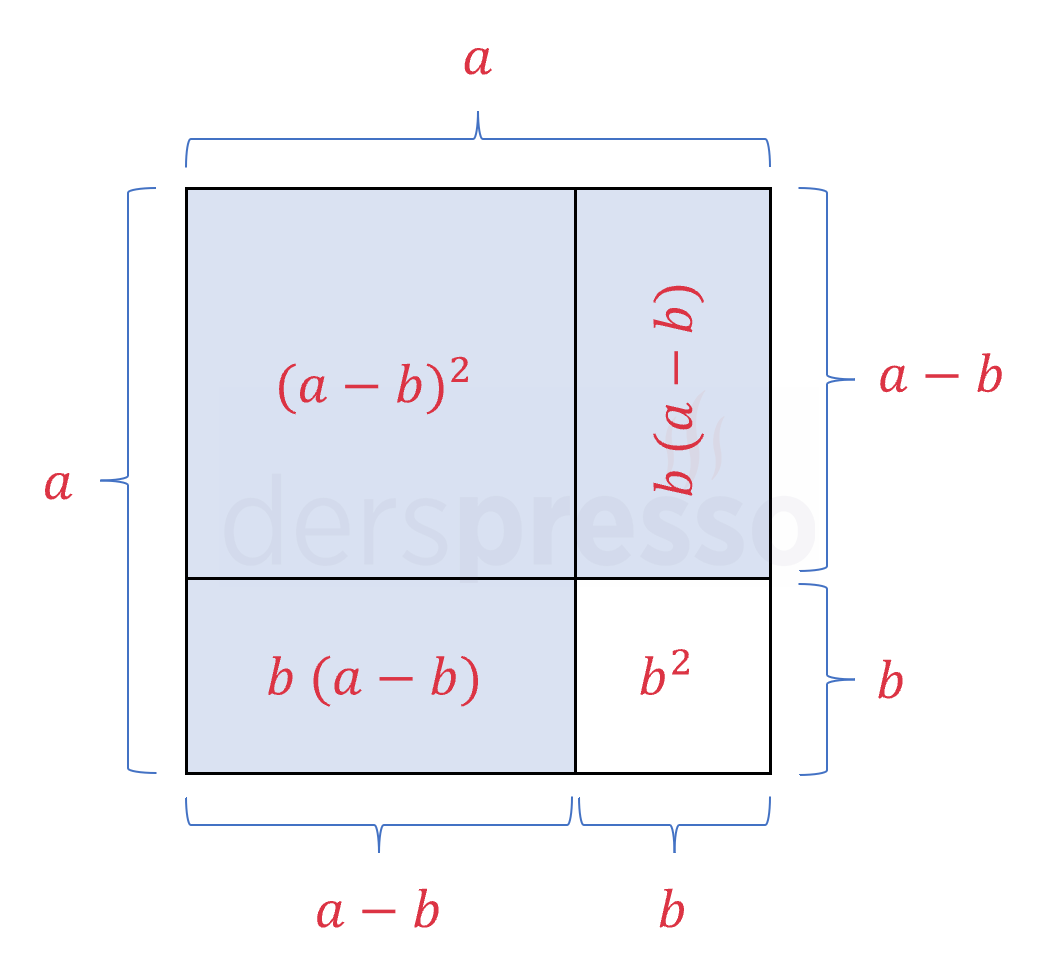
Büyük karenin alanı:

Küçük karenin alanı:

Renkli üç dörtgen:

Büyük kareden küçük karenin alanını çıkarıp renkli üç dörtgenin alanları toplamına eşitleyelim.

İfadenin sağ tarafını parantezine alırsak iki sayının kare farkı özdeşliğini elde ederiz.

Toplam Karesinin Fark Karesinden Farkı

Aşağıda bir kenar uzunluğu birim olan bir büyük kare ve içinde kenar uzunlukları ve birim olan dört küçük dikdörtgen verilmiştir. Renkli işaretlenmiş dört dikdörtgenin alan formülünü büyük kare ile küçük karenin alanları farkı şeklinde yazalım.

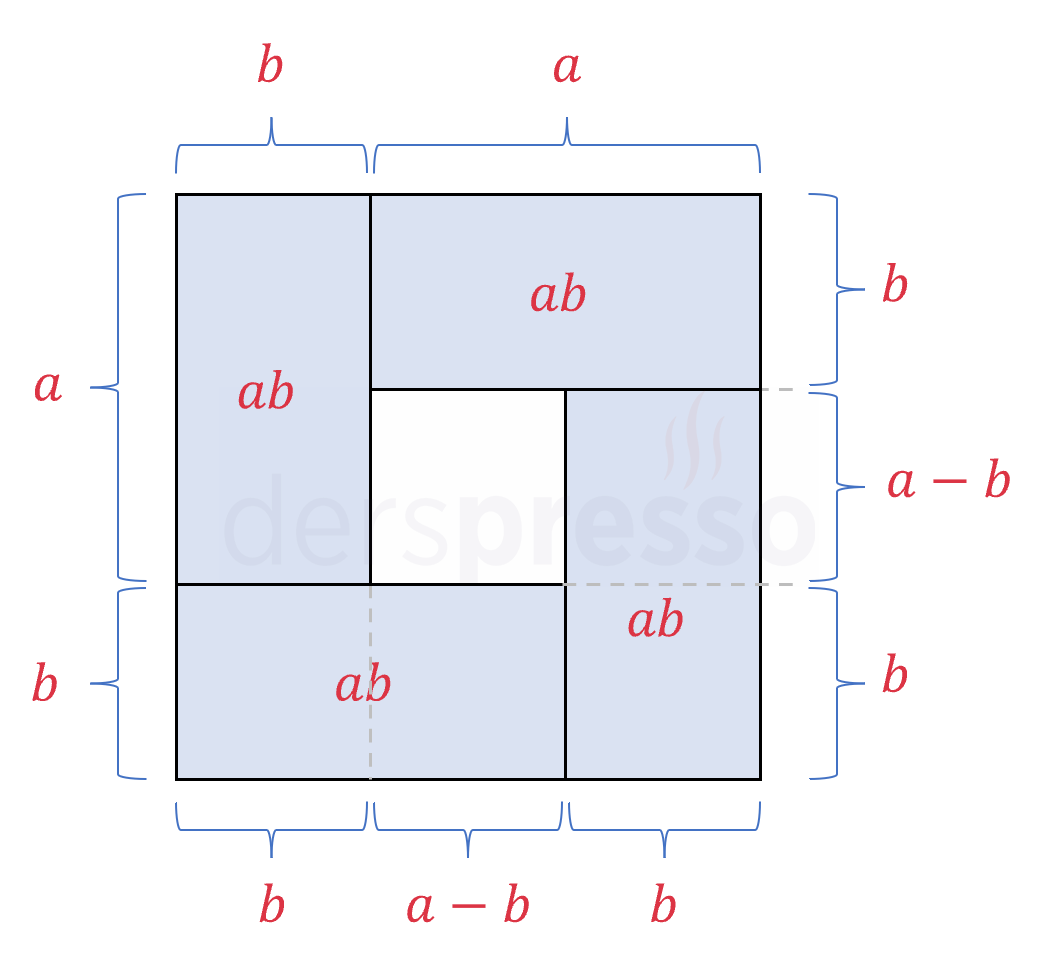
Büyük karenin alanı:

Küçük (beyaz) karenin alanı:

Renkli dört dikdörtgenin alanı:

Büyük kareden küçük karenin alanını çıkarıp renkli dört dikdörtgenin alanları toplamına eşitleyelim.