Üç Terimli İfadeleri Çarpanlarına Ayırma
Benzer terimlerden oluşan iki terimli iki ifadenin çarpımının açılımı üç terimli bir ifade olur.
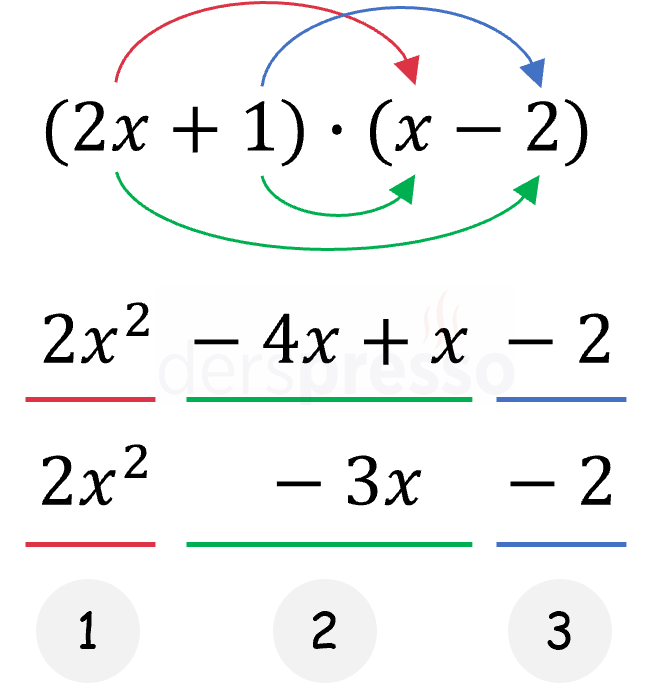
Böyle bir ifadenin benzer terimleri arasındaki çarpımlar (kırmızı ve mavi oklar) iki farklı terim üretirler. Benzer olmayan terimler arasındaki çarpımlar (yeşil oklar) da iki terim üretirler, ancak bu çarpımların sonucu olan terimler benzer oldukları için tek terimde birleşirler.
Bu şekildeki ifadelere ve açılımlarına aşağıdaki örnekler verilebilir.
| Çarpanlar | Açılım |
|---|---|
| \( (x - 2)(x + 1) \) | \( x^2 + x - 2x - 2 \) \( = x^2 - x - 2 \) |
| \( (2x - y)(3x + 2y) \) | \( 6x^2 + 4xy - 3xy - 2y^2 \) \( = 6x^2 + xy- 2y^2 \) |
| \( (2\sin{x} - 3)(\sin{x} + 1) \) | \( 2\sin^2{x} + 2\sin{x} - 3\sin{x} - 3 \) \( = 2\sin^2{x} - \sin{x}- 3 \) |
\( ax^2 + bx + c \) şeklindeki bir ifadenin kökleri reel sayı olacak şekilde çarpanlarına ayrılabilmesi için, ifadenin deltası (diskriminantı) sıfıra eşit ya da sıfırdan büyük olmalıdır (\( \Delta = b^2 - 4ac \ge 0 \)).
Çarpanlara Ayırma Yöntemi
Açılımı verilen üç terimli bir ifadeyi çarpanlarına ayırmak için aşağıdaki yöntem uygulanır.
Üç terimli ifade: \( 2x^2 - x - 3 \)
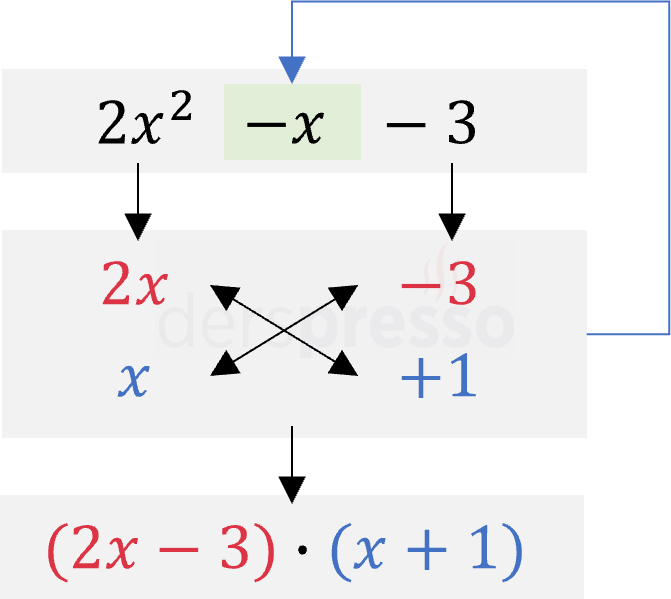
- Çarpanlarına ayrılmak istenen üç terimli ifade ilk satıra yazılır (\( 2x^2 - x - 3 \)).
- Birinci terim (\( 2x^2 \)) iki çarpanına ayrılıp bu çarpanlar altındaki iki satıra yazılır (\( 2x^2 = 2x \cdot x \)).
- Benzer şekilde üçüncü terim (\( -3 \)) iki çarpanına ayrılıp bu çarpanlar altındaki iki satıra yazılır (\( -3 = (-3) \cdot 1 \)).
- Her iki terim çarpanlarına ayrılırken çapraz oklarla gösterilen ifadelerin çarpımlarının toplamının, çarpanlarına ayrılan ifadenin ikinci terimine (\( -x \)) eşitliği sağlanmalıdır (\( 2x \cdot 1 + x \cdot (-3) = 2x - 3x = -x \)). Bu eşitliğin sağlanmadığı durumda 2. ve 3. adımlardaki işlemler farklı çarpanlarla tekrarlanmalıdır.
- Verilen örnekte 4. adımdaki koşulun sağlandığı görülebilir. Buna göre üç terimli ifadenin çarpanları ikinci kutunun ilk satırındaki kırmızı terimlerin toplamı (\( (2x - 3) \)) ile altındaki mavi terimlerin toplamının (\( (x + 1) \)) çarpımı olur (\( (2x - 3)(x + 1) \)).
\( 2x^2 - x - 3 \) \( = (2x - 3)(x + 1) \)
Aşağıdaki ikinci dereceden ifadeleri çarpanlarına ayırınız.
(a) \( x^2 + 4x - 21 \)
(b) \( 2x^2 + 3x - 14 \)
(c) \( 4x^2 + 17x - 15 \)
Çözümü Göster(a) seçeneği:
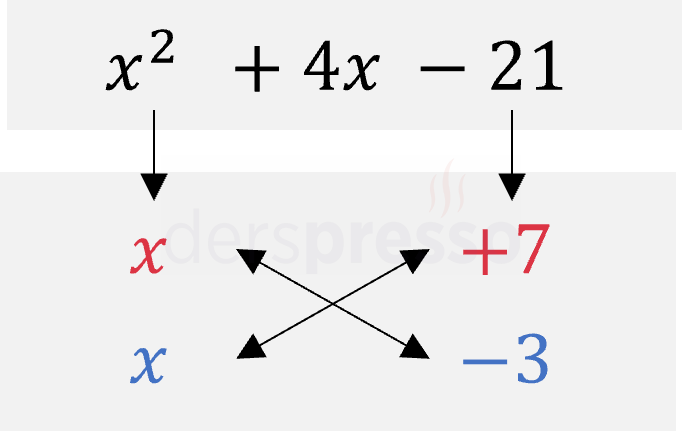
Birinci terimi \( x \) ve \( x \) şeklinde, üçüncü terimi \( +7 \) ve \( -3 \) şeklinde çarpanlarına ayırdığımızda çapraz çarpımların toplamının ikinci terime eşit olduğunu görüyoruz (\( x \cdot (-3) + x \cdot 7 = 4x \)).
Buna göre, verilen ikinci dereceden ifade aşağıdaki şekilde çarpanlarına ayrılır.
\( x^2 + 4x - 21 = (x + 7)(x - 3) \)
(b) seçeneği:
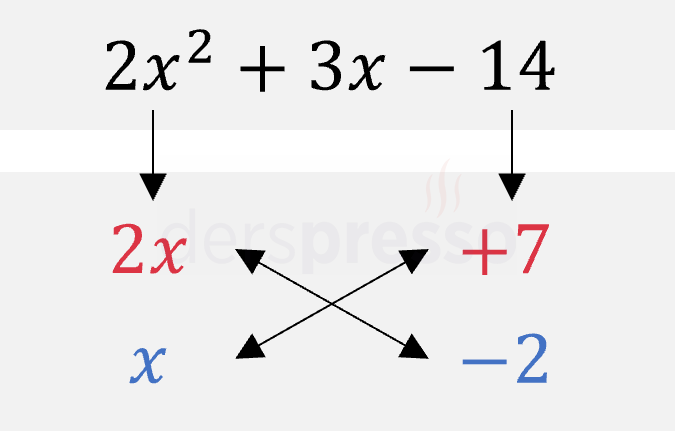
Birinci terimi \( 2x \) ve \( x \) şeklinde, üçüncü terimi \( +7 \) ve \( -2 \) şeklinde çarpanlarına ayırdığımızda çapraz çarpımların toplamının ikinci terime eşit olduğunu görüyoruz (\( 2x \cdot (-2) + x \cdot 7 = 3x \)).
Buna göre, verilen ikinci dereceden ifade aşağıdaki şekilde çarpanlarına ayrılır.
\( 2x^2 + 3x - 14 = (2x + 7)(x - 2) \)
(c) seçeneği:
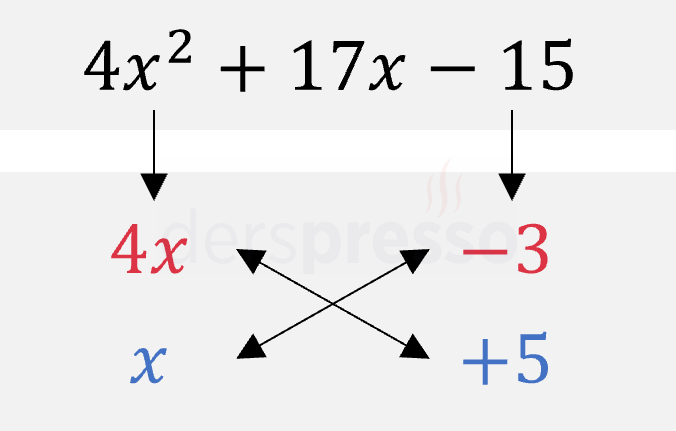
Birinci terimi \( 4x \) ve \( x \) şeklinde, üçüncü terimi \( -3 \) ve \( +5 \) şeklinde çarpanlarına ayırdığımızda çapraz çarpımların toplamının ikinci terime eşit olduğunu görüyoruz (\( 4x \cdot 5 + x \cdot (-3) = 17x \)).
Buna göre, verilen ikinci dereceden ifade aşağıdaki şekilde çarpanlarına ayrılır.
\( 4x^2 + 17x - 15 = (4x - 3)(x + 5) \)
\( 3x^2 + 7xy - 6y^2 \) ifadesini çarpanlarına ayırınız.
Çözümü Göster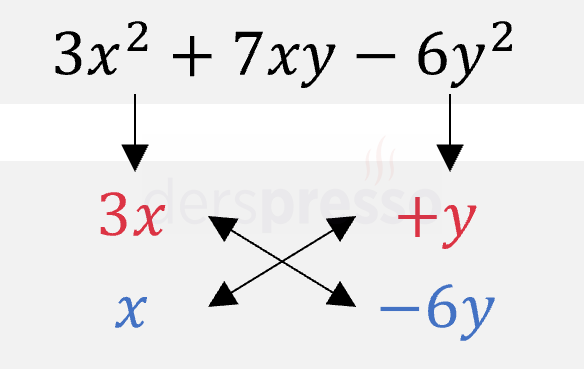
Çarpanlara ayırma yönteminin 4. adımında bahsettiğimiz doğrulamayı uyguladığımızda (\( 3x \cdot (-6y) + x \cdot y = -17xy \ne 7xy \)), yaptığımız çarpanlara ayırma işleminin ilk satırdaki üç terimli ifadenin ikinci terimini vermediğini görüyoruz. Bu durumda aşağıda işlemi farklı çarpanlarla tekrar deneyelim.
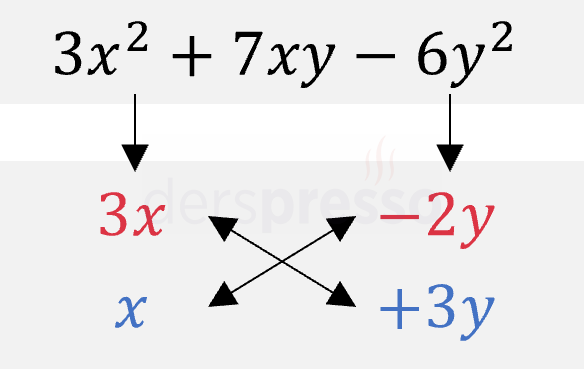
Bu çarpanların (\( 3x \cdot 3y + x \cdot (-2y) = 7xy \)) bize ikinci terimi verdiğini görüyoruz.
Dolayısıyla verilen ikinci dereceden ifade aşağıdaki şekilde çarpanlarına ayrılır.
\( 3x^2 + 7xy - 6y^2 \) \( = (3x - 2y)(x + 3y) \)
\( \dfrac{x^2 + ax + b}{x^2 + 8x + 15} \cdot \dfrac{x^2 + 7x + 10}{x^2 - 9x - 22} = \dfrac{x + 4}{x + 3} \)
olduğuna göre, \( a - b \) ifadesinin değeri kaçtır?
Çözümü GösterVerilen ifadeleri çarpanlarına ayıralım.
\( \dfrac{x^2 + ax + b}{(x + 5)(x + 3)} \) \( \cdot \dfrac{(x + 5)(x + 2)}{(x + 2)(x - 11)} \) \( = \dfrac{x + 4}{x + 3} \)
Pay ve paydadaki ortak çarpanları sadeleştirelim.
\( \dfrac{x^2 + ax + b}{(x + 3)(x - 11)} = \dfrac{x + 4}{x + 3} \)
\( \dfrac{x^2 + ax + b}{x - 11} = x + 4 \)
İçler - dışlar çarpımı yapalım.
\( x^2 + ax + b = (x + 4)(x - 11) \)
\( x^2 + ax + b = x^2 - 7x - 44 \)
İkinci dereceden iki ifadenin her \( x \) değeri için birbirine eşit olması için aynı dereceli terimlerin katsayıları eşit olmalıdır.
\( a = -7, \quad b = -44 \)
\( a - b = -7 - (-44) = 37 \) bulunur.
\( \dfrac{x^2 - 5x + m}{x^2 - 4} \) ifadesi sadeleşebildiğine göre, \( m \) sayısının alabileceği değerlerin toplamı kaçtır?
Çözümü GösterPaydayı çarpanlarına ayıralım.
\( \dfrac{x^2 - 5x + m}{(x - 2)(x + 2)} \)
İfade sadeleşebildiğine göre, payda bulunan ikinci dereceden ifadenin çarpanlarından biri \( x - 2 \) ya da \( x + 2 \) olmalıdır.
Durum 1: \( x - 2 \)
Pay ve paydada sadeleşen çarpanların \( x - 2 \) olduğunu varsayalım. Çarpan teoremine göre, \( x - 2 \) payın bir çarpanı ise \( x = 2 \) değeri payı sıfır yapmalıdır.
\( 2^2 - 5(2) + m = 0 \)
\( m = 6 \)
Bu durumda paydaki ifade aşağıdaki gibi olur ve çarpanlarına ayrılır.
\( x^2 - 5x + 6 = (x - 2)(x - 3) \)
Durum 2: \( x + 2 \)
Pay ve paydada sadeleşen çarpanların \( x + 2 \) olduğunu varsayalım. Çarpan teoremine göre, \( x + 2 \) payın bir çarpanı ise \( x = -2 \) değeri payı sıfır yapmalıdır.
\( (-2)^2 - 5(-2) + m = 0 \)
\( m = -14 \)
Bu durumda paydaki ifade aşağıdaki gibi olur ve çarpanlarına ayrılır.
\( x^2 - 5x - 14 = (x + 2)(x - 7) \)
Buna göre \( m \)'nin alabileceği değerlerin toplamı \( 6 + (-14) = -8 \) olur.