Parametrik Denklemlerin İntegrali
İntegral Uygulamaları
İntegralin parametrik denklemlerdeki bazı uygulamaları aşağıdaki gibidir.
Alan Bulma
Parametrik bir eğrinin belirli bir aralıkta \( x \) ekseni ile arasında kalan alan aşağıdaki formülle bulunur.
\( x = x(t), y = y(t) \) olmak üzere,
\( t_1 \le t \le t_2 \) aralığındaki alan:
\( A = \displaystyle\int_{t_1}^{t_2} y(t)x'(t)\ dt \)
İSPATI GÖSTER
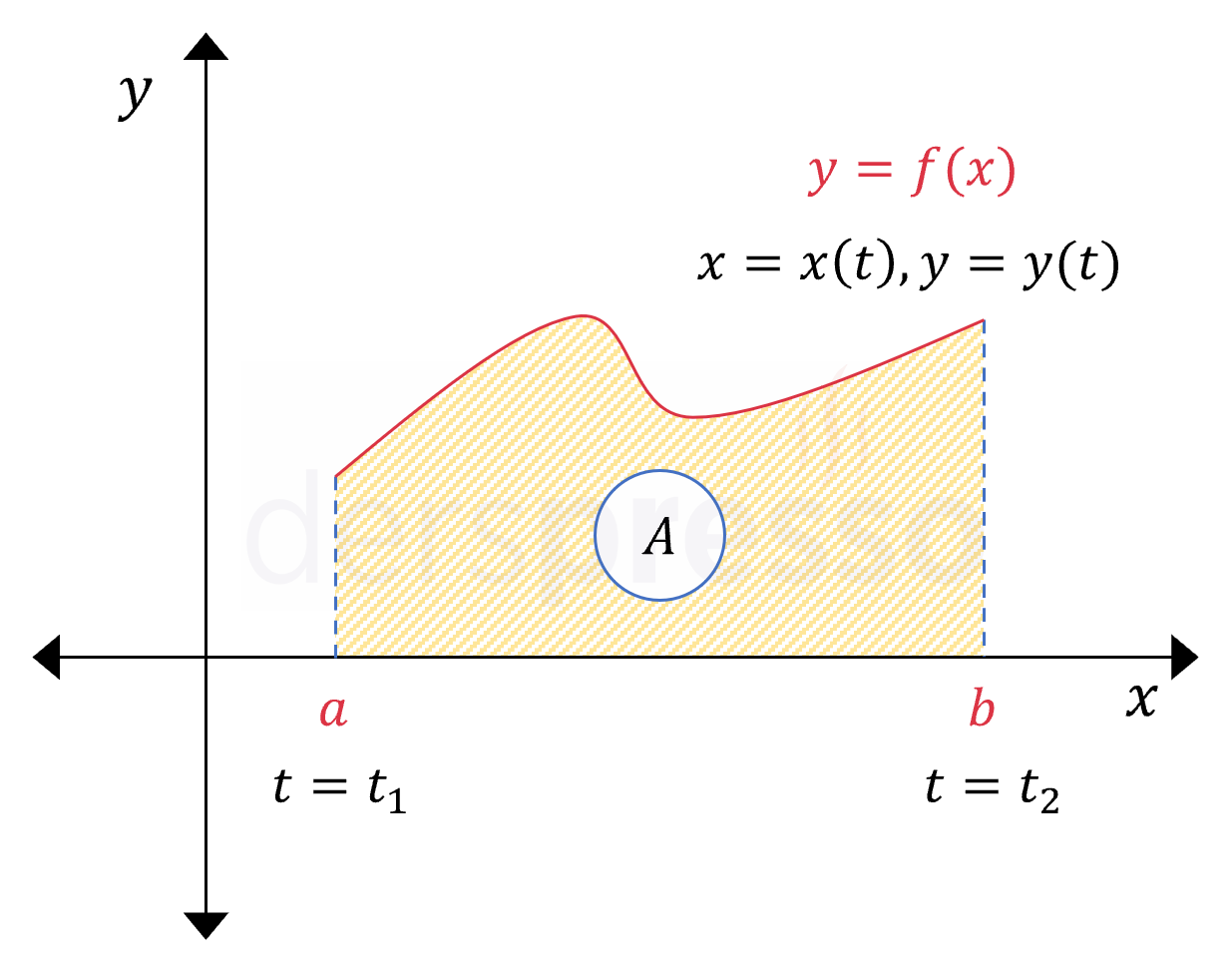
İntegral konusunda \( y = f(x) \) şeklindeki bir fonksiyonun \( x \) ekseni ile arasında kalan alanın formülünün \( f(x) \ge 0 \) olduğu durum için aşağıdaki şekilde olduğunu ispatıyla birlikte göstermiştik.
\( A = \displaystyle\int_a^b {f(x)\ dx} \)
Bu fonksiyonun parametrik denklem karşılığının aşağıdaki şekilde olduğunu varsayalım.
\( x = x(t), \quad y = y(t) \)
Değişken değiştirme yöntemi ile \( x \) değişkenine göre olan bu integrali \( t \) değişkenine çevirelim.
\( y = f(x) = y(t) \)
\( dx = x'(t)\ dt \)
İntegralin \( x = a \) ve \( x = b \) sınır değerlerini veren \( t \) parametre değerlerine \( t_1 \) ve \( t_2 \) diyelim.
\( a = x(t_1), \quad b = x(t_2) \)
Bu değerleri yukarıdaki integral ifadesinde yerine koyalım.
\( A = \displaystyle\int_{t_1}^{t_2} {y(t)x'(t)\ dt} \)
Yukarıdaki formülü kullanabilmemiz için \( x(t) \) denklemi \( t \in [t_1, t_2] \) aralığında türevlenebilir, \( y(t) \) denklemi de aynı aralıkta sürekli olmalıdır.
Bir parametrik denklemin \( x \) ekseni ile arasında kalan alanı bulurken verilen \( t \) değer aralığında aynı bölgenin birden fazla kez taranmadığından emin olunmalıdır. Örneğin alanı \( \pi \) olan birim çemberin \( t \in [0, 2\pi] \) aralığındaki alan integrali \( \pi \) değerini verirken \( t \in [0, 4\pi] \) aralığında \( 2\pi \) değerini verecektir.
Bu formülü bir parametrik eğrinin alan hesaplamasında kullanalım.
Aşağıda tanımı ve grafiği verilen parametrik denklemin \( x \) ekseni ile arasında kalan alanı bulalım.
\( x(\theta) = \sin{\theta} \)
\( y(\theta) = \sin(2\theta) \)

Parametrik eğri iki eksene göre de simetrik olduğu için sadece I. bölgedeki alanı bulup 4 ile çarpabiliriz.
Eğrinin \( (0, 0) \) noktası \( \theta = 0 \) değerinde, \( (1, 0) \) noktası \( \theta = \frac{\pi}{2} \) değerinde oluşur.
\( (\sin{0}, \sin(2 \cdot 0)) = (0, 0) \)
\( (\sin{\frac{\pi}{2}}, \sin(2 \cdot \frac{\pi}{2})) = (1, 0) \)
Dolayısıyla I. bölgedeki alan için integrali \( \theta \in [0, \frac{\pi}{2}] \) aralığında almalıyız.
İntegral alan formülünü yazalım.
\( A = \displaystyle\int_{\alpha}^{\beta} y(\theta)x'(\theta)\ d\theta \)
\( x'(\theta) = \cos{\theta} \)
\( = \displaystyle\int_0^{\frac{\pi}{2}} \sin(2\theta)\cos{\theta}\ d\theta \)
Sinüs iki kat açı formülü ile \( \sin(2\theta) \) ifadesinin açılımını yazalım.
\( = \displaystyle\int_0^{\frac{\pi}{2}} 2\sin{\theta}\cos{\theta}\cos{\theta}\ d\theta \)
\( = \displaystyle\int_0^{\frac{\pi}{2}} 2\sin{\theta}\cos^2{\theta}\ d\theta \)
İfadenin integralini alalım.
\( = (-\dfrac{2\cos^3{\theta}}{3})|_0^{\frac{\pi}{2}} \)
\( = -\dfrac{2\cos^3{\frac{\pi}{2}}}{3} + \dfrac{2\cos^3{0}}{3} \)
\( = -0 + \dfrac{2}{3} = \dfrac{2}{3} \)
Buna göre parametrik eğrinin dört bölgede \( x \) ekseni ile arasında kalan toplam alan \( 4 \cdot \frac{2}{3} = \frac{8}{3} \) olur.
Yay Uzunluğu Bulma
Parametrik bir eğrinin belirli bir aralıktaki yay uzunluğu aşağıdaki formülle bulunur.
\( x = x(t), y = y(t) \) olmak üzere,
\( t_1 \le t \le t_2 \) aralığında eğrinin yay uzunluğu:
\( L = \displaystyle\int_{t_1}^{t_2} \sqrt{(\frac{dx}{dt})^2 + (\frac{dy}{dt})^2}\ dt \)
Yukarıdaki formülü kullanabilmemiz için \( x(t) \) ve \( y(t) \) denklemleri \( t \in [t_1, t_2] \) aralığında sürekli olmalı ve eğri bu aralıkta kendini tekrarlamamalıdır.
Bir parametrik denklemin yay uzunluğunu bulurken verilen \( t \) değer aralığında aynı yayın birden fazla kez tekrarlanmadığından emin olunmalıdır. Örneğin çevresi \( 2\pi \) olan birim çemberin \( t \in [0, 2\pi] \) aralığındaki yay uzunluğu integrali \( 2\pi \) değerini verirken \( t \in [0, 4\pi] \) aralığında \( 4\pi \) değerini verecektir.
Bu formülü bir parametrik eğrinin yay uzunluğu hesaplamasında kullanalım.
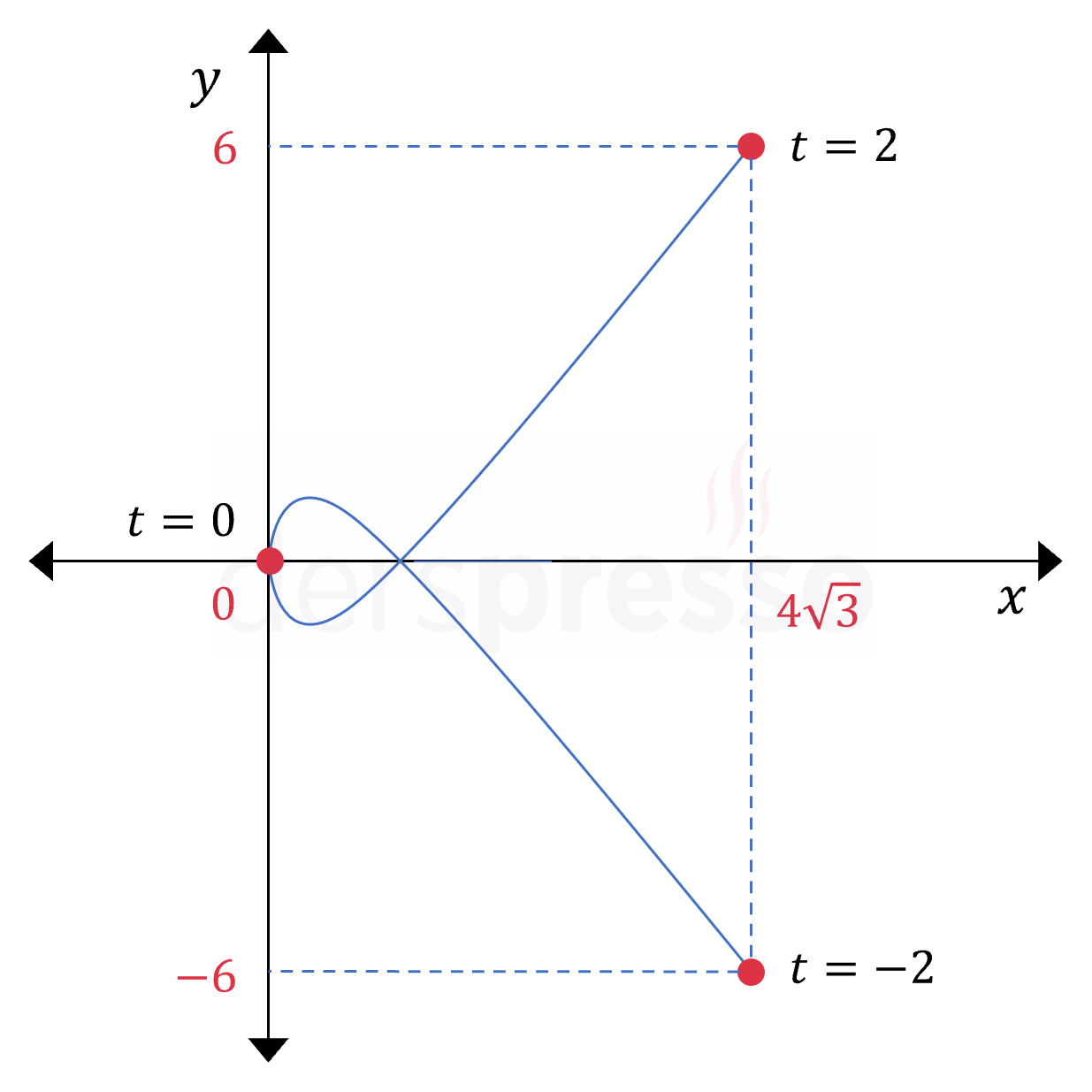
Aşağıda tanımı ve grafiği verilen parametrik denklemin \( -2 \le t \le 2 \) aralığındaki yay uzunluğunu bulalım.
\( x(t) = \sqrt{3}t^2 \)
\( y(t) = t^3 - t \)
İntegral yay uzunluğu formülünü yazalım.
\( L = \displaystyle\int_{t_1}^{t_2} \sqrt{(\frac{dx}{dt})^2 + (\frac{dy}{dt})^2}\ dt \)
\( = \displaystyle\int_{-2}^2 \sqrt{(2\sqrt{3}t)^2 + (3t^2 - 1)^2}\ dt \)
\( = \displaystyle\int_{-2}^2 \sqrt{12t^2 + 9t^4 - 6t^2 + 1}\ dt \)
\( = \displaystyle\int_{-2}^2 \sqrt{9t^4 + 6t^2 + 1}\ dt \)
\( = \displaystyle\int_{-2}^2 \sqrt{(3t^2 + 1)^2}\ dt \)
\( = \displaystyle\int_{-2}^2 \abs{3t^2 + 1}\ dt \)
Mutlak değer içindeki ifade tüm reel sayılarda pozitiftir.
\( = \displaystyle\int_{-2}^2 (3t^2 + 1)\ dt \)
İfadenin integralini alalım.
\( = (t^3 + t)|_{-2}^2 \)
\( = (2^3 + 2) - ((-2)^3 + (-2)) \)
\( = 10 - (-10) = 20 \)
Aşağıda parametrik denklemi verilen eğrinin \( 0 \le t \le \pi \) aralığındaki yay uzunluğunu bulunuz.
\( x(t) = e^t\sin{t} \)
\( y(t) = e^t\cos{t} \)
Çözümü Gösterİntegral yay uzunluğu formülünü yazalım.
\( L = \displaystyle\int_{t_1}^{t_2} \sqrt{(\frac{dx}{dt})^2 + (\frac{dy}{dt})^2}\ dt \)
Türev çarpma kuralı ile denklemlerin türevini alalım.
\( = \displaystyle\int_0^{\pi} \sqrt{(e^t\sin{t} + e^t\cos{t})^2 + (e^t\cos{t} - e^t\sin{t})^2}\ dt \)
\( = \displaystyle\int_0^{\pi} \sqrt{e^{2t}(\sin^2{t} + 2\sin{t}\cos{t} + \cos^2{t}) + e^{2t}(\cos^2{t} - 2\sin{t}\cos{t} + \sin^2{t})}\ dt \)
\( = \displaystyle\int_0^{\pi} \sqrt{e^{2t}(1 + 2\sin{t}\cos{t}) + e^{2t}(1 - 2\sin{t}\cos{t})}\ dt \)
\( = \displaystyle\int_0^{\pi} \sqrt{2e^{2t}}\ dt \)
\( = \displaystyle\int_0^{\pi} \sqrt{2}e^{t}\ dt \)
İfadenin integralini alalım.
\( = \sqrt{2}e^{t}|_0^{\pi} \)
\( = \sqrt{2}e^{\pi} - \sqrt{2}e^{0} \)
\( = \sqrt{2}(e^{\pi} - 1) \) bulunur.
Aşağıda parametrik denklemi verilen eğrinin \( 0 \le t \le 2\pi \) aralığındaki yay uzunluğunu bulunuz.
\( x(t) = \sin{t} - t\cos{t} \)
\( y(t) = \cos{t} + t\sin{t} \)
Çözümü Gösterİntegral yay uzunluğu formülünü yazalım.
\( L = \displaystyle\int_{t_1}^{t_2} \sqrt{(\frac{dx}{dt})^2 + (\frac{dy}{dt})^2}\ dt \)
Türev toplama ve çarpma kuralları ile denklemlerin türevini alalım.
\( = \displaystyle\int_0^{2\pi} \sqrt{(\cos{t} - \cos{t} + t\sin{t})^2 + (-\sin{t} + \sin{t} + t\cos{t})^2}\ dt \)
\( = \displaystyle\int_0^{2\pi} \sqrt{t^2\sin^2{t} + t^2\cos^2{t}}\ dt \)
\( = \displaystyle\int_0^{2\pi} \sqrt{t^2(\sin^2{t} + \cos^2{t})}\ dt \)
\( = \displaystyle\int_0^{2\pi} t\ dt \)
İfadenin integralini alalım.
\( = \dfrac{t^2}{2}|_0^{2\pi} \)
\( = \dfrac{(2\pi)^2}{2} - \dfrac{0^2}{2} \)
\( = 2\pi^2 \) bulunur.
Yüzey Alanı Bulma
Parametrik bir eğrinin belirli bir aralıktaki bölümünü \( x \) ekseni etrafında 360° döndürdüğümüzü varsayalım. Bu şekilde oluşan 3 boyutlu şeklin yanal yüzey alanı aşağıdaki formülle bulunur.
\( x = x(t), y = y(t) \) olmak üzere,
\( t_1 \le t \le t_2 \) aralığındaki yüzey alanı:
\( A = 2\pi \displaystyle\int_{t_1}^{t_2} y(t)\sqrt{(\frac{dx}{dt})^2 + (\frac{dy}{dt})^2}\ dt \)
Parametrik bir eğrinin belirli bir aralıktaki bölümünü \( y \) ekseni etrafında 360° döndürdüğümüzü varsayalım. Bu şekilde oluşan 3 boyutlu şeklin yanal yüzey alanı aşağıdaki formülle bulunur.
\( x = x(t), y = y(t) \) olmak üzere,
\( t_1 \le t \le t_2 \) aralığındaki yüzey alanı:
\( A = 2\pi \displaystyle\int_{t_1}^{t_2} x(t)\sqrt{(\frac{dx}{dt})^2 + (\frac{dy}{dt})^2}\ dt \)
Hacim Bulma
Parametrik bir eğrinin belirli bir aralıktaki bölümünü \( x \) ekseni etrafında 360° döndürdüğümüzü varsayalım. Bu şekilde oluşan 3 boyutlu şeklin hacmi aşağıdaki formülle bulunur.
\( x = x(t), y = y(t) \) olmak üzere,
\( t_1 \le t \le t_2 \) aralığındaki yüzey alanı:
\( V = \pi \displaystyle\int_{t_1}^{t_2} [y(t)]^2x'(t)\ dt \)
Parametrik bir eğrinin belirli bir aralıktaki bölümünü \( y \) ekseni etrafında 360° döndürdüğümüzü varsayalım. Bu şekilde oluşan 3 boyutlu şeklin hacmi aşağıdaki formülle bulunur.
\( x = x(t), y = y(t) \) olmak üzere,
\( t_1 \le t \le t_2 \) aralığındaki yüzey alanı:
\( V = \pi \displaystyle\int_{t_1}^{t_2} [x(t)]^2y'(t)\ dt \)

Yukarıdaki eğrinin parametrik denklemi aşağıda verilmiştir.
\( 0 \le t \le 2\pi \) olmak üzere,
\( x(t) = 2t^2 \)
\( y(t) = 1 + \cos{t} \)
Eğrinin \( x \) ekseni ile arasında kalan taralı bölgenin alanını bulunuz.
Çözümü GösterÖnce eğrinin \( x \) eksenini hangi \( t \) değerinde kestiğini bulalım.
Eğrinin \( x \) eksenini kestiği noktalarda ordinat sıfır olur.
\( y(t) = 0 \)
\( 1 + \cos{t} = 0 \)
\( \cos{t} = -1 \)
\( t = \pi \)
Eğrinin \( y \) eksenini hangi \( t \) değerinde kestiğini bulalım.
Eğrinin \( y \) eksenini kestiği noktalarda apsis sıfır olur.
\( x(t) = 2t^2 = 0 \)
\( t = 0 \)
Buna göre taralı alan eğrinin \( t = 0 \) ve \( t = \pi \) değerleri arasındaki bölgeye karşılık gelir.
Parametrik denklemlerin alan formülünü yazalım.
\( x = x(t), y = y(t) \) olmak üzere,
\( 0 \le t \le \pi \) aralığındaki alan:
\( A = \displaystyle\int_0^{\pi} y(t)x'(t)\ dt \)
\( x'(t) = 4t \)
\( = \displaystyle\int_0^{\pi} (1 + \cos{t}) \cdot 4t\ dt \)
\( = \displaystyle\int_0^{\pi} 4t(1 + \cos{t})\ dt \)
Kısmi integral alma yöntemini kullanalım
\( u \) ve \( dv \) ifadelerini aşağıdaki gibi belirleyelim.
\( u = 4t \)
\( dv = (1 + \cos{t})\ dt \)
Buna göre \( du \) ve \( v \) aşağıdaki gibi olur.
\( du = 4\ dt \)
\( v = t + \sin{t} \)
Değişkenleri kısmi integral formülünde yerine koyalım.
\( \displaystyle\int {u\ dv} = u\ v - \displaystyle\int {v\ du} \)
\( \displaystyle\int_0^{\pi} 4t(1 + \cos{t})\ dt = [4t(t + \sin{t})]|_0^{\pi} - \displaystyle\int_0^{\pi} 4(t + \sin{t})\ dt \)
\( = (4t^2 + 4t\sin{t})|_0^{\pi} - \displaystyle\int_0^{\pi} (4t + 4\sin{t})\ dt \)
Son terimin integralini alalım.
\( = (4t^2 + 4t\sin{t})|_0^{\pi} - (2t^2 - 4\cos{t})|_0^{\pi} \)
\( = [(4\pi^2 + 4\pi\sin{\pi}) - (4(0)^2 + 4(0)\sin{0})] - [(2\pi^2 - 4\cos{\pi}) - (2(0)^2 - 4\cos{0})] \)
\( = [(4\pi^2 + 0) - 0] - [(2\pi^2 + 4) - (0 - 4)] \)
\( = 2\pi^2 - 8 \) bulunur.
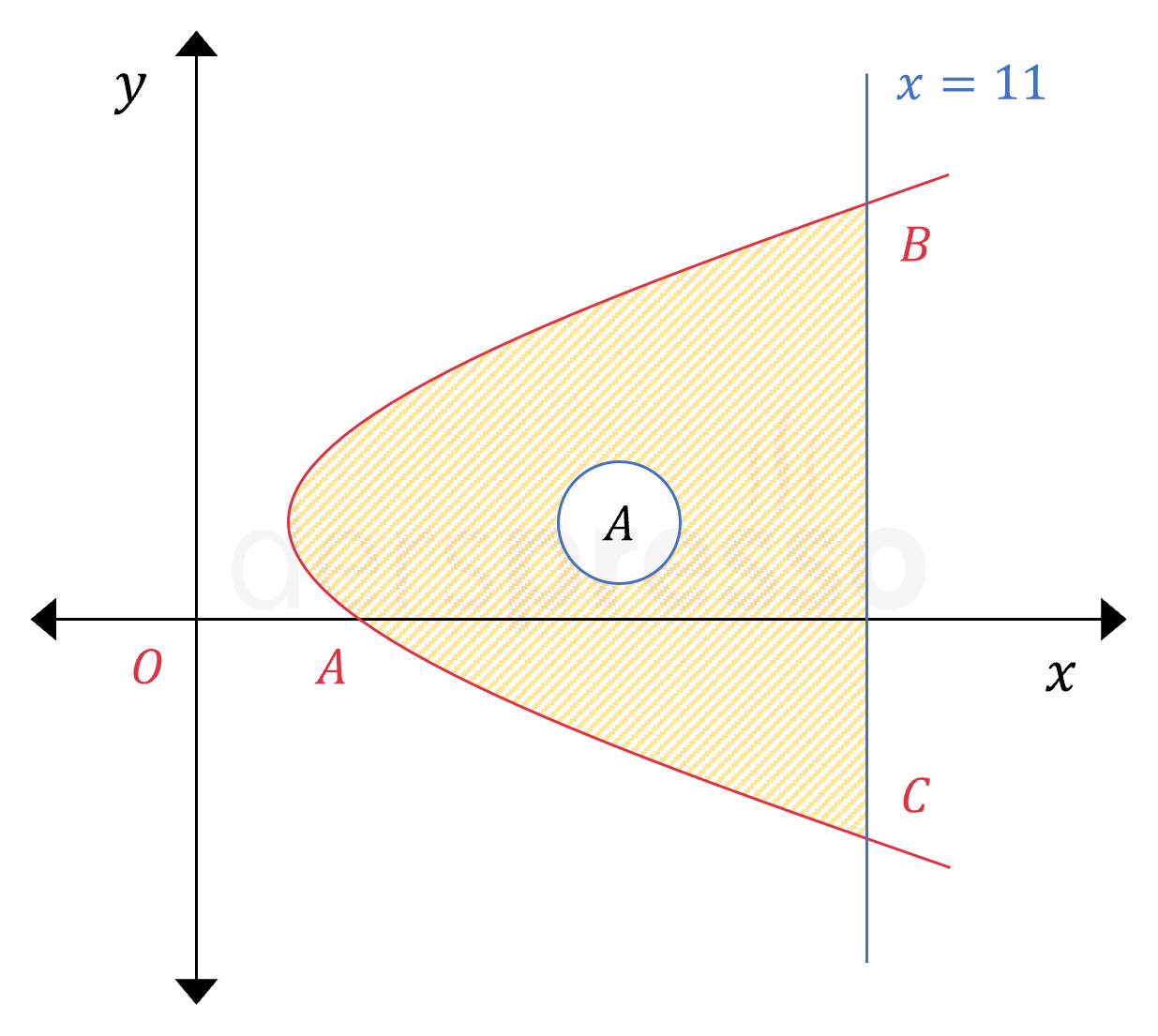
Yukarıdaki eğrinin parametrik denklemi aşağıda verilmiştir.
\( t \in \mathbb{R} \) olmak üzere,
\( x(t) = t^2 + 2 \)
\( y(t) = 3t + 3 \)
Parametrik eğri ile \( x = 11 \) doğrusunun arasında kalan bölgenin alanını bulunuz.
Çözümü GösterÖnce eğrinin \( x \) eksenini kestiği noktayı bulalım.
Eğrinin \( x \) eksenini kestiği noktalarda ordinat sıfır olur.
\( y(t) = 3t + 3 = 0 \)
\( t = -1 \)
\( x(-1) = (-1)^2 + 2 = 3 \)
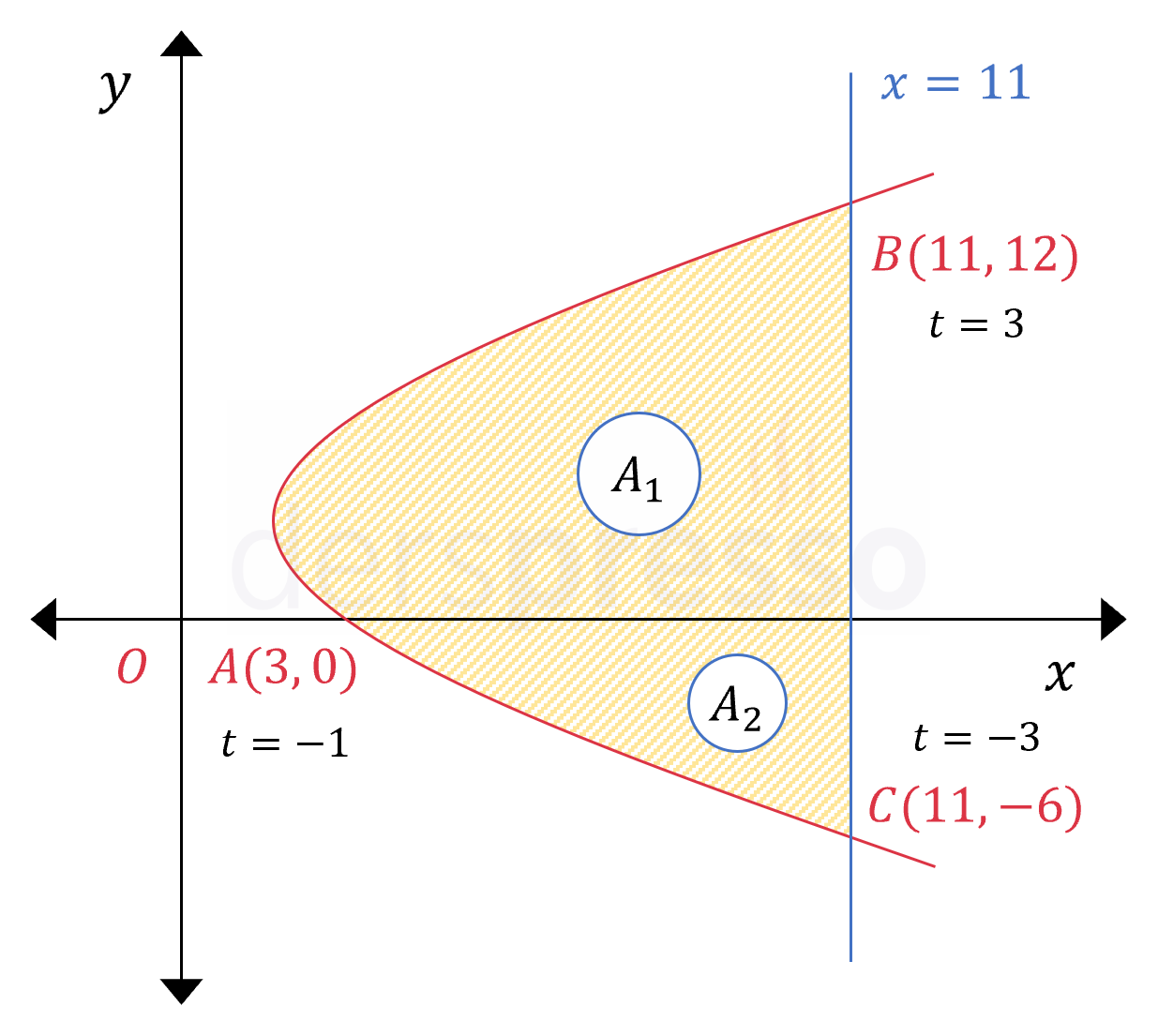
Buna göre eğri \( x \) eksenini \( t = -1 \) değerindeki \( A(3, 0) \) noktasında keser.
Eğrinin \( x = 11 \) doğrusunu kestiği noktaları bulalım.
\( x(t) = t^2 + 2 = 11 \)
\( t = \pm 3 \)
\( y(3) = 3(3) + 3 = 12 \)
\( y(-3) = 3(-3) + 3 = -6 \)
Buna göre eğri \( x = 11 \) doğrusunu \( t = 3 \) değerindeki \( B(11, 12) \) ve \( t = -3 \) değerindeki \( C(11, -6) \) noktalarında keser.
Parametrik denklemlerin alan formülünü yazalım.
Taralı alanı \( A_1 \) ve \( A_2 \) olmak üzere iki bölgeye ayıralım.
Önce \( A_1 \) alanını bulalım.
\( -1 \le t \le 3 \) aralığındaki alan:
\( A_1 = \displaystyle\int_{-1}^3 y(t)x'(t)\ dt \)
\( x'(t) = 2t \)
\( = \displaystyle\int_{-1}^{3} (3t + 3) \cdot 2t\ dt \)
\( = \displaystyle\int_{-1}^{3} (6t^2 + 6t)\ dt \)
İfadenin integralini alalım.
\( = (2t^3 + 3t^2)|_{-1}^3 \)
\( = (2(3)^3 + 3(3)^2) - (2(-1)^3 + 3(-1)^2) \)
\( = (54 + 27) - (-2 + 3) = 80 \)
\( A_2 \) alanını bulalım.
Bir fonksiyonun değerinin negatif olduğu (\( f(x) \lt 0 \)), yani grafiğinin \( x \) ekseninin altında kaldığı bir aralıktaki belirli integrali negatif işaretlidir. Alan pozitif bir büyüklük olduğu için, bu aralıkta fonksiyon grafiği ile \( x \) ekseni arasında kalan alan bu negatif integral değerinin ters işaretlisine eşittir.
\( A_2 = -\displaystyle\int_{-1}^{-3} (6t^2 + 6t)\ dt \)
İfadenin integralini alalım.
\( = -(2t^3 + 3t^2)|_{-1}^{-3} \)
\( = -[(2(-3)^3 + 3(-3)^2) - (2(-1)^3 + 3(-1)^2)] \)
\( = -[(-54 + 27) - (-2 + 3)] = 28 \)
Toplam alan bulduğumuz iki alanın toplamına eşittir.
\( A = A_1 + A_2 \)
\( = 80 + 28 = 108 \) olarak bulunur.
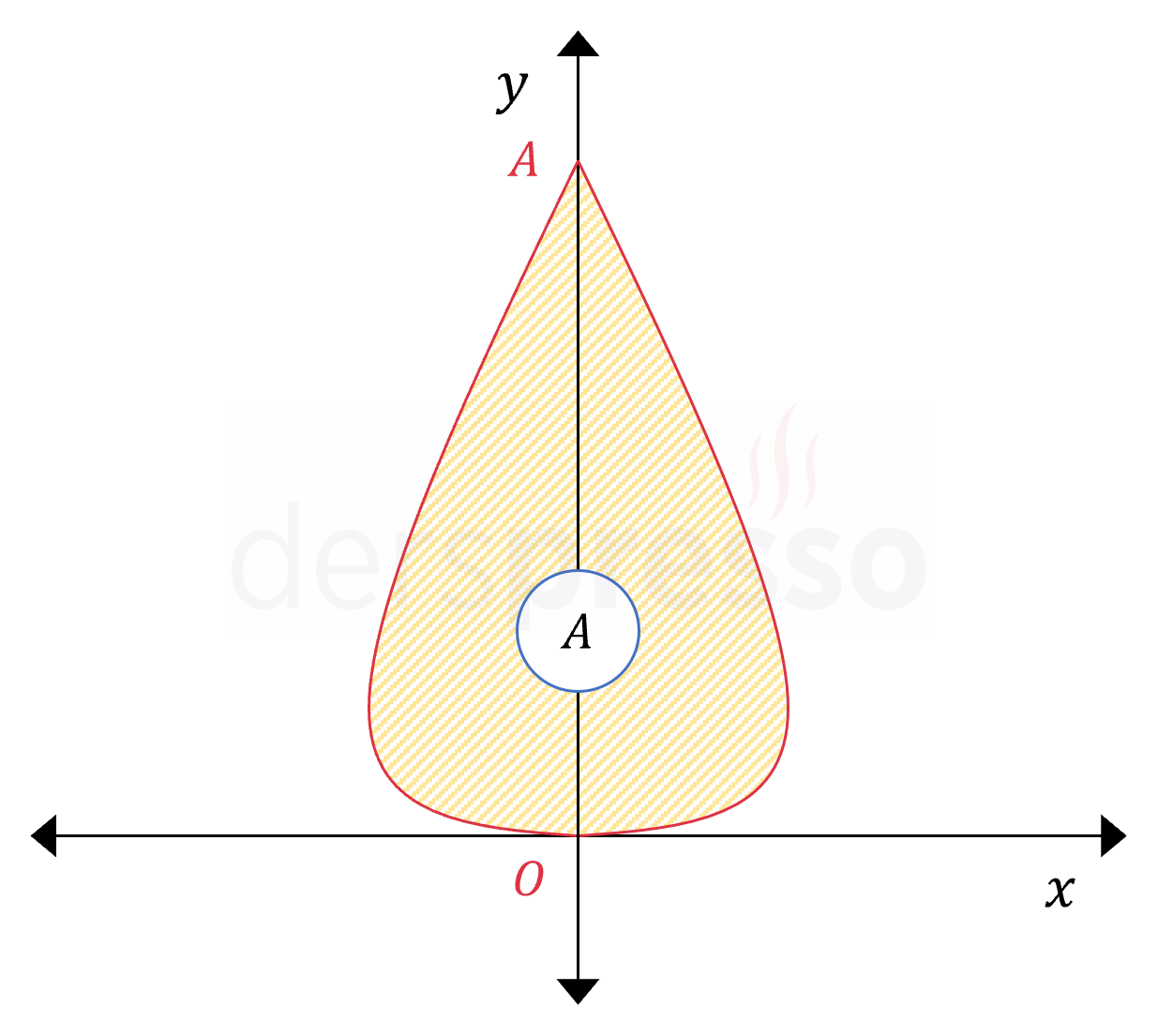
Yukarıdaki eğrinin parametrik denklemi aşağıda verilmiştir.
\( -\pi \le t \le \pi \) olmak üzere,
\( x(t) = 2\sin{t} \)
\( y(t) = t^2 \)
Eğrinin \( y \) ekseni ile arasında kalan taralı bölgenin alanını bulunuz.
Çözümü GösterÖnce eğrinin \( y \) eksenini kestiği noktaları bulalım.
Eğrinin \( y \) eksenini kestiği noktalarda apsis sıfır olur.
\( x(t) = 2\sin{t} = 0 \)
\( t \in \{-\pi, 0, \pi\} \)
\( y(-\pi) = \pi^2 \)
\( y(0) = 0^2 = 0 \)
\( y(\pi) = \pi^2 \)
Buna göre eğri \( y \) eksenini \( t = -\pi \) değerinde \( (0, \pi^2) \) noktasında, \( t = 0 \) değerinde \( (0, 0) \) noktasında ve \( t = \pi \) değerindeki tekrar \( (0, \pi^2) \) noktasında keser.
Eğrinin yönünü bulmak için \( t \)'ye ara değerler verelim.
\( x(-\frac{\pi}{2}) = 2\sin{-\frac{\pi}{2}} = -2 \)
\( y(-\frac{\pi}{2}) = (-\dfrac{\pi}{2})^2 = \dfrac{\pi^2}{4} \)
\( x(\frac{\pi}{2}) = 2\sin{\frac{\pi}{2}} = 2 \)
\( y(\frac{\pi}{2}) = (\dfrac{\pi}{2})^2 = \dfrac{\pi^2}{4} \)
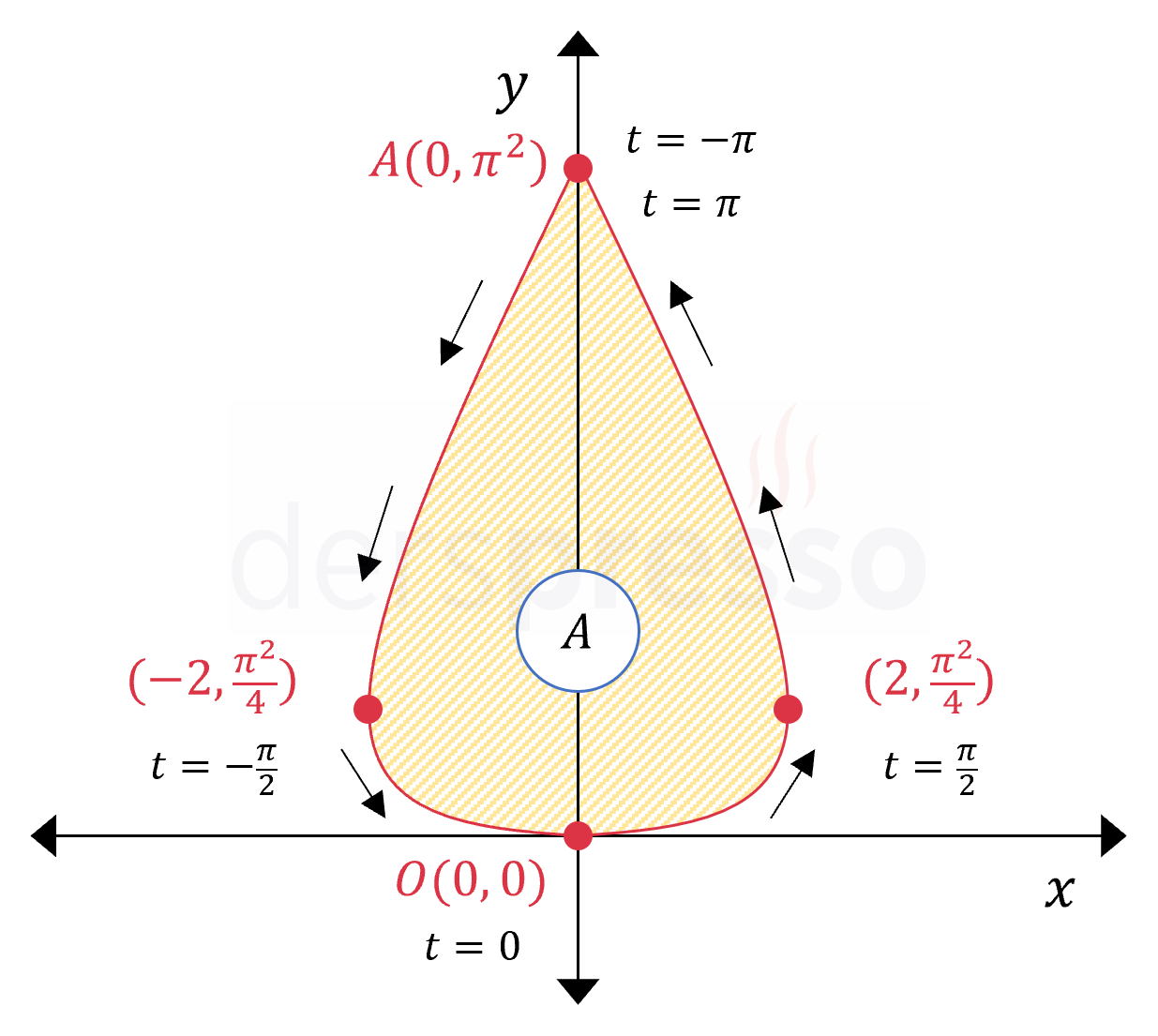
Buna göre istenen alan eğrinin \( t \in [0, \pi] \) aralığında \( y \) ekseni ile arasında kalan alanın 2 katıdır.
Parametrik denklemlerin \( y \) ekseni için alan formülünü yazalım.
\( x = x(t), y = y(t) \) olmak üzere,
\( 0 \le t \le \pi \) aralığındaki alan:
\( A = 2\displaystyle\int_0^{\pi} x(t)y'(t)\ dt \)
\( y'(t) = 2t \)
\( = 2\displaystyle\int_0^{\pi} 2\sin{t} \cdot 2t\ dt \)
\( = 8\displaystyle\int_0^{\pi} t\sin{t}\ dt \)
Kısmi integral alma yöntemini kullanalım
\( u \) ve \( dv \) ifadelerini aşağıdaki gibi belirleyelim.
\( u = t \)
\( dv = \sin{t}\ dt \)
Buna göre \( du \) ve \( v \) aşağıdaki gibi olur.
\( du = dt \)
\( v = -\cos{t} \)
Değişkenleri kısmi integral formülünde yerine koyalım.
\( \displaystyle\int {u\ dv} = u\ v - \displaystyle\int {v\ du} \)
\( 8\displaystyle\int_0^{\pi} t\sin{t}\ dt = 8(-t\cos{t})|_0^{\pi} - 8\displaystyle\int_0^{\pi} -\cos{t}\ dt \)
\( = -8(t\cos{t})|_0^{\pi} + 8\displaystyle\int_0^{\pi} \cos{t}\ dt \)
Son terimin integralini alalım.
\( = -8(t\cos{t})|_0^{\pi} + 8(\sin{t})|_0^{\pi} \)
\( = -8(\pi\cos{\pi} - 0\cos{0}) + 8(\sin{\pi} - \sin{0}) \)
\( = -8(\pi(-1) - 0) + 8(0 - 0) \)
\( = 8\pi \) bulunur.
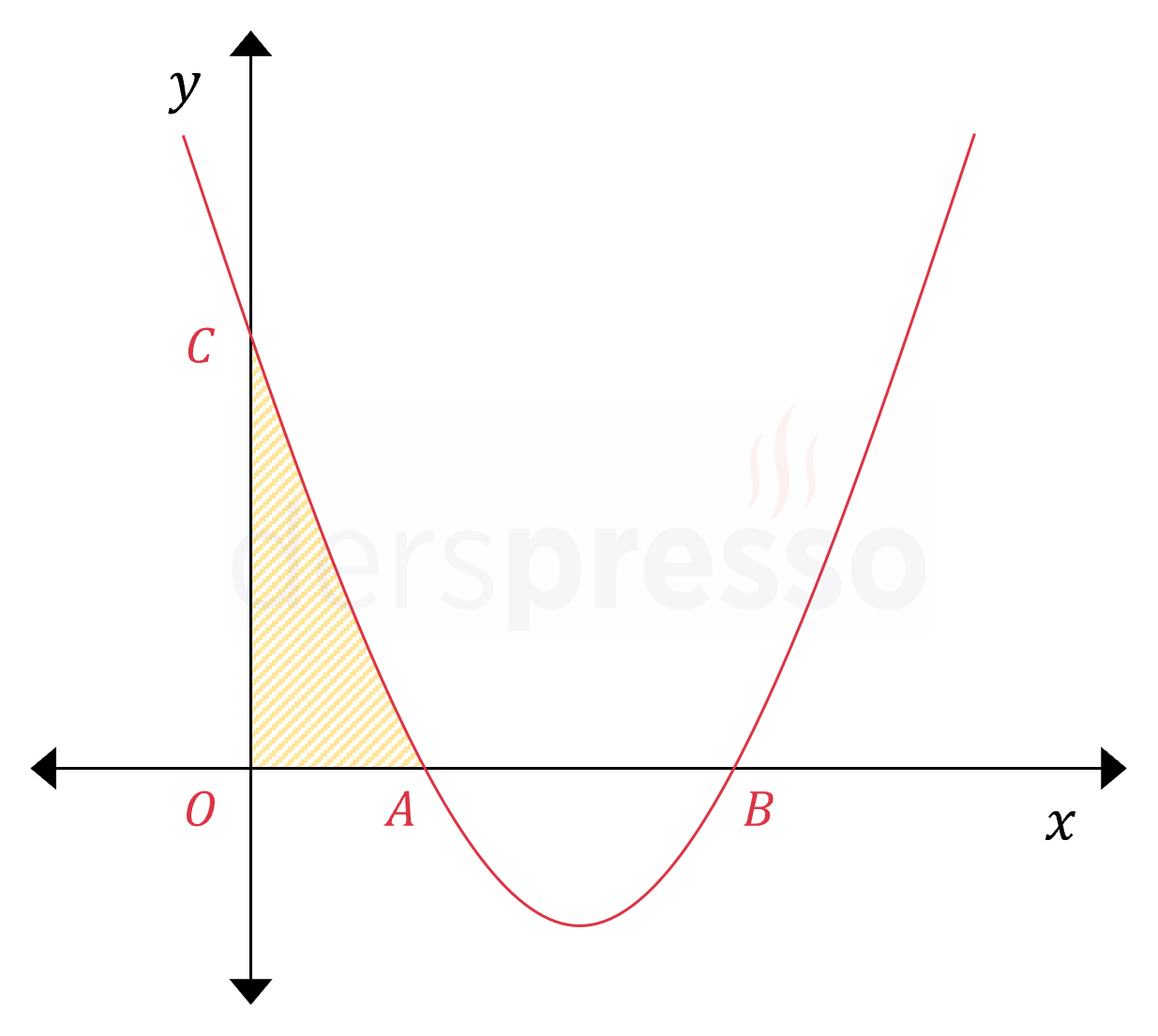
Yukarıdaki eğrinin parametrik denklemi aşağıda verilmiştir.
\( t \in \mathbb{R} \) olmak üzere,
\( x(t) = 4 - 2t \)
\( y(t) = t(t + 3) \)
Buna göre taralı bölgenin alanını bulunuz.
Çözümü GösterÖnce eğrinin \( x \) eksenini kestiği noktaları bulalım.
Eğrinin \( x \) eksenini kestiği noktalarda ordinat sıfır olur.
\( y(t) = 0 \)
\( t(t - 3) = 0 \)
\( t = 0 \) ya da \( t = -3 \)
\( t = 0 \) için:
\( x(0) = 4 - 2(0) = 4 \)
\( t = -3 \) için:
\( x(-3) = 4 - 2(-3) = 10 \)
Buna göre eğri \( x \) eksenini \( A(4, 0) \) ve \( B(10, 0) \) noktalarında keser.
Eğrinin hangi \( t \) değerinde \( y \) eksenini kestiğini bulalım.
Eğrinin \( y \) eksenini kestiği noktalarda apsis sıfır olur.
\( x(t) = 0 \)
\( 4 - 2t = 0 \)
\( t = 2 \)
Buna göre taralı alan \( t = 2 \) ve \( t = 0 \) değerleri arasında oluşan eğrinin altında kalan alana karşılık gelir.
Parametrik denklemlerin alan formülünü yazalım.
\( x = x(t), y = y(t) \) olmak üzere,
\( A = \displaystyle\int_2^0 y(t)x'(t)\ dt \)
\( x'(t) = -2 \)
\( = \displaystyle\int_2^0 (t(t + 3)(-2))\ dt \)
\( = -\displaystyle\int_2^0 (2t^2 + 6t)\ dt \)
Sınırların yer değiştirmesi kuralını uygulayalım.
\( = \displaystyle\int_0^2 (2t^2 + 6t)\ dt \)
İfadenin integralini alalım.
\( = (\dfrac{2t^3}{3} + 3t^2)|_0^2 \)
\( = (\dfrac{2(2)^3}{3} + 3(2)^2) - (\dfrac{2(0)^3}{3} + 3(0)^2) \)
\( = (\dfrac{16}{3} + 12) - 0 = \dfrac{52}{3} \) bulunur.

Yukarıdaki eğrinin parametrik denklemi aşağıda verilmiştir.
\( t \ge 0 \) olmak üzere,
\( x(t) = t^2 \)
\( y(t) = 4t - t^2 \)
Eğri ile \( x \) ekseni arasında kalan taralı alanın \( x \) ekseni etrafında 360° döndürülmesi ile oluşan cismin hacmini bulunuz.
Çözümü GösterÖnce eğrinin \( x \) eksenini kestiği noktaları bulalım.
Eğrinin \( x \) eksenini kestiği noktalarda ordinat sıfır olur.
\( y(t) = 0 \)
\( 4t - t^2 = 0 \)
\( t(4 - t) = 0 \)
\( t = 0 \) ya da \( t = 4 \)
\( t = 0 \) için:
\( x(0) = 0^2 = 0 \)
\( t = 4 \) için:
\( x(1) = 4^2 = 16 \)
Buna göre eğri \( x \) eksenini \( O(0, 0) \) ve \( A(16, 0) \) noktalarında keser.
Buna göre taralı alan \( t = 0 \) ve \( t = 4 \) değerleri arasında oluşan eğrinin altında kalan alana karşılık gelir.
Parametrik denklemlerin hacim formülünü yazalım.
\( x = x(t), y = y(t) \) olmak üzere,
\( 0 \le t \le 4 \) aralığında \( x \) ekseni etrafında döndürülen cismin hacmi:
\( V = \pi\displaystyle\int_0^4 [y(t)]^2x'(t)\ dt \)
\( x'(t) = 2t \)
\( = \pi\displaystyle\int_0^4 (4t - t^2)^2 \cdot 2t\ dt \)
\( = \pi\displaystyle\int_0^4 (16t^2 - 8t^3 + t^4) \cdot 2t\ dt \)
\( = \pi\displaystyle\int_0^4 (32t^3 - 16t^4 + 2t^5)\ dt \)
İfadenin integralini alalım.
\( = \pi \cdot (8t^4 - \dfrac{16t^5}{5} + \dfrac{t^6}{3})|_0^4 \)
\( = \pi \cdot [(8(4)^4 - \dfrac{16(4)^5}{5} + \dfrac{4^6}{3}) - (8(0)^4 - \dfrac{16(0)^5}{5} + \dfrac{0^6}{3})] \)
\( = \pi \cdot [(2048 - \dfrac{16384}{5} + \dfrac{4096}{3}) - 0] \)
\( = \dfrac{2048\pi}{15} \) bulunur.
Yukarıdaki eğrinin parametrik denklemi aşağıda verilmiştir.
\( 0 \le t \le 2\pi \) olmak üzere,
\( x(t) = 2\sin{t} \)
\( y(t) = t^2 \)
Eğri ile \( y \) ekseni arasında kalan taralı alanın \( y \) ekseni etrafında 360° döndürülmesi ile oluşan cismin hacmini bulunuz.
Çözümü GösterÖnce eğrinin \( y \) eksenini kestiği noktaları bulalım.
Eğrinin \( y \) eksenini kestiği noktalarda apsis sıfır olur.
\( x(t) = 2\sin{t} = 0 \)
\( t \in \{-\pi, 0, \pi\} \)
\( y(-\pi) = \pi^2 \)
\( y(0) = 0^2 = 0 \)
\( y(\pi) = \pi^2 \)
Buna göre eğri \( y \) eksenini \( t = -\pi \) değerinde \( (0, \pi^2) \) noktasında, \( t = 0 \) değerinde \( (0, 0) \) noktasında ve \( t = \pi \) değerinde tekrar \( (0, \pi^2) \) noktasında keser.
Eğrinin yönünü bulmak için \( t \)'ye ara değerler verelim.
\( x(-\frac{\pi}{2}) = 2\sin(-\frac{\pi}{2}) = -2 \)
\( y(-\frac{\pi}{2}) = (-\dfrac{\pi}{2})^2 = \dfrac{\pi^2}{4} \)
\( x(\frac{\pi}{2}) = 2\sin{\frac{\pi}{2}} = 2 \)
\( y(\frac{\pi}{2}) = (\dfrac{\pi}{2})^2 = \dfrac{\pi^2}{4} \)
Buna göre istenen hacim eğrinin \( t \in [0, \pi] \) aralığında \( y \) ekseni ile arasında kalan alanın \( y \) ekseni etrafında 360° döndürülmesi ile elde edilir.
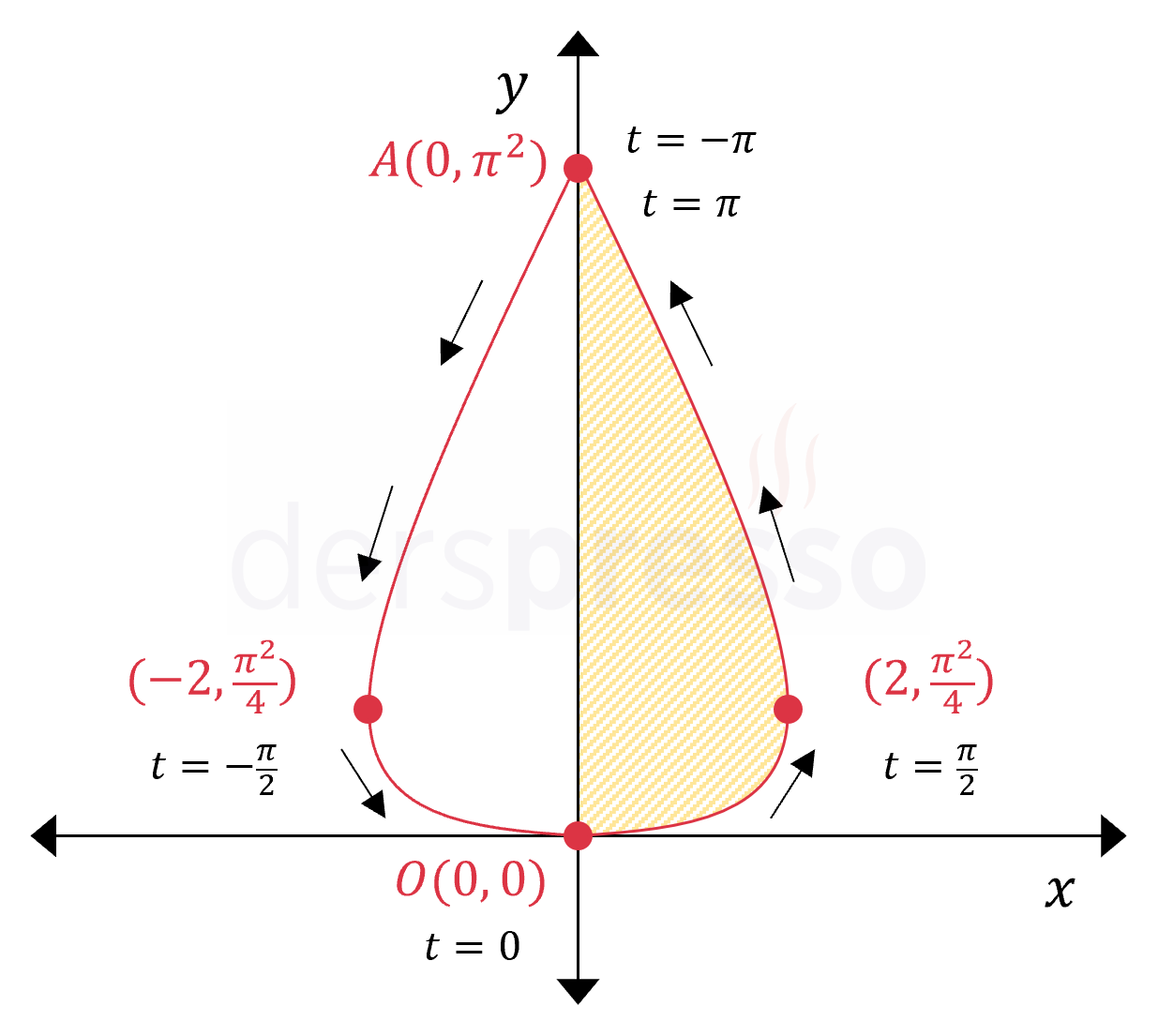
Parametrik denklemlerin \( y \) ekseni için hacim formülünü yazalım.
\( V = \pi\displaystyle\int_0^{\pi} [x(t)]^2 \cdot y'(t)\ dt \)
\( y'(t) = 2t \)
\( = \pi\displaystyle\int_0^{\pi} (2\sin{t})^2 \cdot 2t\ dt \)
\( = 8\pi\displaystyle\int_0^{\pi} t\sin^2{t}\ dt \)
Kosinüs iki kat açı özdeşliğini kullanalım.
\( \cos(2t) = 1 - 2\sin^2{t} \)
\( \sin^2{t} = \dfrac{1 - \cos(2t)}{2} \)
\( = 8\pi\displaystyle\int_0^{\pi} t(\dfrac{1 - \cos(2t)}{2})\ dt \)
\( = 4\pi\displaystyle\int_0^{\pi} t\ dt - 4\pi\displaystyle\int_0^{\pi} t\cos(2t)\ dt \)
Birinci terimin integralini alalım.
\( = 4\pi \cdot (\dfrac{t^2}{2})|_0^{\pi} - 4\pi\displaystyle\int_0^{\pi} t\cos(2t)\ dt \)
\( = 4\pi(\dfrac{\pi^2}{2} - \dfrac{0^2}{2}) - 4\pi\displaystyle\int_0^{\pi} t\cos(2t)\ dt \)
\( = 2\pi^3 - 4\pi\displaystyle\int_0^{\pi} t\cos(2t)\ dt \)
İkinci terimin integralini almak için kısmi integral alma yöntemini kullanalım.
\( u \) ve \( dv \) ifadelerini aşağıdaki gibi belirleyelim.
\( u = t \)
\( dv = \cos(2t)\ dt \)
Buna göre \( du \) ve \( v \) aşağıdaki gibi olur.
\( du = dt \)
\( v = \dfrac{\sin(2t)}{2} \)
Değişkenleri kısmi integral formülünde yerine koyalım.
\( \displaystyle\int {u\ dv} = u\ v - \displaystyle\int {v\ du} \)
\( = 2\pi^3 - 4\pi [(t \cdot \dfrac{\sin(2t)}{2})|_0^{\pi} - \displaystyle\int_0^{\pi} \dfrac{1}{2} \cdot \sin(2t)\ dt] \)
Son terimin integralini alalım.
\( = 2\pi^3 - 4\pi [(t \cdot \dfrac{\sin(2t)}{2})|_0^{\pi} - (-\dfrac{\cos(2t)}{4})|_0^{\pi}] \)
\( = 2\pi^3 - 4\pi [(\pi \cdot \dfrac{\sin(2\pi)}{2} - 0 \cdot \dfrac{\sin{0}}{2}) + (\dfrac{\cos(2\pi)}{4} - \dfrac{\cos{0}}{4})] \)
\( = 2\pi^3 - 4\pi [(\pi \cdot \dfrac{0}{2} - 0 \cdot \dfrac{0}{2}) + (\dfrac{1}{4} - \dfrac{1}{4})] \)
\( = 2\pi^3 \) bulunur.

Yukarıdaki eğrinin parametrik denklemi aşağıda verilmiştir.
\( t \in \mathbb{R} \) olmak üzere,
\( x(t) = t^2 + 2t \)
\( y(t) = t^3 - 16t \)
Eğrinin eksenlerle arasında kalan taralı alanı bulunuz.
Çözümü GösterÖnce eğrinin \( y \) eksenini kestiği noktaları bulalım.
Eğrinin \( y \) eksenini kestiği noktalarda apsis sıfır olur.
\( x(t) = 0 \)
\( t(t + 2) = 0 \)
\( t = 0 \) ya da \( t = -2 \)
\( y(0) = 0^3 - 16(0) = 0 \)
\( y(-2) = (-2)^3 - 16(-2) = 24 \)
Buna göre eğri \( y \) eksenini \( t = 0 \) değerinde \( (0, 0) \) noktasında ve \( t = -2 \) değerinde \( (0, 24) \) noktasında keser.
Eğrinin \( x \) eksenini kestiği noktaları bulalım.
Eğrinin \( x \) eksenini kestiği noktalarda ordinat sıfır olur.
\( y(t) = 0 \)
\( t^3 - 16t = 0 \)
\( t(t - 4)(t + 4) = 0 \)
\( t = 0 \), \( t = 4 \) ya da \( t = -4 \)
\( x(0) = 0^2 + 2(0) = 0 \)
\( x(4) = 4^2 + 2(4) = 24 \)
\( x(-4) = (-4)^2 + 2(-4) = 8 \)
Buna göre eğri \( x \) eksenini \( t = 0 \) değerinde \( (0, 0) \) noktasında, \( t = 4 \) değerinde \( (24, 0) \) noktasında ve \( t = -4 \) değerinde \( (8, 0) \) noktasında keser.
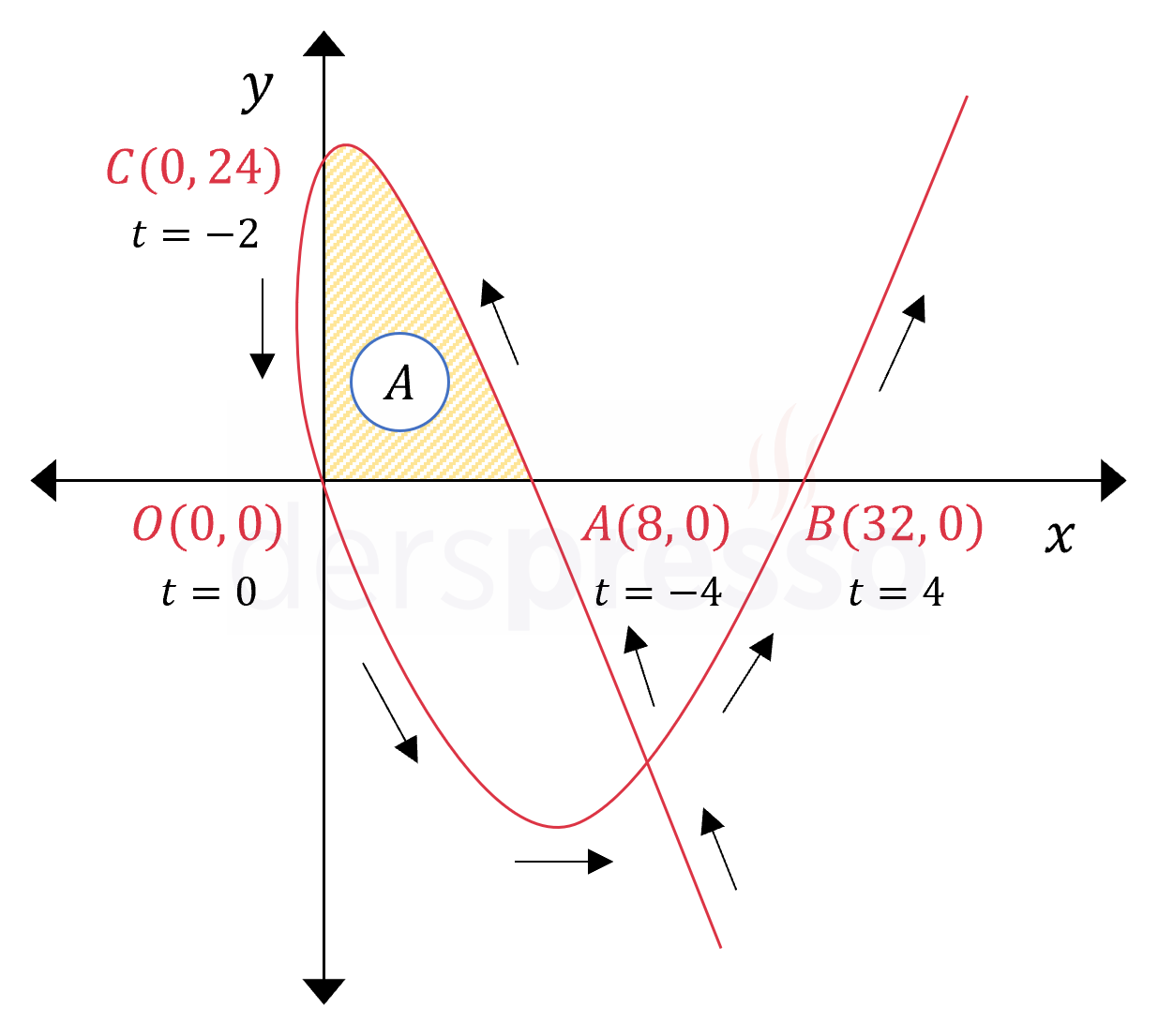
Parametrik denklemlerin alan formülünü yazalım.
Taralı alan \( t = -2 \) ve \( t = -4 \) aralığındaki bölgeye karşılık gelir.
\( x = x(t), y = y(t) \) olmak üzere,
\( -4 \le t \le -2 \) aralığındaki alan:
\( A = \displaystyle\int_{-4}^{-2} y(t)x'(t)\ dt \)
\( x'(t) = 2t + 2 \)
\( = \displaystyle\int_{-2}^{-4} (t^3 - 16t)(2t + 2)\ dt \)
\( = \displaystyle\int_{-2}^{-4} (2t^4 + 2t^3 - 32t^2 - 32t)\ dt \)
İfadenin integralini alalım.
\( = (\dfrac{2t^5}{5} + \dfrac{t^4}{2} - \dfrac{32t^3}{3} - 16t^2)|_{-2}^{-4} \)
\( = (\dfrac{2(-4)^5}{5} + \dfrac{(-4)^4}{2} - \dfrac{32(-4)^3}{3} - 16(-4)^2) - (\dfrac{2(-2)^5}{5} + \dfrac{(-2)^4}{2} - \dfrac{32(-2)^3}{3} - 16(-2)^2) \)
\( = (\dfrac{-2048}{5} + 128 - \dfrac{-2048}{3} - 256) - (\dfrac{-64}{5} + 8 - \dfrac{-256}{3} - 64) \)
\( = (\dfrac{-2048}{5} + 128 - \dfrac{-2048}{3} - 256) - (\dfrac{-64}{5} + 8 - \dfrac{-256}{3} - 64) \)
\( = \dfrac{2176}{15} - \dfrac{248}{15} \)
\( = \dfrac{1928}{15} \) bulunur.