Parametrik Denklemlerin Türevi
\( (x(t), y(t)) \) formundaki bir parametrik eğride aşağıdaki üç temel türevden bahsedilebilir.
| Türev | Açıklama |
|---|---|
| \( dx/dt \) | \( t \) parametresindeki değişime göre \( x \) koordinatının anlık değişim hızı. \( t \) zamanı temsil ediyorsa hareket eden noktanın hızının yatay bileşeni. |
| \( dy/dt \) | \( t \) parametresindeki değişime göre \( y \) koordinatının anlık değişim hızı. \( t \) zamanı temsil ediyorsa hareket eden noktanın hızının düşey bileşeni. |
| \( dy/dx \) | \( x \) değişkenindeki değişime göre \( y \) değişkeninin anlık değişim hızı. Bir diğer ifadeyle, parametrik eğriye ilgili noktada çizilen teğet doğrunun eğimi. |
Aşağıdaki \( (\cos{t}, \sin{t}) \) eğrisi ışığında, bu üç türev işaretlerine göre aşağıdaki şekilde yorumlanabilir.
- \( dx/dt \gt 0 \) ise eğri üzerindeki noktanın hareketi sağa doğru, \( dx/dt \lt 0 \) ise sola doğrudur, \( dx/dt = 0 \) ise noktanın yatay yönde hareketi yoktur. Ek olarak \( dy/dt \ne 0 \) ise nokta yalnızca düşey yönde hareket eder ve eğrinin teğeti o noktada düşeydir.
- \( dy/dt \gt 0 \) ise eğri üzerindeki noktanın hareketi yukarıya doğru, \( dy/dt \lt 0 \) ise aşağıya doğrudur, \( dy/dt = 0 \) ise noktanın düşey yönde hareketi yoktur. Ek olarak \( dx/dt \ne 0 \) ise nokta yalnızca yatay yönde hareket eder ve eğrinin teğeti o noktada yataydır.
- \( dx/dt \) ve \( dy/dt \) aynı işaretli olduğunda \( x \) ve \( y \) birlikte artar ya da azalır (örnekte II. ve IV. bölgeler). Bunun sonucu olarak eğri artan ve \( dy/dx \) pozitif olur (eğriye bu noktada çizilen teğet doğrunun eğimi pozitif olur).
- \( dx/dt \) ve \( dy/dt \) ters işaretli olduğunda \( x \) artarken \( y \) azalır ya da tersi olur (örnekte I. ve III. bölgeler). Bunun sonucu olarak eğri azalan ve \( dy/dx \) negatif olur (eğriye bu noktada çizilen teğet doğrunun eğimi negatif olur).
- \( dx/dt \) ve \( dy/dt \) türevlerinin işareti hareketin yönüne bağlıdır, \( dy/dx \) türevinin işareti ise hareketin yönünden bağımsızdır ve eğriye o noktada teğet olan doğrunun eğimi ile ilgilidir. Buna göre eğrinin hareket yönü tersine çevrilirse \( dx/dt \) ve \( dy/dt \) işaretleri de değişir, ama \( dy/dx \) işareti aynı kalır.
Parametrik Denklemin Birinci Türevi
Bir parametrik denklemde \( y \) değişkeninin \( x \) değişkenine göre türevi (\( \frac{dy}{dx} \)), bu iki değişkenin denklemin parametresine göre türevlerinin (\( \frac{dy}{dt} \) ve \( \frac{dx}{dt} \)) oranına eşittir. Bu türevin belirli bir parametre değerinde tanımlı olması için, her iki koordinat fonksiyonu da bu parametre değerinde türevlenebilir olmalı ve paydada yer alan koordinat fonksiyonunun türevi sıfırdan farklı olmalıdır.
\( dx/dt \ne 0 \) olmak üzere,
\( \dfrac{dy}{dx} = \dfrac{dy/dt}{dx/dt} \)
\( x(t) = t^2 \)
\( y(t) = t^4 - 4t^2 + 5 \)
Parametrik denklemin birinci türevini bulalım.
Pay ve paydadaki türevleri bulalım.
\( \dfrac{dx}{dt} = 2t \)
\( \dfrac{dy}{dt} = 4t^3 - 8t \)
Bulduğumuz ifadeleri türev formülünde yerine koyalım.
\( \dfrac{dy}{dx} = \dfrac{dy/dt}{dx/dt} \)
\( = \dfrac{4t^3 - 8t}{2t} = 2t^2 - 4 \)
İSPATI GÖSTER
\( f \) ve \( g \) fonksiyonları bir \( t = t_0 \) noktası civarında türevlenebilir olmak üzere, aşağıdaki gibi bir parametrik denklem tanımlayalım.
\( x = f(t) \)
\( y = g(t) \)
\( f'(t_0) \ne 0 \) olduğunu varsayalım. Bu durumda \( f \) fonksiyonu \( t = t_0 \) noktası civarında birebirdir ve yerel olarak tersi alınabilir.
\( t = f^{-1}(x) \)
Bu ifadeyi \( y \) koordinat fonksiyonunda yerine koyalım.
\( y = g(f^{-1}(x)) \)
Zincir kuralı ile \( y \) fonksiyonunun türevini alalım.
\( \dfrac{dy}{dx} = g'(f^{-1}(x)) \cdot \dfrac{d}{dx}(f^{-1}(x)) \)
Ters fonksiyon türev kuralını uygulayalım.
\( = g'(f^{-1}(x)) \cdot \dfrac{1}{f'(f^{-1}(x))} \)
\( f^{-1}(x) = t \) yazalım.
\( = g'(t) \cdot \dfrac{1}{f'(t)} \)
\( = \dfrac{g'(t)}{f'(t)} \)
\( = \dfrac{dy/dt}{dx/dt} \)
Bir parametrik denklem kartezyen koordinatları \( (x, y) \) olan belirli bir noktadan birden fazla kez ve farklı parametre değerleri ile geçebileceği için, aynı noktada birden fazla türev değeri oluşabilir.
Aşağıdaki parametrik denklemin birinci türevini bulunuz.
\( x(s) = \sin^3{s} \)
\( y(s) = \cos^3{s} \)
Çözümü GösterÖnce değişkenlerin \( s \) parametresine göre türevini alalım.
\( \dfrac{dx}{ds} = 3\sin^2{s}\cos{s} \)
\( \dfrac{dy}{ds} = -3\cos^2{s}\sin{s} \)
Bulduğumuz ifadeleri türev formülünde yerine koyalım.
\( \dfrac{dy}{dx} = \dfrac{dy/ds}{dx/ds} \)
\( = \dfrac{-3\cos^2{s}\sin{s}}{3\sin^2{s}\cos{s}} \)
\( = -\cot{s} \) bulunur.
\( t \in \mathbb{R} - \{0\} \) olmak üzere,
\( x(t) = \dfrac{1}{2t^2} + \dfrac{1}{t^3} \)
\( y(t) = \dfrac{1}{2t^2} - \dfrac{1}{t^3} \)
olduğuna göre, \( dy/dx \) türevini bulunuz.
Çözümü GösterDenklemleri düzenleyelim.
\( x(t) = \dfrac{t^{-2}}{2} + t^{-3} \)
\( y(t) = \dfrac{t^{-2}}{2} - t^{-3} \)
Değişkenlerin \( t \) parametresine göre türevini alalım.
\( \dfrac{dx}{dt} = \dfrac{(-2) \cdot t^{-3}}{2} + (-3) \cdot t^{-4} \)
\( = -t^{-3} - 3t^{-4} \)
\( \dfrac{dy}{dt} = \dfrac{(-2) \cdot t^{-3}}{2} - (-3) \cdot t^{-4} \)
\( = -t^{-3} + 3t^{-4} \)
Bulduğumuz ifadeleri türev formülünde yerine koyalım.
\( \dfrac{dy}{dx} = \dfrac{dy/dt}{dx/dt} \)
\( = \dfrac{-t^{-3} + 3t^{-4}}{-t^{-3} - 3t^{-4}} \)
\( = \dfrac{-t^{-4}(t - 3)}{-t^{-4}(t + 3)} \)
\( = \dfrac{t - 3}{t + 3} \) bulunur.
\( u = \ln{\tan{x}} \)
\( v = \sqrt{\cos{x}} \)
olduğuna göre, \( du/dv \) türevini bulunuz.
Çözümü Göster\( x \) parametresine bağlı iki fonksiyondan \( u \)'nun \( v \)'ye göre türevi, bu fonksiyonların \( x \)'e göre türevlerinin oranına eşittir.
\( \dfrac{du}{dv} = \dfrac{du/dx}{dv/dx} \)
\( u \) değişkeninin \( x \) değişkenine göre türevini alalım.
\( \dfrac{du}{dx} = \dfrac{(\tan{x})'}{\tan{x}} \)
\( = \dfrac{\frac{1}{\cos^2{x}}}{\frac{\sin{x}}{\cos{x}}} \)
\( = \dfrac{1}{\sin{x}\cos{x}} \)
\( v \) değişkeninin \( x \) değişkenine göre türevini alalım.
\( \dfrac{dv}{dx} = \dfrac{(\cos{x})'}{2\sqrt{\cos{x}}} \)
\( = -\dfrac{\sin{x}}{2\sqrt{\cos{x}}} \)
Bulduğumuz ifadeleri türev formülünde yerine koyalım.
\( \dfrac{du}{dv} = \dfrac{du/dx}{dv/dx} \)
\( = \dfrac{\frac{1}{\sin{x}\cos{x}}}{-\frac{\sin{x}}{2\sqrt{\cos{x}}}} \)
\( = -\dfrac{2}{\sin^2{x}\sqrt{\cos{x}}} \)
\( = -\dfrac{2\csc^2{x}}{\sqrt{\cos{x}}} \) bulunur.
\( x^5 \) ifadesinin \( x^2 \) ifadesine göre türevi nedir?
Çözümü Göster\( x \) değişkenine bağlı iki değişken tanımlayalım.
\( u = x^5, \quad v = x^2 \)
Elde ettiğimiz denklem, \( x \) değişkenine bağlı \( u \) ve \( v \) değişkenlerinden oluşan bir parametrik denklemdir.
Soruda parametrik denklemin \( u \) değişkeninin \( v \) değişkenine göre türevi istenmektedir. Bu türev \( \frac{du}{dv} \) şeklinde ifade edilir.
Parametrik denklemlerin türev formülü aşağıdaki gibidir.
\( \dfrac{du}{dv} = \dfrac{du/dx}{dv/dx} \)
Değişkenlerin \( x \)'e göre türevini alalım.
\( \dfrac{du}{dx} = 5x^4 \)
\( \dfrac{dv}{dx} = 2x \)
Bulduğumuz ifadeleri türev formülünde yerine koyalım.
\( \dfrac{du}{dv} = \dfrac{5x^4}{2x} = \dfrac{5x^3}{2} \)
\( y = 3^{x^3} \) olduğuna göre,
\( \dfrac{d(y^2)}{d(x^2)} \) ifadesinin eşiti nedir?
Çözümü Göster\( y^2 \) ve \( x^2 \) ifadelerini parametrik denklem şeklinde tanımlayalım.
\( u = y^2, \quad v = x^2 \)
\( \dfrac{d(y^2)}{d(x^2)} = \dfrac{du}{dv} \)
\( x \) parametresine bağlı iki fonksiyondan \( u \)'nun \( v \)'ye göre türevi, bu fonksiyonların \( x \)'e göre türevlerinin oranına eşittir.
\( = \dfrac{du/dx}{dv/dx} \)
\( u \) değişkeninin \( x \) değişkenine göre türevini alalım.
\( \dfrac{du}{dx} = \dfrac{d(y^2)}{dx} \)
\( = \dfrac{d(y^2)}{dy} \cdot \dfrac{dy}{dx} \)
\( = 2y \cdot (3^{x^3} \cdot 3x^2 \cdot \ln{3}) \)
\( y = 3^{x^3} \) yazalım.
\( = 2 \cdot 3^{x^3} \cdot 3^{x^3} \cdot 3x^2 \cdot \ln{3} \)
\( = 6x^2 \cdot 3^{2x^3} \cdot \ln{3} \)
\( v \) değişkeninin \( x \) değişkenine göre türevini alalım.
\( \dfrac{dv}{dx} = \dfrac{d(x^2)}{dx} \)
\( = 2x \)
Bulduğumuz ifadeleri türev formülünde yerine koyalım.
\( \dfrac{d(y^2)}{d(x^2)} = \dfrac{du/dx}{dv/dx} \)
\( = \dfrac{6x^2 \cdot 3^{2x^3} \cdot \ln{3}}{2x} \)
\( = 3x \cdot 3^{2x^3} \cdot \ln{3} \) bulunur.
Teğet ve Normal Doğrular
Türevin eğim anlamı parametrik denklemler için de geçerlidir. Buna göre \( (x(t), y(t)) \) parametrik eğrisine \( t = a \) değerindeki \( (x(a), y(a)) \) noktasında çizilen teğet doğrunun eğimi, \( dy/dx \) türevinin \( t = a \) için değerine eşittir.
Aşağıda denklemi verilen parametrik eğriye \( t = \frac{\pi}{4} \) değerinin karşılık geldiği noktada çizilen teğet doğrunun denklemini bulalım.
\( x(t) = 4\cos{t} \)
\( y(t) = 3\sin{t} \)
Değişkenlerin \( t \) parametresine göre türevini alalım.
\( \dfrac{dx}{dt} = -4\sin{t} \)
\( \dfrac{dy}{dt} = 3\cos{t} \)
Değişkenlerin birbirine göre türevini alalım.
\( \dfrac{dy}{dx} = \dfrac{3\cos{t}}{-4\sin{t}} = -\dfrac{3\cot{t}}{4} \)
Türev ifadesinde \( t = \frac{\pi}{4} \) koyarak eğrinin ilgili noktadaki eğimini bulalım.
\( \dfrac{dy}{dx}|_{t = \frac{\pi}{4}} = -\dfrac{3\cot{\frac{\pi}{4}}}{4} = -\dfrac{3}{4} \)
\( t = \frac{\pi}{4} \) değerinin karşılık geldiği \( (x, y) \) noktasını bulalım.
\( x\left( \dfrac{\pi}{4} \right) = 4\cos{\dfrac{\pi}{4}} = \dfrac{4\sqrt{2}}{2} = 2\sqrt{2} \)
\( y\left( \dfrac{\pi}{4} \right) = 3\sin{\dfrac{\pi}{4}} = \dfrac{3\sqrt{2}}{2} \)
\( (2\sqrt{2}, \frac{3\sqrt{2}}{2}) \) noktasından geçen ve eğimi \( -\frac{3}{4} \) olan doğrunun denklemini bulalım.
\( y - \dfrac{3\sqrt{2}}{2} = -\dfrac{3}{4}(x - 2\sqrt{2}) \)
\( y = -\dfrac{3}{4}x + 3\sqrt{2} \)
Parametrik eğrinin grafiği ve bu noktadaki teğeti aşağıdaki şekilde gösterilmiştir.
Bir parametrik eğriye çizilen teğet doğrular, \( dy/dx \) türevinin sıfır olduğu noktalarda yatay olur. Bu noktalarda \( dy/dt \) türevi (hareketin düşey hızı) sıfır, \( dx/dt \) türevi (hareketin yatay hızı) sıfırdan farklı olur. Bu noktalar eğrinin yatay durağan noktalarıdır.
\( \dfrac{dy}{dx} = \dfrac{dy/dt}{dx/dt} = 0 \)
\( \dfrac{dy}{dt} = 0, \quad \dfrac{dx}{dt} \ne 0 \)
Yukarıdaki koşul yatay teğet doğru için gerekli değil, yeterli bir koşuldur. Bir örnek olarak, \( (x(t), y(t)) = (t^3, t^6) \) eğrisi yukarıdaki koşulu sağlamasa da eğriye \( t = 0 \) noktasında çizilen teğet doğru yataydır.
Bir parametrik eğriye çizilen teğet doğrular, \( dx/dy \) türevinin sıfır olduğu noktalarda düşey olur. Bu noktalarda \( dx/dt \) türevi (hareketin yatay hızı) sıfır, \( dy/dt \) türevi (hareketin düşey hızı) sıfırdan farklı olur.
\( \dfrac{dx}{dy} = \dfrac{dx/dt}{dy/dt} = 0 \)
\( \dfrac{dx}{dt} = 0, \quad \dfrac{dy}{dt} \ne 0 \)
Yukarıdaki koşul düşey teğet doğru için gerekli değil, yeterli bir koşuldur. Bir örnek olarak, \( (x(t), y(t)) = (t^6, t^3) \) eğrisi yukarıdaki koşulu sağlamasa da eğriye \( t = 0 \) noktasında çizilen teğet doğru düşeydir.
Aşağıdaki parametrik denklemin yatay durağan noktalarını bulalım.
\( x(t) = -t^2 + 2t + 9 \)
\( y(t) = 3t^4 - 4t^3 - 12t^2 + 15 \)
Değişkenlerin parametreye göre türevini alalım.
\( \dfrac{dx}{dt} = -2t + 2 \)
\( \dfrac{dy}{dt} = 12t^3 - 12t^2 - 24t \)
\( = 12t(t - 2)(t + 1) \)
Bulduğumuz ifadeleri türev formülünde yerine koyalım.
\( \dfrac{dy}{dx} = \dfrac{dy/dt}{dx/dt} \)
\( = \dfrac{12t(t - 2)(t + 1)}{-2(t - 1)} \)
Eğrinin yatay durağan noktaları birinci türev sıfır olduğunda oluşur.
\( \dfrac{dy}{dx} = 0 \)
Bu koşul \( y \) değişkeninin \( t \) parametresine göre türevi sıfırken \( x \) değişkeninin \( t \) parametresine göre türevinin sıfırdan farklı olmasını gerektirir.
\( \dfrac{dy}{dt} = 0, \quad \dfrac{dx}{dt} \ne 0 \)
\( 12t(t + 1)(t - 2) = 0 \)
\( t \in \{ -1, 0, 2 \} \)
Bu \( t \) değerlerinden hiçbiri \( \frac{dx}{dt} \) ifadesini sıfır yapmadığı için eğrinin \( t = -1 \), \( t = 0 \) ve \( t = 2 \) değerlerinde yatay durağan noktaları vardır.
Bu \( t \) değerlerinde oluşan \( (x, y) \) noktalarını bulalım.
\( t = -1 \) için:
\( x(-1) = -(-1)^2 + 2(-1) + 9 = 6 \)
\( y(-1) = 3(-1)^4 - 4(-1)^3 - 12(-1)^2 + 15 = 10 \)
\( t = 0 \) için:
\( x(0) = -(0)^2 + 2(0) + 9 = 9 \)
\( y(0) = 3(0)^4 - 4(0)^3 - 12(0)^2 + 15 = 15 \)
\( t = 2 \) için:
\( x(2) = -(2)^2 + 2(2) + 9 = 9 \)
\( y(2) = 3(2)^4 - 4(2)^3 - 12(2)^2 + 15 = -17 \)
Buna göre \( t = -1 \) değerindeki \( (6, 10) \), \( t = 0 \) değerindeki \( (9, 15) \) ve \( t = 2 \) değerindeki \( (9, -17) \) noktaları eğrinin yatay durağan noktalarıdır.
Parametrik eğrinin grafiği ve yatay durağan noktaları aşağıdaki şekilde gösterilmiştir.
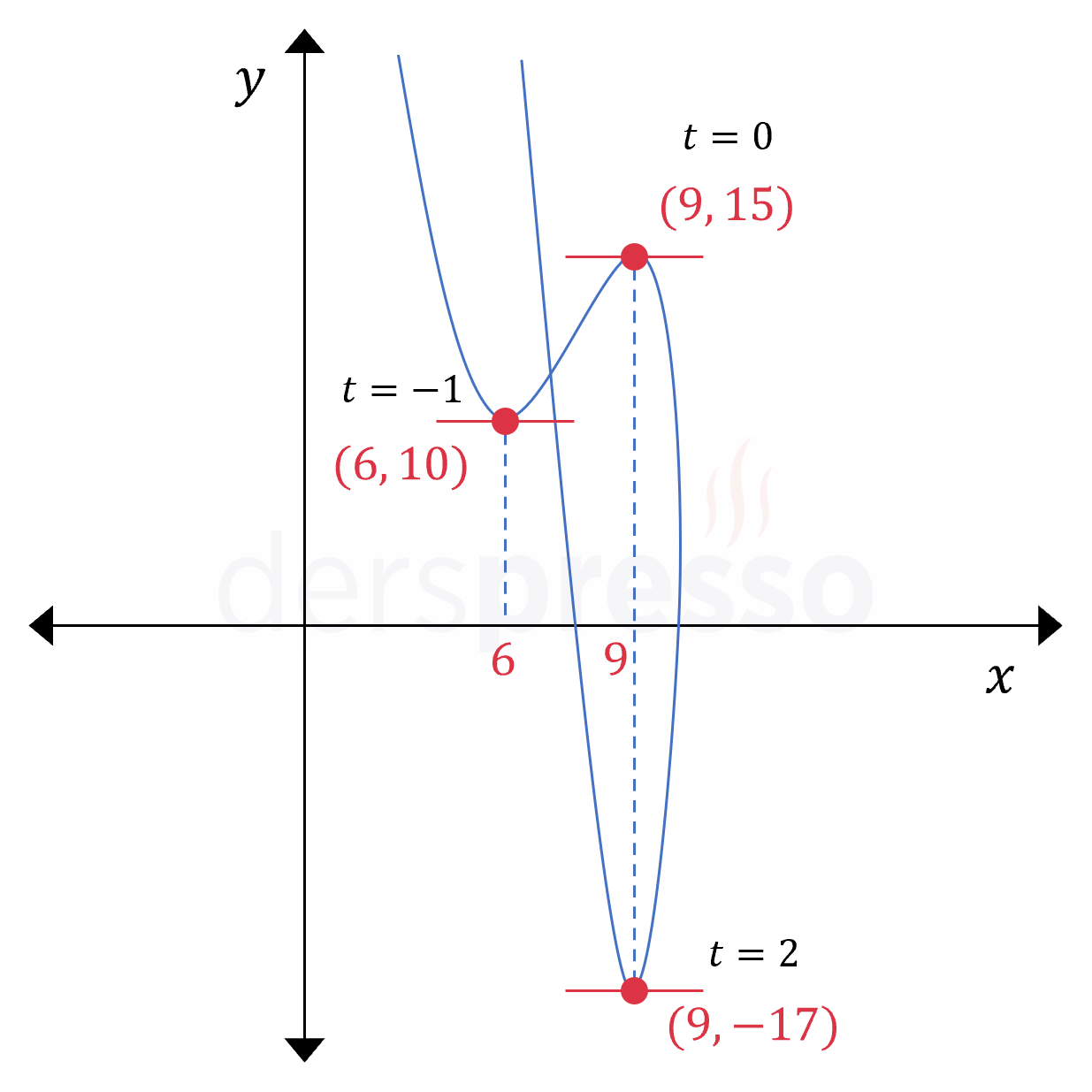
Dikkat edilirse \( x = 9 \) noktasında farklı \( t \) değerleri için birbirinden farklı iki yatay durağan nokta oluşmuştur.
Bir parametrik eğriye belirli bir noktada çizilen normal doğru, bu noktadan geçen ve bu noktadaki teğet doğruyu dik kesen doğrudur.
Minimum ve Maksimum Değerler
Bir parametrik eğride, \( x(t) \)'nin mutlak minimum ve maksimum değerleri geometrik olarak eğrinin en soldaki ve en sağdaki noktalarına, \(y(t) \)'nin mutlak minimum ve maksimum değerleri ise en alttaki ve en üstteki noktalarına karşılık gelir.
Parametrik bir eğrinin \( x \) ve \( y \) koordinatlarının yerel ve mutlak ekstremum değerleri, türev konusunda tek değişkenli fonksiyonlar için öğrendiğimiz yöntemler \( x(t) \) ve \( y(t) \) fonksiyonlarına ayrı ayrı uygulanarak belirlenebilir. Buna göre;
- \( x \) koordinatının yerel ekstremum değerlerini bulmak için öncelikle \( \frac{dx}{dt} \) türevinin sıfır ya da tanımsız olduğu kritik \( t \) değerleri bulunur.
- Birinci (\( \frac{dx}{dt} \)) ya da ikinci (\( \frac{d^2x}{dt^2} \)) türev testi kullanılarak bu kritik değerler yerel minimum ya da maksimum olarak ayrılır.
- \( x(t) \) sürekli ve \( t \) değer aralığı sınırlı ve kapalı ise kritik noktalardaki ve aralığın uç noktalarındaki \( x \) değerleri karşılaştırılarak \( x(t) \) fonksiyonunun mutlak minimum ve maksimum değerleri belirlenir. \( t \) aralığı açık ya da sınırsızsa uç noktalardaki limitler incelenir.
- Aynı işlem \( y(t) \) fonksiyonu için tekrarlanır.
Yukarıdaki işlemlerdeki fonksiyonların ve türevlerinin \( t \) cinsinden olduğuna dikkat edilmelidir.
Aşağıdaki parametrik eğrinin \( x \) ve \( y \) koordinatlarının yerel ve mutlak ekstremumlarını bulalım.
\( -3 \le t \le 3 \) olmak üzere,
\( x(t) = t^3 - 3t \)
\( y(t) = t^3 - 12t \)
\( x \) koordinatının yerel ekstremumlarını bulalım.
Yerel ekstremumların oluşabileceği kritik \( t \) değerlerini bulmak için koordinat fonksiyonunun türevinin sıfır ya da tanımsız olduğu değerler belirlenir.
\( \dfrac{dx}{dt} = 3t^2 - 3 = 0 \)
\( t \in \{ -1, 1 \} \)
Kritik noktaların yerel minimum mu yerel maksimum mu olduğunu anlamak için ikinci türev testini kullanalım.
Bir kritik \( t \) değerinde ikinci türev pozitifse koordinat fonksiyonu yerel minimum, negatifse yerel maksimum değer alır.
\( \dfrac{d^2x}{dt^2} = 6t \)
\( \dfrac{d^2x}{dt^2}\Bigg|_{t=-1} = 6(-1) = -6 \lt 0 \)
\( \dfrac{d^2x}{dt^2}\Bigg|_{t=1} = 6(1) = 6 \gt 0 \)
Buna göre \( x(t) \) fonksiyonu \( t = -1 \) değerinde yerel maksimum, \( t = 1 \) değerinde yerel minimum değeri alır.
Bu \( t \) değerlerindeki \( (x, y) \) koordinatlarını bulalım.
\( t = -1 \) için:
\( x(-1) = (-1)^3 - 3(-1) = 2 \)
\( y(-1) = (-1)^3 - 12(-1) = 11 \)
\( x \) koordinatının yerel maksimum olduğu nokta: \( (2, 11) \)
\( t = 1 \) için:
\( x(1) = 1^3 - 3(1) = -2 \)
\( y(1) = 1^3 - 12(1) = -11 \)
\( x \) koordinatının yerel minimum olduğu nokta: \( (-2, -11) \)
\( t \) tanım aralığının uç değerlerindeki \( (x, y) \) koordinatlarını bulalım.
\( t = -3 \) için:
\( x(-3) = (-3)^3 - 3(-3) = -18 \)
\( y(-3) = (-3)^3 - 12(-3) = 9 \)
\( t = 3 \) için:
\( x(3) = 3^3 - 3(3) = 18 \)
\( y(3) = 3^3 - 12(3) = -9 \)
\( t \in \{ -3, -1, 1, 3 \} \) değerlerindeki \( x \) değerlerini karşılaştırdığımızda \( x(t) \) fonksiyonu için aşağıdaki mutlak ekstremum noktalarını buluruz.
\( x \) koordinatının mutlak minimum olduğu nokta: \( (-18, 9) \)
\( x \) koordinatının mutlak maksimum olduğu nokta: \( (18, -9) \)
\( y \) koordinatının yerel ekstremumlarını bulalım.
\( \dfrac{dy}{dt} = 3t^2 - 12 = 0 \)
\( t \in \{ -2, 2 \} \)
Kritik noktaların yerel minimum mu yerel maksimum mu olduğunu anlamak için ikinci türev testini kullanalım.
\( \dfrac{d^2y}{dt^2} = 6t \)
\( \dfrac{d^2y}{dt^2}\Bigg|_{t=-2} = 6(-2) = -12 \lt 0 \)
\( \dfrac{d^2y}{dt^2}\Bigg|_{t=2} = 6(2) = 12 \gt 0 \)
Buna göre \( y(t) \) fonksiyonu \( t = -2 \) değerinde yerel maksimum, \( t = 2 \) değerinde yerel minimum değeri alır.
Bu \( t \) değerlerindeki \( (x, y) \) koordinatlarını bulalım.
\( t = -2 \) için:
\( x(-2) = (-2)^3 - 3(-2) = -2 \)
\( y(-2) = (-2)^3 - 12(-2) = 16 \)
\( y \) koordinatının yerel maksimum olduğu nokta: \( (-2, 16) \)
\( t = 2 \) için:
\( x(2) = 2^3 - 3(2) = 2 \)
\( y(2) = 2^3 - 12(2) = -16 \)
\( y \) koordinatının yerel minimum olduğu nokta: \( (2, -16) \)
\( t \) tanım aralığının uç değerlerindeki \( (x, y) \) koordinatlarını yukarıda bulmuştuk.
\( t \in \{ -3, -2, 2, 3 \} \) değerlerindeki \( y \) değerlerini karşılaştırdığımızda \( y(t) \) fonksiyonu için aşağıdaki mutlak ekstremum noktalarını buluruz.
Mutlak minimum: \( (2, -16) \)
Mutlak maksimum: \( (-2, 16) \)
Parametrik eğrinin grafiği ve \( x \) ve \( y \) koordinatları için yerel ve mutlak ekstremum noktaları aşağıdaki şekilde gösterilmiştir.
Parametrik Denklemin İkinci Türevi
Bir parametrik denklemde \( y \) değişkeninin \( x \) değişkenine göre ikinci türevi (\( \frac{d^2y}{dx^2} \)), birinci türevin aynı formülle tekrar türevi alınarak elde edilir.
\( dx/dt \ne 0 \) olmak üzere,
\( \dfrac{d^2y}{dx^2} = \dfrac{\frac{d}{dt} (\frac{dy}{dx})}{\frac{dx}{dt}} \)
\( x(t) = t^2 \)
\( y(t) = t^4 - 4t^2 + 5 \)
Yukarıda bu parametrik denklemin birinci türevini aşağıdaki gibi bulmuştuk.
\( \dfrac{dy}{dx} = 2t^2 - 4 \)
Denklemin ikinci türevini bulalım.
Pay ve paydadaki türevleri bulalım.
\( \dfrac{d}{dt} \left(\dfrac{dy}{dx}\right) = 4t \)
\( \dfrac{dx}{dt} = 2t \)
Bulduğumuz ifadeleri türev formülünde yerine koyalım.
\( \dfrac{d^2y}{dx^2} = \dfrac{4t}{2t} = 2 \)
İSPATI GÖSTER
İkinci türev birinci türevin türevine eşittir.
\( \dfrac{d^2y}{dx^2} = \dfrac{d}{dx} \left(\dfrac{dy}{dx}\right) \)
Zincir kuralını uygulayalım.
\( = \dfrac{d}{dt} \left(\dfrac{dy}{dx}\right) \cdot \dfrac{dt}{dx} \)
\( dt/dx \) ifadesinin çarpmaya göre tersini paydaya alalım.
\( = \dfrac{\frac{d}{dt} (\frac{dy}{dx})}{\frac{dx}{dt}} \)
\( x(t) = 3t + 2 \)
\( y(t) = t^2 + 2t \) olduğuna göre,
\( \dfrac{d^2y}{dx^2} \) türevini bulunuz.
Çözümü Göster\( \frac{dy}{dx} \) ifadesi \( y \) değişkeninin \( x \) değişkenine göre birinci türevi, \( \frac{d^2y}{dx^2} \) ifadesi ise ikinci türevidir.
Bir parametrik denklemin birinci türevi aşağıdaki formülle alınır.
\( \dfrac{dy}{dx} = \dfrac{dy/dt}{dx/dt} \)
\( = \dfrac{\frac{d}{dt} (t^2 + 2t)}{\frac{d}{dt} (3t + 2)} \)
\( = \dfrac{2t + 2}{3} = \dfrac{2t}{3} + \dfrac{2}{3} \)
Bir parametrik denklemin ikinci türevi aşağıdaki formülle alınır.
\( \dfrac{d^2y}{dx^2} = \dfrac{\frac{d}{dt}(\frac{dy}{dx})}{\frac{dx}{dt}} \)
\( = \dfrac{\frac{d}{dt}(\frac{2t}{3} + \frac{2}{3})}{\frac{d}{dt} (3t + 2)} \)
\( = \dfrac{\frac{2}{3}}{3} = \dfrac{2}{9} \) bulunur.
\( C \) eğrisinin parametrik denklemi aşağıdaki gibidir.
\( t \in \mathbb{R^+} \) olmak üzere,
\( x(t) = \ln{t} \)
\( y(t) = 6t^3 \)
\( C \) eğrisi üzerindeki bir \( A \) noktasında \( \frac{d^2y}{dx^2} = 432 \) olduğuna göre, \( A \) noktasının koordinatlarını bulunuz.
Çözümü GösterDeğişkenlerin parametreye göre türevini alalım.
\( \dfrac{dx}{dt} = \dfrac{1}{t} \)
\( \dfrac{dy}{dt} = 18t^2 \)
Değişkenlerin birbirine göre birinci türevini bulalım.
\( \dfrac{dy}{dx} = \dfrac{dy/dt}{dx/dt} \)
\( = \dfrac{18t^2}{\frac{1}{t}} = 18t^3 \)
Değişkenlerin birbirine göre ikinci türevini bulalım.
\( \dfrac{d^2y}{dx^2} = \dfrac{\frac{d}{dt}(\frac{dy}{dx})}{\frac{dx}{dt}} \)
\( = \dfrac{\frac{d}{dt} (18t^3)}{\frac{d}{dt} (\ln{t})} = \dfrac{54t^2}{\frac{1}{t}} = 54t^3 \)
\( \dfrac{d^2y}{dx^2} = 432 \) eşitliğini sağlayan \( t \) değerini bulalım.
\( 54t^3 = 432 \)
\( t^3 = 8 \)
\( t = 2 \)
Eğri üzerinde \( t = 2 \) değerindeki noktanın kartezyen koordinatlarını bulalım.
\( x(2) = \ln{2} \)
\( y(2) = 6(2)^3 = 48 \)
\( A \) noktasının koordinatları \( A(\ln{2}, 48) \) olarak bulunur.
Konkavlık ve Büküm Noktaları
Bir parametrik denklem ikinci türevinin pozitif olduğu bir aralıkta yukarı konkavdır, negatif olduğu bir aralıkta ise aşağı konkavdır.
Bir parametrik eğri;
- \( \dfrac{d^2y}{dx^2} \gt 0 \) olan aralıklarda yukarı konkavdır.
- \( \dfrac{d^2y}{dx^2} \lt 0 \) olan aralıklarda aşağı konkavdır.
Sürekli bir parametrik eğrinin farklı aralıklardaki konkavlık durumu aşağıdaki yöntemle bulunur.
- \( \frac{d^2y}{dx^2} \) türevinin sıfır ya da tanımsız olduğu noktalar bulunur.
- Bir işaret tablosu oluşturulur ve birinci maddede bulunan noktaların oluşturduğu aralıkların her birinde ikinci türevin işareti bulunur.
- Eğri ikinci türevin pozitif olduğu aralıklarda yukarı konkav, negatif olduğu aralıklarda aşağı konkavdır.
Bir parametrik eğrinin konkavlık durumunun değiştiği, yani yukarı konkavdan aşağı konkava ya da aşağı konkavdan yukarı konkava döndüğü (bir diğer ifadeyle ikinci türevinin işaret değiştirdiği) noktalara büküm noktası denir. Ek bir koşul olarak, parametrik eğrilerde büküm noktalarında \( \frac{dx}{dt} \) sıfırdan farklı olmalıdır, yani bu noktadaki teğet doğru düşey olmamalıdır.
Sürekli bir parametrik eğrinin büküm noktaları aşağıdaki yöntemle bulunur.
- Eğrinin konkavlık durumu için hazırlanan işaret tablosunda ikinci türevin işaret değiştirdiği \( t \) değerleri bulunur.
- Bu \( t \) değerlerinden \( \frac{dx}{dt} \) türevinin sıfırdan farklı olduğu noktalarda birer büküm noktası oluşur.
Konkavlık geometrik olarak, \( x \)'in artış yönünde eğrinin sola ya da sağa doğru kıvrılması şeklinde yorumlanabilir. Eğri bu yönde izlenirken sola doğru kıvrılıyorsa yukarı konkav, sağa doğru kıvrılıyorsa aşağı konkavdır. Parametrik bir eğride bu yorum yapılırken parametrenin artış yönü değil, \( x \)'in artış yönü dikkate alınmalıdır. Aşağıda bir çemberin farklı bölümlerindeki konkavlık durumu gösterilmiştir.
Aşağıdaki parametrik denklemin aşağı ve yukarı konkav olduğu aralıkları ve büküm noktalarını bulalım.
\( t \in \mathbb{R} \) olmak üzere,
\( x(t) = t^2 + t \)
\( y(t) = t^3 \)
Denklemin birinci türevini bulalım.
\( \dfrac{dy}{dx} = \dfrac{dy/dt}{dx/dt} \)
\( \dfrac{dx}{dt} = 2t + 1 \)
\( \dfrac{dy}{dt} = 3t^2 \)
\( \dfrac{dy}{dx} = \dfrac{3t^2}{2t + 1} \)
Denklemin ikinci türevini bulalım.
\( \dfrac{d^2y}{dx^2} = \dfrac{\frac{d}{dt} (\frac{dy}{dx})}{\frac{dx}{dt}} \)
\( \dfrac{d}{dt} \left( \dfrac{dy}{dx} \right) = \dfrac{d}{dt} \left( \dfrac{3t^2}{2t + 1} \right) \)
\( = \dfrac{6t(2t + 1) - 3t^2(2)}{(2t + 1)^2} \)
\( = \dfrac{6t(t + 1}{(2t + 1)^2} \)
\( \dfrac{d^2y}{dx^2} = \dfrac{\frac{6t(t + 1}{(2t + 1)^2}}{2t + 1} \)
\( = \dfrac{6t(t + 1}{(2t + 1)^3} \)
Bu ifadenin farklı aralıklardaki işaretini bulmak için bir işaret tablosu hazırlayalım.
Eğri ikinci türevin pozitif olduğu aralıklarda yukarı konkav, negatif olduğu aralıklarda aşağı konkavdır.
Yukarı konkav: \( t \in \left( -1, -\dfrac{1}{2} \right) \cup (0, \infty) \)
Aşağı konkav: \( t \in (-\infty, -1) \cup \left( -\dfrac{1}{2}, 0 \right) \)
Eğrinin işaret değiştirdiği \( t \in (-1, \frac{1}{2}, 0) \) değerleri içinde \( t = -\frac{1}{2} \) değerinde \( \frac{dx}{dt} = 0 \) olur, dolayısıyla bu değerde teğet doğru düşeydir ve bir büküm noktası oluşmaz.
Buna göre eğrinin \( t \in (-1, 0) \) değerlerinde büküm noktası vardır.
Büküm noktalarının koordinatlarını bulalım.
\( t = -1 \) için:
\( x(-1) = (-1)^2 + (-1) = 0 \)
\( y(-1) = (-1)^3 = -1 \)
\( t = 0 \) için:
\( x(0) = 0^2 + 0 = 0 \)
\( y(0) = 0^3 = 0 \)
Büküm noktaları: \( (x, y) \in \{ (0, -1), (0, 0) \} \)
Parametrik eğrinin grafiği, yukarı ve aşağı konkav olduğu aralıklar ve büküm noktaları aşağıdaki şekilde gösterilmiştir.
Aşağıdaki parametrik denkleme hangi noktasında çizilen teğet \( y \) eksenine paraleldir?
\( t \in \mathbb{R} \) olmak üzere,
\( x(t) = -t^2 + 2t + 3 \)
\( y(t) = -t^3 + 8t \)
Çözümü GösterBir parametrik eğriye bir noktada çizilen teğetin \( y \) eksenine paralel olması için o noktada \( x \) değişkeninin \( y \) değişkenine göre türevi sıfır olmalıdır.
\( \dfrac{dx}{dy} = \dfrac{dx/dt}{dy/dt} = 0 \)
Bu türev formülünün sıfır olabilmesi için \( \frac{dx}{dt} = 0 \) ve \( \frac{dy}{dt} \ne 0 \) olmalıdır.
\( \dfrac{dx}{dt} = 0 \)
\( -2t + 2 = 0 \)
\( t = 1 \)
Bu değerin \( \frac{dy}{dt} \) ifadesin sıfır yapıp yapmadığını kontrol edelim.
\( \dfrac{dy}{dt} = -3t^2 + 8 \)
\( \dfrac{dy}{dt}|_{t=1} = -3(1)^2 + 8 = 5 \)
Buna göre \( t = 1 \) değerindeki noktada eğriye çizilen teğet \( y \) eksenine paralel olur.
\( t = 1 \) için \( (x, y) \) koordinatlarını bulalım.
\( x(1) = -1^2 + 2(1) + 3 = 4 \)
\( y(1) = -1^3 + 8(1) = 7 \)
Eğriye çizilen teğetin \( y \) eksenine paralel olduğu nokta \( t = 1 \) değerindeki \( (4, 7) \) noktasıdır.
Parametrik eğrinin grafiği ve bu noktada çizilen teğet aşağıdaki şekilde gösterilmiştir.
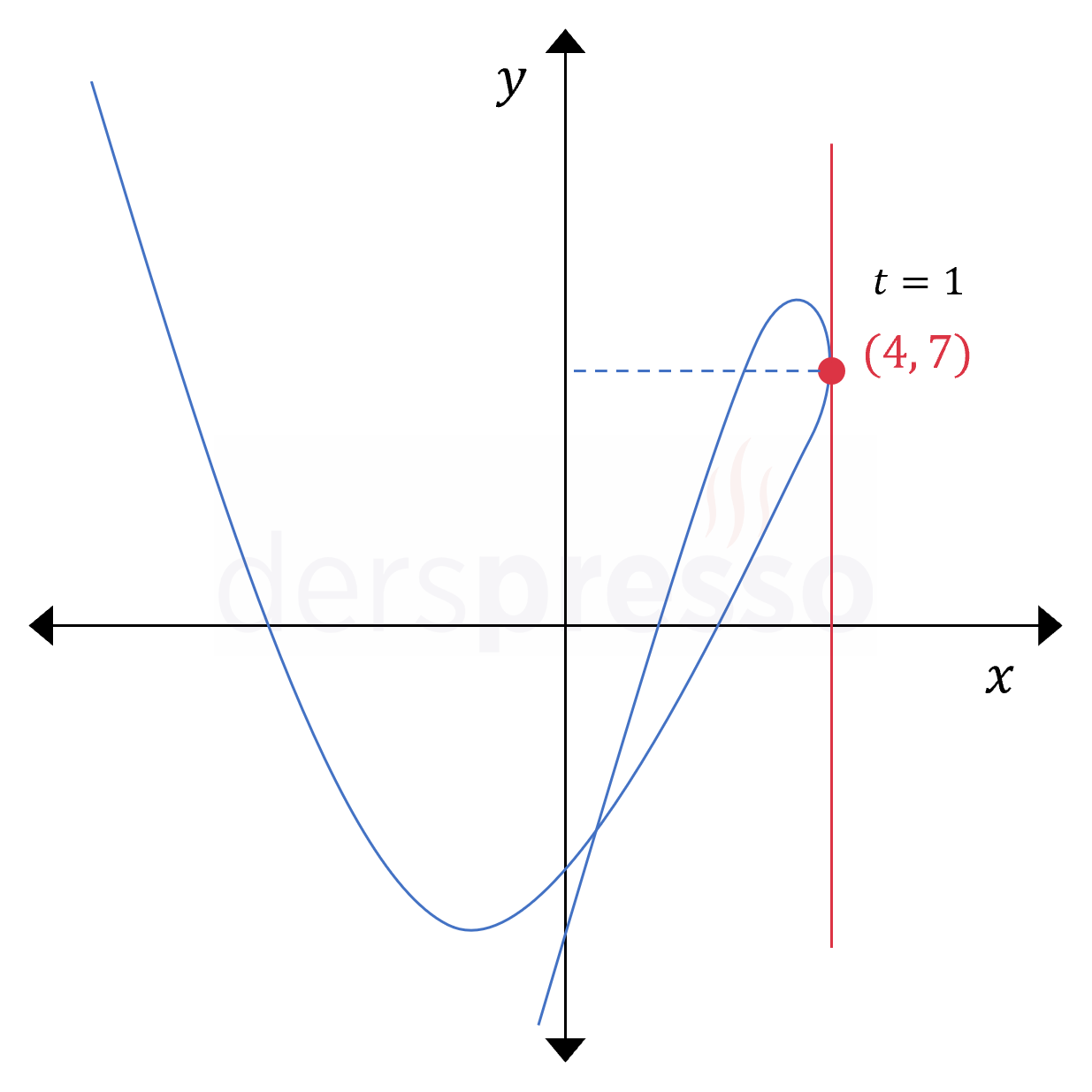
\( C \) eğrisinin parametrik denklemi aşağıda verilmiştir.
\( -\dfrac{1}{2} \lt t \lt \dfrac{1}{2} \) olmak üzere,
\( x(t) = \ln(1 + 2t) \)
\( y(t) = \ln(1 - 2t) \)
\( C \) eğrisi üzerinde eğimi \( -3 \) olan noktanın kartezyen koordinatlarını doğal logaritma cinsinden bulunuz.
Çözümü GösterDeğişkenlerin \( t \) parametresine göre türevini alalım.
\( \dfrac{dx}{dt} = \dfrac{(1 + 2t)'}{1 + 2t} = \dfrac{2}{2t + 1} \)
\( \dfrac{dy}{dt} = \dfrac{(1 - 2t)'}{1 - 2t} = \dfrac{2}{2t - 1} \)
Değişkenlerin birbirine göre türevini alalım.
\( \dfrac{dy}{dx} = \dfrac{dy/dt}{dx/dt} \)
\( = \dfrac{\frac{2}{2t - 1}}{\frac{2}{2t + 1}} = \dfrac{2t + 1}{2t - 1} \)
Bulduğumuz türev ifadesini eğim değeri olan \( -3 \)'e eşitleyelim.
\( \dfrac{2t + 1}{2t - 1} = -3 \)
\( 2t + 1 = -6t + 3 \)
\( 8t = 2 \)
\( t = \dfrac{1}{4} \)
Buna göre eğri üzerinde \( t = \frac{1}{4} \) değerindeki noktada eğim \( -3 \) olur.
Bu \( t \) değerini parametrik denklemde yerine koyarak eğimin \( -3 \) olduğu noktanın kartezyen koordinatlarını bulalım.
\( x\left( \dfrac{1}{4} \right) = \ln\left( 1 + 2 \cdot \dfrac{1}{4} \right) = \ln{\dfrac{3}{2}} \)
\( y\left( \dfrac{1}{4} \right) = \ln\left( 1 - 2 \cdot \dfrac{1}{4} \right) = \ln{\dfrac{1}{2}} \)
İstenen noktanın koordinatları \( (\ln{\frac{3}{2}}, \ln{\frac{1}{2}}) \) olarak bulunur.
\( t \in \mathbb{R} \) olmak üzere,
\( x(t) = t^3 - 5 \)
\( y(t) = 3t^2 + 3t + 7 \)
Yukarıda parametrik denklemi verilen eğrinin durağan noktasındaki ikinci türev değerini bulunuz.
Çözümü GösterBir fonksiyonun birinci türevinin tanımlı ve sıfır olduğu noktalara durağan nokta denir.
Bir parametrik denklemin durağan noktaları kartezyen denklemlerinde olduğu gibi \( y \) değişkeninin \( x \) değişkenine göre türevinin sıfır olduğu noktalarda oluşur.
\( \dfrac{dy}{dx} = \dfrac{dy/dt}{dx/dt} = 0 \)
Parametrik denklemin türev formülü düşünüldüğünde, durağan noktalar \( y \) değişkeninin parametreye göre türevinin sıfır olduğu, ama \( x \) değişkeninin parametreye göre türevinin sıfırdan farklı olduğu noktalardır.
\( \dfrac{dy}{dt} = 0, \quad \dfrac{dx}{dt} \ne 0 \)
Değişkenlerin \( t \) parametresine göre türevini alalım.
\( \dfrac{dx}{dt} = 3t^2 \)
\( \dfrac{dy}{dt} = 6t + 3 \)
Değişkenlerin birbirine göre türevini alalım.
\( \dfrac{dy}{dx} = \dfrac{dy/dt}{dx/dt} \)
\( = \dfrac{6t + 3}{3t^2} = \dfrac{2t + 1}{t^2} \)
\( = \dfrac{2}{t} + \dfrac{1}{t^2} \)
Bulduğumuz birinci türev ifadesini sıfıra eşitleyelim.
\( \dfrac{2t + 1}{t^2} = 0 \)
\( t = -\dfrac{1}{2} \)
Bulduğumuz \( t \) değerinda payda sıfırdan farklı olduğu için eğrinin \( t = -\frac{1}{2} \) değerinde durağan noktası vardır.
Parametrik denklemin ikinci türevini alalım.
\( \dfrac{d^2y}{dx^2} = \dfrac{\frac{d}{dt} (\frac{dy}{dx})}{\frac{dx}{dt}} \)
\( = \dfrac{\frac{d}{dt}(\frac{2}{t} + \frac{1}{t^2})}{\frac{d}{dt} (t^3 - 5)} \)
\( = \dfrac{-\frac{2}{t^2} - \frac{2}{t^3}}{3t^2} \)
\( = -\dfrac{2}{3t^4} - \dfrac{2}{3t^5} \)
Durağan noktadaki ikinci türev değerini bulalım.
\( \dfrac{d^2y}{dx^2}|_{t = -\frac{1}{2}} = -\dfrac{2}{3(-\frac{1}{2})^4} - \dfrac{2}{3(-\frac{1}{2})^5} \)
\( = \dfrac{32}{3} \) bulunur.
\( 0 \le \theta \le 2\pi \) olmak üzere,
\( x(\theta) = 2\theta - \cos{\theta} \)
\( y(\theta) = 1 + \sin{\theta} \)
Yukarıda parametrik denklemi verilen eğrinin durağan noktalarının kartezyen koordinatlarını bulunuz.
Çözümü GösterBir parametrik denklemin durağan noktaları kartezyen denklemlerinde olduğu gibi \( y \) değişkeninin \( x \) değişkenine göre türevinin sıfır olduğu noktalarda oluşur.
\( \dfrac{dy}{dx} = \dfrac{dy/d\theta}{dx/d\theta} = 0 \)
Parametrik denklemin türev formülü düşünüldüğünde, durağan noktalar \( y \) değişkeninin parametreye göre türevinin sıfır olduğu, ama \( x \) değişkeninin parametreye göre türevinin sıfırdan farklı olduğu noktalardır.
\( \dfrac{dy}{d\theta} = 0, \quad \dfrac{dx}{d\theta} \ne 0 \)
Değişkenlerin \( \theta \) parametresine göre türevini alalım.
\( \dfrac{dx}{d\theta} = 2 + \sin{\theta} \)
\( \dfrac{dy}{d\theta} = \cos{\theta} \)
Değişkenlerin birbirine göre türevini alalım.
\( \dfrac{dy}{dx} = \dfrac{dy/d\theta}{dx/d\theta} \)
\( = \dfrac{\cos{\theta}}{2 + \sin{\theta}} \)
Bulduğumuz birinci türev ifadesini sıfıra eşitleyelim.
\( \dfrac{\cos{\theta}}{2 + \sin{\theta}} = 0 \)
\( \cos{\theta} = 0 \)
\( 2 + \sin{\theta} \ne 0 \)
\( \cos{\theta} \) ifadesi \( [0, 2\pi] \) aralığında \( \theta \in \{\frac{\pi}{2}, \frac{3\pi}{2}\} \) değerlerinde sıfır olur. Her iki değerde de paydadaki \( 2 + \sin{\theta} \) ifadesi sıfırdan farklı olur.
Buna göre eğrinin \( \theta \in \{\frac{\pi}{2}, \frac{3\pi}{2}\} \) değerlerinde durağan noktaları vardır.
Bu \( \theta \) değerlerindeki \( (x(\theta), y(\theta)) \) noktalarını bulalım.
\( \theta = \dfrac{\pi}{2} \) için:
\( x\left( \dfrac{\pi}{2} \right) = 2 \cdot \dfrac{\pi}{2} - \cos{\dfrac{\pi}{2}} = \pi \)
\( y\left( \dfrac{\pi}{2} \right) = 1 + \sin{\dfrac{\pi}{2}} = 2 \)
\( \theta = \dfrac{3\pi}{2} \) için:
\( x\left( \dfrac{3\pi}{2} \right) = 2 \cdot \dfrac{3\pi}{2} - \cos{\dfrac{3\pi}{2}} = 3\pi \)
\( y\left( \dfrac{3\pi}{2} \right) = 1 + \sin{\dfrac{3\pi}{2}} = 0 \)
Buna göre eğrinin durağan noktalarının kartezyen koordinatları aşağıdaki gibi bulunur.
\( (x, y) = \{ (\pi, 2), (3\pi, 0) \} \)
Aşağıdaki parametrik denklem bir cismin zamana bağlı konumunu vermektedir.
\( t \in \mathbb{R} \) olmak üzere,
\( x(t) = t^4 - 2t^2 \)
\( y(t) = t^2 - 2t \)
Buna göre bu aracın tamamen durduğu bir noktanın bulunup bulunmadığını, varsa bu noktanın koordinatlarını bulunuz.
Çözümü GösterVerilen \( x(t) \) ve \( y(t) \) denklemleri cismin \( t \) anındaki \( x \) ve \( y \) koordinatlarını vermektedir.
Bu denklemlerin türevi cismin \( x \) ve \( y \) eksenleri boyunca olan hızlarını verir.
Cismin tamamen durması demek yatay ve dikey hızlarının ikisinin birlikte sıfıra eşit olması demektir.
\( \dfrac{dx}{dt} = \dfrac{dy}{dt} = 0 \)
Her iki eksen boyunca hız denklemlerini bulalım.
\( x'(t) = v_x(t) = 4t^3 - 4t \)
\( y'(t) = v_y(t) = 2t - 2 \)
Bu denklemleri ayrı ayrı sıfıra eşitleyelim.
\( v_x(t) = 4t^3 - 4t = 0 \)
\( t(t + 1)(t - 1) = 0 \)
Buna göre cismin \( t = -1 \), \( t = 0 \) ve \( t = 1 \) anlarında \( x \) ekseni boyunca (yatay) hızı sıfır olur.
\( v_y(t) = 2t - 2 = 0 \)
\( t - 1 = 0 \)
Buna göre cismin \( t = 1 \) anında \( y \) ekseni boyunca (dikey) hızı sıfır olur.
Hem yatay hem dikey hızların sıfır olduğu, yani cismin tamamen durduğu zaman \( t = 1 \) anıdır.
Cismin \( t = 1 \) anındaki konumunu bulalım.
\( x(1) = 1^4 - 2(1)^2 = -1 \)
\( y(1) = 1^2 - 2(1) = -1 \)
Buna göre cisim \( (-1, -1) \) noktasında tamamen durur.
Aşağıda denklemi verilen parametrik eğriye \( \theta = \frac{\pi}{8} \) değerindeki noktada çizilen normalin denklemini bulunuz.
\( 0 \le \theta \lt 2\pi \) olmak üzere,
\( x(\theta) = \cos(2\theta) \)
\( y(\theta) = 1 - \sin(2\theta) \)
Çözümü GösterEğriye \( \theta = \frac{\pi}{8} \) değerindeki noktada çizilen teğet doğrunun eğimine \( m_t \), aynı noktadaki normal doğrunun eğimine \( m_n \) diyelim.
Değişkenlerin \( \theta \) parametresine göre türevini alalım.
\( \dfrac{dx}{d\theta} = -2\sin(2\theta) \)
\( \dfrac{dy}{d\theta} = -2\cos(2\theta) \)
Değişkenlerin birbirine göre türevini alalım.
\( \dfrac{dy}{dx} = \dfrac{dy/d\theta}{dx/d\theta} \)
\( = \dfrac{-2\cos(2\theta)}{-2\sin(2\theta)} = \dfrac{\cos(2\theta)}{\sin(2\theta)} \)
Değişkenlerin birbirine göre türevinde \( \theta = \frac{\pi}{8} \) yazarak eğriye bu noktada çizilen teğet doğrunun eğimini bulalım.
\( \dfrac{dy}{dx}|_{\theta = \frac{\pi}{8}} = \dfrac{\cos{\frac{2\pi}{8}}}{\sin{\frac{2\pi}{8}}} \)
\( = \dfrac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}} = 1 = m_t \)
Eğri üzerinde \( \theta = \frac{\pi}{8} \) değerindeki noktanın kartezyen koordinatlarını bulalım.
\( x\left( \dfrac{\pi}{8} \right) = \cos{\dfrac{2\pi}{8}} = \dfrac{\sqrt{2}}{2} \)
\( y\left( \dfrac{\pi}{8} \right) = 1 - \sin{\dfrac{2\pi}{8}} = 1 - \dfrac{\sqrt{2}}{2} \)
Buna göre eğri üzerinde \( \theta = \frac{\pi}{8} \) değerindeki noktanın kartezyen koordinatları \( (\frac{\sqrt{2}}{2}, 1 - \frac{\sqrt{2}}{2}) \) olur ve eğriye bu noktada çizilen teğet doğrunun eğimi \( m_t = 1 \) olur.
Bir noktadaki teğet ve normal doğrular birbirine dik olduğu için eğimlerinin çarpımı -1 olur.
\( m_t \cdot m_n = -1 \)
\( 1 \cdot m_n = -1 \Longrightarrow m_n = -1 \)
\( (\frac{\sqrt{2}}{2}, 1 - \frac{\sqrt{2}}{2}) \) noktasından geçen ve eğimi \( -1 \) olan doğrunun denklemini bulalım.
\( y - y_1 = m_n(x - x_1) \)
\( y - \left( 1 - \dfrac{\sqrt{2}}{2} \right) = -1\left( x - \dfrac{\sqrt{2}}{2} \right) \)
\( y - 1 + \dfrac{\sqrt{2}}{2} = -x + \dfrac{\sqrt{2}}{2} \)
\( y = -x + 1 \) bulunur.
\( C \) eğrisinin parametrik denklemi aşağıda verilmiştir.
\( t \in \mathbb{R} - \{0\} \) olmak üzere,
\( x(t) = t^2 \)
\( y(t) = \dfrac{6}{t} \)
\( C \) eğrisine \( A(4, -3) \) noktasında teğet olan doğrunun eğriyi tekrar kestiğini noktanın kartezyen koordinatlarını bulunuz.
Çözümü GösterÖnce eğriye \( A \) noktasında teğet olan doğrunun denklemini bulalım.
Eğrinin hangi \( t \) değerinde \( (4, -3) \) noktasından geçtiğini bulalım.
\( x(t) = t^2 = 4 \Longrightarrow t = \pm 2 \)
\( y(t) = \dfrac{6}{t} = -3 \Longrightarrow t = -2 \)
Ortak değer \( t = -2 \) olduğu için eğri bu \( t \) değerinde \( A \) noktasından geçer.
Teğet doğrunun eğimini bulmak için parametrik denklemin türevini bulalım.
Değişkenlerin parametreye göre türevini alalım.
\( \dfrac{dx}{dt} = 2t \)
\( \dfrac{dy}{dt} = -\dfrac{6}{t^2} \)
Değişkenlerin birbirine göre türevini bulalım.
\( \dfrac{dy}{dx} = \dfrac{dy/dt}{dx/dt} \)
\( = \dfrac{-\frac{6}{t^2}}{2t} = -\dfrac{3}{t^3} \)
\( t = -2 \) değerindeki türev değerini bulalım.
\( \dfrac{dy}{dx}|_{t = -2} = -\dfrac{3}{(-2)^3} = \dfrac{3}{8} \)
Buna göre parametrik eğriye \( A \) noktasındaki teğet doğrunun eğimi \( \frac{3}{8} \) olarak bulunur.
\( A(4, -3) \) noktasından geçen ve eğimi \( \frac{3}{8} \) olan doğrunun denklemini bulalım.
\( y - y_1 = m(x - x_1) \)
\( y - (-3)) = \dfrac{3}{8}(x - 4) \)
\( 8y + 24 = 3x - 12 \)
\( 3x - 8y - 36 = 0 \)
İkinci adımda teğet doğru ile eğrinin tüm kesişim noktalarını bulalım.
Teğet doğrunun \( C \) eğrisi ile \( t \)'nin hangi değerlerinde kesiştiğini bulmak için parametrik eğri üzerindeki tüm noktaları temsil eden \( (t^2, \frac{6}{t}) \) sıralı ikilisini doğru denkleminde yerine koyalım.
\( 3x - 8y - 36 = 0 \)
\( 3t^2 - 8 \cdot \dfrac{6}{t} - 36 = 0 \)
\( 3t^3 - 48 - 36t = 0 \)
\( t^3 - 12t - 16 = 0 \)
İfadeyi çarpanlarına ayıralım.
\( (t + 2)^2(t - 4) = 0 \)
Doğrunun parametrik eğriye \( t = -2 \) değerinde teğet olduğunu biliyoruz.
Buna göre doğru eğriyi tekrar \( t = 4 \) değerinde keser.
Eğri üzerinde \( t = 4 \) değerindeki noktanın kartezyen koordinatlarını bulalım.
\( x(4) = 4^2 = 16 \)
\( y(4) = \dfrac{6}{4} = \dfrac{3}{2} \)
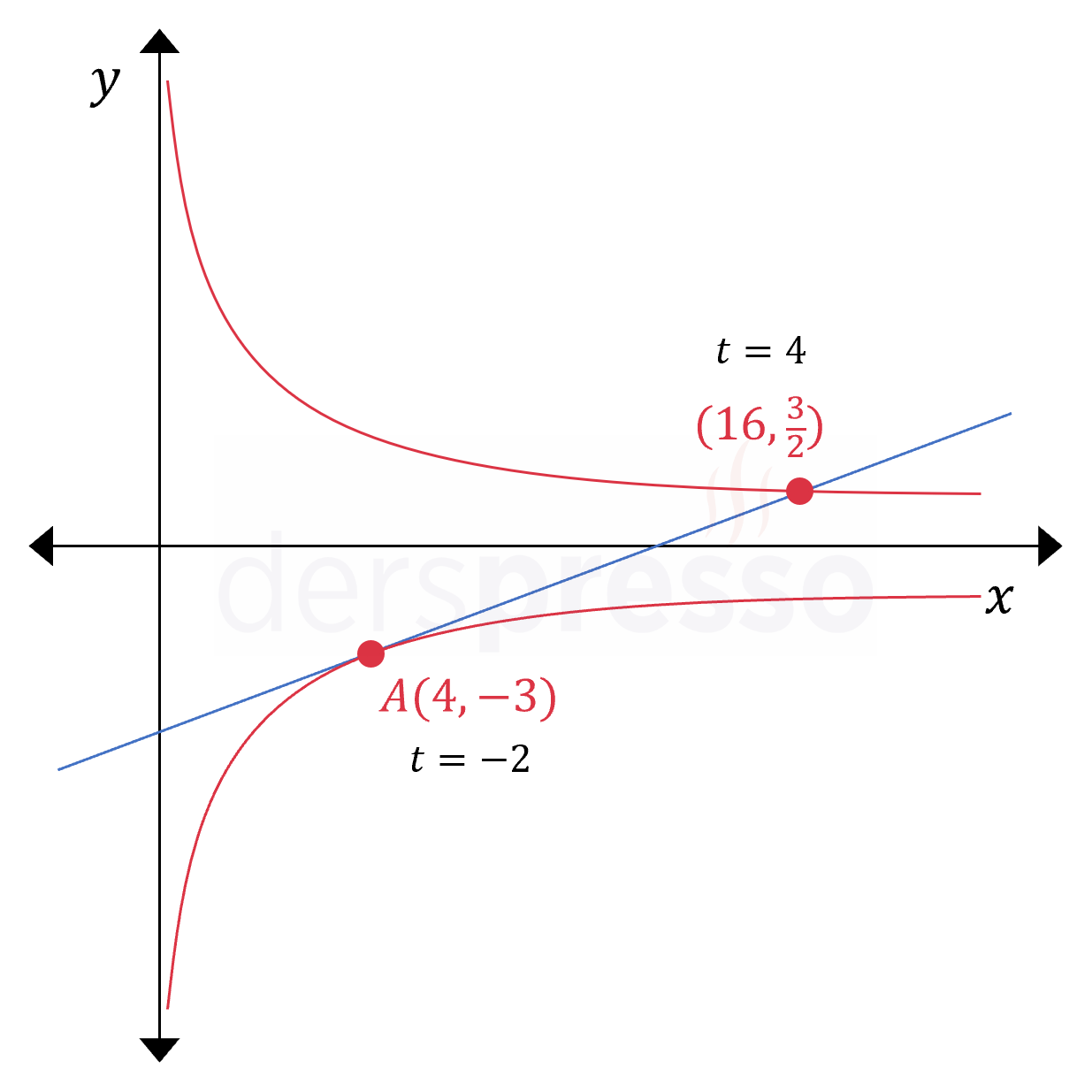
Teğet doğrunun eğriyi tekrar kestiği noktanın kartezyen koordinatları \( (16, \frac{3}{2}) \) olarak bulunur.
Aşağıdaki şekilde \( C \) eğrisiyle \( 3x - 8y - 36 = 0 \) doğrusunun kesişim noktaları gösterilmiştir.
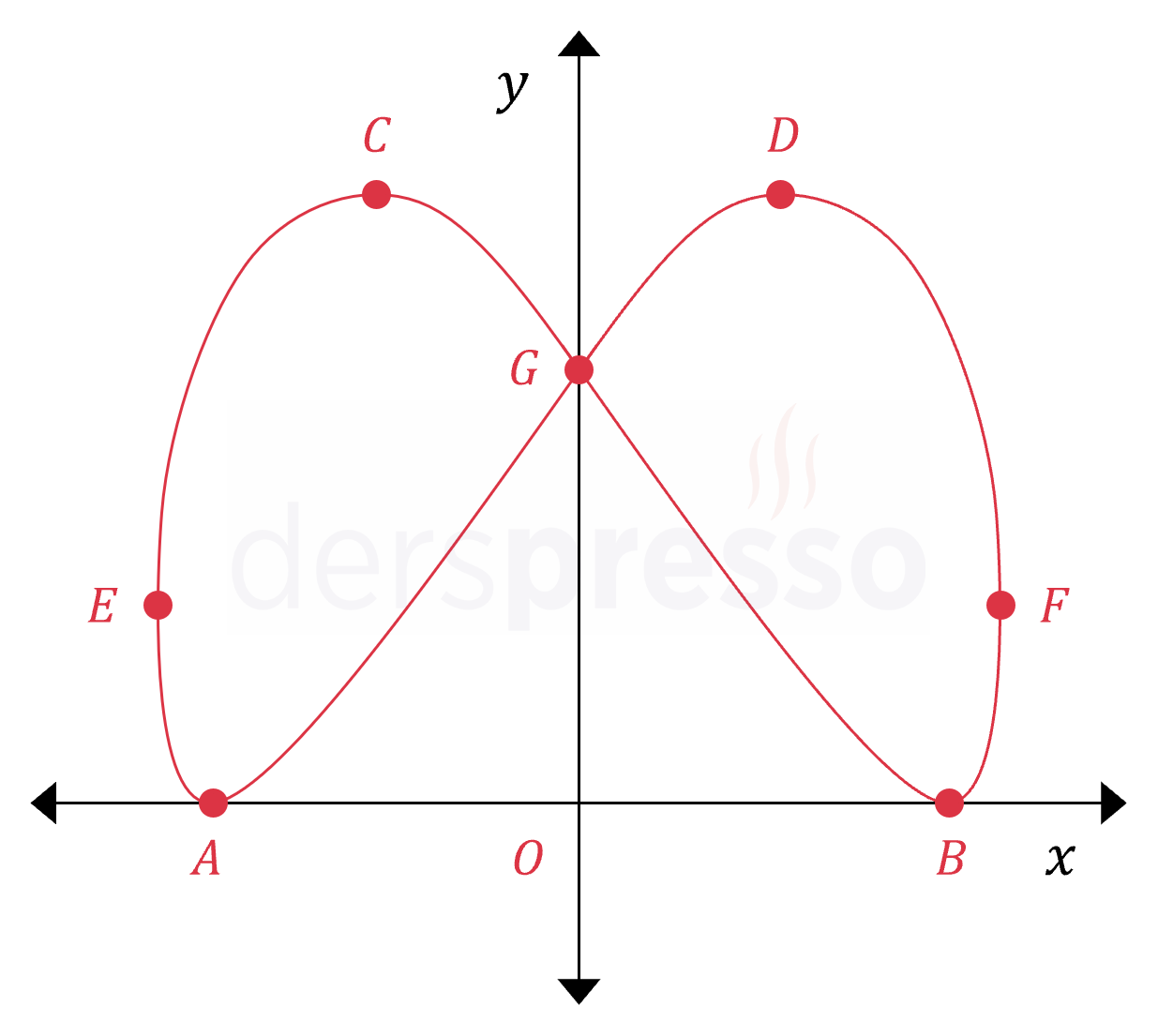
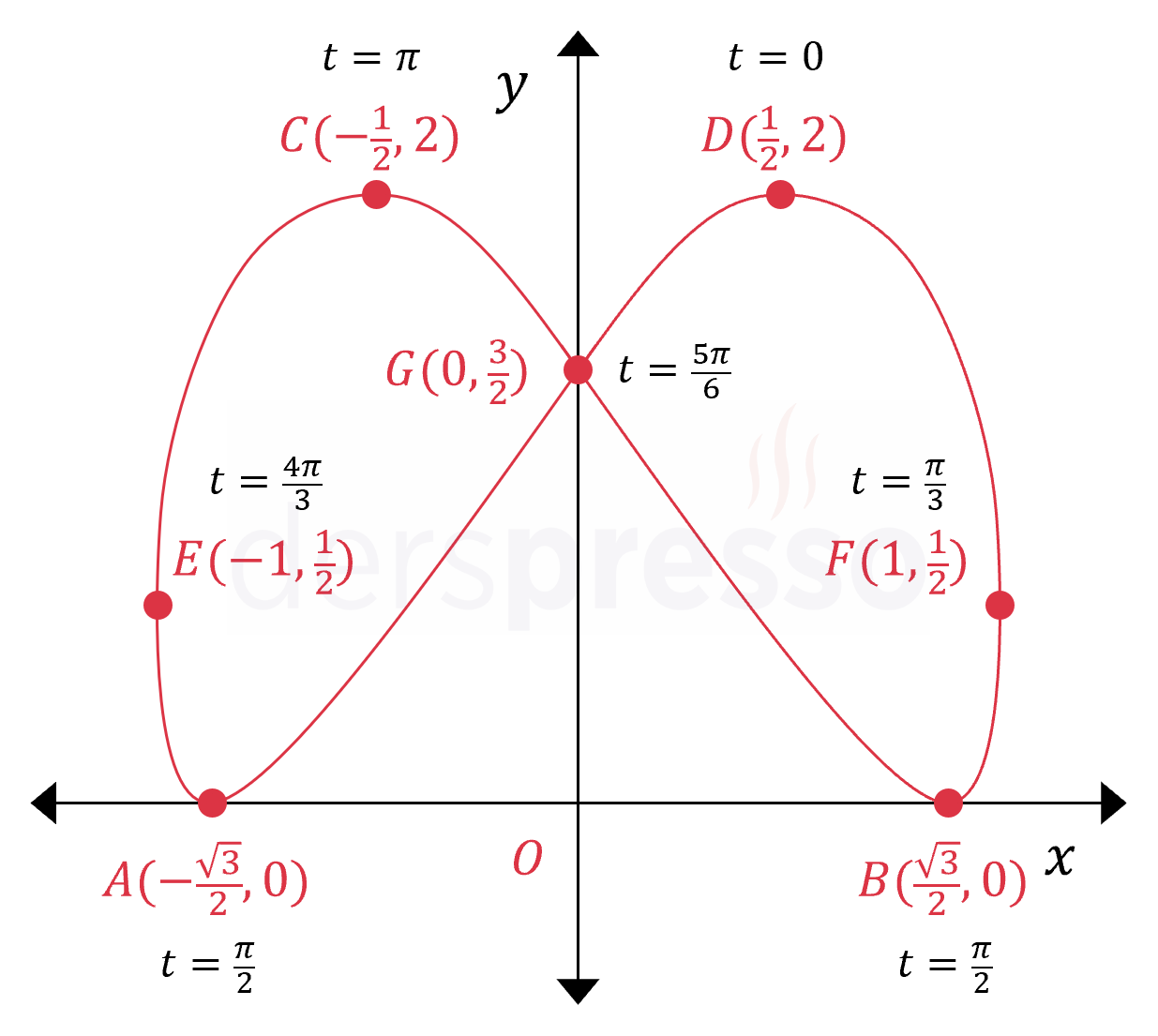
Yukarıdaki eğrinin parametrik denklemi aşağıda verilmiştir.
\( 0 \le t \lt 2\pi \) olmak üzere,
\( x(t) = \sin\left( t + \dfrac{\pi}{6} \right) \)
\( y(t) = 1 + \cos(2t) \)
Grafikte işaretli noktalardan \( A \), \( B \), \( C \) ve \( D \) eğrinin yatay durağan noktaları, \( E \) ve \( F \) dikey durağan noktaları, \( G \) ise eğrinin \( y \) eksenini kestiği noktadır.
Bu yedi noktanın kartezyen koordinatlarını bulunuz.
Çözümü GösterBir fonksiyonun birinci türevinin tanımlı ve sıfır olduğu noktalara durağan nokta denir.
İlk olarak eğrinin yatay durağan noktalarını bulalım.
Bir parametrik denklemin yatay durağan noktaları kartezyen denklemlerinde olduğu gibi \( y \) değişkeninin \( x \) değişkenine göre türevinin sıfır olduğu noktalarda oluşur.
\( \dfrac{dy}{dx} = \dfrac{dy/dt}{dx/dt} = 0 \)
Parametrik denklemin türev formülü düşünüldüğünde, yatay durağan noktalar \( y \) değişkeninin parametreye göre türevinin sıfır olduğu, ama \( x \) değişkeninin parametreye göre türevinin sıfırdan farklı olduğu noktalardır.
\( \dfrac{dy}{dt} = 0, \quad \dfrac{dx}{dt} \ne 0 \)
Değişkenlerin \( t \) parametresine göre türevini alalım.
\( \dfrac{dx}{dt} = \cos\left( t + \dfrac{\pi}{6} \right) \)
\( \dfrac{dy}{dt} = -2\sin(2t) \)
Değişkenlerin birbirine göre türevini alalım.
\( \dfrac{dy}{dx} = \dfrac{dy/dt}{dx/dt} \)
\( = \dfrac{-2\sin(2t)}{\cos(t + \frac{\pi}{6})} \)
Bulduğumuz birinci türev ifadesini sıfıra eşitleyelim.
\( \dfrac{-2\sin(2t)}{\cos(t + \frac{\pi}{6})} = 0 \)
\( -2\sin(2t) = 0, \quad \cos\left( t + \dfrac{\pi}{6} \right) \ne 0 \)
\( \sin(2t) \) ifadesi \( [0, 2\pi) \) aralığında \( t \in \{0, \frac{\pi}{2}, \pi, \frac{3\pi}{2}\} \) değerlerinde sıfır olur. Bu dört değerde de paydadaki \( \cos(t + \frac{\pi}{6}) \) ifadesi sıfırdan farklı olur.
Buna göre eğrinin \( t \in \{0, \frac{\pi}{2}, \pi, \frac{3\pi}{2}\} \) değerlerinde yatay durağan noktaları vardır.
Bu \( t \) değerlerindeki \( (x(t), y(t)) \) noktalarını bulalım.
\( t = 0 \) için:
\( x(0) = \sin\left( 0 + \dfrac{\pi}{6} \right) = \dfrac{1}{2} \)
\( y(0) = 1 + \cos{0} = 2 \)
\( (\frac{1}{2}, 2) \) noktası I. bölgede olduğu için bu nokta \( D \) noktasıdır.
\( t = \dfrac{\pi}{2} \) için:
\( x\left( \dfrac{\pi}{2} \right) = \sin\left( \dfrac{\pi}{2} + \dfrac{\pi}{6} \right) = \dfrac{\sqrt{3}}{2} \)
\( y\left( \dfrac{\pi}{2} \right) = 1 + \cos{\pi} = 0 \)
\( (\frac{\sqrt{3}}{2}, 0) \) noktası \( x \) ekseni üzerinde ve pozitif tarafta olduğu için bu nokta \( B \) noktasıdır.
\( t = \pi \) için:
\( x(\pi) = \sin\left( \pi + \dfrac{\pi}{6} \right) = -\dfrac{1}{2} \)
\( y(\pi) = 1 + \cos(2\pi) = 2 \)
\( (-\frac{1}{2}, 2) \) noktası II. bölgede olduğu için bu nokta \( C \) noktasıdır.
\( t = \dfrac{3\pi}{2} \) için:
\( x\left( \dfrac{3\pi}{2} \right) = \sin\left( \dfrac{3\pi}{2} + \dfrac{\pi}{6} \right) = -\dfrac{\sqrt{3}}{2} \)
\( y\left( \dfrac{3\pi}{2} \right) = 1 + \cos(3\pi) = 0 \)
\( (-\frac{\sqrt{3}}{2}, 0) \) noktası \( x \) ekseni üzerinde ve negatif tarafta olduğu için bu nokta \( A \) noktasıdır.
İkinci adımda eğrinin dikey durağan noktalarını bulalım.
Bir parametrik denklemin dikey durağan noktaları \( x \) değişkeninin \( y \) değişkenine göre türevinin sıfır olduğu noktalarda oluşur.
\( \dfrac{dx}{dy} = 0 \)
Parametrik denklemin türev formülü düşünüldüğünde, dikey durağan noktalar \( x \) değişkeninin parametreye göre türevinin sıfır olduğu, ama \( y \) değişkeninin parametreye göre türevinin sıfırdan farklı olduğu noktalardır.
\( \dfrac{dx}{dt} = 0, \quad \dfrac{dy}{dt} \ne 0 \)
\( \cos\left( t + \dfrac{\pi}{6} \right) = 0 \)
\( k \in \mathbb{Z} \) olmak üzere,
\( t + \dfrac{\pi}{6} = \dfrac{\pi}{2} + \pi k \)
\( t = \dfrac{\pi}{3} + \pi k \)
\( \cos(t + \frac{\pi}{6}) \) ifadesi \( [0, 2\pi) \) aralığında \( t \in \{\frac{\pi}{3}, \frac{4\pi}{3}\} \) değerlerinde sıfır olur.
Bu \( t \) değerlerindeki \( (x(t), y(t)) \) noktalarını bulalım.
\( t = \dfrac{\pi}{3} \) için:
\( x\left( \dfrac{\pi}{3} \right) = \sin\left( \dfrac{\pi}{3} + \dfrac{\pi}{6} \right) = 1 \)
\( y\left( \dfrac{\pi}{3} \right) = 1 + \cos{\dfrac{2\pi}{3}} = \dfrac{1}{2} \)
\( (1, \frac{1}{2}) \) noktası I. bölgede olduğu için bu nokta \( F \) noktasıdır.
\( t = \dfrac{4\pi}{3} \) için:
\( x\left( \dfrac{4\pi}{3} \right) = \sin\left( \dfrac{4\pi}{3} + \dfrac{\pi}{6} \right) = -1 \)
\( y\left( \dfrac{4\pi}{3} \right) = 1 + \cos{\dfrac{8\pi}{3}} = \dfrac{1}{2} \)
\( (-1, \frac{1}{2}) \) noktası II. bölgede olduğu için bu nokta \( E \) noktasıdır.
Üçüncü adımda \( G \) noktasının koordinatlarını bulmak için apsisi sıfır olan noktaları bulalım.
\( x(t) = \sin\left( t + \dfrac{\pi}{6} \right) = 0 \)
\( t + \dfrac{\pi}{6} = \pi k \)
\( t = -\dfrac{\pi}{6} + \pi k \)
\( \sin(t + \frac{\pi}{6}) \) ifadesi \( [0, 2\pi) \) aralığında \( t \in \{\frac{5\pi}{6}, \frac{11\pi}{6}\} \) değerlerinde sıfır olur.
Bu \( t \) değerlerindeki \( (x(t), y(t)) \) noktalarını bulalım.
\( t = \dfrac{5\pi}{6} \) için:
\( x\left( \dfrac{5\pi}{6} \right) = \sin\left( \dfrac{5\pi}{6} + \dfrac{\pi}{6} \right) = 0 \)
\( y\left( \dfrac{5\pi}{6} \right) = 1 + \cos{\dfrac{5\pi}{3}} = \dfrac{3}{2} \)
\( (0, \frac{3}{2}) \) noktası \( y \) ekseni üzerinde ve pozitif tarafta olduğu için bu nokta \( G \) noktasıdır.
Bulduğumuz tüm noktaların kartezyen koordinatları \( t \) değerleri ile birlikte aşağıdaki grafikte işaretlenmiştir.
