Sürekli Fonksiyonlarla İşlemler
Bu bölümde sürekliliği ya da süreksizliği bilinen fonksiyonlar arasındaki işlemler sonucunda elde edilen fonksiyonların süreklilik durumlarını inceleyeceğiz.
Sürekli Fonksiyonlar Arası İşlemler
\( f \) ve \( g \) fonksiyonları \( x = a \) noktasında sürekli fonksiyonlar olmak üzere,
Toplama ve Çıkarma İşlemi
\( (f + g) \) fonksiyonu da \( x = a \) noktasında süreklidir.
\( f(x) = \sin{x} \)
\( g(x) = \cos{x} \)
fonksiyonları tüm reel sayılarda sürekli oldukları için,
\( f(x) + g(x) = \sin{x} + \cos{x} \)
fonksiyonu da tüm reel sayılarda süreklidir.
\( (f - g) \) fonksiyonu da \( x = a \) noktasında süreklidir.
\( f(x) = 2^x \)
\( g(x) = x^2 \)
fonksiyonları tüm reel sayılarda sürekli oldukları için,
\( f(x) - g(x) = 2^x - x^2 \)
fonksiyonu da tüm reel sayılarda süreklidir.
Çarpma İşlemi
\( k \in \mathbb{R} \) olmak üzere, \( (k \cdot f) \) fonksiyonu da \( x = a \) noktasında süreklidir.
\( f(x) = (x - 2)^3 \)
fonksiyonu tüm reel sayılarda sürekli olduğu için,
\( 2 \cdot f(x) = 2(x - 2)^3 \)
fonksiyonu da tüm reel sayılarda süreklidir.
\( (f \cdot g) \) fonksiyonu da \( x = a \) noktasında süreklidir.
\( f(x) = \abs{x} \)
\( g(x) = \sqrt[3]{x} \)
fonksiyonları tüm reel sayılarda sürekli oldukları için,
\( f(x) \cdot g(x) = \abs{x} \cdot \sqrt[3]{x} \)
fonksiyonu da tüm reel sayılarda süreklidir.
Bölme İşlemi
\( g(a) \ne 0 \) olmak üzere, \( \left( \dfrac{f}{g} \right) \) fonksiyonu da \( x = a \) noktasında süreklidir.
\( f(x) = x^2 - 1 \)
\( g(x) = x^3 - 1 \)
fonksiyonları tüm reel sayılarda sürekli oldukları için,
\( \dfrac{f(x)}{g(x)} = \dfrac{x^2 - 1}{x^3 - 1} \)
fonksiyonu da paydayı sıfır yapan \( x \) değerleri hariç süreklidir.
Bileşke İşlemi
\( (f \circ g) \) bileşke fonksiyonu da \( x = a \) noktasında süreklidir.
\( f(x) = x^3 - 1 \)
\( g(x) = 2x + 1 \)
fonksiyonları tüm reel sayılarda sürekli oldukları için,
\( (f \circ g)(x) = f(g(x)) = (2x + 1)^3 - 1 \)
fonksiyonu da tüm reel sayılarda süreklidir.
Sürekli ve Süreksiz Fonksiyonlar Arası İşlemler
Toplama ve Çıkarma İşlemi
\( f \) fonksiyonu bir aralıkta sürekli, \( g \) fonksiyonu aynı aralıkta süreksiz bir fonksiyon ise \( (f + g) \) ve \( (f - g) \) fonksiyonları bu aralıkta süreksizdir.
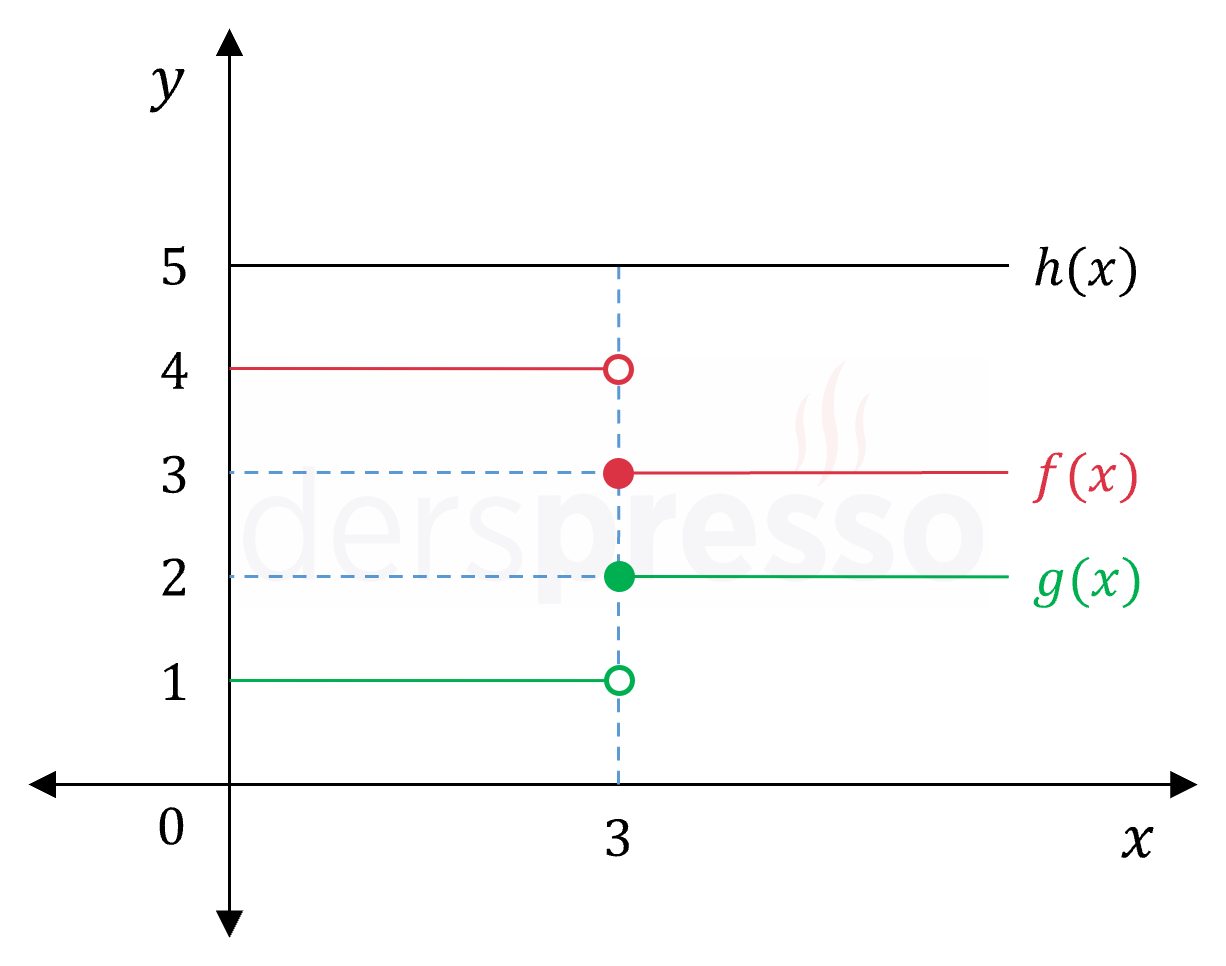
\( f \) ve \( g \) fonksiyonlarının ikisi de bir aralıkta süreksiz ise \( (f + g) \) ve \( (f - g) \) fonksiyonları bu aralıkta sürekli ya da süreksiz olabilir. Aşağıda bir aralıkta süreksiz iki fonksiyonunun toplamı olan diğer bir fonksiyonun bu aralıkta sürekli olmasına bir örnek verilmiştir. Benzer bir örnek süreksiz iki fonksiyonun farkı için de verilebilir.
\( f(x) = \begin{cases} 4 & x \lt 3 \\ 3 & 3 \le x \end{cases} \)
\( g(x) = \begin{cases} 1 & x \lt 3 \\ 2 & 3 \le x \end{cases} \)
\( h(x) = f(x) + g(x) = 5 \)
Çarpma İşlemi
\( f \) fonksiyonu bir aralıkta sürekli, \( g \) fonksiyonu aynı aralıkta süreksiz bir fonksiyon ise \( (f \cdot g) \) fonksiyonu bu aralıkta sadece \( f(x) = 0 \) ise süreklidir, diğer durumlarda süreksizdir.
\( f \) ve \( g \) fonksiyonlarının ikisi de bir aralıkta süreksiz ise \( (f \cdot g) \) fonksiyonu bu aralıkta sürekli ya da süreksiz olabilir. Aşağıda bir aralıkta süreksiz iki fonksiyonunun çarpımı olan diğer bir fonksiyonun bu aralıkta sürekli olmasına bir örnek verilmiştir.
\( f(x) = \begin{cases} -2 & x \lt 0 \\ 3 & 0 \le x \end{cases} \)
\( g(x) = \begin{cases} -3 & x \lt 0 \\ 2 & 0 \le x \end{cases} \)
\( h(x) =f(x) \cdot g(x) = 6 \)
Bölme İşlemi
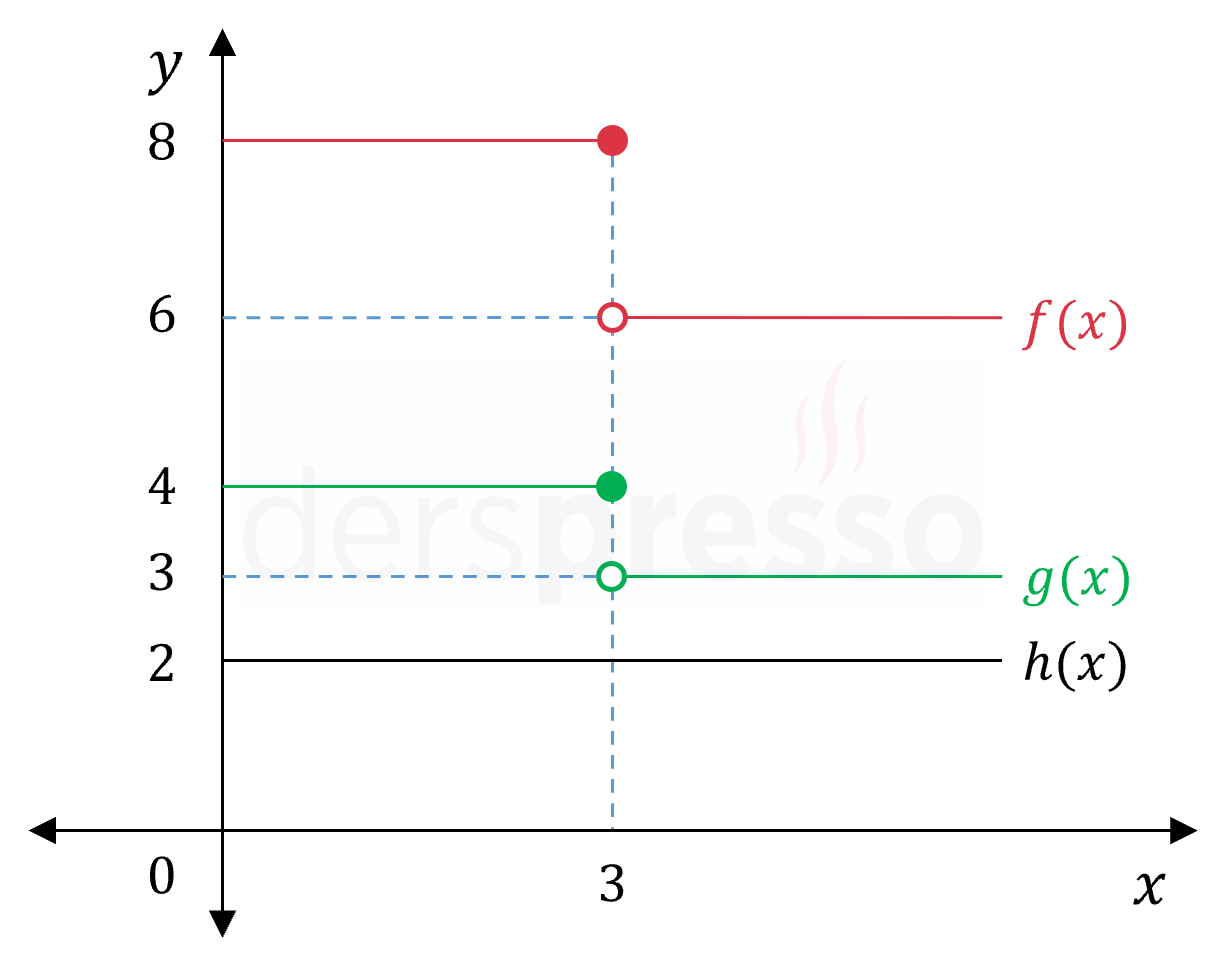
\( f \) ve \( g \) fonksiyonlarının ikisi de bir aralıkta süreksiz ise \( (\frac{f}{g}) \) fonksiyonu bu aralıkta sürekli ya da süreksiz olabilir. Aşağıda bir aralıkta süreksiz iki fonksiyonunun bölümü olan diğer bir fonksiyonun bu aralıkta sürekli olmasına bir örnek verilmiştir.
\( f(x) = \begin{cases} 8 & x \le 3 \\ 6 & 3 \lt x \end{cases} \)
\( g(x) = \begin{cases} 4 & x \le 3 \\ 3 & 3 \lt x \end{cases} \)
\( h(x) = \dfrac{f(x)}{g(x)} = 2 \)
Bileşke İşlemi
\( f \) ve \( g \) fonksiyonlarının ikisi de bir aralıkta süreksiz ise \( (f \circ g) \) bileşke fonksiyonu bu aralıkta sürekli ya da süreksiz olabilir. Aşağıda süreksiz iki fonksiyonunun bileşkesi olan diğer bir fonksiyonun sürekli olmasına bir örnek verilmiştir.
\( f(x) = \begin{cases} -1 & x \lt 0 \\ 1 & 0 \le x \end{cases} \)
\( g(x) = \begin{cases} 2 & x \lt 0 \\ 3 & 0 \le x \end{cases} \)
\( h(x) = (f \circ g)(x) = 1 \)
\( f(x) = \dfrac{5x + 4}{x^2 - 4} + \abs{x^2 - 1} + \dfrac{5}{7 - x} + \sqrt{4x + 8} \)
fonksiyonunun sürekli olduğu en geniş aralık nedir?
Çözümü Göster