Sürekliliğin Grafik Yorumu
Konu tekrarı için: Limitin Grafik Yorumu
Aşağıda \( x = a \) noktasında sürekli birkaç örnek fonksiyonun grafiği verilmiştir.
| Grafik | Açıklama | |
|---|---|---|
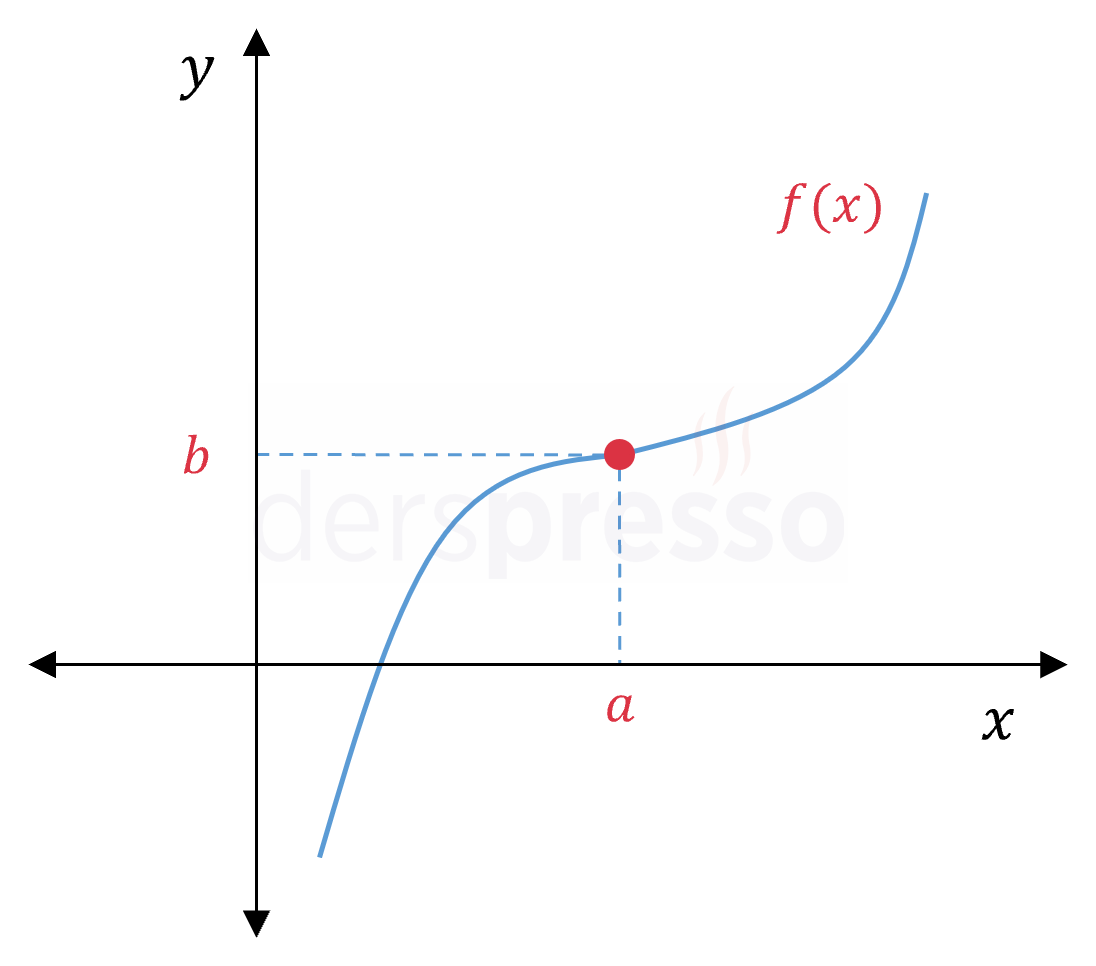
|
\( \lim\limits_{x \to a^-} f(x) = b \) \( \lim\limits_{x \to a^+} f(x) = b \) \( \lim\limits_{x \to a} f(x) = b \) \( f(a) = b \) Fonksiyon \( a \) noktasında tanımlıdır, bu noktada limiti vardır ve limit değeri fonksiyon değerine eşittir, dolayısıyla fonksiyon bu noktada süreklidir. |
|
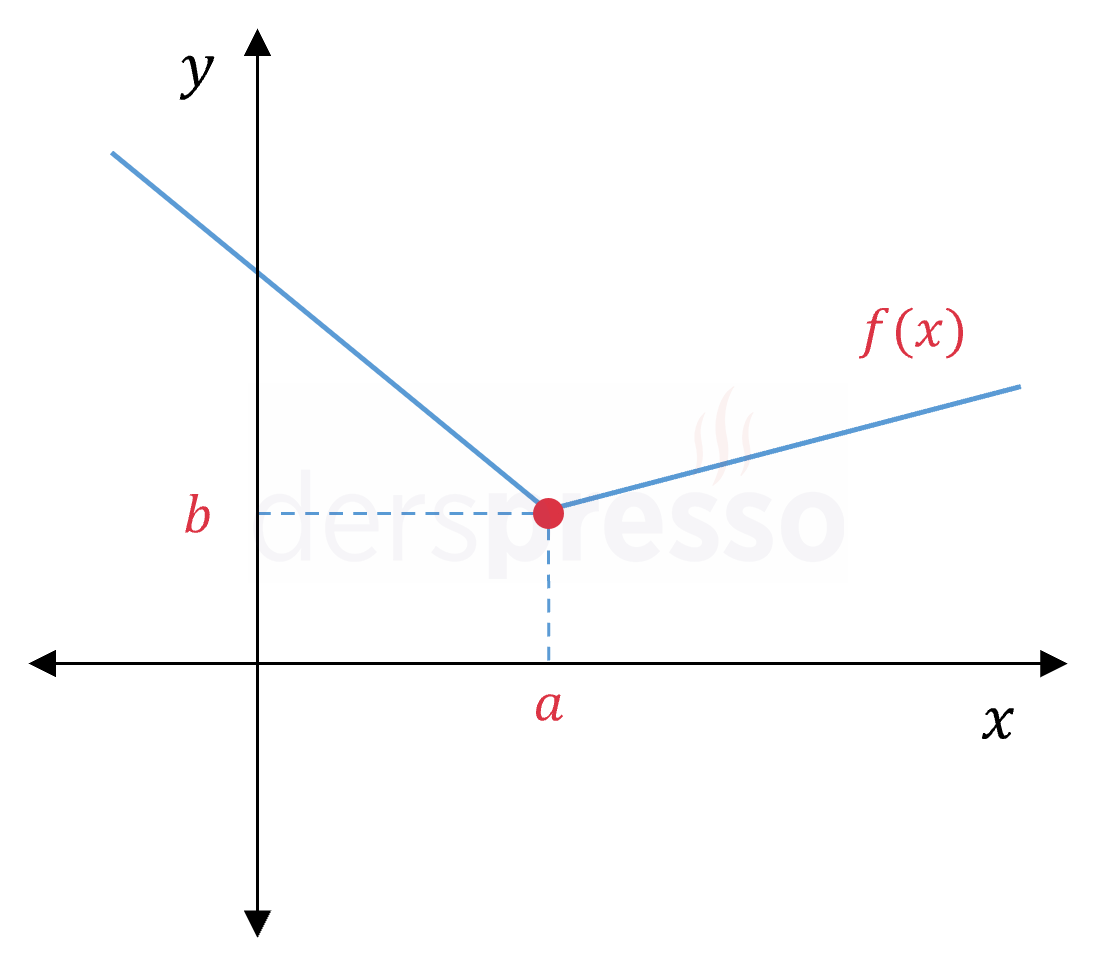
|
\( \lim\limits_{x \to a^-} f(x) = b \) \( \lim\limits_{x \to a^+} f(x) = b \) \( \lim\limits_{x \to a} f(x) = b \) \( f(a) = b \) Parçalı fonksiyon \( a \) noktasında tanımlıdır, bu noktada limiti vardır ve limit değeri fonksiyon değerine eşittir, dolayısıyla fonksiyon bu noktada süreklidir. |
Aşağıda \( x = a \) noktasında süreksiz birkaç örnek fonksiyonun grafiği verilmiştir.
| Grafik | Açıklama |
|---|---|
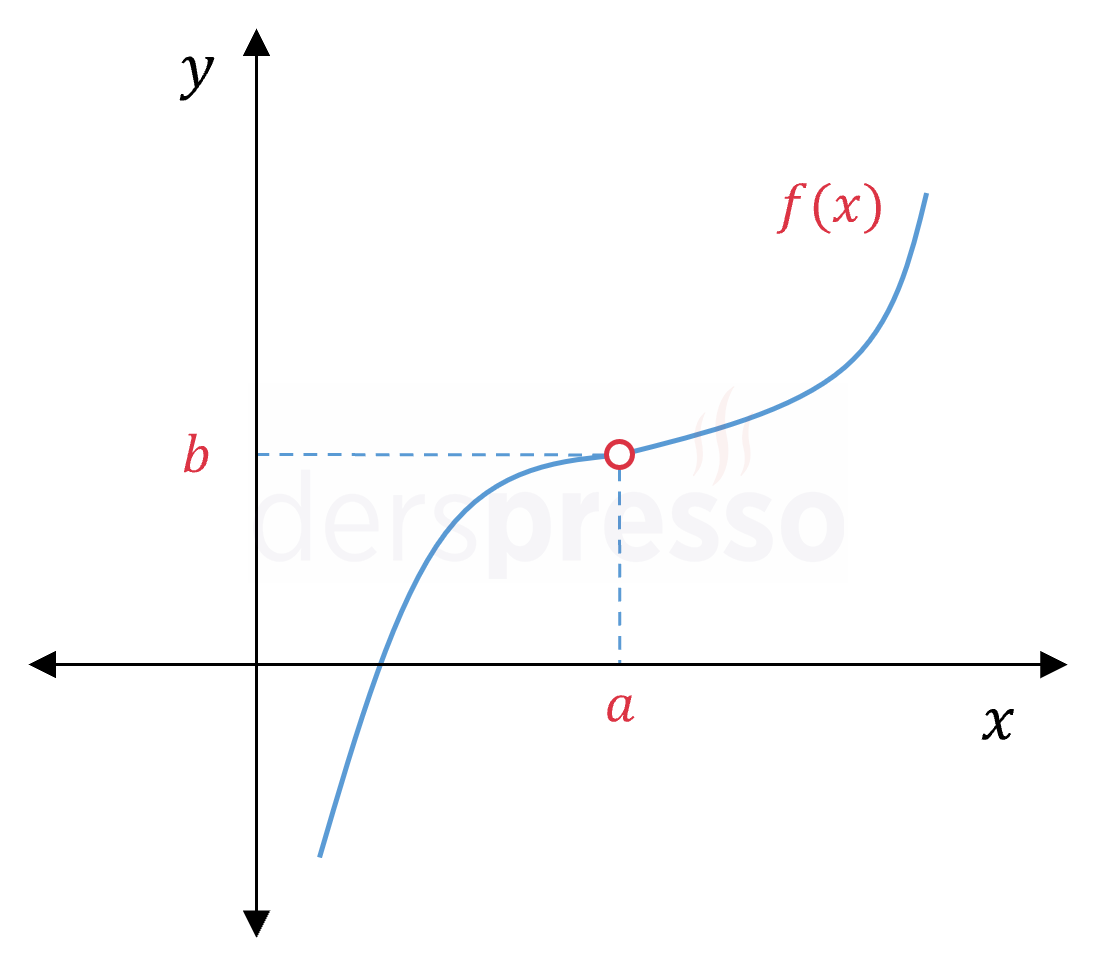
|
\( \lim\limits_{x \to a^-} f(x) = b \) \( \lim\limits_{x \to a^+} f(x) = b \) \( \lim\limits_{x \to a} f(x) = b \) \( f(a) \Longrightarrow \) Tanımsız Limit tanımlı olsa da fonksiyon tanımsız olduğu için fonksiyon bu noktada süreksizdir. |
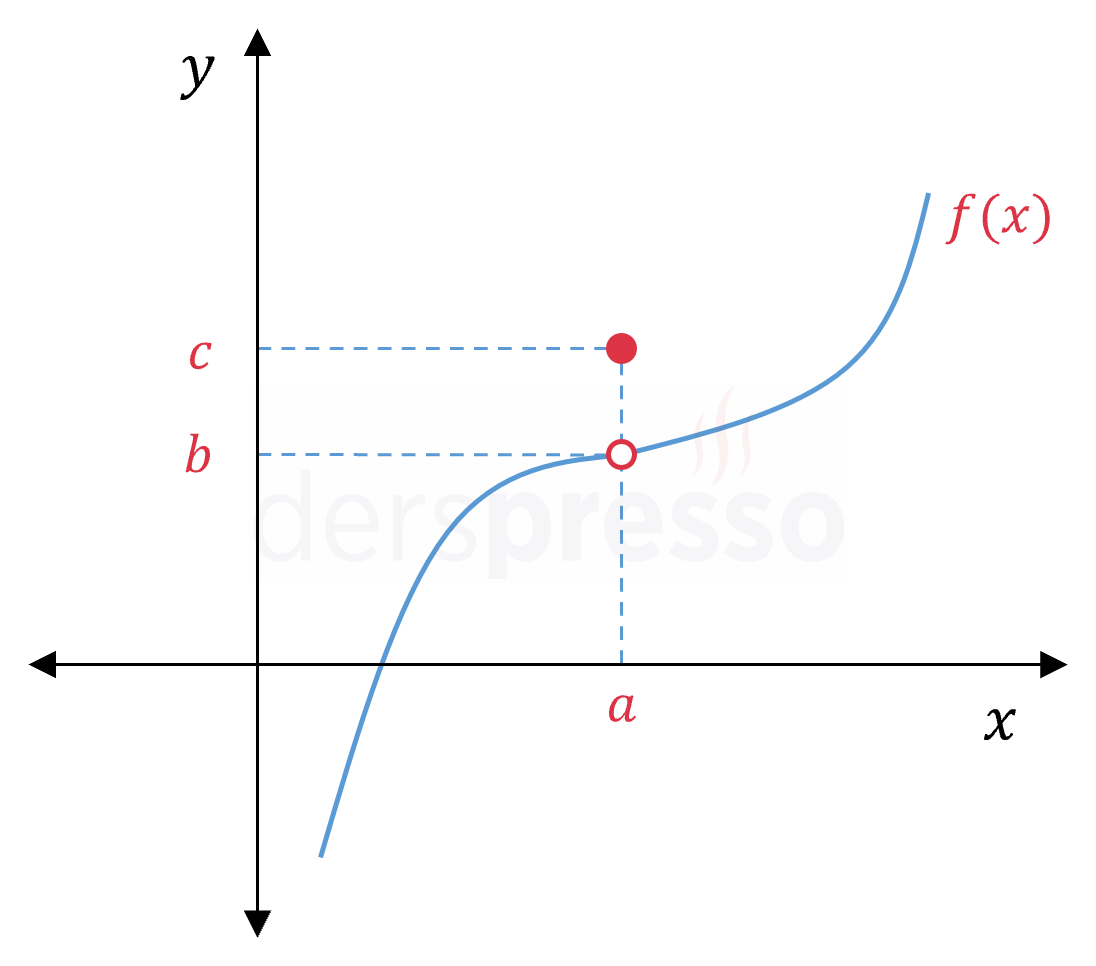
|
\( \lim\limits_{x \to a^-} f(x) = b \) \( \lim\limits_{x \to a^+} f(x) = b \) \( \lim\limits_{x \to a} f(x) = b \) \( f(a) = c \) Limit ve fonksiyon tanımlıdır, ama limit değeri fonksiyon değerine eşit olmadığı için fonksiyon bu noktada süreksizdir. |
|
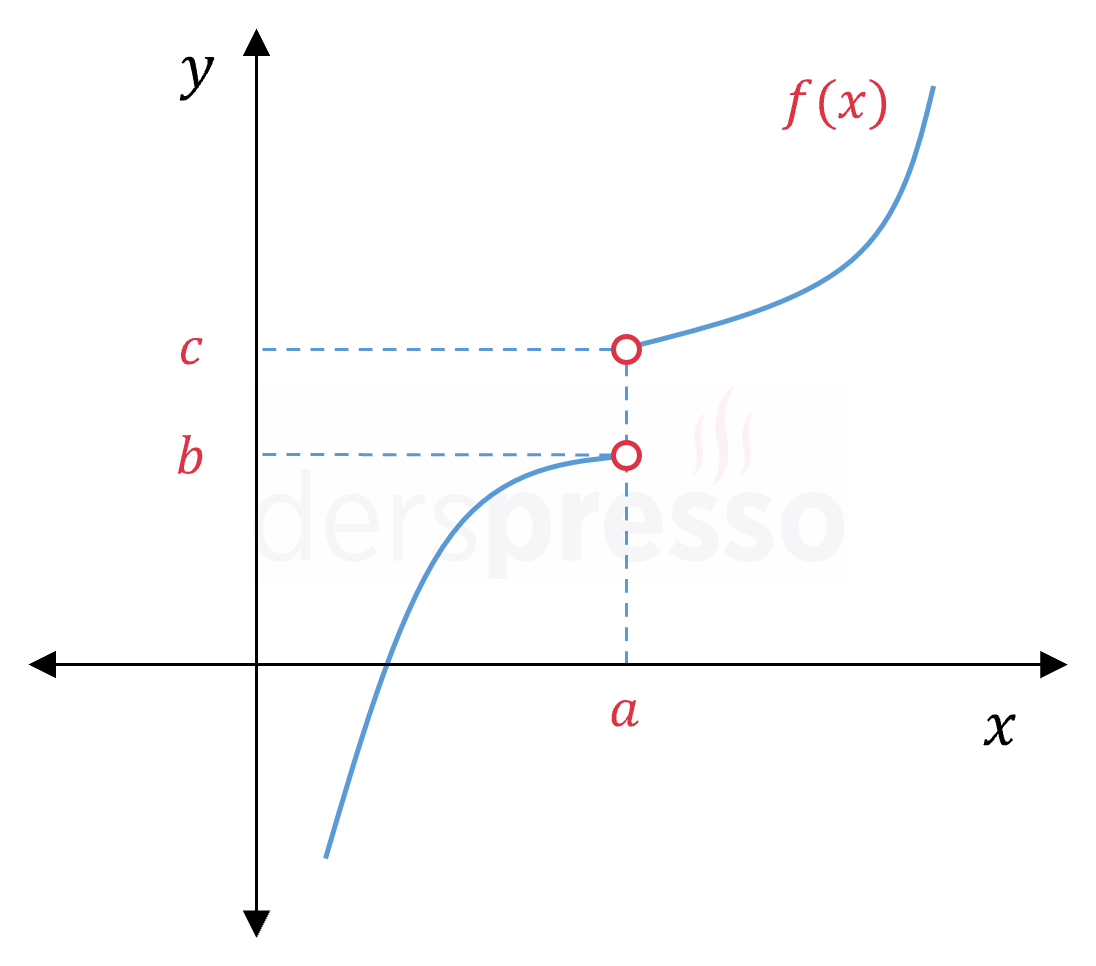
\( \lim\limits_{x \to a^-} f(x) = b \) \( \lim\limits_{x \to a^+} f(x) = c \) \( \lim\limits_{x \to a} f(x) \Longrightarrow \) Tanımsız \( f(a) \Longrightarrow \) Tanımsız Soldan ve sağdan limitler birbirine eşit olmadığı ve fonksiyon tanımsız olduğu için fonksiyon bu noktada süreksizdir. |
|
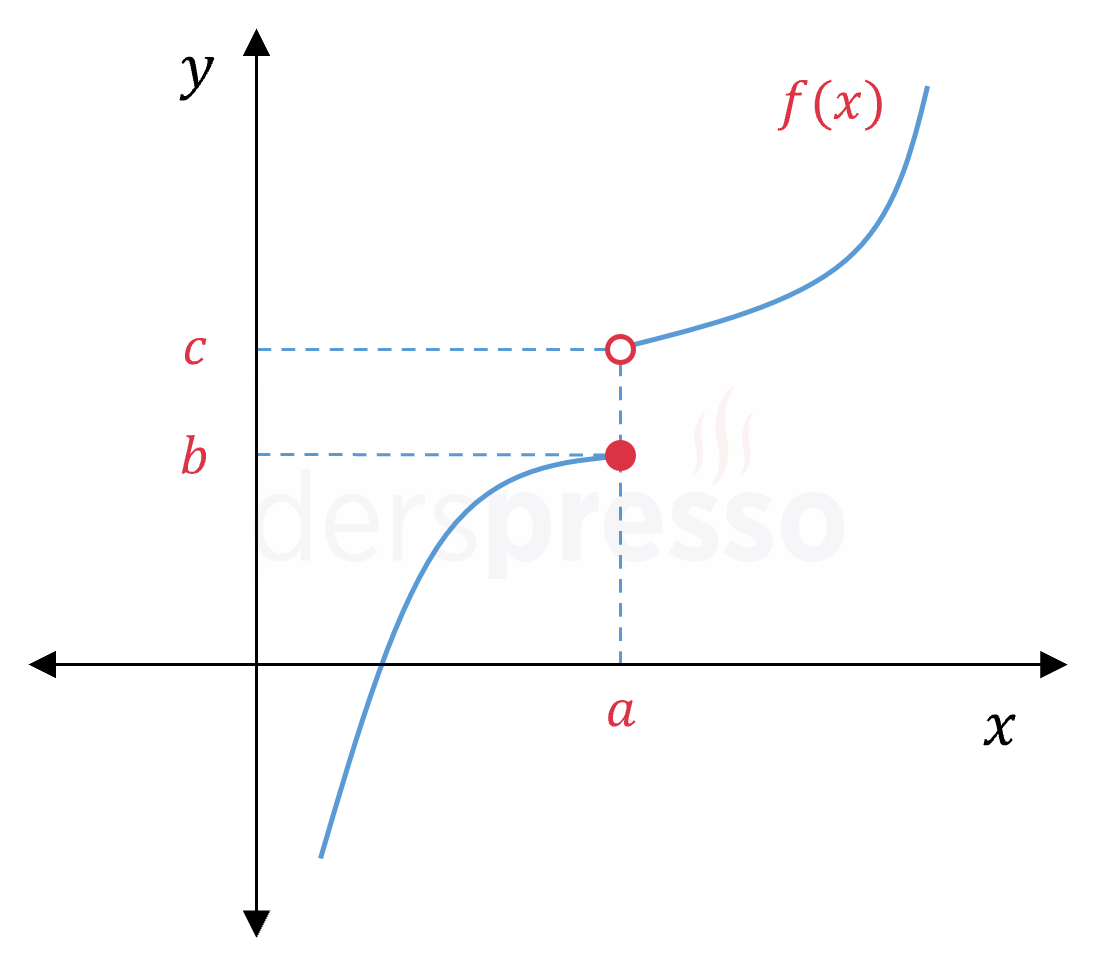
\( \lim\limits_{x \to a^-} f(x) = b \) \( \lim\limits_{x \to a^+} f(x) = c \) \( \lim\limits_{x \to a} f(x) \Longrightarrow \) Tanımsız \( f(a) = b \) Fonksiyon tanımlıdır, ancak soldan ve sağdan limitler birbirine eşit olmadığı için fonksiyon bu noktada süreksizdir. |
|
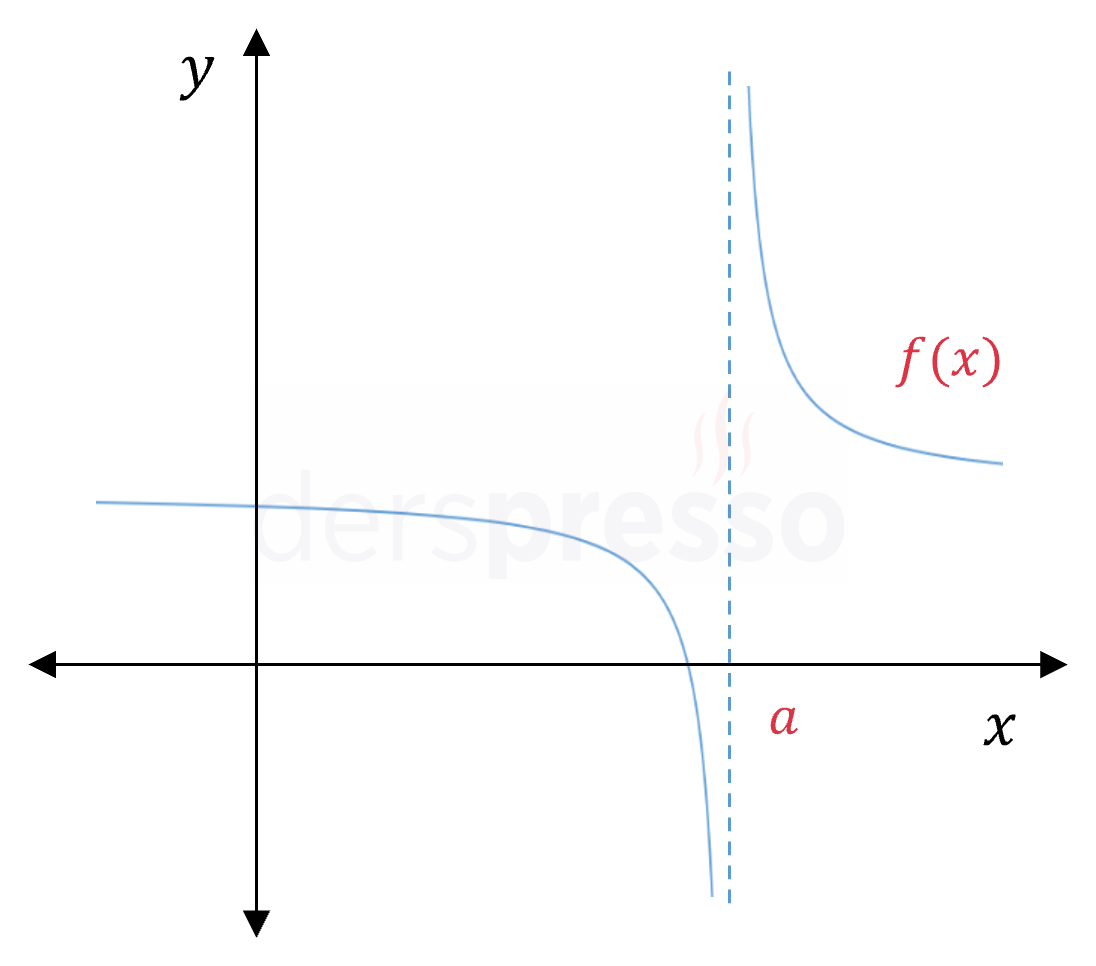
\( \lim\limits_{x \to a^-} f(x) = -\infty \) \( \lim\limits_{x \to a^+} f(x) = +\infty \) \( \lim\limits_{x \to a} f(x) \Longrightarrow \) Tanımsız \( f(a) \Longrightarrow \) Tanımsız Limit ve fonksiyon tanımsızdır, dolayısıyla fonksiyon bu noktada süreksizdir. |
Özel Fonksiyonlar
Fonksiyonlar konusunda gördüğümüz özel fonksiyonlar süreklilik açısından özel olarak incelenmesi gereken fonksiyonlardır.
| Grafik | Açıklama |
|---|---|

|
İşaret fonksiyonu
İşaret fonksiyonu \( x = 0 \) noktasında süreksiz, diğer noktalarda süreklidir. |
|
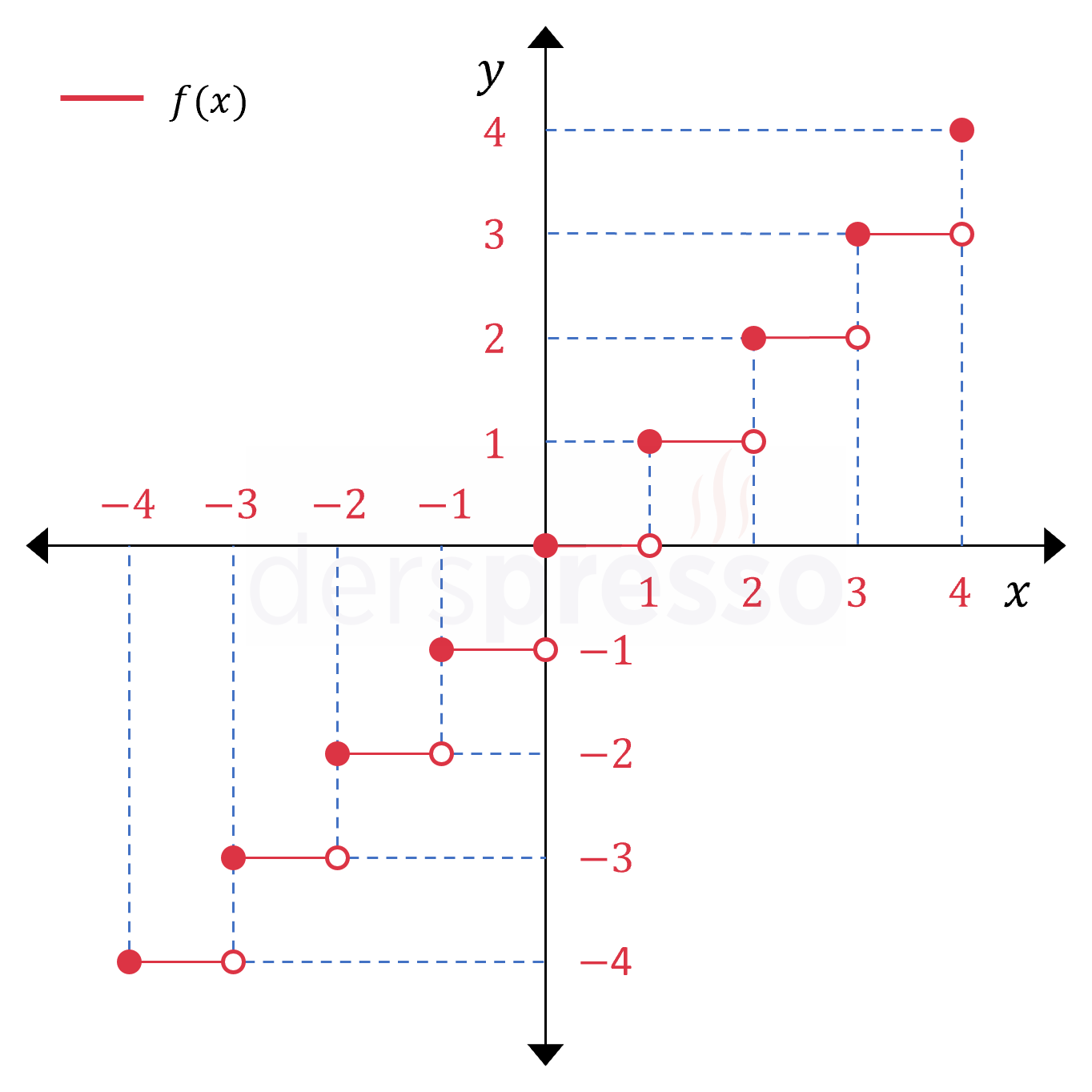
Taban fonksiyonu
Taban fonksiyonu \( x \)'in tam sayı değerlerinde süreksiz, diğer noktalarda süreklidir. Fonksiyon \( x \)'in tam sayı değerlerinde sadece sağdan süreklidir. |
|
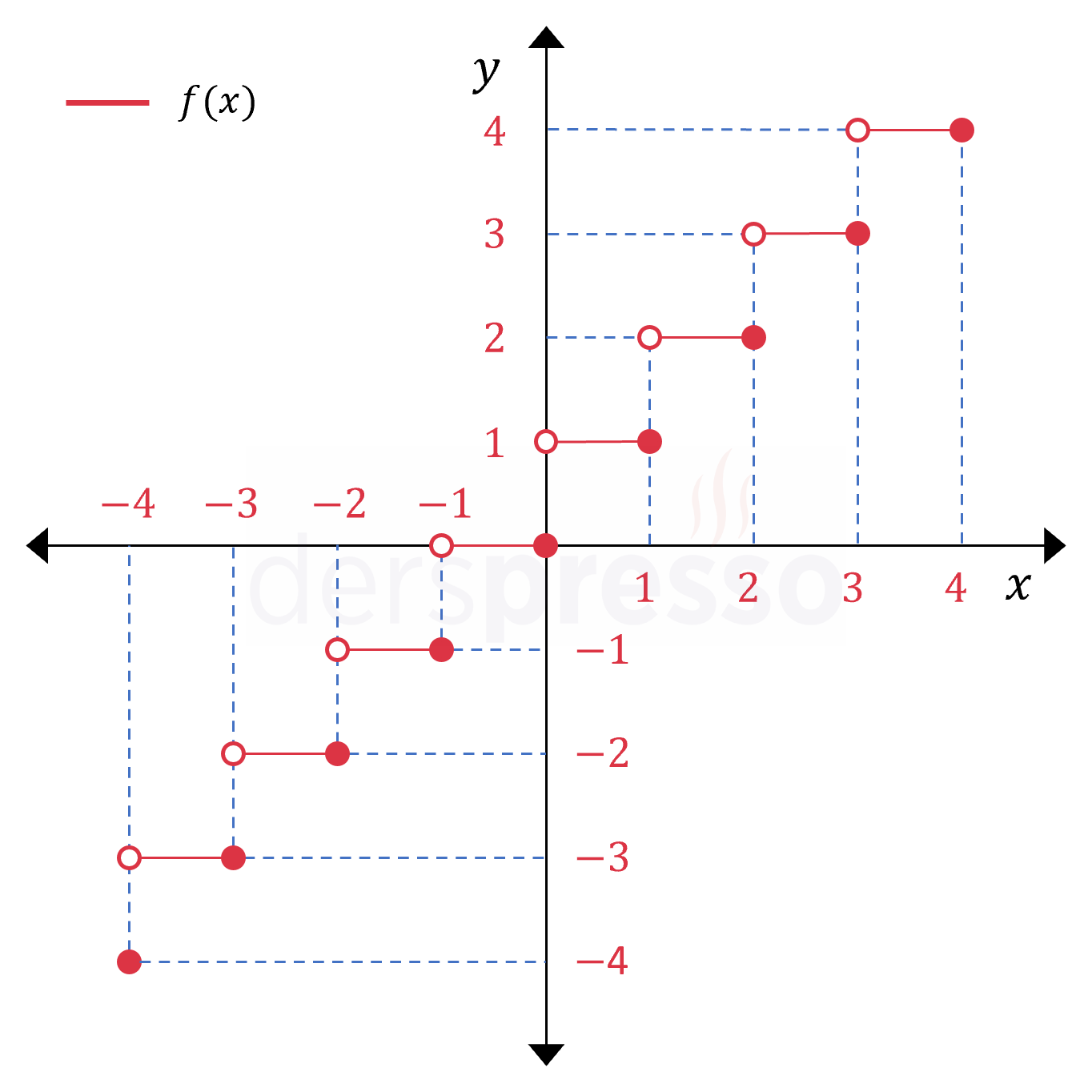
Tavan fonksiyonu
Tavan fonksiyonu \( x \)'in tam sayı değerlerinde süreksiz, diğer noktalarda süreklidir. Fonksiyon \( x \)'in tam sayı değerlerinde sadece soldan süreklidir. |
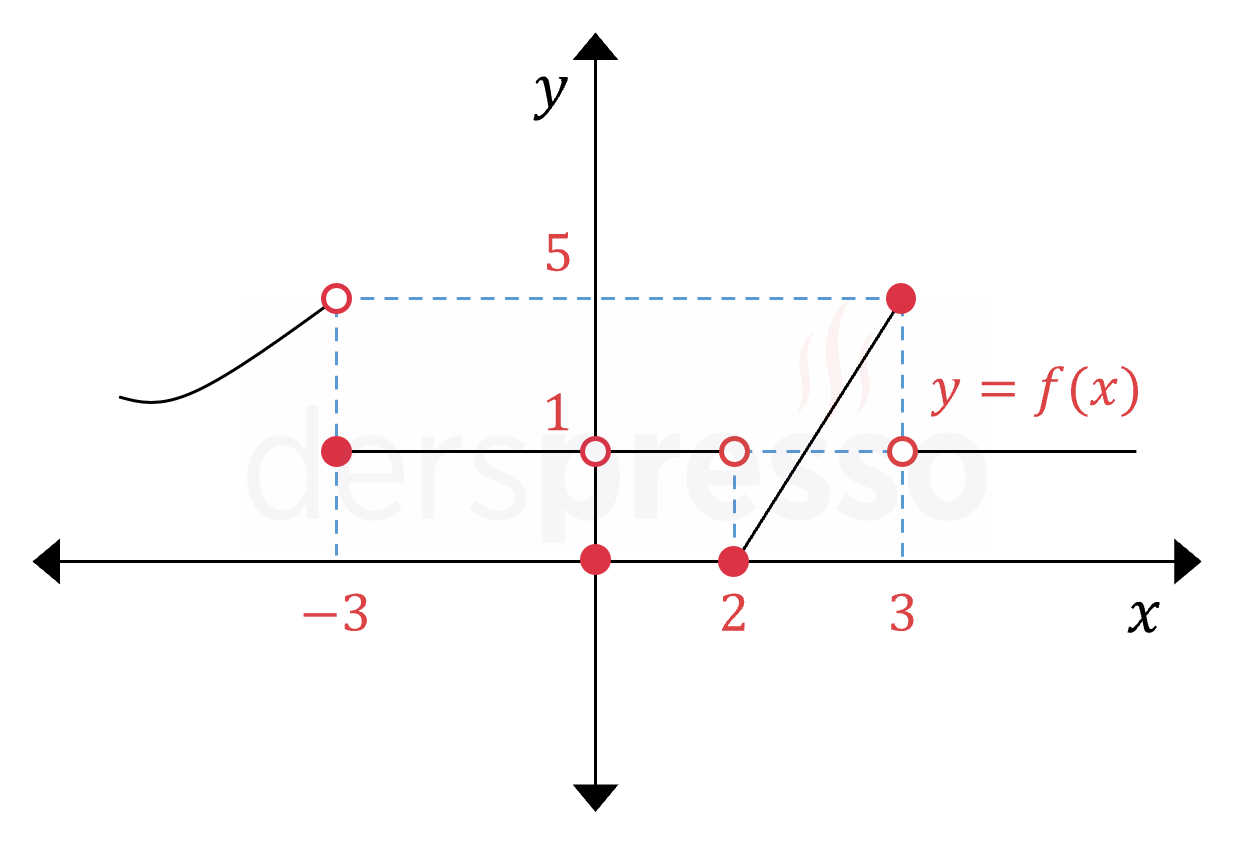
Yukarıda \( y = f(x) \) fonksiyonunun grafiği verilmiştir.
Buna göre aşağıdaki ifadelerden hangileri doğrudur?
I. Fonksiyonun verilen aralıkta 4 noktada limiti yoktur.
II. Fonksiyon verilen aralıkta 4 noktada sürekli değildir.
III. Fonksiyon \( x \in [2, 3] \) aralığında süreklidir.
Çözümü GösterI. öncül:
\( x \in \{ -3, 2, 3 \} \) noktalarında soldan ve sağdan limitler tanımlı olsa da birbirine eşit olmadığı için fonksiyonun bu noktalarda limiti tanımlı değildir.
\( x = 0 \) noktasında ise soldan ve sağdan limitler tanımlı ve birbirine eşit olduğu için fonksiyonun bu noktada limiti tanımlıdır.
I. öncül yanlıştır.
II. öncül:
Verilen grafiğe göre fonksiyon \( x \in \{ -3, 0, 2, 3 \} \) noktalarında sürekli değildir.
II. öncül doğrudur.
III. öncül:
Bir fonksiyon \( (a, b) \) aralığında tüm noktalarda sürekli ise ve ayrıca \( a \) noktasında sağdan ve \( b \) noktasında soldan sürekli ise \( [a, b] \) kapalı aralığında süreklidir.
\( f \) fonksiyonu \( (2, 3) \) açık aralığında süreklidir, ayrıca \( x = 2 \) noktasında sağdan ve \( x = 3 \) noktasında soldan süreklidir. Dolayısıyla fonksiyon \( [2, 3] \) kapalı aralığında süreklidir.
III. öncül doğrudur.
Buna göre II. ve III. öncüller doğrudur.
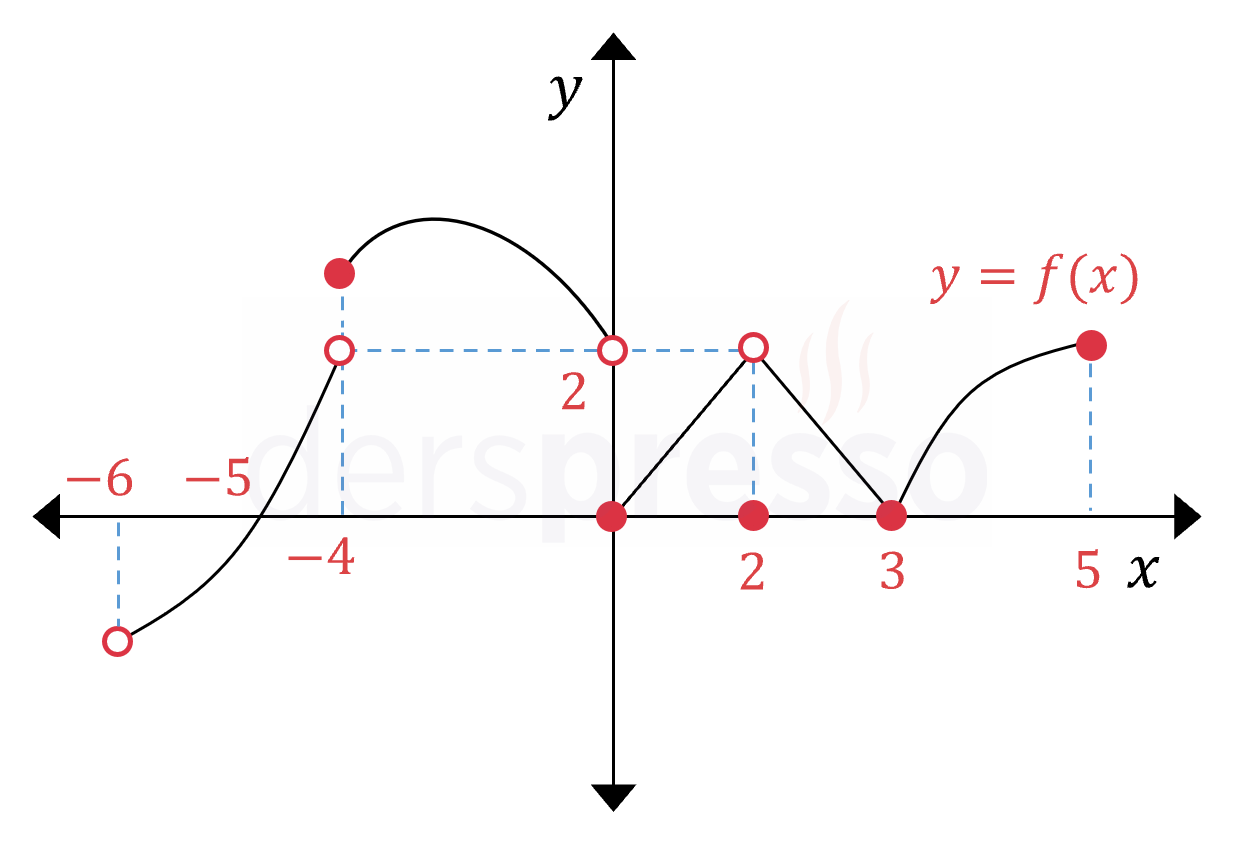
Yukarıda \( (-6, 5] \) aralığında tanımlı \( y = f(x) \) fonksiyonunun grafiği verilmiştir.
Buna göre \( f \) fonksiyonu için aşağıdaki ifadelerden hangileri doğrudur?
I. \( (-6, -4) \) aralığında süreklidir.
II. \( x = -4 \) apsisli noktada süreksizdir.
III. \( x = 2 \) apsisli noktada süreklidir.
IV. \( [3, 5] \) aralığında süreklidir.
Çözümü GösterBir fonksiyonun bir açık aralıkta sürekli olması için fonksiyon bu açık aralıktaki tüm noktalarda sürekli olmalıdır. \( f \) fonksiyonu \( (-6, -4) \) açık aralığındaki tüm noktalarda süreklidir. I. öncül doğrudur.
\( x = -4 \) apsisli noktada fonksiyonun iki taraflı limiti yoktur, dolayısıyla bu noktada fonksiyon süreksizdir. II. öncül doğrudur.
\( x = 2 \) apsisli noktada fonksiyonun iki taraflı limiti tanımlıdır, ancak bu noktadaki fonksiyon değerine eşit değildir. Dolayısıyla \( x = 2 \) noktasında fonksiyon süreksizdir. III. öncül yanlıştır.
Bir fonksiyonun bir kapalı aralıkta sürekli olması için fonksiyon tüm ara noktalarda iki yönlü, uç noktalarda da tek yönlü sürekli olmalıdır. \( f \) fonksiyonu \( (3, 5) \) açık aralığındaki tüm noktalarda süreklidir, ayrıca \( x = 3 \) noktasında sağdan, \( x = 5 \) noktasında soldan süreklidir. IV. öncül doğrudur.
Buna göre I., II. ve IV. öncüller doğrudur.

Yukarıda \( f \) fonksiyonunun grafiği verilmiştir.
Buna göre \( y = \abs{f(x)} \) fonksiyonu \( (-5, 5) \) aralığında apsisi tam sayı olan kaç noktada süreklidir?
Çözümü Göster\( y = \abs{f(x)} \) fonksiyonunun grafiğini oluşturmak için \( x \) ekseninin altında kalan kısmın \( x \) eksenine göre simetriğini alalım.

Bu grafikte \( (-5, 5) \) aralığında apsisi tam sayı olan sürekli noktaları bulalım.
Bir fonksiyonun bir noktada sürekli olması için o noktada soldan ve sağdan limit değerleri birbirine eşit olmalı ve limit değeri o noktadaki fonksiyon değerine eşit olmalıdır.
İstenen koşulları sağlayan 6 nokta vardır.
\( x \in \{ -4, -3, -1, 1, 2, 3 \} \)
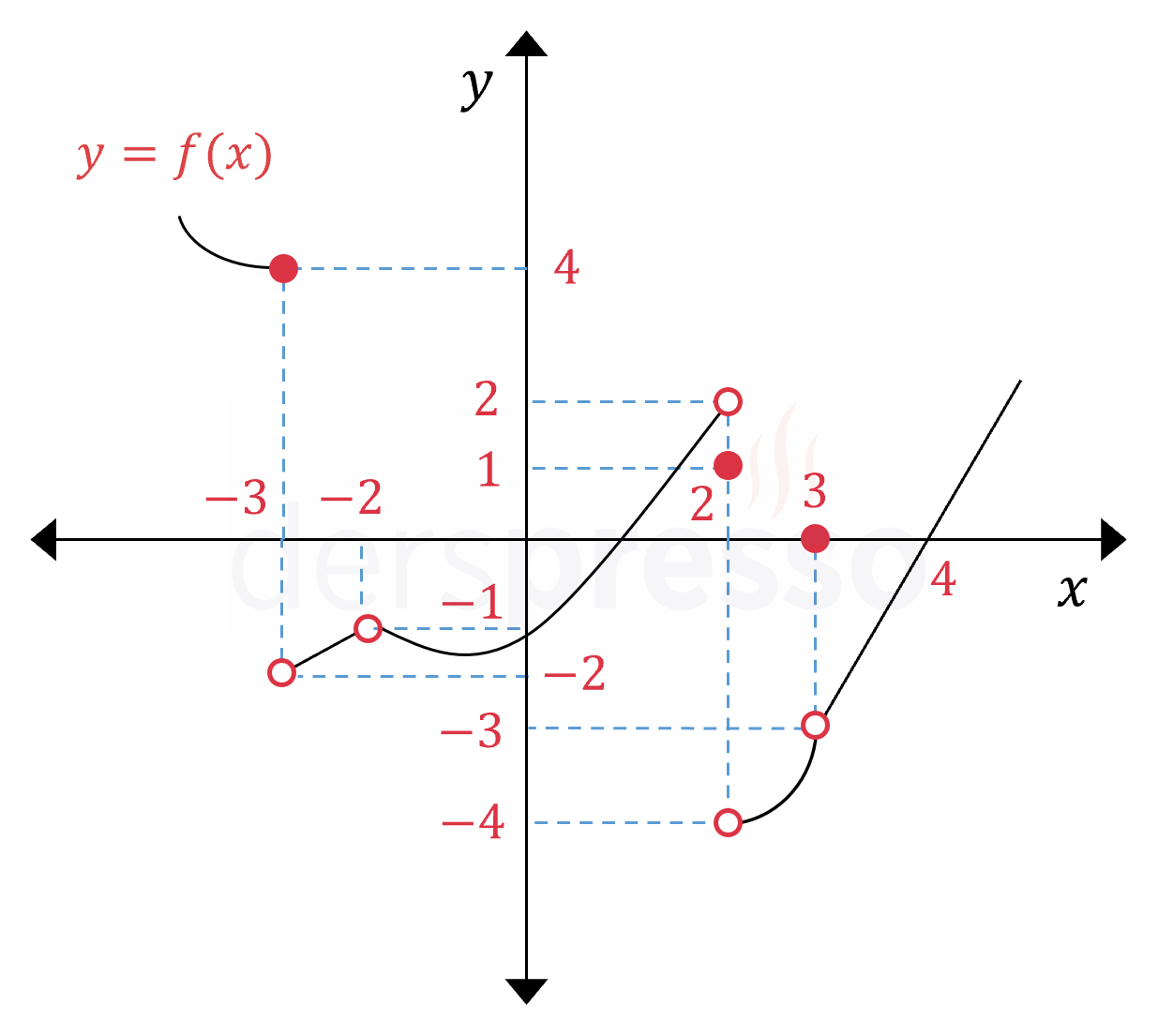
Yukarıda \( y = f(x) \) fonksiyonunun grafiği verilmiştir.
Buna göre, verilen aralıkta fonksiyonun limitinin tanımlı olduğu halde sürekli olmadığı kaç nokta vardır?
Çözümü Göster\( x = -3 \) noktasında fonksiyonun soldan ve sağdan limitleri birbirine eşit olmadığı için iki yönlü limiti yoktur.
\( x = -2 \) noktasında fonksiyonun soldan ve sağdan limitleri birbirine eşit olduğu için limiti tanımlıdır, ancak fonksiyon bu noktada tanımlı olmadığı için sürekli değildir.
\( x = 2 \) noktasında fonksiyonun soldan ve sağdan limitleri birbirine eşit olmadığı için iki yönlü limiti yoktur.
\( x = 3 \) noktasında fonksiyonun soldan ve sağdan limitleri birbirine eşit olduğu için limiti tanımlıdır, ancak bu noktadaki fonksiyon değeri limit değerinden farklı olduğu için fonksiyon bu noktada sürekli değildir.
Buna göre, fonksiyonun limitinin tanımlı olduğu halde sürekli olmadığı \( x = -2 \) ve \( x = 3 \) olmak üzere 2 nokta vardır.
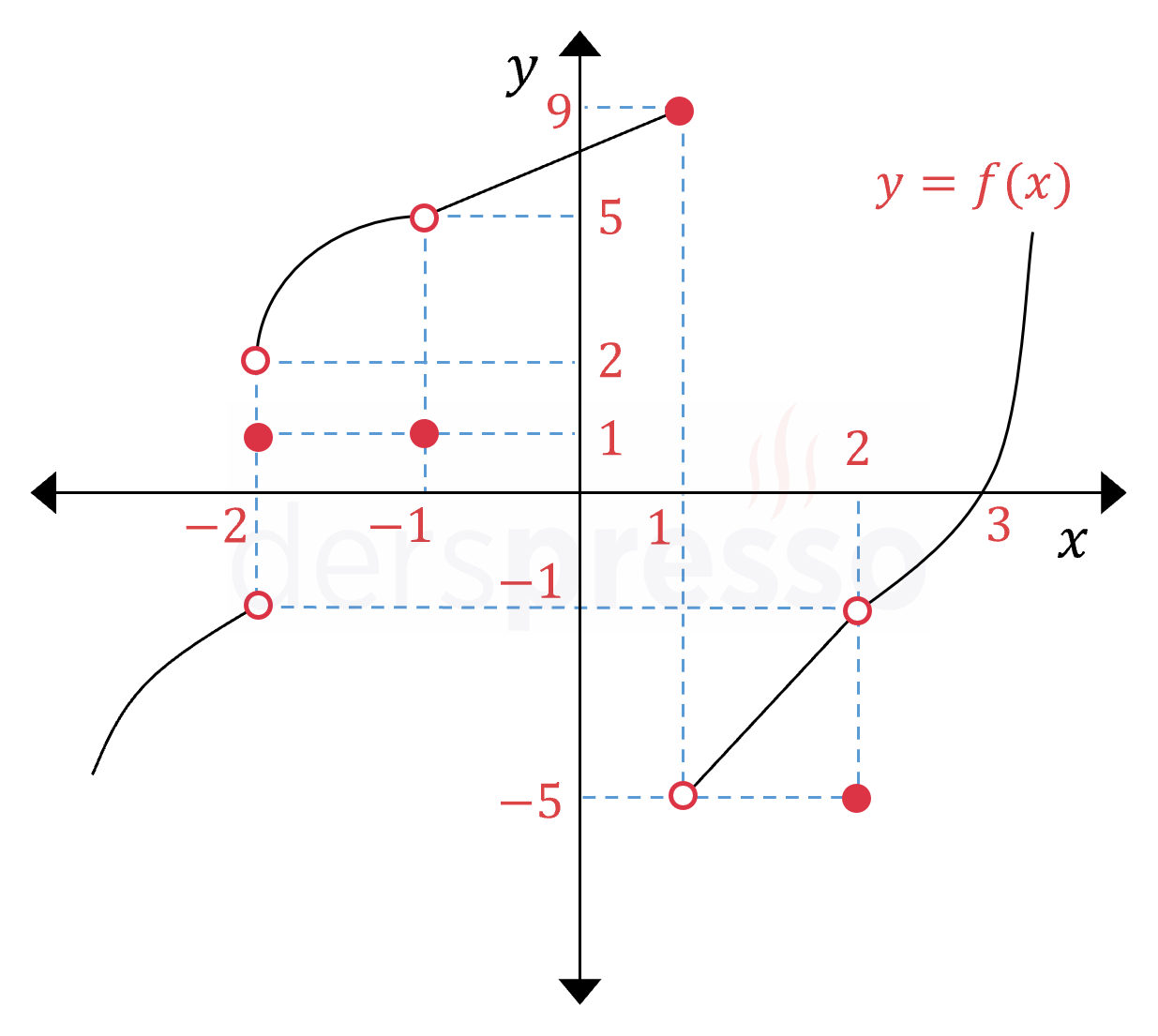
Yukarıda \( y = f(x) \) fonksiyonunun grafiği verilmiştir.
\( g(x) = \dfrac{5x - 3}{f^2(x) - 16} \) fonksiyonu tanımlanıyor.
Buna göre \( g(x) \) fonksiyonu kaç noktada sürekli değildir?
Çözümü Göster\( g \) fonksiyonu \( f \) fonksiyonuna bağlı olduğu için \( f \) fonksiyonunun süreksiz olduğu noktalarda \( g \) fonksiyonu da süreksiz olur.
\( f(x) \) fonksiyonu \( x \in \{-2, -1, 1, 2\} \) noktalarında süreksizdir.
Ek olarak \( g \) fonksiyonu paydasını sıfır yapan noktalarda tanımsız olacağı için bu noktalarda da süreksiz olur.
\( f^2(x) - 16 = 0 \)
\( f(x) = 4 \) ya da \( f(x) = -4 \)
Buna göre \( f \) fonksiyonunun değerinin 4 ya da -4 olduğu noktalarda \( g \) fonksiyonu süreksiz olur.
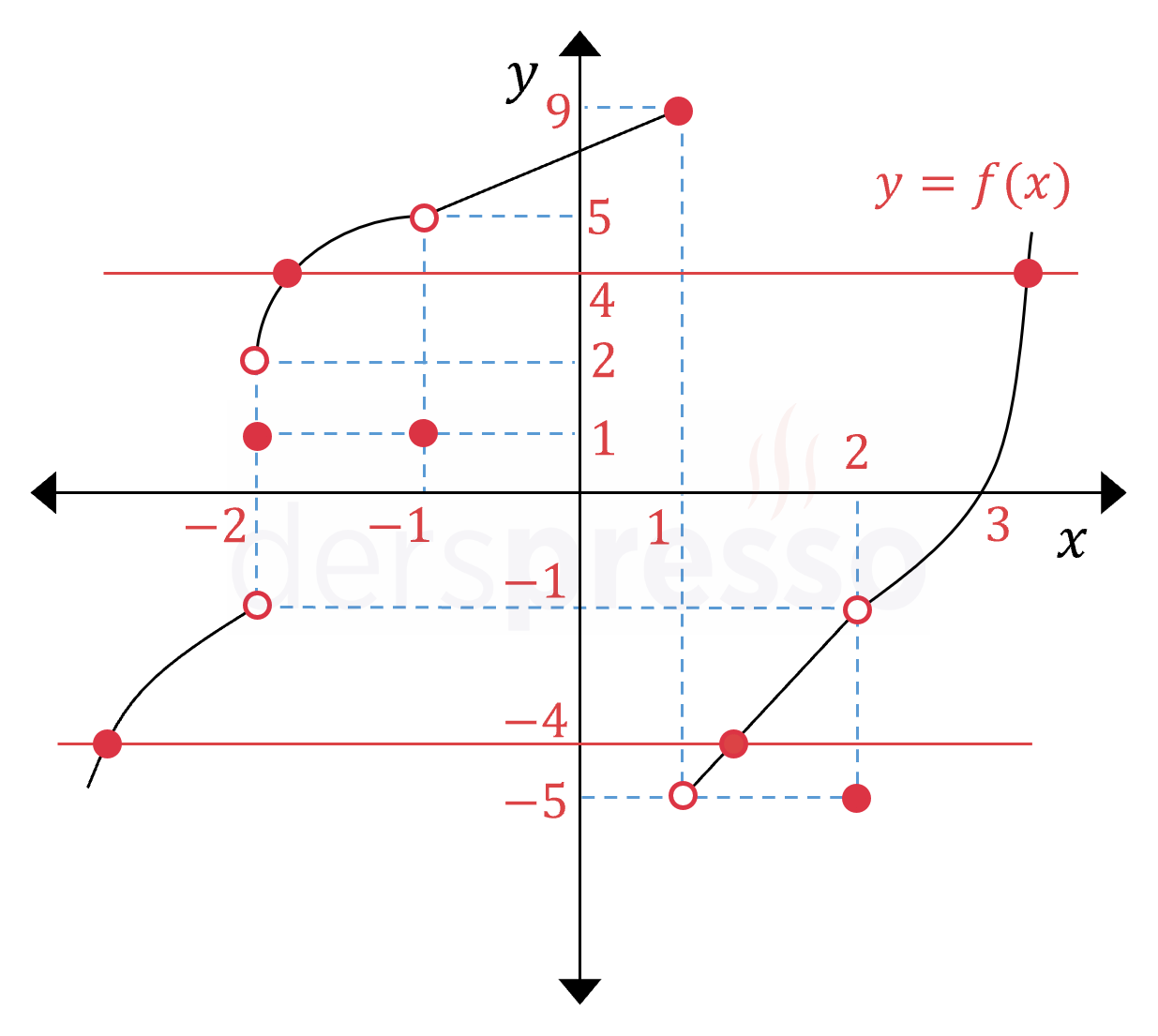
Grafikte görülebileceği gibi, \( y = 4 \) doğrusunun \( f \) eğrisini kestiği 2 noktada \( f(x) = 4 \) olur. Aynı şekilde \( y = -4 \) doğrusunun \( f \) eğrisini kestiği 2 noktada \( f(x) = -4 \) olur.
Buna göre \( g \) fonksiyonu \( 4 + 2 + 2 = 8 \) noktada sürekli değildir.