Denklik Bağıntısı
Bir bağıntı yansıma, simetri ve geçişme özelliklerine sahipse bu bağıntı bir denklik bağıntısıdır.
Bu tanıma göre, \( A \) üzerinde tanımlı aşağıdaki iki bağıntı bu üç özelliğe sahip olduğu için birer denklik bağıntısıdır.
\( A = \{ 1, 2, 3, 4 \} \)
\( R_1 = \{(1, 1), (2, 2), (3, 3), (4, 4)\} \)
\( R_2 = \{(1, 1), (2, 2), (3, 3), (4, 4), \) \( (1, 3), (3, 1), \) \( (2, 4), (4, 2)\} \)
Bir denklik bağıntısında, iki eleman arasında bir ilişki tanımlı ise bu iki eleman bu denklik bağıntısına göre birbirine denktir. Denklik bağıntıları tanımlı oldukları kümenin elemanları arasında bir "eşitlik", "denklik" ya da belirli bir özellikleri açısından "benzerlik" anlamı taşır.
\( x \) ve \( y \) elemanlarının bir \( R \) bağıntısındaki denkliği aşağıdaki şekilde gösterilir.
\( x \equiv y \)
Aşağıda verilen elemanlar arasında belirtilen özelliklerine göre bir denklik ya da benzerlik söz konusu olduğu için, bu kümeleri içeren birer denklik bağıntısı tanımlanabilir.
- 3'e bölündüğünde aynı kalanı veren tam sayılar
- Bir fonksiyona göre görüntüsü aynı olan elemanlar
- Birbirine benzer üçgenler
- Birbirine paralel doğrular
- Doğum günü aynı olan kişiler
- Aynı sınıfta olan öğrenciler
Bir \( A \) kümesi üzerinde tanımlanabilecek en az elemanlı denklik bağıntısı, \( x \in A \) olmak üzere sadece \( (x, x) \) elemanlarından oluşan bağıntıdır. \( A \) üzerinde tanımlanabilecek en çok elemanlı denklik bağıntısı ise \( A \times A \) bağıntısıdır.
Mod 5 işleminin tam sayılarda bir denklik bağıntısı olduğunu gösterelim.
Hatırlatma 1: Mod 5 işlemi bir tam sayının 5'e bölümünden kalanı verir.
Örnek: \( 13 \bmod{5} = 3 \)
Hatırlatma 2: İki sayının 5'e bölümünden kalan aynı ise farkları 5'e tam bölünür (farkları 5'in bir tam sayı katıdır).
\( 5 \mid (a - b) \Leftrightarrow a \equiv b \pmod{5} \)
Örnek: \( 5 \mid (44 - 24) \Leftrightarrow 44 \equiv 24 \pmod{5} \)
Hatırlatma 3: Tüm tam sayılar 0'ı tam böler.
Örnek: \( 5 \mid 0 \)
5'e bölümünden kalanı eşit olan sayılar arasında bir bağıntı tanımlayalım.
\( R = \{(a, b) \mid a, b \in \mathbb{Z}, a \bmod{5} = b \bmod{5}\} \)
\( R \) bağıntısının yansıyan olup olmadığını inceleyelim.
\( \forall a \in \mathbb{Z}, (a, a) \in R \)
Bir sayının 5'e bölümünden kalan kendisinin 5'e bölümünden kalana eşittir.
\( 5 \mid (a - a) \Longrightarrow 5 \mid 0 \)
Buna göre \( R \) yansıyandır.
\( R \) bağıntısının simetrik olup olmadığını inceleyelim.
\( \forall a, b \in \mathbb{Z}, (a, b) \in R \Rightarrow (b, a) \in R \)
\( (a, b) \in R \) ise \( a - b \) farkı 5'in bir tam sayı katı olur.
\( (a, b) \in R \Rightarrow a - b = 5k \)
Eşitliğin taraflarını \( -1 \) ile çarpalım.
\( b - a = 5(-k) \)
\( k \) bir tam sayı olduğu için \( -k \) da bir tam sayıdır. Buna göre \( b - a \) farkı 5'in bir tam sayı katı olarak yazılabilir, dolayısıyla iki sayının 5'e bölümünden kalanlar eşittir.
\( (b, a) \in R \)
Buna göre \( R \) simetriktir.
\( R \) bağıntısının geçişken olup olmadığını inceleyelim.
\( \forall a, b, c \in \mathbb{Z}, (a, b) \in R \land (b, c) \in R \Rightarrow (a, c) \in R \)
\( (a, b) \in R \) ise \( a - b \) farkı 5'in bir tam sayı katı olur.
\( a - b = 5k \)
\( (b, c) \in R \) ise \( b - c \) farkı 5'in bir tam sayı katı olur.
\( b - c = 5m \)
Bulduğumuz iki eşitliğin toplamını alalım.
\( (a - b) + (b - c) = 5k + 5m \)
\( a - c = 5(k + m) \)
\( k \) ve \( m \) tam sayılar olduğu için \( k + m \) de bir tam sayıdır. Buna göre \( a - c \) farkı 5'in bir tam sayı katı olarak yazılabilir, dolayısıyla iki sayının 5'e bölümünden kalanlar eşittir.
\( (a, c) \in R \)
Buna göre \( R \) geçişkendir.
\( R \) bağıntısı tam sayılarda yansıyan, simetrik ve geçişken olduğu için bir denklik bağıntısıdır.
Önceki bölümde yansıyan/simetrik/geçişken iki bağıntının kesişim kümesinin de yansıyan/simetrik/geçişken olduğunu belirtmiştik. Buna göre, iki denklik bağıntısının kesişim kümesi de bir denklik bağıntısıdır.
\( R_1 = \{ (1, 1), (2, 2), (3, 3), (4, 4), \) \( (1, 3), (3, 1) \} \)
\( R_2 = \{ (1, 1), (2, 2), (3, 3), (4, 4), \) \( (2, 4), (4, 2) \} \)
\( R_1 \cap R_2 = \{ (1, 1), (2, 2), \) \( (3, 3), (4, 4) \} \)
Önceki bölümde yansıyan/simetrik/geçişken iki bağıntının birleşim kümesinin yansıyan/simetrik olduğunu, ancak geçişken olmayabileceğini belirtmiştik. Buna göre, iki denklik bağıntısının birleşim kümesi bir denklik bağıntısı olabilir ya da olmayabilir. Aşağıda birleşim kümesi bir denklik bağıntısı olmayan iki denklik bağıntısı örnek olarak verilmiştir. Bu örnekte birleşim kümesinde \( (1, 4) \) ve \( (4, 1) \) elemanları bulunmadığı için birleşim kümesi geçişme özelliğine sahip değildir.
\( R_1 = \{ (1, 1), (2, 2), (3, 3), (4, 4), \) \( (1, 3), (3, 1) \} \)
\( R_2 = \{ (1, 1), (2, 2), (3, 3), (4, 4), \) \( (3, 4), (4, 3) \} \)
\( R_1 \cup R_2 = \{ (1, 1), (2, 2), (3, 3), (4, 4), \) \( (1, 3), (3, 1) \) \( (3, 4), (4, 3) \} \)
Denklik Sınıfları
\( A \) kümesinde tanımlı bir \( R \) denklik bağıntısında \( a \in A \) elemanı ile ilişkili olan tüm elemanların kümesine \( a \) elemanının denklik sınıfı denir ve \( [a]_R \) ile gösterilir.
\( [a]_R = \{x \mid (x, a) \in R\} \)
\( A = \{a, b, c, d, e\} \)
\( R \), \( A \)'da tanımlı bir bağıntı olmak üzere,
\( R = \{(a, a), (b, b), (c, c), (d, d), \) \( (e, e), (a, b), (b, a), (a, c), \) \( (c, a), (b, c), (c, b), (d, e), \) \( (e, d)\} \)
\( R \) bağıntısının iki farklı denklik sınıfı vardır.
\( [a]_R = [b]_R = [c]_R = \{a, b, c\} \)
\( [d]_R = [e]_R = \{d, e\} \)
\( x, y \in A \) olmak üzere, \( x \) ve \( y \) elemanları arasında \( R \) denklik bağıntısına göre bir ilişki tanımlı ise iki eleman bu bağıntıya göre denktir ve denklik sınıfları aynıdır.
\( (x, y) \in R \Leftrightarrow [x]_R = [y]_R \)
\( x \) ve \( y \) elemanlarının denklik sınıflarının ortak bir elemanı varsa bu iki elemanın denklik sınıfları aynıdır ve iki eleman denktir.
\( [x]_R \cap [y]_R \ne \emptyset \Leftrightarrow (x, y) \in R \Leftrightarrow [x]_R = [y]_R \)
Bir denklik bağıntısında \( x \in A \) elemanının denklik sınıfı, \( x \) elemanına denk olan tüm elemanların kümesidir.
- \( A \) kümesinin her elemanı tek bir denklik sınıfının elemanıdır.
- \( A \) kümesinin iki elemanı denk ise denklik sınıfları aynıdır.
- Denklik sınıfları ikili ayrıktır, yani herhangi iki denklik sınıfının kesişim kümesi boş kümedir.
- İki denklik sınıfı ya ayrık ya da eşit kümelerdir.
1. örnekte bir denklik bağıntısı olduğunu gösterdiğimiz mod 5 bağıntısının denklik sınıflarını bulalım.
Mod 5 işleminin \( [0]_R, [1]_R, [2]_R, [3]_R, [4]_R \) olmak üzere 5 denklik sınıfı vardır.
\( [0]_R = \{x \mid x \in \mathbb{Z}, x \equiv 0 \pmod{5}\} \)
\( = \{\ldots, -10, -5, 0, 5, 10, \ldots\} \)
\( [1]_R = \{x \mid x \in \mathbb{Z}, x \equiv 1 \pmod{5}\} \)
\( = \{\ldots, -9, -4, 1, 6, 11, \ldots\} \)
\( \ldots \)
\( [4]_R = \{x \mid x \in \mathbb{Z}, x \equiv 4 \pmod{5}\} \)
\( = \{\ldots, -6, -1, 4, 9, 14, \ldots\} \)
Denklik Sınıflarının Parçalanışları
Sayma konusundaki kümelerin parçalanışı bölümünde bir kümenin parçalanışını; kümenin elemanlarının, her eleman sadece bir alt kümeye dahil olacak, alt kümelerin hiçbiri boş küme olmayacak ve alt kümelerin birleşimi orijinal kümeyi verecek şekilde alt kümelere bölünmesi şeklinde tanımlamıştık.
Bir \( A \) kümesi tanımlayalım ve elemanlarını 4 parçaya/alt kümeye ayıralım.
\( A = \{ 1, 2, 3, 4, 5, 6, 7, 8, 9 \} \)
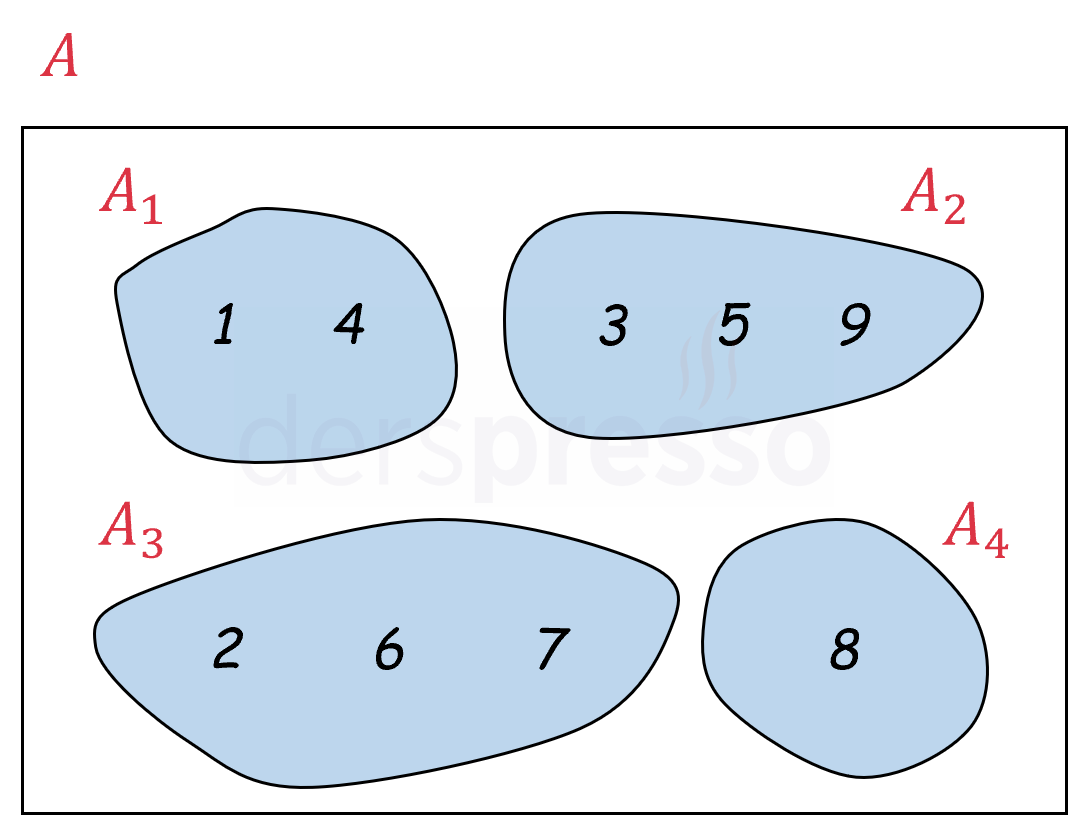
\( A \) kümesinin yukarıdaki örnek parçalanışının küme gösterimi aşağıdaki gibidir.
\( \{ \{1, 4\}, \{3, 5, 9\}, \{2, 6, 7\}, \{8\} \} \)
Kümelerin parçalanışını aşağıdaki şekilde tanımlayabiliriz.
\( A_1, A_2, \ldots, A_k \) kümeleri \( n \) elemanlı \( A \) kümesinin birer alt kümesi ve \( 1 \le k \le n \) olmak üzere,
\( A_1, A_2, \ldots, A_k \) alt kümeleri aşağıdaki üç koşulu sağlıyorsa \( A \) kümesinin bir parçalanışıdır.
(1) \( A_1 \ne \emptyset, A_2 \ne \emptyset, \ldots, A_k \ne \emptyset \)
(2) \( A_1 \cup A_2 \cup \ldots \cup A_k = A \)
(3) \( i \ne j \Longrightarrow A_i \cap A_j = \emptyset \)
Bu tanımdaki birinci koşula göre parçaların (alt kümelerin) hiçbiri boş küme olamaz, ikinci koşula göre parçaların birleşimi \( A \) kümesini verir (hiçbir eleman açıkta kalmaz), üçüncü koşula göre bir eleman sadece tek parçaya ait olabilir (parçalar ikili ayrık kümelerdir).
Bu tanıma göre, \( A \) kümesinde tanımlı bir denklik bağıntısının tüm denklik sınıfları \( A \) kümesinin bir parçalanışıdır. Bir diğer ifadeyle, \( A \) kümesinin her parçalanışı \( A \) kümesinde tanımlı bir denklik bağıntısı oluşturur.
\( A = \{a, b, c, d\} \) üzerinde tanımlı,
\( R = \{(a, a), (b, b), (c, c), (d, d), (a, d), (a, c), (c, a)\} \)
bağıntısının bir denklik bağıntısı olup olmadığını gösterin.
Çözümü GösterBir bağıntı yansıma, simetri ve geçişme özelliklerine sahipse bu bağıntı bir denklik bağıntısıdır.
\( (a, a), (b, b), (c, c), (d, d) \in R \) olduğu için \( R \) yansıma özelliğine sahiptir.
\( (a, d) \in R \) iken \( (d, a) \notin R \) olduğu için \( R \) simetri özelliğine sahip değildir.
\( R \) simetri özelliğine sahip olmadığı için \( A \) üzerinde bir denklik bağıntısı değildir.
\( \mathbb{Z} \) üzerinde tanımlı,
\( R = \{(a, b) \mid a^3 = b^3; a, b \in \mathbb{Z}\} \)
bağıntısının bir denklik bağıntısı olup olmadığını gösterin.
Çözümü GösterBir bağıntı yansıma, simetri ve geçişme özelliklerine sahipse bu bağıntı bir denklik bağıntısıdır.
Her \( a \in \mathbb{Z} \) için \( a^3 = a^3 \) olduğu için \( (a, a) \in R \) olur.
Buna göre \( R \) yansıma özelliğine sahiptir.
\( a, b \in \mathbb{Z} \) olmak üzere, \( (a, b) \in R \) ise \( a^3 = b^3 \) olur. Bu durumda \( b^3 = a^3 \) de doğru olacağı için \( (b, a) \in R \) olur.
Buna göre \( R \) simetri özelliğine sahiptir.
\( a, b, c \in \mathbb{Z} \) olmak üzere, \( (a, b), (b, c) \in R \) ise \( a^3 = b^3 \) ve \( b^3 = c^3 \) olur, dolayısıyla \( a^3 = b^3 = c^3 \) ve \( (a, c) \in R \) olur.
Buna göre \( R \) geçişme özelliğine sahiptir.
\( R \) bağıntısı yansıma, simetri ve geçişme özelliklerine sahip olduğu için bir denklik bağıntısıdır.
Tam sayılar (\( \mathbb{Z} \)) kümesinde tanımlı "\( = \)" bağıntısının denklik bağıntısı olup olmadığını gösterin.
Çözümü GösterTam sayılar kümesinde "\( = \)" bağıntısını tanımlayalım.
\( R = \{ (a, b) \mid a, b \in \mathbb{Z}, a = b\} \)
\( R \) bağıntısının özelliklerini inceleyelim.
Bir tam sayı kendisine eşittir.
\( a = a \)
Buna göre her \( a \in \mathbb{Z} \) için \( (a, a) \in R \) olur, dolayısıyla bağıntının yansıma özelliği vardır.
\( a \) sayısı \( b \) sayısına eşitse \( b \) sayısı da \( a \) sayısına eşittir.
\( a = b \) ise \( b = a \)
Buna göre \( (a, b) \in R \) ise \( (b, a) \in R \) olur, dolayısıyla bağıntının simetri özelliği vardır.
\( a \) sayısı \( b \) sayısına eşitse, \( b \) sayısı da \( c \) sayısına eşitse \( a \) sayısı \( c \) sayısına eşittir.
\( a = b \) ve \( b = c \) ise \( a = c \)
Buna göre \( (a, b) \in R \) ve \( (b, c) \in R \) ise \( (a, c) \in R \) olur, dolayısıyla bağıntının geçişme özelliği vardır.
Sonuç olarak, tam sayılar kümesinde tanımlı "\( = \)" bağıntısının yansıma, simetri ve geçişme özellikleri vardır, dolayısıyla "\( = \)" bağıntısı bir denklik bağıntısıdır.
Tam sayılar (\( \mathbb{Z} \)) kümesinde tanımlı "\( \ne \)" bağıntısının denklik bağıntısı olup olmadığını gösterin.
Çözümü GösterTam sayılar kümesinde "\( \ne \)" bağıntısını tanımlayalım.
\( R = \{ (a, b) \mid a, b \in \mathbb{Z}, a \ne b\} \)
\( R \) bağıntısının özelliklerini inceleyelim.
Bir tam sayı kendisine eşittir.
\( a = a \)
Buna göre her \( a \in \mathbb{Z} \) için \( (a, a) \notin R \) olur, dolayısıyla bağıntının yansıma özelliği yoktur.
\( a \) sayısı \( b \) sayısına eşit değilse \( b \) sayısı da \( a \) sayısına eşit değildir.
\( a \ne b \) ise \( b \ne a \)
Buna göre \( (a, b) \in R \) ise \( (b, a) \in R \) olur, dolayısıyla bağıntının simetri özelliği vardır.
\( a \) sayısı \( b \) sayısına eşit değilse, \( b \) sayısı da \( c \) sayısına eşit değilse \( a \) sayısı \( c \) sayısına eşit olabilir ya da olmayabilir.
\( 1 \ne 3 \) ve \( 3 \ne 1 \) ise \( 1 \ne 1 \) değildir.
Buna göre \( (a, b) \in R \) ve \( (b, c) \in R \) ise \( (a, c) \in R \) olmayabilir, dolayısıyla bağıntının geçişme özelliği yoktur.
Sonuç olarak, tam sayılar kümesinde tanımlı "\( \ne \)" bağıntısının simetri özelliği vardır, yansıma ve geçişme özellikleri ise yoktur, dolayısıyla "\( \ne \)" bağıntısı bir denklik bağıntısı değildir.
\( \mathbb{Z} \) üzerinde tanımlı,
\( R = \{(a, b) \mid a^2 + b^2 \text{ çift sayı}; a, b \in \mathbb{Z}\} \)
bağıntısının bir denklik bağıntısı olup olmadığını gösterin.
Çözümü GösterBir bağıntı yansıma, simetri ve geçişme özelliklerine sahipse bu bağıntı bir denklik bağıntısıdır.
Her \( a \in \mathbb{Z} \) için \( a^2 + a^2 = 2a^2 \) sayısı çifttir, dolayısıyla \( (a, a) \in R \) olur.
Buna göre \( R \) yansıma özelliğine sahiptir.
\( a, b \in \mathbb{Z} \) olmak üzere, \( (a, b) \in R \) ise \( a^2 + b^2 \) çift olur. \( a^2 + b^2 = b^2 + a^2 \) olduğu için \( b^2 + a^2 \) de çift olur ve \( (b, a) \in R \) olur.
Buna göre \( R \) simetri özelliğine sahiptir.
\( a^2 + b^2 \) çift ise \( a \) ve \( b \) sayılarının ya ikisi de çifttir ya da ikisi de tektir.
\( a, b, c \in \mathbb{Z} \) olmak üzere, \( (a, b), (b, c) \in R \) ise \( a^2 + b^2 \) ve \( b^2 + c^2 \) çifttir, buna göre üç sayı ya birlikte çifttir ya da birlikte tektir. \( a \) ve \( c \) birlikte çift ya da birlikte tek oldukları için \( a^2 + c^2 \) çift olur ve \( (a, c) \in R \) olur.
Buna göre \( R \) geçişme özelliğine sahiptir.
\( R \) bağıntısı yansıma, simetri ve geçişme özelliklerine sahip olduğu için bir denklik bağıntısıdır.