Bağıntı İşlemleri
Bu bölümde bağıntılar arasında küme işlemlerini, bir bağıntının tersini ve bağıntılar arasında bileşke işlemini inceleyeceğiz.
Küme İşlemleri
Bağıntılar sıralı ikililerden oluşan kümeler oldukları için aralarında kesişim, birleşim, fark ve tümleyen gibi küme işlemleri yapılabilir.
\( A = \{a, b, c\} \)
\( B = \{1, 2\} \)
\( R \) ve \( S \) bağıntıları, \( A \) kümesinden \( B \) kümesine tanımlı olmak üzere,
\( R = \{(a, 1), (b, 1), (c, 2)\} \)
\( S = \{(a, 1), (b, 2), (c, 2)\} \)
İki bağıntının kesişim kümesi, her iki bağıntıda da bulunan ikililerden oluşur.
\( R \cap S = \{(x, y) \mid (x, y) \in R \land (x, y) \in S\} \)
\( R \cap S = \{(a, 1), (c, 2)\} \)
İki bağıntının birleşim kümesi, bağıntıların en az birinde bulunan ikililerden oluşur.
\( R \cup S = \{(x, y) \mid (x, y) \in R \lor (x, y) \in S\} \)
\( R \cup S = \{(a, 1), (b, 1), (b, 2), (c, 2)\} \)
Bir bağıntının diğer bir bağıntıdan farkı, birinci kümede bulunup ikinci kümede bulunmayan ikililerden oluşur.
\( R - S = \{(x, y) \mid (x, y) \in R \land (x, y) \notin S\} \)
\( R - S = \{(b, 1)\} \)
\( S - R = \{(b, 2)\} \)
Bir bağıntının tümleyeni, bağıntıda bulunmayıp alt kümesi olduğu kartezyen çarpım kümesinin elemanı olan ikililerden oluşur.
\( R' = \{(x, y) \mid (x, y) \notin R \land (x, y) \in A \times B\} \)
\( R' = \{(a, 2), (b, 2), (c, 1)\} \)
\( S' = \{(a, 2), (b, 1), (c, 1)\} \)
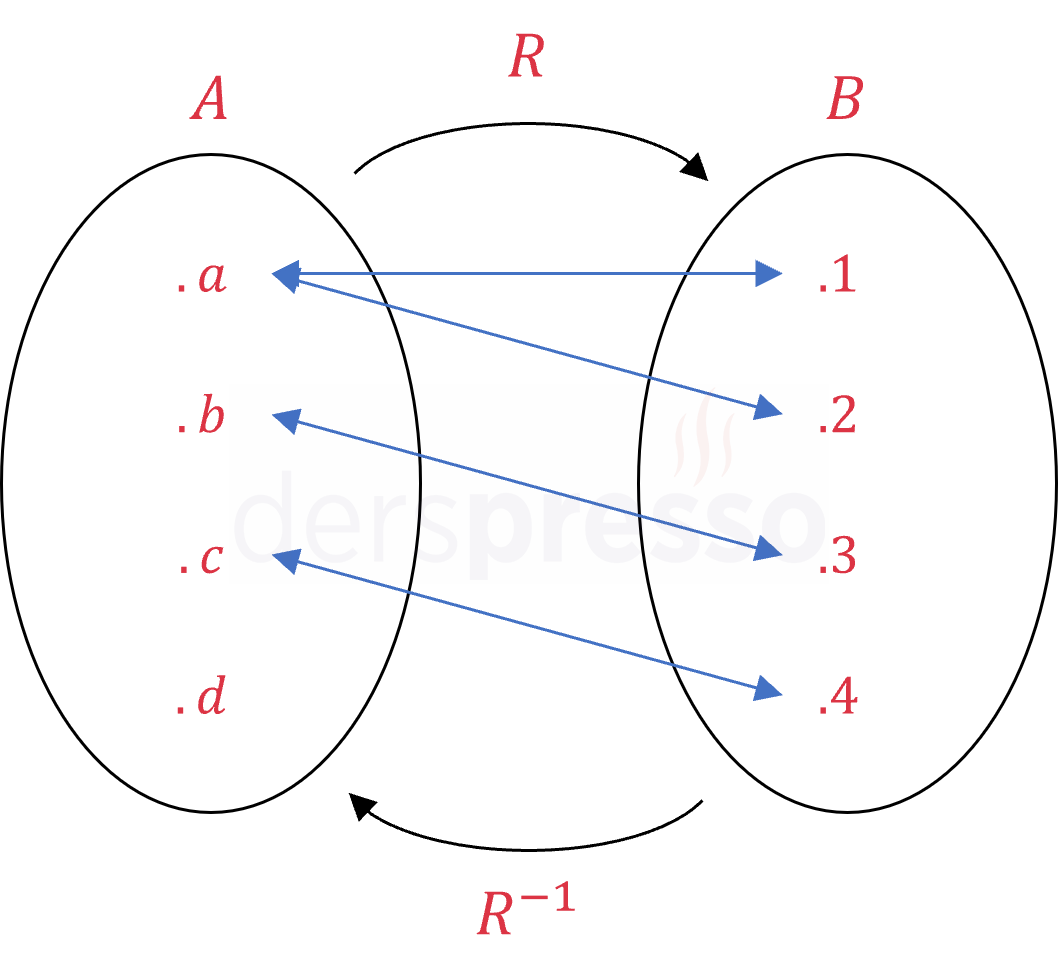
Bir Bağıntının Tersi
Bir \( R \) bağıntısının tüm elemanlarının bileşenlerinin aralarında yer değiştirmesi ile elde edilen bağıntıya \( R \) bağıntısının tersi denir ve \( R^{-1} \) şeklinde gösterilir.
\( R^{-1} = \{(y, x) \mid (x, y) \in R\} \)
\( R = \{(\textcolor{red}{a}, \textcolor{blue}{1}), (\textcolor{red}{a}, \textcolor{blue}{2}), (\textcolor{red}{b}, \textcolor{blue}{3}), (\textcolor{red}{c}, \textcolor{blue}{4})\} \)
\( R^{-1} = \{(\textcolor{blue}{1}, \textcolor{red}{a}), (\textcolor{blue}{2}, \textcolor{red}{a}), (\textcolor{blue}{3}, \textcolor{red}{b}), (\textcolor{blue}{4}, \textcolor{red}{c})\} \)
\( R \) bağıntısı \( A \) kümesinden \( B \) kümesine tanımlı ve \( A \times B \) kartezyen çarpımının bir alt kümesi iken tersi olan \( R^{-1} \) bağıntısı \( B \) kümesinden \( A \) kümesine tanımlıdır ve \( B \times A \) kartezyen çarpımının bir alt kümesidir.
Ters Bağıntı İşlem Kuralları
Bir \( (a, b) \) ikilisi \( R \) bağıntısının elemanı ise \( (b, a) \) ikilisi \( R^{-1} \) bağıntısının elemanıdır.
\( (a, b) \in R \Leftrightarrow (b, a) \in R^{-1} \)
Bir bağıntının ve tersinin eleman sayıları aynıdır.
Bir bağıntının tersinin tersi bağıntının kendisine eşittir.
\( (R^{-1})^{-1} = R \)
İSPATI GÖSTER
\( A \)'dan \( B \)'ye bir \( R \) bağıntısı tanımlayalım.
\( R \) bağıntısının tersinin tersinin kendisine eşit olduğunu gösterelim.
\( (a, b) \in R \) olsun.
Ters bağıntı tanımına göre, bir bağıntının elemanı olan \( (a, b) \) ikilisinin tersi olan \( (b, a) \) ikilisi bağıntının tersinin elemanı olur.
\( (b, a) \in R^{-1} \)
Ters bağıntı tanımına göre, bir bağıntının elemanı olan \( (b, a) \) ikilisinin tersi olan \( (a, b) \) ikilisi bağıntının tersinin elemanı olur.
\( (a, b) \in (R^{-1})^{-1} \)
Buna göre \( R \) bağıntısının tersinin tersi kendisine eşittir.
\( (R^{-1})^{-1} = R \)
İki bağıntının kesişim kümesinin tersi, terslerinin kesişim kümesine eşittir.
\( (R \cap S)^{-1} = R^{-1} \cap S^{-1} \)
İSPATI GÖSTER
\( A \)'dan \( B \)'ye \( R \) ve \( S \) bağıntıları tanımlayalım.
İki bağıntının kesişim kümesinin tersinin, terslerinin kesişim kümesine eşit olduğunu gösterelim.
\( (b, a) \) ikilisi kesişim kümesinin tersinin elemanı olsun.
\( (b, a) \in (R \cap S)^{-1} \)
Ters bağıntı tanımına göre, \( (a, b) \) ikilisi kesişim kümesinin elemanı olur.
\( (a, b) \in R \cap S \)
Kesişim kümesi tanımına göre, \( (a, b) \) ikilisi iki kümenin de elemanı olur.
\( (a, b) \in R \land (a, b) \in S \)
Ters bağıntı tanımına göre, \( (b, a) \) ikilisi iki kümenin tersinin de elemanı olur.
\( (b, a) \in R^{-1} \land (b, a) \in S^{-1} \)
Kesişim kümesi tanımına göre, \( (b, a) \) ikilisi iki kümenin terslerinin kesişim kümesinin elemanı olur.
\( (b, a) \in R^{-1} \cap S^{-1} \)
Buna göre iki bağıntının kesişim kümesinin tersi, terslerinin kesişim kümesine eşittir.
\( (R \cap S)^{-1} = R^{-1} \cap S^{-1} \)
İki bağıntının birleşim kümesinin tersi, terslerinin birleşim kümesine eşittir.
\( (R \cup S)^{-1} = R^{-1} \cup S^{-1} \)
İSPATI GÖSTER
\( A \)'dan \( B \)'ye \( R \) ve \( S \) bağıntıları tanımlayalım.
İki bağıntının birleşim kümesinin tersinin, terslerinin birleşim kümesine eşit olduğunu gösterelim.
\( (b, a) \) ikilisi birleşim kümesinin tersinin elemanı olsun.
\( (b, a) \in (R \cup S)^{-1} \)
Ters bağıntı tanımına göre, \( (a, b) \) ikilisi birleşim kümesinin elemanı olur.
\( (a, b) \in R \cup S \)
Birleşim kümesi tanımına göre, \( (a, b) \) ikilisi iki kümeden en az birinin elemanı olur.
\( (a, b) \in R \lor (a, b) \in S \)
Ters bağıntı tanımına göre, \( (b, a) \) ikilisi iki kümenin tersinden en az birinin elemanı olur.
\( (b, a) \in R^{-1} \lor (b, a) \in S^{-1} \)
Birleşim kümesi tanımına göre, \( (b, a) \) ikilisi iki kümenin terslerinin birleşim kümesinin elemanı olur.
\( (b, a) \in R^{-1} \cup S^{-1} \)
Buna göre iki bağıntının birleşim kümesinin tersi, terslerinin birleşim kümesine eşittir.
\( (R \cup S)^{-1} = R^{-1} \cup S^{-1} \)
Bir bağıntının diğer bir bağıntıdan farkının tersi, bağıntıların terslerinin farkına eşittir.
\( (R - S)^{-1} = R^{-1} - S^{-1} \)
İSPATI GÖSTER
\( A \)'dan \( B \)'ye \( R \) ve \( S \) bağıntıları tanımlayalım.
İki bağıntının farkının tersinin, terslerinin farkına eşit olduğunu gösterelim.
\( (b, a) \) ikilisi fark kümesinin tersinin elemanı olsun.
\( (b, a) \in (R - S)^{-1} \)
Ters bağıntı tanımına göre, \( (a, b) \) ikilisi fark kümesinin elemanı olur.
\( (a, b) \in R - S \)
Fark kümesi tanımına göre, \( (a, b) \) ikilisi birinci kümenin elemanı iken ikinci kümenin elemanı değildir.
\( (a, b) \in R \land (a, b) \notin S \)
Ters bağıntı tanımına göre, \( (b, a) \) ikilisi birinci kümenin tersinin elemanı iken ikinci kümenin tersinin elemanı değildir.
\( (b, a) \in R^{-1} \land (b, a) \notin S^{-1} \)
Elde ettiğimiz ifade \( R^{-1} - S^{-1} \) fark kümesinin tanımıdır.
\( (b, a) \in R^{-1} - S^{-1} \)
Buna göre iki bağıntının farkının tersi, bağıntıların terslerinin farkına eşittir.
\( (R - S)^{-1} = R^{-1} - S^{-1} \)
\( A \)'dan \( B \)'ye tanımlı \( R \) ve \( S \) bağıntıları arasında geçerli olan diğer bazı işlem kuralları aşağıdaki gibidir.
\( R \subseteq S \) ise \( R^{-1} \subseteq S^{-1} \)
\( (A \times B)^{-1} = B \times A \)
Bağıntıların Bileşkesi
\( A \) kümesinden \( B \) kümesine bir \( R \) bağıntısı, \( B \) kümesinden \( C \) kümesine bir \( S \) bağıntısı tanımlayalım.
\( S \circ R \) bileşke bağıntısı \( R \) bağıntısının her elemanının birinci bileşenini, elemanın \( R \) bağıntısına göre görüntüsünün \( S \) bağıntısına göre görüntüsü ile eşler.
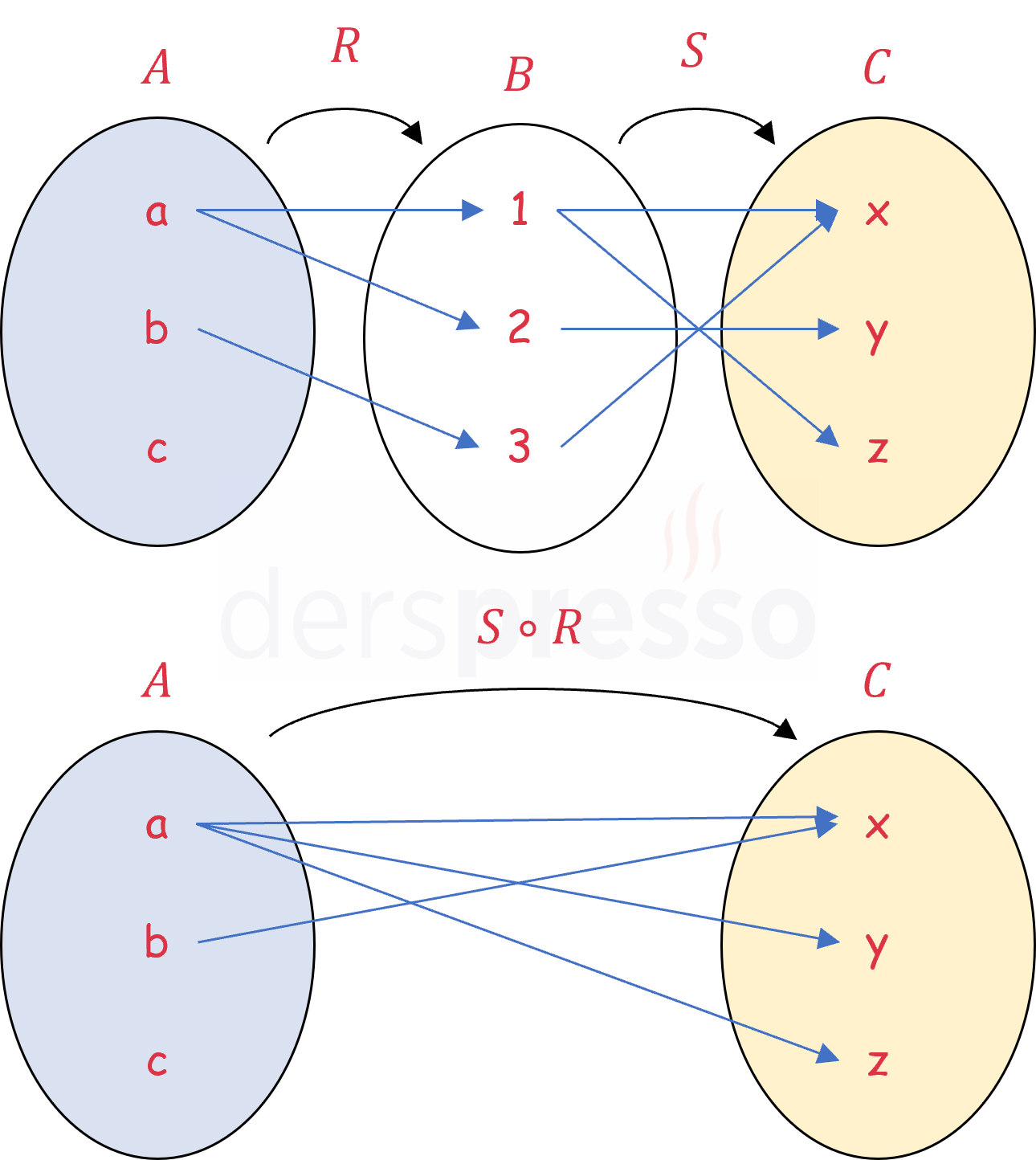
\( S \circ R = \{(x, z) \in A \times C \mid \exists y \in B, (x, y) \in R \land (y, z) \in S\} \)
\( A = \{a, b, c\} \)
\( B = \{1, 2, 3\} \)
\( C = \{x, y, z\} \)
\( R = \{(a, 1), (a, 2), (b, 3)\} \)
\( S = \{(1, x), (1, z), (2, y), (3, x)\} \)
\( S \circ R = \{(a, x), (a, y), (a, z), (b, x)\} \)
Bileşke İşlem Kuralları
İki bağıntının bileşkesinin tersi, bağıntıların terslerinin ters sırada bileşkesine eşittir.
\( (S \circ R)^{-1} = R^{-1} \circ S^{-1} \)
İSPATI GÖSTER
\( A \) kümesinden \( B \) kümesine bir \( R \) bağıntısı, \( B \) kümesinden \( C \) kümesine bir \( S \) bağıntısı tanımlayalım.
\( S \circ R \) için bileşke bağıntı tanımını yazalım.
\( S \circ R = \{(x, z) \in A \times C \mid \exists y \in B, (x, y) \in R \land (y, z) \in S\} \)
Bir bağıntının tersi, bağıntının elemanı olan tüm \( (x, y) \) ikililerini tersine çevirir.
\( (S \circ R)^{-1} = \{(z, x) \mid (x, z) \in S \circ R\} \)
\( = \{(z, x) \in C \times A \mid \exists y \in B, (x, y) \in R \land (y, z) \in S\} \)
Küme tanımını düzenleyelim.
\( = \{(z, x) \in C \times A \mid \exists y \in B, (y, z) \in S \land (x, y) \in R\} \)
\( (x, y) \) ikilisi bir bağıntının elemanı ise \( (y, x) \) ikilisi bağıntının tersinin elemanı olur.
\( = \{(z, x) \in C \times A \mid \exists y \in B, (z, y) \in S^{-1} \land (y, x) \in R^{-1}\} \)
Elde ettiğimiz ifade bağıntıların terslerinin bileşkesinin tanımıdır.
\( = R^{-1} \circ S^{-1} \)
Bileşke bağıntılarla ilgili diğer bazı işlem kuralları aşağıdaki gibidir.
\( T \circ (S \circ R) = (T \circ S) \circ R \)
\( R \circ I_A = I_A \circ R = R \)
Reel sayılarda tanımlı,
\( R = \{ (x, y) \mid x + 2y = 15 \} \) bağıntısı veriliyor.
Buna göre \( R \cap R^{-1} \) kümesini bulunuz.
Çözümü Göster\( R = \{ (x, y) \mid x + 2y = 15 \} \)
\( R^{-1} \) bağıntısı \( R \) bağıntısındaki her \( (x, y) \) elemanı için \( (y, x) \) elemanlarından oluşur.
\( R^{-1} \) bağıntısını bulmak için verilen eşitlikte \( x \) ve \( y \) değişkenlerinin yerini değiştirelim.
\( R^{-1} = \{ (y, x) \mid y + 2x = 15 \} \)
İki bağıntının elemanlarının kesişim kümesini bulmak için denklemleri ortak çözelim.
\( x + 2y = 15 \)
\( y + 2x = 15 \)
İkinci denklemi -2 ile çarpalım ve denklemleri taraf tarafa toplayalım.
\( -3x = -15 \)
\( x = 5 \)
Birinci denklemde \( x = 5 \) yazarak \( y \)'yi bulalım.
\( 5 + 2y = 15 \)
\( y = 5 \)
Buna göre \( R \cap R^{-1} \) kümesinin tek elemanı vardır.
\( R \cap R^{-1} = \{ (5, 5) \} \)