Doğrunun Denkleminin Bulunması
Bir doğruyu çizebilmek için ya doğrunun iki farklı noktası ya da bir noktası ve eğimi bilinmelidir.
- Doğrunun bir noktası ve eğimi
- Doğrunun herhangi iki farklı noktası
- Doğrunun eksenleri kestiği iki nokta
Bir Noktası ve Eğimi Bilinen Doğru
Bir noktası ve eğimi bilinen doğrunun denklemi aşağıdaki formülle bulunabilir.
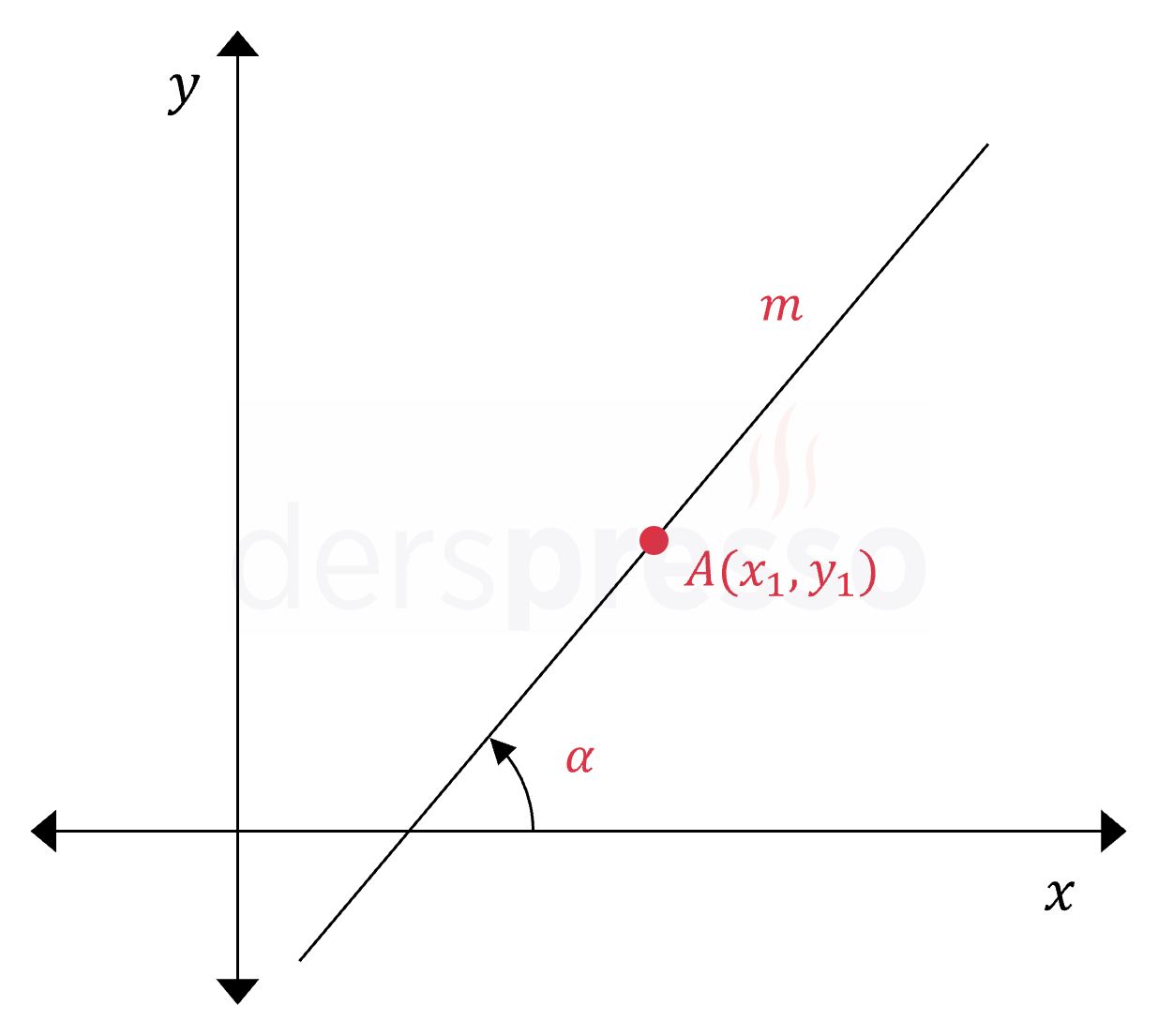
\( A(x_1, y_1) \) noktasından geçen ve eğimi \( m \) olan doğrunun denklemi:
\( y - y_1 = m(x - x_1) \)
\( A(3, -5) \) noktasından geçen ve eğimi \( m = -2 \) olan doğrunun denklemi:
\( y - (-5) = -2(x - 3) \)
\( y + 5 = -2x + 6 \)
\( y = -2x + 1 \)
Bu denklemde \( m \) yalnız bırakıldığında, bu denklemin verilen nokta ile arasındaki eğimin \( m \)'ye eşit olduğu noktaların geometrik yer denklemi olduğu görülebilir.
\( m = \dfrac{y - y_1}{x - x_1} \)
İki Noktası Bilinen Doğru
Farklı iki noktası bilinen doğrunun denklemi aşağıdaki formülle bulunabilir.

\( A(x_1, y_1) \) ve \( B(x_2, y_2) \) noktalarından geçen doğrunun denklemi:
\( \dfrac{y - y_2}{x - x_2} = \dfrac{y_2 - y_1}{x_2 - x_1} \)
\( A(-2, -3) \) ve \( B(4, 9) \) noktalarından geçen doğrunun denklemi ve eğimi:
\( \dfrac{y - 9}{x - 4} = \dfrac{9 - (-3)}{4 - (-2)} \)
\( \dfrac{y - 9}{x - 4} = \dfrac{12}{6} \)
\( y - 9 = 2(x - 4) \)
\( y = 2x + 1 \)
\( m = 2 \)
Bu formülde eşitliğin sağ tarafı verilen iki nokta arasındaki eğime eşit olduğu için bu formül bir noktası ve eğimi bilinen doğru denklemine de dönüştürülebilir.
\( \dfrac{y - y_2}{x - x_2} = \dfrac{y_2 - y_1}{x_2 - x_1} = m \)
Eksenleri Kestiği Noktalar Bilinen Doğru
Bir doğrunun eksenleri kestiği noktalar biliniyorsa yukarıdaki iki noktası bilinen doğrunun denklem formülüne ek olarak aşağıdaki formül de kullanılabilir.

\( \dfrac{x}{x_1} + \dfrac{y}{y_2} = 1 \)
Bu denklem aşağıdaki biçimde de yazılabilir.
\( y_2\ x + x_1\ y = x_1\ y_2 \)
Doğrunun eğimi: \( m = \tan{\alpha} = -\dfrac{y_2}{x_1} \)
Eksenleri \( A(3, 0) \) ve \( B(0, 4) \) noktalarında kesen doğrunun denklemi ve eğimi:
\( \dfrac{x}{3} + \dfrac{y}{4} = 1 \)
\( 4x + 3y = 12 \)
\( y = -\dfrac{4}{3}x + 4 \)
\( m = -\dfrac{4}{3} \)
İSPATI GÖSTER
İki noktası bilinen doğrunun denklemini yazalım.
\( \dfrac{y - y_2}{x - x_2} = \dfrac{y_2 - y_1}{x_2 - x_1} \)
İçleri aralarında yer değiştirelim.
\( \dfrac{y - y_2}{y_2 - y_1} = \dfrac{x - x_2}{x_2 - x_1} \)
Bu iki noktanın bildiğimiz birer koordinatını denklemde yerine koyalım.
\( A(x_1, y_1) = A(x_1, 0) \)
\( B(x_2, y_2) = A(0, y_2) \)
\( \dfrac{y - y_2}{y_2 - 0} = \dfrac{x - 0}{0 - x_1} \)
\( \dfrac{y - y_2}{y_2} = -\dfrac{x}{x_1} \)
Eşitliğin sol tarafını yeniden düzenleyelim.
\( \dfrac{y}{y_2} - \dfrac{y_2}{y_2} = -\dfrac{x}{x_1} \)
\( \dfrac{y}{y_2} - 1 = -\dfrac{x}{x_1} \)
Değişkenli terimleri sol tarafa alırsak eksenleri kestiği noktalar bilinen doğrunun denklemini elde ederiz.
\( \dfrac{x}{x_1} + \dfrac{y}{y_2} = 1 \)
Orijinden Geçen Doğru
Orijinden geçen doğrular \( O(0, 0) \) noktasından geçtiği için sabit terimleri sıfırdır ve denklemleri aşağıdaki formdadır.
\( y = mx + 0 = mx \)
Orijinden geçen ve eğimi \( m = 4 \) olan doğrunun denklemi:
\( y = 4x \)
\( A(2, 3) \) noktasından geçen ve eğimi sıfır olan doğrunun denklemi nedir?
Çözümü GösterEğimi sıfır olan doğru \( x \) eksenine paralel yatay bir doğrudur ve tüm \( x \) değerleri için \( y \) değeri sabittir.
Bu doğru \( A(2, 3) \) noktasından geçtiği için denklemi \( y = 3 \) olur.
Denklemi bir noktası ve eğimi bilinen doğrunun denklem formülü ile de bulabiliriz.
\( y - y_1 = m(x - x_1) \)
\( y - 3 = 0(x - 2) \)
\( y = 3 \)
Analitik düzlemde \( 2x + 3y - 7 = 0 \) doğrusuna paralel olan ve \( A(-1, 2) \) noktasından geçen doğrunun denklemini bulunuz.
Çözümü GösterDenklemi \( ax + by + c = 0 \) formunda olan doğrunun eğimi \( m = -\frac{a}{b} \) olur.
\( 2x + 3y - 7 = 0 \)
\( m = -\dfrac{2}{3} \)
\( 2x + 3y - 7 = 0 \) doğrusuna paralel olan tüm doğruların eğimi birbirine eşittir.
\( A(-1, 2) \) noktasından geçen ve eğimi \( -\frac{2}{3} \) olan doğrunun denklemini bulalım.
\( y - y_1 = m(x - x_1) \)
\( y - 2 = -\dfrac{2}{3}(x - (-1)) \)
\( 3y - 6 = -2x - 2 \)
İstenen doğrunun denklemi aşağıdaki gibi bulunur.
\( 2x + 3y - 4 = 0 \)
Koordinat düzleminde \( A(2, -1) \) ve \( B(-3, 4) \) noktalarından geçen doğrunun üzerindeki ordinatı 7 olan noktanın apsisi kaçtır?
Çözümü GösterOrdinatı 7 olan noktaya \( C \) noktası, apsisine \( a \) diyelim.
\( C(a, 7) \)
İki noktası bilinen doğrunun denklemini bulalım.
\( \dfrac{y - y_2}{x - x_2} = \dfrac{y_2 - y_1}{x_2 - x_1} \)
\( \dfrac{y - 4}{x - (-3)} = \dfrac{4 - (-1)}{(-3) - 2} \)
\( \dfrac{y - 4}{x + 3} = \dfrac{5}{-5} \)
\( y - 4 = -x - 3 \)
\( y = -x + 1 \)
\( C \) noktası bu doğrunun üzerinde olduğuna göre koordinatları doğru denklemini sağlar.
\( 7 = -a + 1 \)
\( a = -6 \)
\( C \) noktasının apsis değeri \( -6 \) olarak bulunur.
Uç noktalar dahil olmak üzere, \( (5, 5) \) ve \( (155, 30) \) noktalarını birleştiren doğru parçası üzerinde koordinatları tam sayı olan kaç nokta bulunur?
Çözümü Gösterİki noktası bilinen doğrunun denklemini bulalım.
\( \dfrac{y - y_1}{x - x_1} = \dfrac{y_2 - y_1}{x_2 - x_1} \)
\( \dfrac{y - 5}{x - 5} = \dfrac{30 - 5}{155 - 5} \)
\( \dfrac{y - 5}{x - 5} = \dfrac{1}{6} \)
\( x - 5 = 6(y - 5) \)
\( x = 6y - 25 \)
Bu eşitlikte \( y \)'nin her tam sayı değeri için \( x \) de bir tam sayı değer alır.
Buna göre her \( y \in [5, 30] \) değeri için doğru parçası üzerinde koordinatları tam sayı olan bir nokta bulunur.
Bu aralıkta \( 30 - 5 + 1 = 26 \) tam sayı \( y \) değeri vardır.
Dolayısıyla verilen iki nokta arasında koordinatları tam sayı olan 26 nokta bulunur.
\( x = 3t + 1 \)
\( y = 2t - 3 \)
şeklinde parametrik denklemi olan doğrunun kapalı denklemi nedir?
Çözümü GösterVerilen parametrik denklemlerde birinci denklemde \( t \)'yi yalnız bırakalım.
\( x = 3t + 1 \)
\( t = \dfrac{x - 1}{3} \)
Bu \( t \) değerini ikinci denklemde yerine koyalım.
\( y = 2t - 3 \)
\( y = 2(\dfrac{x - 1}{3}) - 3 \)
\( y + 3 = 2(\dfrac{x - 1}{3}) \)
\( 3y + 9 = 2x - 2 \)
\( 3y - 2x + 11 = 0 \) bulunur.

Yukarıdaki şekildeki \( d \) doğrusu üzerinde koordinatları toplamı 20 olan noktanın ordinatı kaçtır?
Çözümü Göster\( d \) doğrusunun denklemini bulalım.
\( y = mx + c \)
\( m = \dfrac{3k}{2k} = \dfrac{3}{2} \)
Orijinden geçen doğrunun sabit terimi sıfır olduğu için \( c = 0 \) olur.
Buna göre \( d \) doğrusunun denklemi aşağıdaki gibi olur.
\( y = \dfrac{3}{2}x \)
Koordinatları toplamı 20 olan noktaya \( A(m, n) \) diyelim.
\( A \) noktası doğru üzerinde olduğuna göre, koordinatları doğru denklemini sağlar.
\( n = \dfrac{3}{2}m \)
\( 2n = 3m \)
\( m = 2k \) ve \( n = 3k \) diyelim.
\( A \) noktasının koordinatları toplamı 20 olarak veriliyor.
\( m + n = 20 \)
\( 2k + 3k = 20 \)
\( k = 4 \)
\( A \) noktasının ordinatını bulalım.
\( n = 3k = 3(4) = 12 \) bulunur.
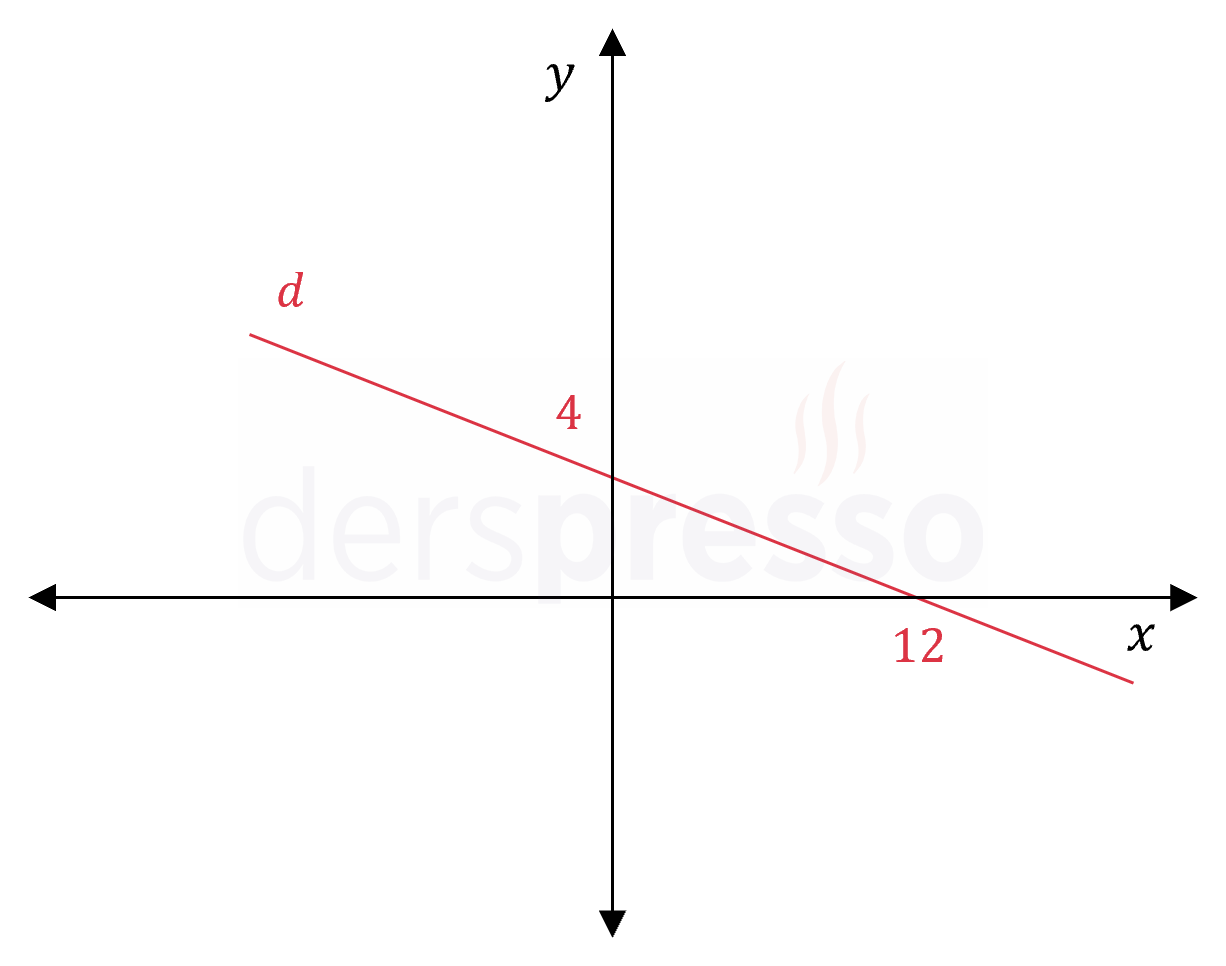
Yukarıdaki şekildeki \( d \) doğrusu üzerinde apsis ve ordinatının mutlak değerleri birbirine eşit olan noktaları bulunuz.
Çözümü Göster\( d \) doğrusunun denklemini yazalım.
Eksenleri kestiği noktalar bilinen doğrunun denklemini yazalım.
\( \dfrac{x}{12} + \dfrac{y}{4} = 1 \)
\( x + 3y = 12 \)
\( y = -\dfrac{1}{3}x + 4 \)
Apsis ve ordinat değerleri birbirine eşit olan noktalar \( A(k, k) \) ve \( B(k, -k) \) şeklinde olan noktalardır.
\( A(k, k) \) şeklinde olan noktalar \( y = x \) doğrusu üzerinde, \( B(k, -k) \) şeklinde olan noktalar \( y = -x \) doğrusu üzerindedir.
\( y = x \) ve \( y = -x \) doğrularını çizelim.
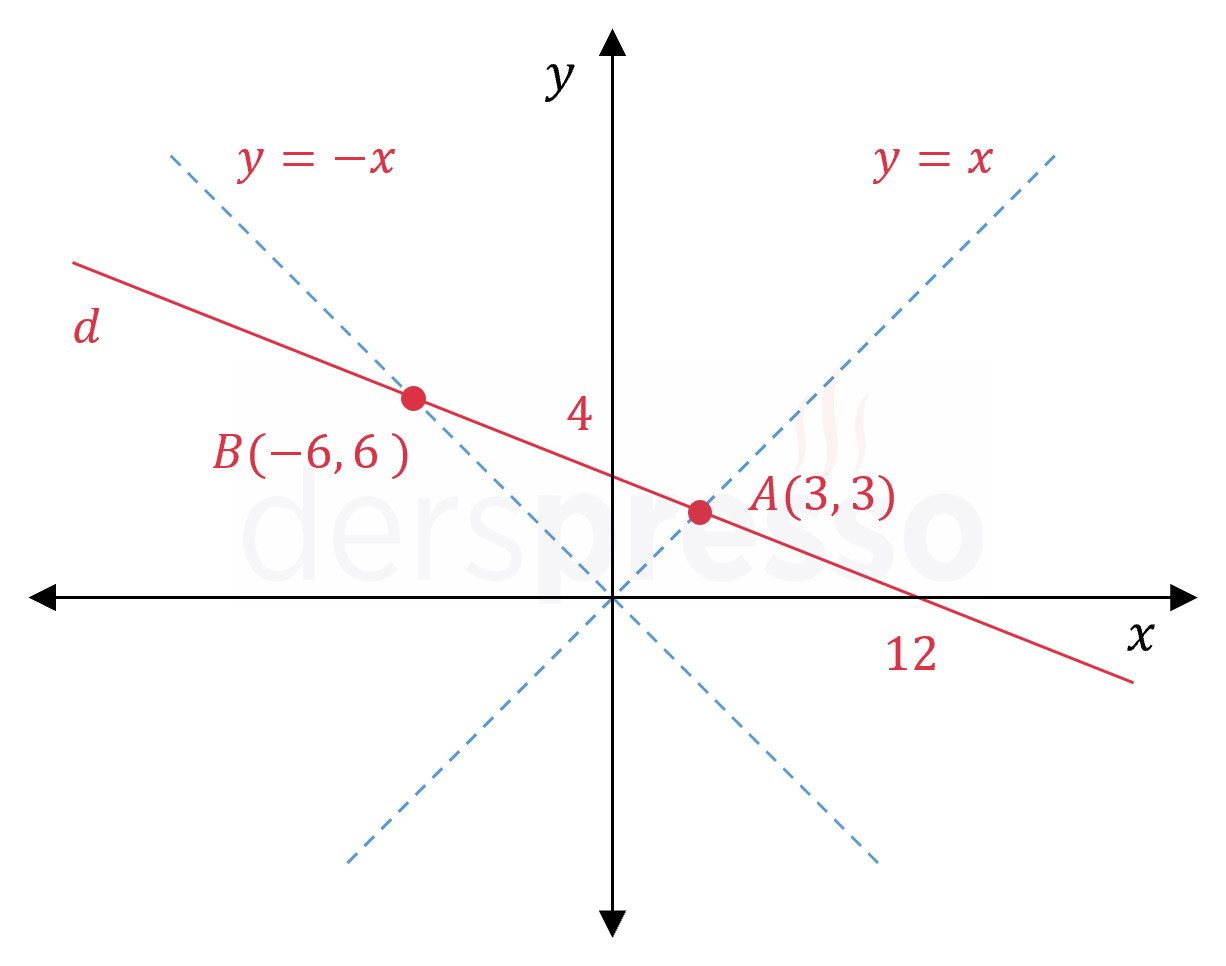
\( A \) noktasının koordinatlarını bulmak için \( d \) doğrusunun denkleminde \( x = k \) ve \( y = k \) yazalım.
\( k = -\dfrac{1}{3}k + 4 \)
\( \dfrac{4}{3}k = 4 \)
\( k = 3 \)
\( A(k, k) = A(3, 3) \)
\( B \) noktasının koordinatlarını bulmak için \( d \) doğrusunun denkleminde \( x = k \) ve \( y = -k \) yazalım.
\( -k = -\dfrac{1}{3}k + 4 \)
\( \dfrac{2}{3}k = -4 \)
\( k = -6 \)
\( B(k, -k) = B(-6, 6) \)
\( d \) doğrusu üzerinde apsis ve ordinatının mutlak değeri birbirine eşit olan iki nokta aşağıdaki gibidir.
\( A(3, 3), \quad B(-6, 6) \)

Birim karelerden oluşan şekildeki düzlemde \( K \) noktasının koordinatları \( (-1, -3) \) olduğuna göre, \( [LM] \) doğrusunun denklemini yazınız.
Çözümü Göster\( K \) noktasının koordinatlarını kullanarak bu düzlemde orijinin ve eksenlerin konumunu belirleyelim.

Birim kareleri kullanarak \( L \) ve \( M \) noktalarının koordinatlarını bulalım.
\( L(2, 2) \)
\( M(7, -4) \)
İki noktası bilinen doğrunun denklemini veren formülü kullanalım.
\( \dfrac{y - y_2}{x - x_2} = \dfrac{y_2 - y_1}{x_2 - x_1} \)
\( \dfrac{y - (-4)}{x - 7} = \dfrac{-4 - 2}{7 - 2} \)
\( \dfrac{y + 4}{x - 7} = \dfrac{-6}{5} \)
\( 5y + 20 = -6x + 42 \)
\( 6x + 5y - 22 = 0 \) bulunur.
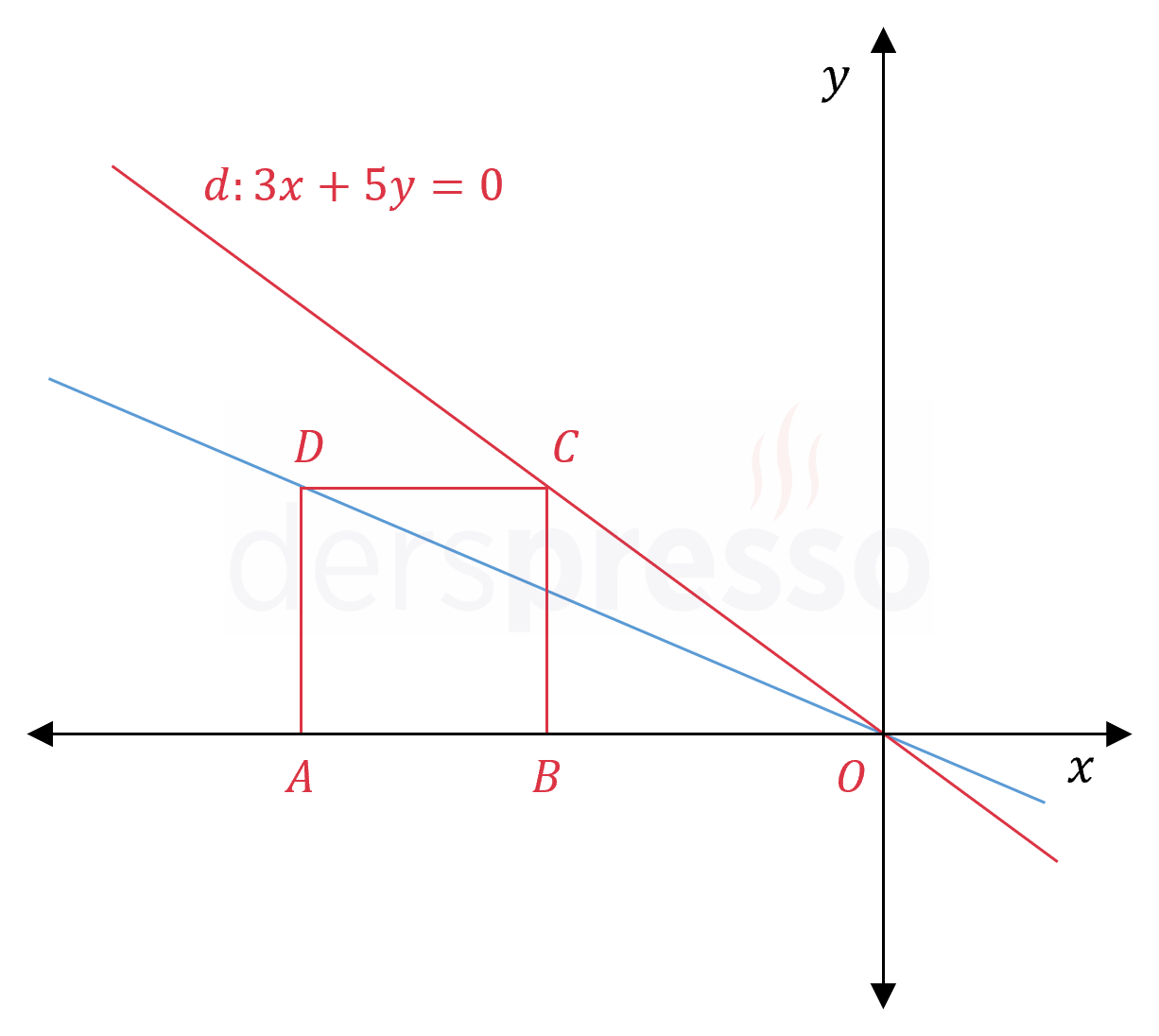
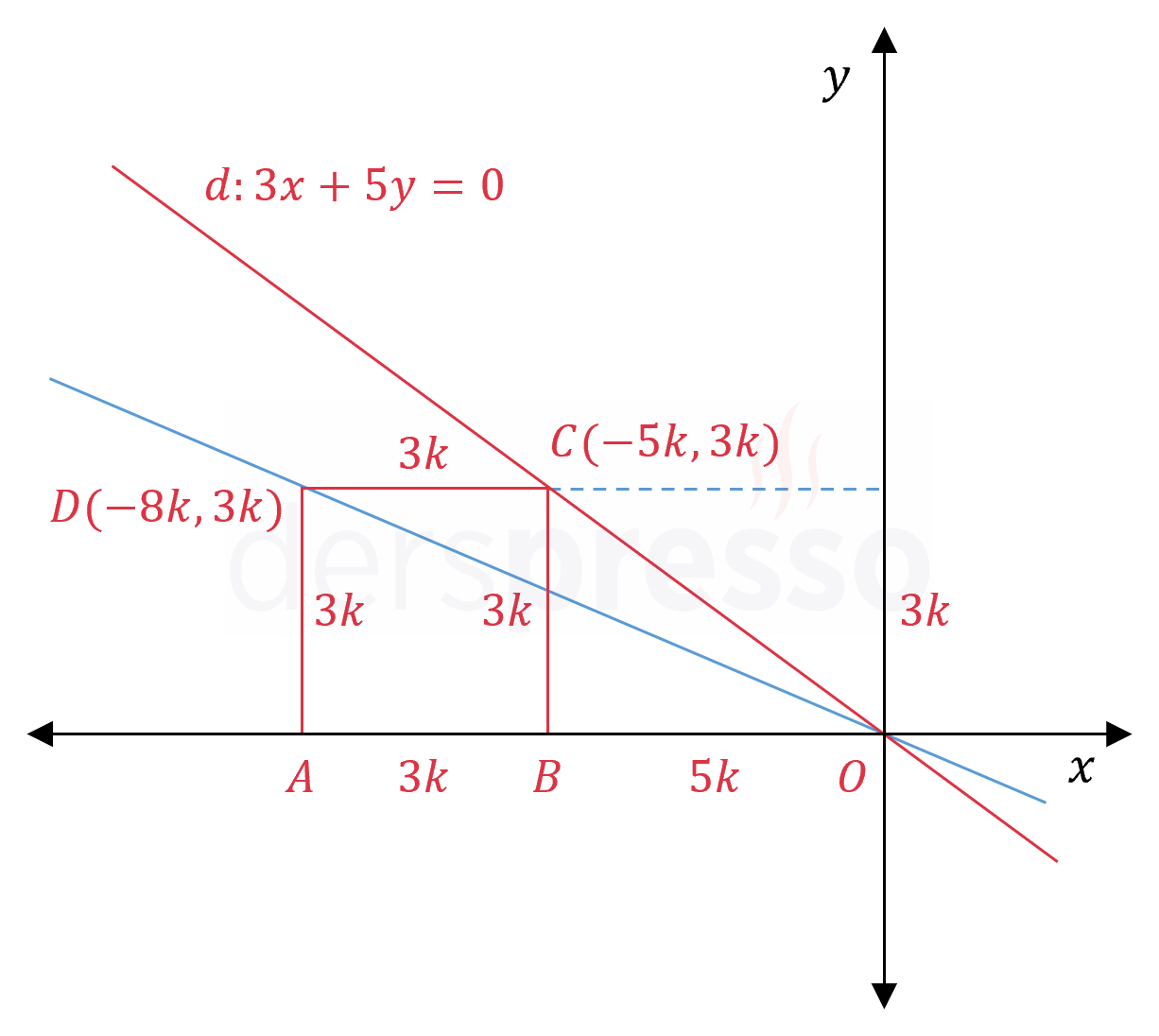
Şekildeki \( ABCD \) karesinin \( C \) köşesi \( d: 3x + 5y = 0 \) doğrusu üzerinde olduğuna göre, \( D \) noktasından ve orijinden geçen doğrunun denklemini bulunuz.
Çözümü Göster\( d \) doğrusunun denkleminini kullanarak \( C \) noktasının koordinatlarını bulalım.
\( C \) noktasının ordinatına \( 3k \) diyelim.
\( 3x = -5(3k) \)
\( x = -5k \)
\( C(-5k, 3k) \)
Buna göre karenin bir kenarının uzunluğu \( 3k \) olur.
\( D(-8k, 3k) \)
\( D \) noktasından ve orijinden geçen doğrunun eğimini bulalım.
\( m = \dfrac{y_2 - y_1}{x_2 - x_1} \)
\( = \dfrac{3k - 0}{-8k - 0} = -\dfrac{3}{8} \)
Orijinden geçen ve eğimi \( m \) olan doğrunun denklemi aşağıdaki formülle bulunur.
\( y = mx \)
\( y = -\dfrac{3}{8}x \)
\( 3x + 8y = 0 \) bulunur.