İki Doğrunun Birbirine Göre Durumu
Denklemleri aşağıdaki gibi olan iki doğrunun birbirine göre durumları üç şekilde olabilir.
\( d_1: a_1x + b_1y + c_1 = 0 \)
\( m_1 = -\dfrac{a_1}{b_1} \)
\( d_2: a_2x + b_2y + c_2 = 0 \)
\( m_2 = -\dfrac{a_2}{b_2} \)
- Doğrular tek bir noktada kesişir.
- Bunun özel bir durumu olarak, doğrular dik kesişir.
- Doğrular çakışıktır.
- Doğrular paraleldir.
Kesişen Doğrular
Eğimleri farklı iki doğru tek bir noktada kesişir. Buna göre eğimleri farklı iki doğrunun denklemlerinin ortak çözüm kümesi bir elemanlıdır ve bu çözüm iki doğrunun kesişim noktasının koordinatlarını verir.
İki doğrunun tek bir noktada kesişme koşulu:
\( m_1 \ne m_2 \)
Bu aynı zamanda doğrunun kapalı denkleminde \( x \) ve \( y \) katsayılarının oranlarının farklı olması anlamına gelir.
\( \dfrac{a_1}{a_2} \ne \dfrac{b_1}{b_2} \)
\( d_1: 2x - 5y + 3 = 0 \)
\( d_2: 3x + 2y - 6 = 0 \)
\( \dfrac{2}{3} \ne \dfrac{-5}{2} \)
Katsayıların oranları farklı olduğu için iki doğru tek bir noktada kesişir.
Dik Kesişen Doğrular
Tek bir noktada kesişen doğruların özel bir durumu olarak, iki doğru aralarındaki açı 90° olacak şekilde (yani dik) kesişebilir. Birbirini dik kesen iki doğrunun eğimleri çarpımı \( -1 \) olur.
Bunun dışında dik kesişen doğruların da eğimleri birbirinden farklıdır.
İki doğrunun dik kesişme koşulu:
\( m_1 \cdot m_2 = -1 \)
\( d_1: 2x - 3y + 3 = 0 \)
\( m_1 = -\dfrac{2}{-3} = \dfrac{2}{3} \)
\( d_2: 3x + 2y - 4 = 0 \)
\( m_2 = -\dfrac{3}{2} \)
\( m_1 \cdot m_2 = \dfrac{2}{3} \cdot -\dfrac{3}{2} = -1 \)
Eğimlerin çarpımı \( -1 \) olduğu için iki doğru tek bir noktada ve dik kesişir.
İSPATI GÖSTER
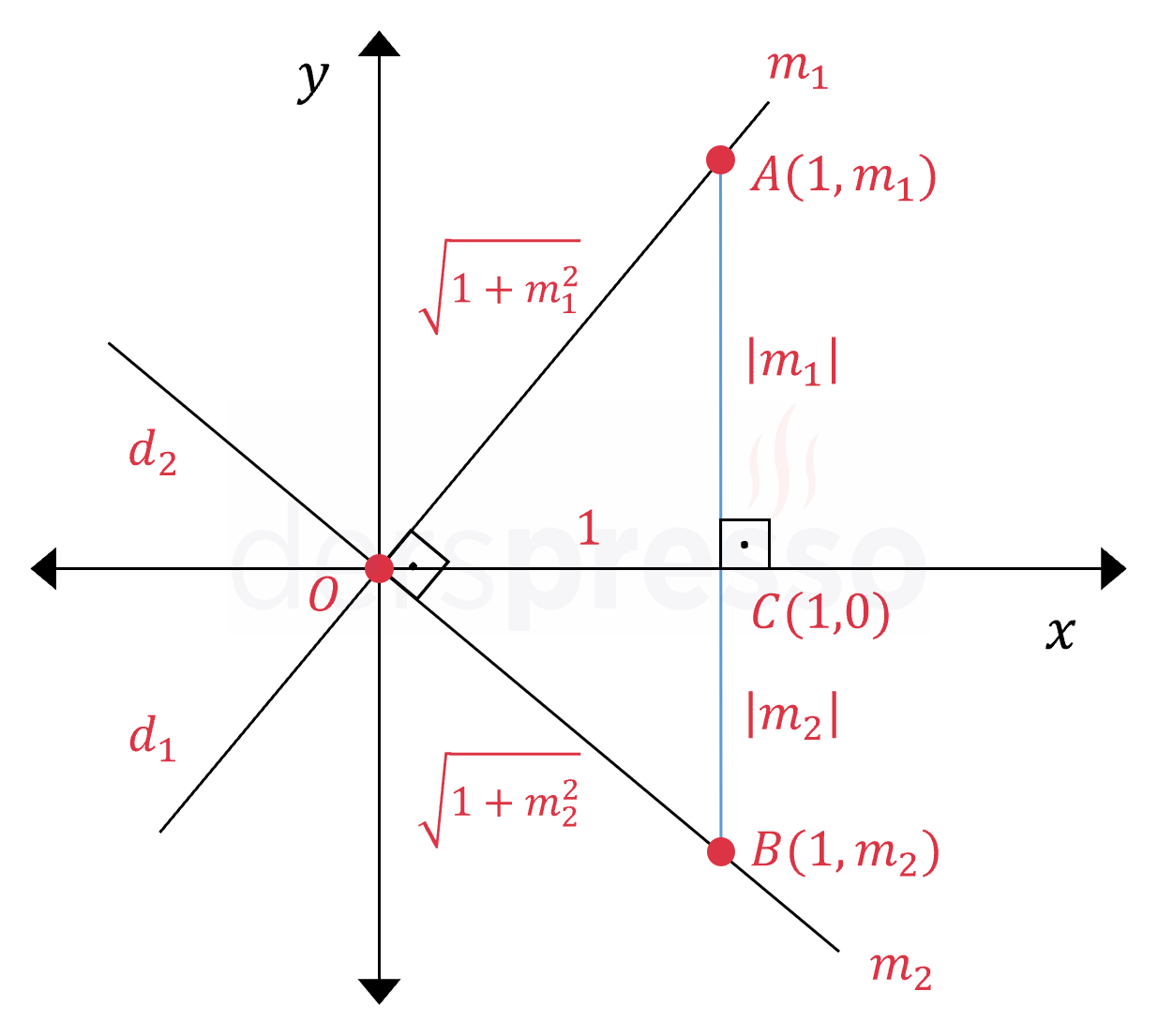
Eğimleri \( m_1 \) ve \( m_2 \) olan iki doğru çizelim. İşlem kolaylığı açısından bu doğruların orijinden geçtiğini varsayalım. Doğruların kesişim noktaları koordinat düzleminde herhangi bir noktaya taşındığında doğruların eğimleri değişmeyeceği için çarpımları da aynı kalacaktır.
\( C(1, 0) \) noktasından \( x \) eksenine dik bir doğru çizelim. \( d_1 \) doğrusunun eğimi \( m_1 \) olduğu için bu doğrunun \( d_1 \) doğrusunu kestiği noktanın koordinatları \( A(1, m_1) \) olur.
\( m_1 = \dfrac{m_1}{1} \)
Benzer şekilde, \( d_2 \) doğrusunun eğimi \( m_2 \) olduğu için bu doğrunun \( d_2 \) doğrusunu kestiği noktanın koordinatları \( B(1, m_2) \) olur.
Dik \( OCA \) üçgeninin hipotenüs uzunluğunu Pisagor teoremi ile hesaplayalım.
\( \abs{OA}^2 = 1^2 + m_1^2 \)
\( \abs{OA} = \sqrt{1^2 + m_1^2} \)
Aynı şekilde dik \( OCB \) üçgeninin hipotenüs uzunluğunu Pisagor teoremi ile hesaplayalım.
\( \abs{OB}^2 = 1^2 + m_2^2 \)
\( \abs{OB} = \sqrt{1^2 + m_2^2} \)
\( OBA \) üçgeni de dik üçgen olduğu için hipotenüs uzunluğunu Pisagor teoremi ile hesaplayalım.
\( \abs{AB}^2 = \abs{OA}^2 + \abs{OB}^2 \)
\( \abs{m_1 - m_2}^2 = \sqrt{1^2 + m_1^2}^2 + \sqrt{1^2 + m_2^2}^2 \)
\( m_1^2 - 2m_1m_2 + m_2^2 = 1^2 + m_1^2 + 1^2 + m_2^2 \)
İki taraftaki ortak terimleri sadeleştirdiğimizde dik doğruların eğimlerinin çarpımını -1 olarak buluruz.
\( -2m_1m_2 = 2 \)
\( m_1m_2 = -1 \)
Bir istisna olarak; yatay (\( x \) eksenine paralel) ve dikey (\( y \) eksenine paralel) iki doğru birbirini dik kesiyor olsa da, eğimleri sırasıyla 0 ve tanımsız olduğu için eğimlerinin çarpımı bu koşulu sağlamaz.
Çakışık Doğrular
Kapalı denklemlerindeki tüm katsayıların oranları birbirine eşit olan iki doğru çakışıktır. Çakışık iki doğrunun denklemlerinin ortak çözüm kümesi sonsuz elemanlıdır ve doğrular üzerindeki tüm noktalardır.
Çakışık doğruların eğimleri eşittir (\( m_1 = m_2 \)), ancak eğimleri eşit iki doğru çakışık olmak zorunda değildir, aşağıda göreceğimiz üzere paralel de olabilir.
İki doğrunun çakışık olma koşulu:
\( \dfrac{a_1}{a_2} = \dfrac{b_1}{b_2} = \dfrac{c_1}{c_2} \)
\( d_1: 2x + y - 3 = 0 \)
\( d_2: -6x - 3y + 9 = 0 \)
\( \dfrac{2}{-6} = \dfrac{1}{-3} = \dfrac{-3}{9} \)
Doğruların tüm katsayılarının oranları eşit olduğu için iki doğru çakışıktır.
Paralel Doğrular
Kapalı denklemlerinin \( x \) ve \( y \) katsayılarının oranları birbirine eşit, sabit terimlerin oranı birbirinden farklı olan iki doğru birbirine paraleldir. Paralel iki doğru hiçbir noktada kesişmez ve bu doğruların denklemlerinin ortak çözüm kümesi boş kümedir.
Paralel doğruların eğimleri eşittir (\( m_1 = m_2 \)).
İki doğrunun paralel olma koşulu:
\( \dfrac{a_1}{a_2} = \dfrac{b_1}{b_2} \ne \dfrac{c_1}{c_2} \)
\( d_1: 2x - 3y + 5 = 0 \)
\( d_2: 6x - 9y - 5 = 0 \)
\( \dfrac{2}{6} = \dfrac{-3}{-9} \ne \dfrac{5}{-5} \)
\( x \) ve \( y \) katsayılarının oranları eşit, sabit terimlerin oranı farklı olduğu için iki doğru paraleldir (kesişmez).
Eğimleri tanımsız olan, yani eğim açıları 90° olan dikey iki doğru bu koşulları sağlamasa da paraleldir ya da çakışıktır.
\( A(1, 2) \) ve \( B(-2, 4) \) noktalarından geçen doğru \( C(-1, a) \) ve \( D(a + 2, 3) \) noktalarından geçen doğruya paralel olduğuna göre, \( a \) kaçtır?
Çözümü GösterParalel doğruların eğimleri eşittir.
\( A \) ve \( B \) noktalarından geçen doğrunun eğimine \( m_{AB} \), \( C \) ve \( D \) noktalarından geçen doğrunun eğimine \( m_{CD} \) diyelim.
\( m_{AB} = \dfrac{4 - 2}{-2 - 1} = -\dfrac{2}{3} \)
\( m_{CD} = \dfrac{3 - a}{a + 2 - (-1)} = \dfrac{3 - a}{a + 3} \)
İki doğrunun eğimi birbirine eşittir.
\( m_{AB} = m_{CD} \)
\( -\dfrac{2}{3} = \dfrac{3 - a}{a + 3} \)
İçler - dışlar çarpımı yapalım.
\( -2a - 6 = 9 - 3a \)
\( a = 15 \) bulunur.
Analitik düzlemde \( K(a, 2) \), \( L(6, 5) \) ve \( M(3, 4) \) noktaları veriliyor.
\( [KL] \perp [LM] \) olduğuna göre, \( a \) kaçtır?
Çözümü Göster\( [KL] \) ve \( [LM] \) doğruları dik kesiştiklerine göre eğimlerinin çarpımı \( -1 \) olur.
\( m_{KL} \cdot m_{LM} = -1 \)
\( m_{KL} \) değerini bulalım.
\( m_{KL} = \dfrac{5 - 2}{6 - a} = \dfrac{3}{6 - a} \)
\( m_{LM} \) değerini bulalım.
\( m_{LM} = \dfrac{4 - 5}{3 - 6} = \dfrac{1}{3} \)
Bu iki eğimin çarpımını \( -1 \)'e eşitleyelim.
\( \dfrac{3}{6 - a} \cdot \dfrac{1}{3} = -1 \)
\( 6 - a = -1 \)
\( a = 7 \) bulunur.
\( (m + 1)x + (n - 3)y + 4 = 0 \) ve \( 3x + 2y - 1 = 0 \) doğruları çakışık olduğuna göre, \( m + n \) toplamı kaçtır?
Çözümü GösterÇakışık doğruların tüm katsayılarının oranı birbirine eşit olur.
\( \dfrac{m + 1}{3} = \dfrac{n - 3}{2} = \dfrac{4}{-1} \)
\( \dfrac{m + 1}{3} = \dfrac{n - 3}{2} = -4 \)
\( m + 1 = -12 \Longrightarrow m = -13 \)
\( n - 3 = -8 \Longrightarrow n = -5 \)
\( m + n = -13 + (-5) = -18 \) bulunur.
Koordinat sisteminde \( d_1: 3x + y - 9 = 0 \) ve \( d_2: -nx + 2y + m = 0 \) doğrularının ortak çözüm kümesi sonsuz elemanlı olduğuna göre, \( n - m \) kaçtır?
Çözümü Göster\( d_1 \) ve \( d_2 \) doğrularının ortak çözüm kümesi sonsuz elemanlı olduğuna göre, bu doğrular çakışıktır.
Çakışık doğruların kapalı denklemlerindeki katsayıların oranı birbirine eşittir.
\( \dfrac{3}{-n} = \dfrac{1}{2} = \dfrac{-9}{m} \)
Birinci ve ikinci oranlar arasında içler - dışlar çarpımı yapalım.
\( \dfrac{3}{-n} = \dfrac{1}{2} \)
\( n = -6 \)
İkinci ve üçüncü oranlar arasında içler - dışlar çarpımı yapalım.
\( \dfrac{1}{2} = \dfrac{-9}{m} \)
\( m = -18 \)
\( n - m \) farkını bulalım.
\( n - m = -6 - (-18) = 12 \) bulunur.
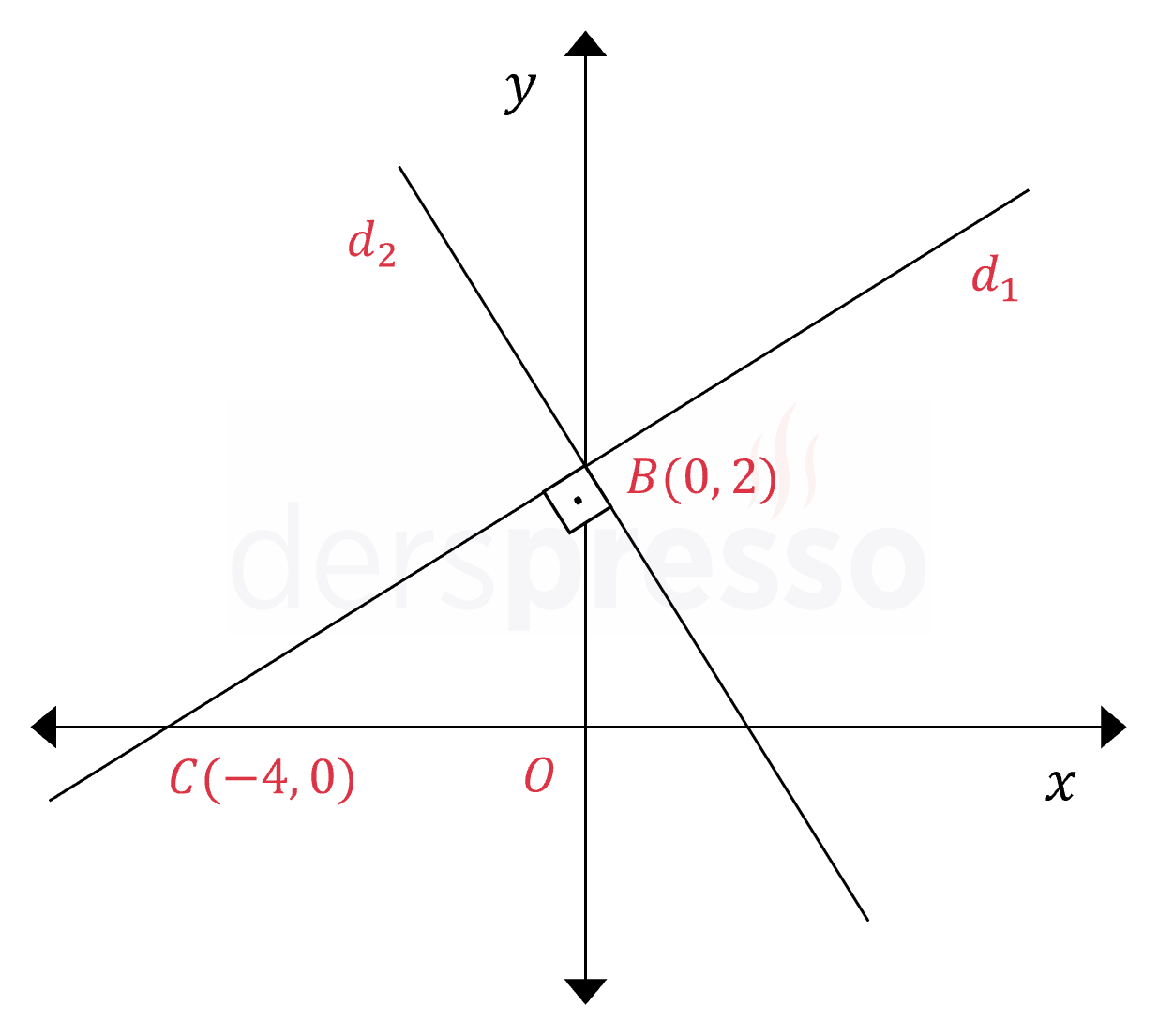
Şekilde verilen \( d_1 \) ve \( d_2 \) doğruları birbirine dik olduğuna göre, \( d_2 \) doğrusunun denklemi nedir?
Çözümü Göster\( d_1 \) ve \( d_2 \) doğrularının eğimlerine sırasıyla \( m_1 \) ve \( m_2 \) diyelim.
\( d_1 \) doğrusunun eğimini \( \widehat{BCO} \) açısının tanjant değeri üzerinden bulabiliriz.
\( m_1 = \tan(\widehat{BCO}) = \dfrac{\abs{BO}}{\abs{OC}} = \dfrac{2}{4} = \dfrac{1}{2} \)
Birbirini dik kesen doğruların eğimleri çarpımı -1'dir.
\( m_1 \cdot m_2 = -1 \)
\( \dfrac{1}{2} \cdot m_2 = -1 \)
\( m_2 = -2 \)
\( B(0, 2) \) noktasından geçen ve eğimi \( m_2 = -2 \) olan doğrunun denklemini bulalım.
\( y - y_1 = m(x - x_1) \)
\( y - 2 = -2(x - 0) \)
\( y = -2x + 2 \) bulunur.
\( A(-2, 6) \) ve \( B(8, 2) \) noktalarını birleştiren doğru parçasının orta dikmesinin \( x \) eksenini kestiği noktanın apsisi nedir?
Çözümü Göster\( A \) ve \( B \) noktalarının orta noktasına \( C(a, b) \) diyelim.
İki noktanın orta noktasının apsis ve ordinat değerleri noktaların apsis ve ordinat değerlerinin aritmetik ortalamasına eşittir.
\( a = \dfrac{-2 + 8}{2} = 3 \)
\( b = \dfrac{6 + 2}{2} = 4 \)
\( C(a, b) = C(3, 4) \)
\( [AB] \) doğru parçasının eğimine \( m_{AB} \) diyelim.
\( m_{AB} = \dfrac{2 - 6}{8 - (-2)} = -\dfrac{2}{5} \)
\( [AB] \) doğru parçası ve \( C \) noktasından çizilen orta dikme birbirine dik olur, dolayısıyla iki doğrunun eğimleri çarpımı \( -1 \) olur.
Çizilen orta dikmenin eğimine \( m_C \) diyelim.
\( m_{AB} \cdot m_C = -1 \)
\( -\dfrac{2}{5} \cdot m_C = -1 \)
\( m_C = \dfrac{5}{2} \)
\( C(3, 4) \) noktasından geçen ve eğimi \( \frac{5}{2} \) olan doğrunun denklemini yazalım.
\( y - y_1 = m(x - x_1) \)
\( y - 4 = \dfrac{5}{2}(x - 3) \)
Bu denklemin \( x \) eksenini kestiği noktayı bulmak için \( y = 0 \) verelim.
\( 0 - 4 = \dfrac{5}{2}(x - 3) \)
\( x - 3 = -\dfrac{8}{5} \)
\( x = \dfrac{7}{5} \)
Buna göre \( [AB] \) doğru parçasının orta dikmesi \( x \) eksenini \( \frac{7}{5} \) apsisli noktada keser.