Analitik Düzlemde Doğru
Tek boyutlu, düz ve her iki yönde sonsuza giden geometrik şekle doğru denir.
Tek bir noktadan sonsuz sayıda doğru geçer. Birbirinden farklı iki noktadan tek bir doğru geçer. Birbirinden farklı üç ya da daha fazla noktadan bir doğru geçebilmesi için bu noktalar doğrusal olmalıdır.

Doğrunun Denklemi
Bir doğrunun denklemi birinci dereceden iki değişkenli denklemdir. Denklemin iki değişkeni doğru üzerindeki noktaların apsis ve ordinat değerlerini temsil eden \( x \) ve \( y \) değişkenleridir. Denklemin birinci dereceden olması değişkenlerin 1 dışında bir kuvvetinin (\( x^2, x^3, \sqrt{x} \) vb.) bulunmaması anlamına gelir.
Bir doğrunun denklemi açık ve kapalı olmak üzere iki şekilde yazılabilir.
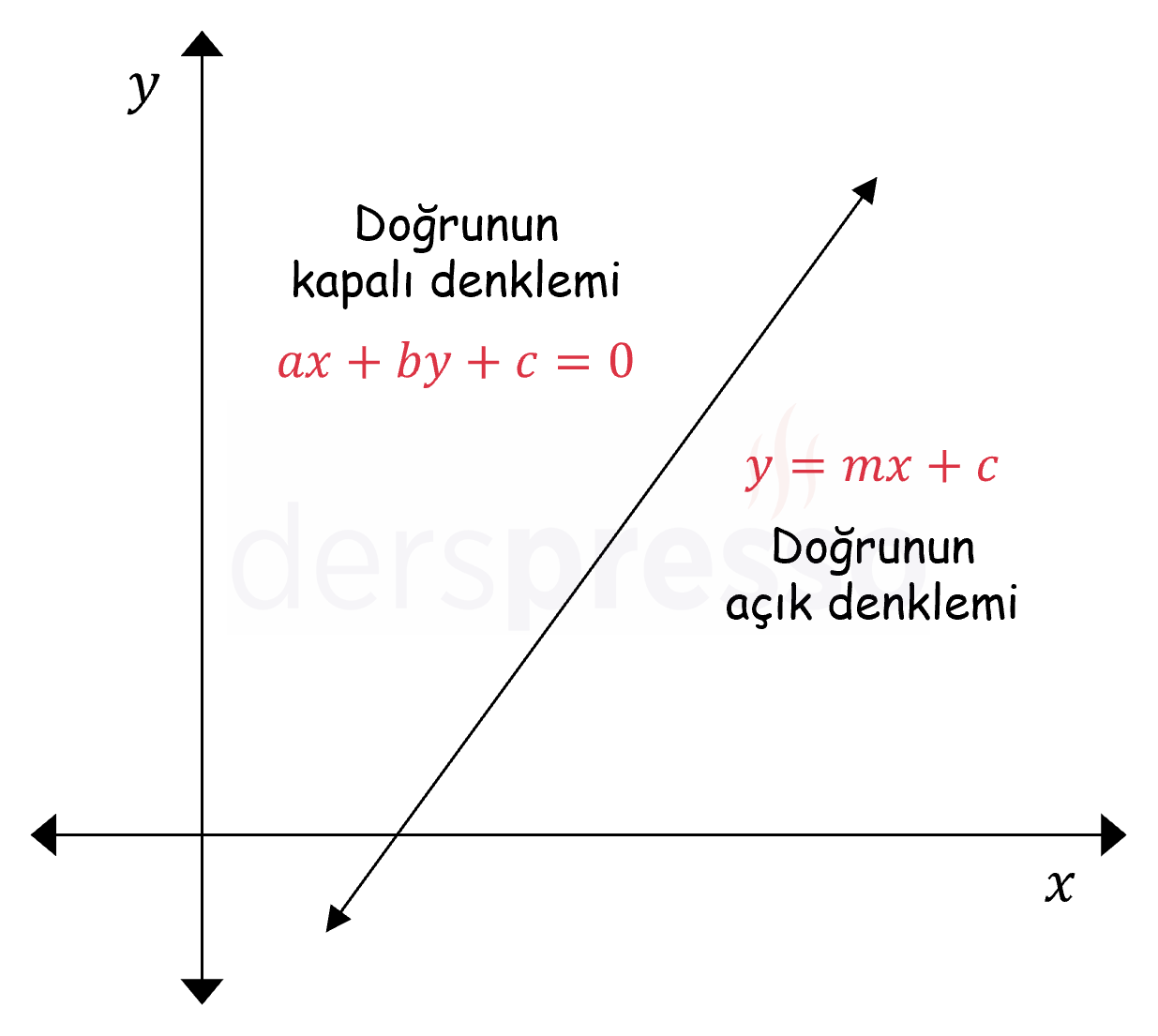
Doğrunun Açık Denklemi
Doğrunun açık denkleminde \( y \) değişkeni katsayısı 1 olacak şekilde yalnız bırakılır.
\( y = mx + c \)
\( y = 3x - 2 \)
\( m = 3, \quad c = -2 \)
Doğrunun Kapalı Denklemi
Doğrunun kapalı denkleminde tüm terimler tek tarafta toplanır ve ifade sıfıra eşitlenir.
\( ax + by + c = 0 \)
\( 3x - y - 2 = 0 \)
\( a = 3, \quad b = -1, \quad c = -2 \)
Kapalı denklemi verilen bir doğrunun açık denklemi, \( y \) değişkeni yalnız bırakılarak aşağıdaki şekilde yazılabilir.
\( ax + by + c = 0 \)
\( y = -\dfrac{a}{b}x - \dfrac{c}{b} \)
\( 5x - 2y - 12 = 0 \)
\( 2y = 5x - 12 \)
\( y = \dfrac{5}{2}x - 6 \)
Aşağıda kapalı denklemleri verilen doğruların açık denklemlerini yazınız.
(a) \( 3x - 2y + 5 = 0 \)
(b) \( 5x + 4y - 7 = 0 \)
(c) \( -4x + \dfrac{y}{3} + 6 = 0 \)
Çözümü GösterKapalı denklemi verilen bir doğrunun açık denklemini elde etmek için \( y \) değişkeni yalnız bırakılır.
(a) seçeneği:
\( 3x - 2y + 5 = 0 \)
\( 2y = 3x + 5 \)
\( y = \dfrac{3}{2}x + \dfrac{5}{2} \)
(b) seçeneği:
\( 5x + 4y - 7 = 0 \)
\( 4y = -5x + 7 \)
\( y = -\dfrac{5}{4}x + \dfrac{7}{4} \)
(c) seçeneği:
\( -4x + \dfrac{y}{3} + 6 = 0 \)
\( \dfrac{y}{3} = 4x - 6 \)
\( y = 12x - 18 \)
\( 3x - 2y + a + 5 = 0 \) doğrusu \( (3, -1) \) noktasından geçtiğine göre, \( a \) kaçtır?
Çözümü GösterBir doğru üzerindeki her noktanın koordinatları doğrunun denklemini sağlar.
\( (3, -1) \) noktasını denklemde yerine koyalım.
\( 3(3) - 2(-1) + a + 5 = 0 \)
\( 9 + 2 + a + 5 = 0 \)
\( a = -16 \) bulunur.
\( A(2k + 3, \frac{k - 5}{2}) \) noktası \( y = \frac{x - 3}{2} \) doğrusu üzerinde olduğuna göre, \( A \) noktasının \( y \) eksenine olan uzaklığı kaçtır?
Çözümü Göster\( A \) noktası verilen doğru üzerinde olduğuna göre koordinatları doğru denklemini sağlar.
\( A \) noktasının koordinatlarını denklemde yerine koyalım.
\( \dfrac{k - 5}{2} = \dfrac{2k + 3 - 3}{2} \)
\( k - 5 = 2k \)
\( k = -5 \)
\( A \) noktasının koordinatlarında \( k = -5 \) değerini yerine koyalım.
\( A(2(-5) + 3, \dfrac{-5 - 5}{2}) = A(-7, -5) \)
Bir noktanın \( y \) eksenine olan uzaklığı, apsisinin mutlak değerine eşittir.
\( \abs{-7} = 7 \) bulunur.
Doğrunun Eksenleri Kestiği Noktalar
Doğrunun \( y \) Eksenini Kestiği Nokta
\( y \) ekseni üzerindeki tüm noktaların apsis değeri sıfır olduğu için, bir doğrunun \( y \) eksenini kestiği noktanın ordinat değeri doğru denkleminde \( x = 0 \) yazılarak bulunabilir.
\( d_1: 2x - 3y + 6 = 0 \)
\( x = 0 \) yazıp denklemi \( y \) için çözelim.
\( 2(0) - 3y + 6 = 0 \)
\( y = 2 \)
Buna göre, doğru \( y \) eksenini \( (0, 2) \) noktasında keser.

Doğrunun açık denklemindeki sabit terim aynı zamanda doğrunun \( y \) eksenini kestiği noktanın ordinatını verir.
Kapalı denklem: \( 2x - 3y + 6 = 0 \)
Açık denklem: \( y = \frac{2}{3}x \textcolor{red}{+ 2} \)
Doğrunun \( x \) Eksenini Kestiği Nokta
\( x \) ekseni üzerindeki tüm noktaların ordinat değeri sıfır olduğu için, bir doğrunun \( x \) eksenini kestiği noktanın apsis değeri doğru denkleminde \( y = 0 \) yazılarak bulunabilir.
\( d_1: 2x - 3y + 6 = 0 \)
\( y = 0 \) yazıp denklemi \( x \) için çözelim.
\( 2x - 3(0) + 6 = 0 \)
\( x = -3 \)
Buna göre, doğru \( x \) eksenini \( (-3, 0) \) noktasında keser.

Özel Bazı Doğrular
Yatay Doğrular
\( x \) eksenine paralel doğruların üzerindeki noktaların ordinat değeri tüm doğru boyunca sabittir, bu yüzden bu doğruların denklemi \( x \) değişkeni içermez ve \( c \) bir reel sayı olmak üzere \( y = c \) şeklinde ifade edilir.
Kendisi de bir yatay doğru olan \( x \) ekseni \( y = 0 \) doğrusuna karşılık gelir.

Dikey Doğrular
\( y \) eksenine paralel doğruların üzerindeki noktaların apsis değeri tüm doğru boyunca sabittir, bu yüzden bu doğruların denklemi \( y \) değişkeni içermez ve \( c \) bir reel sayı olmak üzere \( x = c \) şeklinde ifade edilir.
Kendisi de bir dikey doğru olan \( y \) ekseni \( x = 0 \) doğrusuna karşılık gelir.

1. ve 2. Açıortay Doğruları
Aşağıda grafikleri verilen \( y = x \) ve \( y = -x \) doğruları sırasıyla 1. açıortay ve 2. açıortay doğruları olarak adlandırılır.
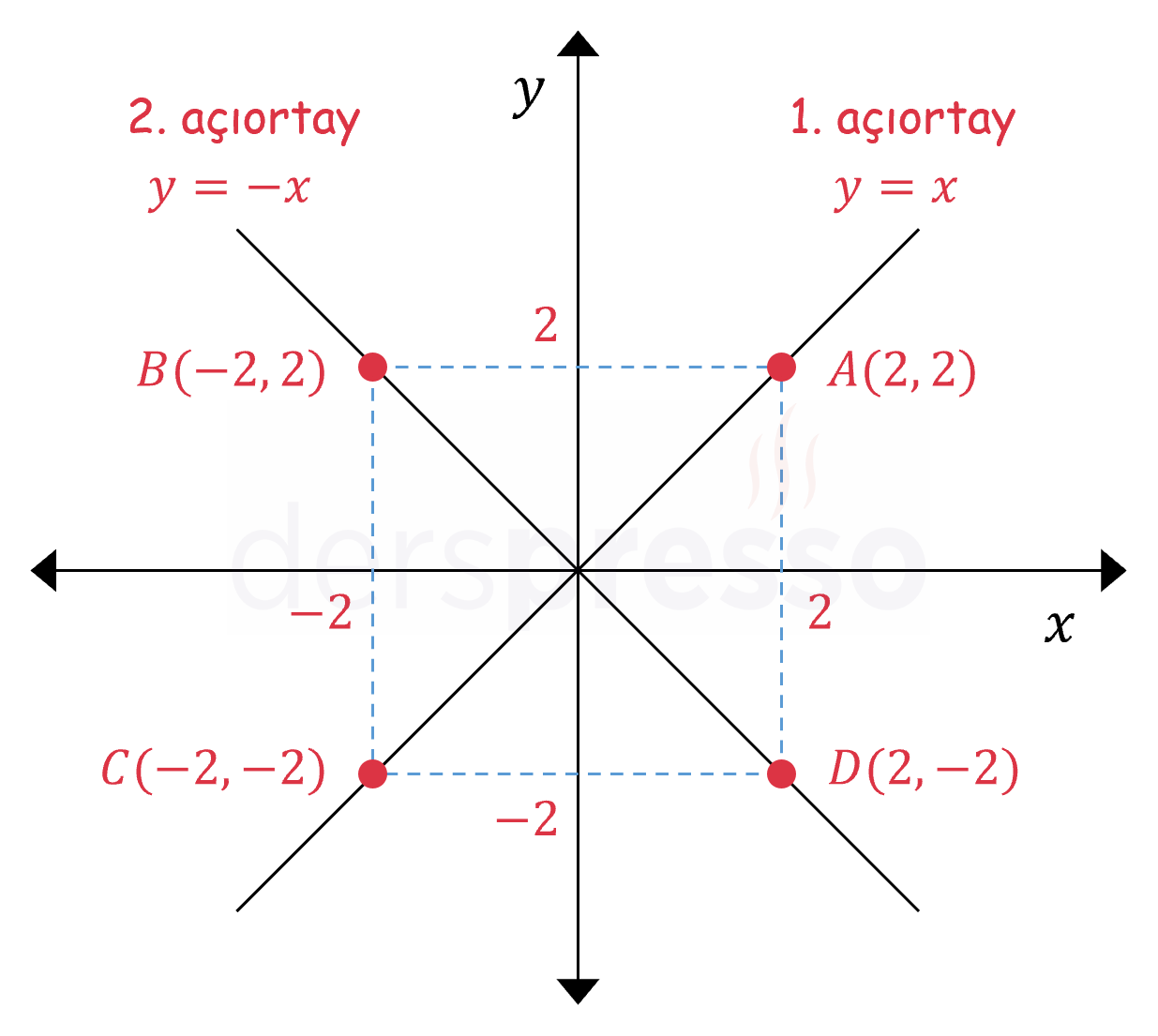
1. açıortay doğrusu üzerindeki noktaların apsis ve ordinat değerleri birbirine eşittir. 2. açıortay doğrusu üzerindeki noktaların apsis ve ordinat değerleri birbirinin ters işaretlisidir. Her iki doğru üzerindeki noktalar eksenlere eşit uzaklıktadır.
Doğrunun Katsayıları
Sabit Terimin Grafiğe Etkisi
Doğrunun açık denklemindeki sabit terim doğrunun \( y \) eksenini kestiği noktanın ordinatını verir. Aşağıdaki grafikte \( x \) katsayıları aynı, sabit terimleri farklı üç doğrunun \( y \) eksenini her doğrunun sabit teriminin belirttiği noktada kestiği görülebilir.

x'in Katsayısının Grafiğe Etkisi
Doğrunun açık denklemindeki \( x \) katsayısı doğrunun dikliğini belirler. Aşağıdaki grafikte sabit terimleri aynı, diklikleri farklı beş doğru \( y \) eksenini aynı noktada kesmektedir.
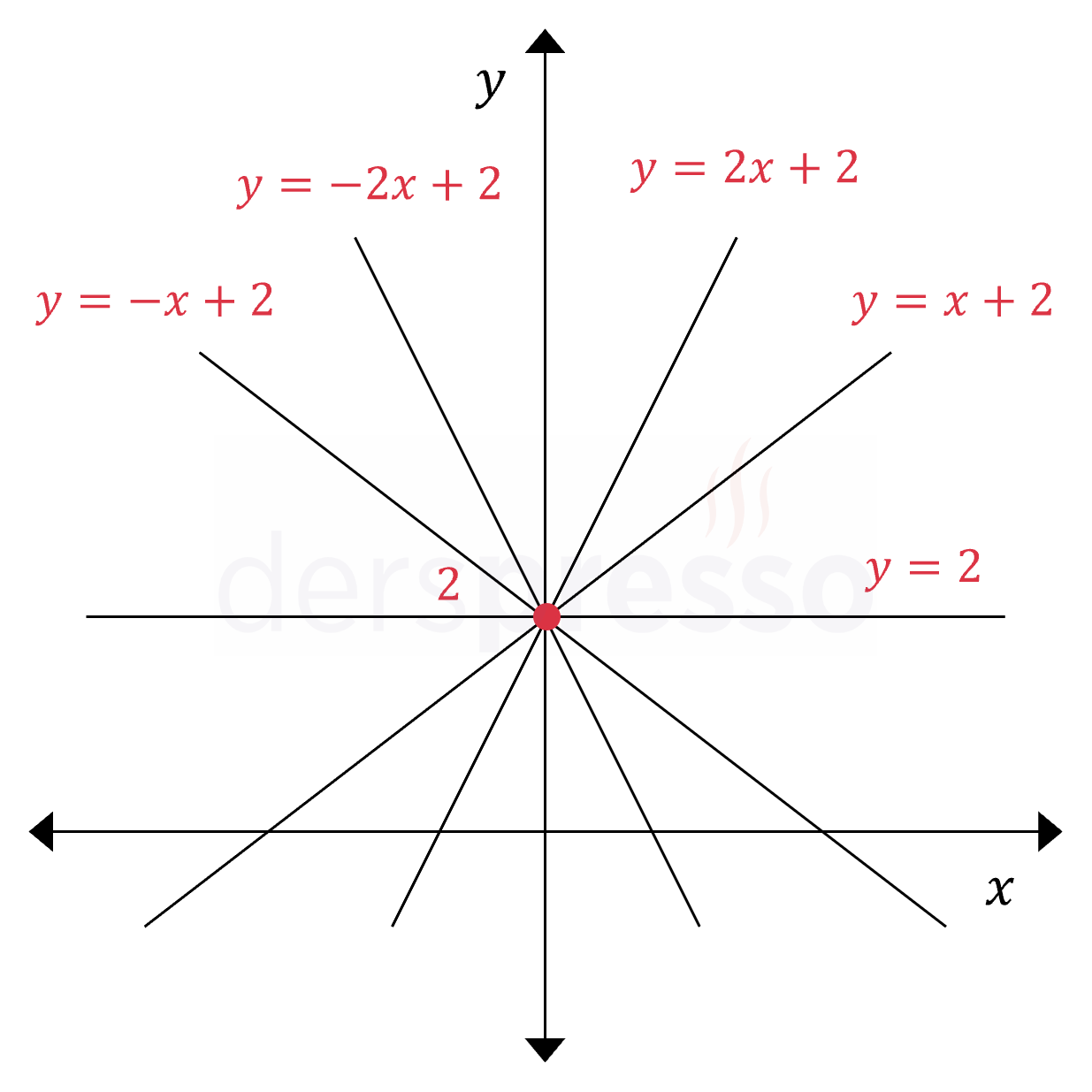
Önümüzdeki bölümde bu dikliği doğrunun eğimi olarak tanımlayacağız.
Aşağıdaki doğruların koordinat eksenlerini kestiği noktaları bulunuz.
(a) \( 2x + 5y - 20 = 0 \)
(b) \( 6x + y = 0 \)
(c) \( y = -4 \)
(d) \( x = 7 \)
Çözümü GösterBir doğrunun \( x \) eksenini kestiği noktanın apsisini bulmak için denklemde \( y = 0 \) yazılır ve denklemi sağlayan \( x \) değeri bulunur.
Bir doğrunun \( y \) eksenini kestiği noktanın ordinatını bulmak için denklemde \( x = 0 \) yazılır ve denklemi sağlayan \( y \) değeri bulunur.
(a) seçeneği:
\( 2x + 5y - 20 = 0 \)
\( y = 0 \) için denklemi çözelim.
\( 2x + 5(0) - 20 = 0 \)
\( x = 10 \)
\( x = 0 \) için denklemi çözelim.
\( 2(0) + 5y - 20 = 0 \)
\( y = 4 \)
Buna göre doğru \( x \) eksenini \( (10, 0) \) noktasında, \( y \) eksenini \( (0, 4) \) noktasında keser.
(b) seçeneği:
\( 6x + y = 0 \)
\( y = 0 \) için denklemi çözelim.
\( 6x + 0 = 0 \)
\( x = 0 \)
\( x = 0 \) için denklemi çözelim.
\( 6(0) + y = 0 \)
\( y = 0 \)
Buna göre doğru \( x \) ve \( y \) eksenlerini \( (0, 0) \) noktasında yani orijinde keser.
(c) seçeneği:
\( y = -4 \)
\( y = -4 \) doğrusu yatay bir doğru olup sadece \( y \) eksenini \( (0, -4) \) noktasında keser.
(d) seçeneği:
\( x = 7 \)
\( x = 7 \) doğrusu dikey bir doğru olup sadece \( x \) eksenini \( (7, 0) \) noktasında keser.
Koordinat düzlemindeki \( 3x - y - 12 = 0 \) doğrusu üzerindeki \( A(n, -3n) \) ve \( B(2m, 3m) \) noktaları arasındaki uzaklık kaç birimdir?
Çözümü Göster\( A \) ve \( B \) noktaları \( 3x - y - 12 = 0 \) doğrusu üzerinde olduğuna göre koordinatları doğru denklemini sağlar.
\( A(n, -3n) \) noktası:
\( 3n - (-3n) - 12 = 0 \)
\( n = 2 \)
\( A(n, -3n) = A(2, -6) \)
\( B(2m, 3m) \) noktası:
\( 3(2m) - 3m - 12 = 0 \)
\( m = 4 \)
\( B(2m, 3m) = B(8, 12) \)
\( \abs{AB} \) uzaklığını bulmak için iki nokta arasındaki uzaklık formülünü kullanalım.
\( \abs{AB} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \)
\( = \sqrt{(8 - 2)^2 + (12 - (-6))^2} \)
\( = \sqrt{360} = 6\sqrt{10} \) bulunur.
Analitik düzlemde \( K(2a + 7, 6) \) ve \( L(4a + 3, -14) \) noktaları veriliyor.
\( [KL] \) doğrusunun orta noktası \( 2y + x - 6 = 0 \) doğrusu üzerinde olduğuna göre, bu noktanın apsis ve ordinatının toplamı kaçtır?
Çözümü Göster\( [KL] \) doğrusunun orta noktasına \( M(x_0, y_0) \) diyelim.
\( M \) noktasının koordinatlarını orta nokta formülü ile bulalım.
\( x_0 = \dfrac{x_1 + x_2}{2} \)
\( = \dfrac{2a + 7 + 4a + 3}{2} \)
\( = 3a + 5 \)
\( y_0 = \dfrac{y_1 + y_2}{2} \)
\( = \dfrac{6 + (-14)}{2} \)
\( = -4 \)
\( M(3a + 5, -4) \)
\( M \) noktası \( 2y + x - 6 = 0 \) doğrusu üzerinde olduğuna göre koordinatları doğru denklemini sağlar.
\( 2(-4) + 3a + 5 - 6 = 0 \)
\( a = 3 \)
\( M \) noktasının koordinatlarında \( a = 3 \) değerini yerine koyalım.
\( M(3(3) + 5, -4) = M(14, -4) \)
\( M \) noktasının koordinatları toplamı \( 14 + (-4) = 10 \) olarak bulunur.
Koordinat düzleminde \( d_1: 12x - 5y + 60 = 0 \) ve \( d_2: 20x + 15y - 180 = 0 \) doğruları ile \( x \) ekseni arasında kalan bölgenin çevresi kaçtır?
Çözümü Göster\( d_1 \) ve \( d_2 \) doğrularının eksenleri kestiği noktaları bulalım.
\( d_1 \) doğrusunun \( y \) eksenini kestiği noktayı bulmak için doğru denkleminde \( x = 0 \) yazalım.
\( 12(0) - 5y + 60 = 0 \)
\( y = 12 \)
\( A(0, 12) \)
\( d_1 \) doğrusunun \( x \) eksenini kestiği noktayı bulmak için doğru denkleminde \( y = 0 \) yazalım.
\( 12x - 5(0) + 60 = 0 \)
\( x = -5 \)
\( B(-5, 0) \)
\( d_2 \) doğrusunun \( y \) eksenini kestiği noktayı bulmak için doğru denkleminde \( x = 0 \) yazalım.
\( 20(0) + 15y - 180 = 0 \)
\( y = 12 \)
\( A(0, 12) \)
\( d_2 \) doğrusunun \( x \) eksenini kestiği noktayı bulmak için doğru denkleminde \( y = 0 \) yazalım.
\( 20x + 15(0) - 180 = 0 \)
\( x = 9 \)
\( C(9, 0) \)
Bu noktaları analitik düzlemde işaretleyelim.
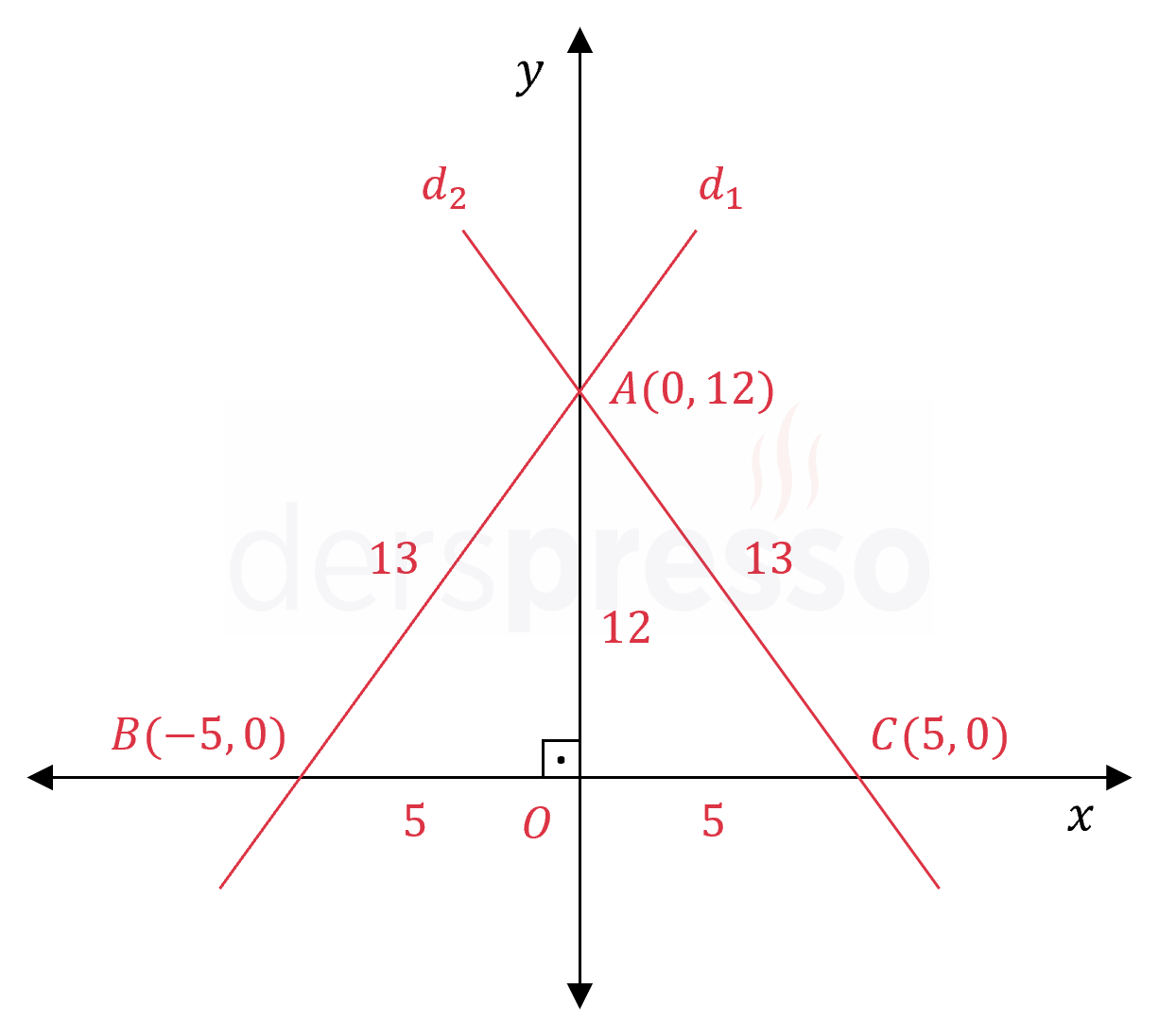
İki doğru \( y \) eksenini aynı noktada kestiği için çevresi istenen bölge bir üçgen olur.
\( AOB \) bir dik üçgen olup aynı zamanda bir 5-12-13 özel üçgenidir.
\( \abs{AB} = 13 \)
\( AOC \) bir dik üçgen olup aynı zamanda bir 9-12-15 özel üçgenidir.
\( \abs{AC} = 15 \)
\( ABC \) üçgeninin çevresini bulalım.
\( \text{Ç}(ABC) = \abs{AB} + \abs{AC} + \abs{BC} \)
\( = 13 + 15 + 5 + 9 \)
\( = 42 \) bulunur.
\( 4x \pm 3y \pm 12 = 0 \) doğrularının oluşturduğu paralelkenarın alanı kaçtır?
Çözümü Göster\( 4x \pm 3y \pm 12 = 0 \) ifadesinin oluşturduğu dört doğruyu yazalım.
\( d_1: 4x + 3y + 12 = 0 \)
\( d_2: 4x + 3y - 12 = 0 \)
\( d_3: 4x - 3y + 12 = 0 \)
\( d_4: 4x - 3y - 12 = 0 \)
Bu doğruların eksenleri hangi noktalarda kestiğini bulalım.
\( d_1 \) doğrusu eksenleri \( C(-3, 0) \) ve \( D(0, -4) \) noktalarında keser.
\( d_2 \) doğrusu eksenleri \( A(3, 0) \) ve \( B(0, 4) \) noktalarında keser.
\( d_3 \) doğrusu eksenleri \( B(0, 4) \) ve \( C(-3, 0) \) noktalarında keser.
\( d_4 \) doğrusu eksenleri \( A(3, 0) \) ve \( D(0, -4) \) noktalarında keser.
Doğruları ve doğruların eksenleri kestiği noktaları analitik düzlemde gösterelim.

Doğruların oluşturduğu paralelkenar, kenar uzunlukları eşit olduğu için aynı zamanda eşkenar dörtgendir.
\( ABCD \) eşkenar dörtgeninin alanı köşegen uzunluklarının çarpımının yarısına eşittir.
\( A(ABCD) = \dfrac{1}{2} \abs{AC} \cdot \abs{BD} \)
\( = \dfrac{1}{2} \cdot 6 \cdot 8 = 24 \) bulunur.
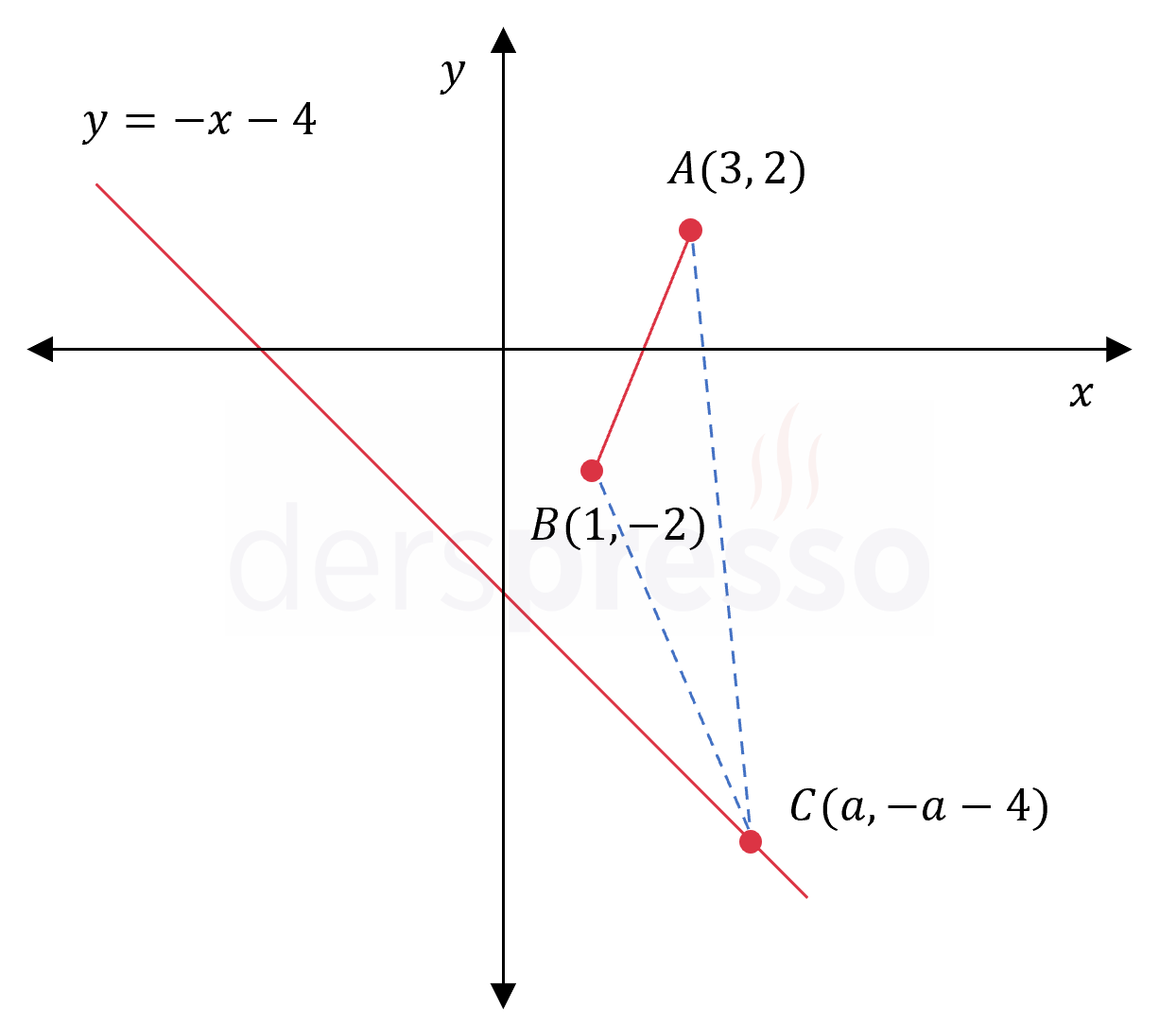
\( ABC \) üçgeninin köşe noktalarından ikisi \( A(3, 2) \) ve \( B(1, -2) \) olup üçüncü \( C \) köşesi \( y = -x - 4 \) doğrusu üzerinde ve IV. bölgededir.
\( ABC \) üçgeninin alanı 12 birimkare olduğuna göre, \( C \) noktasının koordinatları nedir?
Çözümü Göster\( C \) noktasının apsisine \( a \) diyelim.
\( C \) noktası \( y = -x - 4 \) doğrusu üzerinde olduğuna göre ordinatı \( -a - 4 \) olur.
\( C(a, -a - 4) \)
Üç köşesinin koordinatları bilinen üçgenin alan formülünü yazalım.
\( A(ABC) = \dfrac{1}{2} \abs{(x_1y_2 + x_2y_3 + x_3y_1) - (x_2y_1 + x_3y_2 + x_1y_3)} \)
\( A(x_1, y_1) = A(3, 2) \)
\( B(x_2, y_2) = B(1, -2) \)
\( C(x_3, y_3) = C(a, -a - 4) \)
\( A(ABC) = \dfrac{1}{2} \abs{[3(-2) + 1(-a - 4) + a(2)] - [1(2) + a(-2) + 3(-a - 4)]} \)
\( 12 = \dfrac{1}{2} \abs{-6 - a - 4 + 2a - (2 - 2a - 3a - 12)} \)
\( 24 = \abs{6a} \)
Bu eşitlik iki durumda sağlanır.
Durum 1:
\( 6a = 24 \)
\( a = 4 \)
\( C \) noktasının koordinatlarında \( a = 4 \) değerini yerine koyalım.
\( C(4, -4 - 4) = C(4, -8) \)
Bulduğumuz \( C \) noktası IV. bölgededir.
Durum 2:
\( 6a = -24 \)
\( a = -4 \)
\( C \) noktasının koordinatlarında \( a = -4 \) değerini yerine koyalım.
\( C(-4, -(-4) - 4) = C(-4, 0) \)
Bulduğumuz \( C \) noktası \( x \) ekseni üzerindedir.
Buna göre \( C \) noktasının koordinatları \( (4, -8) \) olarak bulunur.