Logaritma Tanımı
\( a^x = b \) eşitliğinde \( x \) değişkenini yalnız bırakarak \( a \) ve \( b \) cinsinden yazmamızı sağlayan işleme logaritma işlemi denir.
\( a \in \mathbb{R^+} - \{ 1 \}, \quad b \in \mathbb{R^+}, \)
\( x \in \mathbb{R} \) olmak üzere,
\( a^x = b \Longleftrightarrow x = \log_a{b} \)
\( 2^x = 3 \Longleftrightarrow x = \log_2{3} \)
\( (\frac{1}{5})^x = 2 \Longleftrightarrow x = \log_\frac{1}{5}{2} \)

\( \log_a{b} \) ifadesindeki \( a \) sayısına logaritmanın tabanı denir. \( \log_a{b} \) ifadesi "logaritma \( a \) tabanında \( b \)" ya da "\( b \)'nin \( a \) tabanında logaritması" şeklinde okunur.
Logaritma işlemi logaritma içindeki değeri (\( b \)) elde etmek için tabanın kaçıncı kuvvetini almamız gerektiğini verir. Bu tanıma göre, \( a^n \) ifadesinin \( a \) tabanında logaritması \( n \)'ye eşittir.
\( \log_a{a^n} = n \)
\( \log_5{1} = \log_5{5^0} = 0 \)
\( \log_5{5} = \log_5{5^1} = 1 \)
\( \log_5{25} = \log_5{5^2} = 2 \)
\( \log_5{125} = \log_5{5^3} = 3 \)
\( \log_5{5^{99}} = 99 \)
\( \log_5{0,2} = \log_{5}{5^{-1}} = -1 \)
\( \log_5{\frac{1}{25}} = \log_5{5^{-2}} = -2 \)
\( \log_5{\sqrt{5}} = \log_5{5^{\frac{1}{2}}} = \frac{1}{2} \)
\( \log_5{\sqrt[3]{25}} = \log_5{5^{\frac{2}{3}}} = \frac{2}{3} \)
Bir taban belirtilmediği durumda logaritma tabanı 10 olarak kabul edilir. Tabanı 10 olan logaritma işlemine onluk logaritma ya da bayağı logaritma denir.
\( \log{b} = \log_{10}{b} \)
Tanımda belirttiğimiz gibi, logaritma işlemi bir üstel ifadenin üssünde bulunan \( x \) değişkenini yalnız bırakmamızı sağlar.
\( 7^{2x - 1} = 12 \)
\( 2x - 1 = \log_7{12} \)
\( x = \dfrac{1 + \log_7{12}}{2} \)
Aşağıdaki ifadelerin sonucunu bulunuz.
(a) \( \log_5{\dfrac{\sqrt{5}}{125}} \)
(b) \( \log_3{\dfrac{81}{\sqrt[3]{9}}} \)
(c) \( \log_{0,5}{\dfrac{1}{\sqrt{32}}} \)
Çözümü GösterVerilen ifadelerde logaritma içini tabanın bir üssü şeklinde yazalım.
(a) seçeneği:
\( \log_5{\dfrac{\sqrt{5}}{125}} = \log_5{\dfrac{5^{\frac{1}{2}}}{5^3}} \)
\( = \log_5{5^{\frac{1}{2} - 3}} \)
\( = \log_5{5^{-\frac{5}{2}}} = -\dfrac{5}{2} \)
(b) seçeneği:
\( \log_3{\dfrac{81}{\sqrt[3]{9}}} = \log_3{\dfrac{3^4}{\sqrt[3]{3^2}}} \)
\( = \log_3{\dfrac{3^4}{3^{\frac{2}{3}}}} \)
\( = \log_3{3^{4-\frac{2}{3}}} \)
\( = \log_3{3^{\frac{10}{3}}} = \dfrac{10}{3} \)
(c) seçeneği:
\( \log_{0,5}{\dfrac{1}{\sqrt{32}}} = \log_{\frac{1}{2}}{\dfrac{1}{\sqrt{2^5}}} \)
\( = \log_{2^{-1}}{\dfrac{1}{2^{\frac{5}{2}}}} \)
\( = \log_{2^{-1}}{2^{-\frac{5}{2}}} \)
\( = \log_{2^{-1}}{(2^{-1})^{\frac{5}{2}}} = \dfrac{5}{2} \)
\( 5^{2x - 1} = 4 \) olduğuna göre, \( x \) kaçtır?
Çözümü Göster\( x \)'i yalnız bırakmak için verilen üstel ifadeyi logaritma ifadesi olarak yazalım.
\( 5^{2x - 1} = 4 \Longleftrightarrow \log_5{4} = 2x - 1 \)
\( 2x = 1 + \log_5{4} \)
\( x = \dfrac{1 + \log_5{4}}{2} \) bulunur.
\( \log_{a^2}{a^6} + \log_\sqrt{a}{a^3} + \log_{a^3}{a^4} \) işleminin sonucu nedir?
Çözümü GösterLogaritma ifadelerinin içini tabanın bir üssü şeklinde yazalım.
\( \log_{a^2}{(a^2)^3} + \log_{\sqrt{a}}{(\sqrt{a})^6} + \log_{a^3}{(a^3)^{\frac{4}{3}}} \)
\( a^n \) ifadesinin \( a \) tabanında logaritması \( n \)'ye eşittir.
\( = 3 + 6 + \dfrac{4}{3} \)
\( = \dfrac{31}{3} \) bulunur.
\( \dfrac{\log_5{\sqrt{125\sqrt{25\sqrt{5}}}}}{\log_2{\sqrt{64\sqrt[5]{16\sqrt{4}}}}} \) işleminin sonucu kaçtır?
Çözümü GösterÖnce paydaki ifadeyi düzenleyelim.
\( \log_5{(5^3 \cdot (5^2 \cdot 5^\frac{1}{2})^\frac{1}{2})^\frac{1}{2}} \)
\( = \log_5{(5^3 \cdot (5^\frac{5}{2})^\frac{1}{2})^\frac{1}{2}} \)
\( = \log_5{(5^3 \cdot 5^\frac{5}{4})^\frac{1}{2}} \)
\( = \log_5{(5^\frac{17}{4})^\frac{1}{2}} \)
\( = \log_5{5^\frac{17}{8}} \)
\( = \dfrac{17}{8} \)
Şimdi paydadaki ifadeyi düzenleyelim.
\( \log_2{(2^6 \cdot (2^4 \cdot (2^2)^\frac{1}{2})^\frac{1}{5})^\frac{1}{2}} \)
\( = \log_2{(2^6 \cdot (2^4 \cdot 2)^\frac{1}{5})^\frac{1}{2}} \)
\( = \log_2{(2^6 \cdot (2^5)^\frac{1}{5})^\frac{1}{2}} \)
\( = \log_2{(2^6 \cdot 2^\frac{5}{5})^\frac{1}{2}} \)
\( = \log_2{(2^6 \cdot 2)^\frac{1}{2}} \)
\( = \log_2{(2^7)^\frac{1}{2}} \)
\( = \log_2{2^\frac{7}{2}} \)
\( = \dfrac{7}{2} \)
İki ifadenin oranını bulalım.
\( \dfrac{\frac{17}{8}}{\frac{7}{2}} = \dfrac{17}{28} \) bulunur.
\( \log_5(25\sqrt[3]{5}\sqrt[4]{125}) \) ifadesinin sonucunu bulunuz.
Çözümü GösterLogaritma içini düzenleyelim.
\( \log_5(25\sqrt[3]{5}\sqrt[4]{125}) = \log_5(5^2 \cdot 5^{\frac{1}{3}} \cdot 5^{\frac{3}{4}}) \)
\( = \log_5{5^{2 + \frac{1}{3} + \frac{3}{4}}} \)
\( = \log_5{5^{\frac{37}{12}}} \)
Logaritma tanımına göre, \( a^n \) ifadesinin \( a \) tabanında logaritması \( n \)'ye eşittir.
\( = \dfrac{37}{12} \) bulunur.
Logaritma Tabanı
Logaritma tabanı (\( a \)) negatif, 0 ya da 1 olamaz.
Logaritma tabanının 0 ya da 1 olamama sebebi, bu değerler için işlem sonucunun belirsiz olmasıdır.
\( x = \log_a{b} \)
\( a = 1 \) ise \( b \) sadece \( 1 \) olabilir.
\( a^x = b \Longrightarrow 1^x = 1 \)
Bu eşitlikte \( x \) herhangi bir değer alabilir, dolayısıyla belirsizdir.
\( a = 0 \) ise \( b \) sadece \( 0 \) olabilir.
\( a^x = b \Longrightarrow 0^x = 0 \)
Bu eşitlikte \( x \) herhangi bir pozitif değer alabilir, dolayısıyla belirsizdir.
Logaritma tabanının negatif olamama sebebi, işlemin kesirli \( x \) değerlerinde reel olmayan sonuçlar üretebilmesidir.
\( x = \log_a{b} \)
\( a = -2 \) ve \( x = \frac{1}{2} \) ise,
\( a^x = b \Longrightarrow (-2)^{\frac{1}{2}} = \sqrt{-2} \)
Reel sayılarda karekök içi negatif olamayacağı için işlem sonucu tanımsızdır.
\( \log_{x - 3}{9} = 2 \) olduğuna göre, \( x \) kaçtır?
Çözümü GösterVerilen logaritma ifadesini üstel ifade olarak yazalım.
\( \log_{x - 3}{9} = 2 \Longleftrightarrow (x - 3)^2 = 9 \)
\( x - 3 = 3 \) veya \( x - 3 = -3 \) olur.
\( x - 3 = 3 \Longrightarrow x = 6 \)
\( x = 6 \) için logaritma tabanı \( 6 - 3 = 3 \) olduğu için \( x = 6 \) geçerli bir çözümdür.
\( x - 3 = -3 \Longrightarrow x = 0 \)
\( x = 0 \) için logaritma tabanı negatif olduğu için \( x = 0 \) geçerli bir çözüm değildir.
\( x = 6 \) bulunur.
\( \log_7{\log_3{\log_2{\log_3(81 \cdot 81)}}} \)
ifadesinin sonucu kaçtır?
Çözümü Gösterİfadenin değerini en içteki logaritma ifadesinden başlayarak hesaplayalım.
\( \log_7{\log_3{\log_2{\log_3(81 \cdot 81)}}} \)
\( = \log_7{\log_3{\log_2{\log_3(3^4 \cdot 3^4)}}} \)
\( = \log_7{\log_3{\log_2{\log_3(3^8)}}} \)
Logaritma tanımına göre \( \log_a{a^n} = n \) olur.
\( = \log_7{\log_3{\log_2{8}}} \)
\( = \log_7{\log_3{\log_2{2^3}}} \)
\( = \log_7{\log_3{3}} \)
\( = \log_7{1} \)
\( = \log_7{7^0} = 0 \) bulunur.
Aşağıda verilen ifadelerin eşitini bulunuz.
(a) \( \log_3{81} - \log_{\sqrt{5}}{25} \)
(b) \( \log_{\frac{1}{3}}{27} + \log_{49}{7} \)
(c) \( \log_{\frac{3}{2}}{\dfrac{4}{9}} + \log_{\frac{1}{2}}{\dfrac{1}{16}} \)
(d) \( \log_6{1} + \log_5{5} \)
Çözümü Göster(a) seçeneği:
\( \log_3{81} - \log_{\sqrt{5}}{25} \)
Logaritma içlerini tabanın bir üssü şeklinde yazalım.
\( = \log_3{3^4} - \log_{\sqrt{5}}{(\sqrt{5})^4} \)
\( = 4 - 4 = 0 \)
(b) seçeneği:
\( \log_{\frac{1}{3}}{27} + \log_{49}{7} \)
Logaritma içlerini tabanın bir üssü şeklinde yazalım.
\( = \log_{\frac{1}{3}}{(\frac{1}{3})^{-3}} + \log_{49}{49^{\frac{1}{2}}} \)
\( = -3 + \dfrac{1}{2} = -\dfrac{5}{2} \)
(c) seçeneği:
\( \log_{\frac{3}{2}}{\dfrac{4}{9}} + \log_{\frac{1}{2}}{\dfrac{1}{16}} \)
Logaritma içlerini tabanın bir üssü şeklinde yazalım.
\( = \log_{\frac{3}{2}}{(\dfrac{3}{2})^{-2}} + \log_{\frac{1}{2}}{(\dfrac{1}{2})^4} \)
\( = -2 + 4 = 2 \)
(d) seçeneği:
\( \log_6{1} + \log_5{5} \)
Logaritma içlerini tabanın bir üssü şeklinde yazalım.
\( = \log_6{6^0} + \log_5{5^1} \)
\( = 0 + 1 = 1 \)
Aşağıdaki eşitliklerdeki bilinmeyen değerini bulunuz.
(a) \( \log_3(3a + 3) = 4 \)
(b) \( 4\log_b{8} - 5 = 7 \)
(c) \( \log_a(6a - 9) = 2 \)
Çözümü Göster(a) seçeneği:
\( \log_3(3a + 3) = 4 \)
\( 3a + 3 = 3^4 = 81 \)
\( 3a = 78 \)
\( a = 26 \)
(b) seçeneği:
\( 4\log_b{8} - 5 = 7 \)
\( 4\log_b{8} = 12 \)
\( \log_b{8} = 3 \)
\( 8 = b^3 \)
\( b = 2 \)
(c) seçeneği:
\( \log_a(6a - 9) = 2 \)
\( a^2 = 6a - 9 \)
\( a^2 - 6a + 9 = 0 \)
\( (a - 3)^2 = 0 \)
\( a = 3 \)
\( \log_4[60 + \log_3(x + 5)] = 3 \)
olduğuna göre, \( x \) kaçtır?
Çözümü GösterDıştaki logaritma ifadesini üstel ifade şeklinde yazalım.
\( \log_4[60 + \log_3(x + 5)] = 3 \)
\( 60 + \log_3(x + 5) = 4^3 = 64 \)
\( \log_3(x + 5) = 64 - 60 = 4 \)
Logaritma ifadesini üstel ifade şeklinde yazalım.
\( x + 5 = 3^4 = 81 \)
\( x = 81 - 5 = 76 \) bulunur.
\( \log{\dfrac{5x + 2}{x - 3}} = 1 \)
olduğuna göre, \( x \) kaçtır?
Çözümü GösterVerilen logaritma ifadesini üstel ifade şeklinde yazalım.
\( \dfrac{5x + 2}{x - 3} = 10^1 = 10 \)
\( 5x + 2 = 10x - 30 \)
\( 5x = 32 \)
\( x = \dfrac{32}{5} \) bulunur.
\( \log_a{64} \) ifadesini tam sayı yapan kaç tane \( a \) tam sayısı vardır?
Çözümü Göster64 sayısını üslü şekillerde yazalım ve ifadeyi tam sayı yapan \( a \) değerlerini bulalım.
Logaritma tabanı negatif, 0 ya da 1 olamaz.
\( \log_2{2^6} = 6 \)
\( \log_4{4^3} = 3 \)
\( \log_8{8^2} = 2 \)
\( \log_{64}{64^1} = 1 \)
Buna göre, \( a \) sayısı 2, 4, 8 ve 64 olmak üzere 4 farklı değer alabilir.
\( a = \log_2{34} \)
\( b = \log_3{99} \)
\( c = \log_5{107} \)
değerlerinin dahil oldukları tam sayı aralıklarını bulunuz.
Çözümü Göster34 sayısı 2'nin bir üssü olarak 32 ve 64 arasındadır.
\( \log_2{32} \lt \log_2{34} \lt \log_2{64} \)
\( \log_2{2^5} \lt \log_2{34} \lt \log_2{2^6} \)
\( 5 \lt a \lt 6 \) bulunur.
99 sayısı 3'ün bir üssü olarak 81 ve 243 arasındadır.
\( \log_3{81} \lt \log_3{99} \lt \log_3{243} \)
\( \log_3{3^4} \lt \log_3{99} \lt \log_3{3^5} \)
\( 4 \lt b \lt 5 \) bulunur.
107 sayısı 5'in bir üssü olarak 25 ve 125 arasındadır.
\( \log_5{25} \lt \log_5{107} \lt \log_5{125} \)
\( \log_5{5^2} \lt \log_5{107} \lt \log_5{5^3} \)
\( 2 \lt c \lt 3 \) bulunur.
\( \log_x{\dfrac{8a}{3b}} = \dfrac{7}{3} \)
\( \log_x{\dfrac{6b}{a}} = \dfrac{5}{3} \)
olduğuna göre, \( x \) değerini bulunuz.
Çözümü Göster\( \log_x{\dfrac{8a}{3b}} = \dfrac{7}{3} \Longrightarrow \dfrac{8a}{3b} = x^{\frac{7}{3}} \)
\( \log_x{\dfrac{6b}{a}} = \dfrac{5}{3} \Longrightarrow \dfrac{6b}{a} = x^{\frac{5}{3}} \)
Elde ettiğimiz ifadeleri taraf tarafa çarpalım.
\( \dfrac{8a}{3b} \cdot \dfrac{6b}{a} = x^{\frac{7}{3}} \cdot x^{\frac{5}{3}} \)
\( 16 = x^{\frac{7}{3} + \frac{5}{3}} \)
\( 16 = x^4 \)
\( x \) logaritma tabanında bulunduğu için negatif değer alamaz, dolayısıyla \( x = -2 \) olamaz.
Buna göre, \( x = 2 \) bulunur.
\( 2^{3x} \cdot 3^{2x} = 5 \) olduğuna göre, \( x \) değerini logaritma cinsinden bulunuz.
Çözümü GösterEşitliğin sol tarafını tek bir tabanda birleştirelim.
\( 2^{3x} \cdot 3^{2x} = 5 \)
\( (2^3)^x \cdot (3^2)^x = 5 \)
Üsleri aynı olan iki ifadenin çarpımında ifadeler tabanlar çarpılarak ve üs korunarak birleştirilebilir.
\( (2^3 \cdot 3^2)^x = 72^x = 5 \)
\( x \)'i yalnız bırakalım.
\( x = \log_{72}{5} \) bulunur.
Aşağıda verilen eşitlikteki \( x \) değişkenini logaritma cinsinden yazınız.
\( 9^{x - 1} = 5^{x + 2} \)
Çözümü Göster\( 9^x\ 9^{-1} = 5^x\ 5^2 \)
\( \dfrac{9^x}{9} = 25 \cdot 5^x \)
\( \dfrac{9^x}{5^x} = 25 \cdot 9 \)
\( (\dfrac{9}{5})^x = 225 \)
\( x = \log_{\frac{9}{5}}{225} \) bulunur.
Logaritma Fonksiyonu
\( f(x) = \log_a{x} \) biçimindeki fonksiyona logaritma fonksiyonu denir.
\( f: \mathbb{R^+} \to \mathbb{R} \)
\( f(x) = \log_a{x} \)
\( f(x) = \log_4{x} \)
\( g(x) = 3\log_2(4x - 1) + 5 \)
Logaritma ve üstel fonksiyonlar birbirlerinin ters fonksiyonlarıdır, dolayısıyla üstel fonksiyonun tanım kümesi logaritma fonksiyonunun görüntü kümesine, üstel fonksiyonun görüntü kümesi de logaritma fonksiyonunun tanım kümesine eşittir.
\( f: \mathbb{R^+} \to \mathbb{R} \)
\( f(x) = \log_a{x} \)
\( f^{-1}: \mathbb{R} \to \mathbb{R^+} \)
\( f^{-1}(x) = a^x \)
\( f(x) = \log_4{x} \) ise,
\( f^{-1}(x) = 4^x \)
Logaritma Değer Tablosu ve Grafiği
\( f(x) = \log_2{x} \) logaritma fonksiyonunun bazı değerleri için değer tablosu aşağıdaki gibidir.
| \( x \) | \( f(x) \) |
|---|---|
| \( \frac{1}{4} \) | \( f(\frac{1}{4}) = \log_2{\frac{1}{4}} = -2 \) |
| \( \frac{1}{2} \) | \( f(\frac{1}{2}) = \log_2{\frac{1}{2}} = -1 \) |
| \( \frac{\sqrt{2}}{2} \) | \( f(\frac{\sqrt{2}}{2}) = \log_2{\frac{\sqrt{2}}{2}} = -\frac{1}{2} \) |
| \( 1 \) | \( f(1) = \log_2{1} = 0 \) |
| \( \sqrt{2} \) | \( f(\sqrt{2}) = \log_2{\sqrt{2}} = \frac{1}{2} \) |
| \( 2 \) | \( f(2) = \log_2{2} = 1 \) |
| \( 4 \) | \( f(4) = \log_2{4} = 2 \) |
| \( 8 \) | \( f(8) = \log_2{8} = 3 \) |
Bu noktaları analitik düzlemde işaretlediğimizde aşağıdaki grafiği elde ederiz.
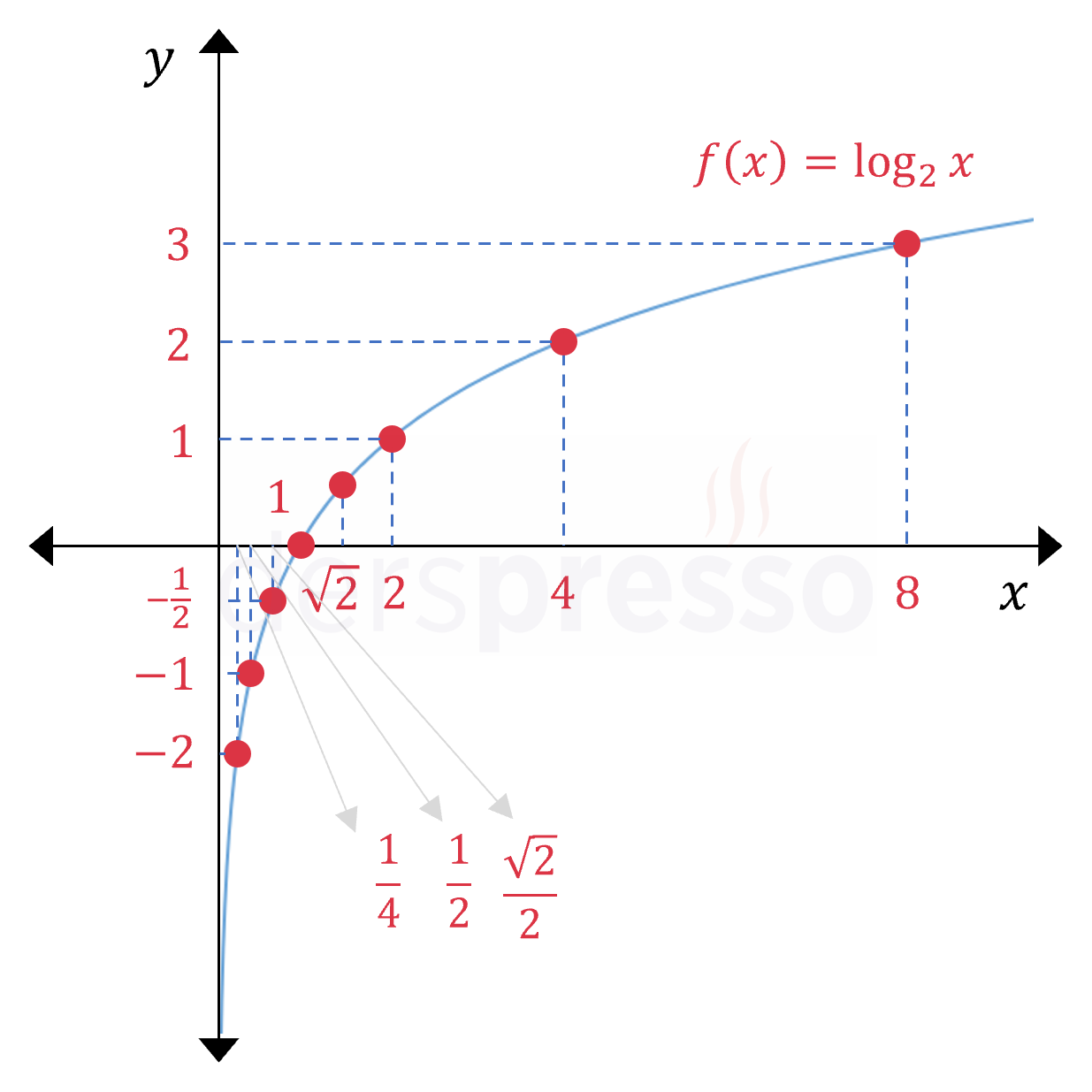
\( f(x) = \log_a{x} \) formundaki tüm logaritma fonksiyonları için \( f(1) = 0 \) olur, dolayısıyla grafikleri \( x \) eksenini \( (1, 0) \) noktasında keser.
Logaritma fonksiyonları \( \mathbb{R^+} \to \mathbb{R} \) için birebir ve örtendir, dolayısıyla ters fonksiyonları tanımlıdır ve üstel fonksiyonlardır.
\( f(x) = 22 + \log_5{x} \)
olduğuna göre, \( (f \circ f)(125) \) kaçtır?
Çözümü Göster\( (f \circ f)(125) = f(f(125)) \)
\( = f(22 + \log_5{125}) \)
\( = f(22 + \log_5{5^3}) \)
\( = f(22 + 3) \)
\( = f(25) \)
\( = 22 + \log_5{25} \)
\( = 22 + \log_5{5^2} \)
\( = 22 + 2 = 24 \) bulunur.
\( f(x) = 2^{3x - 2} \)
olduğuna göre, \( f^{-1}(x) \) nedir?
Çözümü GösterBir fonksiyonun ters fonksiyonunu bulmak için önce \( y = f(x) \) fonksiyonunda \( x \) yalnız kalacak şekilde fonksiyon yeniden düzenlenir.
\( y = f(x) = 2^{3x - 2} \)
\( 3x - 2 = \log_2{y} \)
\( x = \dfrac{\log_2{y} + 2}{3} \)
\( x \) ve \( y \) değişkenlerinin yerleri değiştirdiğimizde elde edeceğimiz yeni fonksiyon \( y = f(x) \) fonksiyonunun ters fonksiyonu olan \( y = f^{-1}(x) \) fonksiyonudur.
\( y = f^{-1}(x) = \dfrac{\log_2{x} + 2}{3} \)
\( f(x) = 2\log(x + 5) \)
olduğuna göre, \( f^{-1}(x) \) nedir?
Çözümü GösterBir fonksiyonun ters fonksiyonunu bulmak için önce \( y = f(x) \) fonksiyonunda \( x \) yalnız kalacak şekilde fonksiyon yeniden düzenlenir.
\( y = f(x) = 2\log(x + 5) \)
\( \dfrac{y}{2} = \log(x + 5) \)
\( x + 5 = 10^{\frac{y}{2}} \)
\( x = 10^{\frac{y}{2}} - 5 \)
\( x \) ve \( y \) değişkenlerinin yerleri değiştirdiğimizde elde edeceğimiz yeni fonksiyon \( y = f(x) \) fonksiyonunun ters fonksiyonu olan \( y = f^{-1}(x) \) fonksiyonudur.
\( y = f^{-1}(x) = 10^{\frac{x}{2}} - 5 \)
\( f(x) = \log_5{x^2} - 2 \)
olduğuna göre, \( f^{-1}(10) \) kaçtır?
Çözümü GösterBir fonksiyonun ters fonksiyonunu bulmak için önce \( y = f(x) \) fonksiyonunda \( x \) yalnız kalacak şekilde fonksiyon yeniden düzenlenir.
\( y = f(x) = \log_5{x^2} - 2 \)
\( y + 2 = \log_5{x^2} \)
\( x^2 = 5^{y + 2} \)
\( x = \sqrt{5^{y + 2}} \)
\( x \) ve \( y \) değişkenlerinin yerleri değiştirdiğimizde elde edeceğimiz yeni fonksiyon \( y = f(x) \) fonksiyonunun ters fonksiyonu olan \( y = f^{-1}(x) \) fonksiyonudur.
\( y = f^{-1}(x) = \sqrt{5^{x + 2}} \)
\( f^{-1}(10) \) değerini bulmak için \( x = 10 \) yazalım.
\( f^{-1}(10) = \sqrt{5^{10 + 2}} = \sqrt{5^{12}} = 5^6 \) bulunur.
\( f(x) = 2^x + a \) ve \( f^{-1}(9) = 2 \)
olduğuna göre, \( f(3) \) kaçtır?
Çözümü GösterBir fonksiyonun ters fonksiyonunu bulmak için önce \( y = f(x) \) fonksiyonunda \( x \) yalnız kalacak şekilde fonksiyon yeniden düzenlenir.
\( y = f(x) = 2^x + a \)
\( y - a = 2^x \)
\( x = \log_2(y - a) \)
\( x \) ve \( y \) değişkenlerinin yerleri değiştirdiğimizde elde edeceğimiz yeni fonksiyon \( y = f(x) \) fonksiyonunun ters fonksiyonu olan \( y = f^{-1}(x) \) fonksiyonudur.
\( y = f^{-1}(x) = \log_2(x - a) \)
\( a \) değerini bulmak için verilen \( f^{-1}(9) = 2 \) değerini kullanalım.
\( f^{-1}(9) = \log_2(9 - a) = 2 \)
\( 2^2 = 9 - a \Longrightarrow a = 5 \)
O halde, \( f(x) = 2^x + 5 \) olur.
\( f(3) = 2^3 + 5 = 13 \) bulunur.
\( f(x) = 5^{2x - 3} \)
\( g(x) = \log_2(6x - 2) \)
olduğuna göre, \( (g \circ f^{-1})(125) \) kaçtır?
Çözümü Göster\( f \) fonksiyonuna göre görüntüsü 125 olan değeri bulalım.
\( f^{-1}(125) = a \Longrightarrow f(a) = 125 \)
\( f(a) = 5^{2a - 3} = 125 = 5^3 \)
Tabanlar eşit olduğu için üsler de eşittir.
\( 2a - 3 = 3 \)
\( a = 3 \)
\( f^{-1}(125) = a = 3 \)
\( (g \circ f^{-1})(125) = g(f^{-1}(125)) \)
\( = g(3) = \log_2(6 \cdot 3 - 2) \)
\( = \log_2{16} = \log_2{2^4} \)
\( = 4 \) bulunur.
\( f(x) = \log_3{x} \)
\( (g \circ f)(x) = 4x + 3 \)
olduğuna göre, \( g(x) \) fonksiyonu nedir?
Çözümü GösterLogaritma fonksiyonunun ters fonksiyonu üstel fonksiyondur.
\( f(x) = y = \log_3{x} \Longrightarrow f^{-1}(x) = 3^x \)
\( (g \circ f)(x) = 4x + 3 \)
Eşitliğin her iki tarafının \( f^{-1} \) ile bileşkesini alalım.
\( g \circ f \circ f^{-1} = (4x + 3) \circ f^{-1} \)
\( f \circ f^{-1} = I \) birim fonksiyonu verir.
\( g(x) = [(4x + 3) \circ f^{-1}](x) \)
\( = 4f^{-1}(x) + 3 \)
\( = 4 \cdot 3^x + 3 \) bulunur.
\( f(x) = \dfrac{5^x - 1}{5^x + 2} \) fonksiyonunun tersini bulunuz.
Çözümü Göster\( f \) fonksiyonunun tersini bulmak için fonksiyonda \( x \)'i yalnız bırakalım.
\( y = \dfrac{5^x - 1}{5^x + 2} \)
\( y \cdot (5^x + 2) = 5^x - 1 \)
\( y \cdot 5^x + 2y = 5^x - 1 \)
\( 5^x - y \cdot 5^x = 2y + 1 \)
\( 5^x \cdot (1 - y) = 2y + 1 \)
\( 5^x = \dfrac{2y + 1}{1 - y} \)
\( x = \log_5{\dfrac{2y + 1}{1 - y}} \)
Elde ettiğimiz ifade \( f \) fonksiyonunun ters fonksiyonudur.
\( f^{-1}(x) = \log_5{\dfrac{2x + 1}{1 - x}} \)
\( n \in \mathbb{Z^+} \) olmak üzere,
\( f(n) = \begin{cases} 1 & \log_9{n} \text{ rasyonelse} \\ 0 & \log_9{n} \text{ rasyonel değilse} \end{cases} \)
fonksiyonu veriliyor.
Buna göre, \( f(1) + f(2) + \ldots + f(750) \) toplamı kaça eşittir?
Çözümü Göster\( \log_9{n} \) ifadesinin rasyonel olması için \( n \) 3'ün bir pozitif tam sayı kuvveti olmalıdır.
Örnek 1: \( \log_9{3} = \dfrac{1}{2} \)
Örnek 2: \( \log_9{27} = \dfrac{3}{2} \)
\( k \in \mathbb{Z^+} \) olmak üzere,
\( n = 3^k \)
\( \log_9{n} = \log_{3^2}{3^k} = \dfrac{k}{2} \)
\( 3^k \) değerinin 1-750 aralığında alabileceği en büyük değeri bulalım.
\( n \le 750 \)
\( 3^k \le 750 \)
\( 3^6 = 729 \le 750 \)
Buna göre, \( \log_9{n} \) ifadesini rasyonel yapan \( k \) değerleri 7 tanedir.
\( k \in \{0, 1, 2, 3, 4, 5, 6\} \)
\( n = 3k \in \{1, 3, 9, 27, 81, 243, 729\} \)
Fonksiyon \( n \in [1, 750] \) aralığında 7 kez 1 değerini alır, diğer \( n \) değerlerinde 0 değerini alır.
Buna göre verilen toplamın sonucu 7 olur.
\( a \in \mathbb{Z^+} \) olmak üzere,
\( \log_{a}{4096} \) ifadesinin sonucunun pozitif tam sayı olmasını sağlayan \( a \) değerlerinin toplamını bulunuz.
Çözümü Göster\( b \in \mathbb{Z^+} \) olmak üzere,
\( \log_{a}{4096} = b \) diyelim.
\( \log_{a}{2^{12}} = b \)
\( 2^{12} = a^b \)
Bu eşitliğe göre, \( a \) pozitif tam sayı olduğundan 2'nin bir tam sayı üssü şeklinde yazılabilmelidir.
\( k \in \mathbb{Z^+} \) olmak üzere,
\( a = 2^k \)
\( 2^{12} = (2^k)^b = 2^{kb} \)
\( 12 = kb \)
Bu eşitliği sağlayan pozitif tam sayı \( b \) değerleri aşağıdaki gibidir.
\( b = 1 \) için:
\( 2^{12} = a^1 \Longrightarrow a = 2^{12} = 4096 \)
\( b = 2 \) için:
\( 2^{12} = a^2 \Longrightarrow a = 2^6 = 64 \)
\( b = 3 \) için:
\( 2^{12} = a^3 \Longrightarrow a = 2^4 = 16 \)
\( b = 4 \) için:
\( 2^{12} = a^4 \Longrightarrow a = 2^3 = 8 \)
\( b = 6 \) için:
\( 2^{12} = a^6 \Longrightarrow a = 2^2 = 4 \)
\( b = 12 \) için:
\( 2^{12} = a^{12} \Longrightarrow a = 2^1 = 2 \)
Bulduğumuz \( a \) değerlerinin toplamını alalım.
\( 2 + 4 + 8 + 16 + 64 + 4096 = 4190 \) bulunur.