İşçi ve Havuz Problemleri
İşçi ve havuz problemlerinde belirli bir işin tamamlanması için çalışan işçi, makine ya da musluk gibi kaynakların kapasiteleri doğrultusunda işin tamamlanma süreleri hesaplanır.
A işçisi bir işi \( a \) günde tamamlıyorsa her gün işin aşağıdaki kadarlık kısmını tamamlar.
1 günde \( \frac{1}{a} \)'lık kısmı
2 günde \( \frac{2}{a} \)'lık kısmı
\( n \) günde \( \frac{n}{a} \)'lık kısmı
A işçisi bir işi \( a \) günde, B işçisi aynı işi \( b \) günde tamamlıyorsa birlikte her gün işin aşağıdaki kadarlık kısmını tamamlarlar.
1 günde \( \frac{1}{a} + \frac{1}{b} \)'lik kısmı
2 günde \( \frac{2}{a} + \frac{2}{b} \)'lik kısmı
\( n \) günde \( \frac{n}{a} + \frac{n}{b} \)'lik kısmı
\( x + 10 \) işçi bir işi 8 günde, \( 6x \) işçi aynı işi 3 günde tamamlıyor.
Her işçi bir günde aynı miktarda iş yaptığına göre \( x \) kaçtır?
Çözümü Göster\( x + 10 \) işçi bir işi 8 günde tamamlıyorsa toplam iş miktarını \( (x + 10) \cdot 8 = 8x + 80 \) olarak ifade edebiliriz.
\( 6x \) işçi aynı işi 3 günde tamamlıyorsa toplam iş miktarını \( 6x \cdot 3 = 18x \) olarak da ifade edebiliriz.
Toplam iş miktarı her iki durumda birbirine eşittir.
\( 8x + 80 = 18x \)
\( 10x = 80 \)
\( x = 8 \) bulunur.
Eşit kapasitedeki 7 işçi günde 5 saat çalışarak bir işi 16 günde bitirdiğine göre, 14 işçi günde 4 saat çalışarak aynı işi kaç günde bitirebilir?
Çözümü GösterToplam iş miktarını aşağıdaki formülle ifade edebiliriz.
Toplam iş = İşçi sayısı x Günlük çalışma saati x Gün sayısı
14 işçinin çalışması gereken gün sayısına \( x \) diyelim.
Toplam iş miktarı her iki durumda birbirine eşittir.
\( 7 \cdot 5 \cdot 16 = 14 \cdot 4 \cdot x \)
\( 5 \cdot 16 = 2 \cdot 4 \cdot x \)
\( x = 10 \) bulunur.
Eşit kapasitedeki bir grup işçiden 4'ü çalışmazsa bir evin inşaatı 80 günde, bu gruba aynı kapasitede 5 işçi daha alınmasıyla birlikte tüm işçiler çalışırsa aynı evin inşaatı 50 günde tamamlanıyor.
İşçiler her gün aynı süre çalıştıklarına göre, bu grup kaç kişiliktir?
Çözümü GösterBu gruptaki işçi sayısına \( x \) diyelim.
Bu işçilerden 4'ü çalışmadığında evin inşaatı 80 günde bitiyorsa toplam iş miktarını \( (x - 4) \cdot 80 \) şeklinde ifade edebiliriz.
İşçilerin yanına 5 işçi daha eklendiğinde evin inşaatı 50 günde tamamlanıyorsa iş miktarını \( (x + 5) \cdot 50 \) şeklinde de ifade edebiliriz.
Toplam iş miktarı her iki durumda birbirine eşittir.
\( (x - 4) \cdot 80 = (x + 5) \cdot 50 \)
\( (x - 4) \cdot 16 = (x + 5) \cdot 10 \)
\( 16x - 64 = 10x + 50 \)
\( 6x = 114 \)
\( x = 19 \)
Buna göre grupta 19 işçi vardır.
Bir fabrikada iki farklı makarna paketleme makinesi vardır. Birinci makine saatte 300 paket makarna paketleyip günde 8 saat çalışabilirken ikinci makine saatte 500 paket makarna paketleyip günde 6 saat çalışabiliyor.
Bu fabrikada birinci makinenin 15 günde paketlediği miktarda makarnayı ikinci makine kaç günde paketler?
Çözümü GösterBirinci makine 15 günde toplam \( 300 \cdot 8 \cdot 15 \) paket makarna paketler.
İkinci makinenin çalışması gereken gün sayısına \( x \) diyelim.
İkinci makine \( x \) günde toplam \( 500 \cdot 6 \cdot x \) paket makarna paketler.
Paketlenen makarna miktarı her iki durumda birbirine eşittir.
\( 300 \cdot 8 \cdot 15 = 500 \cdot 6 \cdot x \)
\( x = 12 \)
Buna göre ikinci makine aynı miktarda makarnayı 12 günde paketler.
Bir halı dokuma fabrikasında 25 işçi günde 9 saat çalışarak 7 günde 300 halı dokuyabiliyor.
Bir süre sonra fabrikadan 10 işçi çıkarılıyor. Kalan işçiler günde 10 saat çalışarak 400 halıyı kaç günde dokuyabilir?
Çözümü GösterDokunan halı sayısı ile toplam çalışma süresi doğru orantılı olduğundan her iki durumda dokunan halı sayılarının oranı, toplam çalışma sürelerinin oranına eşit olmalıdır.
Birinci ve ikinci durumda dokunan halı sayılarının oranını bulalım.
\( \dfrac{300}{400} = \dfrac{3}{4} \)
İkinci durumda 10 işçi çıkarılınca \( 25 - 10 = 15 \) işçi kalır. Bu işçilerin 400 halıyı dokumak için çalışmaları gereken gün sayısına \( x \) diyelim.
Birinci ve ikinci durumda toplam çalışma sürelerinin oranını bulalım.
\( \dfrac{25 \cdot 9 \cdot 7}{15 \cdot 10 \cdot x} \)
Bu iki oran birbirine eşit olmalıdır.
\( \dfrac{3}{4} = \dfrac{25 \cdot 9 \cdot 7}{15 \cdot 10 \cdot x} \)
İçler - dışlar çarpımı yapalım.
\( 3 \cdot 15 \cdot 10 \cdot x = 4 \cdot 25 \cdot 9 \cdot 7 \)
\( x = 14 \)
Buna göre kalan işçiler 400 halıyı 14 günde dokuyabilirler.
Bir grup işçi bir işi 80 günde bitirebiliyor. İşçilerin sayısı 2 katına çıkarılıp günlük çalışma süresi %20 azaltılırsa işçiler bu işi kaç günde bitirebilir?
Çözümü Gösterİşçi sayısına \( x \), günlük çalışma sürelerine işlem kolaylığı açısından \( 10y \) diyelim.
Bu işin tamamlanması için gerekli toplam süreyi \( x \cdot 10y \cdot 80 = 800xy \) şeklinde ifade edebiliriz.
İşçilerin sayısı 2 katına çıkarılınca işçi sayısı \( 2x \) olur.
Günlük çalışma süresi %20 azaltılınca süre \( 10y - 10y \cdot \frac{20}{100} = 8y \) olur.
İkinci durumda işçilerin işi bitirme süresine \( z \) diyelim.
İkinci durumda işin tamamlanması için gerekli toplam süreyi \( 2x \cdot 8y \cdot z = 16xyz \) şeklinde ifade edebiliriz.
Toplam iş miktarı her iki durumda birbirine eşittir.
\( 800xy = 16xyz \)
\( z = 50 \)
Buna göre işçiler işi 50 günde bitirebilirler.
Yiğit bir işi 12 günde, arkadaşı Salih ise 4 günde bitirebilmektedir.
İkisi birlikte çalışırlarsa bu işi kaç günde bitirebilirler?
Çözümü Gösterİş miktarına işlem kolaylığı açısından \( 12x \) birim diyelim.
Yiğit bir günde \( \frac{12x}{12} = x \) birim, Salih bir günde \( \frac{12x}{4} = 3x \) birim iş tamamlamaktadır.
İkisi birlikte çalıştıklarında günde \( x + 3x = 4x \) birim iş tamamlarlar.
Buna göre bu işi birlikte \( \frac{12x}{4x} = 3 \) günde bitirebilirler.
Ali usta bir işi tek başına \( x \) saatte, Mehmet usta ile birlikte 10 saatte tamamlıyor.
Mehmet usta aynı işi Ali ustadan daha uzun sürede tamamladığına göre \( x \) hangi aralıktadır?
Çözümü Gösterİkisi aynı hızda çalışıyor olsalardı her biri ayrı ayrı bu işi 20 saatte tamamlıyor olurlardı.
Ali usta Mehmet ustadan daha hızlı çalıştığı için \( x \) sayısı 20'den küçük olmalıdır.
İkisi birlikte bu işi 10 saatte tamamladıklarına göre, Ali usta işi 10 saatten önce tamamlıyor olamaz.
O halde \( x \) sayısı 10'dan büyüktür.
\( 10 \lt x \lt 20 \) olarak bulunur.
Farklı işlemci gücüne sahip iki bilgisayar birlikte çalışarak bir veri setinin analizini 15 saatte bitirebiliyor.
Birinci bilgisayar tek başına çalışarak bu analizi 24 saatte bitirebildiğine göre, ikinci bilgisayar bu analizi tek başına kaç saatte bitirebilir?
Çözümü GösterToplam iş miktarına \( 120x \) birim diyelim.
Birinci bilgisayar bir saatte \( \frac{120x}{24} = 5x \) birim iş bitirebiliyor.
İki bilgisayar birlikte çalıştığında bir saatte \( \frac{120x}{15} = 8x \) birim iş bitirebiliyor.
Buna göre ikinci bilgisayar bir saatte \( 8x - 5x = 3x \) birim iş yapabiliyor olmalıdır.
İkinci bilgisayar bir saatte \( 3x \) birim iş yapabiliyorsa tüm işi \( \frac{120x}{3x} = 40 \) saatte bitirebilir.
Bir dekorasyon şirketinde boyacı olarak çalışan iki işçiden Sevda, bir saatte Hilal'in boyadığı alanın \( \frac{4}{5} \)'i kadarını boyayabiliyor.
İkisinin birlikte 24 saatte boyadığı bir evi Sevda tek başına kaç saatte boyayabilir?
Çözümü GösterVerilen orana göre Sevda saatte 4 birim boyama yaparken Hilal 5 birim boyama yapabiliyor. Buna göre birlikte saatte \( 4 + 5 = 9 \) birim boyama yaparlar.
Birlikte 24 saatte \( 24 \cdot 9 = 216 \) birim boyama yapabildiklerine göre, bu duvarın 216 birimlik bir çalışma gerektirdiğini söyleyebiliriz.
Buna göre saatte 4 birim çalışma yapabilen Sevda bu duvarı tek başına \( \frac{216}{4} = 54 \) saatte boyayabilir.
Halil bir işin \( \frac{3}{4} \)'ünü 9 günde, Ayça aynı işin \( \frac{2}{3} \)'ünü 16 günde bitirebiliyor.
Buna göre, ikisi birlikte bu işin yarısını kaç günde bitirebilirler?
Çözümü GösterHalil işin \( \frac{3}{4} \)'ünü 9 günde bitiriyorsa tamamını \( 9 \cdot \frac{4}{3} = 12 \) günde bitirebilir.
Ayça işin \( \frac{2}{3} \)'ünü 16 günde bitirebiliyorsa tamamını \( 16 \cdot \frac{3}{2} = 24 \) günde bitirebilir.
İşin tamamına işlem kolaylığı açısından 120 birim diyelim.
Halil tek başına bir günde \( \frac{120}{12} = 10 \) birim, Ayça tek başına bir günde \( \frac{120}{24} = 5 \) birim iş bitirebilir.
Birlikte çalıştıklarında bir günde \( 10 + 5 = 15 \) birim iş bitirebilirler.
İşin yarısı 60 birimdir.
Buna göre birlikte çalıştıklarında işin yarısını \( \frac{60}{15} = 4 \) günde bitirebilirler.
Üç farklı dikiş makinesi birlikte çalıştığında bir miktar perdeyi 4 saatte dikebiliyor.
A makinesi bu perdeleri tek başına 8 saatte, B makinesi 12 saatte dikebildiğine göre, C makinesi bu perdeleri tek başına kaç saatte dikebilir?
Çözümü GösterToplam perde miktarına işlem kolaylığı açısından \( 24x \) birim diyelim.
A makinesi tek başına saatte \( \frac{24x}{8} = 3x \) birim, B makinesi tek başına \( \frac{24x}{12} = 2x \) birim perde dikebiliyor.
Üç makine birlikte saatte \( \frac{24x}{4} = 6x \) birim dikebildiğine göre, C makinesi tek başına saatte \( 6x - 3x - 2x = x \) birim dikebilir.
Buna göre C makinesi bu perdeleri tek başına \( \frac{24x}{x} = 24 \) saatte dikebilir.
Ayşe ve Serhat bir işi sırasıyla \( a \) ve \( 4a \) günde bitirebiliyor, birlikte çalıştıklarında ise aynı işi 16 günde bitirebiliyorlar.
Buna göre Ayşe bu işi tek başına kaç günde bitirebilir?
Çözümü GösterToplam iş miktarına işlem kolaylığı açısından \( 16a \) diyelim.
Ayşe işi \( a \) günde bitirebiliyorsa bir günde \( \frac{16a}{a} = 16 \) birim iş bitirebilir.
Serhat aynı işi \( 4a \) günde bitirebiliyorsa bir günde \( \frac{16a}{4a} = 4 \) birim iş bitirebilir.
Ayşe ve Serhat birlikte çalıştıklarında aynı işi \( 16 \) günde bitirebiliyorsa bir günde \( \frac{16a}{16} = a \) birim iş bitirebilirler.
\( a \) ikisinin bir günde tamamladıkları işin toplamıdır.
\( a = 4 + 16 = 20 \)
Buna göre Ayşe bu işi tek başına \( a = 20 \) günde bitirebilir.
Bir kumaş boyama fabrikasındaki A makinesi 2400 metrekarelik bir kumaşı günde 3 saat çalışarak 10 günde boyayabiliyor. B makinesi ise aynı kumaşın \( \frac{3}{4} \)'ünü günde 5 saat çalışarak 3 günde boyayabiliyor.
A ve B makinelerinin birlikte çalışarak bu kumaşı 2 günde boyayabilmesi için günde kaç saat çalışmaları gerekir?
Çözümü GösterA makinesi 2400 metrekarelik kumaşı \( 3 \cdot 10 = 30 \) saatte boyayabiliyorsa bir saatte \( \frac{2400}{30} = 80 \) metrekare kumaş boyayabilir.
B makinesi \( 2400 \cdot \frac{3}{4} = 1800 \) metrekarelik kumaşı \( 5 \cdot 3 = 15 \) saatte boyayabiliyorsa bir saatte \( \frac{1800}{15} = 120 \) metrekare kumaş boyayabilir.
Buna göre iki makine birlikte çalışarak bir saatte \( 80 + 120 = 200 \) metrekare kumaş boyayabilir.
2400 metrekarelik kumaşı boyamak için iki makinenin birlikte toplam \( \frac{2400}{200} = 12 \) saat çalışması gerekir.
İki makinenin bu işi 2 günde bitirebilmesi için günde \( \frac{12}{2} = 6 \) saat çalışmaları gerekir.
Faruk ve Eray birim zamanda eşit miktarda patik dikmektedir. Faruk sabahtan beri 60 adet patik dikmiştir ve elindeki patikleri tamamlaması için 3 saat daha çalışması gerekmektedir. Eray ise sabahtan beri 140 adet patik dikmiştir ve elindeki patikleri tamamlaması için 5 saat daha çalışması gerekmektedir.
Eray'ın toplamda dikmiş olacağı patik adedi Faruk'unkinin 2 katı olduğuna göre, ikisi birlikte toplam kaç adet patik dikmiş olacaktır?
Çözümü GösterHer birinin bir saatte diktikleri patik adedine \( x \) diyelim.
Faruk'un toplamda dikmiş olacağı patik adedi \( 60 + 3x \) olur.
Eray'ın toplamda dikmiş olacağı patik adedi \( 140 + 5x \) olur.
Eray'ın toplamda dikmiş olacağı patik adedi Faruk'unkinin 2 katına eşittir.
\( 140 + 5x = 2(60 + 3x) \)
\( 140 + 5x = 120 + 6x \)
\( x = 20 \)
Buna göre Faruk'un dikmiş olacağı toplam patik adedi \( 60 + 3x = 120 \), Eray'ınki ise \( 140 + 5x = 240 \) olur.
İkisinin dikmiş olacağı toplam patik adedi \( 120 + 240 = 360 \) olur.
Bir kargo şirketi kapasiteleri farklı üç araçla bir haftada 5880 paket dağıtacaktır.
En büyük araç ile en küçük araç kargoların \( \frac{5}{7} \)'sini, orta büyüklükteki araç ile en küçük araç kargoların \( \frac{1}{2} \)'sini dağıtacaktır.
Buna göre orta büyüklükteki aracın tek başına dağıtacağı paket sayısı kaçtır?
Çözümü GösterBüyük, orta ve küçük araçların bir haftada dağıtacağı paket sayılarına sırasıyla \( a \), \( b \) ve \( c \) diyelim.
Kargoların \( \frac{1}{2} \)'sini \( b \) ve \( c \) araçları dağıtacaksa geriye kalan paketleri \( a \) aracı dağıtacaktır.
\( a = b + c = \dfrac{5880}{2} = 2940 \)
Kargoların \( \frac{5}{7} \)'sini \( a \) ve \( c \) araçları dağıtacaktır.
\( a + c = 5880 \cdot \dfrac{5}{7} = 4200 \)
\( a = 2940 \Longrightarrow c = 1260 \)
\( b + c = 2940 \Longrightarrow b = 1680 \) bulunur.
Birlikte çalışan üç işçiden en hızlı olan işçi diğer iki işçinin toplamının iki katı hızda çalışırken diğer işçilerin çalışma hızları arasında \( \frac{1}{3} \) oranı vardır.
Bu işçilerin birlikte 6 günde bitirdiği bir işi en hızlı çalışan işçi tek başına kaç günde bitirir?
Çözümü GösterEn yavaş çalışan işçinin bir günde tamamladığı iş miktarına \( x \) diyelim.
Orta hızda çalışan işçi ile aralarında \( \frac{1}{3} \) oranı olduğuna göre, orta hızda çalışan işçinin bir günde tamamladığı iş miktarı \( 3x \) olur.
En hızlı çalışan işçi diğer iki işçinin çalışma hızları toplamının iki katı hızda çalıştığına göre, bir günde tamamladığı iş miktarı \( (x + 3x) \cdot 2 = 8x \) olur.
Üç işçi birlikte çalıştığında bir günde bitirdikleri iş miktarı üçünün çalışma hızlarının toplamı, yani \( x + 3x + 8x = 12x \) olur.
Üç işçi birlikte 1 günde \( 12x \) birim iş tamamlıyorsa 6 günde \( 72x \) birim iş tamamlarlar.
Aynı işi en hızlı çalışan işçinin tek başına yapma süresi \( \frac{72x}{8x} = 9 \) gün olur.
Eşit iş gücünde 4 adet A makinesi bir siparişi 6 günde, eşit iş gücünde 6 adet B makinesi aynı siparişi 12 günde tamamlayabiliyor.
Buna göre bir adet A ve bir adet B makinesi aynı siparişi kaç günde tamamlayabilir?
Çözümü Göster4 adet A makinesi siparişi 6 günde tamamlıyorsa 4 adet A makinesi bir günde siparişin \( \frac{1}{6} \)'sını tamamlar, dolayısıyla 1 adet A makinesi bir günde siparişin \( \frac{1}{24} \)'ünü tamamlar.
6 adet B makinesi siparişi 12 günde tamamlıyorsa 6 adet B makinesi bir günde siparişin \( \frac{1}{12} \)'sini tamamlar, dolayısıyla 1 adet B makinesi bir günde siparişin \( \frac{1}{72} \)'sini tamamlar.
Bir adet A ve bir adet B makinesinin siparişi tamamlayabileceği gün sayısına \( t \) diyelim.
\( (\dfrac{1}{24} + \dfrac{1}{72}) \cdot t = 1 \)
\( \dfrac{1}{18} \cdot t = 1 \)
\( t = 18 \) gün bulunur.
Askerde yemekhanede çalışan Osman beş çuval patatesi tek başına 12 saatte, Sinan ise üç çuval patatesi tek başına 8 saatte soyabiliyor.
Osman ve Sinan birlikte yarım saat çalıştıklarında bir çuval patatesin kaçta kaçını soyabilirler?
Çözümü GösterOsman beş çuval patatesi 12 saatte soyuyorsa bir çuvalı \( \frac{12}{5} \) saatte soyar, dolayısıyla 1 saatte bir çuvalın \( \frac{1}{\frac{12}{5}} = \frac{5}{12} \)'ini soyar.
Sinan üç çuval patatesi 8 saatte soyuyorsa bir çuvalı \( \frac{8}{3} \) saatte soyar, dolayısıyla 1 saatte bir çuvalın \( \frac{1}{\frac{8}{3}} = \frac{3}{8} \)'ünü soyar.
Osman ve Sinan birlikte yarım saat çalıştıklarında bir çuval patatesin kaçta kaçını soyabildiklerini bulalım.
\( \dfrac{1}{2} \cdot (\dfrac{5}{12} + \dfrac{3}{8}) = \dfrac{1}{2} \cdot \dfrac{10 + 9}{24} \)
\( = \dfrac{19}{48} \) bulunur.
Bir yenilenebilir enerji tesisinde iki farklı rüzgar türbini 184 MW kapasiteli bir bataryayı şarj etmek için birlikte çalışmaktadır.
Aşağıdaki grafikte türbinlerin çalıştıkları süreye bağlı olarak ürettikleri enerji miktarları verilmiştir.
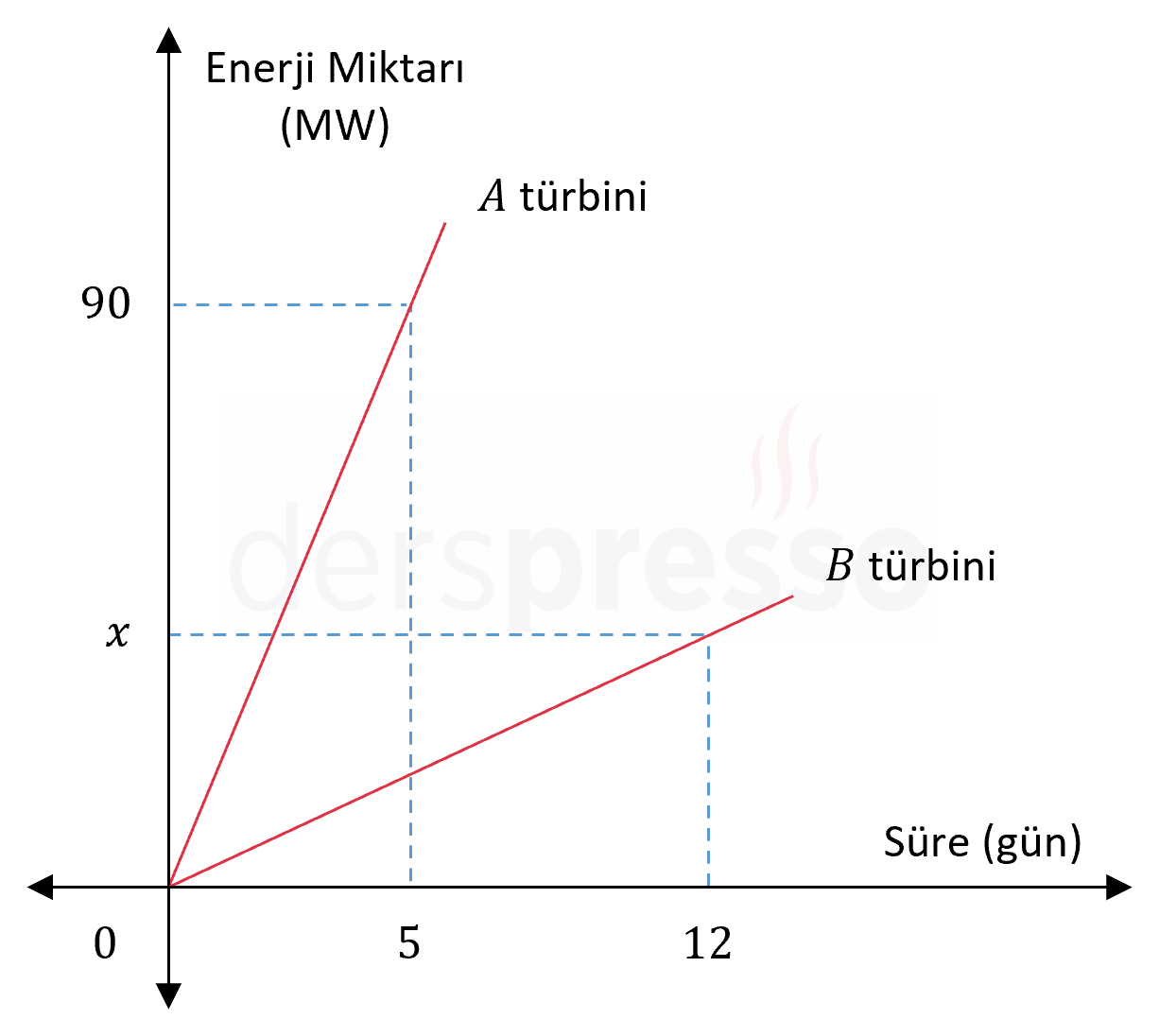
Her iki türbin birlikte çalışarak bataryayı 8 günde tamamen şarj edebildiklerine göre, \( x \) kaçtır?
Çözümü GösterA türbini 5 günde 90 MW enerji ürettiğine göre, bir günde 18 MW, 8 günde \( 8 \cdot 18 = 144 \) MW enerji üretir.
İki türbinin bataryayı birlikte 8 günde şarj edebilmeleri için, B türbini 8 günde \( 184 - 144 = 40 \) MW, günde 5 MW enerji üretmelidir.
\( x \) miktarı B türbininin 12 günde ürettiği enerji miktarıdır.
\( x = 12 \cdot 5 = 60 \) MW bulunur.
Bir fabrikadaki \( a, b, c \) makinalarından \( a \) makinesi belirli bir siparişi tek başına 12 günde, \( a \) ve \( b \) makineleri birlikte 8 günde, üç makine birlikte 5 günde tamamlayabiliyor.
Buna göre aşağıdaki öncüllerden hangileri doğrudur?
I. Üretim kapasitesi en yüksek olan makine \( c \) makinesidir.
II. \( a \) ve \( c \) makineleri birlikte aynı siparişi, \( b \) ve \( c \) makinelerine kıyasla daha kısa sürede tamamlar.
III. \( b \) makinesi bu siparişin yarısını tek başına 10 günde tamamlar.
Çözümü GösterSipariş miktarına \( 120x \) adet diyelim.
\( a \) makinesi \( 120x \) adet üretimi tek başına 12 günde tamamlıyorsa 1 günde \( 10x \) adet üretim yapar.
\( a \) ve \( b \) makineleri \( 120x \) adet üretimi birlikte 8 günde tamamlıyorsa 1 günde \( 15x \) adet üretim yapar.
\( a \) makinesi 1 günde \( 10x \) adet üretim yaptığına göre, \( b \) makinesi 1 günde \( 5x \) adet üretim yapıyordur.
\( a \), \( b \) ve \( c \) makineleri \( 120x \) adet üretimi birlikte 5 günde tamamlıyorsa 1 günde \( 24x \) adet üretim yapar.
\( a \) ve \( b \) makineleri 1 günde \( 15x \) adet üretim yaptığına göre, \( c \) makinesi 1 günde \( 9x \) adet üretim yapıyordur.
Verilen öncülleri inceleyelim.
I. öncül:
"Üretim kapasitesi en yüksek olan makine \( c \) makinesidir."
Üç makinenin bir gündeki üretim adetleri sırasıyla \( 10x, 5x, 9x \) adettir. Buna göre üretim kapasitesi en yüksek olan makine \( a \) makinesidir.
I. öncül yanlıştır.
II. öncül:
"\( a \) ve \( c \) makineleri birlikte aynı siparişi, \( b \) ve \( c \) makinelerine kıyasla daha kısa sürede tamamlar."
\( a \) ve \( c \) makineleri birlikte çalıştıklarında günde \( 19x \) adet üretim yapar.
\( b \) ve \( c \) makineleri birlikte çalıştıklarında ise günde \( 14x \) adet üretim yapar.
\( a \) ve \( c \) makinelerinin toplam kapasitesi daha yüksek olduğu için \( b \) ve \( c \) makinelerine göre aynı siparişi daha kısa sürede tamamlar.
II. öncül doğrudur.
III. öncül:
"\( b \) makinesi bu siparişin yarısını tek başına 10 günde tamamlar"
Toplam sipariş miktarı \( 120x \) adet olduğuna göre siparişin yarısı \( 60x \) adet olur.
\( b \) makinesi günde \( 5x \) adet üretim yaptığına göre, 10 günde \( 50x \) adet üretim yapar.
III. öncül yanlıştır.
Bu durumda sadece II. öncül doğrudur.
Toplam hacmi 56 metreküp olan bir havuzu doldurmak için kullanılan 3 musluktan özdeş ikisi havuzu eşit hızda, üçüncüsü farklı hızda doldurmaktadır.
Bu üç musluk aynı anda açılıyor ve havuzdaki su miktarı belirli bir seviyeye ulaştığında üçüncü musluk kapatılıyor.
Aşağıdaki grafikte havuzdaki su miktarının zamana göre değişimi verilmiştir.

Buna göre üçüncü musluk tek başına havuzu kaç dakikada doldurur?
Çözümü GösterÖzdeş musluklardan her birinin dakikada doldurduğu su miktarına \( a \) metreküp, üçüncü musluğun dakikada doldurduğu su miktarına \( b \) metreküp diyelim.
Grafikte 4. dakikadaki değişime göre, üçüncü musluk 4. dakikada kapatılmıştır.
Buna göre ilk 4 dakika boyunca üç musluk birlikte çalışmıştır.
İlk 4 dakikada üç musluk toplam \( 4 \cdot (2a + b) = 32 \) metreküp su doldurmuştur.
Sonraki 6 dakikada özdeş iki musluk toplam \( 6 \cdot 2a = 56 - 32 = 24 \) metreküp su doldurmuştur.
İki denklemi ortak çözelim.
\( 4 \cdot (2a + b) = 32 \)
\( 2a + b = 8 \)
\( 6 \cdot 2a = 24 \)
\( a = 2 \) metreküp/dk
\( b = 4 \) metreküp/dk
Üçüncü musluğun havuzu tek başına kaç dakikada dolduracağını bulalım.
\( \dfrac{56}{4} = 14 \) dakika bulunur.
Boya ustası Ali, Fuat ve Soner'in günlük ücreti bir saatte boyadıkları alanla doğru orantılı olarak sırasıyla 1000, 1200 ve 1500 liradır.
Üçü birlikte bir binayı 12 saatte boyayabildiklerine göre, Fuat tüm binayı kaç saatte boyar?
Çözümü GösterAli, Fuat ve Soner'in bir saatte boyadıkları alanlara sırasıyla \( a, b, c \) metrekare diyelim.
Bir saatte boyadıkları alanlar 1000, 1200 ve 1500 ile doğru orantılıdır.
\( \dfrac{a}{1000} = \dfrac{b}{1200} = \dfrac{c}{1500} = k \)
Buna göre her birinin bir saatte boyadıkları alanlar sırasıyla \( 1000k, 1200k, 1500k \) metrekaredir.
Boyanacak alana \( x \) metrekare diyelim.
Üçü birlikte çalıştıklarında binayı 12 saatte boyayabiliyorlar.
\( (1000k + 1200k + 1500k) \cdot 12 = x \)
\( 3700k \cdot 12 = x \)
\( k = \dfrac{x}{3700 \cdot 12} \)
Fuat'ın tek başına bir saatte boyayabileceği alanı bulalım.
\( 1200k = 1200 \cdot \dfrac{x}{3700 \cdot 12} = \dfrac{x}{37} \) metrekare
Fuat'ın tek başına \( x \) metrekareyi (tüm binayı) kaç saatte boyayabileceğini bulalım.
\( \dfrac{x}{\frac{x}{37}} = 37 \) saat bulunur.
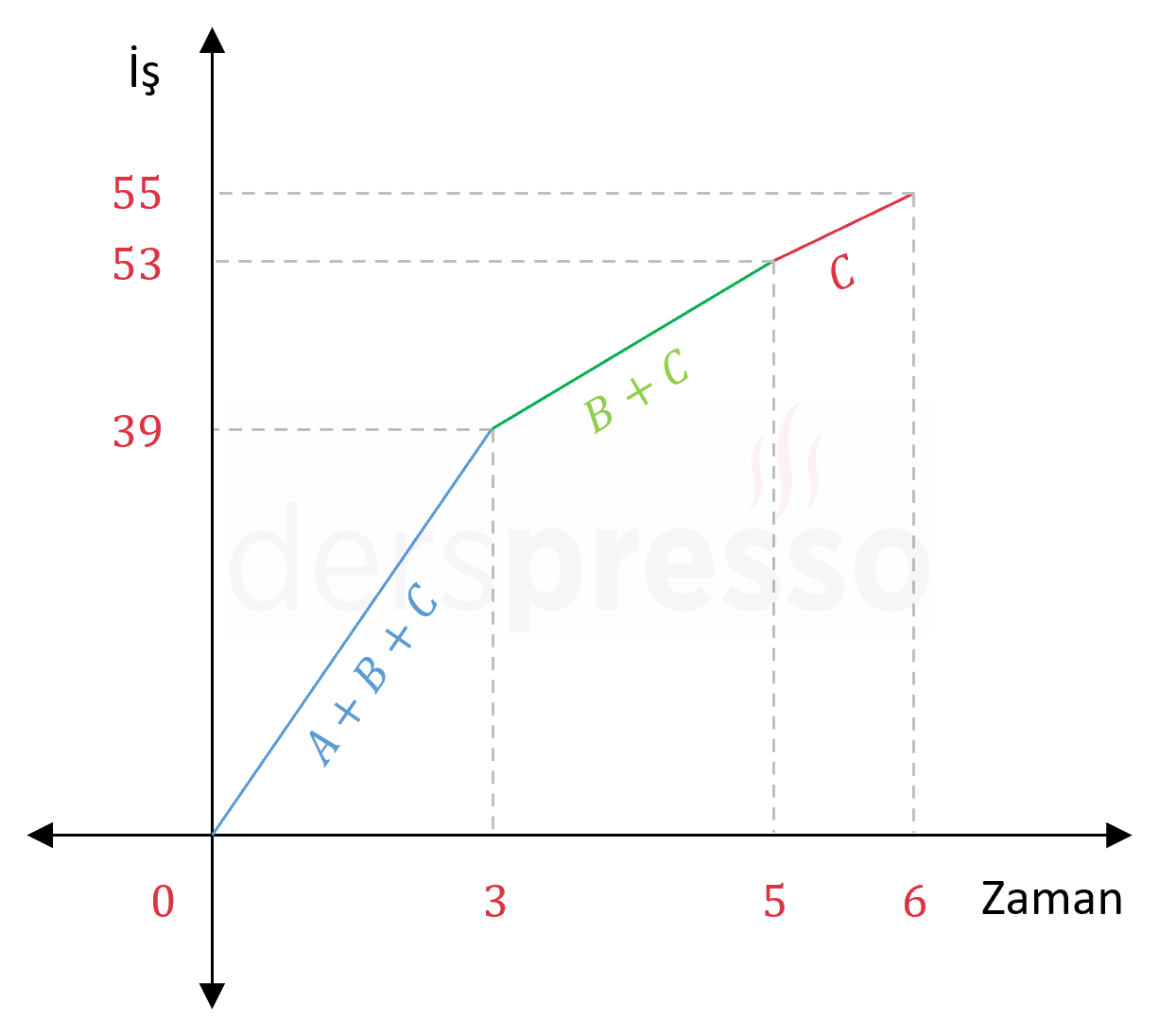
Yukarıdaki grafikte A, B ve C makinelerinin belirli zaman aralıklarında tamamladıkları iş miktarları verilmiştir.
Bu grafiğe göre, ilk 3 saat boyunca üç makine birlikte çalıştırılmış, 3. saat sonunda A makinesi, 5. saat sonunda B makinesi durdurulmuştur.
Buna göre A makinesi 1 saatte kaç birimlik iş tamamlar?
Çözümü GösterA, B ve C makineleri ilk 3 saatte birlikte 39 birimlik iş tamamlamıştır.
A makinesi 3. saat sonunda durdurulduğuna göre, B ve C makineleri sonraki 2 saatte birlikte \( 53 - 39 = 14 \) birimlik iş tamamlamıştır.
Buna göre, B ve C makineleri 1 saatte birlikte 7 birimlik iş tamamlar.
B makinesi 5. saat sonunda durdurulduğuna göre, C makinesi sonraki 1 saatte tek başına \( 55 - 53 = 2 \) birimlik iş tamamlamıştır.
B ve C makineleri birlikte 1 saatte 7 birimlik iş, C makinesi tek başına 1 saatte 2 birimlik iş tamamladığına göre, B makinesi tek başına 1 saatte \( 7 - 2 = 5 \) birimlik iş tamamlar.
B ve C makineleri birlikte 1 saatte 7 birimlik iş tamamladığına göre, 3 saatte \( 3 \cdot 7 = 21 \) birimlik iş tamamlar.
O halde A makinesi 3 saatte \( 39 - 21 = 18 \) birimlik iş tamamlar.
Buna göre A makinesi 1 saatte 6 birimlik iş tamamlar.
Eşit uzunluktaki mumlardan parafin mumu yakıldıktan 10 saat sonra, bal mumu yakıldıktan 16 saat sonra tamamen bitiyor.
Buna göre iki mum beraber yakıldıktan kaç saat sonra birinin boyu diğerinin boyunun \( \frac{5}{2} \) katı olur?
Çözümü GösterMumların uzunluklarına işlem kolaylığı açısından \( 80x \) cm diyelim.
Parafin mumu 10 saatte \( 80x \) cm yanıyorsa 1 saatte \( 8x \) cm yanar.
Bal mumu 16 saatte \( 80x \) cm yanıyorsa 1 saatte \( 5x \) cm yanar.
Mumlardan birinin uzunluğunun diğerinin \( \frac{5}{2} \) katı olması için geçen süreye \( t \) saat diyelim.
\( t \) saat sonra mumların uzunlukları \( 80x - 8xt \) ve \( 80x - 5xt \) olur.
10 saatte yanan mum daha hızlı yandığı için \( t \) anında uzunluğu daha kısa olur.
\( \dfrac{5}{2} \cdot (80x - 8xt) = 80x - 5xt \)
\( 200x - 20xt = 80x - 5xt \)
\( 200 - 20t = 80 - 5t \)
\( t = 8 \) saat bulunur.
Bir kaldırım taşı döşeme işinde aynı iş gücüne sahip 30 işçi 24 günde 800 metrekare kaldırım taşı döşemiştir.
Aynı iş gücüne sahip 6 işçinin 600 metrekarelik bir alana 18 günden daha kısa sürede kaldırım taşı döşeyebilmesi için en az kaç işçi daha işe alınmalıdır?
Çözümü Gösterİşçiler her iki durumda aynı iş gücüne sahip oldukları için, bir işçinin bir saatte döşeyebildiği kaldırım metrekare olarak eşittir.
Gereken işçi sayısına \( x \) diyelim.
\( \dfrac{800}{30 \cdot 24} = \dfrac{600}{18 \cdot x} \)
\( \dfrac{4}{5 \cdot 24} = \dfrac{3}{3 \cdot x} \)
İçler - dışlar çarpımı yapalım.
\( 12x = 360 \)
\( x = 30 \)
İşin 18 günde tamamlanması için 30 işçinin çalışması gerekiyorsa işin 18 günden daha kısa sürede tamamlanması için en az 31 işçi çalışmalıdır.
Buna göre en az \( 31 - 6 = 25 \) işçi daha işe alınmalıdır.
Ahmet bir işi \( k \) saatte, Berfin \( 2k \) saatte, Cem ise \( \frac{3k}{2} \) saatte bitirebiliyor. Ahmet ve Berfin birlikte çalıştıklarında ise aynı işi 14 saatte bitirebiliyorlar.
Buna göre Berfin ve Cem birlikte çalışarak bu işi kaç saatte bitirebilirler?
Çözümü GösterToplam iş miktarına işlem kolaylığı açısından \( 6k \) diyelim.
Ahmet bir saatte \( \frac{6k}{k} = 6 \) birim, Berfin \( \frac{6k}{2k} = 3 \) birim, Cem ise \( \frac{6k}{\frac{3k}{2}} = 4 \) birim iş yapabiliyor.
Ahmet ve Berfin birlikte çalıştıklarında bir saatte \( 6 + 3 = 9 \) birim işi yapabilirler.
Ahmet ve Berfin işi birlikte 14 saatte bitirebiliyorlar.
\( 9 = \frac{6k}{14} \)
\( k = 21 \)
Buna göre toplam iş miktarı \( 6k = 126 \) birimdir.
Berfin saatte 3 birim, Cem saatte 4 birim iş yapabildiğine göre, ikisi birlikte saatte \( 3 + 4 = 7 \) birim iş yapabilirler.
Buna göre ikisi birlikte işi \( \frac{126}{7} = 18 \) günde bitirebilirler.
Ayşe, Ferhat ve Fatma üçü birlikte bir işi 4 günde, Ayşe ve Fatma birlikte 6 günde, Fatma ve Ferhat birlikte 10 günde bitirebiliyor.
Buna göre, Fatma bu işi tek başına kaç günde bitirebilir?
Çözümü GösterYapılan işe işlem kolaylığı açısından 60 birim diyelim.
Ayşe'nin bir günde yaptığı birim işe \( a \), Fatma'nın bir günde yaptığı birim işe \( b \), Ferhat'ın bir günde yaptığı birim işe \( c \) diyelim.
Üçü birlikte çalışarak bu işi 4 günde bitirebiliyorsa üçünün bir günde yaptıkları iş \( \frac{60}{4} = 15 \) birimdir.
\( a + b + c = 15 \)
Ayşe ve Fatma birlikte çalışarak bu işi 6 günde bitirebiliyorsa ikisinin bir günde yaptıkları iş \( \frac{60}{6} = 10 \) birimdir.
\( a + b = 10 \)
Fatma ve Ferhat birlikte çalışarak bu işi 10 günde bitirebiliyorsa ikisinin bir günde yaptıkları iş \( \frac{60}{10} = 6 \) birimdir.
\( b + c = 6 \)
Birinci denklemden ikinci denklemi çıkaralım.
\( a + b + c - (a + b) = 15 - 10 \)
\( c = 5 \)
Bu değeri üçüncü denklemde yerine koyalım.
\( b + c = 6 \Longrightarrow b = 1 \)
Fatma tek başına bir günde 1 birim iş yapabiliyorsa işin tamamını \( \frac{60}{1} = 60 \) günde bitirebilir.
Aynı işlem kapasitesine sahip 15 bilgisayar bir işi birlikte çalışarak 8 saatte bitirebiliyor.
Hepsi aynı anda çalışmaya başladıktan 2 saat sonra bilgisayarlardan bazıları bozulmuş ve kalan bilgisayarlar işi 10 saat daha çalışarak bitirmişlerdir. Buna göre bilgisayarların kaçı bozulmuştur?
Çözümü Göster15 bilgisayar bu işi 8 saatte bitirebiliyorsa işin tamamına \( 15 \cdot 8 = 120 \) birim diyebiliriz.
Bilgisayarların tümü 2 saat çalıştığında \( 15 \cdot 2 = 30 \) birim iş tamamlanmış olur.
Bozulan bilgisayarların sayısına \( x \) diyelim. 2 saat sonra çalışır durumda \( 15 - x \) bilgisayar kalır.
Kalan bilgisayarlar 10 saat çalıştığında \( (15 - x) \cdot 10 \) birim iş yaparlar.
Bilgisayarlar bozulmadan önce ve sonra yapılan iş toplam işe eşittir.
\( 30 + (15 - x) \cdot 10 = 120 \)
\( 150 - 10x = 90 \)
\( x = 6 \)
Buna göre 15 bilgisayardan 6'sı bozulmuştur.
Bir araba fabrikasında kullanılan iki farklı boyama makinesinden birincisi bir arabanın boyasını ikinci makineden 18 dakika önce tamamlıyor. İkisi birlikte bir arabayı boyadıklarında ise bu işlem 12 dakika sürüyor.
Buna göre, ikinci makine tek başına bir arabayı kaç dakikada boyayabilir?
Çözümü GösterBirinci makinenin bir arabayı boyama süresine \( x \) dakika diyelim. Bu durumda ikinci makinenin bir arabayı boyama süresi \( x + 18 \) dakika olur.
Bir arabanın boyamasını 1 birimlik bir iş olarak alalım.
Birinci makine bu bir birim işi \( x \) dakikada bitirebiliyorsa bir dakikada \( \frac{1}{x} \) birim iş yapabilir.
İkinci makine bir birim işi \( x + 18 \) dakikada bitirebiliyorsa bir dakikada \( \frac{1}{x + 18} \) birim iş yapabilir.
İki makine birlikte çalıştıklarında bir arabayı 12 dakikada bitirebiliyorlarsa bir dakikada \( \frac{1}{12} \) birim iş yapabilirler.
İki makinenin bir dakikada ayrı ayrı yaptıkları işin toplamı birlikte yaptıkları işe eşittir.
\( \dfrac{1}{x} + \dfrac{1}{x + 18} = \dfrac{1}{12} \)
\( \dfrac{x + 18}{x(x + 18)} + \dfrac{x}{x(x + 18)} = \dfrac{1}{12} \)
\( \dfrac{2x + 18}{x^2 + 18x} = \dfrac{1}{12} \)
İçler - dışlar çarpımı yapalım.
\( 24x + 216 = x^2 + 18x \)
\( x^2 - 6x - 216 = 0 \)
\( (x - 18)(x + 12) = 0 \)
\( x = 18 \) ya da \( x = -12 \)
İşin tamamlanma süresi negatif olamayacağı için \( x = 18 \) olur.
Buna göre ikinci makine bir arabayı \( x + 18 = 18 + 18 = 36 \) dakikada boyayabilir.
Bir binanın dış cephe camlarını silmek için Can ve Cem isimli iki işçi işe alınıyor. Can tüm camları tek başına 10 günde, Cem ise 20 günde silebiliyor.
Can 4 gün boyunca camları tek başına sildikten sonra Cem izinden dönüyor ve kalan camları birlikte siliyorlar. Buna göre kalan camların silinmesi kaç gün sürer?
Çözümü GösterTüm camları silme işine 20 birimlik bir iş diyelim.
Can tüm camları tek başına 10 günde silebildiğine göre bir günde \( \frac{20}{10} = 2 \) birimlik kısmını silebilir.
Cem tüm camları tek başına 20 günde silebildiğine göre bir günde \( \frac{20}{20} = 1 \) birimlik kısmını silebilir.
İkisi birlikte bir günde \( 2 + 1 = 3 \) birimlik iş yaparlar.
Can 4 gün tek başına çalıştığında işin \( 2 \cdot 4 = 8 \) birimlik kısmını bitirir, geriye \( 20 - 8 = 12 \) birimlik kısmı kalır.
Bu 12 birimlik işi ikisi birlikte günde 3 birimlik iş yaparak \( \frac{12}{3} = 4 \) günde bitirirler.
Bir marangoz atölyesinde çıraklık yapan Eser, ustası ile birlikte bir masayı 12 saatte yapabiliyor.
Yeni bir masaya ikisi birlikte başladıktan 4 saat sonra ustası kalan işi Eser'e bırakıyor. Eser masanın kalanını 32 saatte tamamlayabildiğine göre, usta bir masayı tek başına kaç saatte yapabilir?
Çözümü GösterBir masayı yapmak için gereken toplam işe 96 birim diyelim.
Eser ve ustası birlikte çalıştıklarında masayı 12 saatte yapabiliyorlarsa bir saatte \( \frac{96}{12} = 8 \) birim iş yaparlar.
Birlikte 4 saat çalıştıklarında \( 4 \cdot 8 = 32 \) birim iş tamamlamış olurlar, geriye \( 96 - 32 = 64 \) birim iş kalır.
Eser bu kalan işi 32 saatte tamamlıyorsa bir saatte \( \frac{64}{32} = 2 \) birim iş yapabiliyordur.
Birlikte bir saatte 8 birim iş yaptıklarına göre usta tek başına bir saatte \( 8 - 2 = 6 \) birim iş yapabiliyordur.
Buna göre, usta bir masayı tek başına \( \frac{96}{6} = 16 \) saatte yapabilir.
Bir restoranda aşçıbaşı 3 saatte 16 hamur açabiliyor, yanında çalışan aşçıların her biri 5 saatte 18 hamur açabiliyor.
Bir sipariş için 300 hamuru 12 saatte açmak isteyen aşçıbaşı en az kaç aşçı ile birlikte bu işe başlamalıdır?
Çözümü GösterAşçıbaşı 3 saatte 16 hamur açabiliyorsa saatte \( \frac{16}{3} \) hamur açar.
Bir aşçı 5 saatte 18 hamur açabiliyorsa saatte \( \frac{18}{5} \) hamur açar.
12 saatte 300 hamur açmak için saatte \( \frac{300}{12} = 25 \) hamur açılmalıdır.
Bu iş için aşçıbaşı ile birlikte çalışması gereken aşçı sayısına \( x \) diyelim.
Aşçıbaşı ve \( x \) aşçının bir saatte açması gereken hamur sayısı 25'tir.
\( \dfrac{16}{3} + \dfrac{18}{5} \cdot x = 25 \)
\( \dfrac{80}{15} + \dfrac{54x}{15} = 25 \)
\( 80 + 54x = 375 \)
\( 54x = 295 \)
\( x \approx 5,46... \)
Buna göre işi 12 saatte yetiştirebilmek için aşçıbaşı işe en az 6 aşçı ile başlamalıdır.
Bir havuzu dolduran 3 musluk vardır. Birinci musluk havuzu tek başına 6 saatte, ikinci musluk tek başına 8 saatte, üçüncü musluk tek başına 10 saatte doldurabiliyor.
Havuz boşken üç musluk aynı anda açılıyor ancak birinci musluk 1 saat sonra tıkanıyor. İkinci ve üçüncü musluklar 2 saat daha açık kaldıktan sonra kapatılıyor.
Buna göre 3 saat sonunda havuzun kaçta kaçı dolmuş olur?
Çözümü GösterHavuzun hacmine işlem kolaylığı açısından \( 120x \) diyelim.
Musluklar bir saatte havuzun sırasıyla \( \frac{120x}{6} = 20x \), \( \frac{120x}{8} = 15x \) ve \( \frac{120x}{10} = 12x \) kadarını doldurur.
Üç musluk aynı anda açıldığında bir saatte \( 20x + 15x + 12x = 47x \) kadarını doldurur.
İkinci ve üçüncü musluklar ise bir saatte \( 15x + 12x = 27x \) kadarını, 2 saatte \( 2 \cdot 27x = 54x \) kadarını doldurur.
3 saat sonunda havuzun \( 47x + 54x = 101x \) kadarı dolmuş olur.
Buna göre 3 saat sonunda havuzun \( \frac{101x}{120x} = \frac{101}{120} \) kadarı dolmuş olur.
Aynı uzunluktaki iki mum aynı anda yakılıyor. Sabit bir hızda yanan mumlardan birincisi 10 dakikada, ikincisi 6 dakikada bitmektedir.
Yakıldıktan kaç dakika sonra birinci mumun uzunluğu ikinci mumun uzunluğunun 3 katına eşit olur?
Çözümü GösterMumların uzunluğuna \( h \) birim diyelim.
Birinci mum dakikada \( \frac{h}{10} \) birim, ikinci mum dakikada \( \frac{h}{6} \) birim yanar.
\( t \) dakika sonra birinci mumun uzunluğunun ikinci mumun uzunluğunun 3 katı olduğunu varsayalım.
Mumların \( t \) dakika sonraki uzunluklarını yazalım.
Birinci mum: \( h - \dfrac{h}{10}t \)
İkinci mum: \( h - \dfrac{h}{6}t \)
\( h - \dfrac{h}{10}t = 3(h - \dfrac{h}{6}t) \)
\( h - \dfrac{h}{10}t = 3h - \dfrac{h}{2}t \)
\( \dfrac{4h}{10}t = 2h \)
\( t = \dfrac{10 \cdot 2h}{4h} \)
\( = 5 \) dk bulunur.
Farklı maddelerden yapılmış ve uzunlukları eşit iki mumdan birincisi 2 saatte, diğeri 3 saatte tamamen yanıyor.
Bu iki mum aynı anda saat 12:00'de yakılıyor. Mumlardan birinin uzunluğunun diğerinin uzunluğunun 2 katı olduğu anda saat kaç olur?
Çözümü GösterMumların uzunluğuna \( x \) diyelim.
Mumlar bir dakikada \( \frac{x}{120} \) ve \( \frac{x}{180} \) kadar yanarlar.
\( t \) dakika sonra mumların uzunlukları \( x - \frac{x}{120}t \) ve \( x - \frac{x}{180}t \) olur.
Mumlardan birinin uzunluğunun diğerinin 2 katı olduğu \( t \) değerini bulalım.
2 saatte yanan mum daha hızlı yandığı için \( t \) anında uzunluğu daha kısa olur.
\( 2(x - \dfrac{x}{120}t) = x - \dfrac{x}{180}t \)
\( 2x - \dfrac{xt}{60} = x - \dfrac{xt}{180} \)
\( x = \dfrac{xt}{90} \)
\( t = 90 \) dakika
Mumlar saat 12:00'de yakıldığına göre, saat 13:30'da bir mumun uzunluğu diğer mumun uzunluğunun 2 katı olur.
Bir okuldaki 5. sınıflar arasında yapılan yarışmada verilen görevi 25 kişilik A şubesi 8 saatte, 20 kişilik B şubesi 12 saatte, 15 kişilik C şubesi de 20 saatte tamamlıyor. Her şubedeki öğrenciler eşit verimlilikte çalıştığına göre, şubelerdeki öğrencilerin verimlilikleri arasındaki orantıyı bulunuz.
Çözümü Gösterİşi yapan öğrenci sayısıyla işin tamamlanması için gereken saatin çarpımı, 1 öğrencinin aynı işi tek başına kaç saatte yapabileceğini gösterir.
A şubesinden bir öğrenci işi \( 25 \cdot 8 = 200 \) saatte yapabilir.
B şubesinden bir öğrenci işi \( 20 \cdot 12 = 240 \) saatte yapabilir.
C şubesinden bir öğrenci işi \( 15 \cdot 20 = 300 \) saatte yapabilir.
Bir öğrenci bir işi \( x \) saatte tamamlıyorsa 1 saatte işin \( \frac{1}{x} \) kadarını yapar. Bu da öğrencinin verimliliğini gösterir.
A şubesindeki bir öğrenci bir saatte işin \( \frac{1}{200} \)'ini tamamlar.
B şubesindeki bir öğrenci bir saatte işin \( =\frac{1}{240} \)'ini tamamlar.
C şubesindeki bir öğrenci bir saatte işin \( =\frac{1}{300} \)'ini tamamlar.
Şubelerin verimliliklerinin oranını bulalım.
\( \dfrac{1}{200} : \dfrac{1}{240} : \dfrac{1}{300} \)
\( = \dfrac{1}{20} : \dfrac{1}{24} : \dfrac{1}{30} \)
Sayıları paydaların EKOK'ları ile çarpalım.
\( EKOK(20, 24, 30) = 120 \)
\( = \dfrac{120}{20}: \dfrac{120}{24}: \dfrac{120}{30} \)
\( = 6 : 5 : 4 \) bulunur.
A, B, C muslukları sabit ancak birbirinden farklı hızlarda bir tanka su dolduruyor. Tank üç musluk birlikte açıldığında 2 saatte, sadece A ve B muslukları açıldığında 3 saatte, sadece A ve C muslukları açıldığında 5 saatte doluyor.
Buna göre, tank sadece B ve C muslukları açıldığında kaç saatte dolar?
Çözümü GösterA, B, C musluklarının bir saatte doldurdukları su miktarına sırasıyla \( x, y, z \) diyelim.
Tankın toplam kapasitesi verilen her durumda aynıdır.
\( 2(x + y + z) = 3(x + y) = 5(x + z) \)
\( y \) ve \( z \) değişkenlerini \( x \) cinsinden yazmaya çalışalım.
İlk iki ifade arasındaki eşitliği sadeleştirelim.
\( 2(x + y + z) = 3(x + y) \)
\( 2z = x + y \)
Birinci ve üçüncü ifadeler arasındaki eşitliği sadeleştirelim.
\( 2(x + y + z) = 5(x + z) \)
\( 2y = 3x + 3z \)
\( y = \dfrac{3x + 3z}{2} \)
Bulduğumuz \( y \) değerini \( 2z = x + y \) eşitliğinde yerine koyalım.
\( 2z = x + \dfrac{3x + 3z}{2} \)
\( z = 5x \)
Bulduğumuz \( z \) değerini \( 2y = 3x + 3z \) eşitliğinde yerine koyalım.
\( 2y = 3x + 3(5x) \)
\( y = 9x \)
Soruda sadece B ve C muslukları açıldığında tankın kaç saatte dolacağı soruluyor.
B ve C muslukları açıldığında tankın dolma süresine \( t \) diyelim.
\( (y + z)t = 2(x + y + z) \)
\( y \) ve \( z \) değerlerini \( x \) cinsinden yazalım.
\( (9x + 5x)t = 2(x + 9x + 5x) \)
\( t = \dfrac{30x}{14x} \)
\( = \dfrac{15}{7} \) saat bulunur.
Bir mikrobiyoloji laboratuvarına gelen 5760 örnek 3 haftada inceleniyor. Her hafta bir saatte incelenen örnek sayısı bir önceki haftadan %60 fazla olmasına rağmen araştırmaya hafta boyunca harcanan toplam süre her hafta azaltılıyor.
İlk hafta incelenen 3000 örneğe 40 saat harcanırken son hafta sadece 5 saat harcanıyor. Buna göre ikinci hafta bu araştırmaya kaç saat harcanmıştır? (Not: Örnek başına harcanan süre üç hafta için sabittir.)
Çözümü Gösterİlk hafta bir saatte kaç örnek incelendiğini bulalım.
40 saatte 3000 örnek inceleniyorsa 1 saatte \( \frac{3000}{40} = 75 \) örnek incelenir.
Her hafta bir saatte incelenen örnek sayısı bir önceki haftadan %60 fazla oluyor.
2. hafta bir saatte incelenen örnek sayısını bulalım.
\( 75 + 75 \cdot \dfrac{60}{100} = 120 \) örnek
3. hafta bir saatte incelenen örnek sayısını bulalım.
\( 120 + 120 \cdot \dfrac{60}{100} = 192 \) örnek
3. haftada incelenen örnek sayısı \( 5 \cdot 192 = 960 \) olur.
1. ve 3. haftalarda incelenen toplam örnek sayısı \( 3000 + 960 = 3960 \) olur.
Bu durumda 2. hafta \( 5760 - 3960 = 1800 \) örnek incelenmiştir.
2. hafta 1 saatte 120 örnek incelenmiştir.
Buna göre 2. hafta \( \frac{1800}{120} = 15 \) saat harcanmıştır.