Farklı Nesnelerin Farklı Kutulara Dağıtımı
Bu problem tipinde amaç birbirinden farklı \( n \) nesnenin birbirinden farklı \( k \) kutuya dağıtım sayısını hesaplamaktır. Nesneler birbirinden farklı olduğu için farklı kutulardaki iki nesnenin aralarında yer değiştirmesi yeni bir dağıtıma karşılık gelir. Bu problem tipinde nesnelerin bulundukları kutu içindeki dizilişleri önemli değildir.
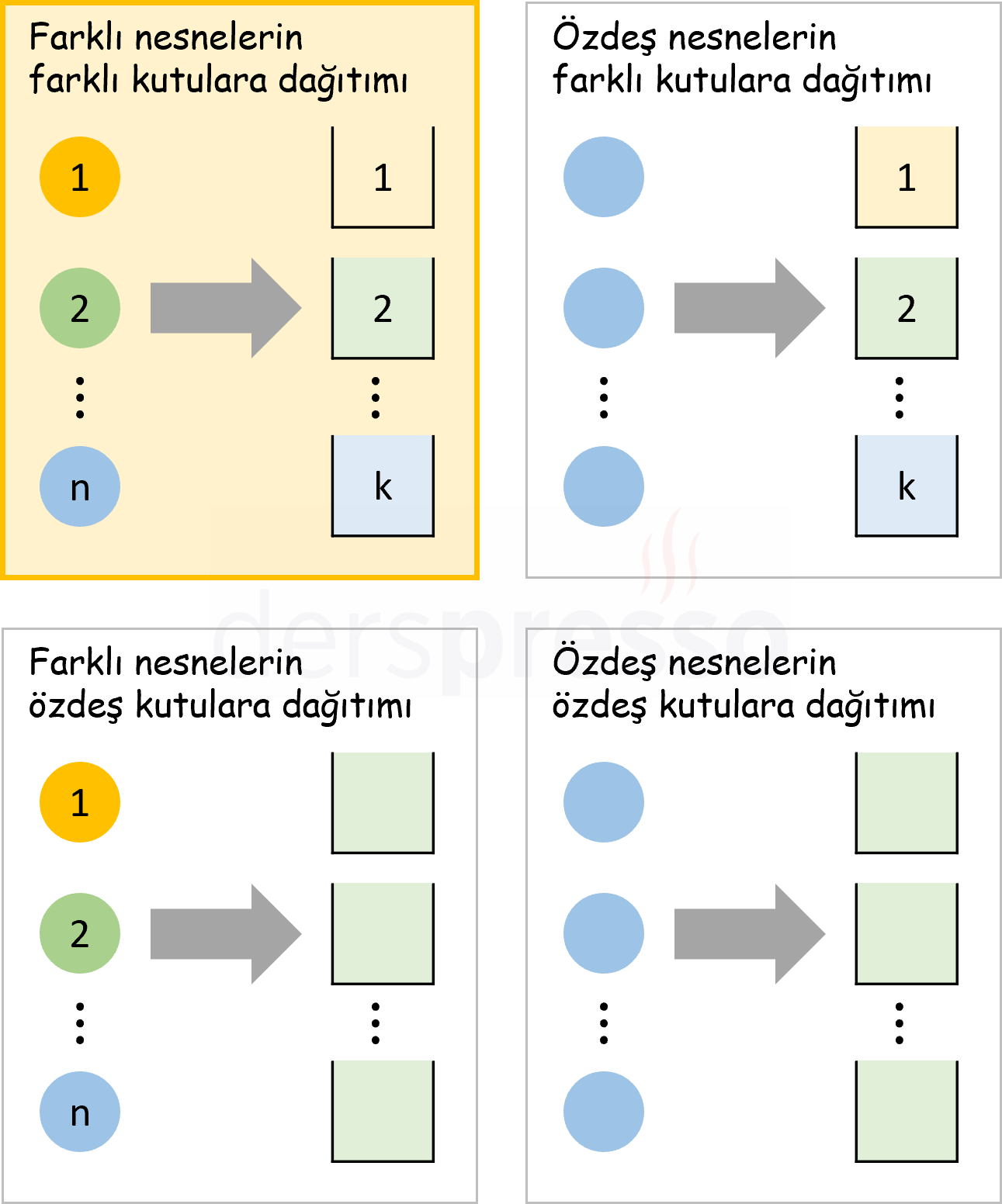
Bu problem tipini her kutuya dağıtılabilecek nesne sayısına göre dört başlık altında inceleyebiliriz.
Her Kutuda Herhangi Bir Sayıda Nesne
Bu problem tipinde nesneler kutulara herhangi bir koşul olmaksızın dağıtılır (bazı kutular boş kalabilir ya da bir kutuya birden fazla nesne konabilir).
\( n \) farklı nesnenin \( k \) farklı kutuya herhangi bir koşul olmaksızın farklı dağıtım sayısı \( = k^n \)
Her nesnenin dağıtımı birbirinden bağımsız olaylar olup her nesne için \( k \) kutudan herhangi biri seçilebilir. Bu bağımsız seçimler \( n \) farklı nesne için tekrarlandığında oluşan farklı dağıtım sayısı çarpma yoluyla sayma konusunda tekrarlayan olaylar başlığı altında incelediğimiz gibi \( \underbrace{k \cdot k \ldots k}_\text{n adet} = k^n \) olur.
4 farklı renkteki top 6 farklı kutuya kaç farklı şekilde atılabilir?
Çözümü GösterSorudaki farklı renkteki toplar farklı nesnelere karşılık gelmektedir.
Topların kutulara dağıtımı konusunda herhangi bir koşul verilmemiştir, yani bazı kutular boş kalabilir ya da bir kutuya birden fazla top atılabilir.
Her top için kutu sayısı kadar farklı seçenek vardır, dolayısıyla tüm topların kutulara dağıtımı çarpma kuralı gereği \( k^n = 6^4 \) farklı şekilde yapılabilir.
5 farklı oyuncak 3 çocuğa herhangi bir koşul olmadan kaç farklı şekilde dağıtılabilir?
Çözümü GösterSorudaki farklı oyuncaklar farklı nesnelere, çocuklar da nesnelerin dağıtılacağı farklı kutulara karşılık gelmektedir.
Oyuncakların çocuklara dağıtımı konusunda herhangi bir koşul verilmemiştir, yani bazı çocuklar oyuncak almayabilir ya da bir çocuğa birden fazla oyuncak verilebilir.
Her oyuncak için çocuk sayısı kadar farklı seçenek vardır, dolayısıyla tüm oyuncakların çocuklara dağıtımı çarpma kuralı gereği \( k^n = 3^5 \) farklı şekilde yapılabilir.
4 mektup 9 posta kutusuna kaç farklı şekilde atılabilir?
Çözümü GösterSorudaki mektuplar farklı nesnelere, posta kutuları da farklı kutulara karşılık gelmektedir.
Mektupların kutulara dağılımı konusunda herhangi bir koşul verilmemiştir, yani bazı posta kutuları boş kalabilir ya da bir posta kutusuna birden fazla mektup atılabilir.
Her mektup için posta kutusu sayısı kadar farklı seçenek vardır, dolayısıyla tüm mektupların posta kutularına dağıtımı çarpma kuralı gereği \( k^n = 9^4 \) farklı şekilde yapılabilir.
8 elemanlı bir kümeden 6 elemanlı bir kümeye kaç farklı fonksiyon tanımlanabilir?
Çözümü GösterTanım kümesinin elemanları farklı nesnelere, bu elemanların eşleneceği değer kümesinin elemanları da farklı kutulara karşılık gelmektedir. Fonksiyon tanımı gereği, yapılacak dağıtımlar (eşlemeler) sonucunda değer kümesinin bir elemanı boşta kalabilir (bir kutu boş kalabilir) ya da tanım kümesinin birden fazla elemanı değer kümesinin aynı elemanı ile eşlenebilir (bir kutuya birden fazla nesne konabilir).
Bu açıdan baktığımızda, problemi herhangi bir koşul olmaksızın farklı nesnelerin farklı kutulara dağıtım problemi olarak modelleyebiliriz.
Buna göre 8 elemanlı bir kümeden 6 elemanlı bir kümeye tanımlanabilecek fonksiyon sayısı \( k^n = 6^8 \) olur, bu da fonksiyonlar konusunda gördüğümüz formülle aynıdır.
Elemanları \( A = \{1, 2, 3, 4, 5\} \) kümesinin elemanları arasından seçilen \( K \), \( L \) ve \( M \) kümeleri aşağıdaki iki koşul sağlanacak şekilde kaç farklı şekilde oluşturulabilir?
\( K \cup L \cup M = A \)
\( K \cap L \cap M = \emptyset \)
Çözümü GösterVerilen kümelerin Venn şeması gösterimi aşağıdaki gibidir.
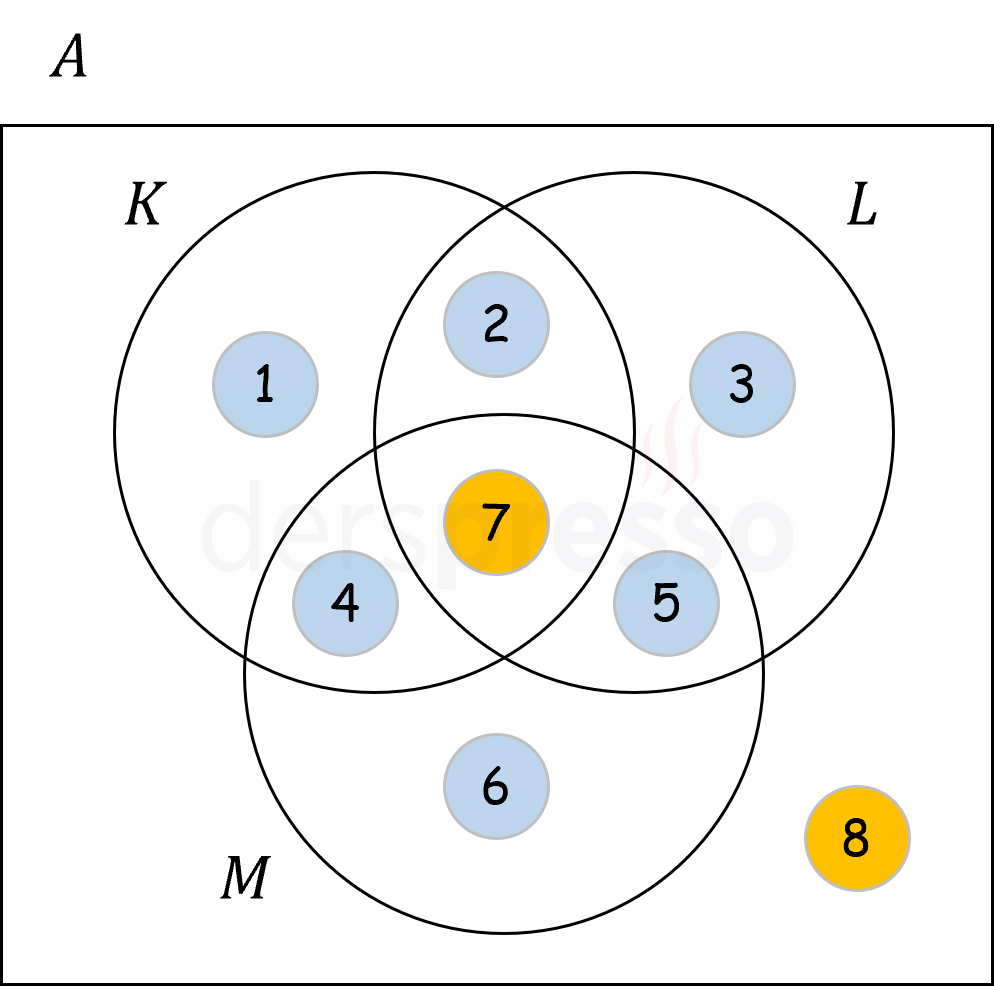
\( A \) kümesinin elemanlarının her biri bu şemada mavi ile işaretli 6 bölgeden birine yerleştirilebilir. Üç kümenin kesişiminin boş küme olma koşulu sebebiyle 7 no'lu bölgeye, bu üç kümenin birleşiminin \( A \) kümesine eşit olma koşulu sebebiyle de 8 no'lu bölgeye bir eleman yerleştirilemez.
Buna göre \( A \) kümesinin 5 elemanını dağıtılacak farklı nesneler, 6 mavi bölgeyi de bu nesnelerin dağıtılacağı farklı kutular olarak kurgulayabiliriz.
Bir kümeye dağıtılacak eleman sayısı ile ilgili bir kısıtlama verilmediği için farklı dağıtım sayısı \( k^n = 6^5 \) olarak bulunur.
Her Kutuda En Fazla Bir Nesne
Bu problem tipinde nesneler kutulara her kutuda en fazla bir nesne olacak şekilde dağıtılır. Her kutuda en fazla bir nesne olabileceği için, bu problemlerde \( n \le k \) koşulunun sağlanması gerekir (nesne sayısı kutu sayısından fazla olamaz), aksi takdirde farklı dağıtım sayısı 0 olur.
\( n \le k \) olmak üzere,
\( n \) farklı nesnenin \( k \) farklı kutuya her kutuda en fazla bir nesne olacak şekilde farklı dağıtım sayısı \( = P(k, n) \)
Her kutuda en fazla bir nesne olabileceği için, bir nesnenin dağıtıldığı bir kutu sonraki dağıtımlar için bir seçenek olamaz, dolayısıyla problem bir permütasyon problemine dönüşmektedir. Buna göre, 1. nesne için \( k \) kutu seçeneği, 2. nesne için \( k - 1 \) kutu seçeneği, \( n \). nesne için de \( k - n + 1 \) kutu seçeneği bulunmaktadır. Birbirinden bağımsız bu seçeneklerin çarpımı sonucunda \( P(k, n) \) farklı dağıtım sayısı oluşur.
8 kişilik bir grup 20 boş koltuk olan bir sinema salonunda kaç farklı şekilde oturabilir?
Çözümü GösterSorudaki kişiler farklı nesnelere, koltuklar da nesnelerin dağıtılacağı farklı kutulara karşılık gelmektedir.
Her koltuğa en fazla bir kişi oturabileceği için, problemi her kutuda en fazla bir nesne olacak şekilde farklı nesnelerin farklı kutulara dağıtım problemi olarak kurgulayabiliriz.
Buna göre birinci kişi için 20, ikinci kişi için 19, üçüncü kişi için 18 koltuk seçeneği vardır. Gruptaki herkes için bunu tekrarladığımızda farklı oturma sayısını \( P(20, 8) = 20 \cdot 19 \cdot \ldots \cdot 14 \cdot 13 \) olarak buluruz.
4 mektup 9 posta kutusuna bir posta kutusuna en fazla bir mektup atılmak koşuluyla kaç farklı şekilde atılabilir?
Çözümü GösterSorudaki mektuplar farklı nesnelere, posta kutuları da farklı kutulara karşılık gelmektedir.
Soruda verilen koşula göre bir posta kutusuna en fazla bir mektup atılabilir, dolayısıyla problemi her kutuda en fazla bir nesne olacak şekilde farklı nesnelerin farklı kutulara dağıtım problemi olarak kurgulayabiliriz.
Buna göre birinci mektup için 9, ikinci mektup için 8, üçüncü mektup için 7 posta kutusu seçeneği vardır. Tüm mektuplar için bunu tekrarladığımızda farklı dağıtım sayısını \( P(9, 4) = 9 \cdot 8 \cdot 7 \cdot 6 \) olarak buluruz.
Her Kutuda En Az Bir Nesne
Bu problem tipinde nesneler kutulara her kutuda en az bir nesne olacak şekilde dağıtılır. Her kutuda en az bir nesne olabileceği için, bu problemlerde \( n \ge k \) koşulunun sağlanması gerekir (nesne sayısı kutu sayısından az olamaz), aksi takdirde farklı dağıtım sayısı 0 olur.
Bu problemin çözümünde sayma konusunda gördüğümüz dahil etme / hariç tutma prensibi kullanılır.
\( A = \{ 1, 2, 3, 4, 5 \} \)
\( B = \{ a, b, c, d \} \)
olmak üzere, \( A \) kümesinden \( B \) kümesine kaç farklı örten fonksiyon tanımlanabilir?
Çözümü GösterBu sorunun "dahil etme / hariç tutma prensibi" ile çözümü için dahil etme - hariç tutma prensibi ve örten fonksiyon sayısı sayfalarını, "ikinci türden Stirling sayıları" ile çözümü için ikinci türden Stirling sayıları sayfalarını inceleyebilirsiniz.
Her Kutuda Tek Bir Nesne
Bu problem tipinde nesneler kutulara her kutuda sadece bir nesne olacak şekilde dağıtılır. Her kutuda sadece bir nesne olabileceği için, bu problemlerde \( n = k \) koşulunun sağlanması gerekir (nesne sayısı kutu sayısına eşit olmalıdır), aksi takdirde farklı dağıtım sayısı 0 olur.
\( n = k \) olmak üzere,
\( n \) farklı nesnenin \( k \) farklı kutuya her kutuda sadece bir nesne olacak şekilde farklı dağıtım sayısı \( = n! \)
"Her Kutuda En Fazla Bir Nesne" ve "Her Kutuda En Az Bir Nesne" problem tiplerinde \( k = n \) aldığımızda da aynı \( n! \) sonucunu elde ederiz.
6 otomobil 6 park yerine kaç farklı şekilde parkedebilir?
Çözümü GösterSorudaki otomobiller farklı nesnelere, park yerleri de nesnelerin dağıtılacağı farklı kutulara karşılık gelmektedir.
Otomobil ve park yeri sayısı eşit olduğu için, problemi her kutuda tek bir nesne olacak şekilde farklı nesnelerin farklı kutulara dağıtım problemi olarak kurgulayabiliriz.
Buna göre birinci otomobil için 6, ikinci otomobil için 5, üçüncü otomobil için 4 park yeri seçeneği vardır. Tüm otomobiller için bunu tekrarladığımızda farklı park sayısını \( 6! = 6 \cdot 5 \cdot \ldots \cdot 2 \cdot 1 \) olarak buluruz.