Limitin Grafik Yorumu
Bir fonksiyonun bir noktadaki limiti ve grafiği ile ilgili farklı bazı durumlar aşağıda verilmiştir.
| Grafik | Açıklama |
|---|---|
|
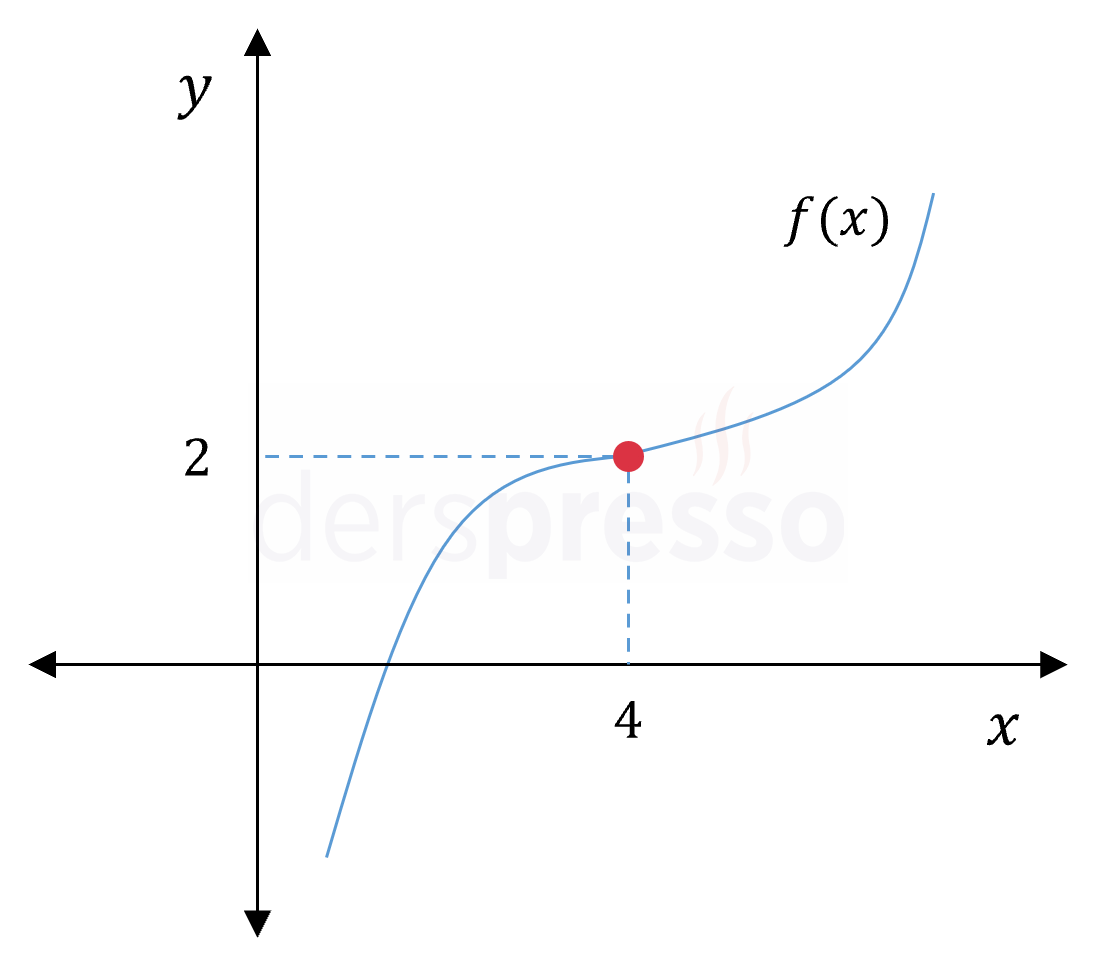
\( \lim\limits_{x \to 4^-} f(x) = 2 \) \( \lim\limits_{x \to 4^+} f(x) = 2 \) \( \lim\limits_{x \to 4} f(x) = 2 \) \( f(4) = 2 \) \( x = 4 \) noktası için soldan ve sağdan limit vardır ve birbirine eşittir, dolayısıyla bu noktada limit vardır. Fonksiyonun bu noktadaki değerinin limit değerine eşit olmasının limite bir etkisi yoktur. |
|
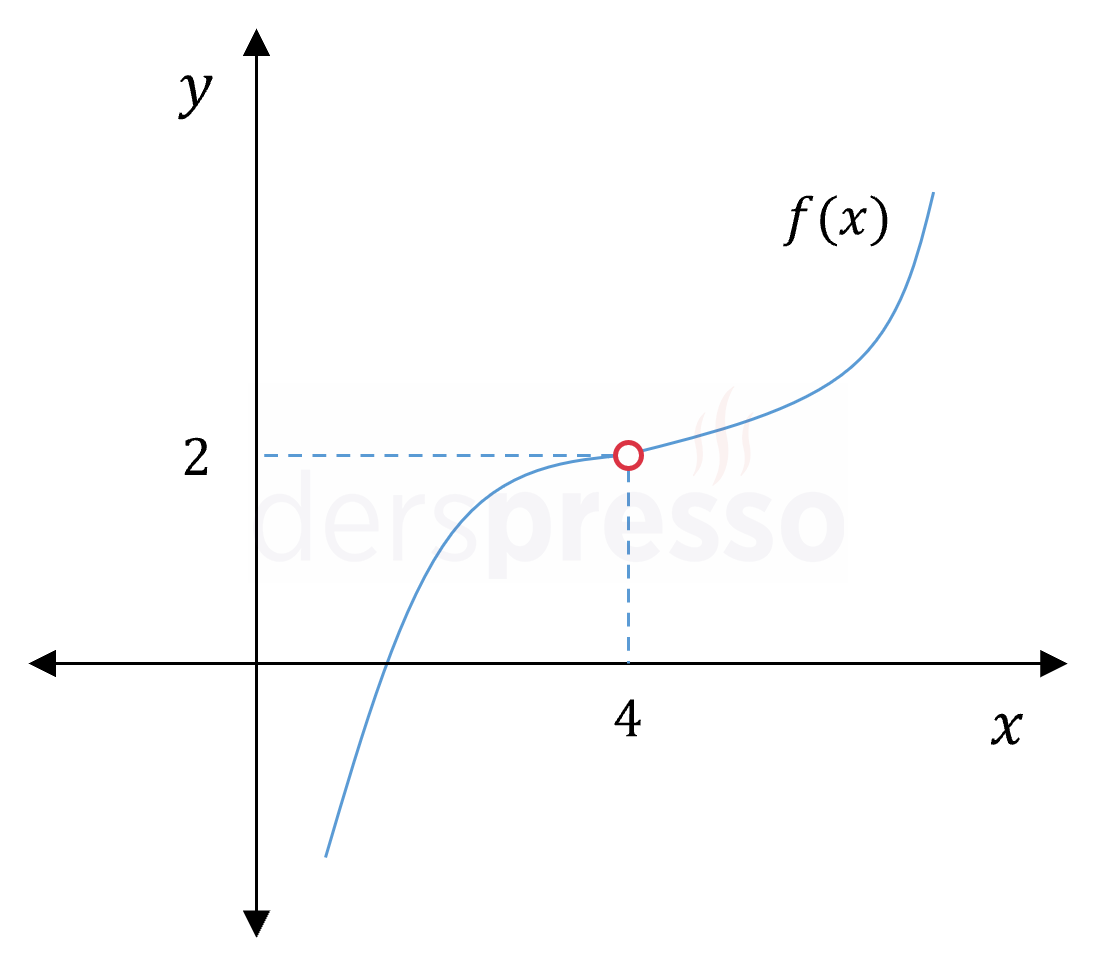
\( \lim\limits_{x \to 4^-} f(x) = 2 \) \( \lim\limits_{x \to 4^+} f(x) = 2 \) \( \lim\limits_{x \to 4} f(x) = 2 \) \( f(4) \Longrightarrow \) Tanımsız \( x = 4 \) noktası için soldan ve sağdan limit vardır ve birbirine eşittir, dolayısıyla bu noktada limit vardır. Fonksiyonun bu noktada tanımsız olmasının limite bir etkisi yoktur. |
|
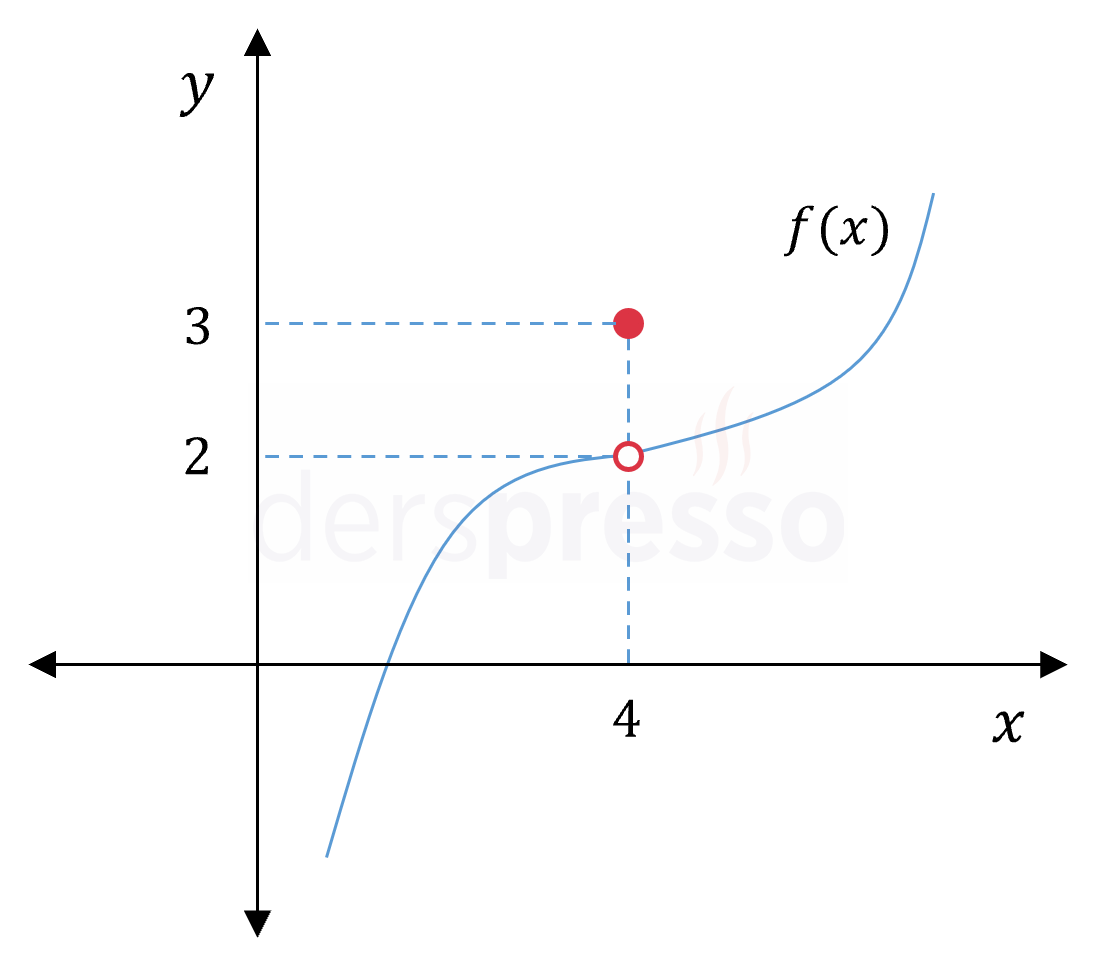
\( \lim\limits_{x \to 4^-} f(x) = 2 \) \( \lim\limits_{x \to 4^+} f(x) = 2 \) \( \lim\limits_{x \to 4} f(x) = 2 \) \( f(4) = 3 \) \( x = 4 \) noktası için soldan ve sağdan limit vardır ve birbirine eşittir, dolayısıyla bu noktada limit vardır. Fonksiyonun bu noktadaki değerinin limit değerinden farklı olmasının limite bir etkisi yoktur. |
|
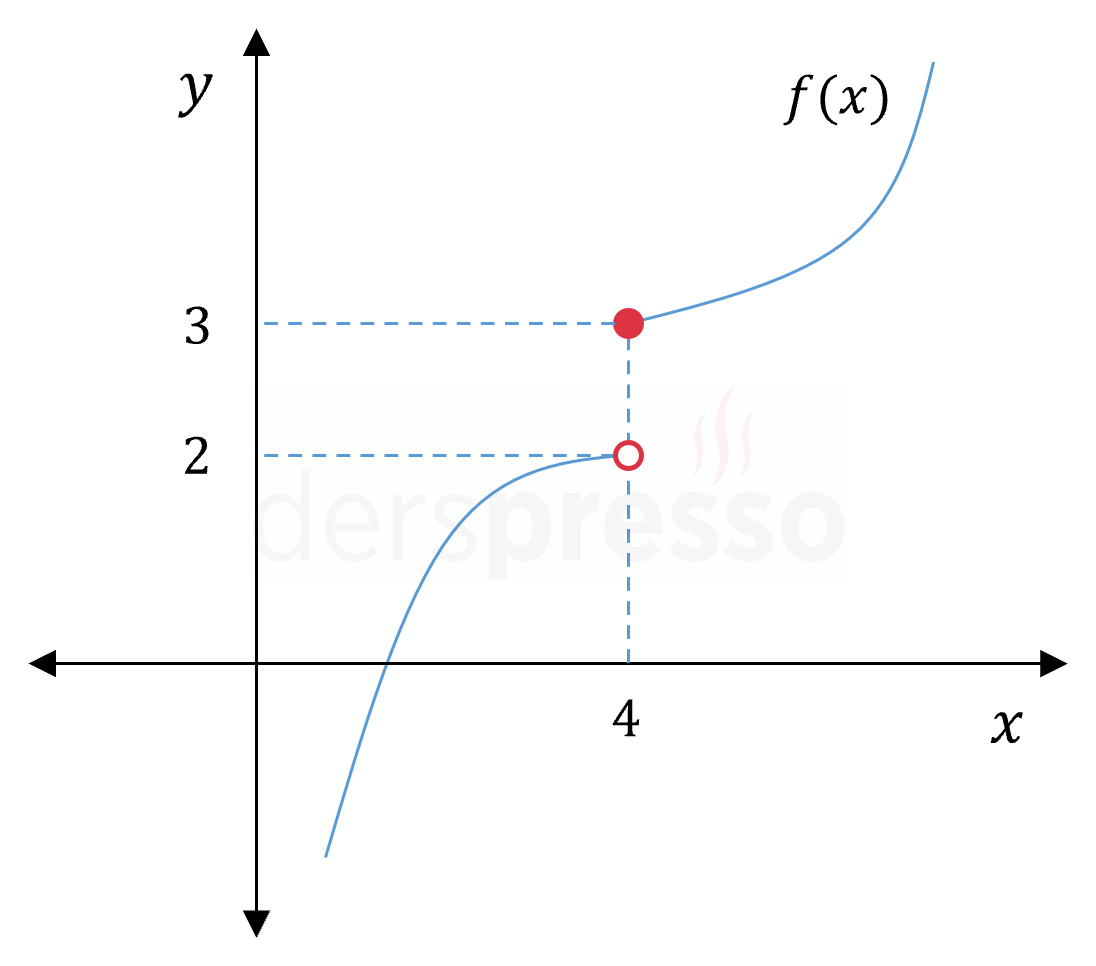
\( \lim\limits_{x \to 4^-} f(x) = 2 \) \( \lim\limits_{x \to 4^+} f(x) = 3 \) \( \lim\limits_{x \to 4} f(x) \Longrightarrow \) Tanımsız \( f(4) = 3 \) \( x = 4 \) noktası için soldan ve sağdan limit vardır, ancak birbirine eşit değildir, dolayısıyla bu noktada iki taraflı limit tanımsızdır. Fonksiyon değerinin bu noktada sağdan limite eşit olmasının limite bir etkisi yoktur. |
|
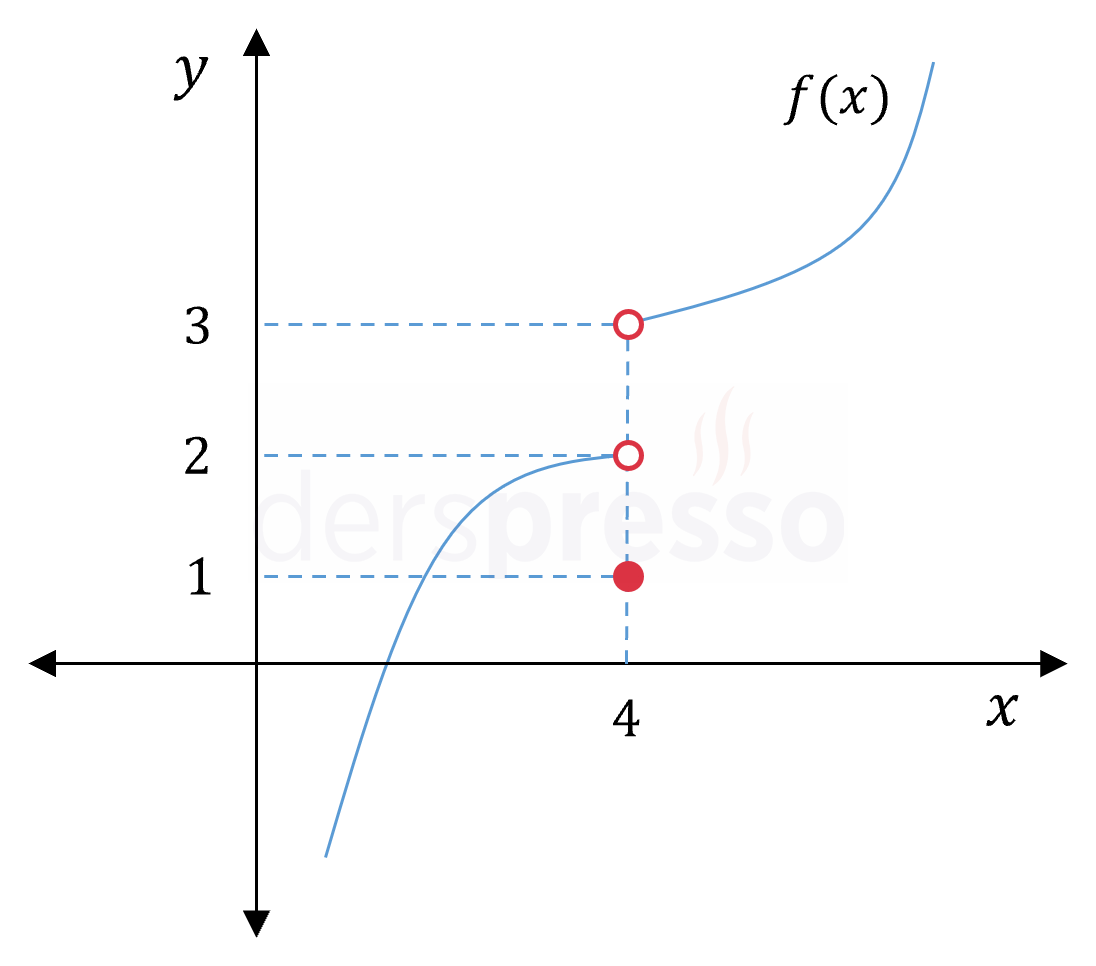
\( \lim\limits_{x \to 4^-} f(x) = 2 \) \( \lim\limits_{x \to 4^+} f(x) = 3 \) \( \lim\limits_{x \to 4} f(x) \Longrightarrow \) Tanımsız \( f(4) = 1 \) \( x = 4 \) noktası için soldan ve sağdan limit vardır, ancak birbirine eşit değildir, dolayısıyla bu noktada iki taraflı limit tanımsızdır. Fonksiyon değerinin bu noktada limit değerlerinden farklı olmasının limite bir etkisi yoktur. |
|
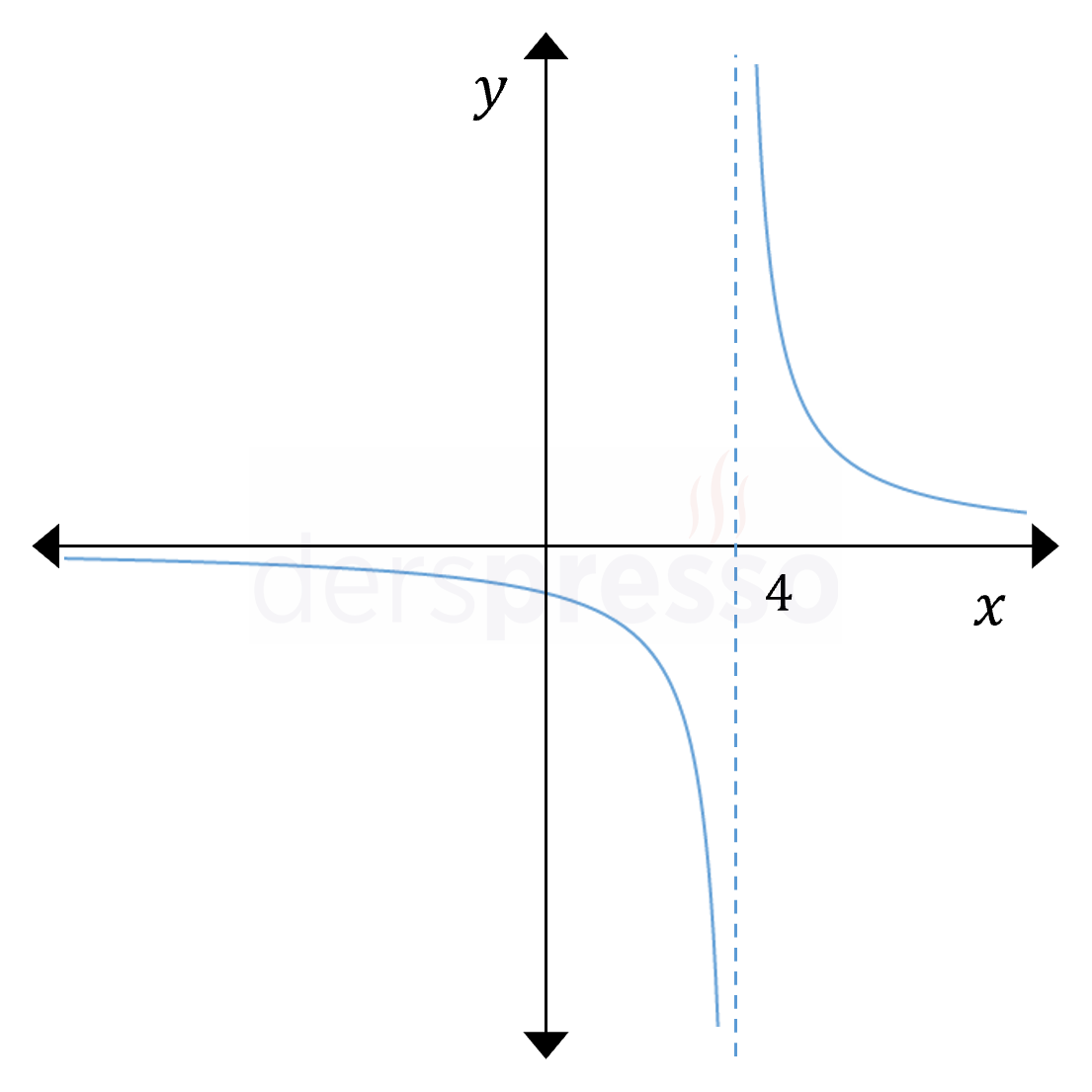
\( \lim\limits_{x \to 4^-} f(x) = -\infty \) \( \lim\limits_{x \to 4^+} f(x) = +\infty \) \( \lim\limits_{x \to 4} f(x) \Longrightarrow \) Tanımsız \( f(4) \Longrightarrow \) Tanımsız \( x = 4 \) noktasına soldan yaklaşırken fonksiyon çok büyük negatif değerler alır, sağdan yaklaşırken çok büyük pozitif değerler alır. Fonksiyonun soldan ve sağdan reel sayı bir limit değeri olmadığı için soldan ve sağdan limitler tanımsızdır. Soldan ve sağdan limit değerleri olarak negatif ve pozitif sonsuz yazmamız bu noktada tek taraflı limitlerin tanımlı olduğu anlamına gelmez. |
|
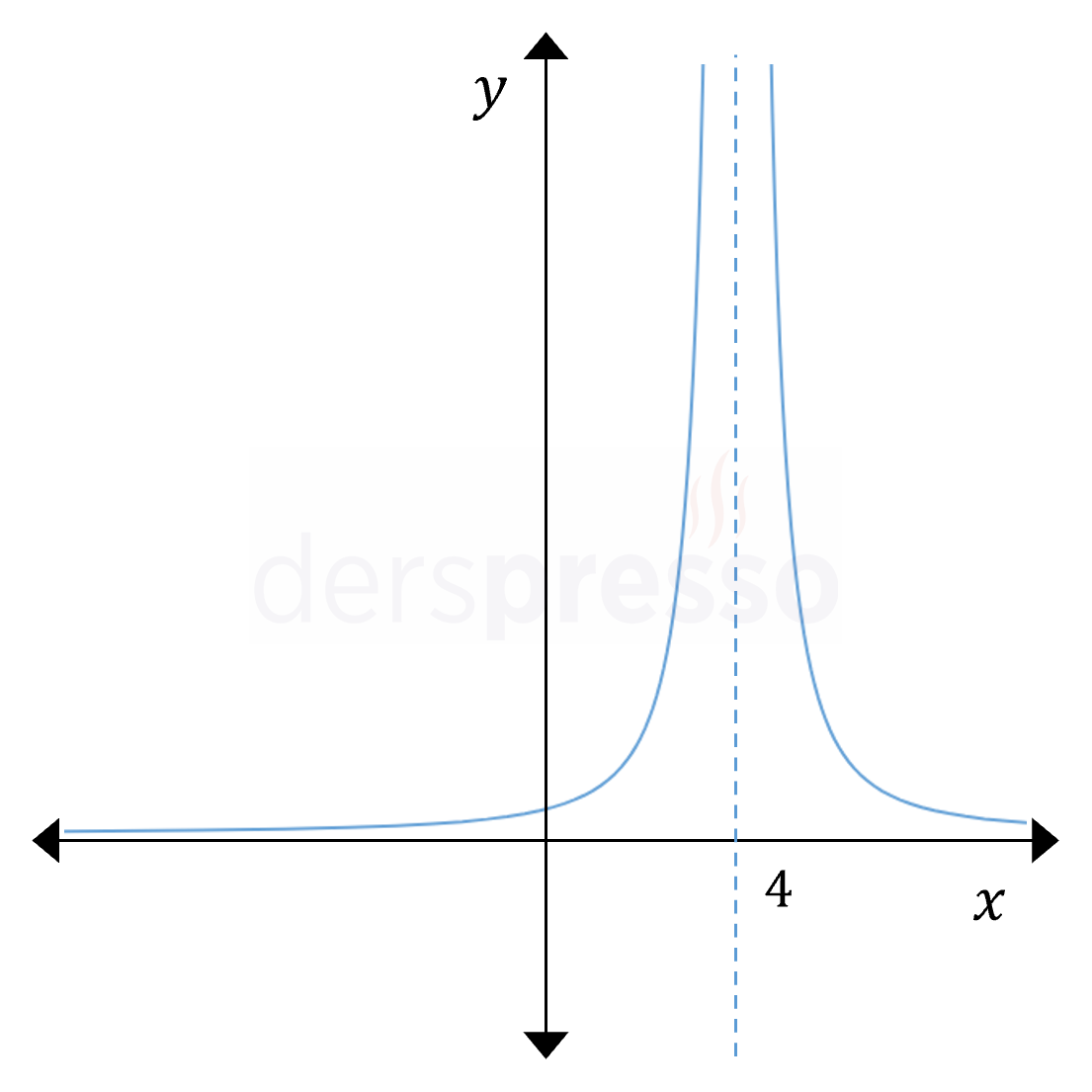
\( \lim\limits_{x \to 4^-} f(x) = +\infty \) \( \lim\limits_{x \to 4^+} f(x) = +\infty \) \( \lim\limits_{x \to 4} f(x) = +\infty \) \( f(4) \Longrightarrow \) Tanımsız Benzer şekilde, \( x = 4 \) noktasında fonksiyonun soldan ve sağdan limitleri tanımsızdır. Soldan ve sağdan limit değerleri olarak pozitif sonsuz yazmamız bu noktada limitin tanımlı olduğu anlamına gelmez. Soldan ve sağdan limitler tanımsız olsa da fonksiyon aynı yönde sonsuza gittiği için iki taraflı limite pozitif sonsuz yazabiliriz, ancak bu da bu noktada iki taraflı limitin tanımlı olduğu anlamına gelmez. |
|
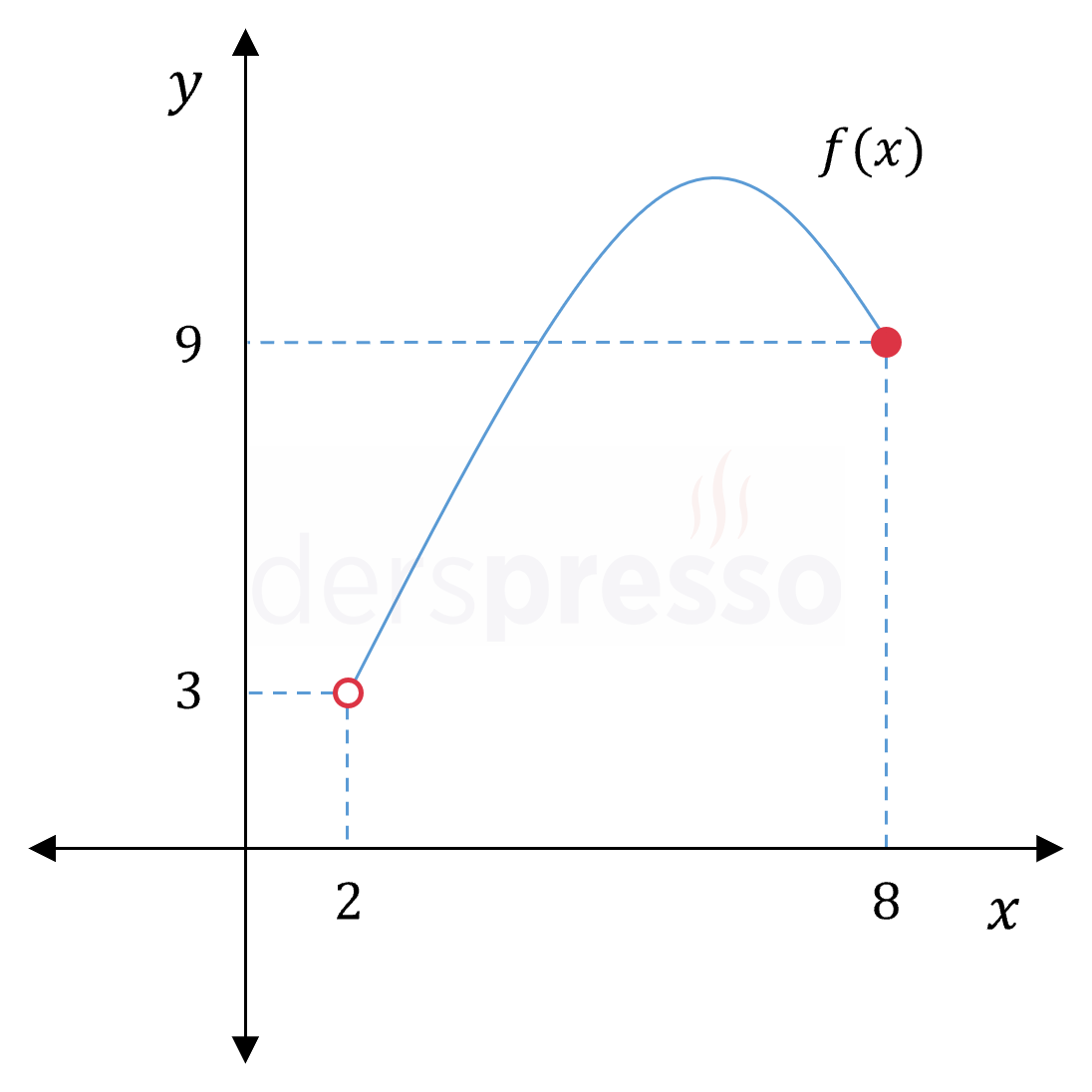
\( f: (2, 8] \to \mathbb{R} \) olmak üzere, \( \lim\limits_{x \to 2^-} f(x) \Longrightarrow \) Tanımsız \( \lim\limits_{x \to 2^+} f(x) = 3 \) \( \lim\limits_{x \to 2} f(x) \Longrightarrow \) Tanımsız \( f(2) \Longrightarrow \) Tanımsız \( \lim\limits_{x \to 8^-} f(x) = 9 \) \( \lim\limits_{x \to 8^+} f(x) \Longrightarrow \) Tanımsız \( \lim\limits_{x \to 8} f(x) \Longrightarrow \) Tanımsız \( f(8) = 9 \) Bir fonksiyonun tanım aralığının uç noktalarında tek taraflı limitler sadece fonksiyonun tanımlı olduğu yönlerde tanımlıdır. İki taraflı limit soldan ve sağdan limitlerin tanımlı ve eşit olmasını gerektirdiği için, uç noktalarda iki taraflı limit tanımlı değildir. |
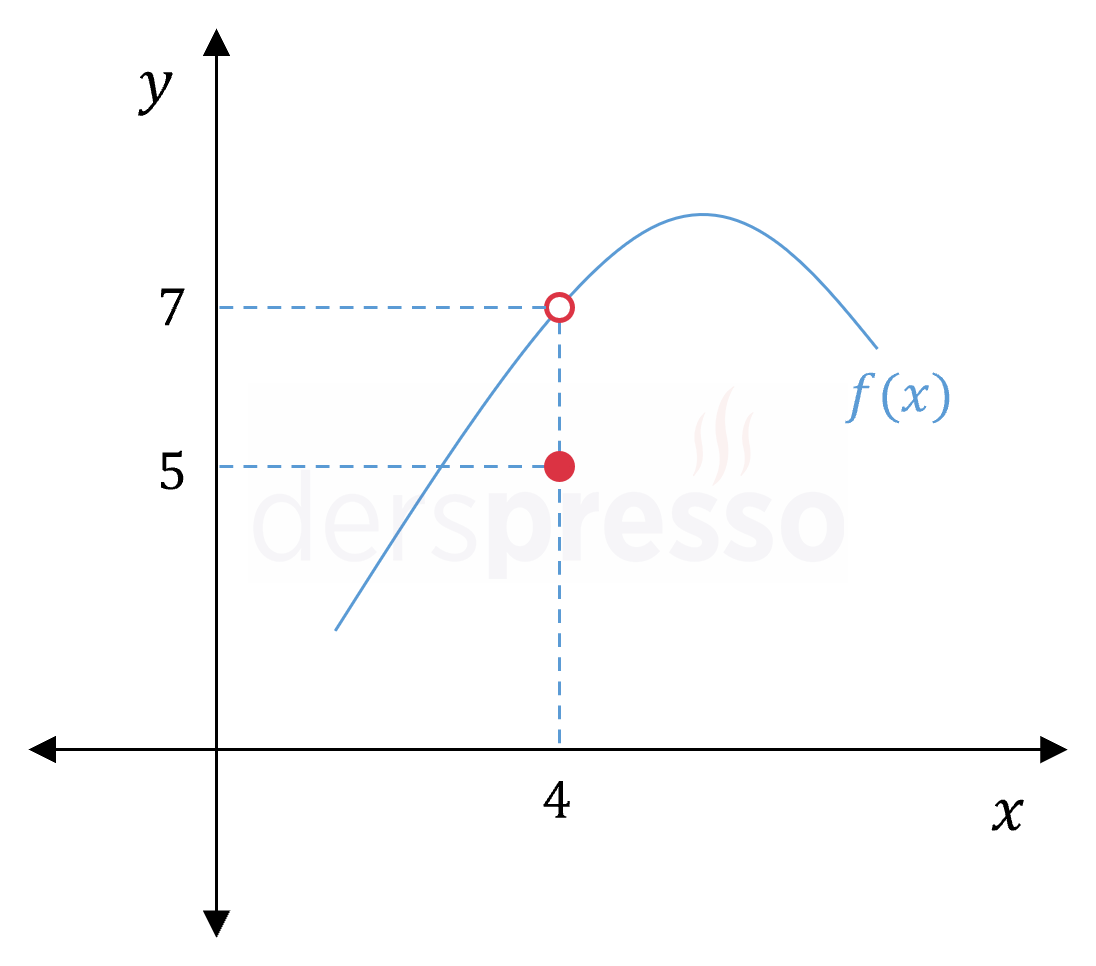
Şekildeki \( f \) fonksiyonu için,
\( f(4) + \lim\limits_{x \to 4} f(x) \) toplamı kaçtır?
Çözümü GösterSoldan ve sağdan limit değerlerini bulalım.
\( \lim\limits_{x \to 4^-} f(x) = 7 \)
\( \lim\limits_{x \to 4^+} f(x) = 7 \)
Soldan ve sağdan limitler tanımlı ve birbirine eşit olduğu için iki taraflı limit tanımlıdır ve değeri soldan ve sağdan limitlerin değerine eşittir.
\( \lim\limits_{x \to 4} f(x) = 7 \)
Bu noktadaki fonksiyon değeri limit değerinden farklıdır.
\( f(4) = 5 \)
Soruda istenen toplamı bulalım.
\( f(4) + \lim\limits_{x \to 4} f(x) = 5 + 7 = 12 \) bulunur.
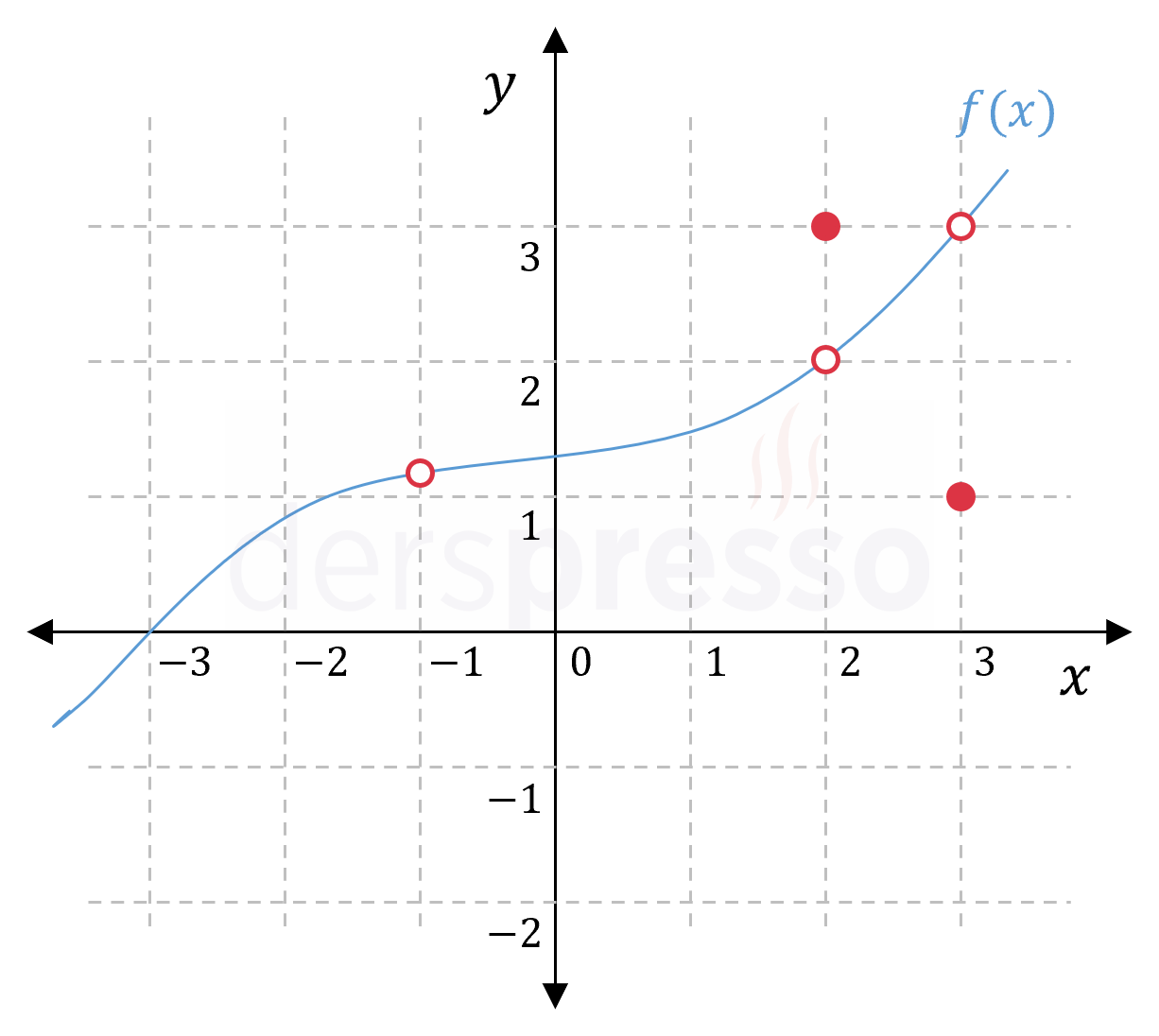
Yukarıda \( f(x) \) fonksiyonunun grafiği verilmiştir.
Buna göre aşağıdakilerden hangileri doğrudur?
I. Verilen aralıkta fonksiyonun tanımsız olduğu 3 nokta vardır.
II. \( \lim\limits_{x \to -3^-} f(x) = \lim\limits_{x \to -3} f(x) \)
III. \( \lim\limits_{x \to 2^+} f(x) = 3 \)
IV. \( \lim\limits_{x \to 3^-} f(x) = 3 \)
Çözümü GösterI. öncül: Bu aralıkta fonksiyon sadece \( x = -1 \) noktasında tanımsızdır, \( x = 2 \) ve \( x = 3 \) noktalarında ise tanımlıdır. Bu öncül yanlıştır.
II. öncül: \( x = -3 \) noktasında fonksiyonun soldan ve sağdan limitleri tanımlı ve sıfıra eşittir, dolayısıyla iki taraflı limiti de tanımlı ve sıfıra eşittir. Buna göre soldan limit iki taraflı limit değerine eşittir. Bu öncül doğrudur.
III. öncül: \( x = 2 \) noktasında sağdan limit değeri 2'dir. Bu noktadaki fonksiyon değeri 3'tür ve bu değerin limite bir etkisi yoktur. Bu öncül yanlıştır.
IV. öncül: \( x = 3 \) noktasında soldan limit değeri 3'tür. Bu öncül doğrudur.
Buna göre II. ve IV. öncüller doğrudur.

Şekildeki \( f \) fonksiyonunun \( [-3, 4] \) aralığındaki tam sayı apsis değerli noktalarındaki var olan limitlerin toplamı kaçtır?
Çözümü GösterHer nokta için soldan, sağdan ve iki taraflı limit değerleri aşağıda verilmiştir. Her noktadaki fonksiyon değerleri limitin varlığını ya da değerini etkilemese de bilgi amaçlı verilmiştir.
\( x = -3 \) noktası için:
\( \lim\limits_{x \to -3^-} f(x) = -1 \)
\( \lim\limits_{x \to -3^+} f(x) = -1 \)
\( \lim\limits_{x \to -3} f(x) = -1 \)
\( f(-3) = -1 \)
Soldan ve sağdan limitler tanımlıdır ve birbirine eşittir, dolayısıyla limit vardır ve değeri \( -1 \)'dir.
\( x = -2 \) noktası için:
\( \lim\limits_{x \to -2^-} f(x) = 0 \)
\( \lim\limits_{x \to -2^+} f(x) = 0 \)
\( \lim\limits_{x \to -2} f(x) = 0 \)
\( f(-2) = 1 \)
Soldan ve sağdan limitler tanımlıdır ve birbirine eşittir, dolayısıyla limit vardır ve değeri \( 0 \)'dır. Fonksiyon değerinin limit değerinden farklı olması limitin tanımlı olmasına engel değildir.
\( x = -1 \) noktası için:
\( \lim\limits_{x \to -1^-} f(x) = 1 \)
\( \lim\limits_{x \to -1^+} f(x) = 3 \)
\( \lim\limits_{x \to -1} f(x) \Longrightarrow \) Tanımsız
\( f(-1) = 3 \)
Soldan ve sağdan limitler tanımlıdır, ancak birbirinden farklıdır, dolayısıyla limit tanımlı değildir.
\( x = 0 \) noktası için:
\( \lim\limits_{x \to 0^-} f(x) = 1 \)
\( \lim\limits_{x \to 0^+} f(x) = 1 \)
\( \lim\limits_{x \to 0} f(x) = 1 \)
\( f(0) = 1 \)
Soldan ve sağdan limitler tanımlıdır ve birbirine eşittir, dolayısıyla limit vardır ve değeri \( 1 \)'dir.
\( x = 1 \) noktası için:
\( \lim\limits_{x \to 1^-} f(x) = -1 \)
\( \lim\limits_{x \to 1^+} f(x) = -1 \)
\( \lim\limits_{x \to 1} f(x) = -1 \)
\( f(1) \Longrightarrow \) Tanımsız
Soldan ve sağdan limitler tanımlıdır ve birbirine eşittir, dolayısıyla limit vardır ve değeri \( -1 \)'dir. Fonksiyonun bu noktada tanımsız olması limitin tanımlı olmasına engel değildir.
\( x = 2 \) noktası için:
\( \lim\limits_{x \to 2^-} f(x) = 0 \)
\( \lim\limits_{x \to 2^+} f(x) = 0 \)
\( \lim\limits_{x \to 2} f(x) = 0 \)
\( f(2) = 0 \)
Soldan ve sağdan limitler tanımlıdır ve birbirine eşittir, dolayısıyla limit vardır ve değeri \( 0 \)'dır.
\( x = 3 \) noktası için:
\( \lim\limits_{x \to 3^-} f(x) = 1 \)
\( \lim\limits_{x \to 3^+} f(x) = 2 \)
\( \lim\limits_{x \to 3} f(x) \Longrightarrow \) Tanımsız
\( f(3) = 3 \)
Soldan ve sağdan limitler tanımlıdır, ancak birbirinden farklıdır, dolayısıyla limit tanımlı değildir.
\( x = 4 \) noktası için:
\( \lim\limits_{x \to 4^-} f(x) = 2 \)
\( \lim\limits_{x \to 4^+} f(x) = 2 \)
\( \lim\limits_{x \to 4} f(x) = 2 \)
\( f(4) = 2 \)
Soldan ve sağdan limitler tanımlıdır ve birbirine eşittir, dolayısıyla limit vardır ve değeri \( 2 \)'dir.
Buna göre var olan limitlerin toplamı \( -1 + 0 + 1 + -1 + 0 + 2 = 1 \) olarak bulunur.
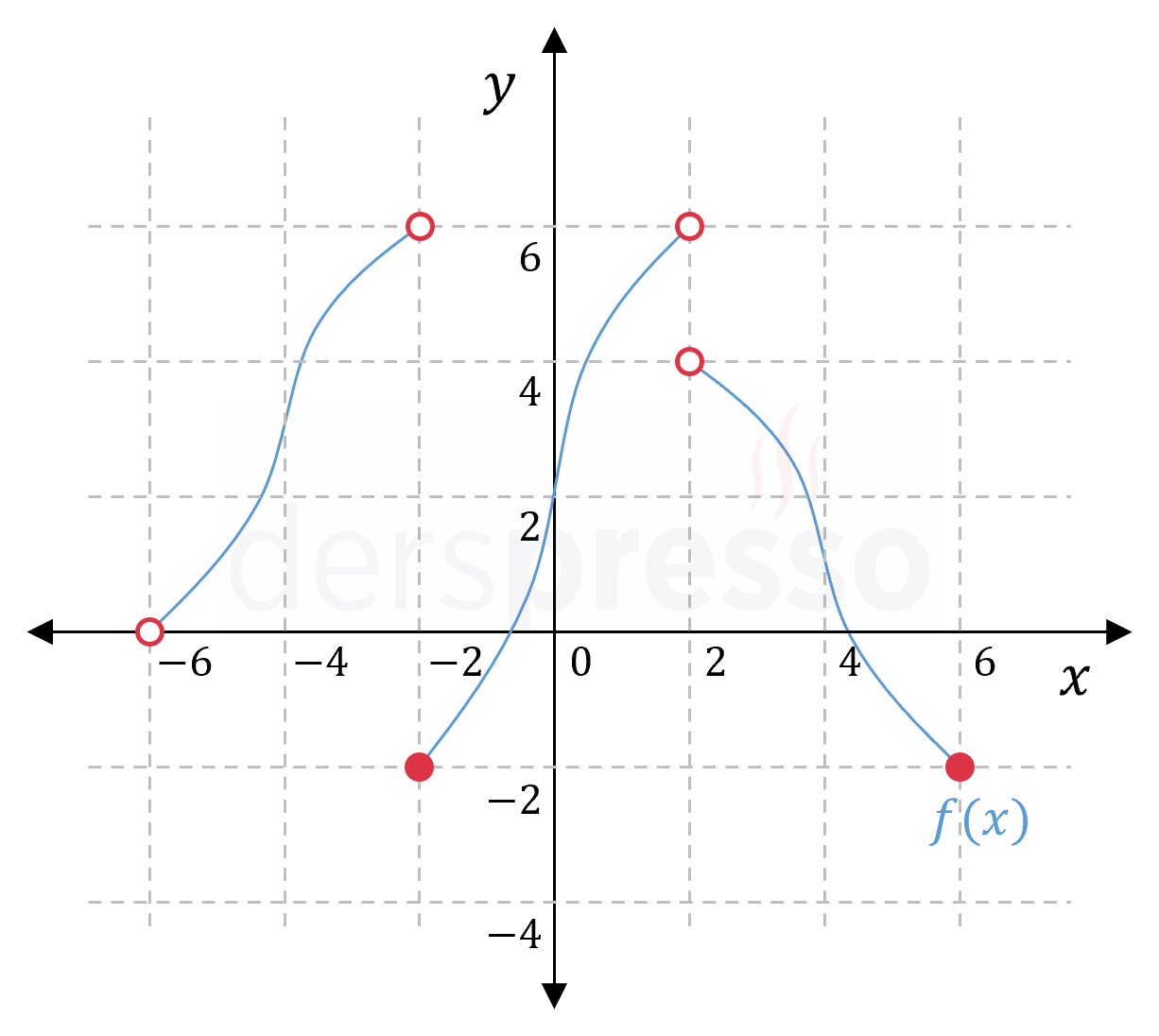
Şekildeki \( f \) fonksiyonu için aşağıdaki toplam kaçtır?
\( \lim\limits_{x \to -6^+} f(x) + \lim\limits_{x \to -2^-} f(x) \) \( + \lim\limits_{x \to 2^+} f(x) \) \( + \lim\limits_{x \to 6^-} f(x) \)
Çözümü Gösterİstenen tek taraflı limit değerleri aşağıdaki gibi olur.
\( \lim\limits_{x \to -6^+} f(x) = 0 \)
\( \lim\limits_{x \to -2^-} f(x) = 6 \)
\( \lim\limits_{x \to 2^+} f(x) = 4 \)
\( \lim\limits_{x \to 6^-} f(x) = -2 \)
Buna göre ifadenin sonucu \( 0 + 6 + 4 + (-2) = 8 \) olarak bulunur.

Yukarıdaki şekilde \( y = f(x) \) fonksiyonunun grafiği verilmiştir.
Buna göre aşağıdaki ifadelerden hangileri doğrudur?
I. \( \lim\limits_{x \to 1^+} f(x - 2) = 2 \)
II. \( \lim\limits_{x \to 2^-} f(3 - x) = 1 \)
III. \( \lim\limits_{x \to 0^-} f(x + 3) = -1 \)
Çözümü GösterI. öncül:
\( x \to 1^+ \) iken \( x - 2 \to -1^+ \) olur.
Buna göre verilen ifade \( f \) fonksiyonunun \( x = -1 \) noktasındaki sağdan limitidir.
\( \lim\limits_{x \to 1^+} f(x - 2) = f(-1^+) \)
Grafiğe göre \( f(-1^+) = 2 \) olduğu için bu öncül doğrudur.
II. öncül:
\( x \to 2^- \) iken \( 3 - x \to 1^+ \) olur.
Buna göre verilen ifade \( f \) fonksiyonunun \( x = 1 \) noktasındaki sağdan limitidir.
\( \lim\limits_{x \to 2^-} f(3 - x) = f(1^+) \)
Grafiğe göre \( f(1^+) = -1 \) olduğu için bu öncül yanlıştır.
III. öncül:
\( x \to 0^- \) iken \( x + 3 \to 3^- \) olur.
Buna göre verilen ifade \( f \) fonksiyonunun \( x = 3 \) noktasındaki soldan limitidir.
\( \lim\limits_{x \to 0^-} f(x + 3) = f(3^-) \)
Grafiğe göre \( f(3^-) = -1 \) olduğu için bu öncül doğrudur.
Buna göre I. ve III. öncüller doğrudur.

Yukarıda \( f \) fonksiyonunun grafiği verilmiştir.
\( g \) fonksiyonu her \( a \in \mathbb{R} \) için aşağıdaki şekilde tanımlanıyor.
\( g(a) = 2f(a) + \lim\limits_{x \to a^+} f(x) + 4 \)
Buna göre \( (g \circ f)(4) \) değeri kaçtır?
Çözümü Göster\( (g \circ f)(x) = g(f(x)) \)
\( (g \circ f)(4) = g(f(4)) \)
Verilen grafiğe göre \( f(4) = 0 \)'dır.
\( g(f(4)) = g(0) \)
Verilen \( g \) fonksiyonu tanımından \( g(0) \)'ı bulalım.
\( g(0) = 2f(0) + \lim\limits_{x \to 0^+} f(x) + 4 \)
Verilen grafikten ihtiyaç duyduğumuz değerleri bulalım.
\( f(0) = 2 \)
\( \lim\limits_{x \to 0^+} f(x) = -2 \)
Bulduğumuz değerleri \( g \) fonksiyonunun tanımında yerlerine yazalım.
\( g(0) = 2 \cdot 2 + (-2) + 4 = 6 \)
Buna göre \( (g \circ f)(4) = 6 \) bulunur.
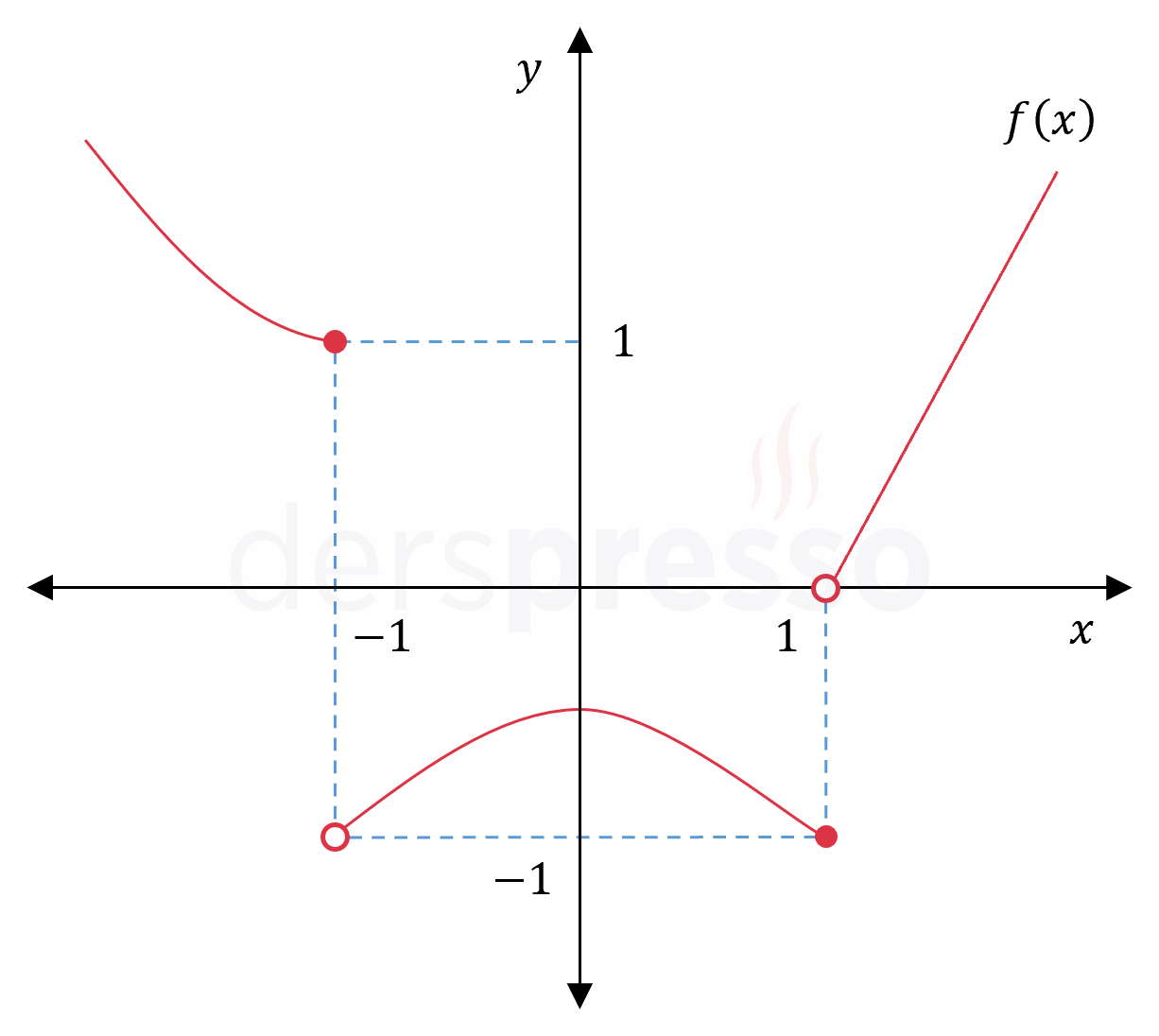
Yukarıda \( f \) fonksiyonunun grafiği verilmiştir.
Buna göre aşağıdaki limit ifadelerinden hangileri tanımlıdır?
I. \( \lim\limits_\limits{x \to -1} \abs{f(x)} \)
II. \( \lim\limits_\limits{x \to -1} f^2(x) \)
III. \( \lim\limits_\limits{x \to -1} f(\abs{x}) \)
Çözümü GösterVerilen öncülleri sırasıyla inceleyelim.
I. öncül:
\( \lim\limits_\limits{x \to -1^-} \abs{f(x)} = 1 \)
\( \lim\limits_\limits{x \to -1^+} \abs{f(x)} = \abs{-1} = 1 \)
Soldan ve sağdan limitler birbirine eşit olduğu için limit tanımlıdır.
II. öncül:
\( \lim\limits_\limits{x \to -1^-} f^2(x) = 1^2 = 1 \)
\( \lim\limits_\limits{x \to -1^+} f^2(x) = (-1)^2 = 1 \)
Soldan ve sağdan limitler birbirine eşit olduğu için limit tanımlıdır.
III. öncül:
\( f(x) \) fonksiyonu \( x = -1 \) noktasına soldan (sağdan) yaklaşırken \( f(\abs{x}) \) fonksiyonu \( x = 1 \) noktasına sağdan (soldan) yaklaşır.
\( \lim\limits_\limits{x \to -1^-} f(\abs{x}) = \lim\limits_\limits{x \to 1^+} f(x) = 0 \)
\( \lim\limits_\limits{x \to -1^+} f(\abs{x}) = \lim\limits_\limits{x \to 1^-} f(x) = -1 \)
Soldan ve sağdan limitler birbirine eşit olmadığı için limit tanımlı değildir.
Bu durumda I. ve II. öncüllerdeki limitler tanımlıdır.