Üstel Fonksiyon Tanımı
\( f(x) = a^x \) şeklindeki fonksiyonlara üstel fonksiyon denir.
\( a \in \mathbb{R^+} - \{ 1 \} \) olmak üzere,
\( f: \mathbb{R} \to \mathbb{R^+} \)
\( f(x) = a^x \)
fonksiyonuna üstel fonksiyon denir.
\( f(x) = 2^x \)
\( g(x) = (\frac{2}{3})^{2x} \)
Üstel fonksiyonların \( x^2, x^3, \ldots \) şeklindeki kuvvet fonksiyonlarından farkı, \( x \) değişkeninin fonksiyonun tabanında değil üssünde yer almasıdır.

Üstel Fonksiyonun Tabanı
Üstel fonksiyonların tabanı negatif, 0 ve 1 olamaz.
Üstel fonksiyonların tabanının 0 ya da 1 olamama sebebi, bu değerlerde fonksiyonun sabit fonksiyona dönüşmesidir.
\( a = 0 \) ve \( x \ne 0 \) için,
\( f(x) = 0^x = 0 \)
\( a = 1 \) için,
\( f(x) = 1^x = 1 \)
Üstel fonksiyonların tabanının negatif olamama sebebi, fonksiyonun kesirli \( x \) değerlerinde reel olmayan sonuçlar verebilmesidir.
\( a = -2 \) için,
\( f(\frac{1}{2}) = (-2)^{\frac{1}{2}} = \sqrt{-2} \notin \mathbb{R} \)
Negatif tabanın yol açtığı bir diğer durum da tam sayı üs değerlerinde fonksiyonun pozitif/negatif değerler arasında gidip gelmesidir.
\( a = -2 \) için,
\( f(1) = (-2)^1 = -2 \)
\( f(2) = (-2)^2 = 4 \)
\( f(3) = (-2)^3 = -8 \)
\( f(4) = (-2)^4 = 16 \)
Üstel Fonksiyon Değer Tablosu ve Grafiği
\( f(x) = 2^x \) üstel fonksiyonunun bazı değerleri için değer tablosu aşağıdaki gibidir.
| \( x \) | \( f(x) = 2^x \) |
|---|---|
| \( -2 \) | \( f(-2) = 2^{-2} = \frac{1}{4} \) |
| \( -1 \) | \( f(-1) = 2^{-1} = \frac{1}{2} \) |
| \( -\frac{1}{2} \) | \( f(-\frac{1}{2}) = 2^{-\frac{1}{2}} = \frac{1}{\sqrt{2}} \) |
| \( 0 \) | \( f(0) = 2^{0} = 1 \) |
| \( \frac{1}{2} \) | \( f(\frac{1}{2}) = 2^{\frac{1}{2}} = \sqrt{2} \) |
| \( 1 \) | \( f(1) = 2^{1} = 2 \) |
| \( 2 \) | \( f(2) = 2^{2} = 4 \) |
| \( 3 \) | \( f(3) = 2^{3} = 8 \) |
Bu noktaları analitik düzlemde işaretlediğimizde aşağıdaki grafiği elde ederiz.
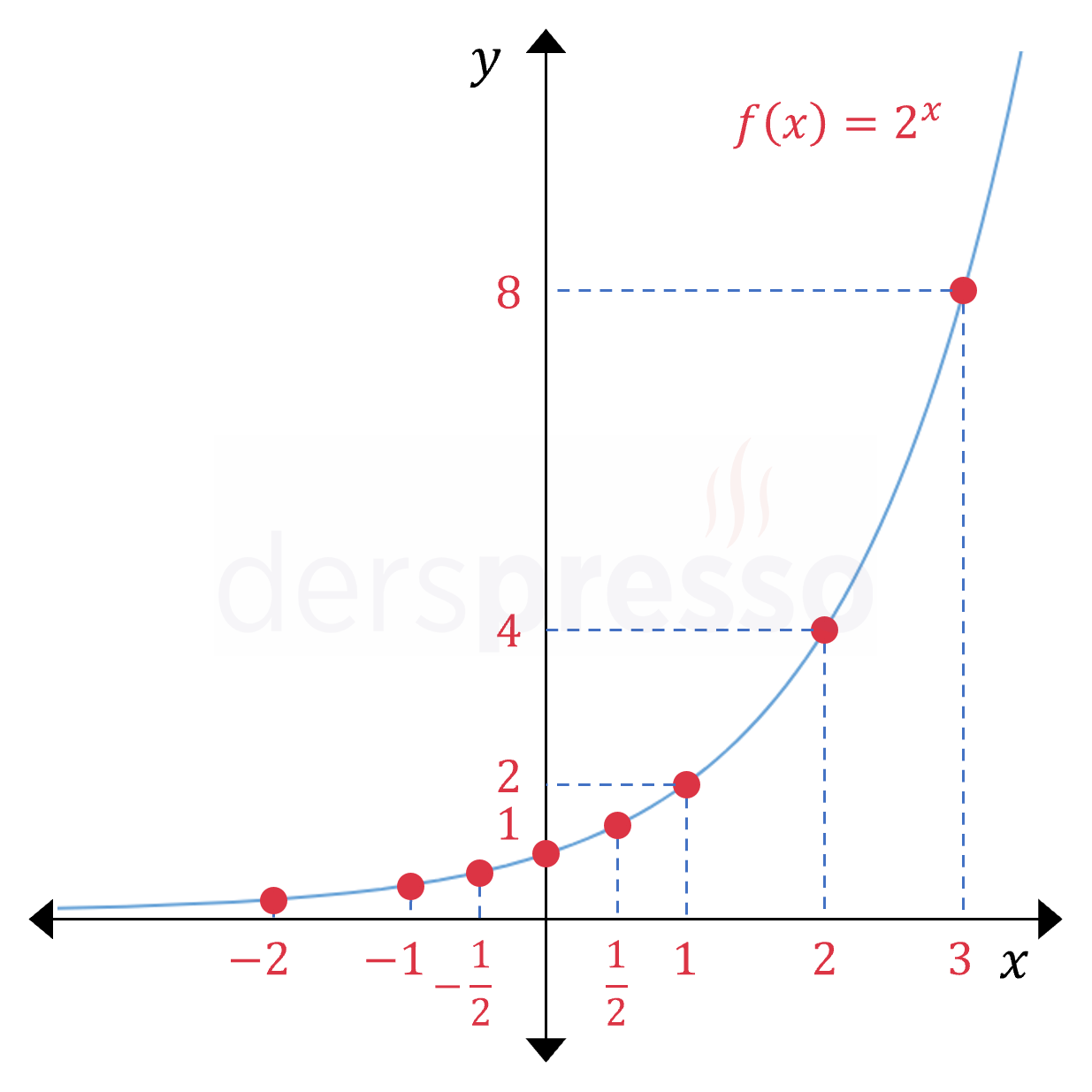
\( f(x) = a^x \) şeklindeki tüm üstel fonksiyonlar için \( f(0) = 1 \) olur, dolayısıyla grafikleri \( y \) eksenini \( (0, 1) \) noktasında keser.
Üstel fonksiyonlar \( \mathbb{R} \to \mathbb{R^+} \) için birebir ve örtendir, dolayısıyla ters fonksiyonları tanımlıdır ve logaritma fonksiyonudur.
Üstel İşlem Kuralları
Üslü ifadeler konusunda gördüğümüz işlem kuralları üstel ifadeler için de geçerlidir.
\( a^x \cdot a^y = a^{x + y} \)
\( \dfrac{a^x}{a^y} = a^{x - y} \)
\( a^x \cdot b^x = (a \cdot b)^x \)
\( \dfrac{a^x}{b^x} = \left( \dfrac{a}{b} \right)^x \)
\( (a^x)^k = a^{kx} \)
\( a^{-x} = \dfrac{1}{a^x} \)
\( e \) Sayısı
Sadece matematikte değil, fizik ve kimya gibi diğer doğa bilimlerinde önemli bir yeri olan sabit \( e \) (Euler) sayısı (e = 2,7182... ) üstel fonksiyonlarda en sık kullanılan taban değerlerinden biridir.
\( f(x) = e^x \)
\( e \) tabanındaki üstel fonksiyonlara doğal üstel fonksiyon da denir.
\( f: \mathbb{R} \to \mathbb{R^+} \)
\( f(x) = (3k - 7)^x \) fonksiyonu veriliyor.
\( f \) bir üstel fonksiyon olduğuna göre, \( k \) değer aralığı nedir?
Çözümü GösterÜstel fonksiyonlarda taban pozitif ve 1'den farklı olur.
Taban pozitif olmalıdır.
\( 3k - 7 \gt 0 \)
\( 3k \gt 7 \)
\( k \gt \dfrac{7}{3} \)
Taban 1 olamaz.
\( 3k - 7 \ne 1 \)
\( 3k \ne 8 \)
\( k \ne \dfrac{8}{3} \)
\( k \) değer aralığı aşağıdaki gibi olur.
\( k \in (\frac{7}{3}, \infty) - \{\frac{8}{3}\} \)
\( 9^x + 9^{x - 1} = 30 \) eşitliğine göre, \( 4^x \) kaça eşittir?
Çözümü Göster\( 9^x + 9^{x - 1} = 30 \)
\( 9^x + \dfrac{9^x}{9} = 30 \)
\( \dfrac{10 \cdot 9^x}{9} = 30 \)
\( 9^x = 27 \)
\( 3^{2x} = 3^3 \)
Tabanları pozitif ve birden farklı iki üstel ifadenin eşitliğinde üsler birbirine eşittir.
\( 2x = 3 \)
\( x = \dfrac{3}{2} \)
Bu \( x \) değerini \( 4^x \) ifadesinde yerine koyalım.
\( 4^x = 2^{2x} \)
\( = 2^{2 \cdot \frac{3}{2}} = 2^3 \)
\( = 8 \) bulunur.
Aşağıdaki fonksiyonlardan hangileri üstel fonksiyondur?
(a) \( f(x) = (-\dfrac{4}{11})^{3x - 4} \)
(b) \( g(x) = -(\sqrt{23})^{x} \)
(c) \( h(x) = x^{3e - 1} \)
(d) \( k(x) = (\dfrac{1}{e})^{5 - x} \)
Çözümü GösterÜstel fonksiyonlarda taban pozitif ve 1'den farklı olur.
Ayrıca üstel fonksiyonlarda taban sabit bir değer, üs ise \( x \) değişkeni içerir.
(a) \( f \) fonksiyonu tabanı negatif olduğu için üstel fonksiyon değildir.
(b) \( g \) fonksiyonu tabanı pozitif ve 1'den farklı olduğu için üstel fonksiyondur.
(c) \( h \) fonksiyonu \( x \) değişkeni üste değil tabanda olduğu için üstel değil kuvvet fonksiyonudur.
(d) \( k \) fonksiyonu tabanı pozitif ve 1'den farklı olduğu için üstel fonksiyondur.
Buna göre \( (b) \) ve \( (d) \) seçeneklerindeki fonksiyonlar üstel fonksiyondur.
\( f(x) = (\dfrac{2k - 9}{4})^x \)
\( g(x) = (41 - 5k)^x \)
fonksiyonları birer üstel fonksiyon olduğuna göre, \( k \)'nın alabileceği tam sayı değerlerin toplamı kaçtır?
Çözümü GösterÜstel fonksiyonlarda taban pozitif ve 1'den farklı olur.
\( f \) fonksiyonu için:
Taban pozitif olmalıdır.
\( \dfrac{2k - 9}{4} \gt 0 \)
\( 2k - 9 \gt 0 \)
\( k \gt \dfrac{9}{2} \)
Taban 1 olamaz.
\( \dfrac{2k - 9}{4} \ne 1 \)
\( 2k - 9 \ne 4 \)
\( k \ne \dfrac{13}{2} \)
\( g \) fonksiyonu için:
Taban pozitif olmalıdır.
\( 41 - 5k \gt 0 \)
\( 5k \lt 41 \)
\( k \lt \dfrac{41}{5} \)
Taban 1 olamaz.
\( 41 - 5k \ne 1 \)
\( k \ne 8 \)
İki fonksiyon için bulduğumuz aralıkların kesişimi \( k \) değer aralığını verir.
\( k \in (\frac{9}{2}, \frac{41}{5}) - \{\frac{13}{2}, 8\} \)
Bu aralıktaki tam sayı değerleri 5, 6 ve 7'dir.
\( 5 + 6 + 7 = 18 \) bulunur.
\( f(x) = (\dfrac{k + 8}{3 - 2k})^x \) bir üstel fonksiyon olduğuna göre, \( k \) değer aralığı nedir?
Çözümü GösterÜstel fonksiyonlarda taban pozitif ve 1'den farklı olur.
Taban pozitif olmalıdır.
\( \dfrac{k + 8}{3 - 2k} \gt 0 \)
Pay ve paydadaki ifadeleri sıfır yapan \( \{-8, \frac{3}{2}\} \) değerleri eşitsizliğin kritik noktalarıdır.
Bu kritik noktalar reel sayı doğrusunda \( (-\infty, -8) \), \( (-8, \frac{3}{2}) \) ve \( (\frac{3}{2}, \infty) \) aralıklarını oluşturur.
Bir işaret tablosu hazırlayalım.

Rasyonel ifade paydayı sıfır yapan \( k = \frac{3}{2} \) değerinde tanımsız, payı sıfır yapan \( k = -8 \) değerinde sıfır olur.
Verilen eşitsizlikte \( \gt \) sembolü kullanıldığı için rasyonel ifadenin pozitif olduğu aralık ve değerler eşitsizliğin çözüm kümesi olur.
\( k \in (-8, \frac{3}{2}) \)
Üstel fonksiyonların tabanı 1 olamaz.
\( \dfrac{k + 8}{3 - 2k} \ne 1 \)
\( k + 8 \ne 3 - 2k \)
\( k \ne -\dfrac{5}{3} \)
\( k \) değer aralığı aşağıdaki gibi olur.
\( k \in (-8, \frac{3}{2}) - \{ -\frac{5}{3} \} \)
\( f(x) = Ae^{\frac{x}{k}} \) eğrisi \( (0, 2) \), \( (4, 12) \) ve \( (m, 72) \) noktalarından geçtiğine göre, \( m \) değerini bulunuz.
Çözümü GösterVerilen denklem bir üstel fonksiyona aittir.
\( A \) ve \( k \) değerlerini bulmak için noktaların koordinatlarını denklemde yerine koyalım.
\( (0, 2) \) noktası için:
\( 2 = Ae^{\frac{0}{k}} \)
\( 2 = A \)
\( (4, 12) \) noktası için:
\( 12 = 2e^{\frac{4}{k}} \)
\( 6 = e^{\frac{4}{k}} \)
Eşitliğin iki tarafının doğal logaritmasını alalım.
\( \ln{6} = \dfrac{4}{k} \)
\( k = \dfrac{4}{\ln{6}} \)
Fonksiyon tanımı aşağıdaki gibi olur.
\( f(x) = 2e^{\frac{\ln{6} \cdot x}{4}} \)
\( m \) değerini bulmak için denklemde \( y = 72 \) yazalım.
\( 72 = 2e^{\frac{\ln{6} \cdot m}{4}} \)
\( 36 = e^{\frac{\ln{6} \cdot m}{4}} \)
Eşitliğin iki tarafının doğal logaritmasını alalım.
\( \ln{36} = \frac{m\ln{6}}{4} \)
\( 4\ln{36} = m\ln{6} \)
\( \ln{36^4} = \ln{6^m} \)
Tabanları aynı iki logaritma ifadesinin eşitliğinde logaritma içleri birbirine eşittir.
\( 36^4 = 6^8 = 6^m \)
\( m = 8 \) bulunur.