Uzayda Doğruya Uzaklık
Bu bölümde uzayda nokta ile doğru ve doğrular arasındaki uzaklığı hesaplama yöntemlerini inceleyeceğiz.
Noktanın Doğruya Uzaklığı
Uzayda noktanın doğruya olan en kısa uzaklığı farklı yöntemlerle bulunabilir. Aşağıda bu yöntemlerden üçünü inceleyeceğiz.
Vektörel Çarpım Yöntemi
Bir \( A \) noktasının \( P_0 \) noktasından geçen ve \( \vec{d} \) vektörüne paralel olan \( L \) doğrusuna olan uzaklığı aşağıdaki formülle bulunur.
\( A \) noktasının \( P_0 \) noktasından geçen ve \( \vec{d} \) vektörüne paralel olan doğruya uzaklığı:
\( d = \dfrac{\norm{\vec{P_0A} \times \vec{d}}}{\norm{\vec{d}}} \)
\( A(4, 8, -3) \) noktasının \( P_0(2, 4, -5) \) noktasından geçen ve \( \vec{d} = (-3, 4, 0) \) vektörüne paralel olan doğruya uzaklığı:
\( \vec{P_0A} = A - P_0 = (4 - 2, 8 - 4, -3 - (-5)) \)
\( = (2, 4, 2) \)
\( \vec{P_0A} \times \vec{d} = (4(0) - 4(2), -3(2) - 2(0), 2(4) - (-3)(4)) \)
\( = (-8, -6, 20) \)
\( \norm{\vec{P_0A} \times \vec{d}} = \sqrt{(-8)^2 + (-6)^2 + 20^2} = 10\sqrt{5} \)
\( \norm{\vec{d}} = \sqrt{(-3)^2 + 4^2 + 0^2} = 5 \)
\( d = \dfrac{10\sqrt{5}}{5} = 2\sqrt{5} \)
İSPATI GÖSTER
\( \vec{d} \) vektörünü başlangıç noktası \( P_0 \) olacak şekilde taşıyalım.
\( \vec{P_0A} \) ve \( \vec{d} \) vektörlerine paralel çizilen \( [CB] \) ve \( [AB] \) doğru parçaları \( P_0ABC \) paralelkenarını oluşturur.
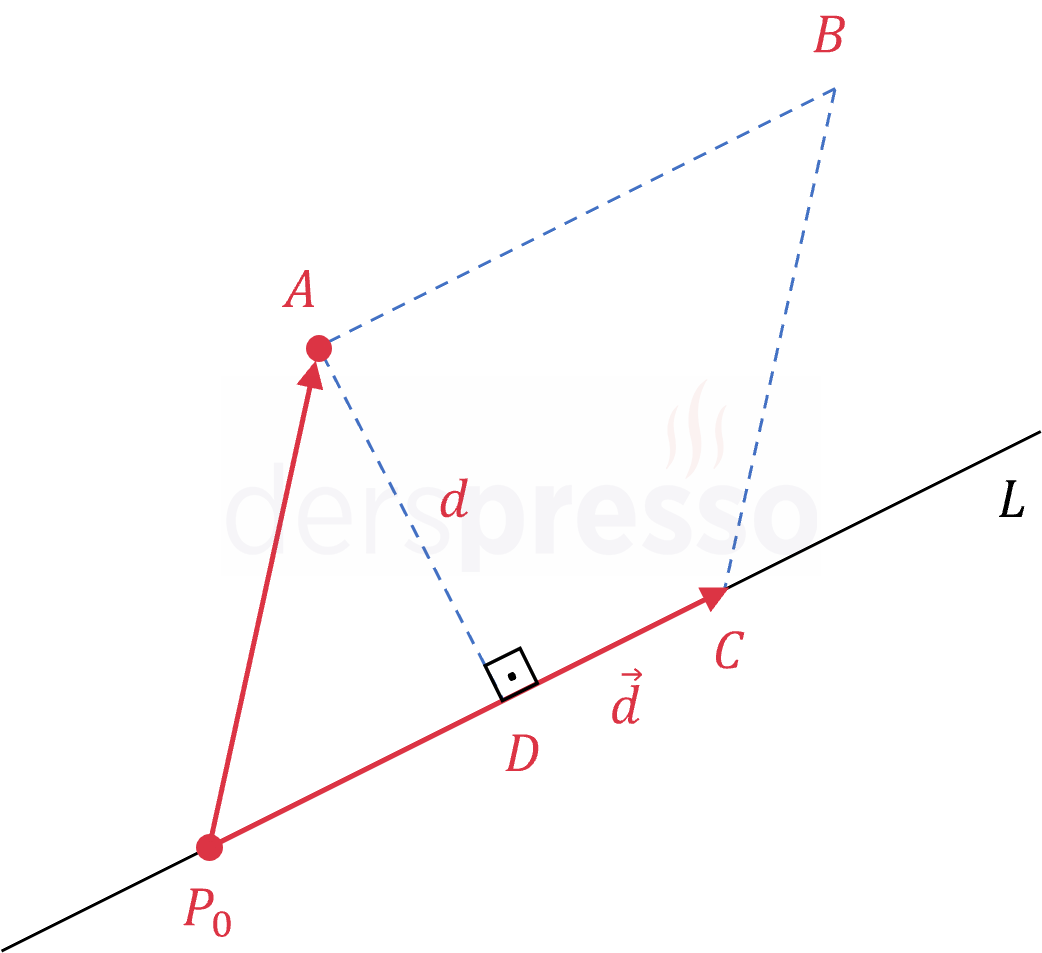
Paralelkenar alan formülüne göre, \( P_0ABC \) paralelkenarının alanı taban ile yüksekliğin çarpımına eşittir.
\( A(P_0ABC) = \norm{\vec{d}}d \)
Vektörel çarpımın geometrik yorumuna göre, bu alan aynı zamanda \( \vec{P_0A} \) ve \( \vec{d} \) vektörlerinin çarpımının normuna eşittir.
\( A(P_0ABC) = \norm{\vec{P_0A} \times \vec{d}} \)
İki alan formülünü birbirine eşitleyelim.
\( \norm{\vec{d}}d = \norm{\vec{P_0A} \times \vec{d}} \)
\( d \) uzunluğunu yalnız bırakalım.
\( d = \abs{AD} = \dfrac{\norm{\vec{P_0A} \times \vec{d}}}{\norm{\vec{d}}} \)
Nokta Çarpımı Yöntemi
\( A \) noktasının \( P_0 \) noktasından geçen ve \( \vec{d} \) vektörüne paralel olan \( L \) doğrusuna olan uzaklığı aşağıdaki yöntemle de bulunabilir.
- \( L \) doğrusunun vektör denklemi bulunur.
- \( A \) noktasından \( L \) doğrusu üzerindeki herhangi bir \( P \) noktasına çizilen \( \vec{n} \) vektörü bulunur.
- \( \vec{n} \) vektörü ile \( \vec{d} \) vektörünün birbirine dik olduğu, dolayısıyla nokta çarpımlarının sıfır olduğu \( t \) değeri bulunur.
- Bu \( t \) değeri ile hesaplanan \( \vec{n} \) vektörünün normu \( A \) noktasının \( L \) doğrusuna olan uzaklığını verir.
Bu yöntemi birinci yöntemde kullandığımız örnek üzerinde uygulayalım.
\( A(4, 8, -3) \) noktasının \( P_0(2, 4, -5) \) noktasından geçen ve \( \vec{d} = (-3, 4, 0) \) vektörüne paralel olan \( L \) doğrusuna uzaklığını bulalım.
\( L \) doğrusunun vektör denklemini bulalım.
\( \vec{r} = (2, 4, -5) + t(-3, 4, 0) \)
\( = (2 - 3t, 4 + 4t, -5) \)
\( A \) noktasından \( L \) noktası üzerindeki herhangi bir \( P \) noktasına çizilen \( \vec{n} \) vektörünün denklemini bulalım.
\( \vec{n} = \vec{AP} = P - A \)
\( = (2 - 3t - 4, 4 + 4t - 8, -5 - (-3)) \)
\( = (-2 - 3t, -4 + 4t, -2) \)
\( \vec{d} \) ve \( \vec{n} \) vektörlerinin nokta çarpımının 0 olduğu \( t \) değerinde iki vektör birbirine dik olur ve \( A \) noktasının \( L \) doğrusuna uzaklığı en küçük değerini alır.
\( \vec{d} \cdot \vec{n} = 0 \)
\( (-3, 4, 0) \cdot (-2 - 3t, -4 + 4t, -2) = 0 \)
\( -3(-2 - 3t) + 4(-4 + 4t) + 0(-2) = 0 \)
\( 6 + 9t - 16 + 16t + 0 = 0 \)
\( t = \dfrac{2}{5} \)
Bu değer için \( \vec{n} \) vektörünü ve normunu bulalım.
\( \vec{n} = (-2 - 3(\dfrac{2}{5}), -4 + 4(\dfrac{2}{5}), -2) \)
\( = (-\dfrac{16}{5}, -\dfrac{12}{5}, -2) \)
\( \norm{\vec{n}} = \sqrt{(-\dfrac{16}{5})^2 + (-\dfrac{12}{5})^2 + (-2)^2} \)
\( = 2\sqrt{5} \)
İzdüşüm Yöntemi
\( A \) noktasının \( P_0 \) noktasından geçen ve \( \vec{d} \) vektörüne paralel olan \( L \) doğrusuna olan uzaklığı aşağıdaki yöntemle de bulunabilir.
- \( \vec{P_0A} \) vektörünün \( \vec{d} \) vektörü üzerindeki izdüşümü olan \( \vec{p} \) vektörü bulunur.
- \( \vec{P_0A} \) ve \( \vec{p} \) vektörlerinin normları kullanılarak Pisagor teoremi ile \( d \) uzunluğu bulunur.
Bu yöntemi birinci yöntemde kullandığımız örnek üzerinde uygulayalım.
\( A(4, 8, -3) \) noktasının \( P_0(2, 4, -5) \) noktasından geçen ve \( \vec{d} = (-3, 4, 0) \) vektörüne paralel olan \( L \) doğrusuna uzaklığını bulalım.
\( \vec{d} \) vektörünü başlangıç noktası \( P_0 \) olacak şekilde taşıyalım.
\( L \) doğrusunun vektör denklemini bulalım.
\( \vec{r} = (2, 4, -5) + t(-3, 4, 0) \)
\( = (2 - 3t, 4 + 4t, -5) \)
\( P_0A \) vektörünü bulalım.
\( \vec{P_0A} = A - P_0 = (4 - 2, 8 - 4, -3 - (-5)) \)
\( = (2, 4, 2) \)
\( \vec{P_0A} \) vektörünün normunu bulalım.
\( \norm{\vec{P_0A}} = \sqrt{2^2 + 4^2 + 2^2} = 2\sqrt{6} \)
\( \vec{P_0A} \) vektörünün \( \vec{d} \) vektörü üzerindeki izdüşümüne \( \vec{p} \) diyelim.
\( \norm{\vec{p}} = \dfrac{\abs{\vec{P_0A} \cdot \vec{d}}}{\norm{\vec{d}}} \)
\( = \dfrac{\abs{2(-3) + 4(4) + 2(0)}}{\sqrt{(-3)^2 + 4^2 + 0^2}} \)
\( = \dfrac{10}{2} = 2 \)
\( P_0AD \) üçgenine Pisagor teoremini uygulayalım.
\( \norm{\vec{P_0A}}^2 = \norm{\vec{p}}^2 + d^2 \)
\( (2\sqrt{6})^2 = 2^2 + d^2 \)
\( d = 2\sqrt{5} \)
Paralel Doğrular Arası Uzaklık
Sırasıyla \( P_1 \) ve \( P_2 \) noktalarından geçen ve \( \vec{d} \) vektörüne paralel olan \( L_1 \) ve \( L_2 \) doğruları arasındaki uzaklık, yukarıda paylaştığımız bir nokta ile doğru arasındaki uzaklık formülünde \( A \) noktası yerine \( P_2 \) noktası kullanılarak bulunabilir.
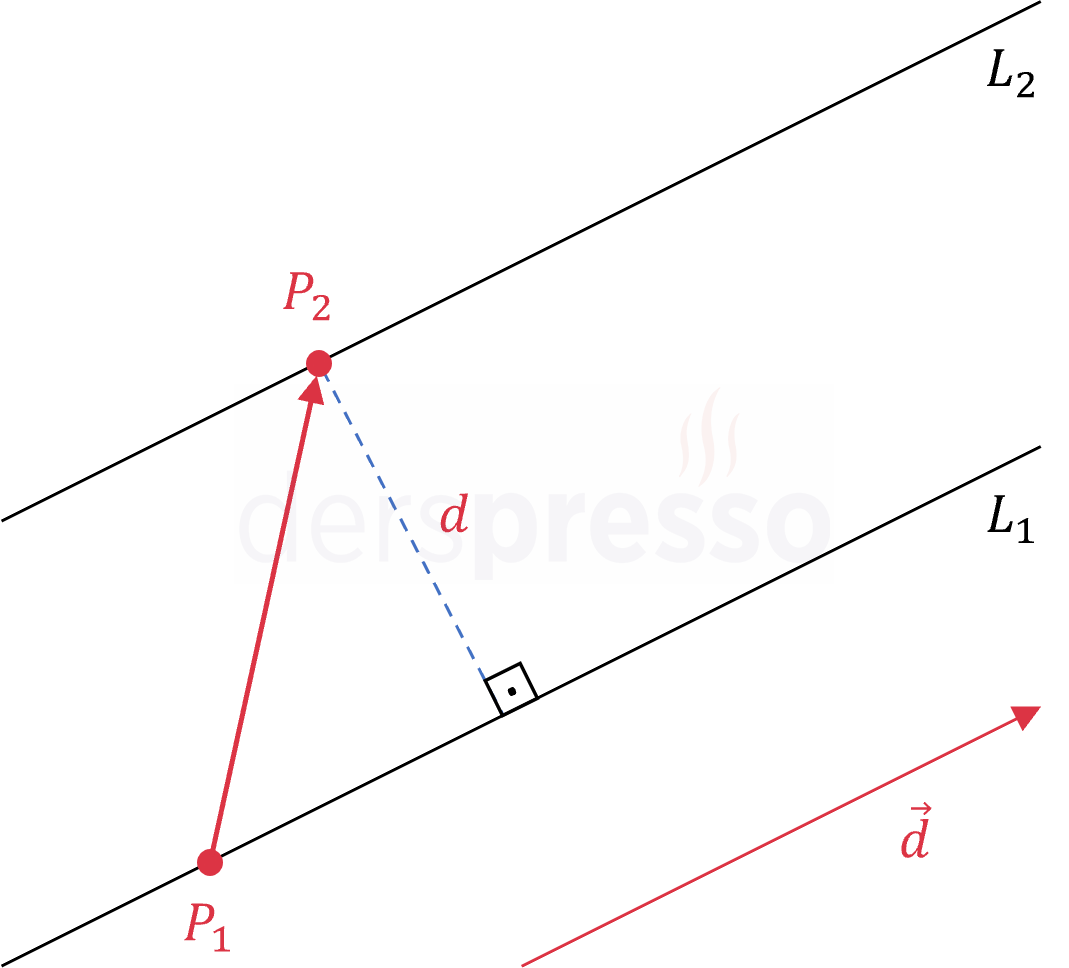
Sırasıyla \( P_1 \) ve \( P_2 \) noktalarından geçen ve \( \vec{d} \) vektörüne paralel olan doğrular arasındaki uzaklık:
\( d = \dfrac{\norm{\vec{P_1P_2} \times \vec{d}}}{\norm{\vec{d}}} \)
Sırasıyla \( P_1(2, 4, -5) \) ve \( P_2(4, 8, -3) \) noktalarından geçen ve ikisi de \( \vec{d} = (-3, 4, 0) \) vektörüne paralel olan \( L_1 \) ve \( L_2 \) doğruları arasındaki uzaklık:
\( L_2 \) noktası üzerindeki herhangi bir nokta olarak \( P_2 \) noktasını seçelim ve vektörel çarpım yöntemi ile \( P_2 \) noktasının \( L_1 \) doğrusuna uzaklığını bulalım.
\( P_2(4, 8, -3) \) noktasının \( P_1(2, 4, -5) \) noktasından geçen ve \( \vec{d} = (-3, 4, 0) \) vektörüne paralel olan doğruya uzaklığı:
\( \vec{P_1P_2} = P_2 - P_1 = (4 - 2, 8 - 4, -3 - (-5)) \)
\( = (2, 4, 2) \)
\( \vec{P_1P_2} \times \vec{d} = (4(0) - 4(2), -3(2) - 2(0), 2(4) - (-3)(4)) \)
\( = (-8, -6, 20) \)
\( \norm{\vec{P_1P_2} \times \vec{d}} = \sqrt{(-8)^2 + (-6)^2 + 20^2} = 10\sqrt{5} \)
\( \norm{\vec{d}} = \sqrt{(-3)^2 + 4^2 + 0^2} = 5 \)
\( d = \dfrac{10\sqrt{5}}{5} = 2\sqrt{5} \)
Aykırı Doğrular Arası Uzaklık
Aykırı (kesişmeyen ve paralel olmayan) iki doğru arasındaki en kısa uzaklık, iki doğruya da dik olan doğrunun uzunluğuna eşittir. Bu uzaklık aşağıdaki formülle bulunur.
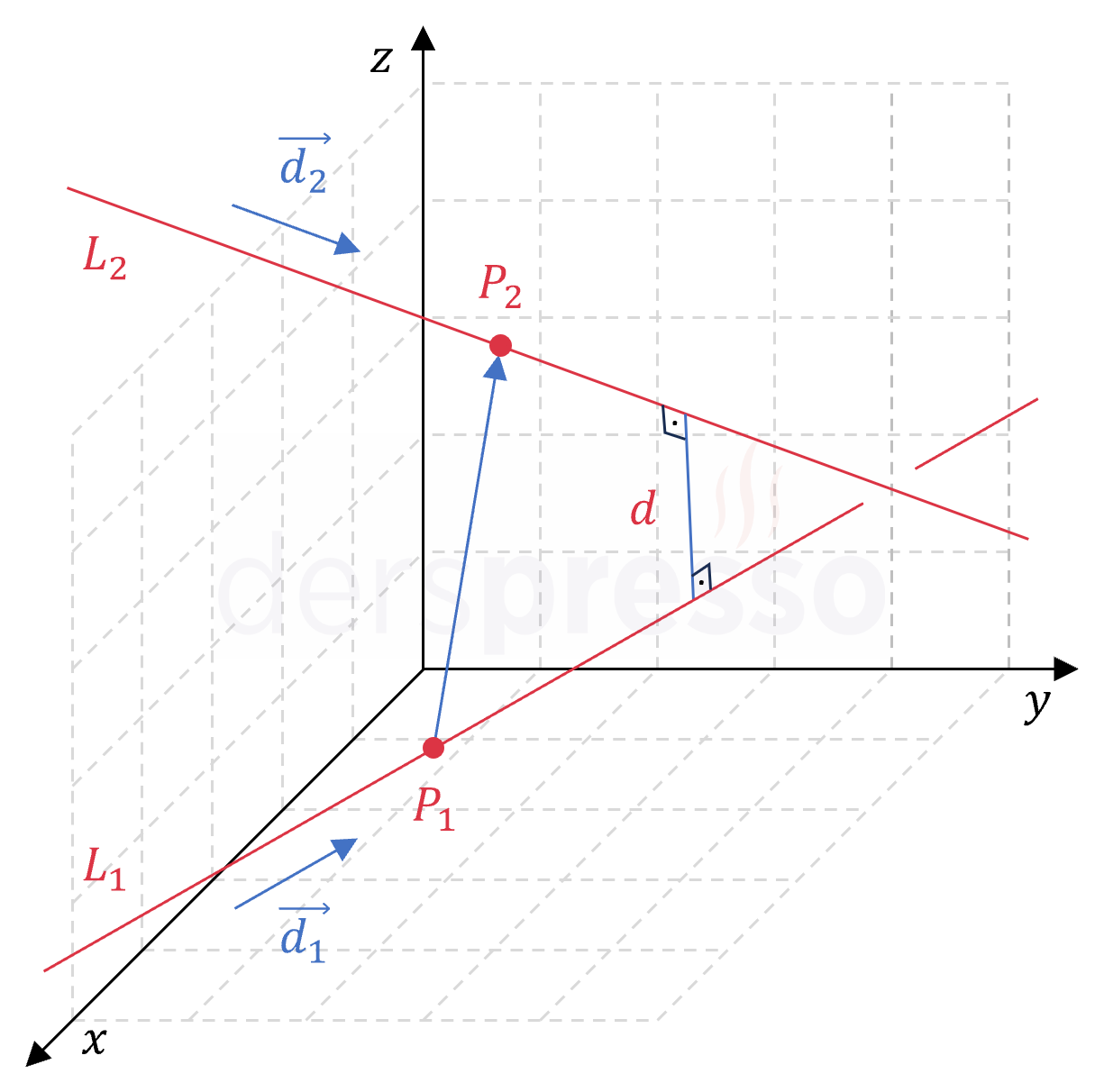
\( P_1 \) noktasından geçen ve \( \vec{d_1} \) vektörüne paralel olan doğru ile \( P_2 \) noktasından geçen ve \( \vec{d_2} \) vektörüne paralel olan doğru arasındaki uzaklık:
\( d = \dfrac{\abs{\vec{P_1P_2} \cdot (\vec{d_1} \times \vec{d_2})}}{\norm{\vec{d_1} \times \vec{d_2}}} \)
\( P_1(3, 2, -1) \) noktasından geçen ve \( \vec{d_1} = (-2, 1, 0) \) vektörüne paralel olan \( L_1 \) doğrusu ile \( P_2(2, 1, 5) \) noktasından geçen ve \( \vec{d_2} = (2, 1, -2) \) vektörüne paralel olan \( L_2 \) doğrusu arasındaki uzaklık:
\( \vec{P_1P_2} = (2 - 3, 1 - 2, 5 - (-1)) \)
\( = (-1, -1, 6) \)
\( \vec{d_1} \times \vec{d_2} = (1(-2) - 1(0), 2(0) - (-2)(-2), -2(1) - 2(1)) \)
\( = (-2, -4, -4) \)
\( \vec{P_1P_2} \cdot (\vec{d_1} \times \vec{d_2}) = (-1, -1, 6) \cdot (-2, -4, -4) \)
\( = -1(-2) + (-1)(-4) + 6(-4) = -18 \)
\( \norm{\vec{d_1} \times \vec{d_2}} = \sqrt{(-2)^2 + (-4)^2 + (-4)^2} = 6 \)
\( d = \dfrac{\abs{-18}}{6} = 3 \)
Aykırı Doğruların En Yakın Noktaları
Aykırı iki doğrunun birbirine en yakın oldukları noktalar (\( A \) ve \( B \) noktaları) aşağıdaki yöntemle bulunur.
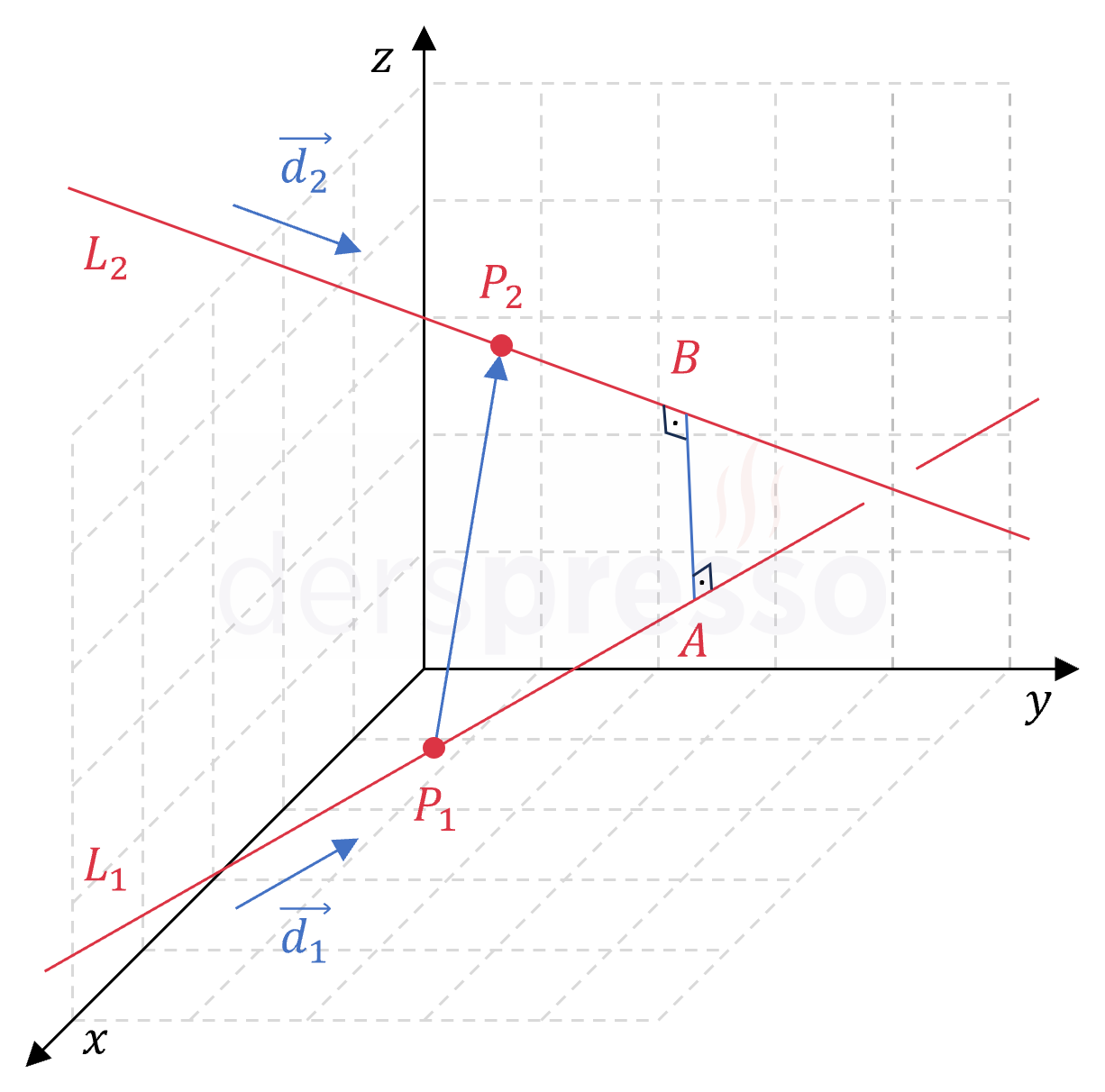
- Aykırı doğruların parametrik denklemleri yazılır. Denklemlerde farklı parametre sembolleri kullanılmalıdır (örneğin \( t \) ve \( s \)).
- Birinci doğru üzerindeki herhangi bir noktadan ikinci doğru üzerindeki herhangi bir noktaya bir vektör tanımlanır.
- "İki aykırı doğru arasındaki en kısa uzaklık iki doğruya da diktir" bilgisi kullanılarak bu vektörün iki doğruya ait doğrultman vektörleri ile nokta çarpımları ayrı ayrı sıfıra eşitlenir.
- Elde edilen iki bilinmeyenli iki denklem ortak çözülür ve doğruların birbirine en yakın oldukları noktalar için parametre değerleri bulunur.
- Bu parametre değerleri doğru denklemlerinde yerine konarak en yakın noktaların koordinatları bulunur.
\( P_1(3, 2, -1) \) noktasından geçen ve \( \vec{d_1} = (-2, 1, 0) \) vektörüne paralel olan \( L_1 \) doğrusu ile \( P_2(2, 1, 5) \) noktasından geçen ve \( \vec{d_2} = (2, 1, -2) \) vektörüne paralel olan \( L_2 \) doğrusunun birbirine en yakın oldukları noktaları bulalım.
\( L_1 \) doğrusunun parametrik denklemini yazalım.
\( x = 3 - 2t \)
\( y = 2 + t \)
\( z = -1 \)
\( L_2 \) doğrusunun parametrik denklemini yazalım.
\( x = 2 + 2s \)
\( y = 1 + s \)
\( z = 5 - 2s \)
İki doğru üzerindeki herhangi iki noktayı temsil eden \( A \) ve \( B \) noktaları arasında bir vektör tanımlayalım.
\( \vec{AB} = B - A \)
\( = (2 + 2s - (3 - 2t), 1 + s - (2 + t), 5 - 2s - (-1)) \)
\( = (2t + 2s - 1, -t + s - 1, -2s + 6) \)
\( L_1 \) ve \( L_2 \) doğruları arasındaki uzaklık en küçük değerini aldığında \( \vec{AB} \) vektörü iki doğruya da dik olduğu için iki doğrunun doğrultman vektörleri ile de nokta çarpımı sıfıra eşit olur.
\( \vec{AB} \) vektörünün \( L_1 \) doğrusuna ait \( \vec{d_1} \) vektörü ile nokta çarpımını sıfıra eşitleyelim.
\( \vec{AB} \cdot \vec{d_1} = 0 \)
\( (2t + 2s - 1, -t + s - 1, -2s + 6) \cdot (-2, 1, 0) = 0 \)
\( (-4t - 4s + 2) + (-t + s - 1) + (0) = 0 \)
\( -5t - 3s = -1 \)
\( \vec{AB} \) vektörünün \( L_2 \) doğrusuna ait \( \vec{d_2} \) vektörü ile nokta çarpımını sıfıra eşitleyelim.
\( \vec{AB} \cdot \vec{d_2} = 0 \)
\( (2t + 2s - 1, -t + s - 1, -2s + 6) \cdot (2, 1, -2) = 0 \)
\( (4t + 4s - 2) + (-t + s - 1) + (4s - 12) = 0 \)
\( 3t + 9s = 15 \)
\( t + 3s = 5 \)
Elde ettiğimiz \( t \) ve \( s \) parametrelerine bağlı iki denklemi ortak çözdüğümüzde aşağıdaki değerleri buluruz.
\( t = -1, \quad s = 2 \)
Bu parametre değerlerini ilgili doğruların parametrik denklemlerinde yerine koyarak \( A \) ve \( B \) noktalarının koordinatlarını bulalım.
\( L_1 \) doğrusunun \( t = -1 \) için koordinatları:
\( A(3 - 2t, 2 + t, -1) \)
\( A(3 - 2(-1), 2 + (-1), -1) \)
\( A(5, 1, -1) \)
\( L_2 \) doğrusunun \( s = 2 \) için koordinatları:
\( B(2 + 2s, 1 + s, 5 - 2s) \)
\( B(2 + 2(2), 1 + 2, 5 - 2(2)) \)
\( B(6, 3, 1) \)
Buna göre iki doğrunun birbirine en yakın oldukları noktalar \( L_1 \) doğrusu üzerindeki \( A(5, 1, -1) \) noktası ile \( L_2 \) doğrusu üzerindeki \( B(6, 3, 1) \) noktasıdır.
Bu iki nokta arasındaki uzaklığı hesapladığımızda yukarıdaki örnekte bulduğumuzu uzaklık değerini buluruz.
\( \norm{\vec{AB}} = \sqrt{(6 - 5)^2 + (3 - 1)^2 + (1 - (-1))^2} \)
\( = \sqrt{1 + 4 + 4} = 3 \)