Düzlemlerin Yaptığı Açılar
Bu bölümde iki düzlemin birbiriyle ve bir doğrunun düzlemle yaptığı açıları inceleyeceğiz.
İki Düzlem Arasındaki Açı
İki düzlemin birbiriyle yaptığı açılardan dar olan açı, düzlemlerin normal vektörlerinin birbiriyle yaptığı açılardan dar olan açıya eşittir.
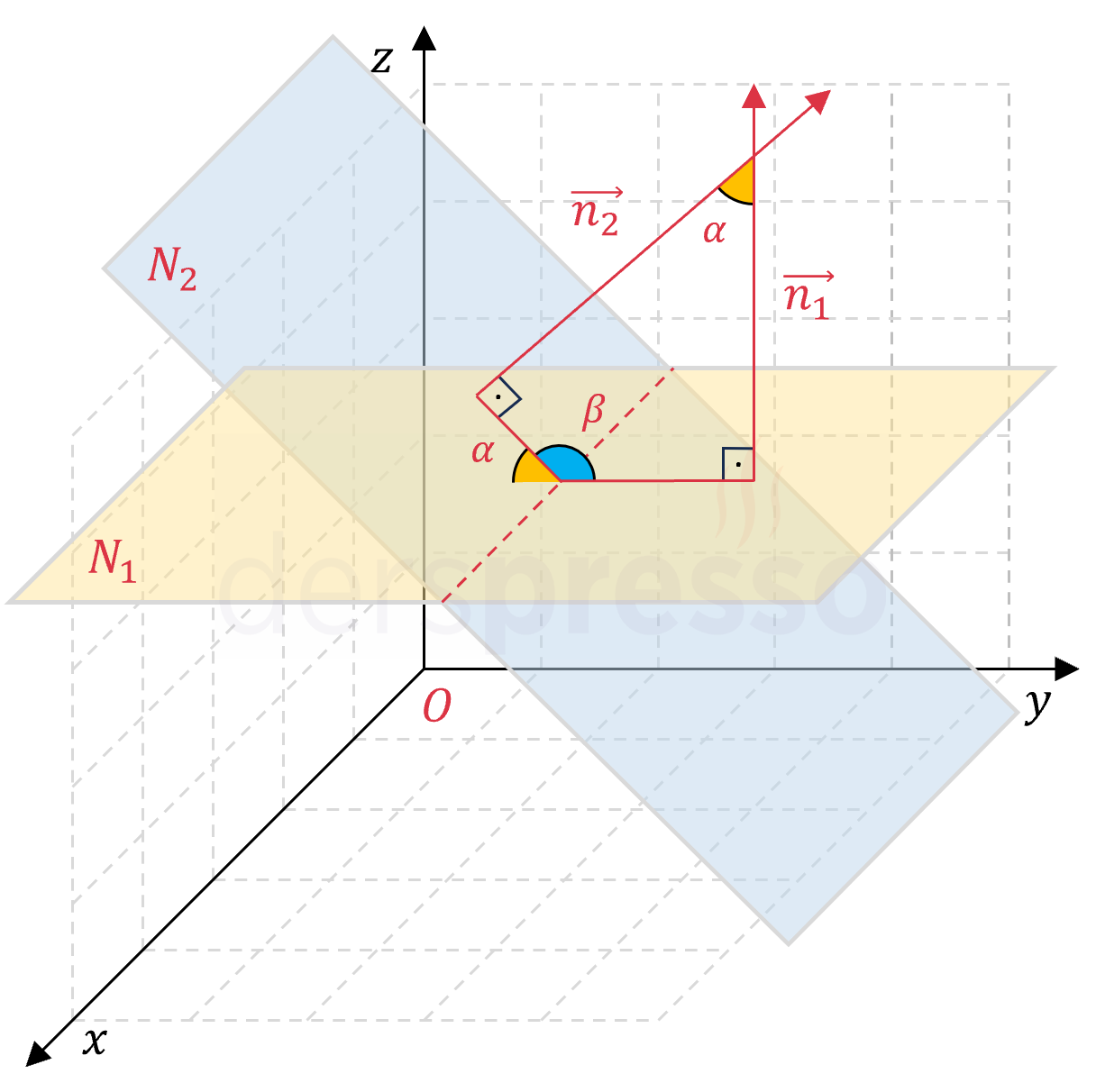
\( \alpha \in [0, \frac{\pi}{2}] \) olmak üzere,
\( \cos{\alpha} = \dfrac{\abs{\vec{n_1} \cdot \vec{n_2}}}{\norm{\vec{n_1}}\norm{\vec{n_2}}} \)
Aşağıda genel denklemleri verilen \( N_1 \) ve \( N_2 \) düzlemleri arasında kalan açıyı bulalım.
\( N_1: x + y - 5 = 0 \)
\( N_2: 2x + y - z - 4 = 0 \)
\( \vec{n_1} = (1, 1, 0) \)
\( \vec{n_2} = (2, 1, -1) \)
\( \vec{n_1} \cdot \vec{n_2} = 1(2) + 1(1) + 0(-1) = 3 \)
\( \norm{\vec{n_1}} = \sqrt{1^2 + 1^2 + 0^2} = \sqrt{2} \)
\( \norm{\vec{n_2}} = \sqrt{2^2 + 1^2 + (-1)^2} = \sqrt{6} \)
\( \cos{\alpha} = \dfrac{\abs{3}}{\sqrt{2}\sqrt{6}} = \dfrac{\sqrt{3}}{2} \)
\( \alpha = \arccos{\dfrac{\sqrt{3}}{2}} = \dfrac{\pi}{6} \)
Bir Doğru ile Düzlem Arasındaki Açı
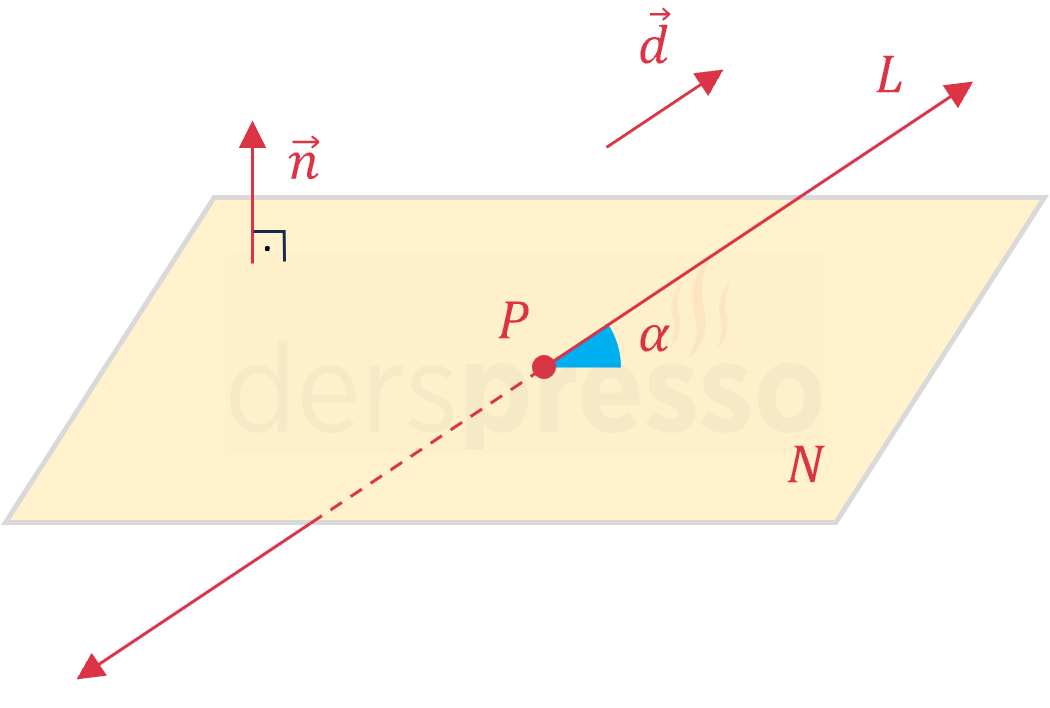
\( \vec{d} \) doğrunun doğrultman, \( \vec{n} \) düzlemin normal vektörü olmak üzere,
\( \sin{\alpha} = \dfrac{\vec{d} \cdot \vec{n}}{\norm{\vec{d}}\norm{\vec{n}}} \)
Aşağıda denklemleri verilen \( L \) doğrusu ve \( N \) düzlemi arasında kalan açıyı bulalım.
\( L: \dfrac{x - 1}{6} = \dfrac{y + 3}{2} = \dfrac{z - 1}{-3} \)
\( N: x - 2y - 2z = -11 \)
\( \vec{d} = (6, 2, -3) \)
\( \vec{n} = (1, -2, -2) \)
\( \vec{d} \cdot \vec{n} = 6(1) + 2(-2) + (-3)(-2) = 8 \)
\( \norm{\vec{d}} = \sqrt{6^2 + 2^2 + (-3)^2} = 7 \)
\( \norm{\vec{n}} = \sqrt{1^2 + (-2)^2 + (-2)^2} = 3 \)
\( \sin{\alpha} = \dfrac{8}{3 \cdot 7} = \dfrac{8}{21} \)
\( \alpha = \arcsin{\dfrac{8}{21}} \)