Uzayda Düzlem
Aşağıdaki nokta ve doğruların birleşimi uzayda tek bir düzlem belirtir.
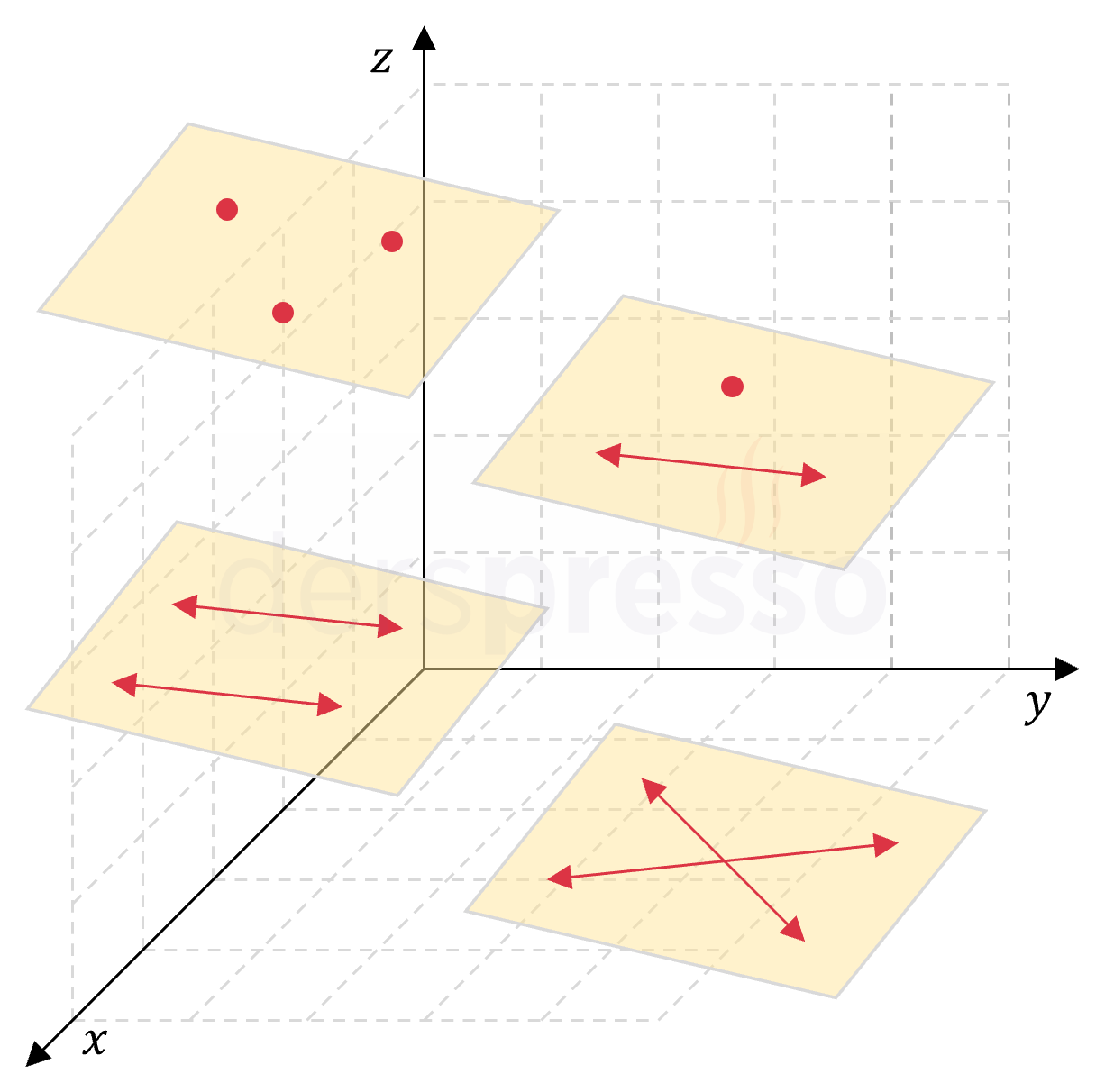
- Doğrusal olmayan üç nokta
- Bir doğru ve bu doğru üzerinde bulunmayan bir nokta
- Birbirinden farklı iki paralel doğru
- Tek bir noktada kesişen iki doğru
Uzayda Düzlem Denklemi
Bir \( N \) düzleminin denklemini bulmak için, önce bu düzlem üzerinde bir \( P_0 \) noktası ve düzleme dik bir \( \vec{n} \) vektörü tanımlayalım.
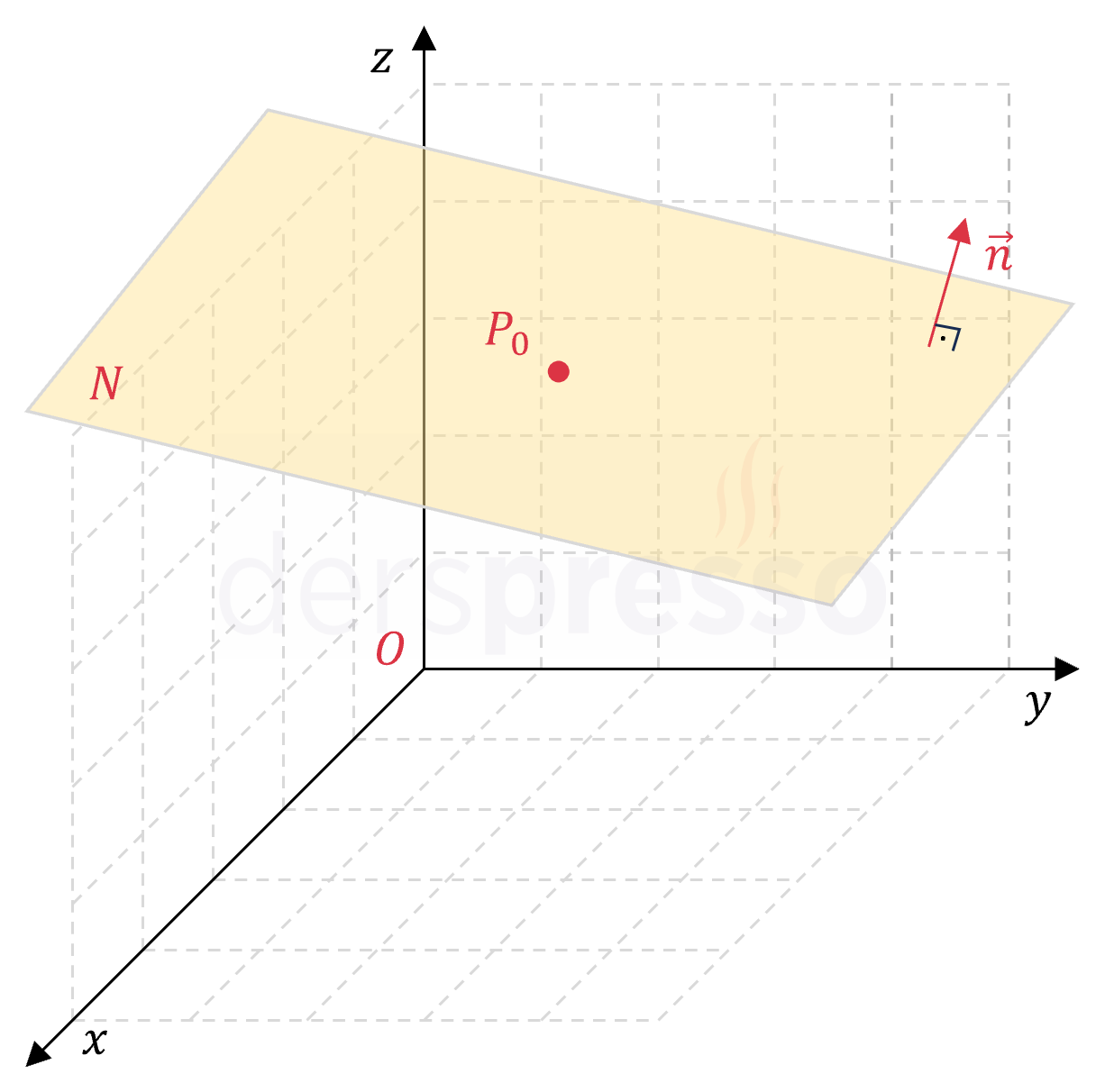
\( P_0(x_0, y_0, z_0) \)
\( \vec{n} = (a, b, c) \)
Bir düzleme dik olan bu \( \vec{n} \) vektörüne normal vektörü denir. Bir düzlemin normal vektörü o düzlem üzerinde bulunan tüm doğrulara diktir.
\( N \) düzlemi üzerindeki herhangi bir noktayı temsil eden bir \( P \) noktası seçelim. \( P_0 \) ve \( P \) noktaları için konum vektörleri sırasıyla \( \vec{r_0} \) ve \( \vec{r} \) olsun.
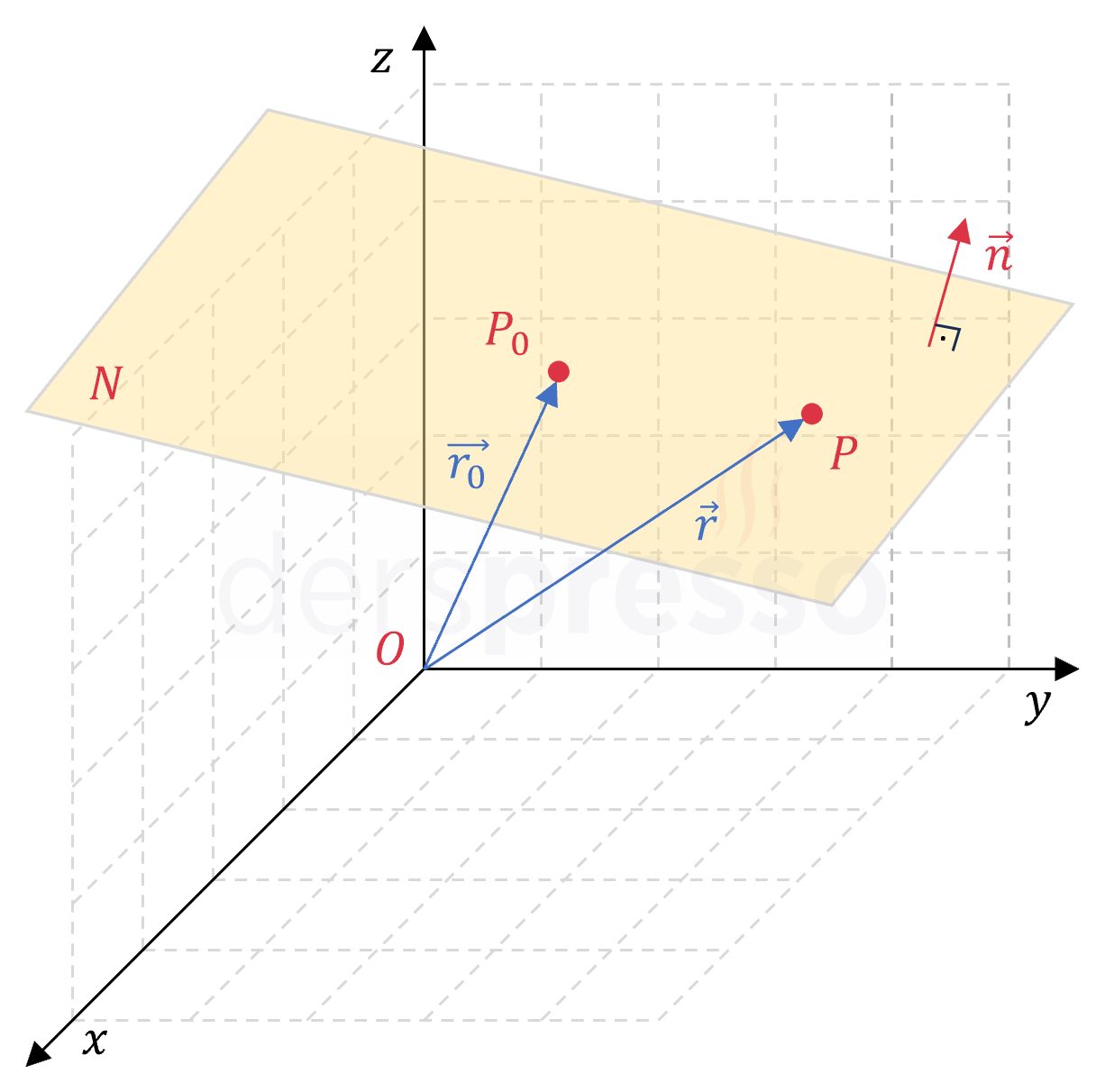
\( P(x, y, z) \)
\( \vec{r_0} = (x_0, y_0, z_0) \)
\( \vec{r} = (x, y, z) \)
\( P \) noktasını \( \vec{r} \) ve \( \vec{r_0} \) vektörlerinin farkı şeklinde yazabiliriz.
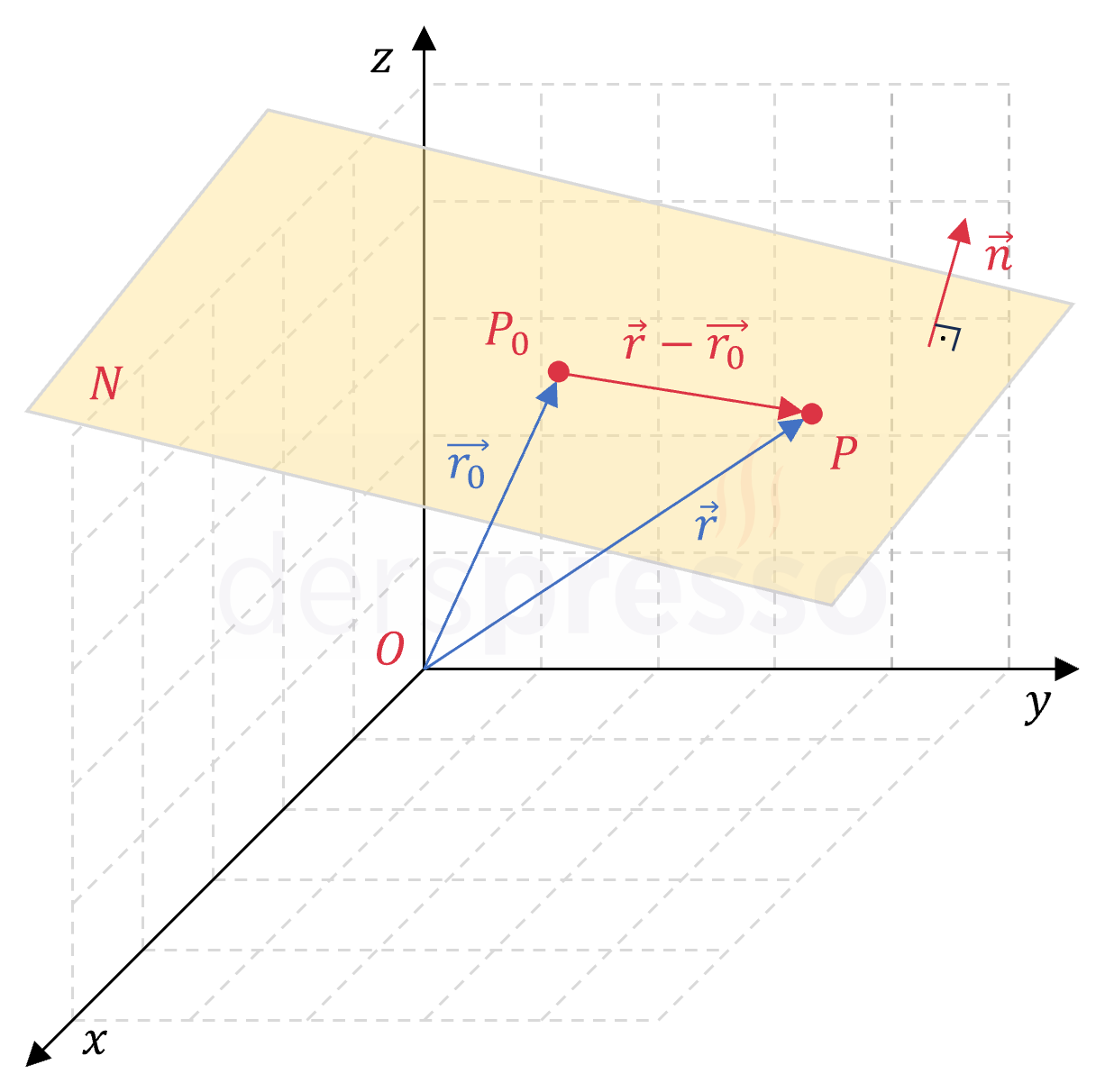
\( \vec{P_0P} = \vec{r} - \vec{r_0} \)
\( \vec{P_0P} \) vektörü \( N \) düzlemi üzerindeki tüm \( P \) noktaları için \( \vec{n} \) vektörüne dik olacağı için, bu iki vektörün nokta çarpımı her zaman sıfıra eşit olur. Bu çarpım aynı zamanda düzlemin vektör denklemini verir.
\( \vec{n} \cdot (\vec{r} - \vec{r_0}) = 0 \)
\( (a, b, c) \cdot (x - x_0, y - y_0, z - z_0) = 0 \)
\( P_0(4, -5, 6) \) noktasından geçen ve \( \vec{n} = (2, -3, 1) \) vektörüne dik olan düzlemin vektör denklemi:
\( (2, -3, 1) \cdot (x - 4, y + 5, z - 6) = 0 \)
Düzlemin vektör denklemindeki nokta çarpım işlemi yapıldığında düzlemin standart denklemi elde edilir.
\( P_0(x_0, y_0, z_0) \) noktasından geçen ve \( \vec{n} = (a, b, c) \) vektörüne dik olan düzlemin standart denklemi:
\( a(x - x_0) + b(y - y_0) + c(z - z_0) = 0 \)
\( P_0(4, -5, 6) \) noktasından geçen ve \( \vec{n} = (2, -3, 1) \) vektörüne dik olan düzlemin standart denklemi:
\( 2(x - 4) - 3(y + 5) + (z - 6) = 0 \)
Düzlemin standart denklemindeki parantezler genişletildiğinde ise düzlemin genel denklemi elde edilir.
\( P_0(x_0, y_0, z_0) \) noktasından geçen ve \( \vec{n} = (a, b, c) \) vektörüne dik olan düzlemin genel denklemi:
\( ax + by + cz + d = 0 \)
\( d = -ax_0 - by_0 - cz_0 \)
\( P_0(4, -5, 6) \) noktasından geçen ve \( \vec{n} = (2, -3, 1) \) vektörüne dik olan düzlemin genel denklemi:
\( d = -2(4) - (-3)(-5) - 1(6) = -29 \)
\( 2x - 3y + z - 29 = 0 \)
\( 4x + y - 4z + 13 = 0 \) düzlemine ait normal vektörü:
\( \vec{n} = (4, 1, -4) \)
İSPATI GÖSTER
Düzlemin standart denklemini yazalım.
\( a(x - x_0) + b(y - y_0) + c(z - z_0) = 0 \)
Parantezleri genişletelim.
\( ax - ax_0 + by - by_0 + cz - cz_0 = 0 \)
Terimleri düzenleyelim.
\( ax + by + cz - ax_0 - by_0 - cz_0 = 0 \)
\( -ax_0 - by_0 - cz_0 \) ifadesi yerine \( d \) değişkeni tanımlayalım.
\( d = -ax_0 - by_0 - cz_0 \) olmak üzere,
\( ax + by + cz + d = 0 \)
Düzlemin Birim Normal Vektörü
Bir düzlemin birim normal vektörü, doğrultusu normal vektör ile aynı ve normu 1 olan vektördür. Birim normal vektör \( \hat{n} \) ile gösterilir.
\( \hat{n} = \dfrac{\vec{n}}{\norm{\vec{n}}} \)
\( \vec{n} = (2, -2, 1) \) normal vektörünün birim normal vektörü:
\( \norm{\vec{n}} = \sqrt{2^2 + (-2)^2 + 1^2} = 3 \)
\( \hat{n} = \dfrac{(2, -2, 1)}{3} \)
\( = (\dfrac{2}{3}, -\dfrac{2}{3}, \dfrac{1}{3}) \)
Düzlemin Normal Formda Denklemi
Düzlem denklemi alternatif olarak düzlemin \( \hat{n} \) birim normal vektörü ve orijine olan dik uzaklığı cinsinden de ifade edilebilir.
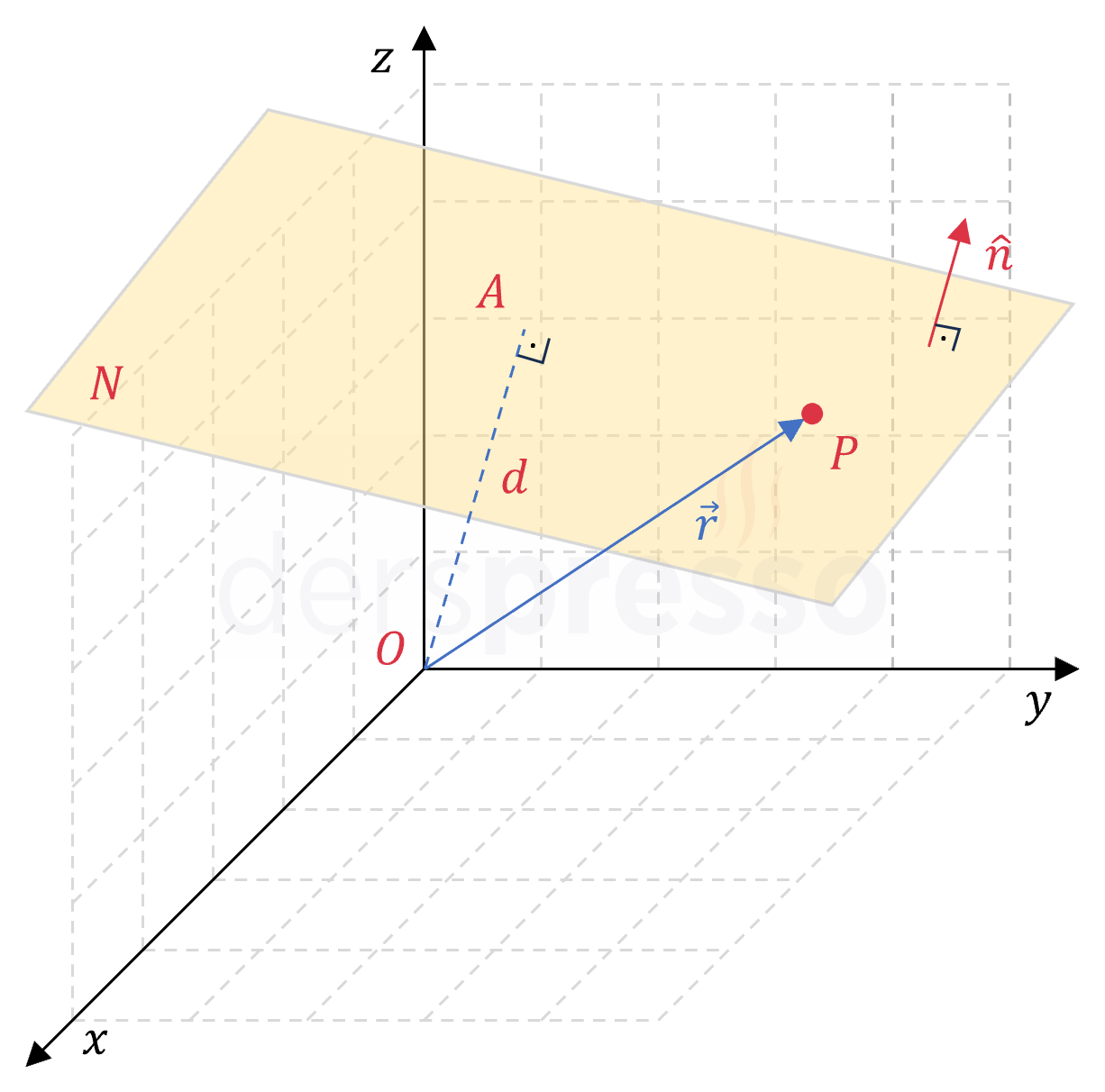
\( \hat{n} \) birim normal vektörüne dik ve orijine uzaklığı \( d \) olan düzlemin normal formdaki denklemi:
\( \vec{r} \cdot \hat{n} = d \)
Normal vektörü \( \vec{n} = (\sqrt{2}, \sqrt{2}, 0) \) ve orijine dik uzaklığı \( d = 5 \) olan düzlemin normal formdaki denklemi:
\( \norm{\vec{n}} = \sqrt{(\sqrt{2})^2 + (\sqrt{2})^2 + 0^2} = 2 \)
\( \hat{n} = \dfrac{1}{2}(\sqrt{2}, \sqrt{2}, 0) \)
\( = (\dfrac{\sqrt{2}}{2}, \dfrac{\sqrt{2}}{2}, 0) \)
\( \vec{r} \cdot (\dfrac{\sqrt{2}}{2}, \dfrac{\sqrt{2}}{2}, 0) = 5 \)
İSPATI GÖSTER
Düzlemin normal formdaki denklemini elde etmek için aşağıdaki tanımlamaları yapalım.
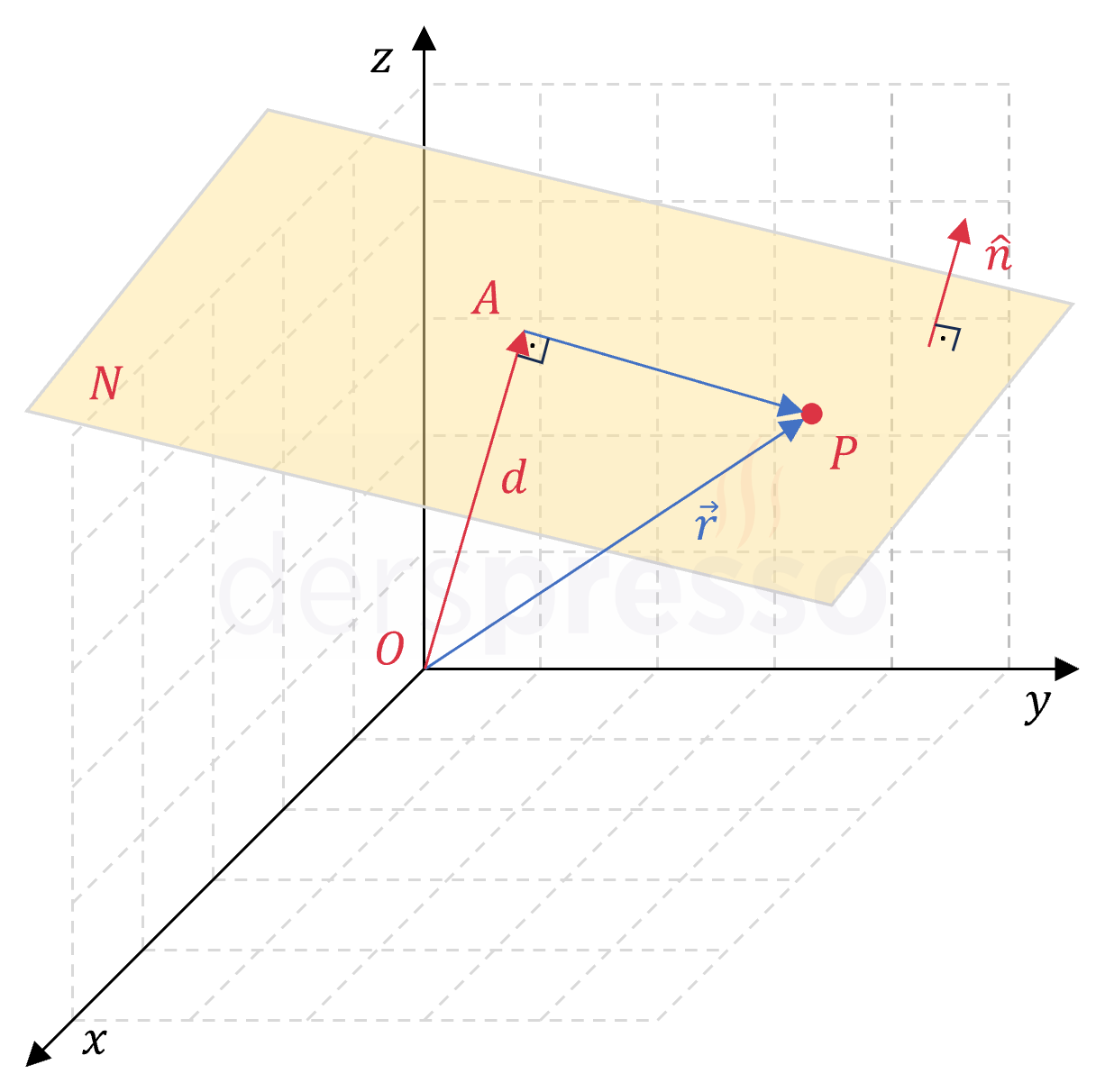
\( \vec{OA} \): Orijinden düzleme dik çizilen vektör
\( d = \abs{OA} \): Düzlemin orijinden dik uzaklığı
\( \hat{n} \): Düzlemin birim normal vektörü
\( P \): Düzlem üzerindeki herhangi bir nokta
\( \vec{r} \): \( P \) noktasına ait konum vektörü
\( \vec{OA} \) vektörü bu vektörün uzunluğu ile aynı doğrultudaki düzlemin birim normal vektörünün çarpımına eşittir.
\( \vec{OA} = d\hat{n} \)
\( \vec{AP} \) ve \( \vec{OA} \) vektörleri birbirine dik olduğu için nokta çarpımları sıfırdır.
\( \vec{AP} \perp \vec{OA} \)
\( \vec{AP} \cdot \vec{OA} = 0 \)
Düzlem üzerindeki herhangi bir noktayı temsil eden \( \vec{r} \) vektörünü iki vektörün toplamı şeklinde yazabiliriz.
\( \vec{r} = \vec{OA} + \vec{AP} \)
\( \vec{AP} = \vec{r} - \vec{OA} \)
Bu ifadeyi nokta çarpım denkleminde yerine koyalım.
\( (\vec{r} - \vec{OA}) \cdot \vec{OA} = 0 \)
\( \vec{OA} = d\hat{n} \) eşitliğini kullanalım.
\( (\vec{r} - d\hat{n}) \cdot d\hat{n} = 0 \)
\( d \gt 0 \) olduğu için sadeleştirebiliriz.
\( (\vec{r} - d\hat{n}) \cdot \hat{n} = 0 \)
Nokta çarpımının dağılma özelliği vardır.
\( \vec{r} \cdot \hat{n} - d\hat{n} \cdot \hat{n} = 0 \)
\( \vec{r} \cdot \hat{n} - d\norm{\hat{n}}^2 = 0 \)
\( \hat{n} \) birim vektördür.
\( \norm{\hat{n}} = 1 \)
\( \vec{r} \cdot \hat{n} = d \)
Eksenleri Kestiği Noktalar Bilinen Düzlem Denklemi
Orijinden geçmeyen ve herhangi bir eksene paralel olmayan, dolayısıyla üç ekseni de kesen bir düzlemin denklemi eksenleri kestiği noktaların koordinatları cinsinden aşağıdaki şekilde ifade edilebilir.
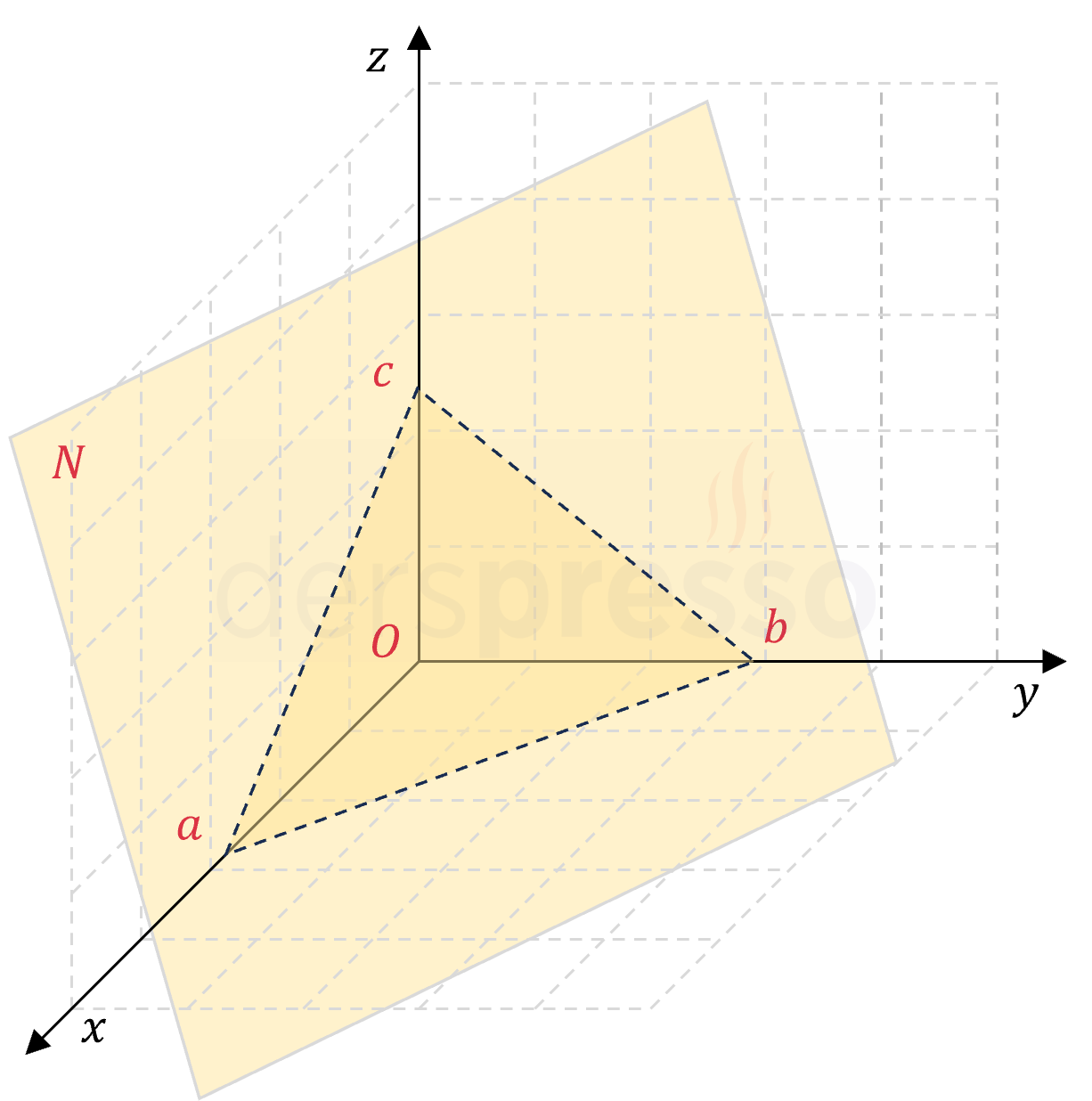
\( A(a, 0, 0) \), \( B(0, b, 0) \) ve \( C(0, 0, c) \) düzlemin eksenleri kestiği noktalar olmak üzere:
\( \dfrac{x}{a} + \dfrac{y}{b} + \dfrac{z}{c} = 1 \)
Eksenleri \( A(16, 0, 0) \), \( B(0, 2, 0) \) ve \( C(0, 0, -8) \) noktalarında kesen düzlemin denklemi:
\( \dfrac{x}{16} + \dfrac{y}{2} + \dfrac{z}{-6} = 1 \)
İSPATI GÖSTER
Düzlemin genel denklemini yazalım.
\( Ax + By + Cz + D = 0 \)
Düzlemin eksenleri kestiği noktalar sırasıyla \( K, L, M \) olsun.
\( K(a, 0, 0), L(0, b, 0), M(0, 0, c) \)
Bu noktaların koordinatlarını sırayla düzlem denkleminde yerine koyalım.
\( K \) noktası:
\( A(a) + B(0) + C(0) + D = 0 \)
\( A = -\dfrac{D}{a} \)
\( L \) noktası:
\( A(0) + B(b) + C(0) + D = 0 \)
\( B = -\dfrac{D}{b} \)
\( M \) noktası:
\( A(0) + B(0) + C(c) + D = 0 \)
\( C = -\dfrac{D}{c} \)
Bu değerleri düzlemin genel denkleminde yerine koyalım.
\( Ax + By + Cz + D = 0 \)
\( -\dfrac{D}{a}x + (-\dfrac{D}{b}y) + (-\dfrac{D}{c}z) + D = 0 \)
Eşitliğin taraflarını \( D \)'ye bölelim.
\( -\dfrac{x}{a} - \dfrac{y}{b} - \dfrac{z}{c} + 1 = 0 \)
İfadeyi düzenleyelim.
\( \dfrac{x}{a} + \dfrac{y}{b} + \dfrac{z}{c} = 1 \)
3 Noktası Bilinen Düzlemin Denklemi
Doğrusal olmayan üç noktası bilinen düzlemin denklemi aşağıdaki yöntemle bulunabilir.
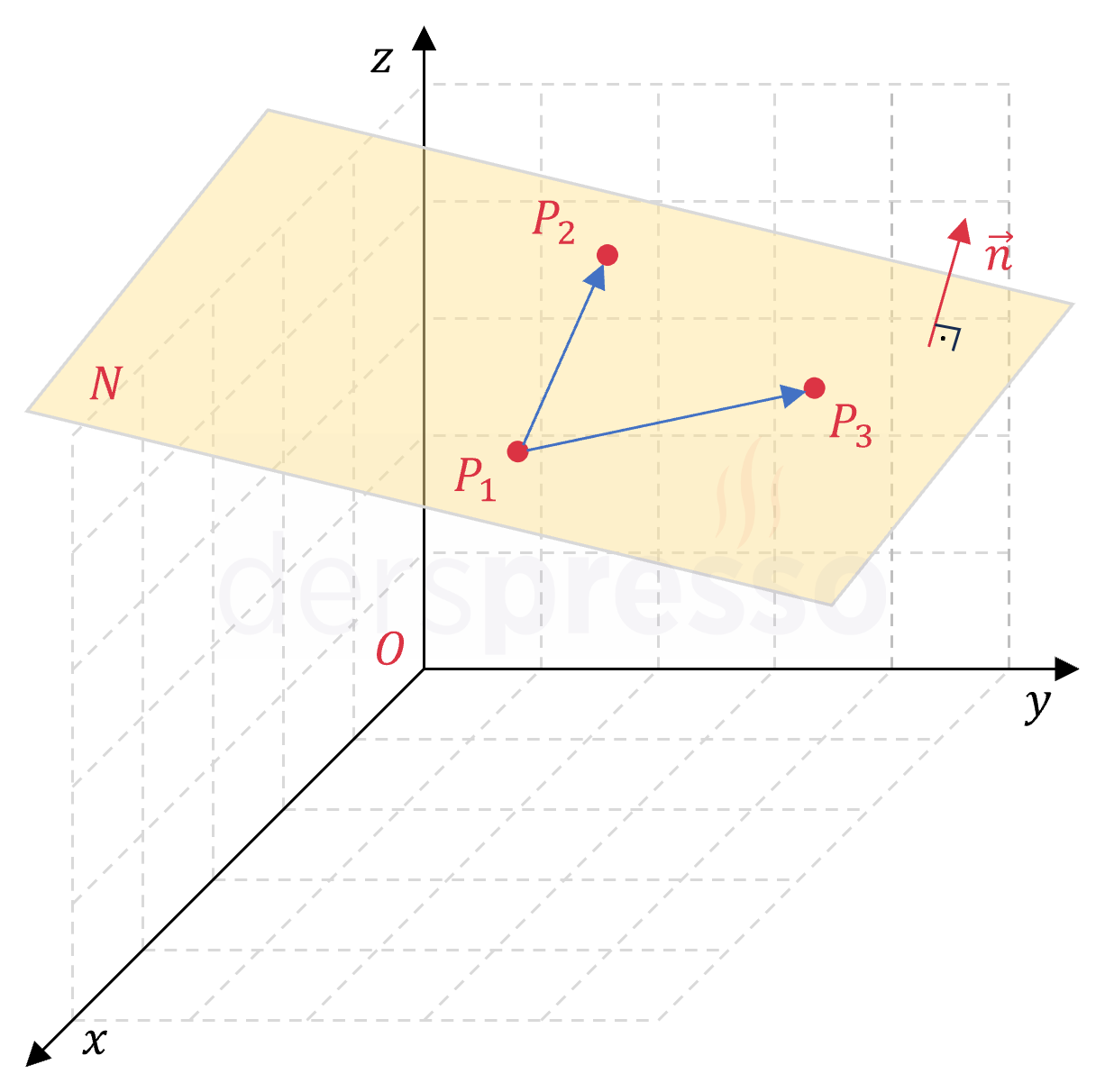
- 3 nokta arasındaki herhangi iki vektör bulunur (örneğin \( \vec{P_1P_2} \) ve \( \vec{P_1P_3} \)).
- Aynı düzlemde bulunan bu iki vektörün vektörel çarpımı düzleme dik olacağı için düzlemin normal vektörü olur (\( \vec{n} = \vec{P_1P_2} \times \vec{P_1P_3} \)).
- 3 noktadan herhangi biri ve normal vektörü kullanılarak düzlemin denklemi bulunur.
\( P_1(-1, 2, -2) \), \( P_2(2, 3, -4) \) ve \( P_3(0, 4, 0) \) noktalarından geçen düzlemin denklemini bulalım.
\( \vec{P_1P_2} \) ve \( \vec{P_1P_3} \) vektörlerini bulalım.
\( \vec{P_1P_2} = (2 - (-1), 3 - 2, -4 - (-2)) \)
\( = (3, 1, -2) \)
\( \vec{P_1P_3} = (0 - (-1), 4 - 2, 0 - (-2)) \)
\( = (-1, 2, 2) \)
\( \vec{P_1P_2} \) ve \( \vec{P_1P_3} \) vektörlerinin vektörel çarpımı düzlemin normal vektörünü verir.
\( \vec{n} = \vec{P_1P_2} \times \vec{P_1P_3} \)
\( = (3, 1, -2) \times (-1, 2, 2) \)
\( = (1(2) - 2(-2), (-1)(-2) - 3(2), 3(2) - (-1)1) \)
\( = (6, -4, 7) \)
\( P_1 \) noktasından geçen ve \( \vec{n} \) vektörüne dik olan düzlemin denklemi:
\( 6(x + 1) - 4(y - 2) + 7(z + 2) = 0 \)
Koordinat Düzlemleri
\( xy \), \( xz \) ve \( yz \) koordinat düzlemlerinin denklemleri aşağıdaki gibidir.
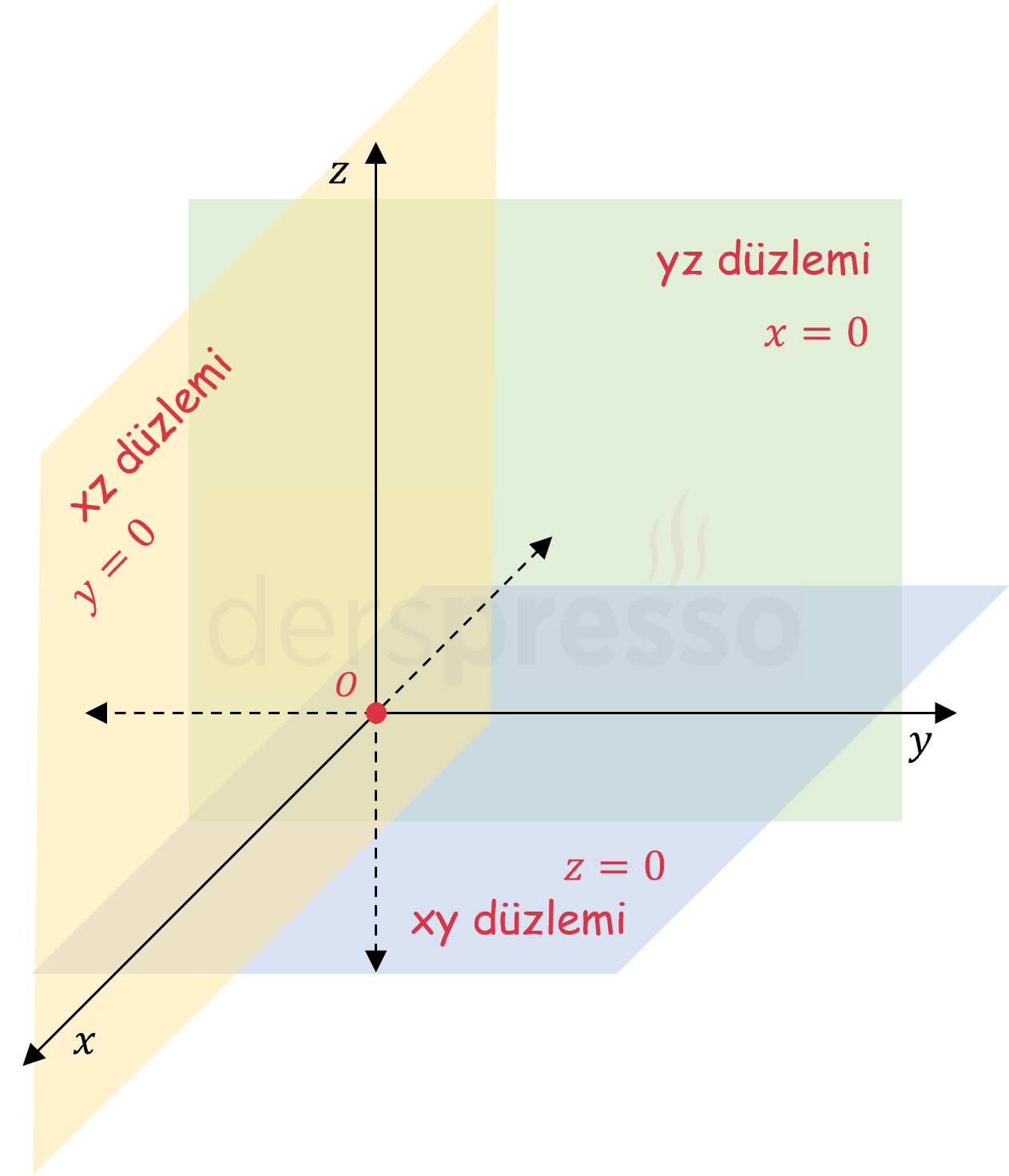
\( xy \) düzlemi:
\( z = 0 \)
\( xz \) düzlemi:
\( y = 0 \)
\( yz \) düzlemi:
\( x = 0 \)
Bir Düzlemin Koordinat Düzlemleri ile Kesişimi
Bir düzlem paralel olmadığı bir koordinat düzlemini bir doğru boyunca keser. Aşağıdaki şekilde \( N \) düzleminin sırasıyla \( xy \), \( xz \) ve \( yz \) düzlemleri ile kesişimi olan \( d_1 \), \( d_2 \) ve \( d_3 \) doğruları gösterilmiştir.
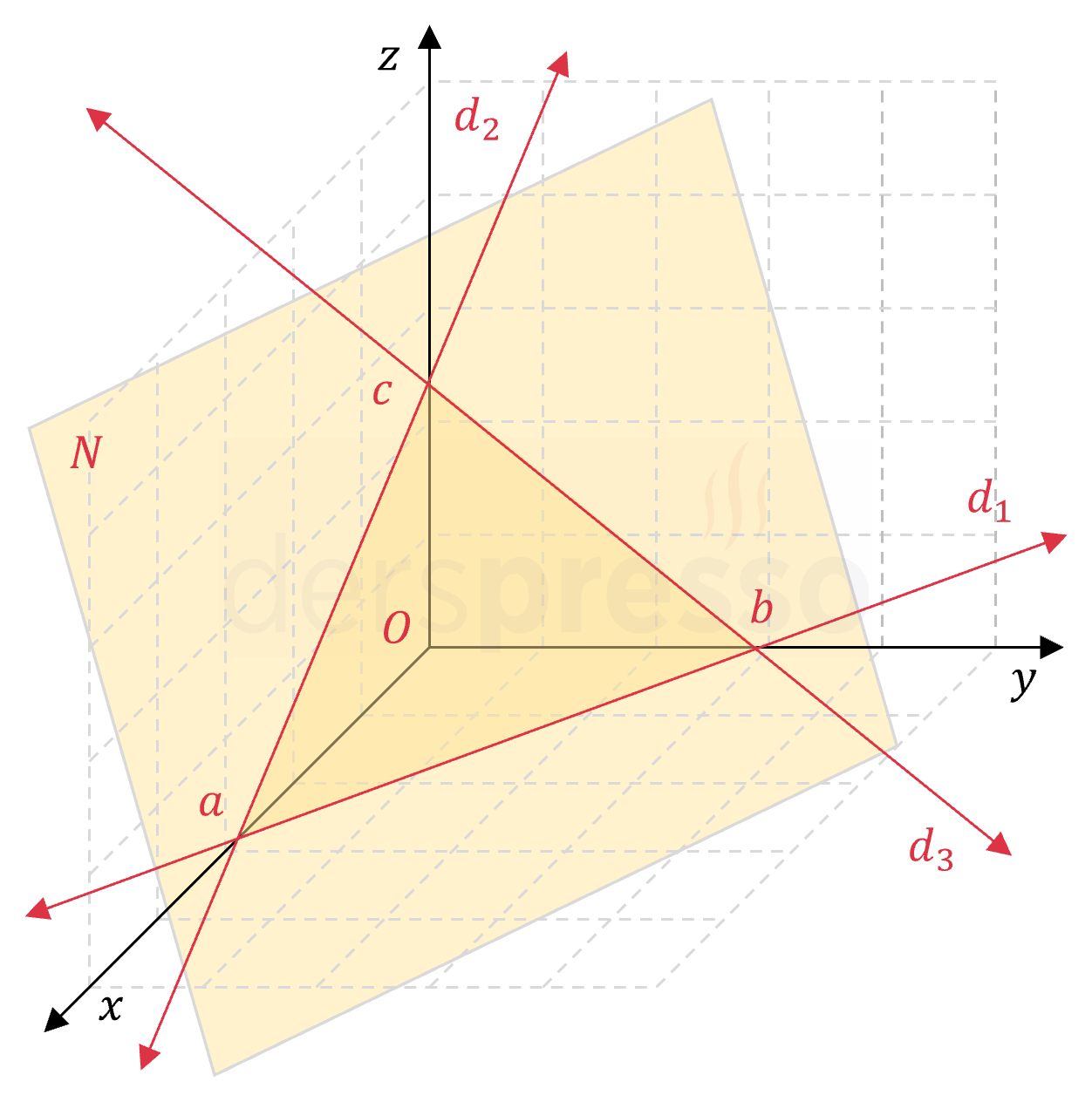
Bir düzlemin \( xy \) koordinat düzlemi ile kesişiminin oluşturduğu doğrunun denklemini bulmak için düzlem denkleminde \( z = 0 \) yazılır. Düzlemin diğer koordinat düzlemleri ile kesişimi de benzer şekilde bulunur.
\( N: 2x + 3y - 4z = 12 \) düzleminin her bir koordinat düzlemi ile kesişiminin oluşturduğu doğru denklemleri:
\( xy \) düzlemi ile kesişim:
\( 2x + 3y = 12, \quad z = 0 \)
\( xz \) düzlemi ile kesişim:
\( 2x - 4z = 12, \quad y = 0 \)
\( yz \) düzlemi ile kesişim:
\( 3y - 4z = 12, \quad x = 0 \)
Bir Düzlemin Koordinat Eksenleri ile Kesişimi
Bir düzlem paralel olmadığı bir koordinat eksenini tek bir noktada keser. Aşağıdaki şekilde \( N \) düzleminin sırasıyla \( x \), \( y \) ve \( z \) eksenleri ile kesişimi olan \( A \), \( B \) ve \( C \) noktaları gösterilmiştir.
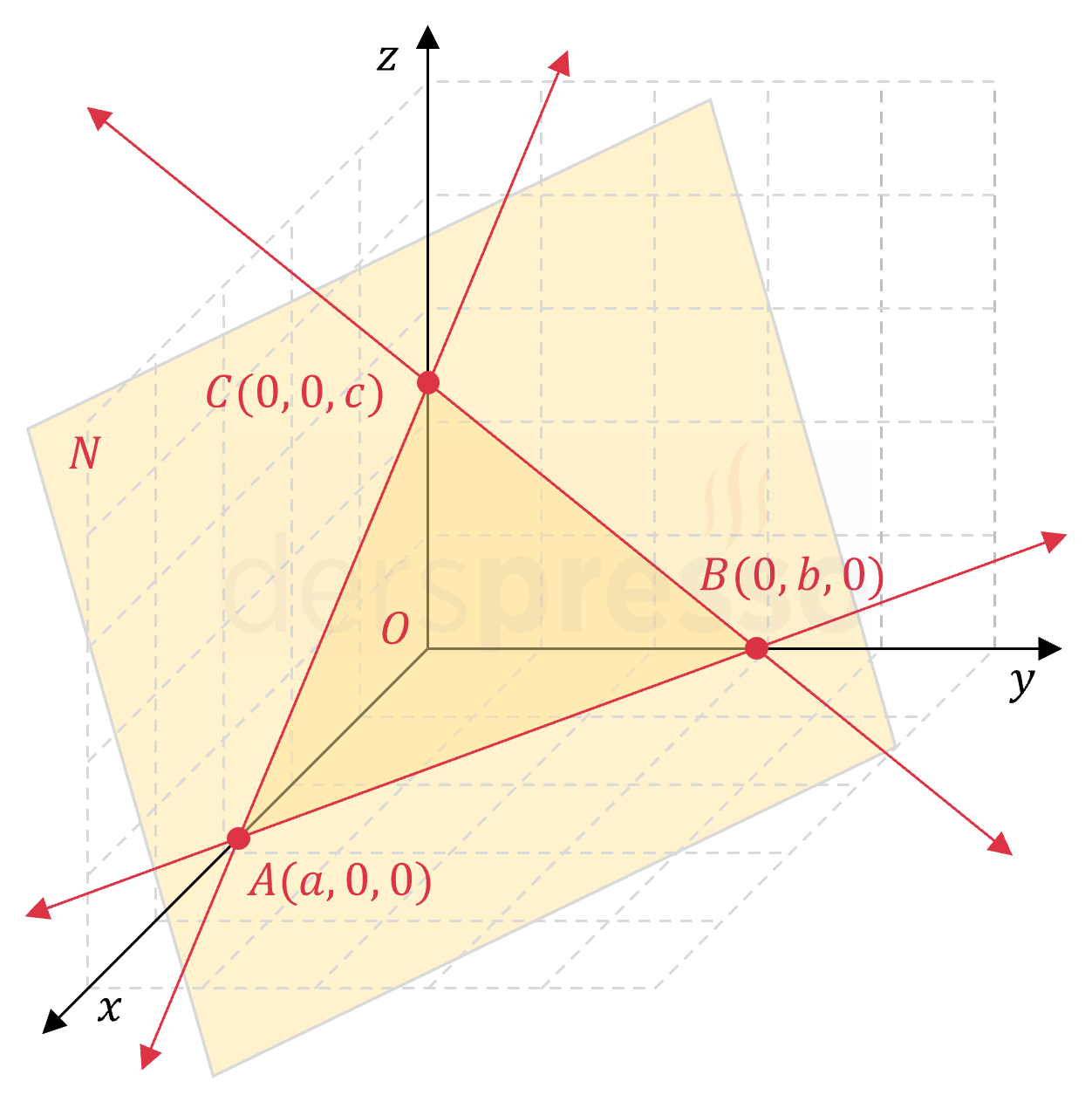
Bir düzlemin \( x \) koordinat ekseni ile kesişimi olan noktayı bulmak için düzlem denkleminde \( y = z = 0 \) yazılır. Düzlemin diğer koordinat eksenleri ile kesişimi de benzer şekilde bulunur.
\( N: 2x + 3y - 4z = 12 \) düzleminin her bir koordinat ekseni ile kesişimi olan noktalar:
\( x \) ekseni ile kesişim:
\( y = z = 0, \quad x = 6 \)
\( A(6, 0, 0) \)
\( y \) ekseni ile kesişim:
\( x = z = 0, \quad y = 4 \)
\( B(0, 4, 0) \)
\( z \) ekseni ile kesişim:
\( x = y = 0, \quad z = -3 \)
\( C(0, 0, -3) \)
Noktanın Düzleme Göre Konumu
Uzayda bir noktanın bir düzleme göre konumu üç şekilde olabilir.
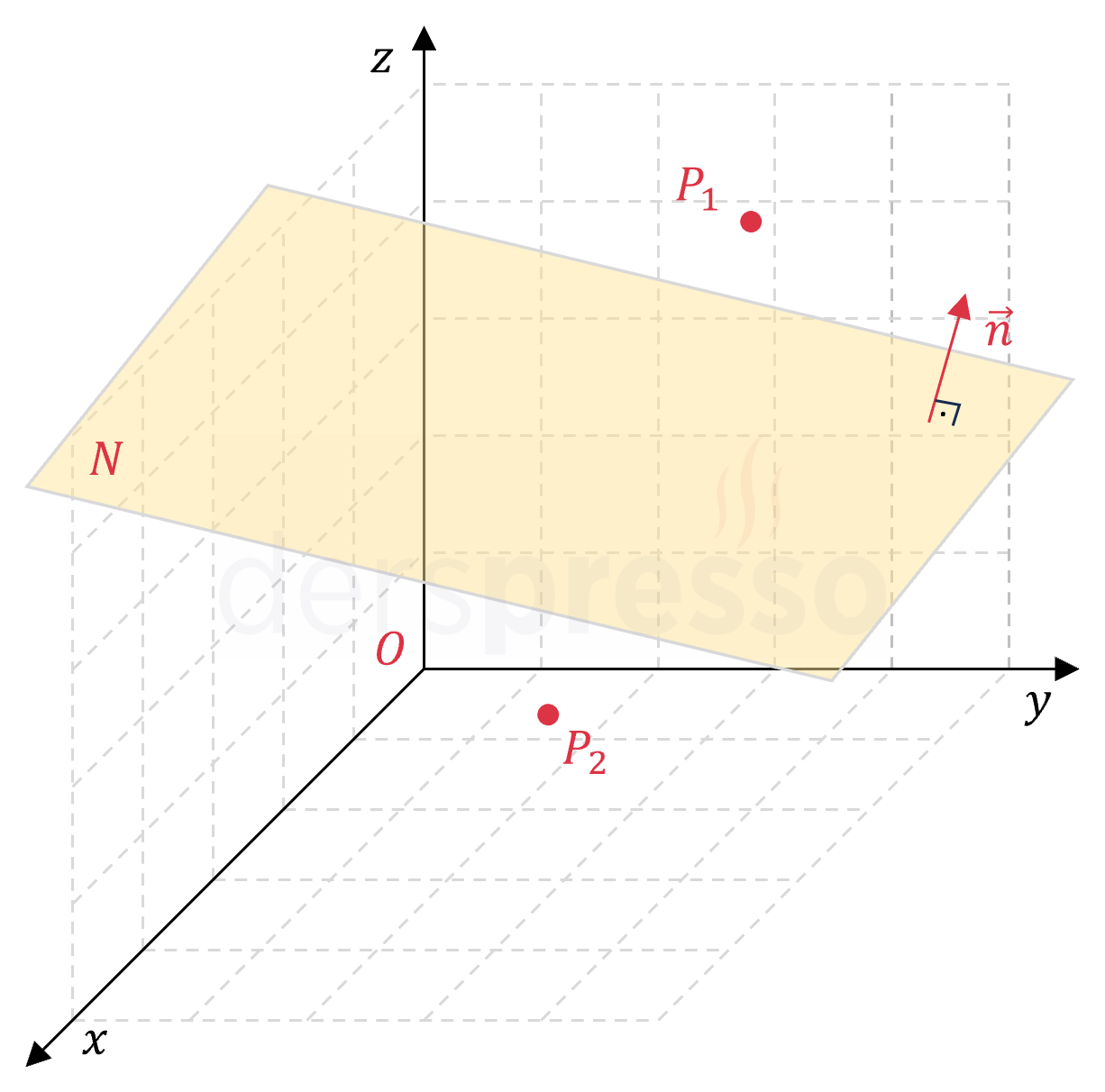
\( P_1(x_1, y_1, z_1) \) noktasının \( ax + by + cz + d = 0 \) düzlemine göre konumu üç şekilde olabilir.
- \( ax_1 + by_1 + cz_1 + d \gt 0 \) ise \( P_1 \) noktası düzleme göre normal vektörünün yönündeki taraftadır.
- \( ax_1 + by_1 + cz_1 + d = 0 \) ise \( P_1 \) noktası düzlemin üzerinde bir noktadır.
- \( ax_1 + by_1 + cz_1 + d \lt 0 \) ise \( P_1 \) noktası düzleme göre normal vektörünün ters yönündeki taraftadır.
\( P_1(1, 2, 2) \) noktasının \( 3x - y + 4z - 12 = 0 \) düzlemine göre konumu:
Noktanın koordinatlarını düzlem denkleminde yerine koyalım.
\( 3(1) - 2 + 4(2) - 12 = -3 \lt 0 \)
Buna göre \( P_1 \) noktası düzleme göre normal vektörünün ters yönündeki taraftadır.
Orijin noktasının \( 2x + 4y - 3z + 3 = 0 \) düzlemine göre konumu:
Noktanın koordinatlarını düzlem denkleminde yerine koyalım.
\( 2(0) + 4(0) - 3(0) + 3 = 3 \gt 0 \)
Buna göre orijin noktası düzleme göre normal vektörünün yönündeki taraftadır.
İSPATI GÖSTER
\( N \) denklemi \( ax + by + cz + d = 0 \) olan bir düzlem ve \( P_1(x_1, y_1, z_1) \) uzayda bir noktadır.
\( N \) düzleminin normal vektörü \( \vec{n} = (a, b, c) \) olur.
\( P(x, y, z) \) noktası \( N \) düzlemi üzerinde herhangi bir nokta olsun.
\( P \) noktasından \( P_1 \) noktasına \( \vec{PP_1} \) vektörü tanımlayalım.
\( \vec{PP_1} = (x_1 - x, y_1 - y, z_1 - z) \)
\( P_1 \) noktası \( N \) düzlemine göre normal vektörünün yönündeki tarafta ise \( \vec{PP_1} \) vektörü ile \( \vec{n} \) normal vektörünün arasındaki açı dar açı olur, dolayısıyla iki vektörün nokta çarpımı pozitif olur.
\( \vec{n} \cdot \vec{PP_1} \gt 0 \)
\( (a, b, c) \cdot (x_1 - x, y_1 - y, z_1 - z) \gt 0 \)
\( a(x_1 - x) + b(y_1 - y) + c(z_1 - z) \gt 0 \)
\( ax_1 - ax + by_1 - by + cz_1 - cz \gt 0 \)
\( ax_1 + by_1 + cz_1 - (ax + by + cz) \gt 0 \)
Parantez içindeki ifade düzlem denklemine göre \( -d \) değerine eşittir.
\( ax_1 + by_1 + cz_1 + d \gt 0 \)
Benzer şekilde, \( P_1 \) noktası \( N \) düzlemine göre normal vektörünün ters yönündeki tarafta ise \( \vec{PP_1} \) vektörü ile \( \vec{n} \) normal vektörünün arasındaki açı geniş açı olur, dolayısıyla iki vektörün nokta çarpımı negatif olur.
\( ax_1 + by_1 + cz_1 + d \lt 0 \)
Bunun bir uygulaması olarak iki noktanın bir düzleme göre konumu iki şekilde olabilir.
\( P_1 \) nokta ve \( P_2 \) noktalarının \( ax + by + cz + d = 0 \) düzlemine göre konumu iki şekilde olabilir.
Noktaların koordinatları \( ax + by + cz + d \) ifadesinde yerine konduğunda elde edilen değerlerin;
- İşaretleri aynı ise iki nokta düzlemin aynı tarafındadır.
- İşaretleri farklı ise iki nokta düzlemin farklı taraflarındadır.
\( P_1(4, 2, 2) \) ve \( P_2(2, -2, 3) \) noktalarının \( 2x - 3y + z - 12 = 0 \) düzlemine göre konumu:
\( P_1 \) noktasının koordinatlarını düzlem denkleminde yerine koyalım.
\( 2(4) - 3(2) + 2 - 6 = -2 \lt 0 \)
\( P_2 \) noktasının koordinatlarını düzlem denkleminde yerine koyalım.
\( 2(2) - 3(-2) + (-3) - 6 = 1 \gt 0 \)
Buna göre \( P_1 \) ve \( P_2 \) noktaları düzlemin farklı taraflarındadır.