İki Çemberin Birbirine Göre Durumu
Bu bölümde iki çemberin birbirine göre farklı kesişim ve teğet durumlarını inceleyeceğiz.
İki Çemberin Kesişimi
Aynı düzlemde bulunan iki çemberin birbiriyle kesişimi üç farklı şekilde olabilir.
- Çemberler iki noktada kesişebilir.
- Çemberler içten ya da dıştan tek bir noktada kesişebilir. Tek bir noktada kesişen çemberlere teğet çemberler denir.
- Çemberler ayrık ya da iç içe olup kesişmeyebilir.

Merkezleri aynı olan çemberlere eş merkezli çemberler denir.

Merkez Doğrusu
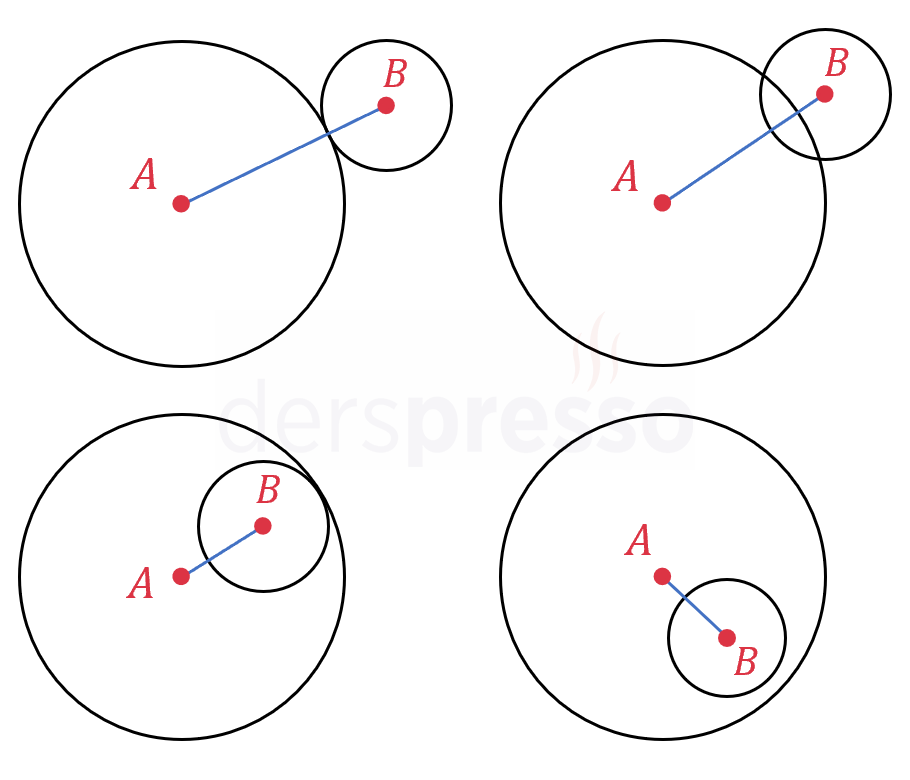
Eş merkezli olmayan iki çemberin merkez noktalarını birleştiren doğru parçasına merkez doğrusu denir. Aşağıdaki şekildeki \( [AB] \) doğru parçası verilen iki çembere ait merkez doğrusudur.

Birbirine göre durumları farklı diğer bazı çember ikililerinin merkez doğruları aşağıdaki şekilde verilmiştir.
Teğet Çemberler
Birbirini tek bir noktada kesen çemberlere teğet çemberler denir.
Aşağıdaki şekildeki gibi biri diğerinin içinde olmayan teğet çemberlere dıştan teğet çember denir.

Aşağıdaki şekildeki gibi biri diğerinin içinde olan teğet çemberlere içten teğet çember denir.

Birbirine içten ya da dıştan teğet olan iki çemberin merkezlerini birleştiren doğru, çemberlerin teğet noktasından geçer.
Ortak Teğetler
İki (ya da daha fazla) çembere teğet olan doğruya bu çemberlerin ortak teğeti denir.
İki çemberin ortak teğeti çemberlerin merkez doğrusunu kesiyorsa bu teğete ortak iç teğet denir, kesmiyorsa ortak dış teğet denir.
Aşağıdaki şekildeki ortak teğet doğruları \( [AB] \) merkez doğrusunu kesmediği için birer ortak dış teğettir.
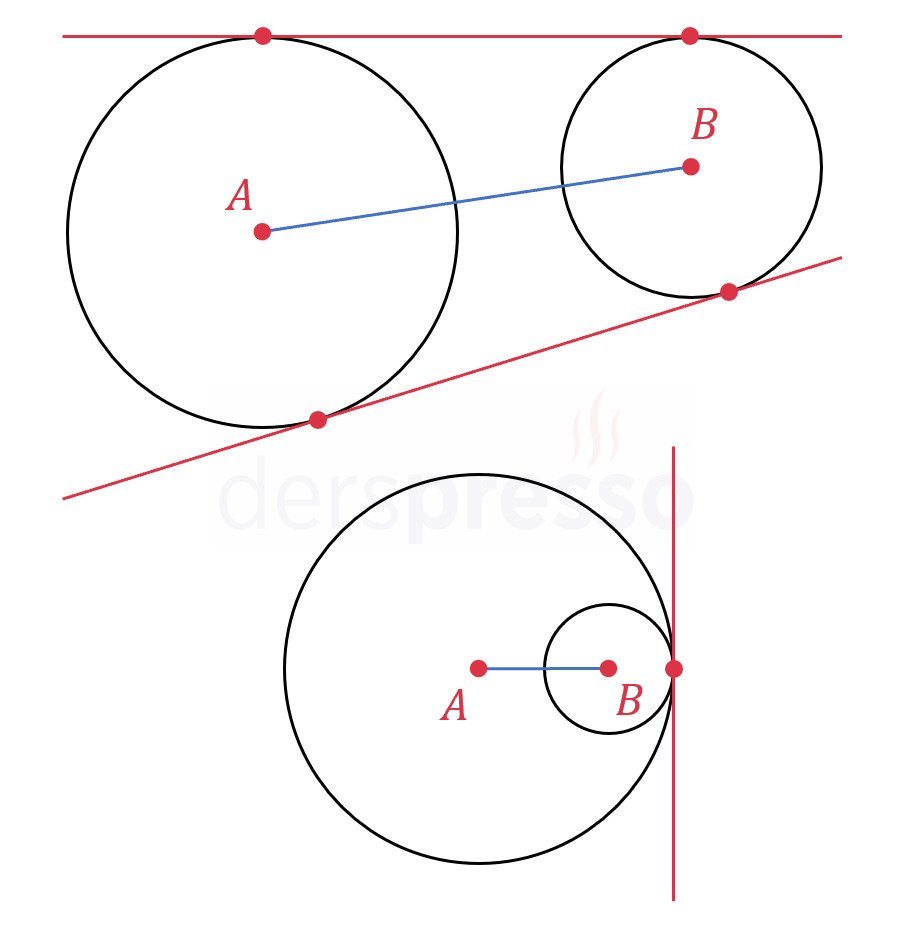
Aşağıdaki şekildeki ortak teğet doğruları \( [AB] \) merkez doğrusunu kestiği için birer ortak iç teğettir.
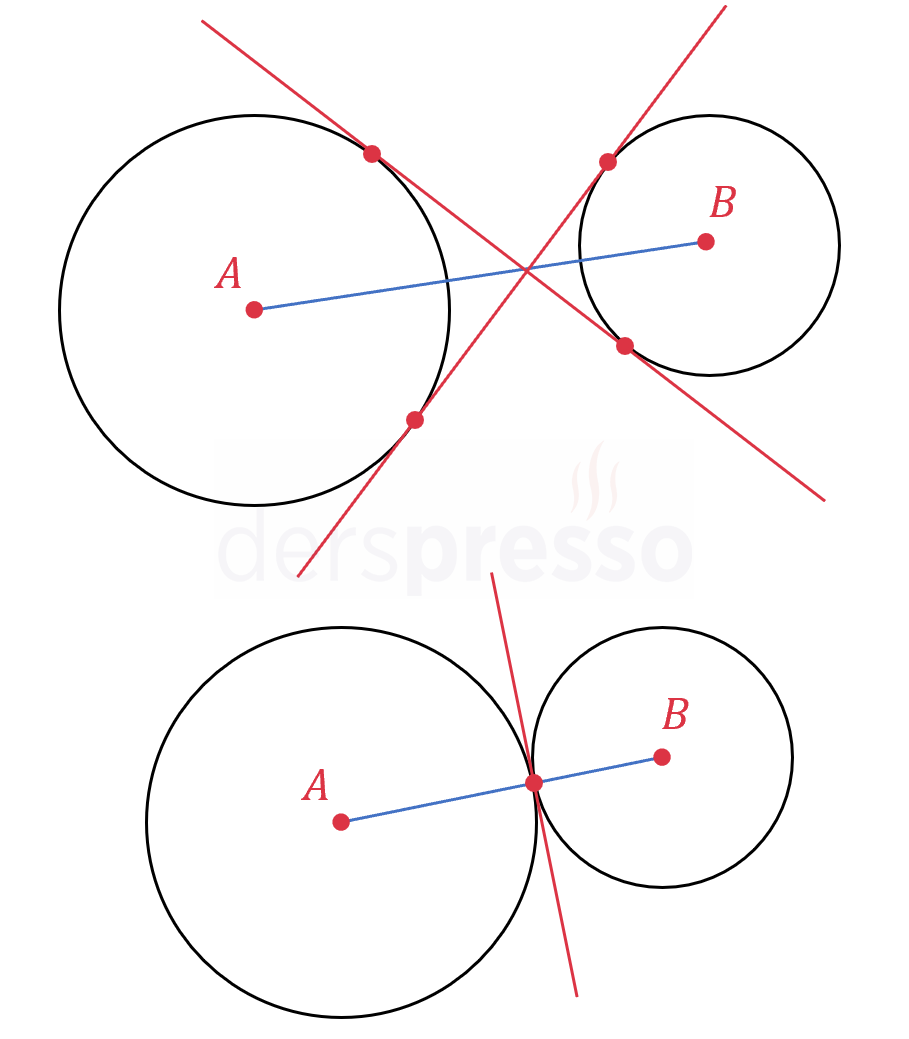
İki çemberin ortak dış teğetlerinin teğet noktaları arasında kalan uzunlukları birbirine eşittir ve bu uzunluk aşağıdaki formülle hesaplanır.
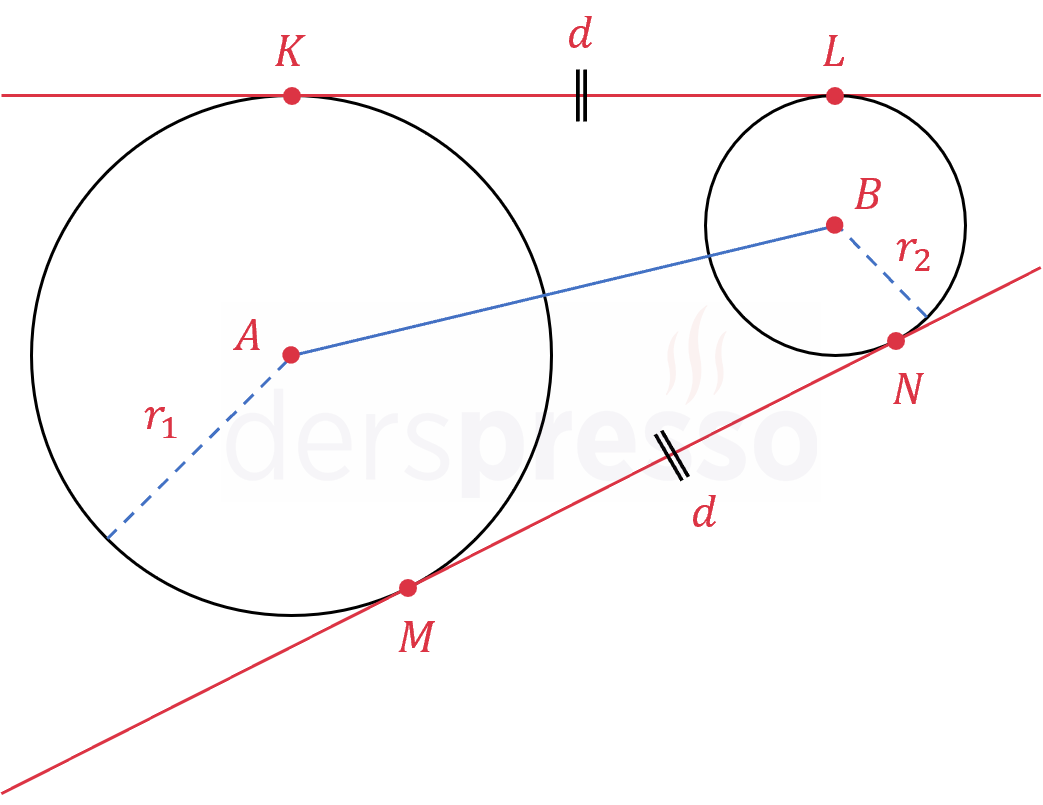
\( r_1, r_2 \) çemberlerin yarıçapları olmak üzere,
\( \abs{KL} = \abs{MN} = d \)
\( \abs{AB}^2 = d^2 + (r_1 - r_2)^2 \)
İSPATI GÖSTER
\( \abs{KL} = d \) diyelim
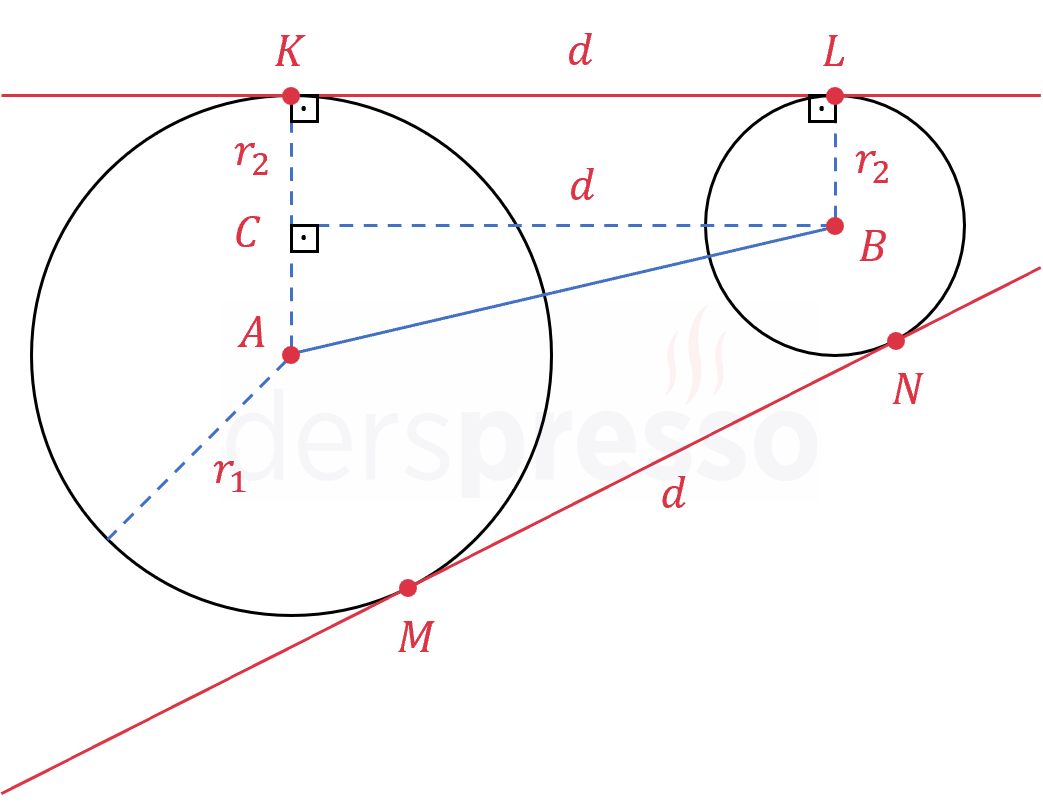
İki çemberin merkezinden \( K \) ve \( L \) teğet noktalarına birer yarıçap çizelim.
\( \abs{AK} = r_1, \quad \abs{BL} = r_2 \)
Çemberin merkezinden teğet noktasına çizilen yarıçap teğeti dik keser.
\( [AK] \perp [KL], \quad [BL] \perp [KL] \)
\( B \) noktasından \( [AK] \) doğru parçasına bir dik indirelim.
\( [CB] \perp [AK] \)
Oluşan \( CKLB \) dörtgeni bir dikdörtgen, \( ACB \) üçgeni bir dik üçgen olur.
\( \abs{CB} = \abs{KL} = d \)
\( \abs{CK} = r_2 \)
\( \abs{AC} = r_1 - r_2 \)
\( ACB \) dik üçgeninde Pisagor teoremini uyguladığımızda ortak teğet uzunluğunu bulabileceğimiz denklemi elde ederiz.
\( \abs{AB}^2 = d^2 + (r_1 - r_2)^2 \)
Aynı yöntemi diğer ortak teğete uyguladığımızda aynı formülü elde ederiz, dolayısıyla her iki ortak teğetin uzunlukları birbirine eşittir.
İki çemberin ortak iç teğetlerinin teğet noktaları arasında kalan uzunlukları birbirine eşittir ve bu uzunluk aşağıdaki formülle hesaplanır.
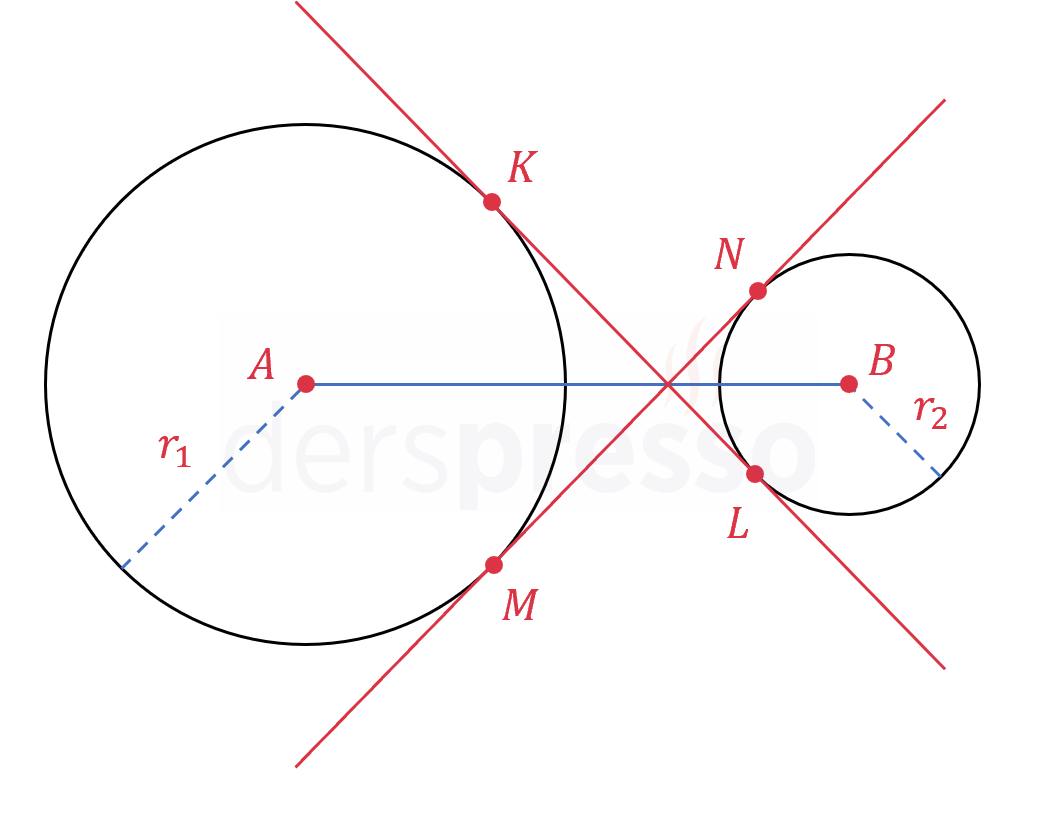
\( r_1, r_2 \) çemberlerin yarıçapları olmak üzere,
\( \abs{KL} = \abs{MN} = d \)
\( \abs{AB}^2 = d^2 + (r_1 + r_2)^2 \)
İSPATI GÖSTER
\( \abs{KL} = d \) diyelim
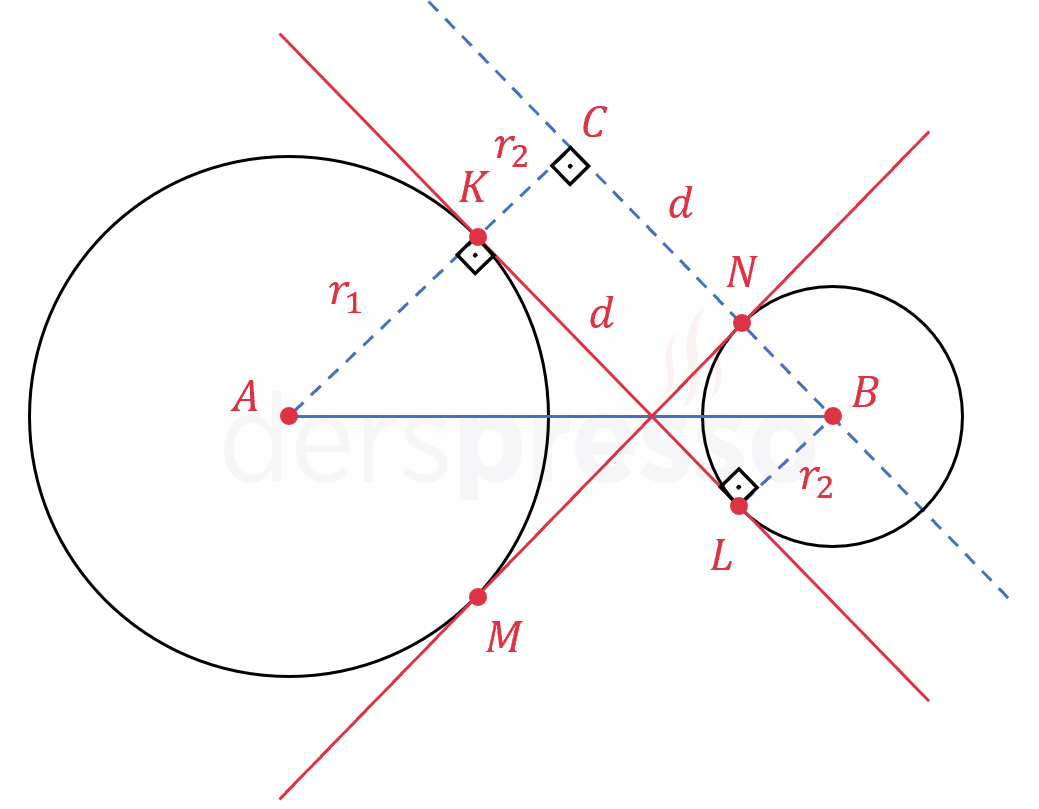
İki çemberin merkezinden \( K \) ve \( L \) teğet noktalarına birer yarıçap çizelim.
\( \abs{AK} = r_1, \quad \abs{BL} = r_2 \)
Çemberin merkezinden teğet noktasına çizilen yarıçap teğeti dik keser.
\( [AK] \perp [KL], \quad [BL] \perp [KL] \)
\( B \) noktasından \( [AK] \) doğru parçasının uzantısına bir dik indirelim.
\( [CB] \perp [AC] \)
Oluşan \( CKLB \) dörtgeni bir dikdörtgen, \( ACB \) üçgeni bir dik üçgen olur.
\( \abs{CB} = \abs{KL} = d \)
\( \abs{CK} = r_2 \)
\( \abs{AC} = r_1 + r_2 \)
\( ACB \) dik üçgeninde Pisagor teoremini uyguladığımızda ortak teğet uzunluğunu bulabileceğimiz denklemi elde ederiz.
\( \abs{AB}^2 = d^2 + (r_1 + r_2)^2 \)
Aynı yöntemi diğer ortak teğete uyguladığımızda aynı formülü elde ederiz, dolayısıyla her iki ortak teğetin uzunlukları birbirine eşittir.
Yarıçapları \( r_1 \) ve \( r_2 \) olan iki çemberin ortak teğetlerinin sayısı çemberlerin yarıçap uzunluklarına ve merkez noktaları arasındaki uzaklığa göre değişiklik gösterir.
| Şekil | Açıklama |
|---|---|
|
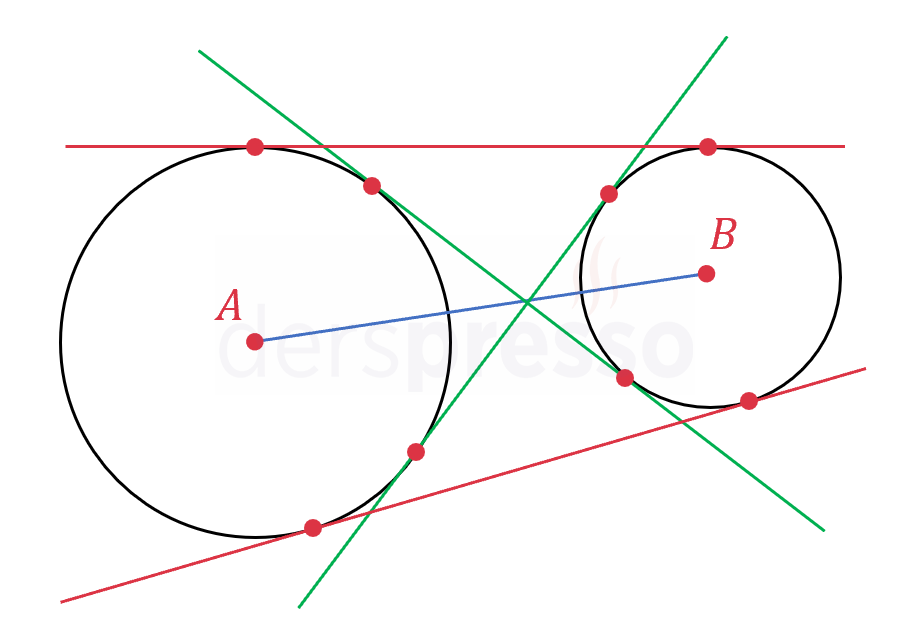
İki ayrık (kesişmeyen ve iç içe olmayan) çember: \( \abs{AB} \gt r_1 + r_2 \) İki dış (kırmızı), iki iç (yeşil) olmak üzere dört ortak teğet |
|
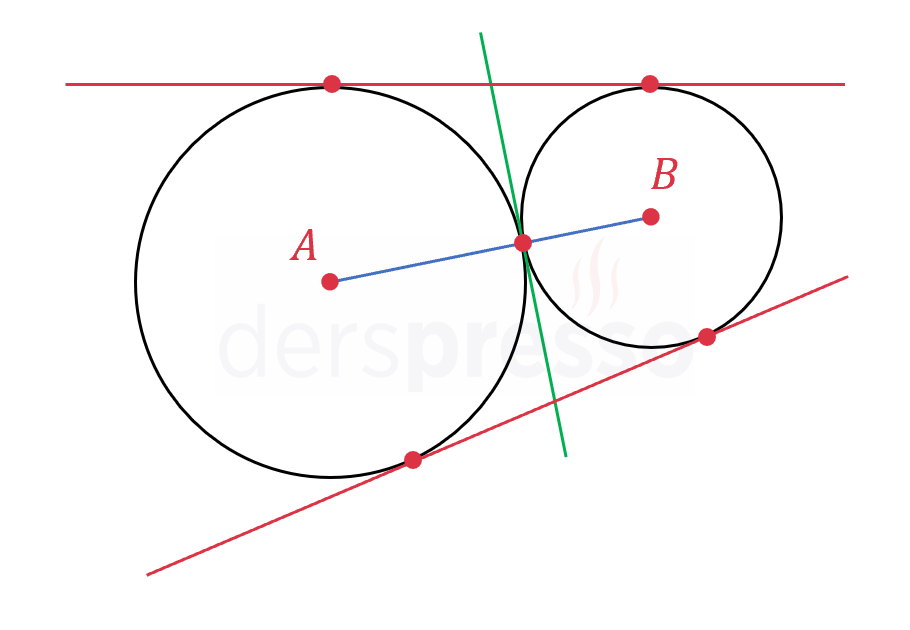
Dıştan teğet iki çember: \( \abs{AB} = r_1 + r_2 \) İki dış (kırmızı), bir iç (yeşil) olmak üzere üç ortak teğet |
|
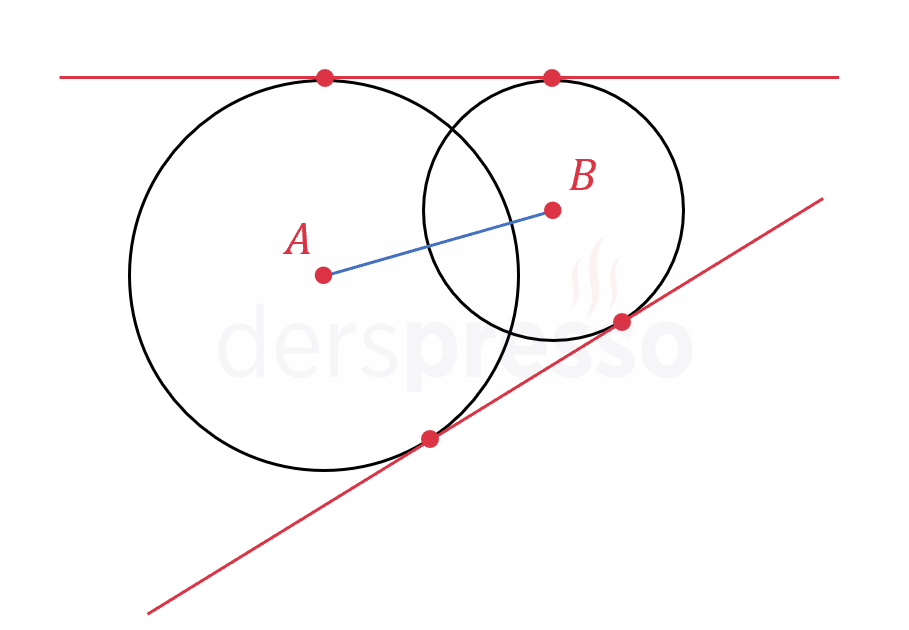
İki noktada kesişen iki çember: \( \abs{r_1 - r_2} \lt \abs{AB} \lt r_1 + r_2 \) İki ortak dış teğet |

|
İçten teğet iki çember: \( \abs{AB} = \abs{r_1 - r_2} \) Bir ortak dış teğet |

|
İç içe ve kesişmeyen iki çember: \( \abs{AB} \lt \abs{r_1 - r_2} \) Sıfır ortak dış teğet |
Teğet İki Çembere Teğet İki Doğru
Birbirine teğet iki çembere teğet iki doğrunun çemberler üzerinde oluşturduğu açı ve yayların ölçüleri arasında aşağıdaki ilişki vardır.
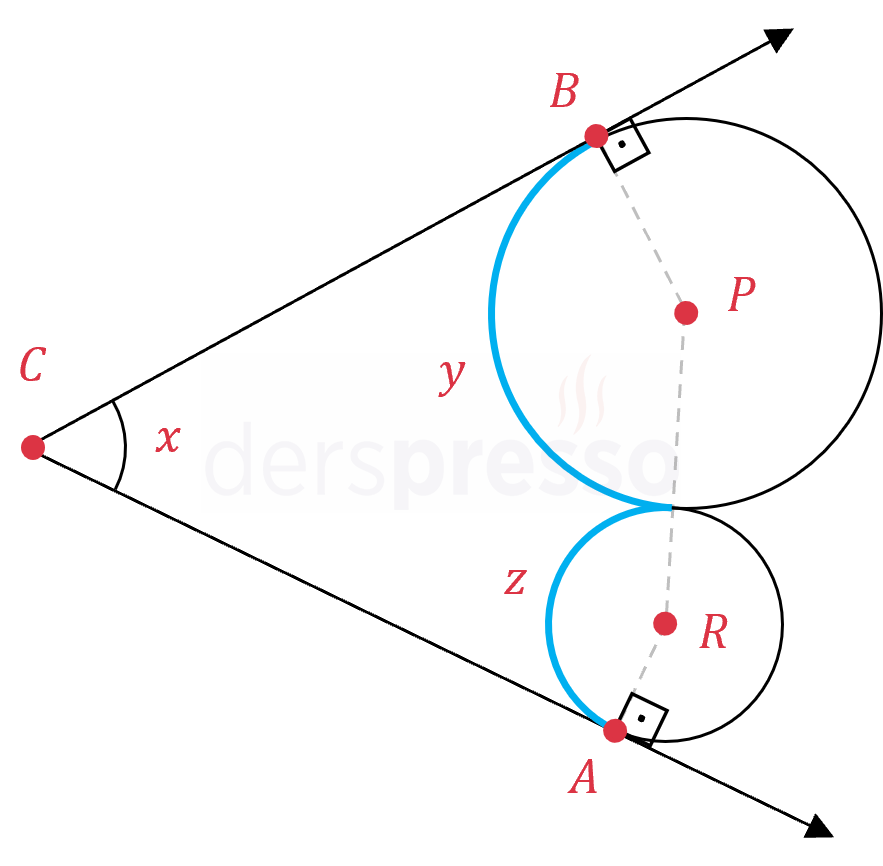
\( x + y + z = 360° \)
İSPATI GÖSTER
\( ARPBC \) beşgeninin iç açılar toplamı \( = (5 - 2) \cdot 180° = 540° \)
\( m(\widehat{CBP}) = m(\widehat{CAR}) = 90° \)
Buna göre beşgenin diğer 3 köşesinin açıları toplamı \( 540 - 180 = 360° \) olur.
\( m(\widehat{ACB}) + m(\widehat{ARP}) + m(\widehat{BPR}) \) \( = 360° \)
Bu toplamda 2. ve 3. terimler aynı zamanda işaretli yayların merkez açıları oldukları için, ölçüleri yayların ölçülerine eşittir.
\( x + y + z = 360° \)
Teğet İki Çembere Teğet Bir Doğru
Birbirine teğet iki çembere teğet bir doğrunun çemberler üzerinde oluşturduğu yayların ölçüleri arasında aşağıdaki ilişki vardır.
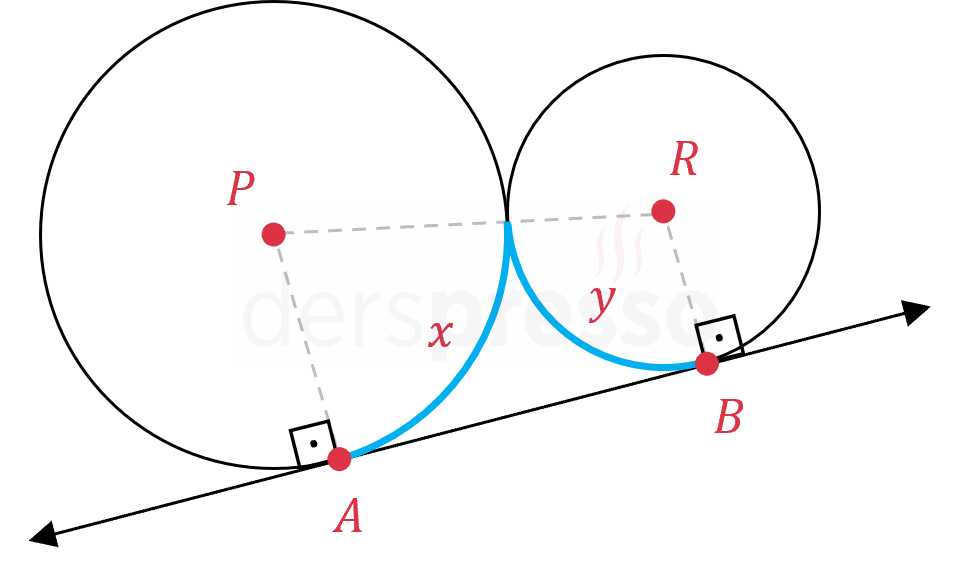
\( x + y = 180° \)
İSPATI GÖSTER
\( APRB \) dörtgeninin iç açılar toplamı \( = (4 - 2) \cdot 180° = 360° \)
\( m(\widehat{BAP}) = m(\widehat{ABR}) = 90° \)
Buna göre dörtgenin diğer 2 köşesinin açıları toplamı \( 360 - 180 = 180° \) olur.
\( m(\widehat{APR}) + m(\widehat{BRP}) = 180° \)
Bu ifadedeki terimler aynı zamanda işaretli yayların merkez açıları oldukları için, ölçüleri yayların ölçülerine eşittir.
\( x + y = 180° \)
İki Çembere Teğet İki Doğru
İki çembere teğet iki doğrunun çemberler üzerinde oluşturduğu yayların ölçüleri arasında aşağıdaki ilişki vardır.
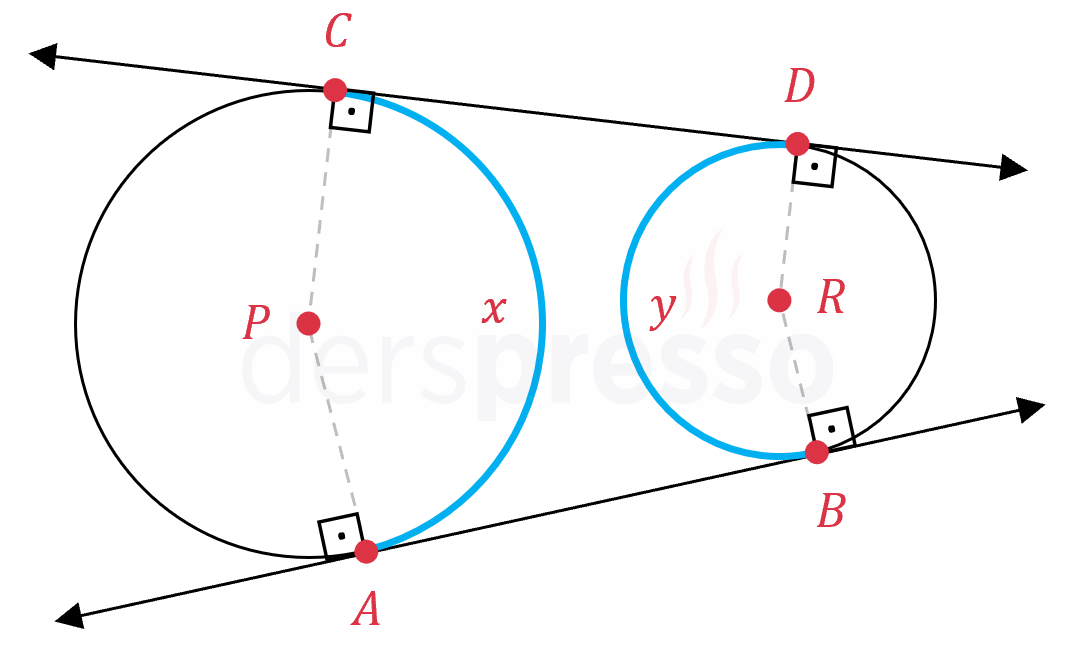
\( x + y = 360° \)
İSPATI GÖSTER
\( APCDRB \) altıgeninin iç açılar toplamı \( = (6 - 2) \cdot 180° = 720° \)
\( m(\widehat{PAB}) = m(\widehat{PCD}) = 90° \)
\( m(\widehat{RDC}) = m(\widehat{RBA}) = 90° \)
Buna göre altıgenin diğer 2 köşesinin açıları toplamı \( 720 - 360 = 360° \) olur.
\( m(\widehat{APC}) + m(\widehat{BRD}) = 360° \)
Bu ifadedeki terimler aynı zamanda işaretli yayların merkez açıları oldukları için, ölçüleri yayların ölçülerine eşittir.
\( x + y = 360° \)
Birbirine Teğet Üç Çember
Birbirine teğet üç çemberin aralarındaki yayların ölçülerinin toplamı 180°'dir.
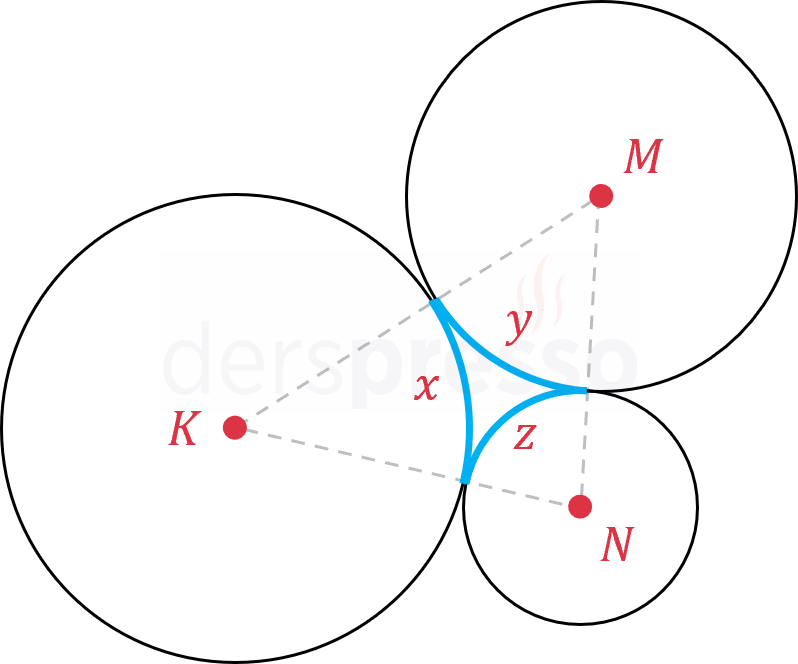
\( x + y + z = 180° \)
İSPATI GÖSTER
\( KMN \) üçgeninin iç açıları toplamı \( = 180° \)
\( m(\widehat{K}) = x \)
\( m(\widehat{M}) = y \)
\( m(\widehat{N}) = z \)
\( x + y + z = 180° \)
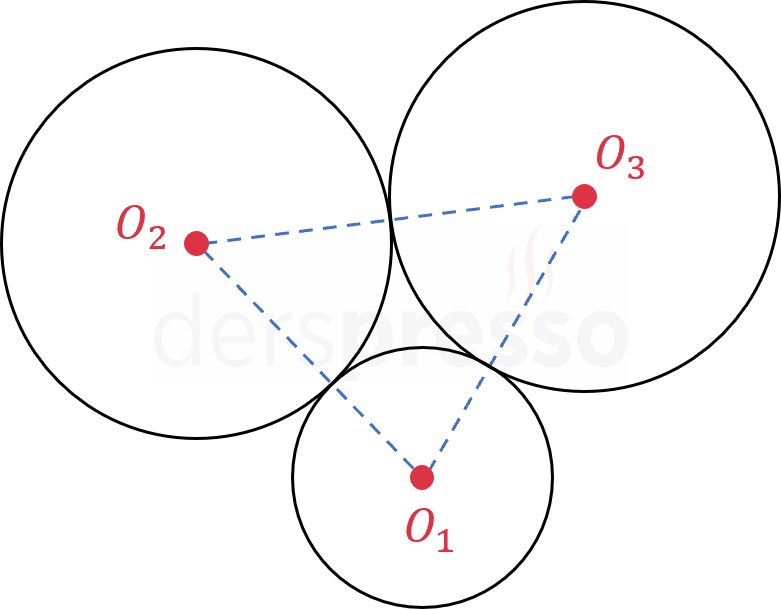
Yarıçapları sırasıyla 4, 6 ve 6 olan \( O_1, O_2, O_3 \) merkezli üç çember birbirine teğet olacak şekilde yerleştiriliyor.
Bu çemberlerin merkezlerini birleştirerek oluşan üçgenin alanı kaçtır?
Çözümü Göster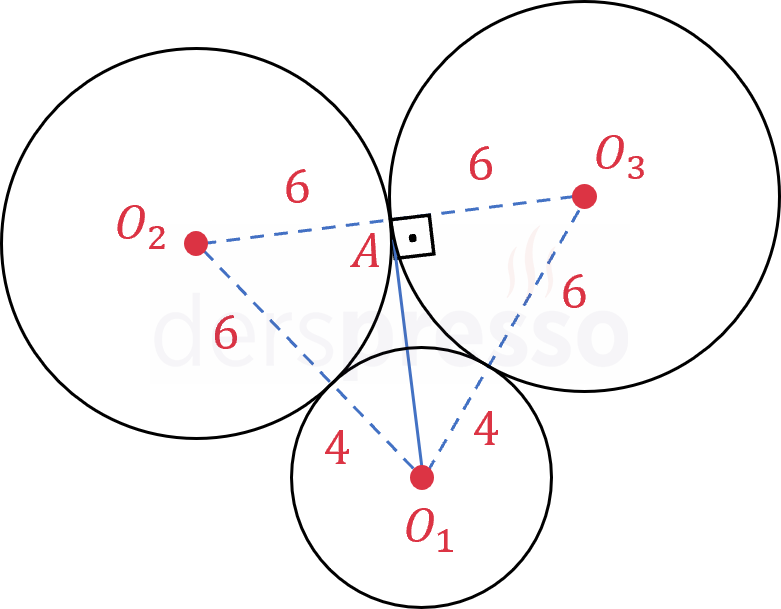
\( O_1O_2O_3 \) üçgeni ikizler üçgendir.
\( O_1O_2O_3 \) üçgeninin alanını hesaplamak için \( O_1 \) köşesinden \( [O_2O_3] \) kenarına bir yükseklik indirelim.
İkizkenar üçgende tabana indirilen yükseklik tabanı ortalar.
\( AO_1O_2 \) üçgeni 3-4-5 Pisagor üçgeninin 2 katı olup yüksekliğinin uzunluğu \( 2 \cdot 4 = 8 \) olur.
Yarıçapların oluşturduğu üçgenin alanını bulalım.
\( A(O_1O_2O_3) = \dfrac{8 \cdot 12}{2} \)
\( = 48 \) bulunur.

Yarıçapları 5 cm ve 15 cm olan iki çember şekildeki gibi birbirine teğettir.
Buna göre bu iki çemberi çevreleyen en kısa halatın uzunluğu kaç cm'dir?
Çözümü GösterÇemberlerin merkezinden halatın çemberlere teğet olduğu noktalara birer yarıçap çizelim.
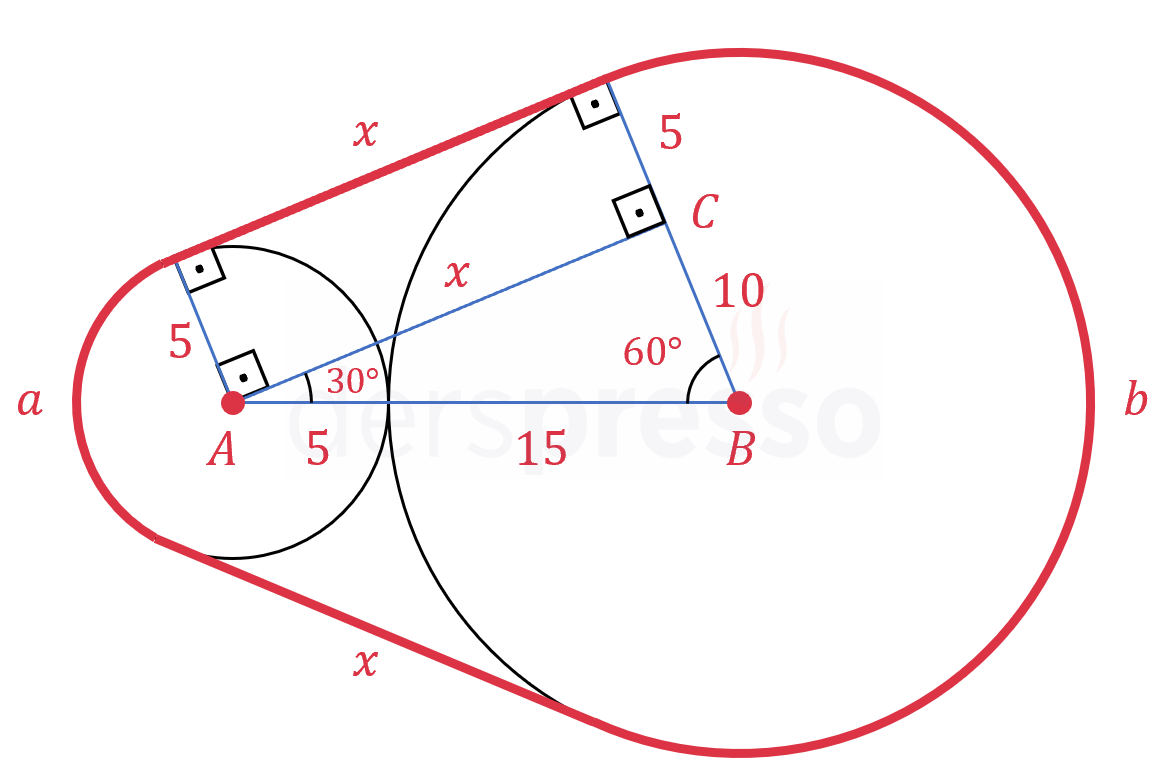
Halatın küçük çemberi çevreleyen kısmının uzunluğuna \( a \) cm, büyük çemberi çevreleyen kısmının uzunluğuna \( b \) cm, iki çember arasında kalan kısımlarının uzunluğuna \( x \) cm diyelim.
Oluşan \( ACB \) dik üçgenindeki kenar orantılarını incelersek \( \widehat{CAB} \) açısının ölçüsünün \( 30° \) olduğunu, dolayısıyla \( ACB \) üçgeninin 30-60-90° üçgeni olduğunu görürüz.
30-60-90 üçgeni özelliğini kullanarak \( x \) uzunluğunu bulalım.
\( x = 10\sqrt{3} \) cm
Halat 2 tane \( x \) uzunluğuna sahip olduğuna göre ikisinin toplam uzunluğu \( 2x = 20\sqrt{3} \) cm olur.
Şimdi halatın çemberleri çevreleyen uzunluğunu bulalım.
Halat küçük çemberde \( 360 - 2(90 + 30) = 120° \) derecelik yayı, yani çemberin \( \frac{1}{3} \)'ünü çevrelemektedir.
Küçük çemberde 120°'lik yayın uzunluğu \( 2\pi \cdot 5 \cdot \frac{1}{3} = \frac{10\pi}{3} \) cm olur.
Halat büyük çemberde \( 360 - 2(60) = 240° \) derecelik yayı, yani çemberin \( \frac{2}{3} \)'ünü çevrelemektedir.
Büyük çemberde 240°'lik yayın uzunluğu \( 2\pi \cdot 15 \cdot \frac{2}{3} = 20\pi \) cm olur.
Halatın toplam uzunluğunu bulalım.
\( = 20\sqrt{3} + \frac{10\pi}{3} + 20\pi \)
\( = 20\sqrt{3} + \dfrac{70\pi}{3} \) cm bulunur.
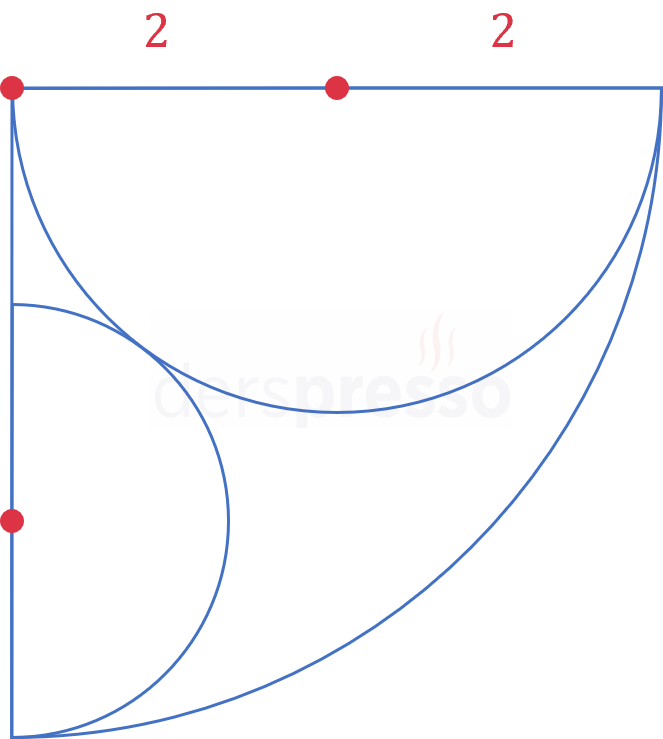
Yukarıdaki şekildeki çeyrek dairenin yarıçapı 4 cm, büyük yarım dairenin yarıçapı 2 cm'dir.
Yarım daireler birbirine teğet olduğuna göre, küçük yarım dairenin yarıçapı kaç cm'dir?
Çözümü GösterDairelerin merkezlerine sırasıyla \( A, B, C \) ve küçük yarım dairenin yarıçapına \( r \) diyelim.
Yarım dairelerin merkezlerini birleştirelim.
Birbirine teğet iki dairenin merkezlerini birleştiren doğru dairelerin teğet noktasından geçer.
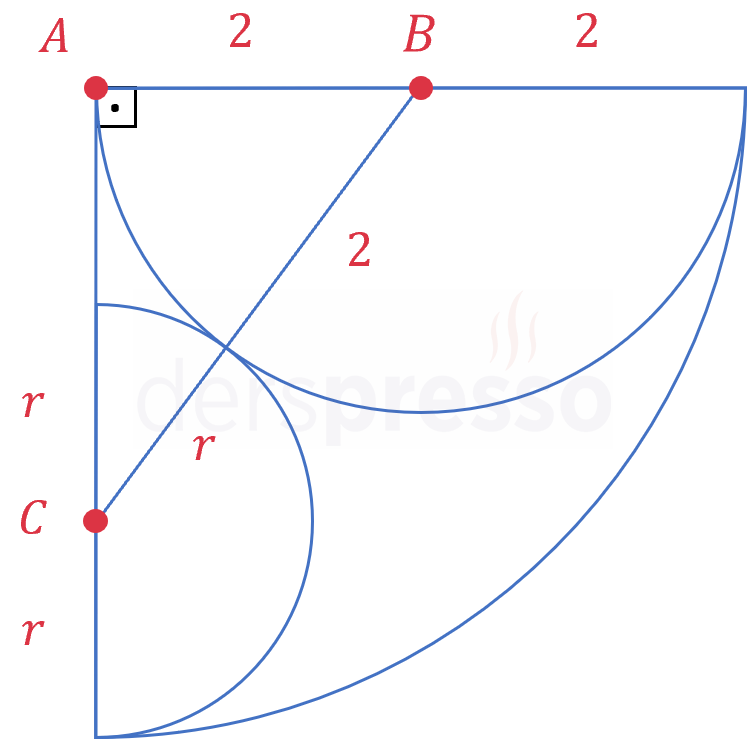
Oluşan \( ABC \) üçgeninde Pisagor teoremini uygulayalım.
\( \abs{AB}^2 + \abs{AC}^2 = \abs{BC}^2 \)
\( 2^2 + (4 - r)^2 = (r + 2)^2 \)
\( 4 + 16 - 8r + r^2 = r^2 + 4r + 4 \)
\( 12r = 16 \)
\( r = \dfrac{4}{3} \) olarak bulunur.

Yarıçap uzunlukları 3 birim olan \( O_1 \) ve \( O_2 \) merkezli iki çember şekilde gösterilmiştir.
İki çemberin içinde kalan \( ABCD \) karesinin köşeleri çemberler üzerinde olduğuna göre, bu karenin alanı kaçtır?
Çözümü Göster\( ABCD \) karesinin merkez noktasına \( E \), bir kenar uzunluğu \( 2a \) diyelim.
\( [O_1O_2] \) yarıçapının karenin \( [AD] \) kenarını kestiği noktaya \( F \) diyelim.

Aşağıdaki uzunluklar çemberlerin yarıçapına eşittir.
\( \abs{O_1O_2} = \abs{AO_2} = 3 \)
\( \abs{EO_2} = \dfrac{3}{2} \)
\( \abs{AB} = 2a \) ve \( E \) noktası karenin merkezidir.
\( \abs{AF} = \abs{FE} = \abs{FD} = a \)
\( A \) karenin köşesi ve \( E \) noktası karenin merkezi olduğundan, \( [AE] \) doğrusu yarım köşegendir. Ayrıca \( AFE \) üçgeni dik ikizkenar üçgendir.
\( m(\widehat{FAE}) = m(\widehat{FEA}) = 45° \)
\( \abs{AE} = a\sqrt{2} \)
\( AEO_2 \) üçgeninde iki kenar ve bir açı değeri bilindiğinden kosinüs alan formülünü kullanarak \( a \) değerini bulabiliriz.
\( \abs{AO_2}^2 = \abs{AE}^2 + \abs{EO_2}^2 - 2\abs{AE}\abs{EO_2}\cos{\widehat{E}} \)
\( m(\widehat{AEF}) = 45° \) olduğu için \( m(\widehat{AEO_2}) = 135° \) olur.
\( 3^2 = (a\sqrt{2})^2 + (\dfrac{3}{2})^2 - 2a\sqrt{2} \cdot \dfrac{3}{2} \cdot \cos{135°} \)
\( 9 = 2a^2 + \dfrac{9}{4} + 3a \)
\( 2a^2 + 3a -\dfrac{27}{4} = 0 \)
Yukarıdaki denklemin kökünü bulmak için kök bulma formülünü kullanalım.
\( x_{1, 2} = \dfrac{-b \pm \sqrt{b^2 - 4ac}}{2a}\)
\( a_{1} = \dfrac{-3 - \sqrt{9 + 4 \cdot 2 \cdot \frac{27}{4} }}{2 \cdot 2}\)
\( = \dfrac{-3 - 3\sqrt{7}}{4} \)
\( a \gt 0 \) olması gerektiği için bu kök geçerli bir çözüm değildir.
\( a_{2} = \dfrac{-3 + \sqrt{9 + 4 \cdot 2 \cdot \frac{27}{4} }}{2 \cdot 2}\)
\( = \dfrac{-3 + 3\sqrt{7}}{4} \)
\( a \) değerini kullanarak karenin alanını bulalım.
\( A(ABCD) = 4a^2 \)
\( = 4(\dfrac{-3 + 3\sqrt{7}}{4})^2 \)
\( = \dfrac{72 - 18\sqrt{7}}{4} \)
\( = 18 - \dfrac{9\sqrt{7}}{2} \) bulunur.

\( O \) merkezli bir çeyrek dairenin içine \( M \) merkezli bir daire şekildeki gibi yerleştiriliyor.
Çeyrek dairenin yarıçapı 4 birim olduğuna göre, yarım dairenin yarıçapı kaçtır?
Çözümü GösterYarım dairenin çeyrek daireye teğet olduğu noktalara \( C \) ve \( D \) diyelim.
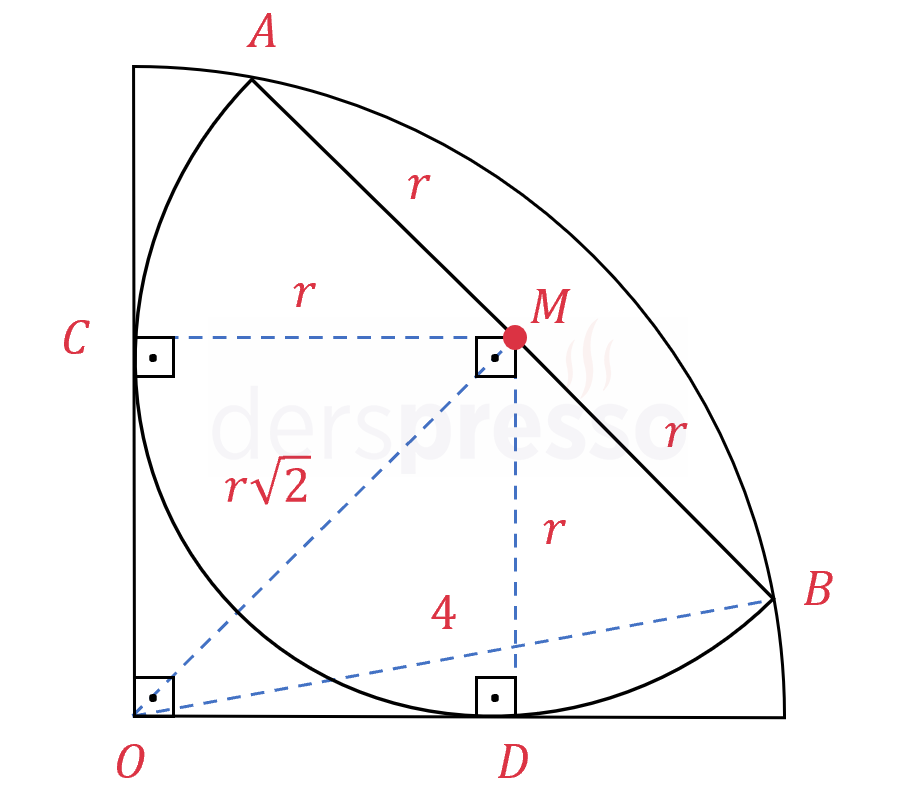
Çeyrek dairenin yarıçap uzunlukları aşağıdaki gibidir.
\( \abs{MA} = \abs{MB} = \abs{MC} = \abs{MD} = r \)
Teğete noktalara çizilen yarıçaplar o teğete diktir.
Böylelikle bir kenar uzunluğu \( r \) olan \( ODMC \) karesi oluşur.
\( ODMC \) karesinin \( [OM] \) köşegen doğrusunu çizelim.
Karenin kenarı \( r \) ise köşegen uzunluğu \( r\sqrt{2} \) olur.
\( \abs{OM} = r\sqrt{2} \)
\( [OB] \) doğrusu çizerek \( OMB \) dik üçgeni oluşturalım.
\( \abs{OB} \) uzunluğu çeyrek dairenin yarıçapıdır.
\( \abs{OB} = 4 \)
\( OMB \) dik üçgeninde Pisagor teoremi uygulayalım.
\( \abs{MB}^2 + \abs{OM}^2 = \abs{OB}^2 \)
\( r^2 + (r\sqrt{2})^2 = 4^2 \)
\( r^2 + 2r^2 = 4^2 \)
\( r^2 = \dfrac{16}{3} \)
\( r = \dfrac{4}{\sqrt{3}} = \dfrac{4\sqrt{3}}{3} \) bulunur.

Yarıçapları 50 birim olan dıştan teğet iki çember ve bu çemberlerin bir ortak dış teğeti arasında şekildeki gibi bir kare tam oturmaktadır.
Buna göre, karenin bir kenar uzunluğu kaçtır?
Çözümü GösterSoldaki çemberin merkezinden doğru ile teğet noktasına \( [OS] \) yarıçapı çizelim.
Karenin \( A \) köşesinden çizdiğimiz yarıçapa bir dikme çizelim.
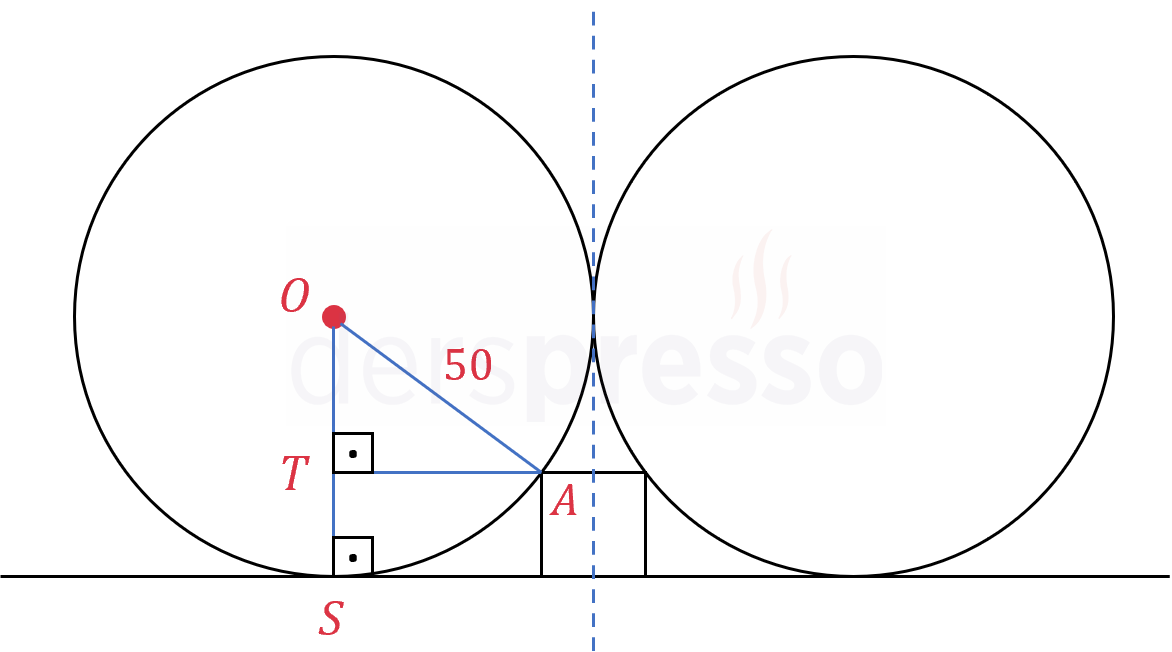
Karenin bir kenar uzunluğuna \( 2a \) diyelim.
Çemberlerin ortak iç teğeti (kesikli çizgi) karenin simetri çizgisidir.
\( \abs{AT} \) uzunluğunu bulalım.
\( \abs{AT} = 50 - \dfrac{2a}{2} = 50 - a \)
\( AOT \) dik üçgeninde Pisagor teoremini kullanarak \( a \) uzunluğunu bulalım.
\( 50^2 = (50 - a)^2 + (50 - 2a)^2 \)
\( 2500 = 2500 - 100a + a^2 + 2500 - 200a + 4a^2 \)
\( 5a^2 - 300a + 2500 = 0 \)
\( a^2 - 60a + 500 = 0 \)
\( (a - 50)(a - 10) = 0 \)
\( a \lt 50 \) olduğu için \( a = 10 \) olur.
Buna göre, karenin bir kenar uzunluğu \( 2a = 20 \) birim bulunur.