Çemberin Uzunluk Özellikleri
Çemberin Dışında Bir Noktadan Çizilen Teğetler
Çemberin dışındaki bir noktadan çembere iki teğet çizilebilir ve bu teğetlerin uzunlukları birbirine eşittir.

\( \abs{AB} = \abs{AC} \)
İSPATI GÖSTER
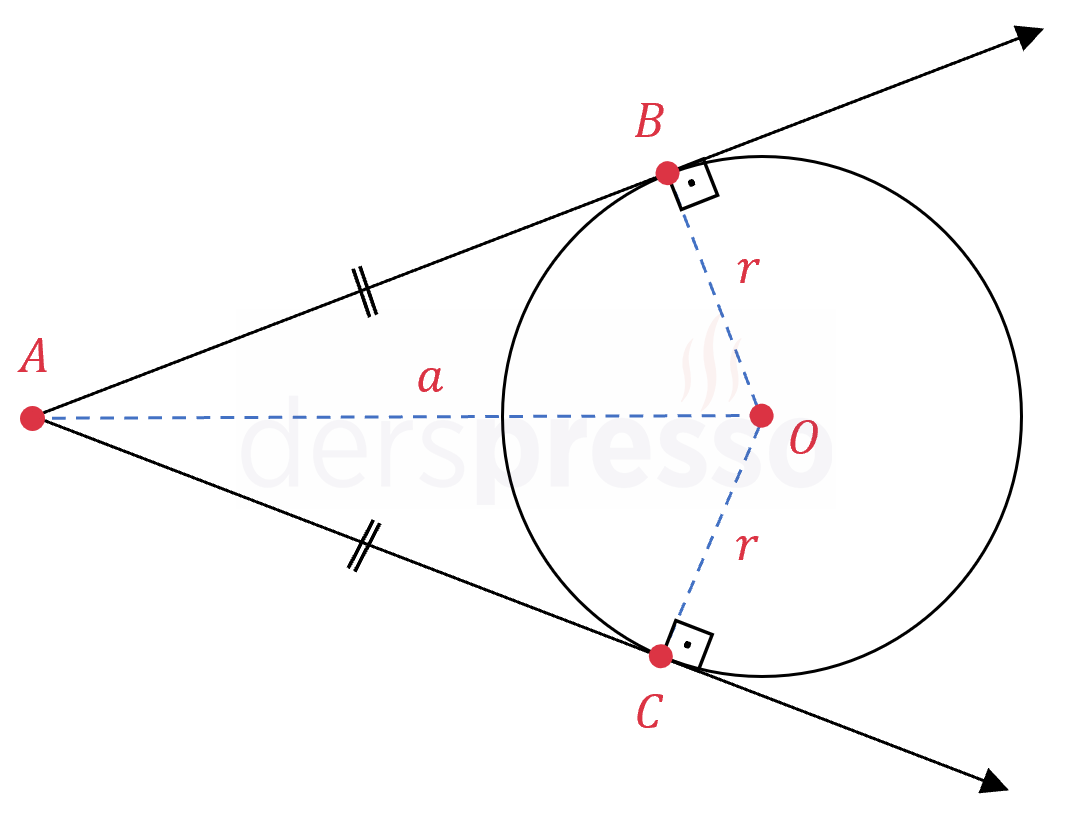
\( A \) noktasından ve teğetlerin çemberi kestiği noktalardan çemberin merkezine doğrular çizelim (mavi kesikli çizgiler).
Çemberin merkezinden teğetlere çizilen doğru parçaları teğeti dik kestiği için iki dik üçgen oluşur.
\( AOB \) üçgeninin teğet uzunluğunu Pisagor teoremini kullanarak yazalım.
\( \abs{AB}^2 + r^2 = a^2 \)
\( \abs{AB} = \sqrt{a^2 - r^2} \)
\( AOC \) üçgeninin teğet uzunluğunu Pisagor teoremini kullanarak yazalım.
\( \abs{AC}^2 + r^2 = a^2 \)
\( \abs{AC} = \sqrt{a^2 - r^2} \)
Buna göre \( A \) noktasından çizilen her iki teğetin uzunluğu birbirine eşittir.
\( \abs{AB} = \abs{AC} \)
Bunun bir sonucu olarak, bu teğetleri kesen ve çembere teğet bir doğru parçasının oluşturduğu üçgenin çevresi, teğetlerden birinin uzunluğunun iki katına eşittir.

\( Ç(ADE) = 2\abs{AB} = 2\abs{AC} \)
İSPATI GÖSTER
Üçgenin çevre formülünü, kenar uzunluklarının toplamı olarak yazalım.
\( Ç(ADE) = \abs{AD} + \abs{AE} + \abs{DE} \)
\( D \) ve \( E \) çemberin dışından çembere çizilen teğetlerin kesişim noktaları oldukları için, aşağıdaki uzunluklar birbirine eşittir.
\( \abs{DF} = \abs{DB} \)
\( \abs{EF} = \abs{EC} \)
Bu eşitlikleri kullanarak, yukarıdaki çevre formülünü aşağıdaki şekilde yazabiliriz.
\( Ç(ADE) = \abs{AD} + \abs{AE} + \abs{DF} + \abs{EF} \)
\( Ç(ADE) = \abs{AD} + \abs{AE} + \abs{DB} + \abs{EC} \)
\( Ç(ADE) = (\abs{AD} + \abs{DB}) + (\abs{AE} + \abs{EC}) \)
\( Ç(ADE) = \abs{AB} + \abs{AC} \)
\( A \) noktası iki teğetin kesişim noktası olduğu için, aşağıdaki uzunluklar birbirine eşittir.
\( \abs{AB} = \abs{AC} \)
Buna göre, verilen çevre formülünü elde ederiz.
\( Ç(ADE) = 2\abs{AB} = 2\abs{AC} \)
Çemberin Dışında Bir Noktadan Çizilen Kesenler
Çemberin dışındaki bir noktadan çembere sonsuz sayıda kesen çizilebilir. Bu kesenlerin ve yine aynı noktadan çembere çizilecek teğetlerin uzunlukları arasında aşağıdaki gibi bir ilişki vardır.

\( {\abs{AB}}^2 = \abs{AC} \cdot \abs{AD} = \abs{AE} \cdot \abs{AF} \)
İSPATI GÖSTER
Kesenlerin Uzunlukları Arasındaki İlişki

Kesenlerin çemberi kestiği noktaları şekildeki gibi birleştiren doğrular çizelim (mavi kesikli çizgiler).
İkisi de \( \overparen{CE} \) yayını gören \( CDE \) ve \( CFE \) çevre açılarının ölçüleri birbirine eşittir.
\( m(\widehat{CDE}) = m(\widehat{CFE}) = c \)
\( ACF \) ve \( AED \) üçgenlerinin ikişer açısı eşit olduğu için üçüncü açıları da eşittir.
\( m(\widehat{ACF}) = m(\widehat{AED}) = b \)
Buna göre üç açıları birbirine eşit olan \( ACF \) ve \( AED \) üçgenleri benzer üçgenlerdir.
\( \overset{\triangle}{ACF} \sim \overset{\triangle}{AED} \)
Benzer üçgenlerin kenar uzunlukları arasındaki orantıyı yazalım.
\( \dfrac{\abs{AC}}{\abs{AE}} = \dfrac{\abs{AF}}{\abs{AD}} \)
\( \abs{AC} \cdot \abs{AD} = \abs{AE} \cdot \abs{AF} \)
Teğet ve Kesen Uzunlukları Arasındaki İlişki

Teğet ve kesenin çemberi kestiği noktaları şekildeki gibi birleştiren doğrular çizelim (mavi kesikli çizgiler).
İkisi de \( \overparen{BC} \) yayını gören \( ABC \) ve \( BDC \) çevre açılarının ölçüleri birbirine eşittir.
\( m(\widehat{ABC}) = m(\widehat{BDC}) = c \)
\( ACB \) ve \( ABD \) üçgenlerinin ikişer açısı eşit olduğu için üçüncü açıları da eşittir, dolayısıyla bu iki üçgen benzer üçgenlerdir.
\( \overset{\triangle}{ACB} \sim \overset{\triangle}{ABD} \)
Benzer üçgenlerin kenar uzunlukları arasındaki orantıyı yazalım.
\( \dfrac{\abs{AC}}{\abs{AB}} = \dfrac{\abs{AB}}{\abs{AD}} \)
\( {\abs{AB}}^2 = \abs{AC} \cdot \abs{AD} \)
Çemberin İçinde Bir Noktadan Çizilen Kirişler
Çemberin içindeki bir noktadan geçen sonsuz sayıda kiriş çizilebilir. Bu noktanın kirişlerde ayırdığı doğru parçalarının uzunlukların çarpımı birbirine eşittir.

\( \abs{AB} \cdot \abs{AE} = \abs{AC} \cdot \abs{AF} = \abs{AD} \cdot \abs{AG} \)
İSPATI GÖSTER
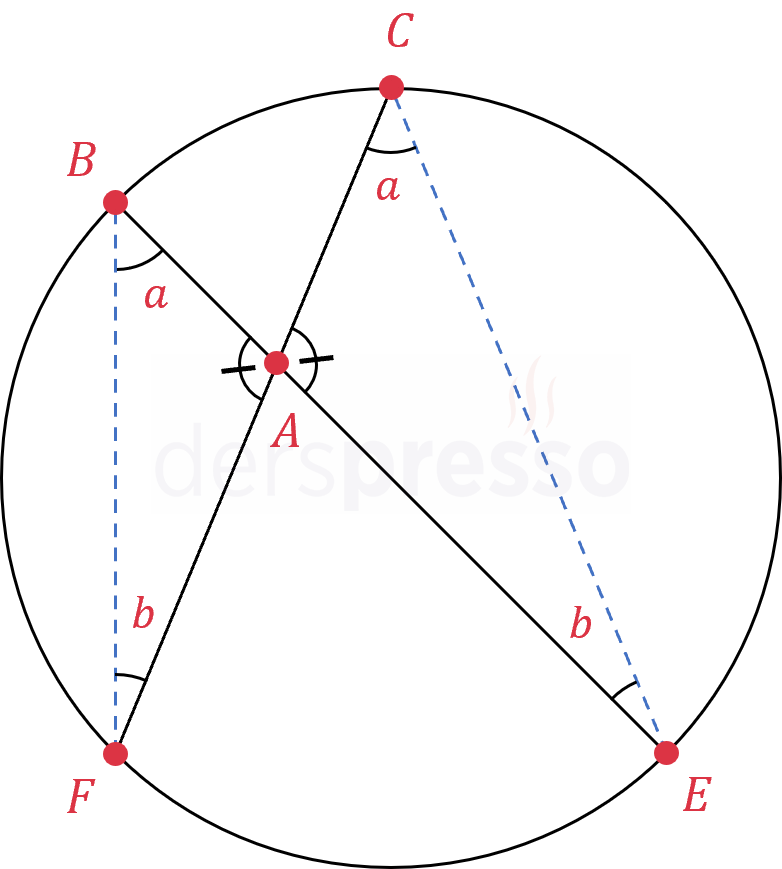
Kirişlerin çemberi kestiği noktaları şekildeki gibi birleştiren doğrular çizelim (mavi kesikli çizgiler).
İkisi de \( \overparen{FE} \) yayını gören \( FBE \) ve \( FCE \) çevre açılarının ölçüleri birbirine eşittir.
\( m(\widehat{FBE}) = m(\widehat{FCE}) = a \)
İkisi de \( \overparen{BC} \) yayını gören \( BFC \) ve \( BEC \) çevre açılarının ölçüleri birbirine eşittir.
\( m(\widehat{BFC}) = m(\widehat{BEC}) = b \)
\( BAF \) ve \( CAE \) üçgenlerinin tüm açıları birbirine eşit olduğu için benzer üçgenlerdir.
\( \overset{\triangle}{BAF} \sim \overset{\triangle}{CAE} \)
Benzer üçgenlerin kenar uzunlukları arasındaki orantıyı yazalım.
\( \dfrac{\abs{AB}}{\abs{AC}} = \dfrac{\abs{AF}}{\abs{AE}} \)
\( \abs{AB} \cdot \abs{AE} = \abs{AC} \cdot \abs{AF} \)
Paralel Kirişlerin Oluşturduğu Yaylar
Paralel iki kiriş arasında kalan iki yayın uzunlukları birbirine eşittir.
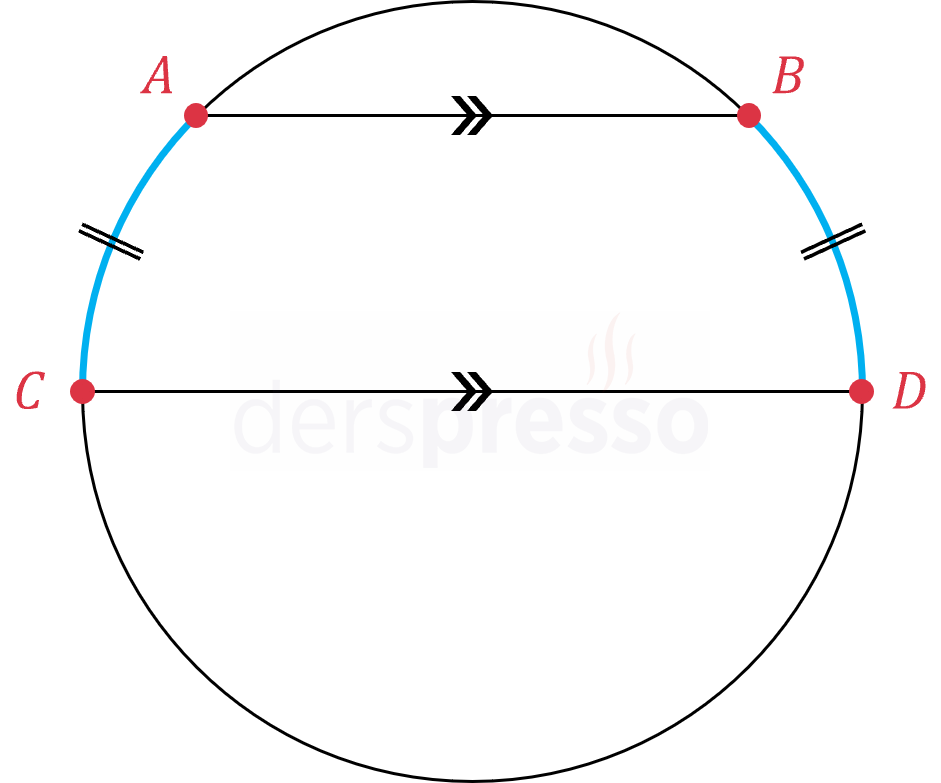
\( \abs{AB} \parallel \abs{CD} \) ise,
\( \abs{\overset{\LARGE\frown}{AC}} = \abs{\overset{\LARGE\frown}{BD}} \)
Eş Kirişlerin Oluşturduğu Yaylar
İki kirişin uzunlukları birbirine eşitse çemberin üzerinde ayırdıkları yayların uzunlukları ve ölçüleri de birbirine eşittir.
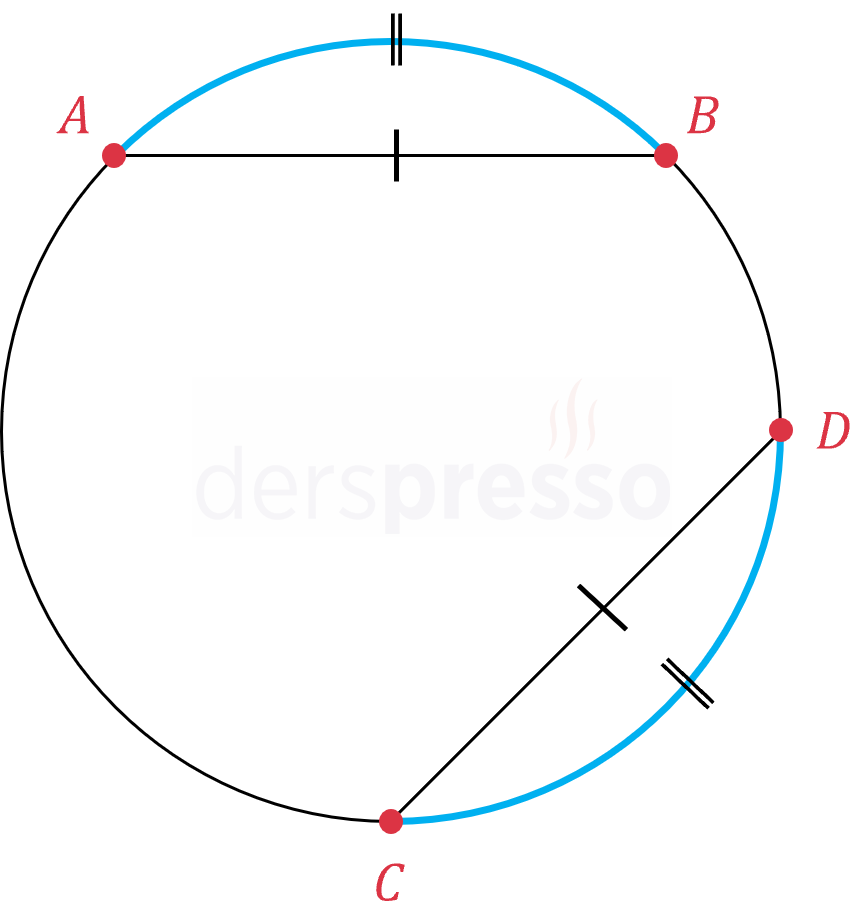
\( \abs{AB} = \abs{DC} \) ise,
\( m(\overset{\LARGE\frown}{AB}) = m(\overset{\LARGE\frown}{DC}) \)
\( \abs{\overset{\LARGE\frown}{AB}} = \abs{\overset{\LARGE\frown}{DC}} \)
Kirişlerin Uzunluğu
Bir çemberin içindeki belirli bir \( K \) noktasından geçen en uzun kiriş çaptır (\( [AB] \)), en kısa kiriş ise bu çapa dik olan kiriştir (\( [CD] \)).

Bir kirişi dik kesen çap hem kirişi hem de kirişin böldüğü yayları ortalar.
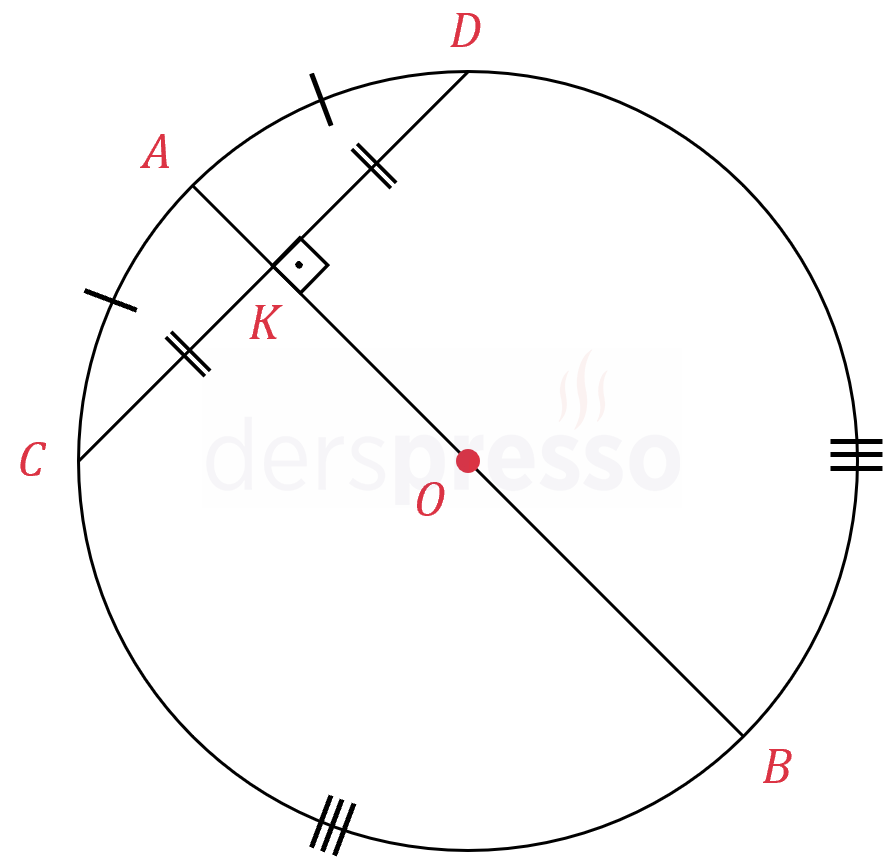
\( O \) çemberin merkezi olmak üzere,
\( \abs{AB} \perp \abs{CD} \) ise,
\( \abs{CK} = \abs{KD} \)
\( \abs{\overset{\LARGE\frown}{CA}} = \abs{\overset{\LARGE\frown}{AD}} \)
\( \abs{\overset{\LARGE\frown}{CB}} = \abs{\overset{\LARGE\frown}{BD}} \)
Bir çemberin kirişleri ile ilgili bazı kurallar aşağıdaki gibidir.
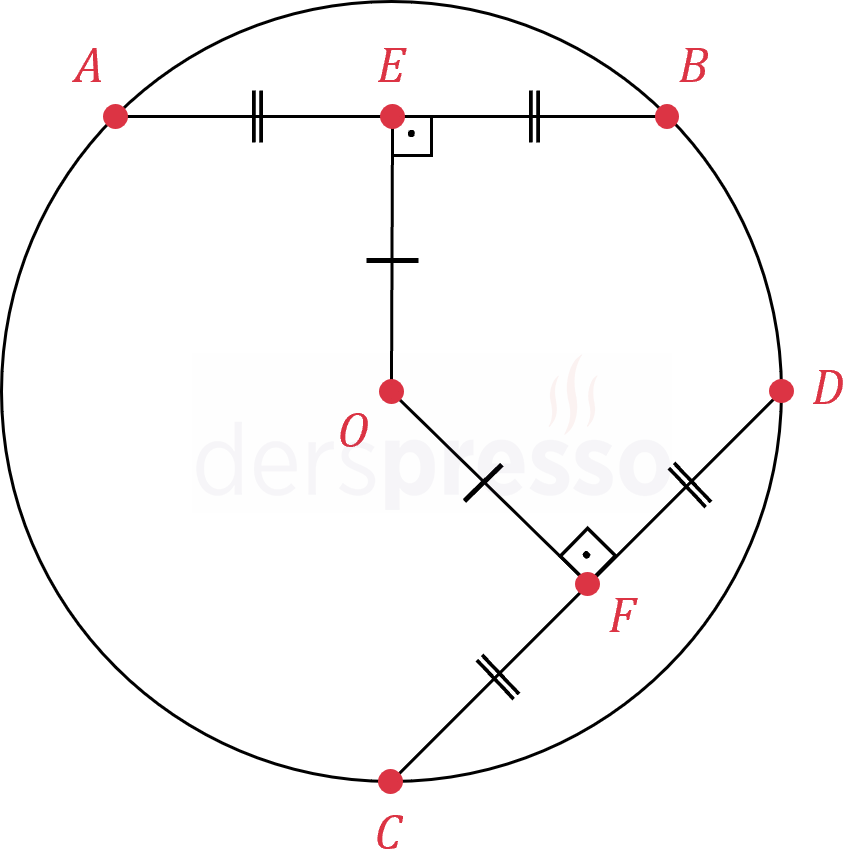
- Bir çemberin kirişinin orta dikmesi çemberin merkezinden geçer.
- Bir çemberin kirişini dik kesen yarıçap kirişi ortalar.
- Bir çemberin aynı uzunluktaki kirişleri çemberin merkezine eşit uzaklıktadır.
- Çemberin merkezine eşit uzaklıktaki kirişlerin uzunlukları birbirine eşittir.
Bir çemberin eş olmayan kirişleri ile ilgili diğer bazı kurallar aşağıdaki gibidir.
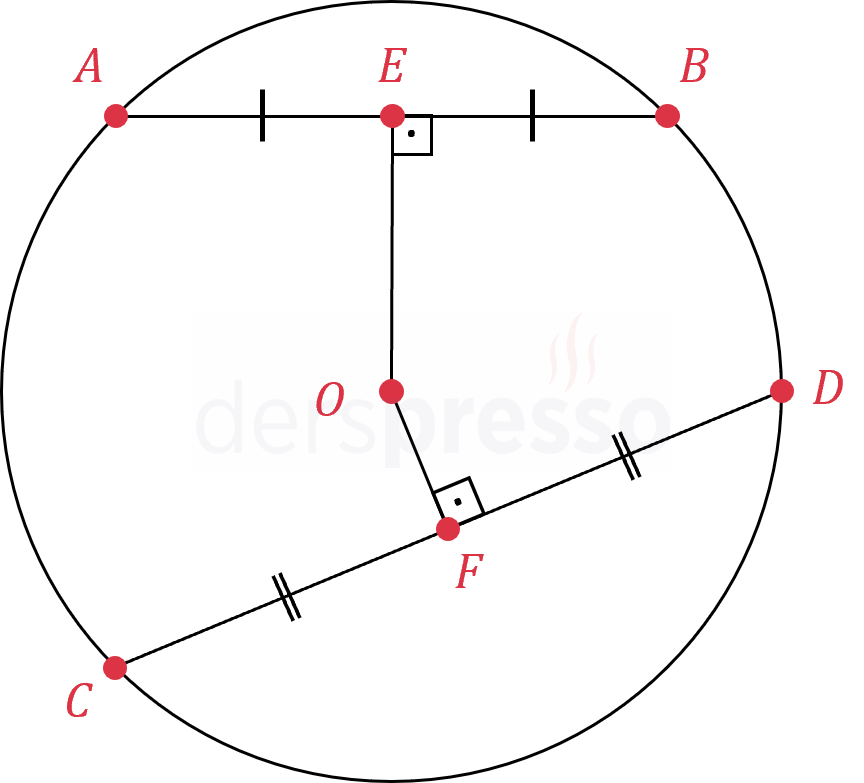
- Çemberin merkezine daha yakın olan kirişler daha uzundur.
- Çemberin merkezine daha yakın olan kirişler çember üzerinde daha uzun bir yay ayırırlar.
\( \abs{OE} \gt \abs{OF} \) ise,
\( \abs{AB} \lt \abs{CD} \)
\( \abs{\overset{\LARGE\frown}{AB}} \lt \abs{\overset{\LARGE\frown}{CD}} \)
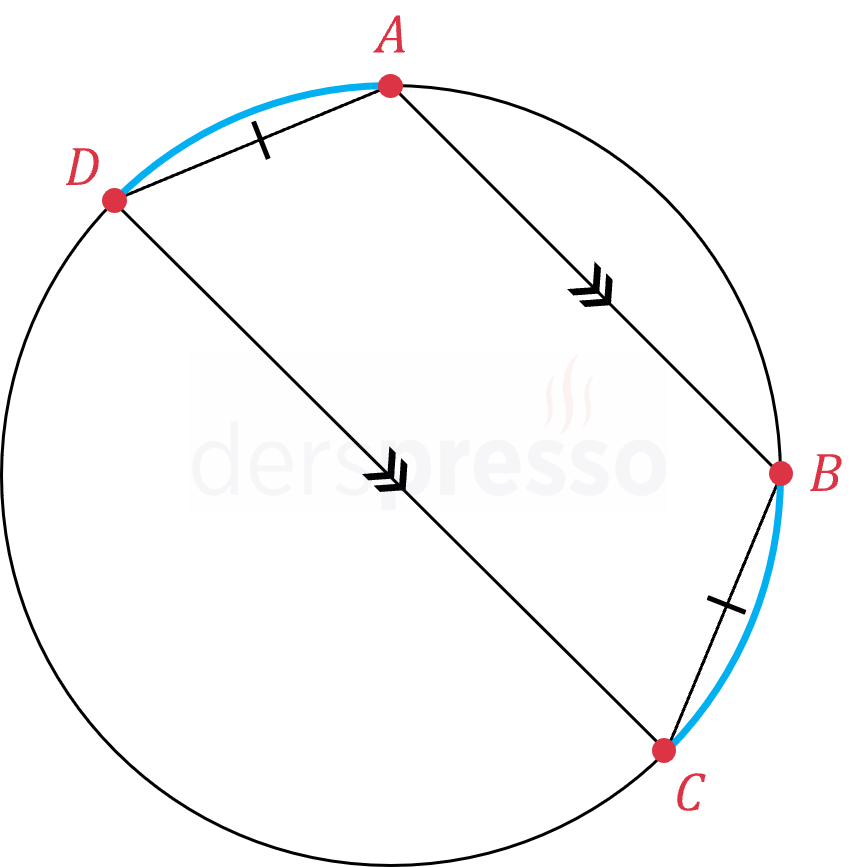
\( [AD] \) ve \( [BC] \) kirişleri eşit uzunlukta ise bu kirişlerin uçlarını birleştiren \( [AB] \) ve \( [DC] \) kirişleri birbirine paralel olur. Benzer şekilde, \( [AB] \) ve \( [DC] \) kirişleri birbirine paralel ise bu kirişlerin uçlarını birleştiren \( [AD] \) ve \( [BC] \) kirişleri eşit uzunlukta olur.
Yarıçap uzunluğu 26 cm olan bir çemberin, birbirine paralel 20 cm ve 48 cm uzunluğundaki kirişlerinin birbirine uzaklıklarının alabileceği değerler toplamı kaçtır?
Çözümü GösterBir çemberin birbirine paralel iki kirişi, çemberin yarıçapına göre ya aynı tarafta ya da farklı taraftadır.
Kirişlerin çemberin yarıçapına göre aynı tarafta olduğu durumu inceleyelim.
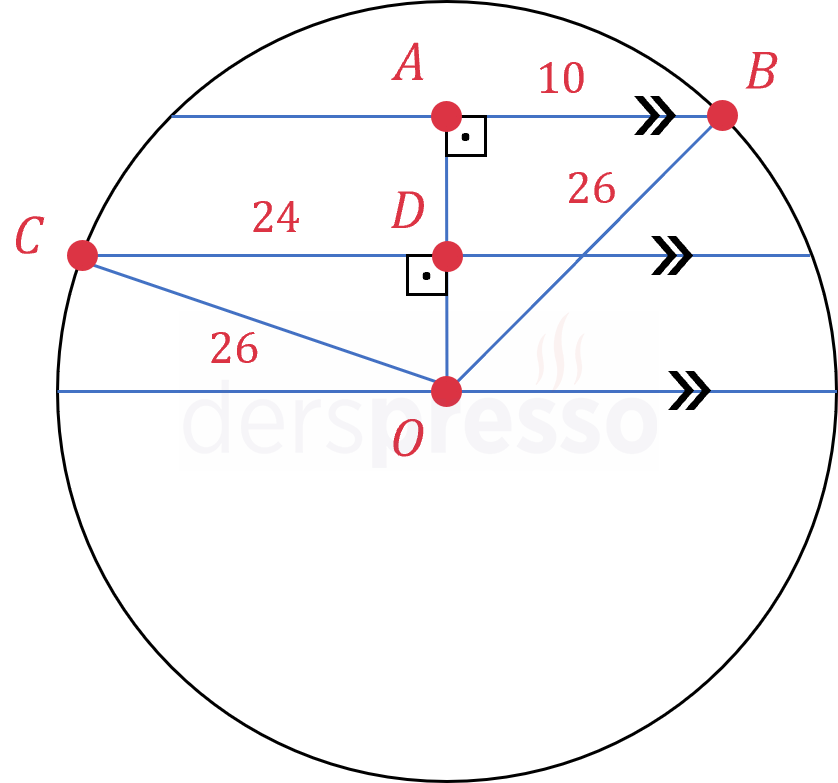
İki kirişe de çemberin merkezinden orta dikme çizelim.
Bu orta dikmeler kirişleri eşit şekilde ikiye böler.
Çemberin merkezini kirişlerin çemberle kesişim noktaları ile birleştirerek dik üçgenler oluşturalım.
Çemberin merkezinden kirişlerin çemberle kesişim noktalarına çizdiğimiz doğrular aynı zamanda yarıçap olduğu için uzunluğu 26 cm'dir.
Oluşan \( OAB \) üçgeni \( 10-24-26 \) üçgeni olduğu için \( \abs{OA} = 24 \) cm olur.
Oluşan \( ODC \) üçgeni \( 10-24-26 \) üçgeni olduğu için \( \abs{OD} = 10 \) cm olur.
Buna göre iki kirişin birbirine uzaklığını bulalım.
\( \abs{AD} = \abs{OA} - \abs{OD} \)
\( = 24 - 10 = 14 \) cm
Kirişlerin çemberin yarıçapına göre farklı tarafta olduğu durumu inceleyelim.
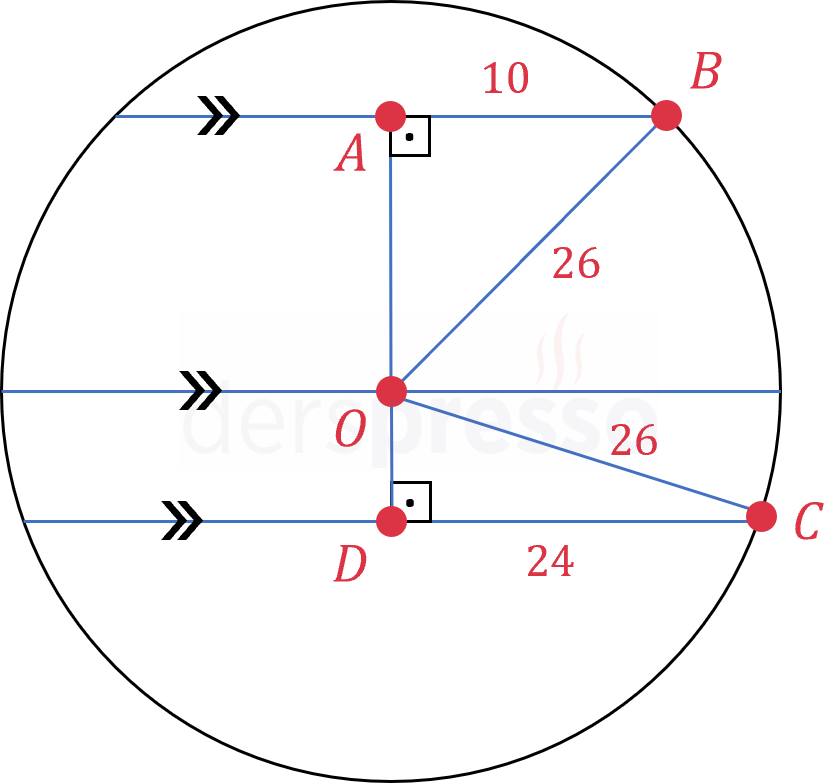
Kirişlerin çemberin yarıçapına göre çemberin aynı tarafta olduğu durumda uyguladığımız adımları tekrar uygulayalım.
İki kirişe de çemberin merkezinden orta dikme çizelim.
Çemberin merkezini kirişlerin çemberle kesişim noktaları ile birleştirerek dik üçgenler oluşturalım.
Oluşan \( OAB \) üçgeni \( 10-24-26 \) üçgeni olduğu için \( \abs{OA} = 24 \) cm olur.
Oluşan \( ODC \) üçgeni \( 10-24-26 \) üçgeni olduğu için \( \abs{OD} = 10 \) cm olur.
Buna göre bu iki kirişin birbirine uzaklığını bulalım.
\( \abs{AD} = \abs{OA} + \abs{OD} \)
\( = 24 + 10 = 34 \) cm
Buna göre kirişlerin birbirine uzaklıklarının alabileceği değerler toplamı \( 34 + 14 = 48 \) olur.
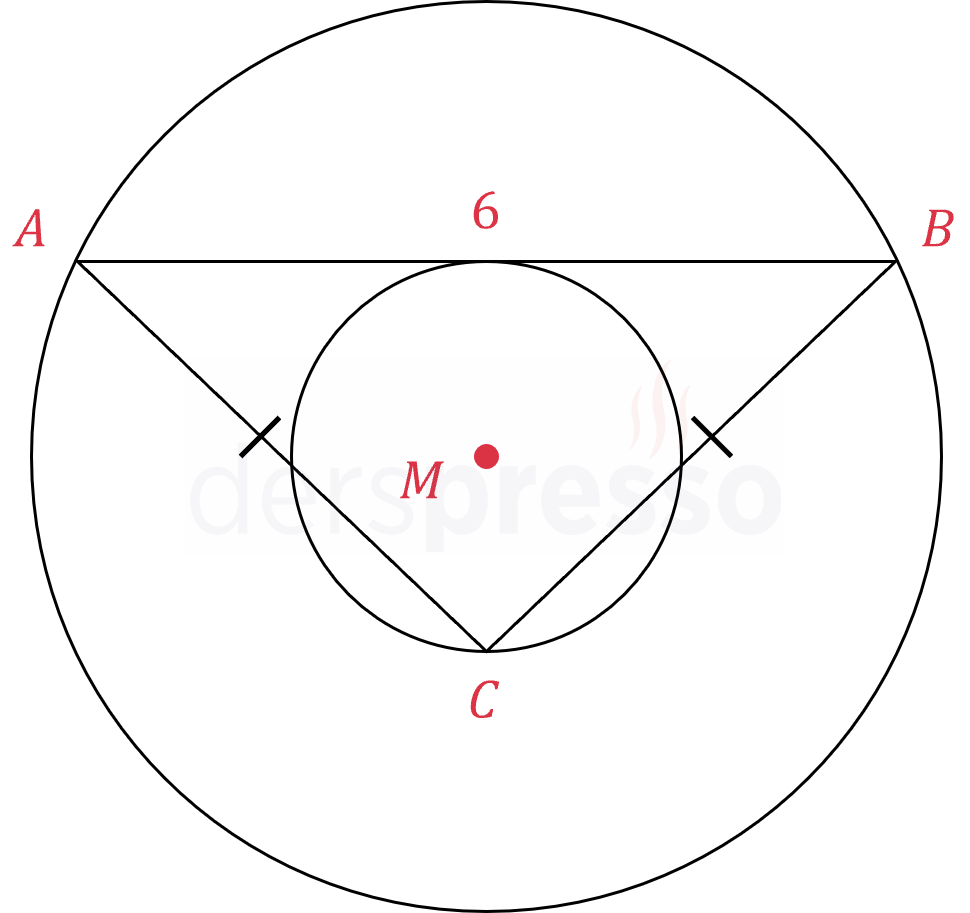
Şekilde merkezleri çakışık iki çember ve \( ABC \) ikizkenar üçgeni verilmiştir. \( C \) noktası küçük çemberin en alt noktasındadır.
Büyük çemberin \( [AB] \) kirişi küçük çembere teğet olup uzunluğu 6 cm'dir.
Büyük çemberin yarıçapı \( 3\sqrt{2} \) cm olduğuna göre, \( ABC \) üçgeninin çevresi kaç cm'dir?
Çözümü GösterKüçük çemberin yarıçapına \( r \) diyelim.
Merkezden \( [AB] \) kirişine indirilen dikme kirişi ortalar ve aynı zamanda küçük çemberin yarıçapıdır.
Merkezden \( B \) noktasına çizilen çizgi büyük çemberin yarıçapı olur.
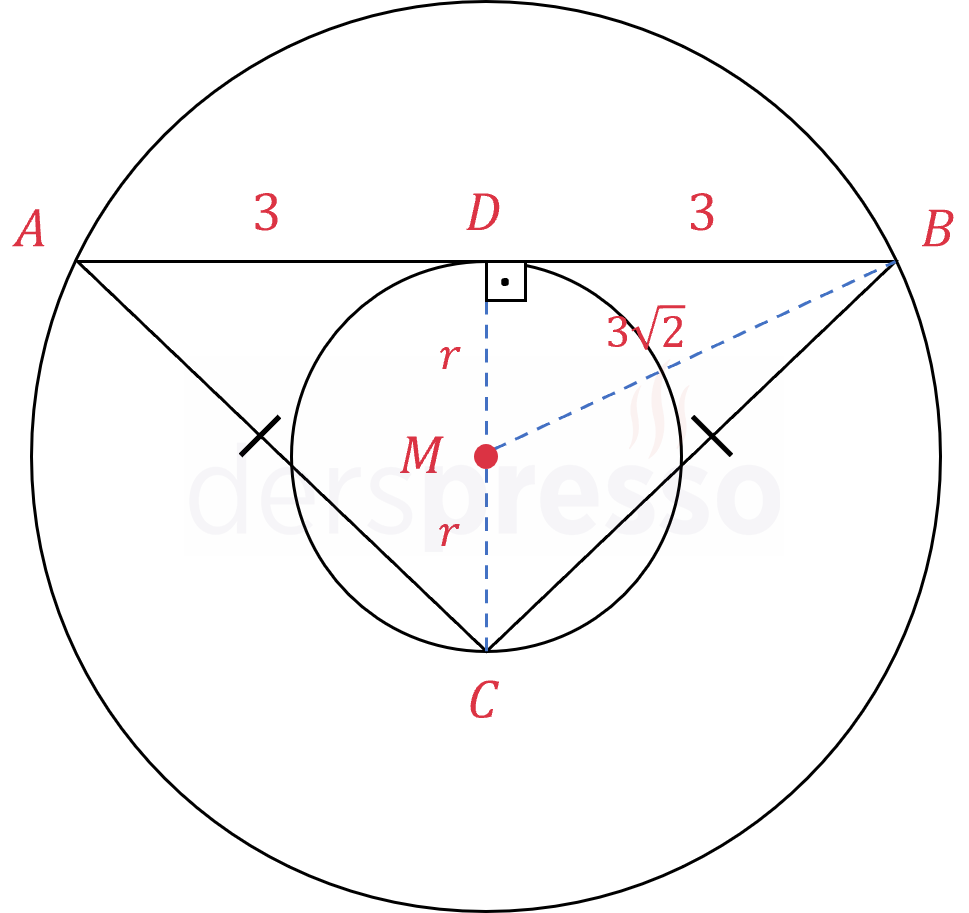
Oluşan \( MBD \) dik üçgeninde Pisagor teoremini kullanarak küçük çemberin yarıçapını bulalım.
\( (3\sqrt{2})^2 = r^2 + 3^2 \)
\( r = 3 \)
\( D \) noktasında merkeze çizilen çizgiyi \( C \) noktasına uzatalım. \( [DC] \) doğru parçası küçük çemberin çapıdır ve yeni bir dik üçgen oluşturur.
\( \abs{DC} = 2r = 6 \)
Yeni dik üçgende Pisagor teoremini kullanarak ikizkenar üçgenin eş kenarlarından birini bulalım.
\( \abs{CB}^2 = 3^2 + 6^2 \)
\( \abs{CB} = 3\sqrt{5} \)
\( ABC \) üçgeninin çevresini bulalım.
\( 6 + 3\sqrt{5} + 3\sqrt{5} = 6 + 6\sqrt{5} \) bulunur.
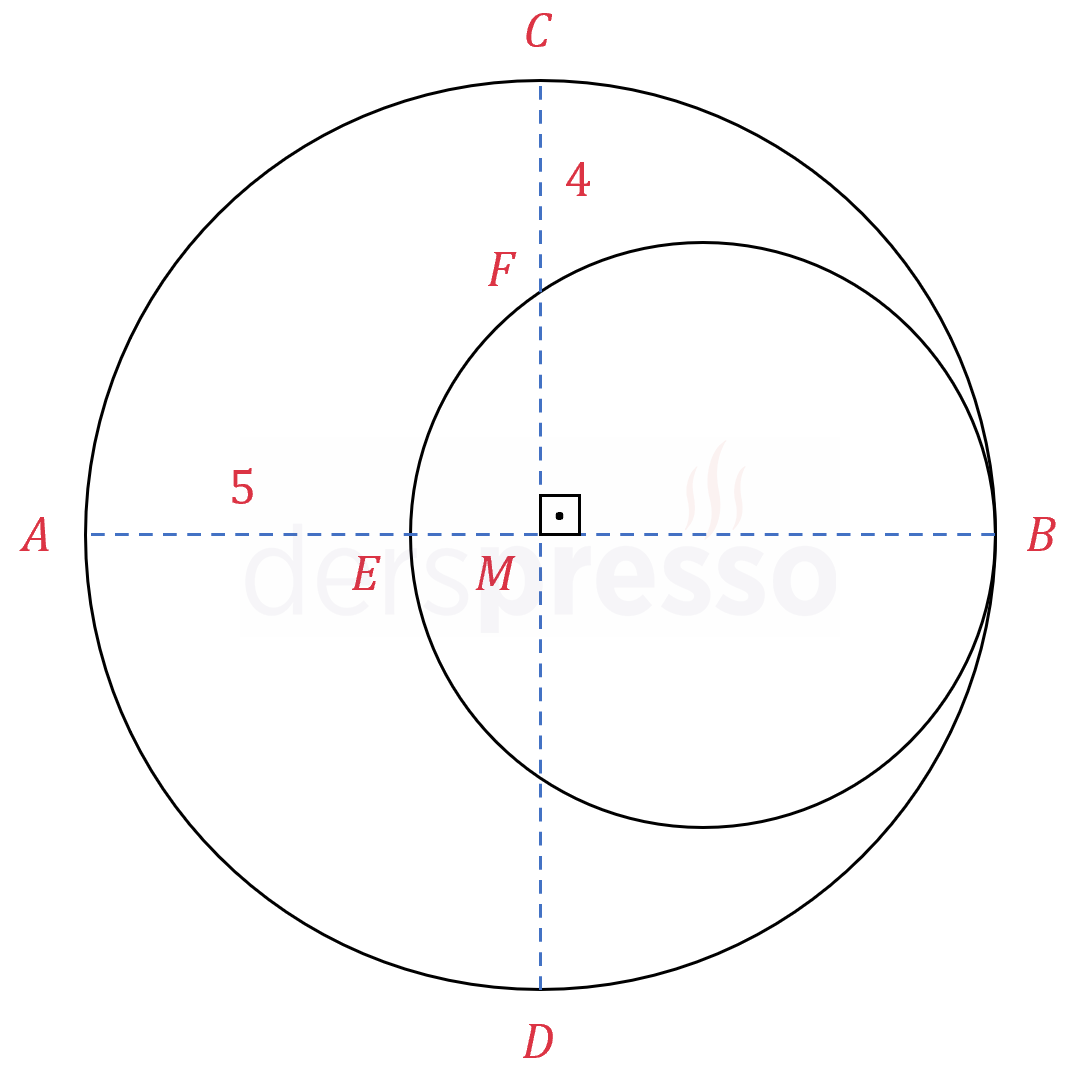
Yukarıdaki şekildeki çemberler \( B \) noktasında teğettir.
Büyük çemberin merkezi \( M \) noktası olup \( AB \) ve \( CD \) çapları birbirine diktir.
\( \abs{AE} = 5 \) ve \( \abs{CF} = 4 \) olduğuna göre, küçük çemberin yarıçapı nedir?
Çözümü GösterKüçük çemberin merkezine \( N \), yarıçapına \( r \), büyük çemberin yarıçapına \( R \) diyelim.
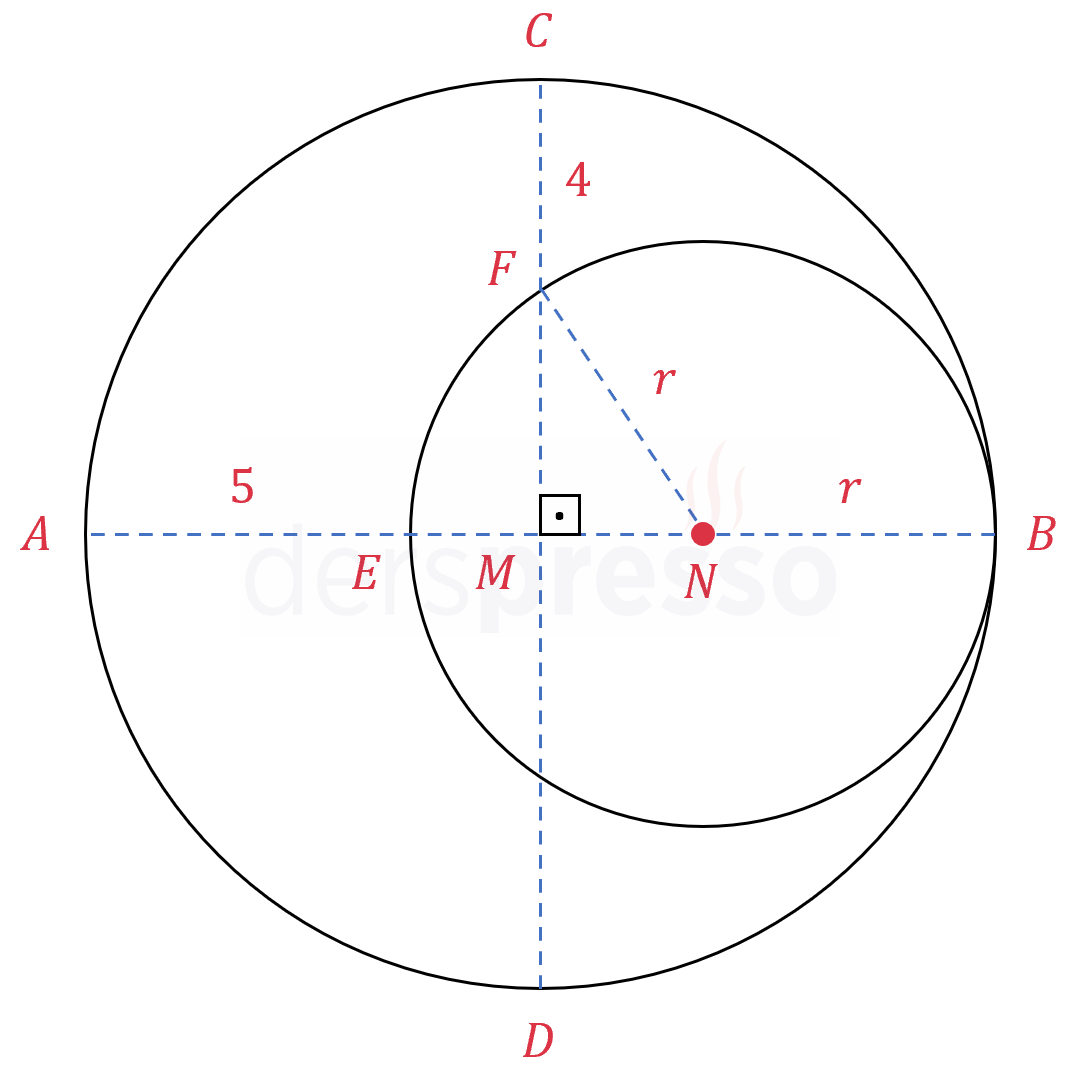
\( \abs{AB} = 2R = 2r + 5 \)
\( R = r + \dfrac{5}{2} \)
\( FMN \) dik üçgenine Pisagor teoremini uygulayalım.
\( \abs{FN}^2 = \abs{FM}^2 = \abs{MN}^2 \)
\( r^2 = (R - 4)^2 + (R - r)^2 \)
\( R = r + \frac{5}{2} \) eşitliğini kullanarak eşitliği \( r \) cinsinden yazalım.
\( r^2 = (r + \dfrac{5}{2} - 4)^2 + (\dfrac{5}{2})^2 \)
\( r^2 = r^2 - 3r + \dfrac{9}{4} + \dfrac{25}{4} \)
\( r = \dfrac{17}{6} \) bulunur.
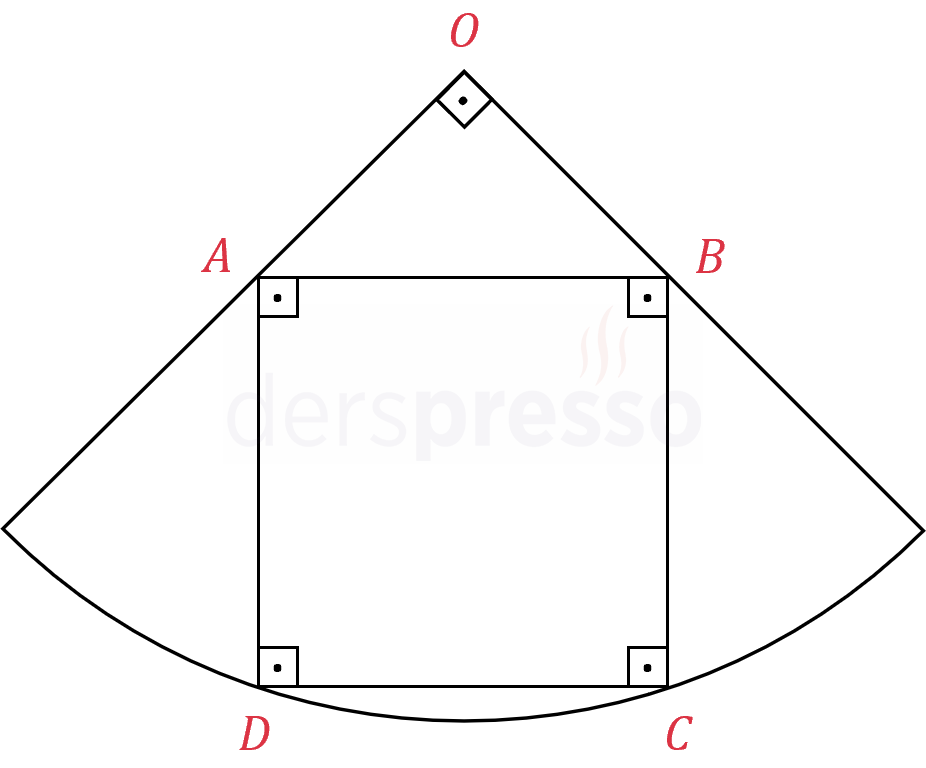
\( O \) merkezli bir çeyrek dairenin içine \( ABCD \) karesi, köşeleri şekildeki gibi çeyrek dairenin yarıçap ve yayı üzerinde olacak şekilde yerleştiriliyor.
\( ABCD \) karesinin alanı 64 birimkare olduğuna göre, \( O \) merkezli çeyrek dairenin yarıçapı kaçtır?
Çözümü GösterDairenin yarıçapına \( r \) diyelim.
\( ABCD \) karesinin alanı 64 birimkare olduğuna göre karenin bir kenarı 8 birimdir.
Çeyrek daireninin merkezinden kareyi simetrik bölecek şekilde \( [OE] \) doğrusu çizelim.

\( \abs{AF} = \abs{FB} = 4 \)
\( [OE] \) bir simetri doğrusu olduğundan çeyrek dairenin merkezindeki 90 derecelik açıyı da iki eş açıya böler.
\( m(\widehat{AOF}) = m(\widehat{BOF}) = 45° \)
Bu durumda \( OFA \) ve \( OFB \) eş ikizkenar üçgenler olur.
\( \abs{AF} = \abs{FB} = \abs{OF} = 4 \)
\( OED \) üçgeni oluşacak şekilde bir \( [OD] \) doğrusu çizelim.
\( [OD] \) aynı zamanda dairenin merkezinden yayına uzanan bir doğru olduğu için yarıçaptır.
\( OED \) üçgeninde Pisagor teoremini kullanarak yarıçapı bulalım.
\( \abs{OE}^2 + \abs{DE}^2 = \abs{OD}^2 \)
\( 12^2 + 4^2 = r^2 \)
\( r^2 = 160 \)
\( r = 4\sqrt{10} \) bulunur.

Yukarıdaki şekilde \( ABCD \) karesi ve karenin içine çizilmiş \( C \) merkezli çeyrek çember verilmiştir.
Yay üzerindeki \( P \) noktasının \( [AB] \) kenarına uzaklığı 6 birim, \( [AD] \) kenarına uzunluğu 12 birim olduğuna göre, \( ABCD \) karesinin bir kenar uzunluğu kaç birimdir?
Çözümü Göster\( ABCD \) karesinin bir kenar uzunluğuna \( x \) diyelim.
\( P \) noktasından \( [BC] \) kenarına bir dikme çizelim.
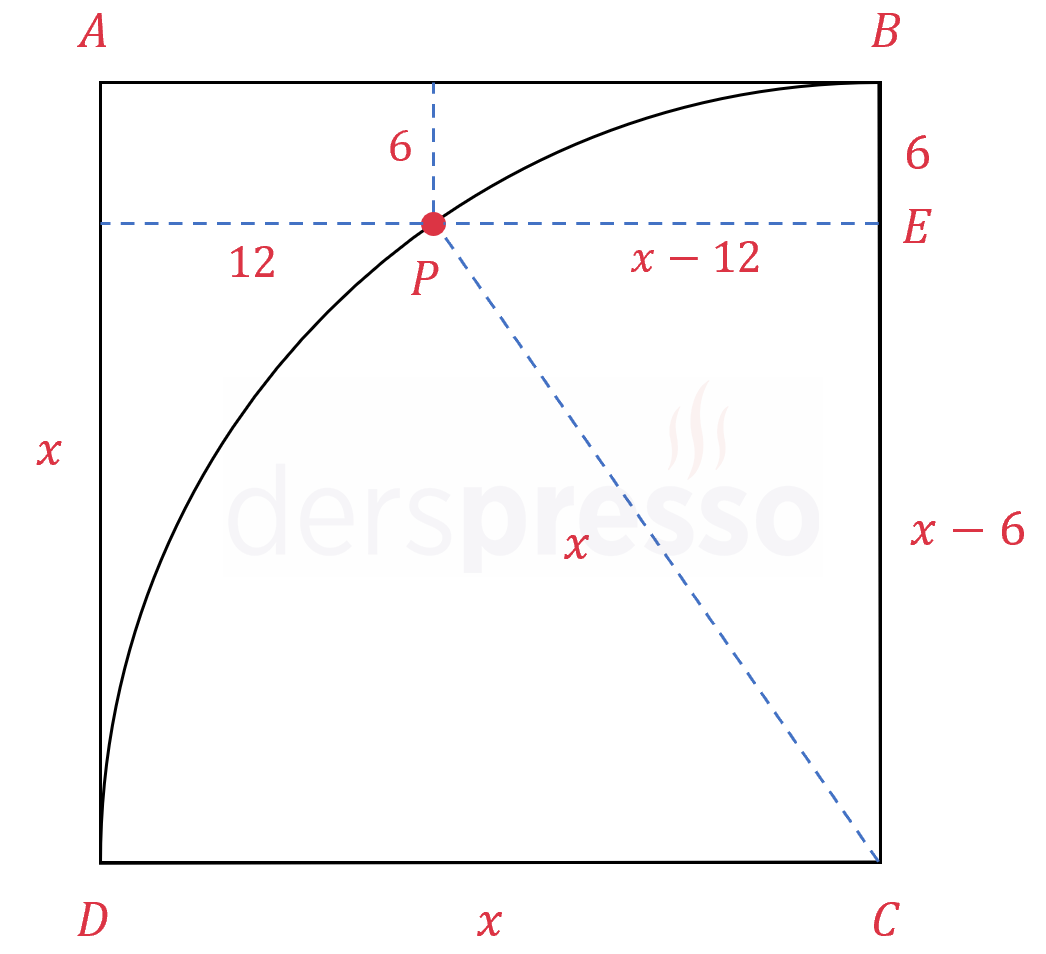
Çeyrek çemberin yarıçapı da \( x \) birim olur.
\( \abs{CP} = x, \quad \abs{PE} = x - 12, \quad \abs{CE} = x - 6 \)
\( PEC \) dik üçgeninde Pisagor teoremini uygulayalım.
\( \abs{PE}^2 + \abs{CE}^2 = \abs{CP} \)
\( (x - 12)^2 + (x - 6)^2 = x^2 \)
\( x^2 - 24x + 144 + x^2 - 12x + 36 = x^2 \)
\( x^2 - 36x + 180 = 0 \)
\( (x - 6)(x - 30) = 0 \)
\( x \gt 12 \) olduğu için \( x = 6 \) olamaz, dolayısıyla \( x = 30 \) olur.
Buna göre, \( ABCD \) karesinin bir kenar uzunluğu 30 birim bulunur.

Yukarıdaki şekildeki \( C_1 \) ve \( C_2 \) çemberlerinin denklemleri \( (x + 13)^2 + y^2 = 25 \) ve \( (x - 26)^2 + y^2 = 100 \) olarak verilmiştir.
\( [A_1L] \) ve \( [KA_2] \) doğru parçaları birbirine paralel olduğuna göre, \( \abs{KL} \) uzunluğu kaç birimdir?
Çözümü GösterDenklemi \( (x - a)^2 + (y - b)^2 = r^2 \) şeklinde verilen çemberin merkezi \( (a, b) \) noktası, yarıçapı \( r \) birimdir.
Buna göre \( C_1 \) çemberinin merkezi \( (-13, 0) \) noktası, yarıçapı 5 birimdir.
\( C_2 \) çemberinin ise merkezi \( (26, 0) \) noktası, yarıçapı 10 birimdir.
\( [A_1L] \parallel [KA_2] \) olduğu için \( A_1LO \) ve \( A_2KO \) benzer üçgenlerdir.
\( \overset{\triangle}{A_1LO} \sim \overset{\triangle}{A_2KO} \)
Üçgenlerin benzerlik oranını bulalım.
İki çemberin merkezleri arasındaki uzaklık \( \abs{A_1A_2} = 26 - (-13) = 39 \) birimdir.
\( \abs{A_1O} = x \) diyelim.
\( \abs{A_2O} = 39 - x \)
\( \dfrac{\abs{A_1L}}{\abs{A_2K}} = \dfrac{\abs{A_1O}}{\abs{A_2O}} \)
\( \dfrac{5}{10} = \dfrac{x}{39 - x} \)
\( 2x = 39 - x \)
\( x = 13 \)
\( A_1LO \) dik üçgenine Pisagor teoremini uygulayalım.
\( 13^2 = \abs{LO}^2 + 5^2 \)
\( \abs{LO} = 12 \)
Üçgenler arası benzerlik oranından \( \abs{OK} = 24 \) birim olur.
\( \abs{KL} = \abs{LO} + \abs{OK} \)
\( = 12 + 24 = 36 \) bulunur.

Bir dikdörtgenin içine yukarıdaki şekildeki gibi iki yarım daire çiziliyor. Bu iki yarım dairenin kesişim noktaları arasındaki uzaklık kaçtır?
Çözümü Göster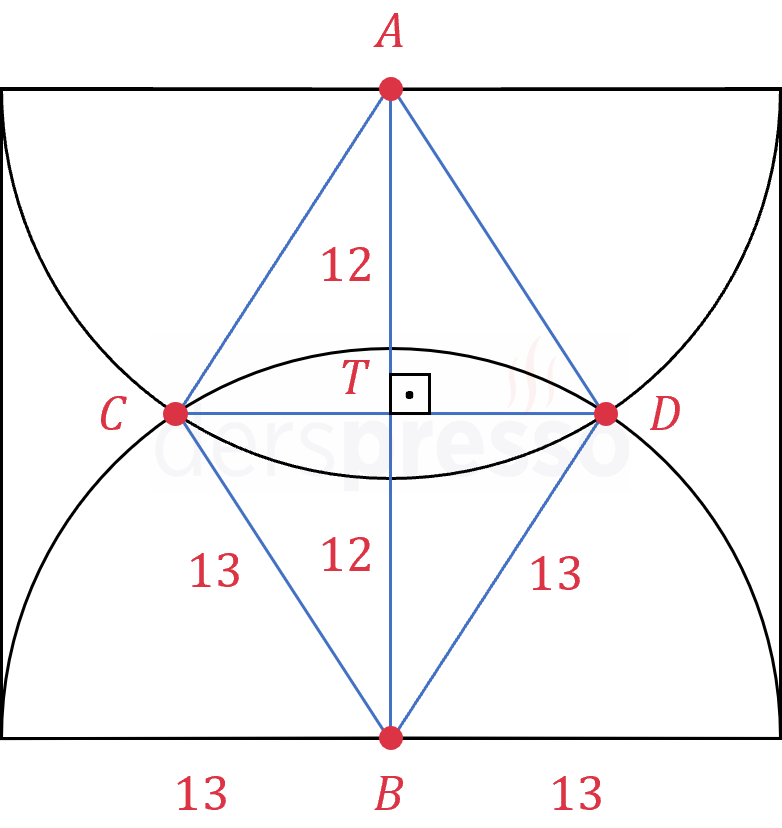
Yarım dairelerin merkezlerine \( A \) ve \( B \), kesişim noktalarına \( C \) ve \( D \) diyelim.
\( [AB] \) ve \( [CD] \) doğru parçalarının kesişim noktasına \( T \) diyelim.
Yarım dairelerin her birinin yarıçap uzunluğu 13 cm'dir.
\( \abs{AC} = \abs{AD} = \abs{BC} = \abs{AD} = 13 \) cm
Buna göre \( ACBD \) bir eşkenar dörtgendir.
\( ACBD \) eşkenar dörtgen ise \( [AB] \) ve \( [CD] \) köşegenleri birbirini dik keser ve ortalar.
\( \abs{AT} = \abs{BT} = 12 \) cm
Eşit uzunluktaki \( [CT] \) ve \( [TD] \) uzunluklarına \( x \) cm diyelim.
\( BTC \) dik üçgeninde Pisagor teoremini uygulayalım.
\( \abs{BT}^2 + \abs{CT}^2 = \abs{BC}^2 \)
\( x^2 + 12^2 = 13^2 \)
\( x^2 = 25 \)
\( x = 5 \)
\( \abs{CD} = 2\abs{CT} = 10 \) cm bulunur.