Çember ve Dairenin Tanımı
Çemberin Tanımı
Bir düzlem üzerinde sabit bir noktaya eşit uzaklıktaki noktalar kümesine çember denir. Çemberin sabit noktasına çemberin merkezi, üzerindeki noktaların merkeze olan uzaklığına yarıçap denir. Yarıçap genellikle \( r \) ile gösterilir.

Bir düzlem üzerinde bir çemberin çizilebilmesi için çemberin merkez noktası ve yarıçap uzunluğunun bilinmesi yeterlidir.
Bir çemberin merkezinden çizilen tüm yarıçapların uzunlukları birbirine eşittir.
Çemberin Temel Elemanları
Bir çemberin temel elemanları şunlardır.

Teğet
Çemberi tek bir noktada kesen doğrulara teğet denir.
Bir teğetin çembere değdiği noktaya teğet noktası denir.

Çemberin merkezinden bir teğet noktasına çizilen yarıçap bu noktadan geçen teğeti dik keser.
Çemberin merkezinden teğet noktasına \( [OT] \) yarıçapını çizelim.

Çizdiğimiz yarıçapın \( d \) doğrusunu dik kestiğini çelişkiyle ispat yöntemiyle ispatlayalım.
Bunun için yarıçapın \( d \) doğrusunu dik kesmediğini varsayalım ve çemberin merkezinden doğruya çizilen dikmenin doğruyu \( P \) noktasında kestiğini varsayalım.
Buna göre \( OPT \) bir dik üçgen olur.
\( m(\widehat{OPT}) = 90° \)
\( m(\widehat{OTP}) \lt 90° \)
Açı - kenar bağıntıları gereği, bir üçgende ölçüsü daha geniş olan açının gördüğü kenar daha uzundur.
\( \abs{OT} \gt \abs{OP} \)
\( \abs{OP} \) uzunluğunu iki doğru parçasının uzunlukları toplamı şeklinde yazalım.
\( \abs{OT} \gt \abs{OR} + \abs{RP} \)
\( \abs{OT} = \abs{OR} = r \)
\( r \gt r + \abs{RP} \)
\( 0 \gt \abs{RP} \)
\( \abs{RP} \) uzunluğunu negatif bir değer olarak bulduk, ancak uzunluk negatif olamaz, dolayısıyla bir çelişki elde etmiş olduk.
Buna göre ispatın başında yaptığımız yarıçapın \( d \) doğrusunu dik kesmediği varsayımı doğru olamaz, dolayısıyla çemberin merkezinden teğet noktasına çizilen yarıçap \( d \) doğrusunu dik kesmelidir.
Yay
Çemberin üzerindeki iki nokta arasında kalan parçaya yay denir. \( A \) ve \( B \) noktaları arasındaki yay \( \overset{\LARGE\frown}{AB} \) şeklinde gösterilir.
Çember üzerindeki iki nokta iki yay belirtir, bunlardan kısa olana minör yay, uzun olana majör yay denir. Bu iki yay üçüncü bir nokta yardımıyla \( \overset{\LARGE\frown}{AMB} \) ve \( \overset{\LARGE\frown}{ANB} \) şeklinde de gösterilebilir.
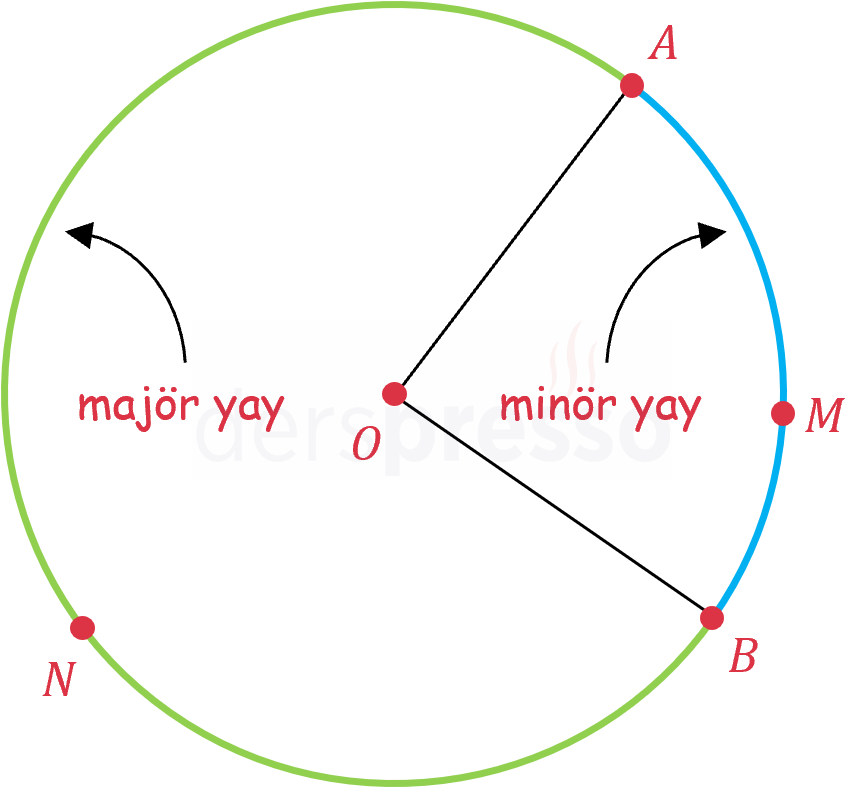
Bir \( \overset{\LARGE\frown}{AB} \) yayının ölçüsü o yayı gören merkez açının ölçüsüne eşittir ve \( m(\overset{\LARGE\frown}{AB}) \) şeklinde gösterilir. Buna göre bir yayın ölçüsü çemberin yarıçapından bağımsızdır.
Aşağıda eş merkezli üç çemberde ölçüleri aynı olan üç yay gösterilmiştir.
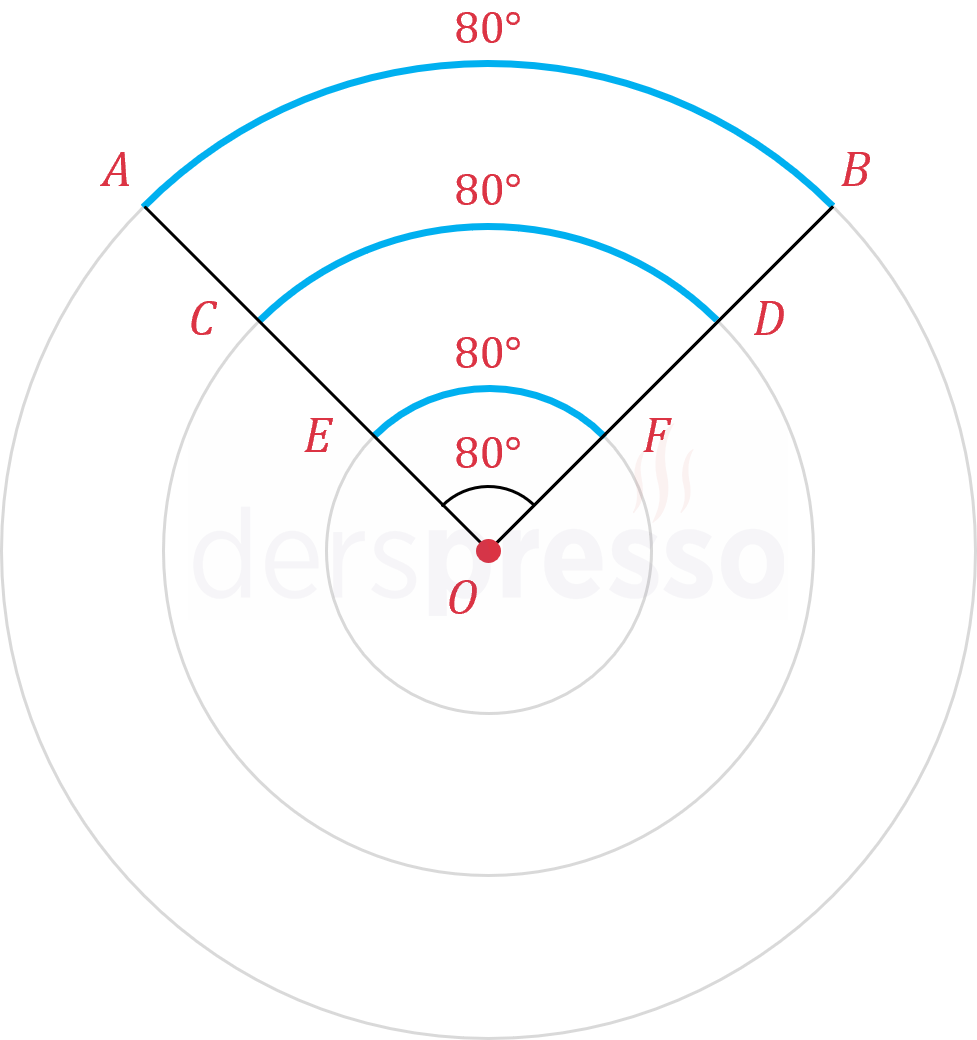
\( m(\overset{\LARGE\frown}{AB}) = m(\overset{\LARGE\frown}{CD}) = m(\overset{\LARGE\frown}{EF}) = 80° \)
Bir \( \overset{\LARGE\frown}{AB} \) yayının uzunluğu o yayın iki ucu arasındaki uzaklığa eşittir ve \( \abs{\overset{\LARGE\frown}{AB}} \) şeklinde gösterilir.
Aşağıda eş merkezli üç çemberde uzunlukları aynı olan üç yay gösterilmiştir.
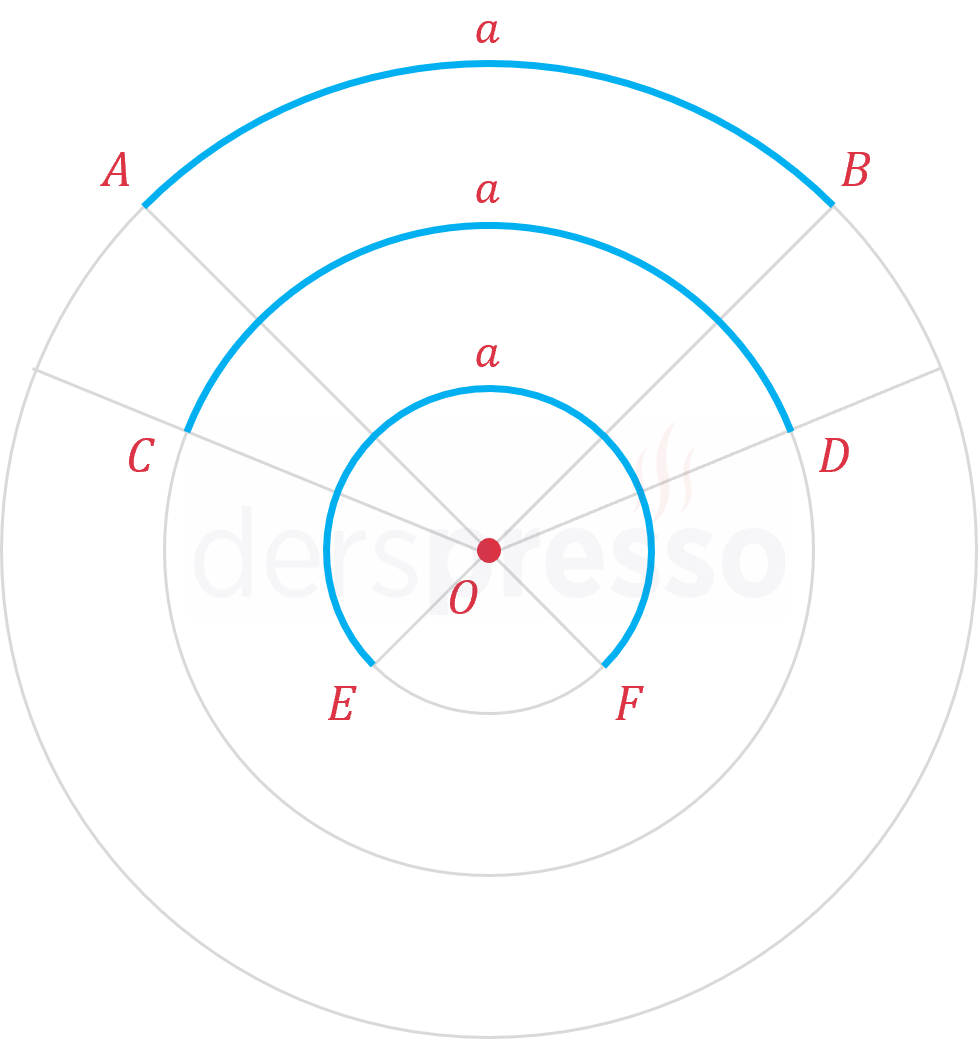
\( \abs{\overset{\LARGE\frown}{AB}} = \abs{\overset{\LARGE\frown}{CD}} = \abs{\overset{\LARGE\frown}{EF}} = a \)
Kiriş
Çemberin üzerindeki iki noktayı birleştiren doğru parçasına kiriş denir. Her kiriş çemberin bir yayının iki ucunu birleştirir.
Kesen
Çemberi iki noktada kesen doğrulara kesen denir. Her kesen çemberin bir kirişini içerir.
Çap
Çemberin merkezinden geçen kirişe çap denir. Bir çemberin çapı o çemberin en uzun kirişidir ve uzunluğu yarıçapın iki katıdır. Çap aynı zamanda çemberi iki eşit parçaya böler.
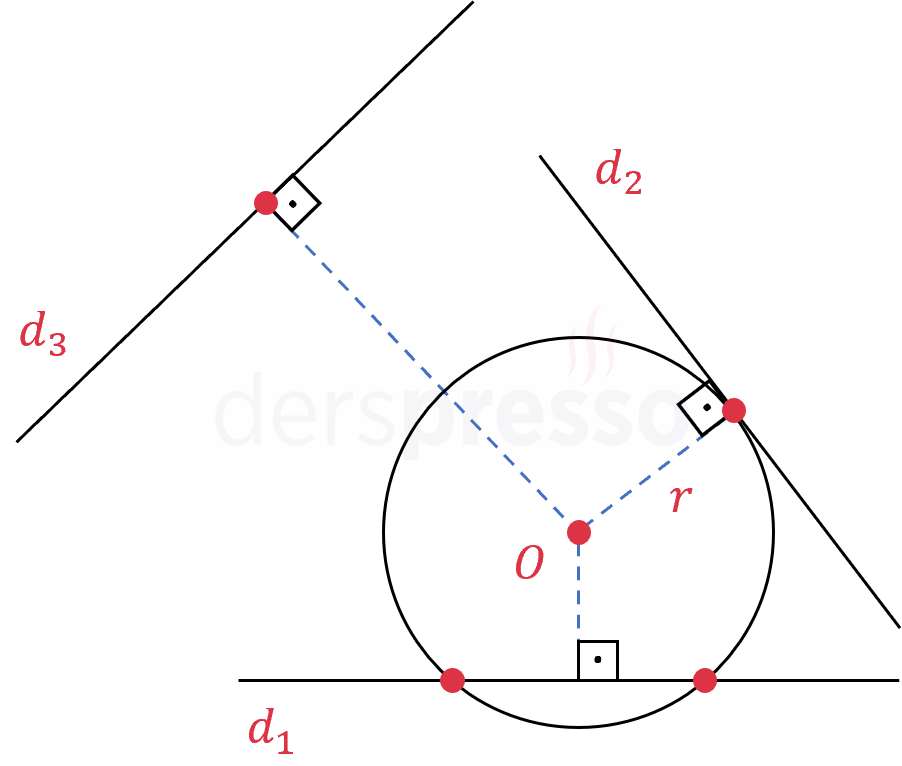
Doğrunun Çembere Göre Durumu
Bir doğru bir çemberi iki noktada kesebilir, bir noktada (teğet) kesebilir ya da hiç kesmeyebilir.
Dairenin Tanımı
Bir çemberden ve çemberin iç bölgesinden oluşan şekle daire denir.
Çemberin iki yarıçapının arasında kalan bölgeye daire dilimi denir.
